八下期中第一章复习

欢迎阅读八年级下册数学期中考试知识点复习第一章证明（二）一. 等腰三角形1. 性质：等边对等角2. 判定：等角对等边3. 推论：“三线合一”4.等边三角形的性质及判定定理例1、已知：如图1所示，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，则∠A 的度数为（）A．30°B．45°C．36°D．72°图1例2、如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（）A.30°B.36°C.45°D.70°已知等腰三角形一角，求其他两角的情况。

注意：等边三角形与轴对称、中心对称的关系。

二.直角三角形（含30°的直角三角形的边的性质）※1. 勾股定理及其逆定理※2. 命题与逆命题※3. 直角三角形全等的判定定理定理：斜边和一条直角边对应相等的两个直角三角形全等（HL）三. 线段的垂直平分线※1. 线段垂直平分线的性质及判定※2.三角形三边的垂直平分线的性质三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等.例1、如图，△ABC中，AB=AC，DE是AB的垂直平分线， AB=8，BC=4，∠A=36°，则∠DBC= ， = ．△BDC的周长C四. 角平分线※1. 角平分线的性质及判定定理※2. 三角形三条角平分线的性质定理性质：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等. 例1、如图，ABC ∆中，DE A AC AB ，， 40=∠=是腰AB 的垂直平分线，求DBC ∠的度数。

平移与旋转轴对称图形的关系例１、如图6－2－13，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝1，将过的路径为BD ，则Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE ，点B 经图中阴影部分的面积是__________．第二章 一元一次不等式和一元一次不等式组一. 不等关系准确“翻译”不等式,正确理解“非负数”、“不小于”等数学术语.非负数 <===> 大于等于0(≥0) <===> 0和正数 <===> 不小于0非正数 <===> 小于等于0(≤0) <===> 0和负数 <===> 不大于0二. 不等式的基本性质注意：有且仅当不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。

第一章小结与复习知识结构框图一、全等三角形的判定及性质1、性质：全等三角形对应相等、对应相等；2、判定：分别相等的两个三角形全等（SSS）；分别相等的两个三角形全等（ASA）；分别相等的两个三角形全等（SSS）；相等的两个三角形全等（AAS）；相等的两个直角三角形全等（HL）；二、等腰三角形1、性质：等腰三角形的两个底角相等（即------------------）。

2、判定：有两个角相等的三角形是等腰三角形（即----------------------）3、推论：等腰三角形、、互相重合（即“”）4、等边三角形的性质及判定定理性质定理：等边三角形的三个角都相等，并且每个角都等于；等边三角形是轴对称图形，有条对称轴。

判定定理：（1）有一个角是60°的--------三角形是等边三角形；（2）三个角都----------的三角形是等边三角形。

三、直角三角形1、勾股定理及其逆定理定理：直角三角形的两条直角边的等于的平方。

逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是2、含30°的直角三角形的边的性质定理：在直角三角形中，如果一个锐角等于30°，那么等于的一半。

3、直角三角形斜边的中线等于的一半。

四、线段的垂直平分线性质：垂直平分线上的点到的距离相等；判定：到一条线段两个端点距离相等的点在这条线段的。

三角形三边的垂直平分线的性质：三角形三条边的垂直平分线相交于一点，并且这一点到三个顶点的距离相等。

．五、角平分线的距离相等；性质：角平分线上的点到判定：在一个角内部，且到角两边的距离相等的点，在这个角的平分线上。

三角形角平分线的性质定理：性质：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等。

这个点叫内心。

六、方法总结：）角平分线的性质定理：角211）证明线段相等的方法：）可证明它们所在的两个三角形全等；（）中垂线5）等角对等边；4）等腰三角形三线合一的性质；平分线上的点到角两边的距离相等；3 的性质定理：线段垂直平分线上的点到线段两端点的距离相等。

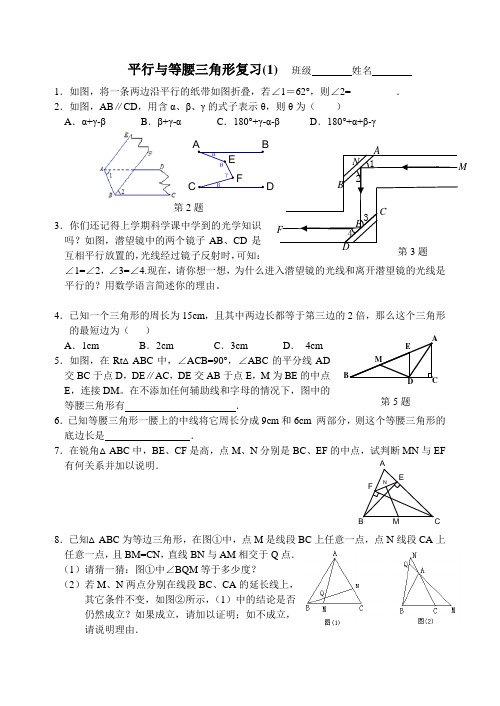
CD平行与等腰三角形复习(1) 班级 姓名1．如图，将一条两边沿平行的纸带如图折叠，若∠1＝62°，则∠2=_________． 2．如图，AB ∥CD ，用含α、β、γ的式子表示θ，则θ为（ ）A ．α+γ-βB ．β+γ-αC ．180°+γ-α-βD ．180°+α+β-γ3．你们还记得上学期科学课中学到的光学知识吗？如图，潜望镜中的两个镜子AB 、CD 是互相平行放置的，光线经过镜子反射时，可知：∠1=∠2，∠3=∠4.现在，请你想一想，为什么进入潜望镜的光线和离开潜望镜的光线是平行的？用数学语言简述你的理由。

4．已知一个三角形的周长为15cm ，且其中两边长都等于第三边的2倍，那么这个三角形的最短边为（ ） A ．1cm B ．2cm C ．3cm D ． 4cm 5．如图，在Rt △ABC 中，∠ACB=90°，∠ABC 的平分线AD 交BC 于点D ，DE ∥AC ，DE 交AB 于点E ，M 为BE 的中点E ，连接DM 。

在不添加任何辅助线和字母的情况下，图中的等腰三角形有 ．6．已知等腰三角形一腰上的中线将它周长分成9cm 和6cm 两部分，则这个等腰三角形的底边长是 ．7．在锐角△ABC 中，BE 、CF 是高，点M 、N 分别是BC 、EF 的中点，试判断MN 与EF 有何关系并加以说明．8．已知△ABC 为等边三角形，在图①中，点M 是线段BC 上任意一点，点N 线段CA 上任意一点，且BM=CN ，直线BN 与AM 相交于Q 点． （1）请猜一猜：图①中∠BQM 等于多少度？ （2）若M 、N 两点分别在线段BC 、CA 的延长线上，其它条件不变，如图②所示，（1）中的结论是否仍然成立？如果成立，请加以证明；如不成立，请说明理由．第2题第3题第5题BAECDMB练习1．下列图形中，∠1与∠2不是同位角的是（ ）2．如图，已知AB ∥CD ，AC ⊥BC ，图中与∠CAB 互余的角有（ ） A ．1个 B ．2个 C ．3个 D ．4个 3．如图, 已知直线 25,115,//=∠=∠A C CD AB , 则=∠E ( )A ． 70ºB ．80ºC ．90ºD ．100º4．如图，放置的两平面镜α、β的夹角为θ，入射光线AO 平行与β入射到α上经过两次反射后的出射光线O’B 平行于α，则交θ= ．5．如图，C 是直线MN 上的一点，AC ⊥BC ，BD//AC ，交MN 于点D ，AE//BC ，交MN 于E ，则∠BDC+∠AEC=（ ） A ．50° B ．90° C ．120° D ．180° 6．如图，一条公路修到湖边时，需拐弯绕湖而过，如果第一次拐的∠A 是120°，第二次拐的∠B 是150°，第三次拐的角是∠C ，这时的道路恰好和第一次拐弯之前的道路平行，则∠C= ．7．一船向正东方向航行,行至A 处折向南偏东60°方向航行,行至B 处后,若该船仍向正东方向行驶，则须向 (填”左”或”右”)转 度． 8．如图，是屋架设计图的一部分，点D 是斜梁AB 的中点，立柱BC 、DE 垂直于横梁AC ，BC=4m ，∠A=30°，则DE 等于（ ）A ．1mB ．2mC ．3mD ．4m9．等腰三角形的顶角为84°，则一腰上的高与底边所成角的度数是 ． 10．在一个正方体的两个面上画两条对角线AB 、AC ，这两条对角线的夹角等于 度． 11．如图，已知在等边三角形ABC 中，D 是AC 的中点，，E 是BC 延长线上的一点，且CE=CD ，DM⊥BC ，垂足为M ，证明：M 是BC 的中点．第2题第3题 第4题 第5题 第6题平行与等腰三角形练习 班级 姓名1．将一直角三角板与两边平行的纸条如图所示放置，下列结论中正确的个数是（ ）（1）∠1＝∠2； （2）∠3＝∠4； （3）∠2+∠4＝90°； （4）∠4+∠5＝180°A ．1B ．2C ．3D ．42．一架飞机向北飞行，两次改变方向后，前进的方向与原来的航行方向平行，已知第一次向左拐50°，那么第二次向右拐（ ） A ．40° B ．50° C ．130° D ．150°3．如图，把一长方形纸片ABCD 沿EG 折叠后，点A 、B 分别落在A ′、B ′的位置上，EA ′与BC 相交于点F 。

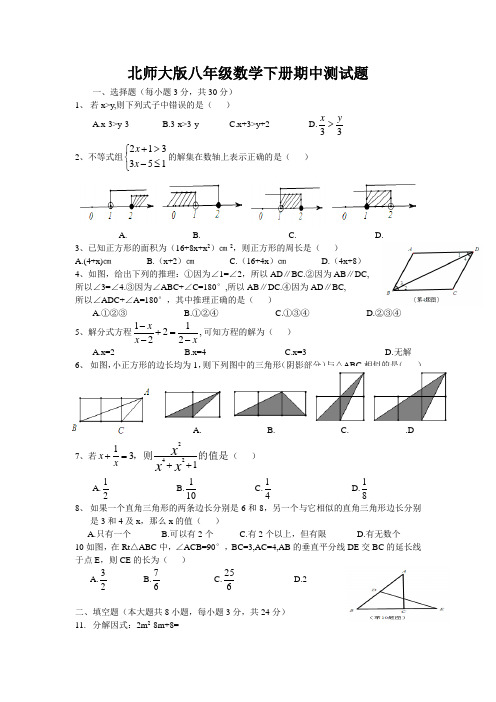
北师大版八年级数学下册期中测试题一、选择题（每小题3分，共30分）1、 若x>y,则下列式子中错误的是（ ）A.x-3>y-3B.3-x>3-yC.x+3>y+2D.33y x > 2、不等式组⎩⎨⎧≤->+153312x x 的解集在数轴上表示正确的是（ ）A. B. C. D.3、已知正方形的面积为（16+8x+x 2）㎝2，则正方形的周长是（ ）A.(4+x)㎝B.（x+2）㎝C.（16+4x ）㎝D.（4x+8）4、如图，给出下列的推理：①因为∠1=∠2，所以AD ∥BC.②因为AB ∥DC, 所以∠3=∠4.③因为∠ABC+∠C=180°,所以AB ∥DC.④因为AD ∥BC,所以∠ADC+∠A=180°，其中推理正确的是（ ）A.①②③B.①②④C.①③④D.②③④5、解分式方程,21221xx x -=+--可知方程的解为（ ） A.x=2 B.x=4 C.x=3 D.无解6、 如图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC 相似的是（ ）A. B. C. .D 7、若的值是，则131242++=+x x x x x （ ） A.21 B.101 C.41 D.81 8、 如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3和4及x ，那么x 的值（ ）A.只有一个B.可以有2个C.有2个以上，但有限D.有无数个 10如图，在Rt △ABC 中，∠ACB=90°，BC=3,AC=4,AB 的垂直平分线DE 交BC 的延长线于点E ，则CE 的长为（ ）A.23B.67C.625 D.2二、填空题（本大题共8小题，每小题3分，共24分）11. 分解因式：2m 2-8m+8=_________12. 若的值为那么分式bb a b b a +=-,352__________ 13. 一次函数y=kx+2的图象过点（-1，-2）.则当x______时，函数值不小于6.14. 如图，直线m ∥n ，∠1=55°，∠2=45°，则∠3的度数为_________15. 如图，CD 是△ACB 的角平分线，过B 点作BE ⊥CD,垂足为E ，过E 点作EF ∥AB 交CB 于点F ，已知∠A=43°∠ACB=58°，则∠FEB 的度数为________.16. 已知关于x 的不等式组,1250⎩⎨⎧>-≥-x a x 只有四个整数解，则实数a 的取值范围是_______ 18. 如图，△ABC 与△A ＇B ＇C ＇是位似图形，且顶点都在格点上，则位似中心的坐标是_______三、解答题19、先化简，再求值:22,24224222+=⎪⎭⎫ ⎝⎛+---÷--x x x x x x x 其中20、（本题满分8分）给出三个多项式：x x x xx x 221,1421,1221222-++-+.请你选择你最喜欢的两个多项式进行加法运算，并把结果因式分解.21、（本题满分10分）小明想利用太阳光测量楼高，他带着皮尺来到一栋楼下，发现对面墙上有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：如示意图，小明边移动边观察，发现站到点E处时，可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠，且高度恰好相同.此时，测得小明落在墙上的影子高度CD=1.2m，CE=0.8m,CA=30m（点A、E、C在同一直线上）.已知小明的身高EF是1.7m，请你帮小明求出楼高AB（结果精确到0.1m）22、（本题满分10分）如图，梯形ABCD中AB∥CD,且AB＝2CD，E、F分别是AB、BC的中点，EF与BD相交于点M.⑴试说明△EDM∽△FBM；⑵若DB=9，求BM.23、铭润超市用5000元购进一批新品种的苹果进行试销，由于销售状况良好，超市又调拨11000元资金购进该品种苹果，但这次的进货价比试销时每千克多了0.5元，购进苹果的数量是试销时的2倍. ⑴试销时该品种苹果的进货价是每千克多少元？⑵如果超市将该品种苹果按每千克7元的定价出售，当大部分苹果售出后，余下的400千克按定价的七折（“七折”即定价的70%）售完，那么超市在这两次苹果销售中共盈利多少元？24、如图，在等腰梯形ABCD中，∠C=60°,AD∥BC,且AD=DC，E、F分别在AD、DC的延长线上，且DE=CF，AF、BE交于点P..⑴求证：AF=BE；⑵求出∠BPF的度数25、一批货物准备运往某地，有甲、乙、丙三辆卡车可雇用，已知甲、乙、丙三辆车每次运货量不变，且甲、乙两车单独运这批货物分别用2a次，a次能运完；若甲、丙两车合运相同次数运完这批货物时，甲车共运了180吨；若乙、丙两车合运相同次数运完这批货物时，乙车共运了270吨．问：(1)乙车每次所运货物量是甲车每次所运货物量的几倍？(2)现甲、乙、丙合运相同次数把这批货物运完时，货主应付车主运费各多少元？(按每运1吨付运费20元计算)四、综合探索题（12分）26.阅读下面短文：如图6所示，△ABC是直角三角形，∠C＝90°，现将△ABC补成矩形，使△ABC的两个顶点为矩形一边的两个端点，第三个顶点落在矩形这一边的对边上，那么符合要求的矩形可以画出两个：矩形ACBD和矩形AEFB(如图7)解答下列问题(1)设图7中矩形ACBD和矩形AEFB的面积为S1，S2，则S1_______S2(填“＞”“＝”或“＜”)(2)如图8所示，△ABC是钝角三角形，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出_______个．图8利用图8把它画出来．(3)如图9所示，△ABC是锐角三角形且三边满足BC＞AC＞AB，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出_______个．利用图9把它画出来．图9(4)在(3)中所画的矩形中，哪一个周长最小，为什么？。

期中考试复习----第一章《机械运动》单元复习题八（）班姓名1. 下列单位换算的写法中正确的是( )A.3 cm=3 cm÷100=0.03 mB.3 cm=3× m=0.03 mC.70 μm=70 mm÷1 000 mm=0.07 mmD.70 μm=70÷1 000=0.07 mm2.下列亲密的“伙伴”中,长度最接近3 cm的是( )A.橡皮擦B.中性笔C.直尺D.三角板1.下列现象中,不属于机械运动的是( )A.冰融化成水B.流星划过夜空C.河水不停地流动D.秋天,树叶飘落3.2018年2月2日,我国第一颗电磁监测试验卫星“张衡一号”在酒泉卫星发射中心由长征二号丁运载火箭发射升空并成功入轨。

在卫星升空的过程中,以下列哪个物体为参照物,卫星是静止的( )A.发射架B.运载火箭C.太阳D.地球4.(2018·龙岩期中)世界短跑名将跑完100 m只需9.8 s,一辆汽车以30 km/h 的速度行驶,羚羊的奔跑速度是20 m/s。

比较这三者的速度由大到小排列顺序是( )A.运动员、羚羊、汽车B.汽车、羚羊、运动员C.汽车、运动员、羚羊D.羚羊、运动员、汽车5.由匀速直线运动公式v=可知,匀速直线运动的速度( )A.与路程成正比B.与时间成正比C.随路程和时间的变化而变化D.与路程和时间无关6.手机百度发现,利川—恩施(普快)全程61公里,运行38分钟。

据此推算,该路段普快列车运行的平均速度约为 ( )A.96 km/hB.61 km/hC.38 km/hD.1.6 km/h7.在“测量物体运动的平均速度”实验中,当小车自斜面顶端滑下时开始计时,滑至斜面底端时停止计时。

如图所示,此过程中小车的平均速度是( )A.90 m/sB.0.09 m/sC.0.9 cm/sD.9 m/s8.如图是小明做“测量物体运动的平均速度”的实验情境,小车通过同一斜面A、B、C三点的时刻如图所示,已知秒表每格为1 s,B点是全程AC的中点。

第一章第1节：模型、符号的建立与作用【知识梳理】1.模型的含义、意义和作用（1）含义：人们通过一定的科学方法，建立一个适当的模型来反映和代替客观对象，并通过研究这个模型来揭示客观对象的形态、特征和本质，这种方法叫模型法。

构建模型常常可以帮助人们认识和理解一些不能直接观察到的事物。

它的类型有：①某种物体的放大或缩小的复制品；②可以是一幅图、一张表或是一个计算机软件；③有的模型不是简单地表示一个具体事物，而是表示一个过程，如描述水的三态变化的示意图“水的三态变化模型”。

④有的模型是抽象的，如一些数学公式或某些特定的词。

（2）意义和作用：帮助人们认识和理解一些不能直接观察到的事物。

2.符号的含义、意义和作用（1）含义：是指有一定意义的图形、文字等。

如数学运算符号、电路元件符号等。

（2）意义和作用：用符号能简单明了地表示事物；用符号可避免由于外形不同引起的混乱；用符号可避免表达的文字语言不同而引起的混乱。

3.对液态水与气态水的状态模型（表示水分子）的观察。

（1）液态水温度降低时会变成固态的冰，而温度升高时会变成气态的水蒸气。

（2）液态水变成气态水时，构成物质的分子没有发生变化，但是分子之间的距离发生了变化。

（3）在液态水变成气态水的过程中，没有新物质生成，因此，这是物理变化。

第2节：物质与微观粒子模型（1）【知识梳理】1.分子的定义和性质（1）分子的定义：分子是构成物质的一种微粒。

在由分子构成的物质中，分子是保持物质化学性质的最小粒子。

（2）分子的性质：分子很小（肉眼不能看见，需通过扫描隧道显微镜等显微设备来观察）、分子在不断地作无规则运动、分子间有间隔、同种分子化学性质相同。

2.用分子观点解释物理变化和化学变化由分子构成的物质，发生物理变化时分子本身未变。

发生化学变化时，分子本身发生变化，变成其它物质的分子。

3.原子的定义：原子是化学变化中的最小粒子。

即在化学变化中原子不能再分。

4.物质的构成与化学性质（1）物质通常是由分子构成的，如水、氢气、氧气等分别由水分子、氢分子、氧分子等构成。

第一章复习一、填空题(每空3分，共36分)1．在△ABC中，AB＝AC，∠A＝44°，则∠B＝度．2．等腰三角形的一个角为50°，则顶角是度．3．如图，AB＝AD，只需添加一个条件，就可以判定△ABC≌△ADE.4．已知等腰三角形两条边的长分别是3和6，则它的周长等于．5．如图，在△ABC中，∠C＝90°，D为BC上的一点，且DA＝DB，DC＝AC．则∠B＝度．(第3题图) (第5题图) (第6题图) 6．如图,△ABC中,∠ACB＝90°,CD⊥AB于点D,∠A＝30°,BD＝1.5cm，则AD= cm．7．在△ABC中，∠A:∠B:∠C＝1:2:3，AB＝6cm，则BC＝cm．8．在△ABC中，AB＝AC，∠BAC＝120°，延长BC到D，使CD＝AC，则∠CDA ＝度.9．等边△ABC的周长为12cm，则它的面积为cm2．10．如图，ED为△ABC的AC边的垂直平分线，且AB=5，△BCE的周长为8，则BC＝.(第10题图) (第11题图)11．如图，在△ABC中，∠C＝90°，∠B＝15°，AB的垂直平分线交BC于D，交AB于E，若DB＝10cm，则AC＝.12．命题“角平分线上的点到这个角的两边的距离相等”的逆命题是。

二、选择题(每空3分，共24分)13．下列条件中能判定△ABC≌△DEF的是( )A．AB＝DE，BC＝EF，∠A＝∠D B．∠A＝∠D，∠B＝∠E，∠C＝∠F C．AC＝DF，∠B＝∠F，AB＝DE D．∠B＝∠E，∠C＝∠F，AC＝DF 14．下列命题中正确的是( )A．有两条边相等的两个等腰三角形全等B．两腰对应相等的两个等腰三角形全等C．两角对应相等的两个等腰三角形全等D．一边对应相等的两个等边三角形全等15．对“等角对等边”这句话的理解，正确的是( )A．只要两个角相等，那么它们所对的边也相等B．在两个三角形中，如果有两个角相等，那么它们所对的边也相等C．在一个三角形中，如果有两个角相等，那么它们所对的边也相等D．以上说法都是错误的16．以下各组数为三角形的三条边长，其中能作成直角三角形的是( )A．2，3，4 B．4，5，6 C．1，2，3D．2，2，417．如图，△ABC与△BDE都是等边三角形，AB<BD．若△ABC不动，将△BDC绕B点旋转，则在旋转过程中，AE与CD的大小关系为( )A．AE＝CD B．AE>CD C AE<CD D．无法确定（第17题图）（第18题图）18．如图，△ABC中，AC＝BC，直线l经过点C，则( )A．l垂直AB B．l平分AB C．l垂直平分AB D．不能确定19．三角形中，若一个角等于其他两个角的差，则这个三角形是( )A．钝角三角形B．直角三角形C．锐角三角形D．等腰三角形20．已知△ABC中，A B＝AC，AB的垂直平分线交AC于D，△ABC和△DBC的周长分别是60 cm和38 cm，则△ABC的腰和底边长分别为( )A．24 cm和12 cm B．16 cm和22 cm C．20 cm和16 cm D．22 cm和16 cm三、解答题(6+6+6+6+8+8分，共40分)21．如图，在△ABC中，∠ACB＝90°，BC＝15，AC＝20，CD是高．(1)求AB的长；(2)求△ABC的面积；(3)求CD的长．22．已知：如图，点D是△ABC内一点，AB＝AC，∠1＝∠2．求证：AD平分∠BAC．23．已知：如图，△ABC和△CDE都是等边三角形，点D在BC边上．求证：AD＝BE．24．求证：等腰三角形两腰上的中线的交点到底边两个端点的距离相等．25．已知：如图，等腰三角形ABC中，AC＝BC，∠ACB＝90°，直线l经过点C(点A、B都在直线l的同侧)，AD⊥l，BE⊥l，垂足分别为D、E．你知道线段AD、DE、BE的关系吗？证明你的结论。

不等式一、不等关系：1、定义凡用符号连接的式子叫做不等式．2、列不等式是数学化与符号化的过程，列不等式注意找到问题中不等关系的词，如：“正数(>0)”,“负数（<0）”，“非正数（≤0）”，“非负数（≥0）”，“超过(>0)”，“不足（<0）”，“至少（≥0）”，“至多（≤0）”，“不大于（≤0）”，“不小于（≥0）”3、不等号具有方向性，其左右两边不能随意交换。

c≥可转换为cd≤b>，da<可转换为ab二、不等式的基本性质：性质1 性质2 性质3不等式有3个基本性质，以这三个基本性质为依据，可求得不等式的解——即对不等式进行变形，最终化为“x<a”或“x>a”的形式。

三、不等式的解（集）1、能使不等式成立的-________________________，叫做不等式的解。

2、一个含有_____________________________，组成这个不等式的解集。

不等式的解集，包含两方面的含义：1）未知数取解集中的任何一个值时，不等式都成立；2）未知数取解集外的任何一个值时，不等式都不成立。

3、求____________________的过程叫做解不等式。

4、不等式的解集可在数轴上直观表示。

用数轴表示不等式的解集，应记住规律：大于向画，小于向画，有等号（≤，≥）画，无等号（<,>）画。

四、一元一次不等式和它的解法1．一元一次不等式左右两边都是___，只含有一个未知数，并且未知数的最高次数是____，像这样的不等式．叫做一元一次不等式．2．一元一次不等式标准形式ax+b＜0或ax+b≤0，ax+b＞0或ax+b≥0(a≠0)．3．解一元一次不等式的一般步骤：1）去______（根据不等式的基本性质2、3）2）去__________（根据整式运算法则）3）______（根据不等式基本性质1）4）__________（根据整式运算法则）5）_______________（根据不等式的基本性质2、3）4、根据实际问题列不等式并求解，主要有以下环节：（1）审题，找出不等关系；（2）设未知数；（3）列出不等式；（4）求出不等式的解集；（5）找出符合题意的值；（6）作答。