matlab里的模糊工具箱绘制隶属度函数曲线导入到word的方法

matlab对数据分段隶属函数处理在Matlab中，数据分段隶属函数是一种用于处理数据的方法。

它可以将数据分为多个不同的段落，并为每个段落分配一个隶属度。

这种方法在数据处理和分析中非常有用，可以帮助我们更好地理解和利用数据。

数据分段隶属函数的基本原理是将数据按照一定的规则进行分段，并为每个段落分配一个隶属度。

这个隶属度表示数据在该段落中的归属程度。

通过隶属度，我们可以对数据进行分类、聚类和预测等操作，从而更好地理解数据的特征和规律。

在Matlab中，可以使用一些函数来实现数据分段隶属函数的处理。

例如，可以使用fuzzy分段函数来进行数据分段，并使用fuzzy隶属函数来计算每个数据点在每个段落中的隶属度。

通过这种方法，我们可以将数据分为多个不同的段落，并为每个段落分配一个相应的隶属度。

数据分段隶属函数在实际应用中有很多用途。

例如，在数据挖掘中，我们可以使用数据分段隶属函数来对数据进行分类和聚类，从而找到数据中的潜在模式和规律。

在机器学习中，数据分段隶属函数可以用于构建模型和进行预测。

在信号处理中，数据分段隶属函数可以用于对信号进行分析和处理。

除了以上应用，数据分段隶属函数还可以用于其他领域的数据处理和分析。

例如，在金融领域，可以使用数据分段隶属函数来进行股票价格的预测和交易策略的制定。

在医疗领域，可以使用数据分段隶属函数来进行疾病的诊断和治疗方案的选择。

在环境科学领域，可以使用数据分段隶属函数来进行气候变化的研究和预测。

数据分段隶属函数是一种非常有用的数据处理方法，可以帮助我们更好地理解和利用数据。

在Matlab中，我们可以使用一些函数来实现数据分段隶属函数的处理。

这种方法在数据挖掘、机器学习、信号处理等领域有广泛的应用。

通过数据分段隶属函数的处理，我们可以更好地理解数据的特征和规律，进而做出更准确的预测和决策。

希望本文对您理解数据分段隶属函数的处理方法有所帮助。

控制理论与控制工程《智能控制基础》课程实验报告专业：控制理论和控制工程班级：双控研2016 姓名：洪帅任课教师：马兆敏2016年 12 月 4 日第一部分：模糊控制实验一模糊控制的理论基础实验实验目的：1 练习matlab中隶属函数程序的编写，同时学习matlab数据的表达、格式、文件格式、存盘2 学习matlab中提供的典型隶属函数及参数改变对隶属度曲线的影响3 模糊矩阵合成仿真程序的学习4 模糊推理仿真程序实验内容（1）要求自己编程求非常老，很老，比较老，有点老的隶属度函数。

1隶属函数编程试验结果如图1-1图1-1隶属度函数曲线（2）完成思考题P80 2-2 写出W及V两个模糊集的隶属函数，并绘出四个仿真后的曲线。

仿真曲线见图1-2，图1-2隶属度函数曲线2 典型隶属函数仿真程序学习下列仿真程序，改变各函数中的参数，观察曲线的变化，并总结各种隶属函数中其参数变化是如何影响曲线形状变换的。

M=1 M=3M=3 M=4M=5 M=6图1-3 M 在1、2、3、4、5、6时的图形2 模糊矩阵合成仿真程序：学习P31例2-10，仿真程序如下，（1） 完成思考题P81 2-5，并对比手算结果。

完成思考题P81 2-4，并对比手算结果。

（2） 2-5：(1) Matlab 结果如下①②③P81 2-5手算结果：P=⎥⎦⎤⎢⎣⎡7.02.09.06.0 Q=⎥⎦⎤⎢⎣⎡4.01.07.05.0 R=⎥⎦⎤⎢⎣⎡7.07.03.02.0 S=⎥⎦⎤⎢⎣⎡5.06.02.01.0(P Q) R=⎥⎦⎤⎢⎣⎡4.04.06.06.0(PUQ) S=⎥⎦⎤⎢⎣⎡5.06.05.06.0 (P S)U(Q S)=⎥⎦⎤⎢⎣⎡5.06.05.06.0总结：手算结果和MATLAB 运行结果一致。

(2) （2）思考题P81 2-4 Matlab 运行结果如下：P81 2-4题手算结果如下：()300200104.001104.0200300++++-+-+-=e ZE μ ()30203.010103.010*******++++-+-+-=e PS μ()()300200104.003.010*******++++-+-+-=⋂e e PS ZE μμ()()30203.010101104.0200300++++-+-+-=⋃e e PS ZE μμ总结：手算结果和MATLAB 运行结果一致。

MATLAB中的模糊逻辑应用技巧绪论近年来，随着人工智能技术的不断发展与应用，模糊逻辑作为一种弥补了传统二值逻辑的不足的方法，被广泛应用于各个领域。

MATLAB作为一种功能强大的数学计算软件，提供了丰富的工具箱，使得模糊逻辑的建模和分析变得更加方便和高效。

本文将重点介绍MATLAB中模糊逻辑的应用技巧。

一、模糊集合的定义与表示在MATLAB中，模糊集合可以通过使用fuzzy工具箱来定义和表示。

在定义模糊集合时，我们需要明确模糊集合的隶属度函数以及对应的隶属度值。

可以使用trimf函数、trapmf函数、gaussmf函数等来定义隶属度函数的形状，并通过给定参数来确定具体的形状。

例如，我们可以使用trimf函数来定义一个三角隶属度函数，代码如下：```matlabx = 0:0.1:10;y = trimf(x, [3 5 7]);plot(x, y);```通过上述代码，我们可以绘制出一个在[3, 5, 7]范围内的三角形隶属度函数。

二、模糊关系的建立与描述在MATLAB中，可以使用fuzzy工具箱来建立和描述模糊关系。

模糊关系可以通过关联隶属度函数的模糊集合来定义，可以是矩阵形式或规则形式。

矩阵形式的模糊关系可以通过编写代码实现。

例如，我们可以建立一个三维矩阵表示的模糊关系，代码如下：```matlabx1 = 0:0.1:10;x2 = 0:0.1:10;x3 = 0:0.1:10;R = zeros(length(x1), length(x2), length(x3));for i = 1:length(x1)for j = 1:length(x2)for k = 1:length(x3)R(i, j, k) = min(trimf(x1(i), [2 3 4]), trimf(x2(j), [5 6 7]), trimf(x3(k), [8 9 10]));endendend```通过上述代码，我们可以建立一个三维矩阵表示的模糊关系，其中每个元素表示了一个具体的隶属度值。

在Matlab中使用模糊C均值聚类进行图像分析的技巧在图像分析领域，模糊C均值聚类（FCM）是一种常用的工具，它可以帮助我们发现图像中隐藏的信息和模式。

通过使用Matlab中的模糊逻辑工具箱，我们可以轻松地实现FCM算法，并进行图像分析。

本文将介绍在Matlab中使用FCM进行图像分析的技巧。

首先，让我们简要了解一下FCM算法。

FCM是一种基于聚类的图像分割方法，它将图像的像素分为不同的聚类，每个聚类代表一类像素。

与传统的C均值聚类算法不同，FCM允许像素属于多个聚类，因此能够更好地处理图像中的模糊边界。

在Matlab中使用FCM进行图像分析的第一步是加载图像。

可以使用imread函数将图像加载到Matlab的工作区中。

例如，我们可以加载一张名为“image.jpg”的图像：```matlabimage = imread('image.jpg');```加载图像后，可以使用imshow函数显示图像。

这可以帮助我们对图像有一个直观的了解：```matlabimshow(image);```接下来，我们需要将图像转换为灰度图像。

这是因为FCM算法通常用于灰度图像分析。

可以使用rgb2gray函数将彩色图像转换为灰度图像：```matlabgrayImage = rgb2gray(image);```在使用FCM算法之前，我们需要对图像进行预处理。

预处理的目的是消除图像中的噪声和不必要的细节，从而更好地提取图像中的特征。

常用的图像预处理方法包括平滑、锐化和边缘检测等。

Matlab中提供了许多图像预处理函数。

例如，可以使用imnoise函数向图像中添加高斯噪声：```matlabnoisyImage = imnoise(grayImage, 'gaussian', 0, 0.01);```还可以使用imfilter函数对图像进行平滑处理。

常见的平滑方法包括均值滤波和高斯滤波：```matlabsmoothImage = imfilter(noisyImage, fspecial('average', 3));```一旦完成预处理步骤，我们就可以使用模糊逻辑工具箱中的fcm函数执行FCM算法。

控制理论与控制工程《智能控制基础》课程实验报告专业：控制理论和控制工程班级：双控研2016姓名：洪帅任课教师：马兆敏2016年12 月4 日第一部分：模糊控制实验一模糊控制的理论基础实验实验目的：1 练习matlab中隶属函数程序的编写，同时学习matlab数据的表达、格式、文件格式、存盘2 学习matlab中提供的典型隶属函数及参数改变对隶属度曲线的影响3 模糊矩阵合成仿真程序的学习4 模糊推理仿真程序实验内容（1）要求自己编程求非常老，很老，比较老，有点老的隶属度函数。

1隶属函数编程试验结果如图1-1图1-1隶属度函数曲线（2）完成思考题P80 2-2 写出W及V两个模糊集的隶属函数，并绘出四个仿真后的曲线。

仿真曲线见图1-2，图1-2隶属度函数曲线2 典型隶属函数仿真程序学习下列仿真程序，改变各函数中的参数，观察曲线的变化，并总结各种隶属函数中其参数变化是如何影响曲线形状变换的。

M=1 M=3M=3 M=4M=5 M=6图1-3 M 在1、2、3、4、5、6时的图形2 模糊矩阵合成仿真程序：学习P31例2-10，仿真程序如下，（1） 完成思考题P81 2-5，并对比手算结果。

完成思考题P81 2-4，并对比手算结果。

（2） 2-5：(1) Matlab 结果如下①②③P81 2-5手算结果：P=⎥⎦⎤⎢⎣⎡7.02.09.06.0 Q=⎥⎦⎤⎢⎣⎡4.01.07.05.0 R=⎥⎦⎤⎢⎣⎡7.07.03.02.0 S=⎥⎦⎤⎢⎣⎡5.06.02.01.0(PοQ)οR=⎥⎦⎤⎢⎣⎡4.04.06.06.0(PUQ)οS=⎥⎦⎤⎢⎣⎡5.06.05.06.0(PοS)U(QοS)=⎥⎦⎤⎢⎣⎡5.06.05.06.0总结：手算结果和MATLAB运行结果一致。

(2)（2）思考题P81 2-4 Matlab运行结果如下：P81 2-4题手算结果如下：()3020104.01104.02030++++-+-+-=eZEμ()30203.01013.0102030++++-+-+-=ePSμ()()3020104.03.0102030++++-+-+-=⋂eePSZEμμ()()30203.01011104.02030++++-+-+-=⋃eePSZEμμ总结：手算结果和MATLAB运行结果一致。

模糊PID基本原理及matlab仿真实现（新⼿！新⼿！新⼿！）有关模糊pid的相关知识就把⾃⼰从刚接触到仿真出结果看到的⼤部分资料总结⼀下，以及⼀些⾃⼰的ps以下未说明的都为转载内容在讲解模糊PID前，我们先要了解PID控制器的原理（本⽂主要介绍模糊PID的运⽤,对PID控制器的原理不做详细介绍）。

PID控制器（⽐例-积分-微分控制器）是⼀个在⼯业控制应⽤中常见的反馈回路部件，由⽐例单元P、积分单元I和微分单元D组成。

PID控制的基础是⽐例控制；积分控制可消除稳态误差，但可能增加超调；微分控制可加快⼤惯性系统响应速度以及减弱超调趋势。

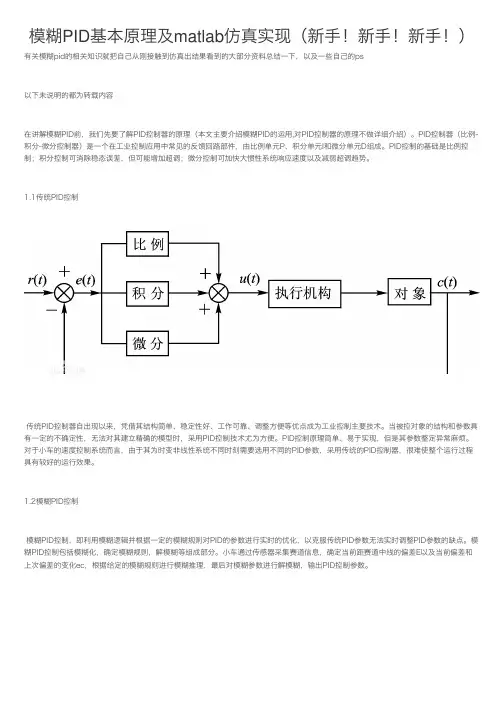
1.1传统PID控制传统PID控制器⾃出现以来，凭借其结构简单、稳定性好、⼯作可靠、调整⽅便等优点成为⼯业控制主要技术。

当被控对象的结构和参数具有⼀定的不确定性，⽆法对其建⽴精确的模型时，采⽤PID控制技术尤为⽅便。

PID控制原理简单、易于实现，但是其参数整定异常⿇烦。

对于⼩车的速度控制系统⽽⾔，由于其为时变⾮线性系统不同时刻需要选⽤不同的PID参数，采⽤传统的PID控制器，很难使整个运⾏过程具有较好的运⾏效果。

1.2模糊PID控制模糊PID控制，即利⽤模糊逻辑并根据⼀定的模糊规则对PID的参数进⾏实时的优化，以克服传统PID参数⽆法实时调整PID参数的缺点。

模糊PID控制包括模糊化，确定模糊规则，解模糊等组成部分。

⼩车通过传感器采集赛道信息，确定当前距赛道中线的偏差E以及当前偏差和上次偏差的变化ec，根据给定的模糊规则进⾏模糊推理，最后对模糊参数进⾏解模糊，输出PID控制参数。

2.1模糊化模糊控制器主要由三个模块组成：模糊化，模糊推理，清晰化。

具体如下图所⽰。

⽽我们将⼀步步讲解如何将模糊PID算法运⽤到智能车上。

（最好⽤笔⼀步步⾃⼰写⼀遍）⾸先我们的智能车会采集到赛道的相关数据，例如摄像头车，其采集到的数据经过算法处理之后会得到与中线的偏差E，以及当前偏差和上次偏差的变化（差值）EC两个值（即此算法为2维输⼊，同理也可以是1维和3维，但2维更适合智能车）。

如何在Matlab中进行模糊聚类分析在数据分析领域，模糊聚类分析是一种常用的技术，它可以应用于各种领域的数据处理和模式识别问题。

而Matlab作为一种功能强大的数据分析工具，也提供了丰富的函数和工具箱，以支持模糊聚类分析的实施。

1. 引言模糊聚类分析是一种基于模糊集理论的聚类方法，与传统的硬聚类方法不同，它允许样本属于多个聚类中心。

这种方法的优势在于可以更好地应对数据中的不确定性和复杂性，对于某些模糊或模糊边界问题具有更好的解释能力。

2. 模糊聚类算法概述Matlab提供了多种模糊聚类算法的实现，其中最常用的是基于模糊C均值（Fuzzy C-Means，FCM）算法。

FCM算法的基本思想是通过最小化聚类后的模糊划分矩阵与原始数据之间的距离来确定每个样本所属的聚类中心。

3. 数据预处理与特征提取在进行模糊聚类分析之前，需要对原始数据进行预处理和特征提取。

预处理包括数据清洗、缺失值处理和异常值处理等；特征提取则是从原始数据中抽取出具有代表性和区分性的特征，用于模糊聚类分析。

4. 模糊聚类分析步骤在Matlab中，进行模糊聚类分析通常包括以下步骤：(1) 初始化聚类中心：通过随机选择或基于某种准则的方法初始化聚类中心。

(2) 计算模糊划分矩阵：根据当前的聚类中心，计算每个样本属于各个聚类中心的隶属度。

(3) 更新聚类中心：根据当前的模糊划分矩阵，更新聚类中心的位置。

(4) 判断终止条件：通过设置一定的终止条件，判断是否达到停止迭代的条件。

(5) 输出最终结果：得到最终的聚类结果和每个样本所属的隶属度。

5. 模糊聚类结果评估在进行模糊聚类分析后，需要对聚类结果进行评估以验证其有效性和可解释性。

常用的评估指标包括模糊划分矩阵的聚类有效性指标、外部指标和内部指标等。

通过这些指标的比较和分析，可以选择合适的模糊聚类算法和参数设置。

6. 模糊聚类的应用模糊聚类分析在诸多领域中都有广泛的应用。

例如，在图像处理中，可以利用模糊聚类方法对图像进行分割和识别；在生物信息学中，可以应用于基因表达数据的分类和模式识别等。

区间二型模糊集 matlab
区间二型模糊集是指在模糊集理论中的一种特殊类型，它具有
两个模糊数作为其元素。

在Matlab中，我们可以使用模糊逻辑工具
箱（Fuzzy Logic Toolbox）来处理区间二型模糊集。

首先，我们需要定义区间二型模糊集的隶属函数。

隶属函数描
述了元素属于模糊集的程度。

在Matlab中，可以使用fuzzy集合函
数（fuzzy set functions）来定义和创建隶属函数，例如使用
trimf函数来创建三角隶属函数，gauss2mf函数创建二项式隶属函
数等。

接着，我们可以使用fuzzy集合对象（fuzzy set objects）来
表示区间二型模糊集。

可以使用addvar函数来添加输入/输出变量，使用addmf函数来添加隶属函数，以及使用addrule函数来添加模
糊规则。

在处理区间二型模糊集时，我们可以利用Matlab中的模糊推理（fuzzy inference）功能来进行模糊推理和模糊控制。

可以使用fuzzy系统对象（fuzzy system objects）来建立和评估模糊系统。

除了使用Matlab自带的模糊逻辑工具箱，还可以在Matlab中编写自定义的函数和算法来处理区间二型模糊集。

这包括定义隶属函数的数学表达式，实现模糊推理算法等。

总之，在Matlab中处理区间二型模糊集，可以通过使用模糊逻辑工具箱提供的函数和对象，或者编写自定义的算法来实现。

希望这些信息对你有所帮助。

第6章 模糊逻辑6.1 隶属函数6.1.1 高斯隶属函数函数 gaussmf格式 y=gaussmf(x,[sig c])说明 高斯隶属函数的数学表达式为：222)c x (e )c ,;x (f σ−−=σ，其中c ,σ为参数，x 为自变量，sig 为数学表达式中的参数σ。

例6-1>>x=0:0.1:10;>>y=gaussmf(x,[2 5]); >>plot(x,y)>>xlabel('gaussmf, P=[2 5]')结果为图6-1。

gaussmf, P=[2 5]图6-16.1.2 两边型高斯隶属函数函数 gauss2mf格式 y = gauss2mf(x,[sig1 c1 sig2 c2])说明 sig1、c1、sig2、c2为命令1中数学表达式中的两对参数 例6-2>>x = (0:0.1:10)';>>y1 = gauss2mf(x, [2 4 1 8]); >>y2 = gauss2mf(x, [2 5 1 7]); >>y3 = gauss2mf(x, [2 6 1 6]); >>y4 = gauss2mf(x, [2 7 1 5]); >>y5 = gauss2mf(x, [2 8 1 4]);>>plot(x, [y1 y2 y3 y4 y5]);>>set(gcf, 'name', 'gauss2mf', 'numbertitle', 'off');结果为图6-2。

6.1.3 建立一般钟型隶属函数函数 gbellmf 格式 y = gbellmf(x,params)说明 一般钟型隶属函数依靠函数表达式b 2|ac x |11)c ,b ,a ;x (f −+=这里x 指定变量定义域范围，参数b 通常为正，参数c 位于曲线中心，第二个参数变量params 是一个各项分别为a ，b 和c 的向量。

一、概述在工程建模和系统分析中，经常需要对实际数据进行拟合，并获取与之相匹配的传递函数。

MATLAB作为一种强大的工程计算软件，提供了丰富的工具和函数来实现这一目标。

本文将介绍MATLAB如何对给定数据进行传递函数拟合，并探讨在不同情况下的应用方法和注意事项。

二、基本原理在进行数据拟合时，传递函数（Transfer Function）是一个常用的数学模型，表示系统的输入与输出之间的关系。

传递函数通常以分子多项式和分母多项式的比值形式表示，是系统动态特性的重要描述工具。

在MATLAB中，可以利用tf函数来创建传递函数，并利用lsim函数进行拟合。

三、数据导入在进行传递函数拟合之前，首先需要将实际数据导入MATLAB。

可以使用MATLAB内置的导入工具，或者编写自定义的数据读取函数来实现。

确保数据的格式正确并无误，以便后续的拟合操作。

四、传递函数拟合1. 传递函数的创建使用tf函数可以创建传递函数对象，其基本语法为：G = tf(num, den)其中num为分子多项式的系数向量，den为分母多项式的系数向量。

通过传递函数对象G，可以方便地进行后续的拟合和分析操作。

2. 数据格式化在进行传递函数拟合之前，需要将待拟合的数据格式化为MATLAB支持的格式。

通常使用时间序列数据的形式，确保数据的采样频率和时间间隔正确。

3. 传递函数拟合利用lsim函数可以对给定的数据进行传递函数拟合，其基本语法为：[ysim, t] = lsim(G, u, t)其中G为传递函数对象，u为系统的输入信号，t为时间向量。

通过lsim函数得到的ysim即为拟合后的输出数据，可以与原始数据进行对比分析。

五、案例分析以一个简单的电路为例，考虑其输入与输出之间的传递函数关系。

假设已经获取了该电路的输入-输出数据，现在需要利用MATLAB对其进行传递函数拟合。

1. 数据导入首先将实际测量得到的电路输入-输出数据导入MATLAB，并确保数据的准确性和完整性。

MATLAB⽣成Word⽂档⼀、创建Microsoft Word服务器1. 创建Microsoft Word服务器try% 若Word服务器已经打开，返回其句柄WordWord = actxGetRunningServer('Word.Application');catch% 创建⼀个Microsoft Word服务器，返回句柄WordWord = actxserver('Word.Application');end2. 设置对象属性设置Word服务器为可见状态set(Word, 'Visible', 1); %或Word.Visible = 1;⼆、建⽴Word⽂本⽂档1. 新建空⽩⽂档%调⽤Add⽅法建⽴⼀个空⽩⽂档，并返回其句柄DocumentDocument = Word.Documents.Add;2. 页⾯设置%查看PageSetup接⼝的所有属性Document.PageSetup.get%页⾯设置Document.PageSetup.TopMargin =60;%上边距60磅Document.PageSetup.BottomMargin =45;%下边距45磅Document.PageSetup.LeftMargin =45;%左边距45磅Document.PageSetup.RightMargin =45;%右边距45磅%查看枚举类型属性VerticalAlignment的属性值Document.PageSetup.set('VerticalAlignment')3. 写⼊⽂字Content接⼝Content接⼝有很多属性和⽅法，可通过Content.get和Content.methodsview命令查看；Start属性⽤来获取或设定⽂字内容的起始位置，End属性⽤来获取或设定⽂字内容的终⽌位置，Text属性⽤来写⼊⽂字内容，Font属性⽤于字体设置，Paragraphs属性⽤于段落设置。

实验一熟悉模糊工具箱一、目的和要求1.目的(1)通过本次实验，进一步了解模糊控制的基本原理、模糊模型的建立和模糊控制器的设计过程。

(2)掌握MATLAB模糊逻辑工具箱的图形用户界面设计模糊控制器的过程。

2.要求（1）充分理解实验内容，并独立完成实验报告。

（2）实验报告要求：实验题目、实验具体内容、结果分析、收获或不足。

二、实验内容1、利用matlab中的模糊逻辑工具箱提供的图形用户界面（GUI）工具设计一个两输入、一输出的模糊控制器，控制器的要求如下：（1）设模糊控制器的输入变量为：误差E和误差变化EC，输出量为U。

（2）隶属度函数：◆隶属度函数均为三角函数◆E、EC和U的模糊语言变量集均为{NB,NM,NS,ZO,PS,PM,PB}◆E和EC论域为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}◆U的论域为{-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7}（3）控制规则表如下：表1 模糊控制表三．实验步骤模糊逻辑工具箱提供的图形用户界面（GUI）工具有五个：模糊推理系统（FIS）编辑器；隶属函数编辑器；模糊规则编辑器；模糊规则观察器；输出曲面观察器。

1.模糊控制器结构设计FIS处理系统有多少个输入变量，输出变量，名称是什么，模糊算子“与”(min，prod乘积，custom自定义)，“或”(max大，probor 概率统计方法，custom)，推理方法（min，prod，custom），聚类方法（max，probor，sum，custom），解模糊的方法（centroid 质心法，bisector中位线法，middle of maximum，largest of maximum，smallest of maximum）。

Matlab的FIS界面如图3所示。

图3 模糊推理系统（FIS）界面2.隶属函数编辑器：确定各个变量的论域和显示范围（左下角编辑区内），如图4所示。

模糊PID控制器设计和仿真步骤：各变量隶属度函数的确定第一步：各变量隶属度函数的确定1、 用于PID 参数调整的模糊控制器采用二输入三输出的形式。

该控制器是以误差E 和误差变化率EC 作为输入，PID 控制器的三个参数P、I、D 的修正△KP、△KI、△KD 作为输出，如图1；2、 取输入E 和EC 和输出△KP、 △KI、△KD 模糊子集为{NB,NM,NS,ZO,PS,PM,PB}，其论域为[-6,6],量化等级为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；如图23、 在模糊逻辑工具箱的隶属度函数编辑器中，选择输入量E，EC 隶属函数为高斯型（gaussmf）,输出△KP、△KI、△KD 的隶属函数为三角形（trimf），如图2和3。

图1图2图3第二步：根据图4规则建立模糊规则表，如图5：图4图5第三步：设置参数：与方式与方式 (And method)为min ；或方式（Or method)为max ；推理推理 (Implication)为min ；合成；合成 (Aggregation)为max ；去模糊（Defuzzification)为重心平均法（centroid ）。

）。

第四步：保存该FIS 文件，取名为FuzzyPID.fis第五步：在MA MATLABTLAB 的M 文件编辑器里建立一个名为FuzzyPID.m 的文件，其内容为：martrix=readfis （‘Fuzzypid.fis ’），并运行。

，并运行。

第六步：打开SIMULINK ，新建一个Model ，选择一个Subsystem ，在其中编辑模块，如图6，并设置模糊化因子KE=KEC=0.01，解模糊因子KP=0.5，KI=KD=0.01，并在Fuzzy Logic Controller 模块的Parameters 中输入readfis('FuzzyPID.fis')：图6第七步：返回到新建的Model 中，按照如图7所示建立模糊PID 控制器，其中，控制器，其中，PID PID 初始值为KP0=20，KI0=1.35，KD0=3.7，传递函数为：图7第八步：保存为FuzzyPID.mdl 并运行。