六年级奥数第5讲 还原法解题资料
- 格式:ppt
- 大小:182.51 KB
- 文档页数:16

还原问题(1)【小学四年级奥数】添加时间:2012年11月02日浏览:1449次顿悟教育小学奥数培优训练营来自:顿悟教育网杨老师专题简析对于有些问题,当顺着题目条件的叙述去寻找解法时,往往有一定的困难,但是,如果改变思考顺序,从问题叙述的最后结果出发,一步一步倒着思考,一步一步往回算,原来加的用减,减的用加,原来乘的用除,除的用乘,那么问题便容易解决。
这种解题方法叫做还原法或逆推法,用还原法解题的问题叫做还原问题。
1、定义:一个数通过一系列的运算后得到一个答案,求这个数。
也就是已知一个数的变化过程和最后结果,求原来的数,通常称此类问题叫“还原问题”。
2、解题方法:解答“还原问题”一般采用倒推法,简单地说:就是倒过来想。
我们可以采用从结果出发,按它变化的相反方向一步步倒着想,直到解决问题。
同时也可以利用线段图、表格、示意图等方式来帮助理解题意。
例题精讲例1、一个数减24加上15,再乘以8得432。
求这个数。
分析:这个问题可以看成(□—24+15)×8=432,求出□,我们倒着看,如果乘以8以前的数应该是432÷8=54,54是在这个数减24以后栽加15得到的,如果不加15,那么差应该是54-15=39,39是这个数减24以后得到的,如果不减24,那么这个数是39+24=63.解:432÷8-15+24=63答:这个数是63.【练习1】1、一个数加上3,乘以3,再减去3,最后除以3,结果还是3。
求这个数。
2、一个数的4倍加上6减去10,再乘以2得88。
求这个数。
3、一个数缩小3倍,再缩小2倍得80。
求这个数。
例2、马小虎在做一道整数减法题时,把减数个位上的3看成8,把减数十位上的7看成1,结果算得差是216,你知道正确的差应该是几吗?分析:像这种问题,我们要分析清楚错误的差与正确的差多少,多算的要减去,少算的要补上。
马小虎错把减数个位上的3看成8,多减了8-3=5,那么差就少减了5,这个5要补上,他把减数十位上的7看成1,少减了70-10=60,那么差就增加了60,这个60要减去。

2019年六年级奥数还原问题指点迷津有些数学问题,叙述某一个未知量,经过一系列的已知变化后变成另一个已知数量,而要求原来的未知量。
解答这类问题的关键在于“还原”。
从最后一个已知数出发,逐步递推回去直至推出问题的答案。
这种解决问题的方法叫做逆推法,也叫还原法。
范例点拨例1 有甲、乙两堆小球,按下面的规律移动,第一次从甲堆拿出和乙堆同样多的小球放到乙堆;第二次从乙堆拿出和甲堆剩下的同样多的小球放到甲堆。
照这样移动四次以后,甲、乙两堆的小球刚好都是16个。
甲、乙两堆小球原来各有多少个?思路提示:从最后一个条件出发,进行逆推。
尝试解答:例2 张华在一本存折中支出生活费。
第一次取出存款的51,第二次取出余下的41,第三次又取出余下的31,这时存折中还剩200元。
他原有存款多少元?思路提示:从最后剩200元,可推出第三次取之前的钱数,再求出第一次取出后的钱数,进而求出他原来的存款钱数。
尝试解答:例 3 一段公路,第一次修了全长的31又31km ,第二次修了剩下的41又41km ,第三次修了剩下的21又21km 。
这段公路长多少千米?思路提示:从最后的问题入手,倒推回去。
先求出第二次剩下的千米数,再求出第一次剩下的千米数,最后求公路的全长。
尝试解答:例4 甲、乙、丙三人各有若干本书,甲给乙、丙两人一部分书,使两人书的本数增加1倍,然后乙也照样送给甲、丙两人,最后丙也照这样送给甲、乙两人。
结果甲有书48本,是丙的书本数的54,乙的本数是丙的书本数的1571。
甲、乙、丙三人原来各有多少本数?思路提示:我们可以计算出最后三人书的本数,再用逆推法求出最初三人书的本数。
尝试解答:触类旁通1.从第一堆橘子里拿一半放到第二堆里,拿出35个放到第三堆里,又拿出剩下的一半放到第四堆里,最后又从第一堆里拿出2个吃掉,这时第一堆里还有48个。
第一堆里原来有橘子多少个?2.四个袋子里共有168粒棋子,现在把棋子作如下的调整:丁袋调3粒到丙袋,丙袋调6粒到乙袋,乙袋调6粒到甲袋,甲袋调2粒到丁袋。

小学奥数趣味学习《还原问题》典型例题及解答还原问题是典型应用题之一,指已知某数经过四则运算的结果,要求出某数的应用题。
解题思路和方法:解这类问题应按题目所述顺序的逆序,施行所述运算的逆运算,就可列出算式。
简言之就是反其道而行之就能算出结果。
例题1:将一个数先加上6,然后乘6,再减去6,最后除以6,结果还是6,那么这个数是多少?解:1、本题考查的是一个量多次变换还原,关键是从最后的结果出发,根据加减乘除的逆运算进行解答。
2、由最后的结果出发,除以6商是6,那么之前就是6×6=36;减去6是36,那么之前是36+6=42;乘6是42,那么之前是42÷6=7;加上6是7,那么之前数7-6=1。
例题2:修路队修一条路,第一天修了全长的一半多20米,第二天修了余下的一半少15米,第三天修了50米,还剩30米没有修,这条路全长多少米?解:1、本题考查的是一半与整体关系还原,关键是抓住最后的数量,从后往前推理。
2、根据题意,如果第二天正好修了余下的一半,则剩下(30+50-15)=65(米),用65×2=130(米)就是第一天修完余下的长度;又因为第一天修了全长的一半多20米,如果第一天正好修了全长的一半时,则剩下的是130+20=150(米),这样得出剩下的长度的2倍就是全长,即150×2=300(米)。
例题3:甲、乙、丙三人各有连环画若干本,如果甲给乙、丙各5本,乙给甲、丙各10本,丙给甲、乙各15本后,那么三人所拥有的连环画一样多,都是35本,原来甲、乙、丙各有连环画多少本?解:1、本题考查的是多个量之间的还原关系,我们通常采用列表的方式倒推解决此类问题。
2、根据题意我们可以列表如下:3、最后每人都有35本,因为丙给甲、乙各15本,所以丙给甲、乙前,丙有35+15×2=65(本),甲、乙各有35-15=20(本)。
4、因为乙给甲、丙各10本,所以乙给甲、丙前,乙有20+10×2=40(本),甲有20-10=10(本),丙有65-10=55(本)。

有一类问题,告诉我们最后的结果,让我们从结果出发,根据已知条件和现有的知识,一步步倒着分析推理,直到退还到原来的出发点。
这类问题叫做还原问题;这样逆向推理,解决问题的方法叫做还原法(也叫倒推法)。
解决还原问题的基本思路是:一步一步退回去。
也就是说,原来加的,退回去用减;原来减的,退回去用加;原来乘的,退回去用除;原来除的,退回去用乘。
还原法的精髓就是先找原运算的逆运算。
原问题,所以根据我们的基本思路:一步步往回退,从结果5出发,做除的逆运算乘,接着做减的逆运算加,然后做乘的逆运算除,最后做加的逆运算减,即可得最初的数。
解答(1)如果没有除以5,这个数是:5×5=25(2)如果没有减去5,这个数是:25+5=30(3)如果没有乘以5,这个数是:30÷5=6(4)如果没有加上5,这个数是:6-5=1综合算式:(5×5+5)÷5-5=(25+5)÷5-5=30÷5-5=6-5=1答:这个数为1。
[例3] 小东在做整数加法运算时,把一个加数个位上的7看成了1,把另一个加数十位上的3看成了8,结果所得的和是342,请问这道题的正确答案应该是多少?思路剖析把个位上的7看成了l,那么和就减少了(7-1)=6,把十位上的3看成了8,那么和就增加了(8-3)×10=50,再根据加和减的互逆关系,把错误的和加上减少的,减去增加的,就可得出正确的答案。
解答要求这道题的正确答案是多少,可以先求出当把个位上7看成1时,和减少了多少,还需要求出当把十位上的3看成8时,和增加了多少?(1)把个位上的7看成1时,和减少了:7-l=6(2)把十位上的3看成8时,和增加了:【例‘1】李老师在黑板上写了若干个从l开始的连续正整数l,2,3,…然后擦掉其中一个,剩下的数的平均数是10.8。
那么,被擦掉的那个正整数是多少?分析与解答以上分数的分子表示去掉一个正数的和,分母表示个数。

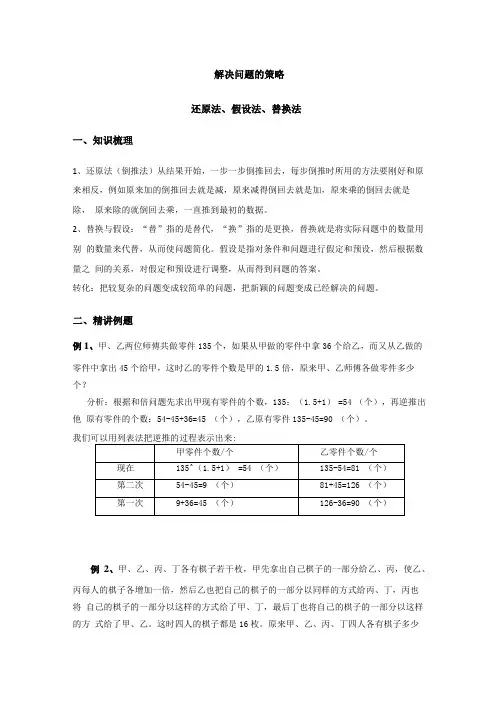
解决问题的策略还原法、假设法、替换法一、知识梳理1、还原法(倒推法)从结果开始,一步一步倒推回去,每步倒推时所用的方法要刚好和原来相反,例如原来加的倒推回去就是减,原来减得倒回去就是加,原来乘的倒回去就是除,原来除的就倒回去乘,一直推到最初的数据。
2、替换与假设:“替”指的是替代,“换”指的是更换,替换就是将实际问题中的数量用别的数量来代替,从而使问题简化。
假设是指对条件和问题进行假定和预设,然后根据数量之间的关系,对假定和预设进行调整,从而得到问题的答案。
转化:把较复杂的问题变成较简单的问题,把新颖的问题变成已经解决的问题。
二、精讲例题例1、甲、乙两位师傅共做零件135个,如果从甲做的零件中拿36个给乙,而又从乙做的零件中拿出45个给甲,这时乙的零件个数是甲的1.5倍,原来甲、乙师傅各做零件多少个?分析:根据和倍问题先求出甲现有零件的个数,135:(1.5+1)=54 (个),再逆推出他原有零件的个数:54-45+36=45 (个),乙原有零件135-45=90 (个)。
例2、甲、乙、丙、丁各有棋子若干枚,甲先拿出自己棋子的一部分给乙、丙,使乙、丙每人的棋子各增加一倍,然后乙也把自己的棋子的一部分以同样的方式给丙、丁,丙也将自己的棋子的一部分以这样的方式给了甲、丁,最后丁也将自己的棋子的一部分以这样的方式给了甲、乙。
这时四人的棋子都是16枚。
原来甲、乙、丙、丁四人各有棋子多少枚?分析:最后一次四人的棋子都是16枚,每次变化中,有一人的棋子数未动,有两人的棋子数增加一倍,倒推时应除以“2”,另一个人的棋子数减少了两人增加的总数。
我们可以用列表法进行倒推:例3、王师傅和李师傅一起打一份稿件。
王师傅打5分钟,李师傅打6分钟,两人一共打了757个字。
已知王师傅每分钟比李师傅多打15个字。
王师傅每分钟打多少个字?李师傅每分钟打多少个字?分析:王师傅每分钟比李师傅多打15个字,王师傅5分钟就比李师傅多打了15*5=75个字,757-75=682,也就是李师傅在11(5+6)分钟打了682个字,每分钟打682/11=62个字,王师傅每分钟打15+62=77个字。


还原问题知识导航还原问题是逆解应用题,还原问题先提出一个未知量,经过一系列的运算,最后给出另一个已知量,要求求出原来的未知数量。
解题时,从最后一个已知量出发,逐步进行逆推性运算,即原来是加的,运算时就减;原来是减的,运算时就加;原来是乘的,运算时就除;原来是除的,运算时就乘。
列综合算式时,要特别注意运算顺序,为此要正确使用括号。
如小莉要把一个包装精美的盒子打开。
她先拆开最外层的彩纸;接着打开纸盒,纸盒里有一个绒布盒;再打开绒布盒一看,里面是两支“派克”金笔。
妈妈说,这礼物是送给大学老师的,要小莉把它重新包装起来。
小莉是按这样的顺序做的:先把两支笔放入绒布盒→盖上绒布盒,并把它放进纸盒→盖上纸盒,并用彩纸封好。
小莉重新包装的步骤(顺序)恰好与她打开这盒礼物的顺序相反。
这是生活中常会遇到的“还原问题”。
在数学中,还原问题也很多。
【例1】一次数学考试后,李军问于昆数学考试得多少分。
于昆说:“用我得的分数减去8加上10,再除以7,最后乘以4,得52。
”小朋友,你知道于昆得多少分吗?【例2】某数加上5,乘以5,减去5,除以5,其结果等于5。
求这个数。
【例3】在做一道加法试题时,某学生把个位上的5看作9,把十位上的8看作3,结果“和”得123。
正确的答案是多少?【例4】小马虎做一道减法题,把被减数十位的6当作9,把减数个位的3当作5,结果是217,正确的答案是多少?【例5】妈妈从超市买回几个面包。
第一天吃了全部的一半又半个,第二天吃了余下的一半又半个,第三天吃了再余下的一半又半个,恰好吃完。
妈妈从超市买回多少个面包?【例6】一群猴子分一堆桃子,第一个猴子取走了一半零一个,第二个猴子取走剩下的一半零一个,……直到第七个猴子按上述方式取完后恰好取尽。
这堆桃子一共有多少个?【例7】有一根铁丝,第一次用去它的一半少1米,第二次用去剩下的一半多1米,最后还剩2.5米,这根铁丝原来长多少米?【例8】有一堆西瓜第一次搬走一半,第二次搬走剩下的一半多3个,第三次搬走剩下的一半少3个,第四次搬走剩下的一半多3个,第五次搬走剩下的一半,最后还剩3个,这堆西瓜原有多少个?【例9】书架分上、中、下三层,一共分放192本书。

有一类问题,告诉我们最后的结果,让我们从结果出发,根据已知条件和现有的知识,一步步倒着分析推理,直到退还到原来的出发点。
这类问题叫做还原问题;这样逆向推理,解决问题的方法叫做还原法(也叫倒推法)。
解决还原问题的基本思路是:一步一步退回去。
也就是说,原来加的,退回去用减;原来减的,退回去用加;原来乘的,退回去用除;原来除的,退回去用乘。
还原法的精髓就是先找原运算的逆运算。
原问题,所以根据我们的基本思路:一步步往回退,从结果5出发,做除的逆运算乘,接着做减的逆运算加,然后做乘的逆运算除,最后做加的逆运算减,即可得最初的数。
解答(1)如果没有除以5,这个数是:5×5=25(2)如果没有减去5,这个数是:25+5=30(3)如果没有乘以5,这个数是:30÷5=6(4)如果没有加上5,这个数是:6-5=1综合算式:(5×5+5)÷5-5=(25+5)÷5-5=30÷5-5=6-5=1答:这个数为1。
[例3] 小东在做整数加法运算时,把一个加数个位上的7看成了1,把另一个加数十位上的3看成了8,结果所得的和是342,请问这道题的正确答案应该是多少?思路剖析把个位上的7看成了l,那么和就减少了(7-1)=6,把十位上的3看成了8,那么和就增加了(8-3)×10=50,再根据加和减的互逆关系,把错误的和加上减少的,减去增加的,就可得出正确的答案。
解答要求这道题的正确答案是多少,可以先求出当把个位上7看成1时,和减少了多少,还需要求出当把十位上的3看成8时,和增加了多少?(1)把个位上的7看成1时,和减少了:7-l=6(2)把十位上的3看成8时,和增加了:【例‘1】李老师在黑板上写了若干个从l开始的连续正整数l,2,3,…然后擦掉其中一个,剩下的数的平均数是10.8。
那么,被擦掉的那个正整数是多少?分析与解答以上分数的分子表示去掉一个正数的和,分母表示个数。


小学奥数,如何用画图法解决还原问题?
一个未知数量,经过几次的变化过程变成另外一个结果,从结果出发,根据过程变化情况倒推还原出初始数量,这种类型题目被称为还原问题,也叫倒推问题(逆运算)。
借助画倒推图法,过程形象直观,直接进行逆运算即可。
我是王老师,致力于小学数学的精品问答!倒推来解决问题,相对于设方程,更锻炼逆向思维的能力。
今天就依据列题详细讲解如何画倒推图解题。
还原问题
【基本题型】:一个数,加上2,减去5,乘4,除以3后结果为20,求这个数?
① 先画过程图,数量的每一步状态用方框来表示,开始未知就在框中画个问号,过程变化用箭头表示,箭头上方写上过程数学表达式(运算符号和数量)。
结果直接表示数字,如下图示。
② 画倒推图,从结果出发逐步向前倒推,倒推时箭头方向改变,运算符号为原来的逆运算,直至求出开始状态,这样就完成了整个倒推过程。
你学会了吗?
倒推时,也可简化为写在原来方框下面。
如下图
来个复杂点的
【复杂题型】:菜商原有若干大白菜,第一天卖出了原有大白菜的一半;第二天运进200千克;第三天卖出现有白菜的一半又30千克,结果剩余白菜的3倍是1800千克。
求原来菜商有多少千克的大白菜?
画图,过程图要根据文字描述仔细分析,转化为数学表达式。
第一天:卖出原来大白菜一半→ ÷2
第二天:运进来200千克,是增加了200kg → 200
第三天:卖出现有白菜的一半和30千克,不妨化两步→ ÷2 → -30
结果:剩余白菜的3倍是1800,剩余×3 → 1800。
可以画图了。
还原问题知识要点在数学问题中,经常遇到这样的应用题:一个数或者一种量,通过一步一步的变化最后得到结果,要我们求最初的数或量。
如果按照一般的解题方法来求解这种题就比较困难,但如果从结果出发,沿着它的变化规律,利用加法与减法,乘法与除法的互逆关系,一步一步的倒着往前推,直到求出最初的数或量。
这样思考问题的方法叫还原法,这样的问题叫还原问题。
解答这类问题的关键在于“还原”。
“还原”的基本途径是:从最后一个已知数开始,逐步逆推回去。
原题为加,倒推里为减;原题为减,倒推时为加;原题为乘,倒推时为除;原题为除,倒推时为乘。
此类应用题也可以根据原题的叙述顺序,列出等量关系式按列方程解应用题的方法进行解答。
典例解析及同步练习典例1 某商场周日出售液晶电视机。
上午售出总数的一半多10台,下午售出剩下的一半多15台,还剩40台。
商场这天原有液晶电视机多少台?解析:从“下午售出剩下的一半多15台”和“还剩下40台”向前倒推。
40台和下午多卖的15台合起来,即40+15=55(台)(如图),正好是上午售出后剩下的一半,那么55×2=110(台)就是上午售后剩下的台数,而110台和10台合起来,即110+10=120(台),又正好是总数的一半,那么120×2=240(台),就是原来液晶电视机的台数。
10台 15台 40台上午售出下午售出还剩解:【(40+15)×2+10】×2=240(台)答:商场这天原有液晶电视机240台。
举一反三训练11、小明的爷爷说:“把我的年龄加上25,除以4,再减去23,最后乘25,恰好是半百。
”你知道小明的爷爷今年多少岁吗?2、小军用自己的零花钱的一半买了一本故事书,后来妈妈又给了他4元6角,他又拿出其中的一半多2角买了一本连环画,结果还剩5元6角,小军原来有多少元?3、冬冬去银行取款,第一次取出了存款的一半还多5元,第二次取了余下的一半少10元,这时存折上还剩下125元,冬冬原有存款多少元?4、超市运来一批苹果,上午卖出总数的一半少15个,下午又卖出剩下的一半少20个,还剩下140个苹果,这批苹果一共有多少个?典例2 甲、乙、丙、丁四人各有故事书若干本,甲将自己的故事书拿一部分给乙、丙、丁,使他们的书增加1倍,然后,乙又拿出一部分故事书使甲、乙、丙的书增加1倍,然后,丙又拿出一部分故事书使得甲、乙、丁的书增加1倍,最后,丁也拿出一部分故事书使得甲、乙、丙的书增加1倍时,甲、乙、丙、丁手中都有32本书。
还原问题一有一位老人说:“把我的年龄加上12,再用4除,再减去15后乘以10,恰好是100岁。
”这位老人有多少岁呢?解这个题目要从所叙述的最后结果出发,利用已给条件一步步倒着推算,同学们不难看出,这位老人的年龄是(100÷10+15)×4—12=88(岁)。
从这一例子可以看出,对于有些问题,当顺着题目条件的叙述去寻找解法时,往往有一定的困难,但是,如果改变思考顺序,从问题叙述的最后结果出发,一步一步倒着思考,一步一步往回算,原来加的用减,减的用加,原来乘的用除,除的用乘,那么问题便容易解决。
这种解题方法叫做还原法或逆推法,用还原法解题的问题叫做还原问题。
入门题:1、小刚的奶奶今年年龄减去7后,缩小9倍,再加上2后,扩大10倍,恰好是100岁,小刚的奶奶今年多少岁?2、一个数的3倍加上6,再减去9,最后乘以2,结果得60。
求这个数。
3、商场出售洗衣机,上午售出总数的一半多10台,下午售出剩下的一半多20台,还剩95台,这个商场原来有洗衣机多少台?4、小明、小强和小勇三个人共有故事书60本。
如果小强向小明借3本后,又借给小勇5本,结果三个人的故事书的本数相等。
这三个人原来各有故事书多少本?5、王亮和李强各有画片若干张。
如果王亮拿出和李强同样多的画片给李强,李强再拿出和王亮同样多的画片给王亮,这时两个人都有24张。
问王亮和李强原来各有画片多少张?练习题:1、粮库内有一批大米,第一次运出总数的一半多3吨,第二次运出剩下的一半多5吨,还剩下4吨。
问粮库原有大米多少吨?2、爸爸买了一些橘子,全家人第一天吃了这些橘子的一半多1个,第二天吃了剩下的一半多1个,第三天又吃了剩下的一半多1个,还剩下1个。
问爸爸买了多少个橘子?3、甲、乙、丙、丁四个小朋友有彩色玻璃球100颗,甲给乙13颗,乙给丙18颗,丙给丁16颗,丁给甲2颗后四人的个数相等。
他们原来各有玻璃球多少颗?4、书架分为上、中、下三层,共放192本书。
6-1-2.还原问题(一)教学目标六年级奥数还原问题〈一〉学生版1. 掌握用倒推法解单个变量的还原问题.2. 了解用倒推法解多个变量的还原问题.3. 培养学生“倒推”的思想.知识点拨一、还原问题已知一个数,经过某些运算之后,得到了一个新数,求原来的数是多少的应用问题,它的解法常常是以新数为基础,按运算顺序倒推回去,解出原数,这种方法叫做逆推法或还原法,这种问题就是还原问题.还原问题又叫做逆推运算问题.解这类问题利用加减互为逆运算和乘除互为逆运算的道理,根据题意的叙述顺序由后向前逆推计算.在计算过程中采用相反的运算,逐步逆推.二、解还原问题的方法在解题过程中注意两个相反:一是运算次序与原来相反;二是运算方法与原来相反.方法:倒推法。
口诀:加减互逆,乘除互逆,要求原数,逆推新数.关键:从最后结果出发,逐步向前一步一步推理,每一步运算都是原来运算的逆运算,即变加为减,变减为加,变乘为除,变除为乘.列式时还要注意运算顺序,正确使用括号.例题精讲模块一、计算中的还原问题【例 1】一个数的四分之一减去5,结果等于5,则这个数等于_____。
【例 2】某数先加上3,再乘以3,然后除以2,最后减去2,结果是10,问:原数是多少?【巩固】有一个数,如果用它加上6,然后乘以6,再减去6,最后除以6,所得的商还是6,那么这个数是。
【巩固】一个数减16加上24,再除以7得36,求这个数.你知道这个数是几吗?【巩固】少先队员采集树种子,采得的个数是一个有趣的数.把这个数除以5,再减去25,还剩25,你算一算,共采集了多少个树种子?【例 3】学学做了这样一道题:某数加上10,乘以10,减去10,除以10,其结果等于10,求这个数.小朋友,你知道答案吗?【巩固】学学做了这样一道题:一个数加上3,减去5,乘以4,除以6得16,求这个数.小朋友,你知道答案吗?【巩固】一次数学竞赛颁奖会上,小刚问老师:“我得了多少分?”老师说:“你的得分减去6后,缩小2倍,再加上10后,扩大2倍,恰好是100分”.小刚这次竞赛得了多少分?【例 4】牛老师带着37名同学到野外春游.休息时,小强问:“牛老师您今年多少岁啦?”牛老师有趣地回答:“我的年龄乘以2,减去16后,再除以2,加上8,结果恰好是我们今天参加活动的总人数.”小朋友们,你知道牛老师今年多少岁吗?【巩固】小智问小康:“你今年几岁?”小康回答说:“用我的年龄数减去8,乘以7,加上6,除以5,正好等于4. 请你算一算,我今年几岁?”【巩固】在小新爷爷今年的年龄数减去15后,除以4,再减去6之后,乘以10,恰好是100,问:小新爷爷今年多少岁数?【巩固】学学和思思在游玩时,遇到一位小神仙,他们问这位神仙:“你一定不到100岁吧!”谁知这位神仙摇摇头说:“你们算算吧!把我的年龄加上75,再除以5,然后减去15,再乘以10,恰好是2000岁.”小朋友,你知道这位神仙现在有多少岁吗?【例 5】在电脑里先输入一个数,它会按给定的指令进行如下运算:如果输入的数是偶数,就把它除以2;如果输入的数是奇数,就把它加上3.同样的运算这样进行了3次,得出结果为27.原来输入的数可能是.【例 6】假设有一种计算器,它由A、B、C、D四种装置组成,将一个数输入一种装置后会自动输出另一个数。