当前位置：文档之家 › 量子力学第一章 PPT

量子力学第一章 PPT

  • 格式：ppt
  • 大小：5.87 MB
  • 文档页数：119

下载文档原格式

  / 119

合集下载

量子力学 第1章-1-2(第3讲)

量子力学 第1章-1-2(第3讲)

越来越多的实验事实证明，波函数的位相是非常重要的物理 概念，只限于统计解释还不能完全穷尽对波函数的认识。
量子波函数的概率解释有不足
玻恩的概率解释：“波函数的振幅的平方是粒 子被发现的概率” 。不是完整诠释，只关注 所谓的可观察量（振幅），忽略了相位（因为 不属于可观察量）。
杨振宁说，规范场论就是相位场。相位是其根 本。振幅与相位合起来用复数表示。
x=0
dx
由于
d 2(x,t)
dx2
0
x0
故 x 0 处，粒子出现概率最大。
注意
（1）归一化后的波函数
(r , t
)
仍有一个模为一的因
子 ei 不定性（ δ为实函数）。
若 r,t 是归一化波函数，那末， r,tei 也是
归一化波函数，与前者描述同一概率波。
（2）只有当概率密度 (r,t) 对空间绝对可积时，才
2
(r,t) dx
A2
ea2x2 dx
A2
1
a2
归一化常数
1/ 2
A a/
归一化的波函数1/ 2Fra bibliotek1a2x2 i t
(r,t) a / e 2 2
（2）概率分布： (x, t) (x, t) 2 a ea2x2
（3）由概率密度的极值条件
d(x, t) a 2a2 xea2x2 0
相位是复杂性之源，相位导致纠缠，纠缠导致 记忆与电子相干。自由度的纠缠和相干，往往 会造就许多意想不到的结果。
作业题
1. 下列一组波函数共描写粒子的几个不同状态? 并指出每
个状态由哪几个波函数描写。
1 ei2x / , 4 ei3x / ,
2 ei2x/ , 5 ei2x / ,

第一章 量子力学基础

第一章 量子力学基础

氧化锆晶体的X射线衍射图 (Debye-Scherrer图)
de Broglie还利用他的关系式为Bohr的轨道角动 量量子化条件
h mvr n 2
作了一个解释：由这一条件导出的
nh h S 2r n n mv p
表明圆轨道周长S是波长的整数倍，这正是在圆周上形 成稳定的驻波所需要的，如同琴弦上形成驻波的条件是 自由振动的弦长为半波长的整数倍一样. 尽管这种轨迹确定的轨道被不确定原理否定了， 但“定态与驻波相联系”的思想还是富有启发性的.
测物理量. 波函数应具有品优性 , 包括单值性、连续性 、平方可积性.
波函数的概率解释
例如, 坐标与相应的动量分量、方位角与动量矩等.
不确定原理可以用不同的方式来阐述, 最容易理解也 最常用的是电子的单缝衍射实验:
波是不确定性的表现
单 缝 衍 射
这个象征着科学 的标志, 迄今仍被有 些人认为是原子模型 的真实图像. 实际上, 它只是照耀过科学历 程的星光:
由于坐标与相应 的动量分量不可能同 时精确测定, 所以， 原子中的电子不可能 具有这种轨迹确切的 轨道.
(photoelectric effect), 后来导致了光的粒子学说. 1889年, 斯托列托夫提出获得光电流的电池方案(下图G为电 流表, V为电压表; C为阴极, A为阳极):
1898年，P.勒纳特确认放电粒子为电子, 并于1902年指出: 1.入射光线的频率低于一定值就不会放出光电子; 2.光电子的动能与光强度无关而与光的频率成正比; 3.光电流强度与光强成正比。
de Broglie波不仅对建立量子
力学和原子、分子结构理论有重要
意义，而且在技术上有重要应用.
使用de Broglie波的电子显微镜分辨率

量子力学_第一章_周世勋

量子力学_第一章_周世勋

1864年 光和电磁现象之间的联系 光的波动性
（二）经典物理学的困难

20世纪初 经典理论遇到了一些严重的困难 （1）黑体辐射问题 （2）光电效应 （3）氢原子光谱
黑体辐射
黑体：能完全吸收一切频率入射电磁 波 （广义光波） 的物体
能 量 密 度
黑体辐射：由这样的空腔小孔发 出的辐射就称为黑体辐射。
h 6.62606896 1034 J s
基于上述假定，普朗克得到了与实验符合很好的黑体辐射公式：
能 量 密 度
8hv3 v dv c3 Planck 线
1 e
hv 1 K BT
dv
吸收或发射电磁能量的不连续概念，经典力学是无法理解的 当时并未引起较多人的注意 用量子假设解决经典困难的是A. Einstein
3. v v0
光愈强，单位时间产生的光电子愈多
光的本性认识：1. Maxwell, Hertz等人工作，肯定了光是电磁波 2. 光电效应，黑体辐射，体现了光的粒子性
光是粒子性和波动性的统一体
• 虽然爱因斯坦对光电效应的解释是对Planck量 子概念的极大支持，但是Planck不同意爱因斯坦的 光子假设，这一点流露在Planck推荐爱因斯坦为普 鲁士科学院院士的推荐信中。 “ 总而言之，我们可以说，在近代物理学结出 硕果的那些重大问题中，很难找到一个问题是爱因 斯坦没有做过重要贡献的，在他的各种推测中，他 有时可能也曾经没有射中标的，例如，他的光量子 假设就是如此，但是这确实并不能成为过分责怪他 的理由，因为即使在最精密的科学中，也不可能不 偶尔冒点风险去引进一个基本上全新的概念 ”
20 sin
2

2
其中 称为电子的Compton波长。

第1章-量子力学的诞生PPT课件

第1章-量子力学的诞生PPT课件
2。1921年， Einstein 因为对光电效应的研究和数学物理 理论的卓越贡献而获奖。
1907年， Einstein 和Debye把能量不连续的概念应用于 固体物理中原子的振动，成功地解决了当温度T->0K时， 固体比热趋于零的现象。
2021/3/12
18
量子理论突破2-原子结构
2021/3/12
2021/3/12
6
2021/3/12
7
2021/3/12
8
量子理论的突破1-黑体辐射
黑体：能吸收射到其上的全部辐射的物体，这 种物体就称为绝对黑体，简称黑体。
黑体辐射：由这样的空腔小孔 发出的辐射就称为黑体辐射。
辐射热平衡状态: 处于某一温 度 T 下的腔壁，单位面积所 发射出的辐射能量和它所吸 收的辐射能量相等时，辐射 2达021到/3/1热2 平衡状态。
1. 成绩构成 平时成绩*50% + 期末成绩*50% 平时成绩：期中考试成绩 + 作业
2. 答疑每周一次
2021/3/12
3
什么是量子力学
2021/3/12
4
几点要求：
1. 作业必须交：做习题是理论物理课程的实验课。
2. 课前预习和课后的复习。
2021/3/12
5
The size of things
2.电子的能量只是与光的频率有
关，与光强无关，光强只决定电
子数目的多少。按照光的电磁理
论，光的能量只决定于光的强度
2021/3/12
13
而与频率无关。
实验发现光电效应有两个特征：
1.临界频率v0: 只有当光的频率 才有光电子发射出来。
大于某一定值v0 时，
2.电子的能量只是与光的频率有关，与光强无关，光强只

chapter1总结.ppt

chapter1总结.ppt

假设Ⅴ：Pauli原理
§ 1.2 量子力学在简单体系中的应用
一维势箱

n (x)
2 l
sin
n
l
x；En
n2h2 8ml 2
(0 x l；n 1,2,3)
立方势箱
nz,ny,nz (x, y, z)
8 a3
sin
nx
a
x
sin
ny
a
y sin
nz
a
z；
Enz , ny , nz
h2 8ma2
(nx2
ny2
nz2 )
(0 x, y, z a；nx , ny , nz 1,2,3 )
简并能级；简并态；简并度
第二章 原子结构和性质
Chapter 2 The structure and properties of atoms
例题：
• 1.微观粒子体系的定态波函数所描述的状态 是（ ）
• A. 波函数不随时间变化的状态 • B．几率密度不随时间变化的状态 • C. 自旋角动量不随时间变化的状态 • D. 粒子势能为零的状态
• (北师大) 简答: 1.波函数的合格条件
•
2. Pauli原理
• 选择：1.一维谐振子的势能表达式 为 V 1 kx2 ，则该体系的定态S方程式中
2
的哈密顿算符为（ ）
原子光谱
-Bohr “玻尔假说”
2. 实物粒子的波粒二向性
粒 子 性
= h v 波
动
p= h /λ 性
h h
p mv
德布罗意(de Broglie)波长
3. 物质波统计解释
玻恩（Born）提出实物微粒波的统计解释 －几率波

量子力学课件(完整版)

量子力学课件(完整版)

Light beam
metal
electric current
11
能量量子化的假设
造成以上难题的原因是经典物理学认为 能量永远是连续的。
如果能量是量子化的，即原子吸收或发 射电磁波，只能以“量子”的方式进行， 那末上述问题都能得到很好的解释。
12
能量量子化概念对难题的解释
原子寿命 ①原子中的电子只能处于一系列分立的能级之中。
18
当 kT hc（高频区）
E(, T)

2hc2 5
e hc
kT
Wein公式
当 kT hc（低频区）
E(, T)

2c 4
kT
Rayleigh–Jeans公式
19
能量量子化概念对难题的解释
对光电效应的解释
如果电子处于分立能级且入射光的能 量也是量子化的，那么只有当光子的能 量（E =hυ）大于电子的能级差，即E =hυ > En－Em时，光电子才会产生。如 果入射光的强度足够强，但频率υ足够 小，光电子是无法产生的。
2 , k 2 / ,
得到 d 2 0,所以，t x(t)
dk 2 m
物质波包的观点夸大了波动性的一面，抹杀 了粒子性的一面，与实际不符。
45
（2）第二种解释：认为粒子的衍射行为是大 量粒子相互作用或疏密分布而产生的行为。 然而，电子衍射实验表明，就衍射效果 而言， 弱电子密度＋长时间＝强电子密度＋短时间 由此表明，对实物粒子而言，波动性体 现在粒子在空间的位置是不确定的，它是以 一定的概率存在于空间的某个位置。
2
这面临着两个问题：
1、信号电磁波所覆盖的区域包括大量的 元件，每个元件的工作状态有随机性，但 器件的响应具有统计性；

量子力学课件完整版(适合初学者)

量子力学课件完整版(适合初学者)
2
利用
得到
E h , p k , h / 2 , 2 , k 2 / ,
d 2 2 0, 所以，t x(t ) dk m
物质波包的观点夸大了波动性的一面，抹杀 了粒子性的一面，与实际不符。
45
（2）第二种解释：认为粒子的衍射行为是大 量粒子相互作用或疏密分布而产生的行为。 然而，电子衍射实验表明，就衍射效果 而言， 弱电子密度＋长时间＝强电子密度＋短时间 由此表明，对实物粒子而言，波动性体 现在粒子在空间的位置是不确定的，它是以 一定的概率存在于空间的某个位置。
37
参考书目
曾谨言《量子力学》，科学出版社 周世勋《量子力学教程》，高等教育出版 社
38
量子力学 第二章 波函数及薛定谔方程
39
2.1 波函数及其统计解释
40
一、自由粒子的波函数
自由粒子指的是不受外力作用，静止或匀速运动 的质点。因此，其能量E 和动量 p pe 都是常量。 根据德布罗意波粒二象性的假设，自由粒子的频 率和波长分别为
4
1.1 经典物理学的困难
5
19世纪末，物理学界建立了牛顿力 学、电动力学、热力学与统计物理， 统称为经典物理学。其中的两个结论 为 1、能量永远是连续的。 2、电磁波（包括光）是这样产生的： 带电体做加速运动时，会向外辐射电 磁波。
6
经典物理学的成就
牛顿力学-支配天体和力学对象的运动； 杨氏衍射实验-确定了光的波动性； Maxwell方程组的建立-把光和电磁现象建立在 牢固的基础上； 统计力学的建立。
46
3、概率波
粒子的波动性可以用波函数来表示， 其中，振幅 ( x, y, z) | ( x, y, z) | ei ( x, y,z ) 表示波动在空间一点(x,y,z)上的强弱。 | ( x, y, z) |2 应该表示粒子出现在点 所以， (x,y,z)附近的概率大小的一个量。 因此，粒子的波函数又称为概率波。

清华大学 大学物理 普通物理量子力学(1)PPT课件

清华大学 大学物理 普通物理量子力学(1)PPT课件
l0,1,2,;ml,l1,,0,,l1,l
正交、归一化条件：
2
d sin d Y l*m (,)Y lm (,)llm m
00
Y lm (, )Nlm (P co )eim s
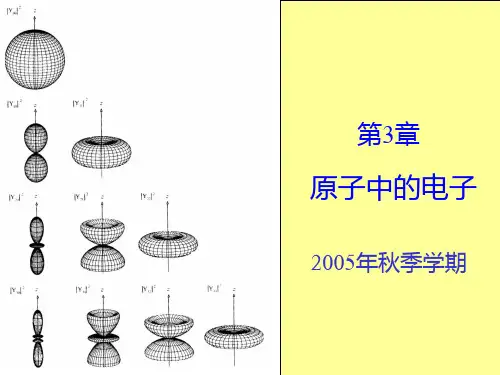
当l=0,1,2时的球谐函数：
Y00
1
4
Y10
3 cos 4
Y11
3 sinei 8
Y20
5 (3cos21) 15
因而其空间的取向是量子化的。
Lz z（ B ）
例如：l = 2，m0,1, 2
2
L
L 2(21) 6
0
Lz0, , 2
2
L只有五种可能的取向。
对 z 轴旋转对称
【例】求解 Lˆ z 的本征值问题。
Lˆz Lz
idd()Lz()
d()
i Lzd
通解为
()
i
Ae
Lz
下面用波函数所满足的条件，定特解。
( )应该单值：
e e e e iLz
i Lz(2π)
i Lz
i Lz2π
i
e Lz 2π 1
2Lz
m2π
本征值： Lz m ,m0， 1， 2， …
归一化因子
本征波函数： ()Aiem 1 eim 2
【思考】设某体系绕对称轴转动（平面转子），转动 惯量为I，求该体系的转动能量和波函数。
§3.2 氢原子的量子力学处理 一、氢原子光谱的实验规律
Y21
15sincosei 8
Y22
15 sin2e2i 32
二、角动量的空间量子化 （space quantization）
角动量的大小为：
L l(l 1) ，l = 0, 1, 2, 3, …
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

核式模型
1913年
丹麦 玻尔
氢原子理论的建立
从此原子说迅速发展，1900年普朗克提出量子论
1924-1927年
建立了量子力学，原子物理在 量子力学的基础上日益完善。
原子的质量与大小：
1、原子的质量
原子的绝对质量（以碳原子为例：碳原子的原子量为12，1mol
碳原子的总质量为12克）
MA
A NA
12103 6.021023
1、南大，柯善哲等《量子力学》；蔡建华《量子力学》 2、复旦，苏汝铿《量子力学》；周世勋《量子力学教程》 3、北大，曾谨言《量子力学》(卷 I)；《量子力学导论》
英文教科书
1、 D. J. Griffiths, Introduction to Quantum Mechanics 2.、W. Greiner, Quantum Mechanics – An Introduction
真正从实验上确定电子的存在，是在1897年由汤姆逊
作出的。
• D、E之间加上电场后射线发生偏移，可判断阴极射线带负电。 在放电管周围加磁场，可使束点由P2回到P1。磁力与电力大小相 等，方向相反。
Hev Ee
可得阴极射线速度
vE/H
• 去掉电场，由于磁力作用，射线将构成一圆形轨道，若半径为 r ，则射线内的粒子（质量为）受到的离心力为
r
3
N
A
A
，所以
由此可得原子的半径公式：
r 3 3A
4 N A
元素 Li Al Cu S Pb
质量数A 7 27 63 32 207
质量密度 0.7 2.7 8.9 2.07 11.34
原子半径 r/nm 0.16 0.16 0.14 0.18 0.19
布朗运动与佩林实验：
1827年，苏格兰植物学家R·布朗发现水中的花粉及其它悬 浮的微小颗粒不停地作不规则的曲线运动，称为布朗运动。 1877年，J·德耳索提出这些微小颗粒是受到周围分子的不 平衡的碰撞而导致的运动。 1905年，爱因斯坦导出布朗运动平均自由程公式，并给出 了测量阿伏伽德罗常数的方法 1908年，法国物理学家佩林实验证实，并测量出阿常数
量子力学
参考书
1、《窥探上帝的秘密：量子史话》 作者：杨建邺 2、《寻找薛定谔的猫》 作者：（美）格里宾 翻译：张广才 3、《量子纠缠》 作者：（美）克莱格 翻译：刘先珍 4、《量子世界-写给所有人的量子物理》作者：(美)福特 译: 王菲 5、《量子史话》 作者：（美）霍夫曼 翻译：马元德
中文教科书
布朗运动也就成为原子分子论的有力实验证据，并成为 分子运动论和统计力学发展的基础。
Ludwig Edward Boltzmann，玻尔兹曼坚信原子 分子的存在，并建立了分子运动论，于1906年 自杀身亡。
§2 电子的发现
1874年斯通尼明确指出：原子所带电荷为一基本电荷的 整数倍，1891年提出用“电子”这一名字来命名电荷的 最小单位。并通过阿伏加德罗常数推算出这一基本电荷 的近似值。
1.981026 kg
法拉第电解定律
原子量的单位： u=碳原子质量/12=MA/12 2、原子的大小
密里根油滴实验
对于任一种原子，1mol原子的质量为A克，包含有NA个原子。
假定该原子的质量密度为ρ(g/cm3)，那么A克原子的总体积为 A/
假如单原子体积为（r为原子半径）则 4 r 3
3
4 3
F mv2 r
离心力与磁力相平衡 Hev mv2 / r
由此可得射线内粒子的荷质比
e v m rH
电子的电荷和质量
电子电荷的精确测定是在1910年由密立根通过著名的“密 立根油滴实验”作出的。当时的测定值为
主张物质不可无限分割
主张物质可以无限分割
我国 外国
战国时期的墨家《墨经》 战国时期的儒家《中庸》
古希腊物理学家德谟克利特 提出原子这一概念并把它当
作物质的最小单元
战国时期的公孙龙 “一尺之棰，日取其半，万世不竭
”
同时代的亚里士多德等认为物质 是连续的，可以无限分割
19世纪人们开始认识到，原子只是物质结构的一个 层次，导致这一结论的重要发现有：
时间 1666年 1806年 1807年 1808年 1811年 1826年 1833年
人物
重要发现
英国 牛顿
光谱：为以后研究原子提供国 道尔顿
化学上的倍比定律，并提出原子论
法国 盖.吕萨克 意大利 阿伏伽德罗
英国 布朗
气体化合的简比定律
阿伏伽德罗假说：同体积气体在 同温同压下分子数相同。
量子力学的前导课程：
普通物理；理论力学；电动力学；统计力学 微积分；常微分方程；偏微分方程；线性代数
量子力学所涉及的哲学问题：
1.决定论：自然规律是偶然的还是严格决定性的？ 2.局域性/可分离性：相互作用都是局部性的还是有超距的？ 3.因果律 4.现实性 5.完全性：存在一个万有理论吗？
目录
第一章 量子力学的诞生背景--实验基础 第二章 量子力学原理(I)--波函数和 Schrodinger 方程 第三章 量子力学原理(II)--力学量算符 第四章 量子力学的三维形式--中心力场 第五章 量子力学理论的表示--态和力学量表象 第六章 量子力学的应用(I)--电子自旋与角动量 第七章 量子力学的应用(II)--微扰与变分方法 第八章 量子力学的应用(III)--电磁场中的粒子 第九章 量子力学原理(III)--全同粒子系 第十章 量子力学的应用(IV)—量子跃迁 第十一章 量子力学的应用(V)—散射
第一章 量子力学的诞生背景
§1 物质的原子性 §2 电子的发现 §3 原子的核式结构 §4 光的波粒二象性 §5 原子态的量子化 §6 实物粒子的波粒二象性
§1 物质的原子性
原子学说的建立：“原子”一词来自希腊文，意思是
“不可分割的”。严复在翻译《穆勒名学》一书时，首 次把“原子”一词介绍到我国，当时他把“Atom”译为 莫破，把“Atom Theory”译为莫破质点论。
布朗运动
英国 法拉第
提出电的基本单元存在
以上为物质微粒说---原子说的诞生创造了条件
1867年 俄国 门捷列夫
元素周期表
1885年 瑞士 巴耳末
氢光谱规律
1887年 德国 赫兹
光电效应
1895年 荷兰 伦琴
X射线
1896年 法国 贝克勒尔
放射性
1897年 英国 汤姆逊
证明电子的存在
1911年 英国 卢瑟福