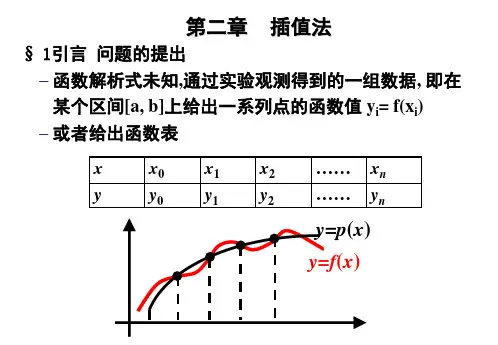
插值法

插值法的最简单计算公式全文共四篇示例，供读者参考第一篇示例：插值法是一种常用的数值计算方法，用于通过已知数据点推断出未知数据点的值。

在实际问题中，往往会遇到数据点不连续或者缺失的情况，这时就需要通过插值法来填补这些数据点，以便更准确地进行计算和分析。

插值法的最简单计算公式是线性插值法。

线性插值法假设数据点之间的变化是线性的，通过已知的两个数据点来推断出中间的未知数据点的值。

其计算公式为：设已知数据点为(x0, y0)和(x1, y1)，需要插值的点为x，其在(x0, x1)之间，且x0 < x < x1，插值公式为：y = y0 + (y1 - y0) * (x - x0) / (x1 - x0)y为插值点x对应的值，y0和y1分别为已知数据点x0和x1对应的值。

通过这个线性插值公式，可以方便地计算出中间未知点的值。

举一个简单的例子来说明线性插值法的应用。

假设有一组数据点为(1, 2)和(3, 6)，现在需要插值得到x=2时的值。

根据线性插值公式，我们可以计算出：y = 2 + (6 - 2) * (2 - 1) / (3 - 1) = 2 + 4 * 1 / 2 = 2 + 2 = 4当x=2时，线性插值法得到的值为4。

通过这个简单的例子，可以看出线性插值法的计算公式的简单易懂，适用于很多实际问题中的插值计算。

除了线性插值法，还有其他更复杂的插值方法，如多项式插值、样条插值等，它们能够更精确地拟合数据并减小误差。

在一些简单的情况下，线性插值法已经足够满足需求，并且计算起来更加直观和方便。

在实际应用中，插值法经常用于图像处理、信号处理、数据分析等领域。

通过插值法，可以将不连续的数据点连接起来，填补缺失的数据，使得数据更加完整和连续，方便后续的处理和分析。

插值法是一种简单而有效的数值计算方法，其中线性插值法是最简单的计算公式之一。

通过这个简单的公式，可以方便地推断出未知数据点的值，并在实际应用中发挥重要作用。

插值法是一种通过已知数据点来估计未知数据点值的方法。

最简单的插值方法之一是线性插值，其公式如下：
对于两个已知数据点 (x1, y1) 和 (x2, y2)，要找到在 x 轴上位于 x1 和 x2 之间的某个点 x 的对应 y 值，线性插值的计算公式为：
\[ y = y1 + \frac{(x - x1)}{(x2 - x1)} \times (y2 - y1) \]
如果将这个表达式简化一下，可以得到：
\[ y = m(x - x1) + y1 \]
其中 m 是斜率，计算方式为：
\[ m = \frac{y2 - y1}{x2 - x1} \]
更一般地，对于多项式插值，比如拉格朗日插值或牛顿插值等，公式会更复杂，涉及更多的数据点和高阶多项式函数。

但在线性插值的情况下，上述公式是最基本且易于理解的插值计算方法。

插值法的最简单计算公式全文共四篇示例，供读者参考第一篇示例：插值法是数值分析领域中常用的一种方法，它可以用来估计未知函数在给定点处的值。

插值法的基本思想是基于已知数据点，构建一个多项式函数来逼近未知函数的值。

在实际应用中，插值法常常被用来对离散数据进行平滑处理，或是用来预测未来的数据。

最简单的插值方法之一是线性插值法。

线性插值法假设未知函数在两个已知数据点之间是线性变化的，即可以通过这两个点之间的直线来估计未知函数在中间点处的值。

线性插值的计算公式如下：设已知数据点为(x0, y0)和(x1, y1)，要估计中间点x处的函数值y，则线性插值公式为：\[y = y0 + \frac{x - x0}{x1 - x0} * (y1 - y0)\]这个公式的推导比较简单，可以通过代入已知数据点计算出来。

如果已知数据点为(0, 1)和(2, 3)，要估计在x=1处的函数值，根据线性插值公式，计算如下：在x=1处的函数值为2。

线性插值法的优点是简单易懂，计算速度快，并且可以比较精确地估计函数值。

但是线性插值法的精度受限于已知数据点之间的线性关系，如果函数在两个数据点之间发生了急剧变化，线性插值法可能无法准确估计函数值。

除了线性插值法，还有许多其他更复杂的插值方法，如拉格朗日插值、牛顿插值、三次样条插值等。

这些方法在不同的情况下可以提供更精确的函数估计值，但也需要更复杂的计算步骤。

插值法是一种常用的数值分析方法，可以帮助我们更好地处理数据和预测未知函数的值。

在实际应用中，可以根据具体情况选取合适的插值方法来进行计算。

第二篇示例：插值法是一种用于估算未知数值的方法，它基于已知数据点之间的关系进行推断。

在实际应用中，插值法经常用于数据处理、图像处理、数学建模和预测等领域。

插值法的计算公式通常比较复杂，但是我们可以通过简化的方式来理解和计算插值结果。

最简单的插值方法之一是线性插值法。

在线性插值法中，我们假设已知数据点之间的关系是线性的，然后通过线性方程来估算未知点的数值。

插值法考核原理
插值法的原理是根据等比关系建立一个方程，然后解方程计算得出所要求的数据。

具体来说，假设与A1对应的数据是B1，与A2对应的数据是B2，A 介于A1和A2之间，已知与A对应的数据是B，则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A的数值。

此外，插值法也称为内插法，是利用函数f(x)在某区间中插入若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f(x)的近似值。

如果这特定函数是多项式，就称它为插值多项式。

插值法的原理也可以理解为数学内插法，即直线插入法。

其原理是若
A(i1,b1),B(i2,b2)为两点，则点P(i,b)在上述两点确定的直线上。

而工程上常用的为i在i1,i2之间，从而P在点A、B之间，故称直线内插法。

数学内插法说明点P反映的变量遵循直线AB反映的线性关系。

如需了解更多关于插值法考核原理的信息，建议查阅数学类书籍或咨询数学专家。

插值法的研究及应用插值法是数值计算中常用的一种方法，其主要作用是利用已知数据的特征来估计未知数据的情况。

插值法的研究和应用在各个领域都有着重要的作用，下面我们将从定义、应用和优缺点三个方面来展开讨论。

1. 定义插值法是一种数值分析方法，采用给定的数据点构造一个插值函数，使该函数能够通过已知的数据点并且在未知的数据点上具有平滑性。

插值法通常用于研究样本数据，通过样本数据预测未来或者未知数据点的值。

插值法根据不同的逼近函数可以分为拉格朗日插值法、牛顿插值法、分段插值法等。

在实际应用中，由于样本数据的种类各异，选择适合的插值法对于保证插值函数的准确性至关重要。

2. 应用插值法是数值计算中非常常见的技术，可以应用于各个领域。

以下是插值法在某些领域的具体应用：2.1. 数学在数学中，插值法可以用于实现函数逼近和积分计算等。

例如在微积分中，为了计算某个函数的面积或者弧长，我们需要拟合出该函数的近似函数。

往往要借助于插值法来完成这个任务。

此外，插值法还在微积分中发挥着重要作用，比如根据已知点分段拟合一阶或者二阶函数，从而计算导数或者曲率等数学概念。

2.2. 工程在工程学上，插值法的应用十分广泛。

例如在测量上，经常需要通过记录的数据点建立精准的计量模型。

插值法可以将稀疏的测量数据处理成一系列流畅的数据点，有助于更好地理解测量数据。

在通信领域，插值法还可以用于数字信号的重构和平滑。

通过将采样后的离散信号插值到连续信号中，我们可以得到更精细的信号波形，从而更准确地还原信号。

3. 优缺点3.1. 优点插值法的主要优点在于其简单易懂、易于实现。

在数值计算中，插值法是一种非常重要的技术，可以快速而有效地分析大量数据。

此外，插值法能够通过现有数据点得到平滑的插值函数，从而减少了数据误差并且提高了计算精度。

3.2. 缺点然而，插值法也有着一些缺点。

首先，插值函数的精度大大依赖于已知数据的数量和分布。

如果样本数据缺乏一定的数量，可能会导致插值函数的精度下降。

插值法计算公式例子
插值法计算公式
数学内插法即“直线插入法”。

其原理是，若A（i1，b1），B（i2，b2）为两点，则点P（i，b）在上述两点确定的直线上。

而工程上常用的为i在i1，i2之间，从而P在点A、B之间，故称“直线内插法”。

数学内插法说明点P反映的变量遵循直线AB反映的线性关系。

上述公式易得。

A、B、P三点共线，则：（b-b1）/（i-i1）=（b2-b1）/（i2-i1）=直线斜率，变换即得所求。

内插法原理
内插法原理：学内插法即“直线插入法”。

其原理是，若
A(i1,b1),B(i2,b2)为两点，则点P(i,b)在上述两点确定的直线上。

内插法
内插法又称插值法。

根据未知函数f（x）在某区间内若干点的函数值，作出在该若干点的函数值与f（x）值相等的特定函数来近似原函数f （x），进而可用此特定函数算出该区间内其他各点的原函数f（x）的近似值，这种方法，称为内插法。

按特定函数的性质分，有线性内
插、非线性内插等；按引数（自变量）个数分，有单内插、双内插和三内插等。

线性内插是假设在二个已知数据中的变化为线性关系，因此可由已知二点的座标(a, b)去计算通过这二点的斜线。

通俗地讲，线性内插法就是利用相似三角形的原理，来计算内插点的数据。

插值法的简化公式插值法是一种用于在有限数据点之间计算函数值的数学方法。

在插值法中，我们使用一些中间值来代替未观测到的数据点，从而构建出一个函数来拟合数据。

插值法有许多不同的形式，其中最常见的是线性插值、二次插值和三次插值等。

在线性插值中，我们使用一个线性函数来拟合数据点。

具体来说，我们可以用以下公式来计算线性插值函数:f(x) = a0 + a1*x其中，a0 和 a1 是拟合函数的两个系数，而 x 是我们要计算的自变量。

这个公式可以帮助我们在数据点之间计算函数值，特别是当我们只有很少的数据点时，线性插值法可以很好地拟合数据并帮助我们预测未观测到的结果。

在二次插值中，我们使用一个二次函数来拟合数据点。

具体来说，我们可以用以下公式来计算二次插值函数:f(x) = a0*x^2 + a1*x + a2其中，a0、a1 和 a2 是拟合函数的三个系数，而 x 是我们要计算的自变量。

与线性插值法不同，二次插值法可以更好地拟合陡峭的曲线，因此在处理一些复杂的函数时非常有用。

在三次插值中，我们使用一个三次函数来拟合数据点。

具体来说，我们可以用以下公式来计算三次插值函数:f(x) = a0*x^3 + a1*x^2 + a2*x + a3其中，a0、a1、a2 和 a3 是拟合函数的四个系数，而 x 是我们要计算的自变量。

三次插值法可以更好地拟合复杂的曲线，并且比二次插值法更具鲁棒性，因此在处理一些高度复杂的函数时非常有用。

无论是线性插值、二次插值还是三次插值，插值法的核心思想就是使用一些中间值来代替未观测到的数据点，从而构建出一个函数来拟合数据。

这些公式可以帮助我们在数据点之间计算函数值，特别适用于当我们只有很少的数据点时。

插值法是如何计算的插值法的计算原理【2017-2018最新会计实务】【2017-2018年最新会计实务经验总结，如对您有帮助请打赏！不胜感激！】插值法是计算实际利率的一种方法.是使未来现金流量现值等于债券购入价格的折现率.插值法(或称插插补法、内插法)是财务分析和决策中常用的财务管理方法之一. 插值法的原理是根据比例关系建立一个方程,然后,解方程计算得出所要求的数据.假设与A1对应的数据是B1,与A2对应的数据是B2,现在已知与A对应的数据是B,A介于A1和A2之间,则可以按照(A1-A)/(A1-A2)=(B1-B)/(B1-B2)计算得出A 的数值,其中A1、A2、B1、B2、B都是已知数据.验证如下:根据:(A1-A)/(A1-A2)=(B1-B)/(B1-B2)可知:(A1-A)=(B1-B)/(B1-B2)×(A1-A2)A=A1-(B1-B)/(B1-B2)×(A1-A2)=A1+(B1-B)/(B1-B2)×(A2-A1)例如某人向银行存入5000元,在利率为多少时才能保证在未来10年中每年末收到750元?5000/750=6.667 或 750*m=5000 查年金现值表 i=8%,系数为6.710 i=9%,系数为6.418 说明利率在8%-9%之间,设为x%(x%-8%)/(9%-8%)=(6.667-6.71)/(6.418-6.71)计算得出 x=8.147.后语点评：会计学作为一门操作性较强的学科、每一笔会计业务处理和会计方法的选择都离不开基本理论的指导。

为此，要求我们首先要熟悉基本会计准则，正确理解会计核算的一般原则，并在每一会计业务处理时遵循一般原则的要求。

会计学的学习，必须力求总结和应用相关技巧，使之更加便于理解和掌握。

学习时应充分利用知识的关联性，通过分析实质，找出核心要点。

要深入钻研，过细咀嚼，独立思考，切忌囫囵吞枣，人云亦云，随波逐流，粗枝大叶，浅尝辄止。