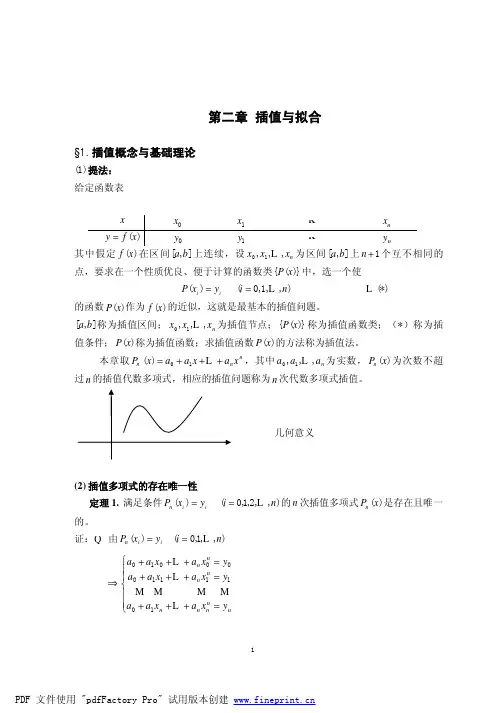
当前位置：文档之家 › 计算方法 插值法(一)

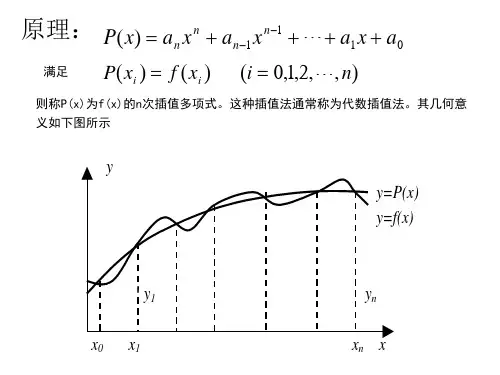
计算方法 插值法(一)

  • 格式：ppt
  • 大小：1.74 MB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

计算方法 1插值方法

计算方法 1插值方法
1.1 问题的提法
1. 插值问题 函数y=f(x)给出一组函数值 yi f ( xi ) ,
x: y: x0 x1 x2 …… xn y0 y1 y2 …… yn
i 0,1,, n
其中x0 ,x1,x2 ,…,xn是区间[a,b]上的互异点，要构造一个简 单的函数 p(x) 作为f (x)的近似表达式，使满足 p(xi ) yi , i 0,1, ,n (插值原则、插值条件 ) 这类问题称为插值问题。 p(x)-----f (x)的插值函数, f (x) -----被插值函数 x0 ,x1,x2 ,…,xn -----插值节点 求插值函数的方法称为插值法。 若x∈[a,b]，需要计算f (x) 的近似值p(x),则称 x为插值点。
同理可得
( x x0 )( x x2 ) l1 ( x ) ( x1 x0 )( x1 x2 )
( x x0 )( x x1 ) l2 ( x) ( x2 x0 )( x2 x1 )
于是求得
p2 ( x) y0 l0 ( x) y1l1 ( x) y2 l2 ( x)
1 线性插值----n=1时的代数多项式插值
已知f(x0 )=y0 ，f(x1)=y1 , x0≠x1 要构造线性函数 p1(x) ,使它满足插值条件 p1(x0)=y0 , p1(x1)=y1 .
x y x0 y0 x1 y1
y1 y0 p1 ( x ) y0 ( x x0 ) （线性插值多项式） x1 x0 x x0 x x1 p1 ( x ) y0 y0 y0 l0 ( x ) y1 l1 ( x ) x0 x1 x1 x （拉格朗日线性插值多项式）
且lj (x) (j=0,1,2)，是一个二次函数.

计算方法 插值法Lagrange插值

计算方法 插值法Lagrange插值
xi , i 0,1,..., n
的n次插值基函数
以n+1个n次基本插值多项式lk(x)(k 0,1, … , n) 为基础，可直接写出满足插值条件
P(xi ) f(x i ) (i 0,1,2, … , n)
的n次代数插值多项式：
P(x) l0(x)y 0 l1(x)y1 … ln(x)yn
B(x1, f(x1))
x0
x1
由解析几何知道,这条直线用点斜式表示为
改写为
p(x)
y0
y1 x1
y0 x0
(x
x0)
p(x)
x x1 x0 x1
y0
x x0 x1 x0
y1
为了便于推广，记
推导
l0(x)
x x1 , x0 x1
l1(x )
x x0 x1 x0
线性插值 基函数
或者写成：
(i 0,1,2)
其几何意义是用经过3个点
(x0, y0 ), (x1, y1), (x2, y2 )
的抛物线 y P(x) 用以近似计算 y f(x)
y=f(x)
y
y = L 2 (x)
y0
y1
x0
x1
y2 x
x2
P(x)的系数 a0 , a1, a2 直接由插值条件决定，即
a0 , a1, a2 满足代数方程组：
(x 0 x1)(x 0 x2 )
从而导出 l0(x)
(x (x 0
x1)(x x2 ) x1)(x 0 x2 )
类似地可以构造出插值多项式 l1(x )和l2 (x )
于是确定了3个抛物插值的基函数：
l0(x)
(x (x 0
x1)(x x1)(x

[转载]插值算法（一）：各种插值方法比较

[转载]插值算法（一）：各种插值方法比较

[转载]插值算法（⼀）：各种插值⽅法⽐较原⽂地址：插值算法（⼀）：各种插值⽅法⽐较作者：稻草⼈确定性随机性确定性随机性趋势⾯（⾮精确）回归（⾮精确）泰森（精确）克⾥⾦（精确）密度估算（⾮精确）反距离权重（精确）薄板样条（精确）整体拟合利⽤现有的所有已知点来估算未知点的值。

局部插值使⽤已知点的样本来估算位置点的值。

确定性插值⽅法不提供预测值的误差检验。

随机性插值⽅法则⽤估计变异提供预测误差的评价。

对于某个数据已知的点，精确插值法在该点位置的估算值与该点已知值相同。

也就是，精确插值所⽣成的⾯通过所有控制点，⽽⾮精确插值或叫做近似插值，估算的点值与该点已知值不同。

1、反距离加权法（Inverse Distance Weighted）反距离加权法是⼀种常⽤⽽简单的空间插值⽅法，IDW是基于“地理第⼀定律”的基本假设:即两个物体相似性随他们见的距离增⼤⽽减少。

它以插值点与样本点间的距离为权重进⾏加权平均，离插值点越近的样本赋予的权重越⼤，此种⽅法简单易⾏，直观并且效率⾼，在已知点分布均匀的情况下插值效果好，插值结果在⽤于插值数据的最⼤值和最⼩值之间，但缺点是易受极值的影响。

2、样条插值法（Spline）样条插值是使⽤⼀种数学函数，对⼀些限定的点值，通过控制估计⽅差，利⽤⼀些特征节点，⽤多项式拟合的⽅法来产⽣平滑的插值曲线。

这种⽅法适⽤于逐渐变化的曲⾯，如温度、⾼程、地下⽔位⾼度或污染浓度等。

该⽅法优点是易操作，计算量不⼤，缺点是难以对误差进⾏估计，采样点稀少时效果不好。

样条插值法⼜分为张⼒样条插值法（Spline with Tension）规则样条插值法（Regularized Spline）薄板样条插值法 (Thin-Plate Splin)3、克⾥⾦法（Kriging）克⾥⾦⽅法最早是由法国地理学家Matheron和南⾮矿⼭⼯程师Krige提出的，⽤于矿⼭勘探。

这种⽅法认为在空间连续变化的属性是⾮常不规则的，⽤简单的平滑函数进⾏模拟将出现误差，⽤随机表⾯函数给予描述会⽐较恰当。

插值法

插值法


i 0 i j
n
x x
j
x xi
i
将 l j ( x)代入
P P
n
( x) l j ( x) y
j 0
n
j
中得
n
( x)
j 0 n
n
( x x0)(x x1)...(x x j 1)(x x j 1)...(x xn ) ( x j x0)( x j x1)...(x j x j 1)( x j x j 1)...(x j xn )y
于是
(x-x1)(x-x2) (x-x0)(x-x2) (x-x0)(x-x1) P2(x)=-----------------y0 + -----------------y1 + ------------------y2 ...(6) (x0-x1)(x0-x2) (x1-x0)(x1-x2) (x2-x0)(x2-x1)
而ai(i=0,1,2,…,n)的系数行列式是Vandermonde行 列式
1 V( x0 , x1 ,...,x n ) 1 ... 1
n i 1
x x x x
0 1
2 0 2
... ... ... ...
1
x x x
n 0 n
1
...
n
...
2 n
...
n n
x x
i
=
( x x )
0.01892 =0.314567+ ——— (0.0167) =0.330365 . 0.02
其截断误差得
其中 M 2

R1 ( x)
// 1
M
2

计算方法Chapter01 - 插值方法

计算方法Chapter01 - 插值方法

若函数族
中的函数 ( x) 满足条件
( xi ) = f ( xi ),
i = 0,1,, n
（ 1）
n ( x ) x f ( x ) 则称 为 在 中关于节点 i i =0 的一个插值函数。
f ( x) ——被插值函数； [a, b] ——插值区间；
xi in=0 ——插值节点； 式（1）——插值条件.
x12 x1n
2 n x2 x2
范德蒙行列式
x
2 n


n n
V=
x
0 i j n

( x j xi )
10
插值多项式的存在唯一性（续）
V= ( x j xi ) 0 i j n
由于 x0 , x1 , x2 , ..., xn 是 n 1 个互异的节点，即：
求插值函数(x)的问题称为插值问题。
5
插值问题
于是人们希望建立一个简单的而便于计算的函数 (x) 使其近似的代替 f (x)。
y 被插值函数 f (x) 插值函数 (x)
插值节点 0 x0 x1 x2 x3
… …… xn x
6
插值区间
多项式插值问题
对于不同的函数族Φ 的选择，得到不同的插值问题
( x0 , y0 ) 0
p2(x)
x0
x1
x2
x
19
抛物线插值（续）
p2 ( x ) = y0l0 ( x ) y1l1 ( x ) y2l2 ( x )
( x x1 )( x x2 ) ( x0 x1 )( x0 x2 )
( x x0 )( x x2 ) ( x1 x0 )( x1 x2 ) ( x x0 )( x x1 ) ( x2 x0 )( x2 x1 )

数值计算方法第四章插值1

数值计算方法第四章插值1

代数插值
代数插值
当f(x)是次数不超过n的多项式时,给定n+1个节点,其n次插值多项式就是f(x)本身.
代数插值几何意义
拉格朗日插值 逐次线性插值 牛顿插值 等距节点插值 反插值 埃尔米特插值 分段插值法 三次样条插值
拉格朗日插值 线性插值
格朗日插值 抛物线插值
基函数之和为1.
拉格朗日插值 n次插值
当插值点x∈(a,b)时称为内插，否则称为外插。
内插的精度高于外插的精度。
拉格朗日插值余项
余项 设函数f(x)在包含节点x0 , x1 ,…, xn的区间[a,b]上有n+1阶导数，则
拉格朗日插值
活动14
写出3次拉格朗日插值多项式及余项
拉格朗日插值
拉格朗日插值
作业5
已知函数表
应用拉格朗日插值公式计算f(1.300)的近似值.
数值计算方法
苏 强
江苏师范大学连云港校区
数学与信息工程学院 E-mail: 412707233@
数值计算方法 第四章 插值与曲线拟合
没有明显的解析表达式
使用不便的解析表达式
简单函数代替
插值问题
插值问题
代数插值 插值函数
被插值函数 插值节点
插值区间
三角多项式插值 有理函数插值
代数插值
抛物线插值
三点插值
拉格朗日插值 抛物线插值
抛物线插值
三点插值
拉格朗日插值 抛物线插值
拉格朗日插值 n次插值
称为关于节点
的n次插值基函数.
拉格朗日插值n次插值
基函数的个数等于节点数.
n+1个节点的基函数是n次代数多项式 基函数和每一个节点都有关。节点确定，基函数就唯一的确定。 基函数和被插值函数无关

插值法例题计算过程

插值法例题计算过程摘要：1.插值法的基本概念和应用场景2.插值法的计算步骤和注意事项3.插值法在财务管理中的实际运用案例4.插值法在实际问题中的优缺点分析正文：插值法是一种数学方法，通过在已知数据点之间构建插值函数来逼近或预测未知数据。

在财务管理等领域具有广泛的应用。

接下来，我们将详细介绍插值法的计算步骤，并通过一个实际案例来说明其应用。

一、插值法的基本概念和应用场景插值法是基于已有的数据点（如(x1, y1)，(x2, y2)，(xn, yn)）来构造一个插值函数，以便在未知点处预测函数值。

插值法可以应用于诸如财务管理等领域，解决诸如净现值计算等问题。

二、插值法的计算步骤和注意事项1.确定插值函数：根据已知数据点选择合适的插值函数，如线性插值、二次插值等。

2.构建插值表：将已知数据点代入插值函数，计算出对应的函数值，并构建插值表。

3.插入未知点：将要求的点的横坐标x代入插值函数，得到所求的函数值。

4.注意事项：在选择插值函数时，应注意数据的分布情况，避免出现龙格现象；同时，插值表的密度和精度也直接影响插值结果的准确性。

三、插值法在财务管理中的实际运用案例假设我们有一个投资项目，其净现值随折现率变化而变化。

已知当折现率为12%时，净现值为116530；当折现率为10%时，净现值为121765。

我们可以使用插值法来计算其他折现率下的净现值。

四、插值法在实际问题中的优缺点分析优点：插值法简单易行，计算速度快，适用于大量数据处理。

缺点：插值法的精度受限于已知数据点的质量和分布，以及所选插值函数的类型。

在某些情况下，插值法可能无法很好地逼近真实函数。

总之，插值法作为一种有效的数学方法，在财务管理等领域具有广泛的应用。

通过掌握插值法的计算步骤和注意事项，我们可以更好地解决实际问题。

数值分析与计算方法 第一章 插值法


同 理 ： (t) 至 少 有n 个 互 异 零 点；
(t) 至 少 有n 1 个 零 点 ；
(n1) (t ) 至 少 有 一 个 零 点 ； 即 (a ，b)，
(n1) (
)
R(n1) n
(
)
K ( x)n1(n1) (
)
R(n1) n
(
)
K ( x) (n
1)!
f (n1) ( ) K ( x) (n 1)! 0
x x0 x1 x2 xn ， y f ( x)？ y y0 y1 y2 yn
（1）有的函数没有表达式，只是一种表格函数，而我们需要的 函数值可能不在该表格中。
（2）如果函数表达式本身比较复杂，计算量会很大；
对于这两种情况，我们都需要寻找一个计算方便且表达简单
的函数 P x来近似代替 f ( x)，求 P x 的方法称为插值法。
Ln1( x)
为此我们考虑对Lagrange插值多项式进行改写； ——由唯一性，仅是形式上的变化
期望：Ln ( x) 的计算只需要对Ln1( x)作一个简单的修正.
考虑 h( x) Ln ( x) Ln1( x) h( x) 是次数 n 的多项式，且有
h( x j ) Ln ( x j ) Ln1( x j ) 0 ，j 0 ，1，2 ，L ，n 1 ；
)
3
)
1 2
(x
(
4
6
6
)( x
)(
4
3
)
3
)
1
(
x
6
)(
x
4
)
2
(
3
6
)(
3
4
)
3 2

计算方法 插值法


例见 P.74 例 1。 (2) 差商与牛顿基本插值多项式 考虑到拉格朗日插值的缺点：增加新的结点，需重新计算，工作量较大！ 改进的方向：选取形式： a 0 + a1 ( x − x0 ) + a 2 ( x − x0 )( x − x1 ) + L + a n ( x − x0 )( x − x1 ) L ( x − xn −1 ) ； （称之为 n 次牛顿插值多项式） 记 N n ( x) = a 0 + a1 ( x − x0 ) + a 2 ( x − x0 )( x − x1 ) + L + a n ( x − x0 )( x − x1 ) L ( x − x n −1 ) 为了给出 a i 简明计算表达式，引入差商（或均差）概念。 定义 1.
第二章 插值与拟合
§1.插值概念与基础理论
(1) 提法： 给定函数表 x y = f ( x) x0 y0 x1 y1
K K
xn yn
其中假定 f ( x) 在区间 [a, b] 上连续，设 x0 , x1 , L, x n 为区间 [a, b] 上 n + 1 个互不相同的 点，要求在一个性质优良、便于计算的函数类 {P ( x)} 中，选一个使 P ( xi ) = y i (i = 0,1,L, n) L (*) 的函数 P( x) 作为 f ( x) 的近似，这就是最基本的插值问题。 [a, b] 称为插值区间； x0 , x1 , L, x n 为插值节点； {P ( x)} 称为插值函数类；（*）称为插 值条件； P( x) 称为插值函数；求插值函数 P( x) 的方法称为插值法。 本章取 Pn ( x) = a 0 + a1 x + L + a n x n ，其中 a 0 , a1 , L, a n 为实数， Pn ( x) 为次数不超 过 n 的插值代数多项式，相应的插值问题称为 n 次代数多项式插值。

数值计算方法插值法


f[x1,x2,x3] …
f[x0,x1,x2 ,x3]
例阶2.1差1商求值f(xi)= x3在节点 x=0, 2, 3, 5, 6上的各
解xi :
计算得如下表 f[xi] f[xi,xi+1]
f[xi,xi+1,xi+2 ]
f[xi,xi+1,xi+2 ,xi+2]
00
28
80 4 20
27 8 19 19 4 5
an x0 n an1x0 n1 a1x0 a0 f (x0 )
an x1n
an1
x n1 1
a1x1 a0
f (x1 )
an xn n an1xn n1 a1xn a0 f (xn )
这是惟一一个性关说于明待，定不参论数用何种方法来构a造的0，,n+也a11阶不, 线论性用, 方何an种形式来表示插值多项式,
由线性代数知,任何一个不高于n次的多项式, 都可以表示成函数
1, x x0 , (x x0 )(x x1 ),, (x x0 )(x x1 )(x xn1 )
的线性组合, 也就是说, 可以把满足插值条件 p(xi)=yi (i=0,1,…,n)的n次插值多项式, 写成如下形式
a0 a1(x x0) a2(x x0)(x x1) an (x x0)(x x1)(x xn1)
f[x0 , x1]=
f(x1)- f(x0) x1 – x0
f[x1 , x0]
f(x0)- f(x1) =
x0 – x1
f x0 , x1, x2 f x1, x2 , x0 f x0 , x2 , x1
性质3 若f[x, x0, x1 , …, xk ]是 x 的 m 次多项式, 则 f[x, x0, x1 ,…, xk , xk+1]是 x 的 m-1 次多项式
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9
基本概念:
已知函数表
函数y=插f(值x)不节知点道或很复杂
构造 P(x)，使 P(xi ) yi f (xi ) i 0,1,2,, n
Pn (x)
插值条件 Def：P(x) 是插值函数，f(x)为被插值函数（原函数）
Pn (x) sk sin c (x xk )
三角函数
Pm,n (x)
的插值多项式 Pn (x) a0 a1x a2 x2 an xn 存在且唯一。
当 n 很大时，通过直接解线性方程组求插值多项式不是好方法! 拉格朗日插值、牛顿插值、埃特肯插值、埃尔米特插值、样条插值
12
§ 2.1 拉格朗日插值 /* Lagrange interpolation */
－理论价值大于应用价值 • 此插值问题可表述为如下：
13
2.1.1 线性插值与抛物线插值（由已知节点的数量决定）
一、线性插值－点斜式 已知两个节点 x0 ,x1
问题
已知函数y=f(x)在点x0,x1上的值为y0,y1，求作一次式 L1(x)，使满足条件
L1(x0 ) y0 , L1(x1) y1
× × ×
x0
x1 x2
x3
x4 x
即多项式 Pn(x) 的系数a0，a1，a2，… ，an满足线性方程组
a0 a1 x0 a2 x02 an x0n y0
a0 a1 x1 a2 x12
an x1n
y1
a0 a1 xn a2 xn2 an xnn yn
a0, a1,a2,, an是否有解？是否唯一？
上机作业邮箱：jsff2_nju@
上节课内容
计算方法简介 误差，误差来源，误差估计 数值稳定性/误差的传播和积累 数值计算一些注意原则
浮点数 (float point numbers)
计算机只能代表有限、离散的数字！ 现代计算硬件上用来表示数字的标准方法是二进制
浮点数在计算机上的储存
南京大学大气科学学院《计算方法》
第二章 插值法和数值逼近
授课老师：汪名怀
问题提出:
表示两个变量 x ,y 内在关系一般由函数式 y=f(x) 表示，但在实际问 题中，通常有两种情况：
1 函数解析表达式 f(x) 已知，但函数形式很复杂，不便于计算， 但又需要计算多点处的函数值。
2 实验或测量得到的采样值（函数表），函数 关系式 y=f(x)未知，需要知道非采样点的值。 如果想求不在表上的函数值，怎么办?
构造一个新的 x 与 y 的函数关系式 ŷ = p(x) 代替原函数式 y = f(x) 进行求
解,称为函数逼近,即数据建模过程。
便于计算，精度高
8
函数逼近的两种主要形式：插值、拟合
函数逼近－插值法
是数值分析的基本工具，是数值积分、数值微分、非线性方 程求根和微分方程数值解的重要基础，许多求解计算公式都 是以插值为基础导出的
浮点数的IEEE标准：舍入误差
当x在计算机中要求超过p个尾数位时，引起舍入误差
e* = x* - x （绝对误差）
计算机中的估计值
x*
e* < 2- p * 2E e Machine precision
相对误差 x* - x < 2- p = e
x
更多浮点数的内容见：
https:///wiki/Floating_point#IEEE_754:_floating_point_in_modern_computers
11
1 x0 x02 x0n
V 1 x1 x12
x1n
n1
n
xi x j
(x j xi ) 0
1 xn xn2 xnni0 ji1由Cramer法则可知，
a0,a1,a2,...,an有唯 一解
定理1. 若插值节点 xi x j (i j) ，则满足插值条件 Pn (xi ) yi i 0,1,2,, n
Pm ( x) qn (x)
amxm am1xm1 a1x a0 bnxn bn1xn1 b1x b0
有理函数
非线性
Pn ( x) a0 a1x a2 x2 an xn
代数多项式
10
y
代数多项式P(x) 的是否存在？是否唯一？
×
×
设代数插值多项式为 Pn ( x) a0 a1 x a2 x2 an xn 且满足 Pn (xi ) yi i 0,1,2,, n
上机实习作业
１.提交时间：作业布置下来两周内（如无特殊情况，晚交的作业做 零分处理。有特殊情况的，需要提前得到授课老师许可，一事一议） （一般是周三）。 ２.提交内容：书面报告、源代码、源代码流程图及运行结果截图 ３.源代码要求：简洁、清楚、有较好的注释（助教能够运行程序并 复制结果）。 ４.完成作业要求：鼓励同学之间讨论、合作完成作业，但最终程序、 报告需要自己独立完成。如和别的同学交流过，请在上交作业中列 出一起合作交流过的同学名字。如发现上交作业雷同，雷同作业做 零分处理。 5. 编程语言：尽量选择Fortran或C语言，不建议使用Matlab。
求作次数 n 多项式 Ln (x) ，使满足插值条件
Ln xi yi ,(i 0,1,, n)
即为拉格朗日（Lagrange）插值。
拉格朗日（Lagrange）插值公式的基本思想是：把构造插值多项式 的问题转化为构造n +1个插值基函数li(x)(i=0,1,…, n)。 •插值区间I=[min(x0,x2,…,xn), max] •当所求插值点xI, 称内插(Interpolation) •当所求插值点xI, 称外推(Extrapolation)
符号位
尾数位
这里位数（bit）指一个二进制位
指数位
指数E的范围： [L, U] （基本决定了计算机能代表数字的范围）
浮点数的IEEE标准
现代计算机硬件上的浮点数标准来自IEEE的浮点数算法（采纳于1985）
单精度：１符号位，23尾数位 (~7个十进位数字），及8个指数位 单精度指数位数只有254个不同E值，其中一些位数用来代表一些特 殊数字，如Inf (infinity, 1/0), NaN (Not a number, 0/0, inf/inf) 双精度：１符号位，52尾数位 (~16个十进位数字），及11个指数位