关于分段函数定积分的计算

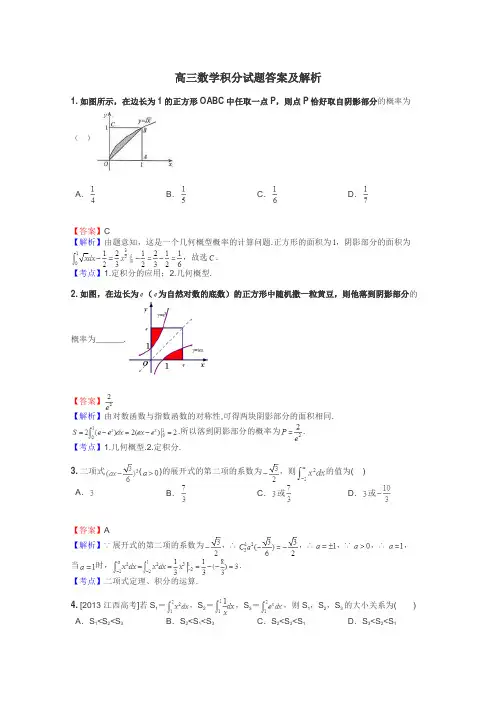
高三数学积分试题答案及解析1.如图所示，在边长为1的正方形OABC中任取一点P，则点P恰好取自阴影部分的概率为（）A．B．C．D．【答案】C【解析】由题意知，这是一个几何概型概率的计算问题.正方形的面积为，阴影部分的面积为，故选．【考点】1.定积分的应用；2.几何概型.2.如图，在边长为（为自然对数的底数）的正方形中随机撒一粒黄豆，则他落到阴影部分的概率为______.【答案】【解析】由对数函数与指数函数的对称性,可得两块阴影部分的面积相同..所以落到阴影部分的概率为.【考点】1.几何概型.2.定积分.3.二项式()的展开式的第二项的系数为，则的值为( ) A．B．C．或D．或【答案】A【解析】∵展开式的第二项的系数为，∴，∴，∵，∴，当时，.【考点】二项式定理、积分的运算.4. [2013·江西高考]若S1＝，S2＝，S3＝，则S1，S2，S3的大小关系为()A．S1<S2<S3B．S2<S1<S3C．S2<S3<S1D．S3<S2<S1【答案】B【解析】S1＝＝x3＝，S2＝＝lnx＝ln2，S3＝＝e x＝e2－e＝e(e－1)>e>，所以S2<S1<S3，故选B.5. [2014·琼海模拟]如图所示，则由两条曲线y＝－x2，x2＝－4y及直线y＝－1所围成图形的面积为________．【答案】【解析】由图形的对称性，知所求图形的面积是位于y轴右侧图形面积的2倍．由得C(1，－1)．同理，得D(2，－1)．故所求图形的面积S＝2{[－－(－x2)]dx＋[－－(－1)]dx}＝2[－]＝2[－(－x)]＝.6.如图，阴影区域是由函数的一段图象与x轴围成的封闭图形，那么这个阴影区域的面积是（）A．B．C．D．【答案】Ｂ【解析】根据余弦函数的对称性可得，曲线从到与x轴围成的面积与从到与轴围成的面积相等，∴由函数的一段图象与轴围成的封闭图形的面积，，故选B．【考点】定积分求面积。

定积分专项训练1、计算定积分⎠⎛01(e x ＋2x)d x = ．2、计算定积分421dx x ⎰= ．3、计算定积分=+⎰-213d )(x x x ．4、计算定积分40(|1||3|)x x dx -+-=⎰ __________.5、计算定积分121(sin )x x dx -+=⎰___________6、计算定积分2)x dx -=⎰_______________．7、设20lg 0()30ax x f x x t dt x >⎧⎪=⎨+⎪⎩⎰…，若((1))1f f =，则a = ．8、曲线22y x =与x 轴及直线1x =所围图形的面积为 ．10、由曲线y =，直线2y x =-及y 轴所围成的图形的面积为 。

11、由直线x=0,3,3==-y x ππ与曲线y=cosx 所围成的封闭图形的面积 。

12、曲线3cos (0)2y x x π=≤≤与坐标轴所围成的面积是________. 13、已知e 是自然对数的底数，⎩⎨⎧≤+>=.0,130,)(x x x e x f x ，计算定积分⎰-42)(x d x f =．14、设0a >.若曲线y =,0x a y ==所围成封闭图形的面积为2a ，则a =______.15、求下列定积分：(1)⎠⎛0a (3x 2－x ＋1)d x (2)⎠⎛12(e 2x ＋1x )d x 解： 解：姓名（）班级（）定积分专项训练1、计算定积分10(2)+⎰x e x dx = 。

被积函数22,x x e x e x ++的原函数为1121200(2)()1)(0).x x e x dx e x e e +=++-+=⎰｜＝(e2、计算定积分421dx x⎰= 。

3、计算定积分=+⎰-21 3d )(x x x ．4、【答案】10 分三段逐一求积分。

5、计算定积分121(sin )x x dx -+=⎰___________【方法总结】1.计算简单定积分的步骤：(1)把被积函数变为幂函数、正弦函数、余弦函数、指数函数与常数的和或差； (2)利用定积分的性质把所求的定积分化为若干个定积分的和或差； (3)分别用求导公式求出F (x )，使得F ′(x )＝f (x )； (4)利用牛顿－莱布尼兹公式求出各个定积分的值； (5)计算所求定积分的值． 2.求定积分的常用技巧：(1)求被积函数，要先化简，再求积分．(2)求被积函数为分段函数的定积分，依据定积分“对区间的可加性”，分段积分再求和．(3)对于含有绝对值符号的被积函数，要先去掉绝对值号才能积分． 6、计算定积分20)x dx -=⎰_______________．【解析】：2dx ⎰等于圆224x y +=在第一象限的面积π，则2222201)22x dx dx xdx x ππ⎡⎤=-=-=-⎢⎥⎣⎦⎰⎰⎰.7、设20lg 0()30ax x f x x t dt x >⎧⎪=⎨+⎪⎩⎰…，若((1))1f f =，则a = ．【思路点拨】分段函数问题通常需要分步进行计算或判断，从1x =算起是解答本题的突破口.【精讲精析】答案：1因为10x =>，所以(1)lg10f ==，又因为230()3af x x t dt x a =+=+⎰，所以3(0)f a =，所以31a =，1a =．8、曲线22y x =与x 轴及直线1x =所围图形的面积为 ． 【答案】23【解析】依题意得知，曲线22y x =与x 轴及直线1x =所围图形的面积为123100222|33x dx x ==⎰.【解析】解：由微积分基本定理，可知由曲线32,x y x y ==围成的封闭图形的面积为12334100111(x x )dx x x |3412-=-=⎰ 10、由曲线y =，直线2y x =-及y 轴所围成的图形的面积为 。

定积分的基本计算方法定积分是微积分中的重要概念，它在各个领域都有着广泛的应用。

在学习定积分的基本计算方法之前，我们首先需要了解定积分的定义和性质。

定积分是对一个区间上的函数进行积分运算，其结果表示该函数在该区间上的“累积效应”。

定积分的计算方法包括定积分的基本性质、定积分的几何意义、定积分的计算公式等内容。

首先，定积分的基本性质是其线性性和可加性。

即定积分具有线性运算和可加性，这使得我们可以通过分段函数的积分来计算复杂函数的定积分。

其次，定积分的几何意义是曲线下面积的计算。

对于给定的函数$f(x)$，其在区间$[a,b]$上的定积分$\int_{a}^{b}f(x)dx$表示函数曲线与$x$轴之间的面积。

这一性质使得定积分在几何和物理问题中有着广泛的应用。

定积分的计算公式包括基本积分公式、换元积分法、分部积分法等。

其中，基本积分公式是我们计算定积分的基础，而换元积分法和分部积分法则是在计算复杂函数的定积分时常用的方法。

在实际应用中，我们经常会遇到一些特殊的函数，如三角函数、指数函数、对数函数等。

针对这些特殊函数，我们需要掌握它们的定积分计算方法，以便能够准确地计算出定积分的值。

除了基本计算方法外，定积分还有一些重要的性质和定理，如定积分中值定理、定积分中的平均值定理等。

这些定理不仅有助于我们理解定积分的概念，还可以帮助我们在实际问题中进行定积分的计算和应用。

总之，定积分的基本计算方法是微积分学习的重要内容，它不仅有着理论上的重要性，还有着广泛的应用价值。

通过对定积分的基本计算方法的学习和掌握，我们可以更好地理解定积分的概念和性质，为将来的学习和工作打下坚实的基础。

定积分复习重点定积分的考查频率不是很高，本讲复习主要掌握定积分的概念和几何意义，使用微积分基本定理计算定积分，使用定积分求曲边图形的面积和解决一些简单的物理问题等． 1.定积分的运算性质1212(1)()()().(2)[()()]()().(3)()()()().bbaab bb aaab c baackf x dx k f x dx k f x f x dx f x dx f x dx f x dx f x dx f x dx =±=±=+⎰⎰⎰⎰⎰⎰⎰⎰为常数其中a<c<b2．微积分基本定理如果()f x 是区间[a ，b]上的连续函数，并且'()()F x f x =，那么()()()baf x dx F b F a =-⎰，这个结论叫微积分基本定理，又叫牛顿—莱布尼兹公式。

3.求定积分的方法（1）利用微积分基本定理就定积分 ①对被积分函数,先简化,再求定积分.例如：230(1-2sin)2d πθθ⎰注：322()3x x '=，(-cos )sin x x '=②分段函数,分段求定积分,再求和.（被积函数中带有绝对值符号时，计算的基本思路就是用分段函数表示被积函数，以去掉绝对值符号，然后应用定积分对积分区间的可加性，分段进行计算）1．计算积分⎰---322|32|dx x x解1. 由于在积分区间]3,2[-上，被积函数可表示为⎩⎨⎧≤<-----≤≤---=--.31,)32(,12,32|32|222x x x x x x x x 所以⎰---322|32|dx x x 13)32()32(312122=-----=⎰⎰---dx x x dx x x .（2）利用定积分的几何意义求定积分如定积分12014x dx π-=⎰，其几何意义就是单位圆面积的14。

（课本P60 B 组第一题） (3)利用被积函数的奇偶性a. 若()f x 为奇函数，则()0aa f x dx -=⎰；b. 若()f x 为偶函数，则0()()a aa f x dx f x dx-=⎰⎰2；其中0a >。

定积分与微积分基本定理教学重点：定积分的概念、定积分的几何意义．求简单的定积分,微积分基本定理的应用教学难点：定积分的概念、求曲边图形面积．一．定积分的概念回忆前面曲边图形面积，变速运动的路程等问题的解决方法，这几个问题都有什么共同点呢？分割→以直代曲→求和→取极限（逼近一般地，设函数()f x 在区间[,]a b 上连续，分割 用分点0121i i n a x x x x x x b -=<<<<<<<=L L 将区间[,]a b 等分成n 个小区间，每个小区间长度为x ∆（b ax n-∆=）， 以直代曲 在每个小区间[]1,i i x x -上取一点()1,2,,i i n ξ=L ，每份小曲边梯形的面积近似为()i f x ξ∆ 求和：11()()nnn i i i i b aS f x f nξξ==-=∆=∑∑取极限 如果x ∆无限接近于0（亦即n →+∞）时，上述和式n S 无限趋近于常数S ，那么称该常数S 为函数()f x 在区间[,]a b 上的定积分。

记为：()baS f x dx =⎰其中()f x 成为被积函数，x 叫做积分变量，[,]a b 为积分区间，b 积分上限，a 积分下限。

思考 定积分()baf x dx ⎰是一个常数还是个函数？即n S 无限趋近的常数S （n →+∞时）称为()baf x dx ⎰，而不是n S ．常见定积分 曲边图形面积：()baS f x dx =⎰；变速运动路程21()t t S v t dt =⎰；变力做功 ()baW F r dr=⎰理解 本来 面积=底⨯高 路程=速度⨯时间 功=力⨯位移因为都是不规则的，所以都用先分割，再以直代曲，这样就可以相乘了，再求和 ，再取极限。

二．定积分的几何性质 定积分()baf x dx ⎰表示由直线,(),0x a x b a b y ==≠=和曲线()y f x =所围成的曲边梯形(如图中的阴影部分)的面积，。

§2 微积分基本定理学习目标 1.直观了解并掌握微积分基本定理的含义.2.会利用微积分基本定理求函数的积分．知识点 微积分基本定理(牛顿—莱布尼茨公式)思考1 已知函数f (x )＝2x ＋1，F (x )＝x 2＋x ，则ʃ10(2x ＋1)d x 与F (1)－F (0)有什么关系？答案 由定积分的几何意义知，ʃ10(2x ＋1)d x ＝12×(1＋3)×1＝2，F (1)－F (0)＝2，故ʃ10(2x ＋1)d x ＝F (1)－F (0)．思考2 对一个连续函数f (x )来说，是否存在唯一的F (x )，使得F ′(x )＝f (x )?答案 不唯一．根据导数的性质，若F ′(x )＝f (x )，则对任意实数c ，都有[F (x )＋c ]′＝F ′(x )＋c ′＝f (x )．梳理 (1)微积分基本定理①条件：f (x )是区间[a ，b ]上的连续函数，并且F ′(x )＝f (x )； ②结论：ʃb a f (x )d x ＝F (b )－F (a )；③符号表示：ʃb a f (x )d x ＝F (x )|b a ＝F (b )－F (a )．(2)常用函数积分公式表1．若F ′(x )＝f (x )，则F (x )唯一．( × )2．微积分基本定理中，被积函数f (x )是原函数F (x )的导数．( √ )3．应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数．( √ )类型一 求定积分命题角度1 求简单函数的定积分 例1 求下列定积分．(1)ʃ21⎝⎛⎭⎫1x －3cos x d x ； (2)2π2sin cos d 22x x x⎛⎫- ⎪⎝⎭⎰； (3)ʃ30(x －3)(x －4)d x .考点 利用微积分基本定理求定积分 题点 利用微积分基本定理求定积分 解 (1)ʃ21⎝⎛⎭⎫1x －3cos x d x ＝(ln x －3sin x )|21 ＝(ln 2－3sin 2)－(ln 1－3sin 1)＝ln 2－3sin 2＋3sin 1.(2)∵⎝⎛⎭⎫sin x 2－cos x 22＝1－2sin x 2cos x 2 ＝1－sin x ， ∴2π2sin cos d 22x x x ⎛⎫- ⎪⎝⎭⎰＝π20(1sin )d x x ⎰－＝π20(cos )|x x ＋＝⎝⎛⎭⎫π2＋cos π2－(0＋cos 0)＝π2－1. (3)∵(x －3)(x －4)＝x 2－7x ＋12，∴ʃ30(x －3)(x －4)d x ＝ʃ30(x 2－7x ＋12)d x＝⎪⎪⎝⎛⎭⎫13x 3－72x 2＋12x 30＝⎝⎛⎭⎫13×33－72×32＋12×3－0＝272. 反思与感悟 (1)当被积函数为两个函数的乘积或乘方形式时一般要转化为和的形式，便于求得原函数F (x )．(2)由微积分基本定理求定积分的步骤 第一步：求被积函数f (x )的一个原函数F (x )； 第二步：计算函数的增量F (b )－F (a )． 跟踪训练1 求下列定积分．(1)ʃ21⎝⎛⎭⎫x －x 2＋1x d x ； (2)π222cos sin d 22x x x ⎛⎫- ⎪⎝⎭⎰；(3)ʃ94x (1＋x )d x .考点 利用微积分基本定理求定积分 题点 利用微积分基本定理求定积分解 (1)ʃ21⎝⎛⎭⎫x －x 2＋1x d x ＝⎪⎪⎝⎛⎭⎫12x 2－13x 3＋ln x 21＝⎝⎛⎭⎫12×22－13×23＋ln 2－⎝⎛⎭⎫12－13＋ln 1＝ln 2－56.(2)π222cos sin d 22x x x ⎛⎫- ⎪⎝⎭⎰＝π20cos d x x ⎰＝π20sin |x ＝1. (3)ʃ94x (1＋x )d x ＝ʃ94(x ＋x )d x ＝3292421|32x x ⎛⎫+ ⎪⎝⎭＝322219932⎛⎫⨯+⨯ ⎪⎝⎭－322214432⎛⎫⨯+⨯ ⎪⎝⎭＝2716.命题角度2 求分段函数的定积分 例2 求下列定积分：(1)f (x )＝⎩⎪⎨⎪⎧sin x ，0≤x ≤π2，1，π2≤x ≤2，x －1，2<x ≤4，求ʃ40f (x )d x ；(2)ʃ20|x 2－1|d x .考点 分段函数的定积分 题点 分段函数的定积分 解(1)ʃ40f (x )d x ＝π2sin d x x ⎰＋2π21d x ⎰＋ʃ42(x －1)d x＝π20(cos )|x －＋2π2|x ＋⎪⎪⎝⎛⎭⎫12x 2－x 42＝1＋⎝⎛⎭⎫2－π2＋(4－0)＝7－π2. (2)ʃ20|x 2－1|d x ＝ʃ10(1－x 2)d x ＋ʃ21(x 2－1)d x＝ ⎪⎪⎝⎛⎭⎫x －13x 310＋⎪⎪⎝⎛⎭⎫13x 3－x 21＝2. 反思与感悟 分段函数定积分的求法(1)利用定积分的性质，转化为各区间上定积分的和计算．(2)当被积函数含有绝对值时，常常去掉绝对值号，转化为分段函数的定积分再计算．跟踪训练2 (1)ʃ1－1e |x |d x ＝_______.(2)已知f (x )＝⎩⎪⎨⎪⎧2x ＋e x，0≤x ≤1，x －1x ，1<x ≤2，则ʃ20f (x )d x ＝______.考点 分段函数的定积分 题点 分段函数的定积分 答案 (1)2e －2 (2)e ＋32－ln 2解析 (1)ʃ1－1e |x |d x ＝ʃ0－1e －x d x ＋ʃ10e xd x＝－e －x |0－1＋e x |10＝－e 0＋e 1＋e 1－e 0＝2e －2.(2)ʃ20f (x )d x ＝ʃ10(2x ＋e x )d x ＋ʃ21⎝⎛⎭⎫x －1x d x ＝(x 2＋e x )|10＋⎪⎪⎝⎛⎭⎫12x 2－ln x 21＝(1＋e)－(0＋e 0)＋⎝⎛⎭⎫12×22－ln 2－⎝⎛⎭⎫12×1－ln 1 ＝e ＋32－ln 2.类型二 利用定积分求参数例3 (1)已知t >0，f (x )＝2x －1，若ʃt 0f (x )d x ＝6，则t ＝________. (2)已知2≤ʃ21(kx ＋1)d x ≤4，则实数k 的取值范围为________． 考点 微积分基本定理的应用 题点 利用微积分基本定理求参数 答案 (1)3 (2)⎣⎡⎦⎤23，2解析 (1)ʃt 0f (x )d x ＝ʃt 0(2x －1)d x ＝t 2－t ＝6， 解得t ＝3或－2，∵t >0，∴t ＝3. (2)ʃ21(kx ＋1)d x ＝⎪⎪⎝⎛⎭⎫12kx 2＋x 21＝32k ＋1. 由2≤32k ＋1≤4，得23≤k ≤2.引申探究1．若将例3(1)中的条件改为ʃt 0f (x )d x ＝f ⎝⎛⎭⎫t 2，求t . 解 由ʃt 0f (x )d x ＝ʃt 0(2x －1)d x ＝t 2－t ， 又f ⎝⎛⎭⎫t 2＝t －1，∴t 2－t ＝t －1，得t ＝1.2．若将例3(1)中的条件改为ʃt 0f (x )d x ＝F (t )，求F (t )的最小值． 解 F (t )＝ʃt 0f (x )d x ＝t 2－t ＝⎝⎛⎭⎫t －122－14(t >0)， 当t ＝12时，F (t )min ＝－14.反思与感悟 (1)含有参数的定积分可以与方程、函数或不等式综合起来考查，先利用微积分基本定理计算定积分是解决此类综合问题的前提．(2)计算含有参数的定积分，必须分清积分变量与被积函数f (x )、积分上限与积分下限、积分区间与函数F (x )等概念．跟踪训练3 (1)已知x ∈(0,1]，f (x )＝ʃ10(1－2x ＋2t )d t ，则f (x )的值域是________．(2)设函数f (x )＝ax 2＋c (a ≠0)．若ʃ10f (x )d x ＝f (x 0)，0≤x 0≤1，则x 0的值为________．考点 微积分基本定理的应用 题点 利用微积分基本定理求参数 答案 (1)[0,2) (2)33解析 (1)f (x )＝ʃ10(1－2x ＋2t )d t ＝(t －2xt ＋t 2)|10＝－2x ＋2，x ∈(0,1]． ∴f (x )的值域为[0,2)．(2)∵ʃ10f (x )d x ＝ʃ10(ax 2＋c )d x＝⎪⎪⎝⎛⎭⎫13ax 3＋cx 10＝a 3＋c . 又f (x 0)＝ax 20＋c ，∴a 3＝ax 20，即x 0＝33或－33. ∵0≤x 0≤1，∴x 0＝33.1．若ʃa 1⎝⎛⎭⎫2x ＋1x d x ＝3＋ln 2，则a 的值是( ) A ．5 B ．4 C ．3 D ．2 考点 微积分基本定理的应用 题点 利用微积分基本定理求参数 答案 D解析 ʃa 1⎝⎛⎭⎫2x ＋1x d x ＝ʃa 12x d x ＋ʃa 11xd x ＝x 2|a 1＋ln x |a 1＝a 2－1＋ln a ＝3＋ln 2，解得a ＝2.2．π2312sin d 2θθ⎛⎫- ⎪⎝⎭⎰等于( )A ．－32 B ．－12 C.12 D.32考点 利用微积分基本定理求定积分 题点 利用微积分基本定理求定积分 答案 D 解析π2312sin d 2θθ⎛⎫- ⎪⎝⎭⎰＝π3cos d θθ⎰＝π30sin |θ＝32. 3．设f (x )＝⎩⎪⎨⎪⎧x 2，0≤x ≤1，2－x ，1<x ≤2，则ʃ20f (x )d x 等于( )A.34 B.45 C.56D ．不存在考点 分段函数的定积分 题点 分段函数的定积分 答案 C解析 ʃ20f (x )d x ＝ʃ10x 2d x ＋ʃ21(2－x )d x ＝ ⎪⎪13x 310＋⎪⎪⎝⎛⎭⎫2x －12x 221＝56. 4．已知函数f (x )＝x n ＋mx 的导函数f ′(x )＝2x ＋2，则ʃ31f (－x )d x ＝________.考点 微积分基本定理的应用 题点 微积分基本定理的综合应用 答案 23解析 ∵f (x )＝x n ＋mx 的导函数f ′(x )＝2x ＋2， ∴nx n －1＋m ＝2x ＋2，解得n ＝2，m ＝2， ∴f (x )＝x 2＋2x ，则f (－x )＝x 2－2x ，∴ʃ31f (－x )d x ＝ʃ31(x 2－2x )d x＝⎪⎪⎝⎛⎭⎫13x 3－x 231＝9－9－13＋1＝23. 5．求函数f (a )＝ʃ10(6x 2＋4ax ＋a 2)d x 的最小值．考点 微积分基本定理的综合应用 题点 微积分基本定理的综合应用解 ∵ʃ10(6x 2＋4ax ＋a 2)d x ＝(2x 3＋2ax 2＋a 2x )|10＝2＋2a ＋a 2，∴f (a )＝a 2＋2a ＋2＝(a ＋1)2＋1， ∴当a ＝－1时，f (a )有最小值1.1．求定积分的一些常用技巧(1)对被积函数，要先化简，再求积分．(2)若被积函数是分段函数，依据定积分“对区间的可加性”，分段积分再求和． (3)对于含有绝对值符号的被积函数，要去掉绝对值符号才能积分．2．由于定积分的值可取正值，也可取负值，还可以取0，而面积是正值，因此不要把面积理解为被积函数对应图形在某几个区间上的定积分之和，而是在x 轴下方的图形面积要取定积分的相反数.一、选择题1．ʃ21⎝⎛⎭⎫e x ＋1x d x 等于( ) A ．e 2－ln 2 B ．e 2－e －ln 2 C ．e 2＋e ＋ln 2D ．e 2－e ＋ln 2考点 利用微积分基本定理求定积分 题点 利用微积分基本定理求定积分 答案 D解析 ʃ21⎝⎛⎭⎫e x ＋1x ＝(e x ＋ln x )|21 ＝(e 2＋ln 2)－(e ＋ln 1)＝e 2－e ＋ln 2. 2．若π2(sin cos )d x a x x ⎰－＝2，则实数a 等于( )A ．－1B ．1C ．－ 3D. 3考点 微积分基本定理的应用 题点 利用微积分基本定理求参数 答案 A 解析π2(sin cos )d x a x x ⎰－＝π20(cos sin )|x a x －－＝0－a －(－1－0)＝1－a ＝2， ∴a ＝－1，故选A.3．若S 1＝ʃ21x 2d x ，S 2＝ʃ211xd x ，S 3＝ʃ21e xd x ，则S 1，S 2，S 3的大小关系为( ) A ．S 1<S 2<S 3 B ．S 2<S 1<S 3 C ．S 2<S 3<S 1D ．S 3<S 2<S 1考点 利用微积分基本定理求定积分 题点 利用微积分基本定理求定积分答案 B解析 因为S 1＝ʃ21x 2d x ＝⎪⎪13x 321＝13×23－13＝73， S 2＝ʃ211xd x ＝ln x |21＝ln 2， S 3＝ʃ21e x d x ＝e x |21＝e 2－e ＝e(e －1)．又ln 2<ln e ＝1，且73<2.5<e(e －1)，所以ln 2<73<e(e －1)，即S 2<S 1<S 3.4．ʃ30|x 2－4|d x 等于( )A.213B.223C.233D.253 考点 分段函数的定积分 题点 分段函数的定积分 答案 C解析 ∵|x 2－4|＝⎩⎪⎨⎪⎧x 2－4，2≤x ≤3，4－x 2，0≤x ≤2，∴ʃ30|x 2－4|d x ＝ʃ32(x 2－4)d x ＋ʃ20(4－x 2)d x＝ ⎪⎪⎝⎛⎭⎫13x 3－4x 32＋⎪⎪⎝⎛⎭⎫4x －13x 320＝⎣⎡⎦⎤(9－12)－⎝⎛⎭⎫83－8＋⎣⎡⎦⎤⎝⎛⎭⎫8－83－0 ＝－3－83＋8＋8－83＝233.5．若函数f (x )，g (x )满足ʃ1－1f (x )g (x )d x ＝0，则称f (x )，g (x )为区间[－1,1]上的一组正交函数．给出三组函数：①f (x )＝sin 12x ，g (x )＝cos 12x ；②f (x )＝x ＋1，g (x )＝x －1； ③f (x )＝x ，g (x )＝x 2.其中为区间[－1,1]上的正交函数的组数为( ) A ．0 B ．1 C ．2 D ．3 考点 微积分基本定理的应用 题点 微积分基本定理的综合应用解析 对于①，ʃ1－1sin 12x cos 12x d x ＝ʃ1－112sin x d x ＝0， 所以①是区间[－1,1]上的一组正交函数；对于②，ʃ1－1(x ＋1)(x －1)d x ＝ʃ1－1(x 2－1)d x ≠0，所以②不是区间[－1,1]上的一组正交函数；对于③，ʃ1－1x ·x 2d x ＝ʃ1－1x 3d x ＝0，所以③是区间[－1,1]上的一组正交函数．6．若f (x )＝x 2＋2ʃ10f (x )d x ，则ʃ10f (x )d x 等于() A ．－13 B ．－1C.13 D ．1考点 利用微积分基本定理求定积分题点 利用微积分基本定理求定积分答案 A解析 ∵f (x )＝x 2＋2ʃ10f (x )d x ，∴ʃ10f (x )d x ＝ ⎪⎪⎝⎛⎭⎫13x 3＋2x ʃ10f (x )d x 10＝13＋2ʃ10f (x )d x ，∴ʃ10f (x )d x ＝－13.7．设f (x )＝⎩⎪⎨⎪⎧x 2，x ≤0，cos x －1，x >0，则ʃ1－1f (x )d x ＝________. 考点 分段函数的定积分题点 分段函数的定积分答案 sin 1－23解析 ʃ1－1f (x )d x ＝ʃ0－1x 2d x ＋ʃ10(cos x －1)d x＝⎪⎪13x 30－1＋(sin x －x )|10＝⎣⎡⎦⎤13×03－13×(－1)3＋[(sin 1－1)－(sin 0－0)] ＝sin 1－23. 8．已知f (x )＝3x 2＋2x ＋1，若ʃ1－1f (x )d x ＝2f (a )成立，则a ＝________.考点 微积分基本定理的应用题点 利用微积分基本定理求参数答案 －1或13解析 ʃ1－1f (x )d x ＝(x 3＋x 2＋x )|1－1＝4， 2f (a )＝6a 2＋4a ＋2，由题意得6a 2＋4a ＋2＝4，解得a ＝－1或13. 9.从如图所示的长方形区域内任取一个点M (x ，y )，则点M 取自阴影部分的概率为________．考点 微积分基本定理的应用题点 微积分基本定理的综合应用答案 13解析 长方形的面积为S 1＝3，S 阴＝ʃ103x 2d x ＝x 3|10＝1，则P ＝S 阴S 1＝13.10．设f (x )＝⎩⎪⎨⎪⎧lg x ，x >0，x ＋ʃa 03t 2d t ，x ≤0，若f (f (1))＝1，则a ＝____________. 考点 微积分基本定理的应用题点 利用微积分基本定理求参数答案 1解析 因为x ＝1>0，所以f (1)＝lg 1＝0.又当x ≤0时，f (x )＝x ＋ʃa 03t 2d t ＝x ＋t 3|a 0＝x ＋a 3，所以f (0)＝a 3.因为f (f (1))＝1，所以a 3＝1，解得a ＝1.11．设f (x )是一次函数，且ʃ10f (x )d x ＝5，ʃ10xf (x )d x ＝176，则f (x )的解析式为________． 考点 微积分基本定理的应用题点 利用微积分基本定理求参数答案 f (x )＝4x ＋3解析 ∵f (x )是一次函数，∴设f (x )＝ax ＋b (a ≠0)，∴ʃ10f (x )d x ＝ʃ10(ax ＋b )d x ＝ʃ10ax d x ＋ʃ10b d x＝12a ＋b ＝5， ʃ10xf (x )d x ＝ʃ10x (ax ＋b )d x＝ʃ10(ax 2)d x ＋ʃ10bx d x ＝13a ＋12b ＝176. ∴⎩⎨⎧ 12a ＋b ＝5，13a ＋12b ＝176，解得⎩⎪⎨⎪⎧a ＝4，b ＝3. ∴f (x )＝4x ＋3. 12．已知α∈⎣⎡⎦⎤0，π2，则当ʃα0(cos x －sin x )d x 取最大值时，α＝________. 考点 微积分基本定理的应用题点 微积分基本定理的综合应用答案 π4解析 ʃα0(cos x －sin x )d x ＝(sin x ＋cos x )|α0＝sin α＋cos α－1＝2sin ⎝⎛⎭⎫α＋π4－1. ∵α∈⎣⎡⎦⎤0，π2，则α＋π4∈⎣⎡⎦⎤π4，34π， 当α＋π4＝π2，即α＝π4时， 2sin ⎝⎛⎭⎫α＋π4－1取得最大值． 三、解答题13．已知f (x )＝ʃx －a (12t ＋4a )d t ，F (a )＝ʃ10[f (x )＋3a 2]d x ，求函数F (a )的最小值．考点 微积分基本定理的应用题点 微积分基本定理的综合应用解 因为f (x )＝ʃx －a (12t ＋4a )d t ＝(6t 2＋4at )|x －a＝6x 2＋4ax －(6a 2－4a 2)＝6x 2＋4ax －2a 2，F (a )＝ʃ10[f (x )＋3a 2]d x ＝ʃ10(6x 2＋4ax ＋a 2)d x＝(2x 3＋2ax 2＋a 2x )|10＝a 2＋2a ＋2＝(a ＋1)2＋1≥1.所以当a ＝－1时，F (a )取到最小值为1.四、探究与拓展14．已知函数f (x )＝⎩⎨⎧ (x ＋1)2，－1≤x ≤0，1－x 2，0<x ≤1，则ʃ1－1f (x )d x 等于( ) A.3π－812B.4＋3π12C.4＋π4D.－4＋3π12 考点 分段函数的定积分题点 分段函数的定积分答案 B解析 ʃ1－1f (x )d x ＝ʃ0－1(x ＋1)2d x ＋ʃ101－x 2d x ，ʃ0－1(x ＋1)2d x ＝ ⎪⎪13(x ＋1)30－1＝13， ʃ101－x 2d x 以原点为圆心，以1为半径的圆的面积的四分之一， 故ʃ101－x 2d x ＝π4， 故ʃ1－1f (x )d x ＝13＋π4＝4＋3π12. 15．已知f ′(x )是f (x )在(0，＋∞)上的导数，满足xf ′(x )＋2f (x )＝1x2，且ʃ21[x 2f (x )－ln x ]d x ＝1. (1)求f (x )的解析式；(2)当x >0时，证明不等式2ln x ≤e x 2－2.考点 微积分基本定理的应用题点 微积分基本定理的综合应用(1)解 由xf ′(x )＋2f (x )＝1x2，得 x 2f ′(x )＋2xf (x )＝1x， 即[x 2f (x )]′＝1x， 所以x 2f (x )＝ln x ＋c (c 为常数)，即x 2f (x )－ln x ＝c .又ʃ21[x 2f (x )－ln x ]d x ＝1，即ʃ21c d x ＝1，所以cx |21＝1，所以2c －c ＝1，所以c ＝1.所以x 2f (x )＝ln x ＋1，所以f (x )＝ln x ＋1x 2. (2)证明 由(1)知f (x )＝ln x ＋1x 2(x >0)， 所以f ′(x )＝1x ×x 2－2x (ln x ＋1)x 4＝－2ln x －1x 3， 当f ′(x )＝0时，x ＝12e -，f ′(x )>0时，0<x <12e -，f ′(x )<0时，x >12e -，所以f (x )在120,e -⎛⎫ ⎪⎝⎭上单调增，在12e ,-⎛⎫+∞ ⎪⎝⎭上单调减．所以f (x )max ＝12e f -⎛⎫ ⎪⎝⎭＝e 2， 所以f (x )＝ln x ＋1x 2≤e 2， 即2ln x ≤e x 2－2.。

定积分计算的方法与技巧摘要：定积分是积分学的重要组成部分，其概念抽象、难以理解、解题方法灵活多变。

本文讨论了定积分计算的各种方法与技巧。

关键词：定积分换元积分法分部积分法计算方法定积分与不定积分是积分学的两个组成部分，定积分不仅是积分学的基础，而且是概率统计、复变函数等课程的重要知识工具.定积分概念抽象、定理较多，学生不仅在理论学习中难以理解掌握，在定积分计算中难度也很大，往往面对一个题目，不知如何下手.因此，本文通过对各种题型、各种解题方法的分析研究，讨论了定积分计算的方法与技巧，希望对初学者有所帮助.一、利用定积分定义计算定积分定积分的思想方法是：“分割、取近似、求和、求极限”，实质是在连续区间上求和，我们通过例子来说明定积分定义的含义.例1.用定积分定义计算：edx.解：将区间［0，1］n等分，分成n个小区间［，］，则每个小区间的长为Δx=，并取ξ=为右端点（i=1，2，…，n），得到：原式=f（ξ）Δx=e•==e-1.注：一般来说，用定义计算定积分是十分麻烦的，实际计算中，并不用上述方法.二、利用定积分性质估算定积分的值例2.估算定积分（1+sinx）dx的值解：f（x）=1+sinx在［，π］上的最大值为f（）=2，最小值为f（π）=1，即：1≤1+sinx≤2，所以：π=1×（-）≤（1+sinx）dx≤2×（-）=2π.三、利用Newton-Leibniz公式计算定积分设f（x）在［a，b］上连续，且F′（x）=f（x），则f（x）dx=F（b）-F（a），这就是Newton-Leibniz公式.由此看出：Newton-Leibniz公式刻画了定积分与不定积分的紧密联系，它使得计算定积分时，只要找到被积函数f（x）的某个原函数F（x），F（x）在b，a两点的函数值的差就是所求的定积分.Newton-Le ibniz公式是最基本的定积分计算公式，而找到f（x）的原函数F（x）是应用这个公式的关键，所以，熟练使用Newton-Leibniz公式的关键是对不定积分的计算相当熟练.例3.计算定积分：（1）dx；（2）dx.解：（1）原式=（3x+）dx=［x+arctanx］=1+（2）原式=dx=tanx|=1四、利用定积分对积分区间的可加性计算定积分如果被积函数含有绝对值或平方根时，应按绝对值内或被开方式子的正负号将积分区间分段求定积分的代数和.同样，对分段函数的定积分，也应该按分段情况逐段积分.例4.计算定积分：（1）；（2）f（x）dx，其中f（x）=x+1，x≤1x，x＞1解：（1）原式==（cosx-sinx）dx+（sinx-cosx）dx=［sinx+cosx］+［-cosx-sinx］=2（-1）（2）f（x）dx=（x+1）dx+xdx=［x+x］+［x］=五、利用换元积分法计算定积分不定积分的换元积分法有两种类型，同样定积分的换元积分法也有两种类型：当用第一类换元积分法求定积分时，若未引进新的积分变量，则积分上、下限不变；当用第二类换元积分法求定积分时，由于引入了新的积分变量，因此，积分上、下限要作相应改变.例5.计算定积分：（1）（1-sinθ）dθ；（2）dx；（3）dx；（4）已知dx=，求a.解：（1）原式=dθ+（1-cosθ）dcosθ=π+［cosθ-cosθ］=π-（2）原式=d（x-1）=［（x-1）+arcsin（x-1）］=（3）令x=π-t，则原式=（-dt）=dt-dt所以，原式=dt=-［arctan（cost）］=.（4）令=t，即x=ln（t+1），dx=dt，则:原式=•dt=2arctant|=π-2arctan，由-2arctan=得：arctan=，所以a=ln2.六、利用分部积分法计算定积分分部积分法的公式为：uv′dx=［uv］-u′vdx，而如何确定恰当的u，v与不定积分的思想完全相同，当u，v选择不恰当时，很难算出定积分，具体求解时，有时须先换元，再分部积分.例6.计算定积分：dx解：令x=sint，dx=costdt，则：原式=costdt=-（cott）′tdt=-tcott|+cottdt=π+ln3.七、对称区间上的定积分的计算由公式f（x）dx=［f（x）+f（-x）］dx=2f（x）dx，f（x）为偶函数0，f（x）为奇函数，可计算对称区间上的定积分或者可化为对称区间上的定积分.例7.计算定积分：（1）I=sin（lnx）dx；（2）I=dx解：（1）令t=lnx，则I=esintdt=sint（e+e）dt=（e-e）（2）令t=lnx并应用得arctanu+arctan=得：I=（arctane+arctane）sintdt=sintdt=.注：从上例看出：对积分上限、下限互为倒数的区间［，a］上的定积分f（x）dx，可引入变换t=lnx，化为对称区间［-lna，lna］上的定积分f（x）dx=ef （e）dt.定积分的计算方法很多，除上面介绍的方法外，还有周期函数的定积分计算，建立递推公式计算定积分，等等，同时定积分的各计算方法不是孤立的，很多题目都可能是几种计算方法联合使用，只有多练习才能熟能生巧.。

实例分析分段函数的微积分典型问题在高等数学的学习过程中，分段函数作为函数中特殊的一类，对其理解和接受都存在一定难度，同时也是高等数学教学中的重点和难点。

为了突破这一难点，就要掌握分段函数在分界点处的各种性质，进而利用微积分计算等方法进行求解。

1 分段函数和微积分分段函数是指在不同的定义域区间具备不同解析式的函数，即不能用同一解析式进行表达的函数。

归根结底，分段函数也是一个函数，其图像也是唯一的。

而分段函数在分界点的性质变化正是其难点所在，也是其本身特殊性所在，因此为了研究分段函数，首要的研究目标就是分段函数的分界点，而微积分在高等数学中也占据着重要的地位，是研究函数有关概念和性质的数学分支，能够使得分段函数中分界点的相关计算有据可依。

两者的互相补充为高等数学的解题带来了便捷。

2 分段函数微积分问题归类与分析2.1 一元分段函数微积分2.1.1 对一元分段函数在分界点处的极限判断对于一元函数分界点处极限的判断，主要是依据分段函数的表达形式。

若函数表达形式在分界点的左右不同，就可以依据分段函数在分界点处左右极限来判断，当极限存在且相等时，该点存在极限；若不存在或者两者不相等时，则该点不存在极限。

若分界点左右的函数表达方式相同，就可直接运用计算极限的常用方法将极限计算出来。

举例说明：例1：已知函数=，求（1）；（2）。

解析：由分段函数表达式可知，x=1为该分段函数的分界点，当x<1和x>1时，所对应的解析式也不同。

所以针对（1）问，应该讨论当x趋近于1时的左右极限。

因此x时，x<1，此时；而当x时，x>1，此时，因此则有函数的左极限与右极限相等，即=1，因此=1，进而得到。

2.1.2 对一元函数在分界点处的连续性判断函数在某一点具有连续性的充要条件是函数在该点同时满足左连续和右连续。

高等数学中也正是依据这个条件来判断分段函数中分界点处的函数连续性。

其具体解决步骤为：第一步，利用左右连续的定义进行分界点左右连续情况的判断；第二步，根据结果进行判断，当左右都连续则证明该分界点连续，若其中有一个不连续或者左右极限不存在或者函数在该分界点不存在定义，即可判断该点不连续。

1.4.2 微积分基本定理(一) 学案（含答案）1.4.2微积分基本定理微积分基本定理一一学习目标1.直观了解并掌握微积分基本定理的含义.2.会利用微积分基本定理求函数的积分知识点微积分基本定理已知函数fx2x1，Fxx2x.思考1fx与Fx有何关系答案Fx2x1fx思考220fxdx与F2F0有何关系答案20fxdx202x1dx122156，F2F06.20fxdxF2F0梳理1微积分基本定理条件Fxfx，且fx在a，b上可积结论bafxdxFbFa 符号表示bafxdxFx|baFbFa2常见函数的定积分公式baCdxCx|baC 为常数；baxndx1n1xn1|ban1；basinxdxcosx|ba；bacosxdxsinx|ba；ba1xdxlnx|baba0；baexdxex|ba；baaxdxaxlna|baa0，且a11若Fxfx，则Fx唯一2微积分基本定理中，被积函数fx是原函数Fx的导数3应用微积分基本定理求定积分的值时，被积函数在积分区间上必须是连续函数类型一求定积分命题角度1求简单函数的定积分例1求下列定积分1102xexdx；2211x3cosxdx；3220sincosd22xxx；430x3x4dx.解1102xexdxx2ex|101e10e0e.2211x3cosxdxlnx3sinx|21ln23sin2ln 13sin1ln23sin23sin1.3sinx2cosx2212sinx2cosx21sinx，22200sincosd1sind22xxxxx20cos|xx2cos20cos021.4x3x4x27x12，30x3x4dx30x27x12dx13x372x212x30133372321230272.反思与感悟1当被积函数为两个函数的乘积或乘方形式时一般要转化为和的形式，便于求得函数Fx2由微积分基本定理求定积分的步骤第一步求被积函数fx的一个原函数Fx第二步计算函数的增量FbFa跟踪训练1求下列定积分121xx21xdx；22220cossind22xxx；394x1xdx.解121xx21xdx12x213x3lnx2112221323ln21213ln1ln256.22220cossind22xxx20cosdxx20sin|x1.394x1xdx94xxdx3292421|32xx3222199323222144322716.命题角度2求分段函数的定积分例21求函数fxsinx，0x2，1，2x2，x1，2x4在区间0,4上的定积分；2求定积分20|x21|dx.解140fxdx20sindxx221dx42x1dx20cos|x22|x12x2x421224072.2|x21|1x2，x0，1，x21，x1，2，又xx331x2，x33xx21，20|x21|dx10|x21|dx21|x21|dx101x2dx21x21dxxx3310x33x211138 321312.反思与感悟分段函数的定积分的求法1利用定积分的性质转化为各区间上定积分的和计算2当被积函数含有绝对值时，常常去掉绝对值符号，转化为分段函数的定积分再计算跟踪训练21fx12x，0x1，x2，1x2，求20fxdx.解20fxdx1012xdx21x2dxxx2|1013x3|21273133.2求22|x2x|dx的值解|x2x|x2x，2x0，xx2，0x1，x2x，10，fx2x1，若t0fxdx6，则t________.2已知221kx1dx4，则实数k的取值范围为________答案13223，2解析1t0fxdxt02x1dxt2t6，解得t3或2，t0，t3.221kx1dx12kx2x2132k1.由232k14，得23k2.引申探究1若将本例1中的条件改为t0fxdxft2，求t.解由t0fxdxt02x1dxt2t，又ft2t1，t2tt1，得t1.2若将本例1中的条件改为t0fxdxFt，求Ft的最小值解Ftt0fxdxt2tt12214t0，当t12时，Ftmin14.反思与感悟1含有参数的定积分可以与方程.函数或不等式综合起来考查，先利用微积分基本定理计算定积分是解决此类综合问题的前提2计算含有参数的定积分，必须分清积分变量与被积函数fx.积分上限与积分下限.积分区间与函数Fx等概念跟踪训练3已知x0,1，fx1012x2tdt，则fx的值域是________答案0,2解析fx1012x2tdtt2xtt2|102x2x0,1fx的值域为0,21若a12x1xdx3ln2，则a的值是A5B4C3D2答案D解析a12x1xdxa12xdxa11xdxx2|a1lnx|a1a21lna3ln2，解得a2.223012sind2等于A32B12C.12D.32答案D解析23012sind230cosd30sin|32.3已知fxax2bxca0，且f12，f00，10fxdx2.求a，b，c的值解f12，abc2，fx2axb，f0b0，10fxdx10ax2cdx13ax3cx1013ac2，由可得a6，b0，c4.4已知fx4x2，0x2，cosx，2x，计算0fxdx.解0fxdx202ddfxxfxx20242dcosdxxxx取F1x2x22x，则F1x4x2；取F2xsinx，则F2xcosx.所以20242dcosd,xxxx22202122|sin||1,2xxx即0fxdx1221.1求定积分的一些常用技巧1对被积函数，要先化简，再求积分2若被积函数是分段函数，依据定积分“对区间的可加性”，分段积分再求和3对于含有绝对值符号的被积函数，要去掉绝对值符号才能积分2由于定积分的值可取正值，也可取负值，还可以取0，而面积是正值，因此不要把面积理解为被积函数对应图形在某几个区间上的定积分之和，而是在x轴下方的图形面积要取定积分的相反数。

定积分常见问题一、关于含“变上限积分”的问题321(1)()x x F x =⎰例、求下列导数32(2)()x x F x =⎰220(3)()()xF x tf x t dt =-⎰2例、求下列极限2221(1)lim(1)x t xx t e dt x -→∞+⎰求 2204()(2)lim,()(0)0,(0)2xx tf x t dtf x f f x→-'==⎰求连续，3例1(1)()()()sin f x f tx dt f x x x =+⎰求连续函数，使之满足1ln 1(2)()0()()1xt f x dt x f x f t x =>++⎰、设，其中，求 ()()3213()0(),1()8,()3f x f x xg x g t dt x f x >=-⎰（）设在可微。

其反函数为且求二、定积分计算的有关问题411(1)例、（常见形式积分）4(2)1cos 2xdx x π+⎰12(3). 24(4)(0)aadx a x >⎰ln 0(5)⎰0(6)a例2、（分段函数，绝对值函数）[(1)()b a xdx a b <⎰ 0,02(2)(),()(),2x l kx x f x x f t dt l c x l ⎧≤≤⎪⎪=Φ=⎨⎪≤≤⎪⎩⎰、设求 10(3)t t x dt -⎰sin ,02(4).()(),(0)0(),()0,2xx x f t g x t dt x x f x x g x x ππ⎧≤<⎪⎪-≥≥==⎨⎪≥⎪⎩⎰其中当时，而例3（对称区间上积分）11(1)(1sin )()x x x e e dx --++⎰(1212(2)sin ln x x x dx -⎡⎢⎣⎰ 244sin (3)1x xdx eππ--+⎰ ()4[]()()baf x dx f xg x +⎰例、形如的积分42(1)⎰sin 2sin cos 0(2)xx x e dxe e π+⎰ 2(3),1()dxtgx πλ+⎰例5、（由三角有理式与其他初等函数通过四则成复合而成的函数的积分）22022001.(sin )(cos ))2.(sin )(sin )21331,24223.sin cos ,1342,1253n nf x dx f x dx xf x dx f x dxn n n n n xdx xdx n n n n n ππππππππ==--⎧⋅⋅⋅⎪⎪-==⎨--⎪⋅⋅⎪-⎩⎰⎰⎰⎰⎰⎰常用结论，为正偶自然数为大于的正奇数，2(sin )(1)(sin )(cos )f x dx f x f x π+⎰2π⎰101020sin cos (2)4sin cos x x dx x x π---⎰、 2(3)ln sin xdx π⎰320sin (4)1cos x x dx x π+⎰ 2220sin (5),sin cos n n n n x x I dx n N x x π+=∈+⎰计算 640(6)sin cos x x xdxπ⎰[]2(7)(),,()()sin ,()1cos xf x f x f x xdx f x x ππππ--=++⎰设在上连续且满足求1210011(8)(1)x dx --⎰求(9)n π⎰2sin (10)()sin ,().x t xF x e tdt F x A B C D π+=⎰则是（）正常数负常数恒为零不是常数例6 利用适当变量代换计算积分4(1)ln(1)tgx dx π+⎰ 120ln(1)(2)1x dx x ++⎰ 200(3)sin n x xdx π⎰ 20(4)(1)(1)dxx x α+∞++⎰求例7（其它）22(1)()[0,]()cos ()()2f x f x x x f t dt f x ππ=+⎰、设在上连续，且，求212(2)()()2()()f x x x f x dx f x dx f x =-+⎰⎰设，求120(3)()()arcsin(1),(01),()y y x y x x x y x dx '==-≤≤⎰设满足求22011(4)()(2)arctan ,(1)1,()2x f x tf x t dt x f f x dx -==⎰⎰、设连续，且满足求的值2200cos sin cos (5),,(2)1x x xdx A dx x x ππ=++⎰⎰已知：求220(6)()ln(12cos )(),()F a a x a dx F a F a π=-+-⎰设，求(2)(),()a xay a y f x edy f x dx --=⎰⎰(7)、设求1(8)(1)m n x x dx -⎰例8、计算下列广义积分（基本题）2(1),1dxx +∞-∞+⎰1(2),e 2ln (3),1xdx x+∞+⎰51(4) 1(5)cos(ln ),x dx ⎰例90(1)0)pt te dt p p +∞->⎰（是常数，且2(2).(1)xx xe dx e +∞--+⎰例10、计算下列广义积分（广义积分变量代换例）3(1)⎰23202ln(1)(2)(1)x x dx x +∞++⎰22200200.cos sin (1)(1)1sin sin (2),()2x x xdx A A dx x x x x dx dxx x π+∞+∞+∞+∞++=⎰⎰⎰⎰例11已知广义积分收敛于，试用表示广义积分的值已知求 经典例题例1求3321lim)n n n →∞++．解 将区间[0,1]n 等分，则每个小区间长为1i x n∆=，然后把2111n n n =⋅的一个因子1n 乘入和式中各项．于是将所求极限转化为求定积分．即3321lim)n n n →∞+=31lim )n n n n →∞+=34=⎰．例2 0⎰=_________．解法1 由定积分的几何意义知，0⎰等于上半圆周22(1)1x y -+= (0y ≥)与x 轴所围成的图形的面积．故0⎰=2π． 解法2 本题也可直接用换元法求解．令1x -=sin t （22t ππ-≤≤），则⎰=22tdt ππ-⎰=2tdt =2202cos tdt π⎰=2π 例3 比较12x e dx ⎰，212x e dx ⎰，12(1)x dx +⎰．解法1 在[1,2]上，有2x x e e ≤．而令()(1)x f x e x =-+，则()1x f x e '=-．当0x >时，()0f x '>，()f x 在(0,)+∞上单调递增，从而()(0)f x f >，可知在[1,2]上，有1x e x >+．又1221()()f x dx f x dx =-⎰⎰，从而有2111222(1)x x x dx e dx e dx +>>⎰⎰⎰．解法2 在[1,2]上，有2xx e e ≤．由泰勒中值定理212!xe e x x ξ=++得1x e x >+．注意到1221()()f x dx f x dx =-⎰⎰．因此2111222(1)x x x dx e dx e dx +>>⎰⎰⎰．例4 估计定积分22xxe dx -⎰的值．解 设 2()xxf x e -=, 因为 2()(21)xxf x e x -'=-, 令()0f x '=，求得驻点12x =, 而 0(0)1f e ==, 2(2)f e =, 141()2f e -=,故124(),[0,2]ef x e x -≤≤∈,从而2122422xxee dx e --≤≤⎰,所以21024222x xe edx e ---≤≤-⎰.例5 设()f x ，()g x 在[,]a b 上连续，且()0g x ≥，()0f x >．求lim (ban g x →∞⎰．解 由于()f x 在[,]a b 上连续，则()f x 在[,]a b 上有最大值M 和最小值m ．由()0f x >知0M >，0m >．又()0g x ≥，则()b ag x dx (b ag x ≤⎰()bag x dx ≤．由于1n n ==，故lim (ban g x →∞⎰=()bag x dx ⎰．例6求sin lim n pnn xdx x+→∞⎰, ,p n 为自然数． 解法1 利用积分中值定理 设 sin ()xf x x=, 显然()f x 在[,]n n p +上连续, 由积分中值定理得 sin sin n p n x dx p x ξξ+=⋅⎰, [,]n n p ξ∈+, 当n →∞时, ξ→∞, 而sin 1ξ≤, 故sin sin lim lim 0n pnn x dx p xξξξ+→∞→∞=⋅=⎰．解法2 利用积分不等式 因为sin sin 1lnn pn p n p nn n x x n pdx dx dx x x x n++++≤≤=⎰⎰⎰, 而limln0n n pn→∞+=,所以 sin lim 0n pnn xdx x+→∞=⎰． 例7 求10lim 1nn x dx x→∞+⎰．解法1 由积分中值定理()()()()bbaaf xg x dx f g x dx ξ=⎰⎰可知101n x dx x +⎰=111n x dx ξ+⎰，01ξ≤≤．又11lim lim01n n n x dx n →∞→∞==+⎰且11121ξ≤≤+， 故10lim 01n n x dx x→∞=+⎰． 解法2 因为01x ≤≤，故有01nn x x x≤≤+．于是可得110001nn x dx x dx x ≤≤+⎰⎰．又由于110()1n x dx n n =→→∞+⎰． 因此10lim 1nn x dx x→∞+⎰=0． 例8 设函数()f x 在[0,1]上连续，在(0,1)内可导，且3414()(0)f x dx f =⎰．证明在(0,1)内存在一点c ，使()0f c '=．证明 由题设()f x 在[0,1]上连续，由积分中值定理，可得3413(0)4()4()(1)()4f f x dx f f ξξ==-=⎰，其中3[,1][0,1]4ξ∈⊂．于是由罗尔定理，存在(0,)(0,1)c ξ∈⊂，使得()0f c '=．证毕．例9 （1）若22()x t xf x e dt -=⎰，则()f x '=___；（2）若0()()xf x xf t dt =⎰，求()f x '=___．()()()[()]()[()]()v x u x d f t dt f v x v x f u x u x dx''=-⎰． 解 （1）()f x '=422x x xe e ---；（2） 由于在被积函数中x 不是积分变量，故可提到积分号外即0()()xf x x f t dt =⎰，则可得()f x '=0()()xf t dt xf x +⎰．例10 设()f x 连续，且31()x f t dt x -=⎰，则(26)f =_________．解 对等式310()x f t dt x -=⎰两边关于x 求导得32(1)31f x x -⋅=，故321(1)3f x x -=，令3126x -=得3x =，所以1(26)27f =． 例11 函数1()(3(0)x F x dt x =>⎰的单调递减开区间为_________．解 ()3F x'=()0F x '<3>，解之得109x <<，即1(0,)9为所求．例12 求0()(1)arctan xf x t tdt =-⎰的极值点．解''得1x =，0x =．列表如下：故1x =为()f x 的极大值点，0x =为极小值点．例13 已知两曲线()y f x =与()y g x =在点(0,0)处的切线相同，其中2arcsin 0()xt g x e dt -=⎰，[1,1]x ∈-，试求该切线的方程并求极限3lim ()n nf n→∞．解 由已知条件得2(0)(0)0t f g e dt -===⎰，且由两曲线在(0,0)处切线斜率相同知(0)(0)1f g =''===．故所求切线方程为y x =．而3()(0)3lim ()lim33(0)330n n f f n nf f n n →∞→∞-'=⋅==-． 例14 求 22000sin lim(sin )x x xtdtt t t dt→-⎰⎰；解 22000sin lim (sin )x x xtdtt t t dt→-⎰⎰=2202(sin )lim (1)(sin )x x x x x x →-⋅⋅-=220()(2)lim sin x x x x→-⋅-=304(2)lim 1cos x x x →-⋅-=2012(2)lim sin x x x→-⋅=0．注 此处利用等价无穷小替换和多次应用洛必达法则．例15 试求正数a 与b，使等式201lim1sin x x x b x →=-⎰成立． 解2001lim sin x x x b x →-⎰=20x →=20lim 1cos x x x b x →→-2011cos x x b x →==-，由此可知必有0lim(1cos )0x b x →-=，得1b =．又由2011cos x x x →==-， 得4a =．即4a =，1b =为所求． 例16 设sin 20()sin x f x t dt =⎰，34()g x x x =+，则当0x →时，()f x 是()g x 的（ ）．A ．等价无穷小．B ．同阶但非等价的无穷小．C ．高阶无穷小．D ．低阶无穷小．解法1 由于 22300()sin(sin )cos lim lim()34x x f x x xg x x x →→⋅=+ 2200cos sin(sin )lim lim34x x x x x x →→=⋅+ 22011lim 33x x x →==． 故()f x 是()g x 同阶但非等价的无穷小．选B ． 解法2 将2sin t 展成t 的幂级数，再逐项积分，得到 sin 223370111()[()]sin sin 3!342x f x t t dt x x =-+=-+⎰，则344340001111sin (sin )sin ()1342342lim lim lim ()13x x x x x x f x g x x x x→→→-+-+===++． 例17 证明：若函数()f x 在区间[,]a b 上连续且单调增加，则有()baxf x dx ⎰()2baa b f x dx +≥⎰．证法1 令()F x =()()2xxaa a x tf t dt f t dt +-⎰⎰，当[,]t a x ∈时，()()f t f x ≤，则 ()F x '=1()()()22x a a x xf x f t dt f x +--⎰=1()()22xax a f x f t dt --⎰≥1()()22x a x a f x f x dt --⎰=()()22x a x a f x f x ---0=． 故()F x 单调增加．即 ()()F x F a ≥，又()0F a =，所以()0F x ≥，其中[,]x a b ∈． 从而()F b =()()2bba a ab xf x dx f x dx +-⎰⎰0≥．证毕． 证法2 由于()f x 单调增加，有()[()()]22a b a bx f x f ++--0≥，从而 ()[()()]22baa b a b x f x f dx ++--⎰0≥． 即()()2baa b x f x dx +-⎰()()22b a a b a b x f dx ++≥-⎰=()()22b a a b a bf x dx ++-⎰=0．故()baxf x dx ⎰()2baa b f x dx +≥⎰． 例18 计算21||x dx -⎰．分析 被积函数含有绝对值符号，应先去掉绝对值符号然后再积分． 解 21||x dx -⎰＝021()x dx xdx --+⎰⎰＝220210[][]22x x --+＝52．注 在使用牛顿－莱布尼兹公式时,应保证被积函数在积分区间上满足可积条件．如 33222111[]6dx x x --=-=⎰，则是错误的．错误的原因则是由于被积函数21x在0x =处间断且在被积区间内无界.例19 计算220max{,}x x dx ⎰．分析 被积函数在积分区间上实际是分段函数212()01x x f x x x ⎧<≤=⎨≤≤⎩． 解 23212221201011717max{,}[][]23236x x x x dx xdx x dx =+=+=+=⎰⎰⎰例20 设()f x 是连续函数，且10()3()f x x f t dt =+⎰，则()________f x =． 解 因()f x 连续，()f x 必可积，从而1()f t dt ⎰是常数，记1()f t dt a =⎰，则()3f x x a =+，且11(3)()x a dx f t dt a +==⎰⎰．所以2101[3]2x ax a +=，即132a a +=， 从而14a =-，所以 3()4f x x =-．例21 设23, 01()52,12x x f x x x ⎧≤<=⎨-≤≤⎩，0()()x F x f t dt =⎰，02x ≤≤，求()F x , 并讨论()F x 的连续性．解 （1）求()F x 的表达式．()F x 的定义域为[0,2]．当[0,1]x ∈时，[0,][0,1]x ⊂, 因此23300()()3[]xxxF x f t dt t dt t x ====⎰⎰．当(1,2]x ∈时，[0,][0,1][1,]x x =, 因此, 则1201()3(52)xF x t dt t dt =+-⎰⎰=31201[][5]x t t t +-=235x x -+-，故32, 01()35,12x x F x x x x ⎧≤<⎪=⎨-+-≤≤⎪⎩． (2) ()F x 在[0,1)及(1,2]上连续, 在1x =处，由于211lim ()lim(35)1x x F x x x ++→→=-+-=, 311lim ()lim 1x x F x x --→→==, (1)1F =． 因此, ()F x 在1x =处连续, 从而()F x 在[0,2]上连续．例22 计算21-⎰．由于积分区间关于原点对称，因此首先应考虑被积函数的奇偶性．解21-⎰=211--+⎰⎰．由于2是偶函数，而是奇函数，有10-=⎰, 于是21-⎰=214⎰=04⎰=1044dx-⎰⎰由定积分的几何意义可知4π=⎰, 故2114444dxππ-=-⋅=-⎰⎰．例23计算3412ee⎰．解3412ee⎰=34e3412ee⎰==3412ee=6π．例24计算4sin1sinxdxxπ+⎰．解4sin1sinxdxxπ+⎰=42sin(1sin)1sinx xdxxπ--⎰=244200sintancosxdx xdxxππ-⎰⎰=244200cos(sec1)cosd xx dxxππ---⎰⎰=44001[][tan]cosx xxππ--=24π-注此题为三角有理式积分的类型，也可用万能代换公式来求解，请读者不妨一试．例25计算2a⎰，其中0a>．解2a⎰=20a⎰，令sinx a a t-=，则2a⎰=3222(1sin)cosa t tdtππ-+⎰=3222cos0a tdtπ+⎰=32aπ．注 ，一般令sin x a t =或cos x a t =． 例26 计算a⎰，其中0a >．解法1 令sin x a t =，则a⎰2cos sin cos tdt t tπ=+⎰201(sin cos )(cos sin )2sin cos t t t t dt t t π++-=+⎰ 201(sin cos )[1]2sin cos t t dt t t π'+=++⎰[]201ln |sin cos |2t t t π=++=4π． 解法2 令sin x a t =，则a⎰=2cos sin cos tdt t tπ+⎰．又令2t u π=-，则有20cos sin cos t dt t t π+⎰=20sin sin cos u du u u π+⎰．所以，a⎰=22001sin cos []2sin cos sin cos t t dt dt t tt t ππ+++⎰⎰=2012dt π⎰=4π．注 如果先计算不定积分，再利用牛顿-莱布尼兹公式求解,则比较复杂，由此可看出定积分与不定积分的差别之一．例27 计算ln 0⎰．解 设u =2ln(1)x u =+，221udx du u =+，则ln 0⎰=22220(1)241u u u du u u +⋅=++⎰22222200442244u u du du u u +-=++⎰⎰2221284du du u =-=+⎰⎰4π-． 例28 计算220()xd tf x t dt dx -⎰，其中()f x 连续． 分析 要求积分上限函数的导数，但被积函数中含有x ，因此不能直接求导，必须先换元使被积函数中不含x ，然后再求导．解 由于220()xtf x t dt -⎰=2221()2x f x t dt-⎰． 故令22x t u -=，当0t =时2u x =；当t x =时0u =，而2dt du =-，所以220()x tf x t dt -⎰=201()()2x f u du -⎰=201()2x f u du ⎰，故220()x d tf x t dt dx -⎰=201[()]2x d f u du dx ⎰=21()22f x x⋅=2()xf x ． 错误解答220()x d tf x t dt dx -⎰22()(0)xf x x xf =-=． 错解分析 这里错误地使用了变限函数的求导公式，公式()()()xad x f t dt f x dx 'Φ==⎰中要求被积函数()f t 中不含有变限函数的自变量x ，而22()f x t -含有x ，因此不能直接求导，而应先换元．例29 计算30sin x xdx π⎰．解30sin x xdx π⎰30(cos )xd x π=-⎰3300[(cos )](cos )x x x dx ππ=⋅---⎰30cos 6xdx ππ=-+⎰6π=-． 例30 计算120ln(1)(3)x dx x +-⎰．解120ln(1)(3)x dx x +-⎰=101ln(1)()3x d x +-⎰=1100111[ln(1)]3(3)(1)x dx x x x +-⋅--+⎰ =101111ln 2()2413dx x x -++-⎰11ln 2ln324=-． 例31 计算20sin x e xdx π⎰．解 由于2sin xe xdx π⎰20sin xxde π=⎰220[sin ]cos xx e x e xdx ππ=-⎰220cos x e e xdx ππ=-⎰， （1）而20cos xe xdx π⎰20cos xxde π=⎰220[cos ](sin )xx e x e x dx ππ=-⋅-⎰20sin 1x e xdx π=-⎰， （2）将（2）式代入（1）式可得20sin xe xdx π⎰220[sin 1]x e e xdx ππ=--⎰,故20sin xe xdx π⎰21(1)2e π=+．例32 计算10arcsin x xdx ⎰．解 10arcsin x xdx ⎰210arcsin ()2x xd =⎰221100[arcsin ](arcsin )22x x x d x =⋅-⎰210142π=-⎰． （1） 令sin x t =，则21⎰20sin t π=⎰220sin cos cos ttdt tπ=⋅⎰220sin tdt π=⎰ 201cos22t dt π-==⎰20sin 2[]24t t π-4π=． （2）将（2）式代入（1）式中得1arcsin x xdx =⎰8π． 例33 设()f x 在[0,]π上具有二阶连续导数，()3f π'=且0[()()]cos 2f x f x xdx π''+=⎰，求(0)f '．解 由于0[()()]cos f x f x xdx π''+⎰0()sin cos ()f x d x xdf x ππ'=+⎰⎰[]000{()sin ()sin }{[()cos ]()sin }f x x f x xdx f x x f x xdx ππππ'''=-++⎰⎰()(0)2f f π''=--=．故 (0)f '=2()235f π'--=--=-． 例34（97研） 设函数()f x 连续，1()()x f xt dt ϕ=⎰，且0()limx f x A x→=（A 为常数）， 求()x ϕ'并讨论()x ϕ'在0x =处的连续性．分析 求()x ϕ'不能直接求，因为10()f xt dt ⎰中含有()x ϕ的自变量x ，需要通过换元将x从被积函数中分离出来，然后利用积分上限函数的求导法则，求出()x ϕ'，最后用函数连续的定义来判定()x ϕ'在0x =处的连续性． 解 由0()limx f x A x→=知0lim ()0x f x →=，而()f x 连续，所以(0)0f =，(0)0ϕ=．当0x ≠时，令u xt =，0t =，0u =；1t =，u x =．1dt du x=，则()()xf u du x xϕ=⎰，从而02()()()(0)xxf x f u dux x xϕ-'=≠⎰．又因为02()()(0)()limlimlim22xx x x f u du x f x A x x x ϕϕ→→→-===-⎰，即(0)ϕ'=2A．所以 ()x ϕ'=02()(),0,02x xf x f u du x x Ax ⎧-⎪≠⎪⎨⎪=⎪⎩⎰． 由于22000()()()()lim ()limlim lim xxx x x x xf x f u duf u du f x x xx x ϕ→→→→-'==-⎰⎰=(0)2A ϕ'=． 从而知()x ϕ'在0x =处连续．注 这是一道综合考查定积分换元法、对积分上限函数求导、按定义求导数、讨论函数在一点的连续性等知识点的综合题．而有些读者在做题过程中常会犯如下两种错误： （1）直接求出2()()()xxf x f u dux xϕ-'=⎰，而没有利用定义去求(0)ϕ'，就得到结论(0)ϕ'不存在或(0)ϕ'无定义，从而得出()x ϕ'在0x =处不连续的结论．（2）在求0lim ()x x ϕ→'时，不是去拆成两项求极限，而是立即用洛必达法则，从而导致()()()1lim ()lim ().22x x xf x f x f x x f x x ϕ→→'+-''==又由0()limx f x A x→=用洛必达法则得到0lim ()x f x →'=A ，出现该错误的原因是由于使用洛必达法则需要有条件：()f x 在0x =的邻域内可导．但题设中仅有()f x 连续的条件，因此上面出现的0lim ()x f x →'是否存在是不能确定的．例35（00研） 设函数()f x 在[0,]π上连续，且()0f x dx π=⎰，0()cos 0f x xdx π=⎰．试证在(0,)π内至少存在两个不同的点12,ξξ使得12()()0f f ξξ==．分析 本题有两种证法：一是运用罗尔定理，需要构造函数0()()xF x f t dt =⎰，找出()F x的三个零点，由已知条件易知(0)()0F F π==，0x =，x π=为()F x 的两个零点，第三个零点的存在性是本题的难点．另一种方法是利用函数的单调性，用反证法证明()f x 在(0,)π之间存在两个零点．证法1 令0()(),0xF x f t dt x π=≤≤⎰，则有(0)0,()0F F π==．又00()cos cos ()[cos ()]()sin f x xdx xdF x xF x F x xdx ππππ==+⎰⎰⎰()sin 0F x xdx π==⎰，由积分中值定理知，必有(0,)ξπ∈，使得()sin F x xdx π⎰=()sin (0)F ξξπ⋅-．故()sin 0F ξξ=．又当(0,),sin 0ξπξ∈≠，故必有()0F ξ=． 于是在区间[0,],[,]ξξπ上对()F x 分别应用罗尔定理，知至少存在1(0,)ξξ∈，2(,)ξξπ∈，使得12()()0F F ξξ''==，即12()()0f f ξξ==．证法2 由已知条件0()0f x dx π=⎰及积分中值定理知必有10()()(0)0f x dx f πξπ=-=⎰，1(0,)ξπ∈，则有1()0f ξ=．若在(0,)π内，()0f x =仅有一个根1x ξ=，由0()0f x dx π=⎰知()f x 在1(0,)ξ与1(,)ξπ内异号，不妨设在1(0,)ξ内()0f x >，在1(,)ξπ内()0f x <，由()cos 0f x xdx π=⎰，0()0f x dx π=⎰，以及cos x 在[0,]π内单调减，可知：100()(cos cos )f x x dx πξ=-⎰=11110()(cos cos )()(cos cos )f x x dx f x x dx ξπξξξ-+-⎰⎰0>．由此得出矛盾．故()0f x =至少还有另一个实根2ξ，12ξξ≠且2(0,)ξπ∈使得 12()()0.f f ξξ==例36 计算2043dxx x +∞++⎰．分析 该积分是无穷限的的反常积分，用定义来计算．解2043dx x x +∞++⎰=20lim 43t t dx x x →+∞++⎰=0111lim ()213t t dx x x →+∞-++⎰ =011lim [ln ]23t t x x →+∞++=111lim (ln ln )233t t t →+∞+-+ =ln 32． 例37计算3+∞⎰．解3+∞⎰2233sec tan sec tan d ππθθθθθ+∞=⎰⎰23cos 1d ππθθ==⎰ 例38计算42⎰．分析 该积分为无界函数的反常积分，且有两个瑕点，于是由定义，当且仅当32⎰43⎰均收敛时，原反常积分才是收敛的．解 由于32⎰32lim aa +→⎰32lim aa +→⎰=32lim[arcsin(3)]a a x +→-=2π．43⎰=34lim bb -→⎰34lim bb -→⎰=34lim[arcsin(3)]b b x -→-=2π． 所以42⎰22πππ=+=．例39计算0+∞⎰．分析 此题为混合型反常积分，积分上限为+∞，下限0为被积函数的瑕点． 解t =，则有+∞⎰＝50222(1)tdt t t +∞+⎰＝50222(1)dt t +∞+⎰，再令tan t θ=，于是可得5022(1)dt t +∞+⎰＝25022tan (tan 1)d πθθ+⎰＝2250sec sec d πθθθ⎰＝230sec d πθθ⎰ ＝32cos d πθθ⎰＝220(1sin )cos d πθθθ-⎰＝220(1sin )sin d πθθ-⎰＝3/21[sin sin ]3πθθ-＝23． 例40计算21⎰． 解 由于221112111()d x x x +-==⎰⎰⎰，可令1t x x=-，则当x =t =；当0x -→时，t →+∞；当0x +→时，t →-∞；当1x =时，0t =；故有21010211()()12()d x d x x x x x--=++-⎰⎰⎰022dtt +∞-∞=+⎰⎰1arctan )2π=+ ． 注 有些反常积分通过换元可以变成非反常积分，如例32、例37、例39；而有些非反常积分通过换元却会变成反常积分，如例40，因此在对积分换元时一定要注意此类情形．例41 求由曲线12y x =，3y x =，2y =，1y =所围成的图形的面积．分析 若选x 为积分变量，需将图形分割成三部分去求，如图5－1所示，此做法留给读者去完成．下面选取以y 为积分变量． 解 选取y 为积分变量，其变化范围为[1,2]y ∈，则面积元素为dA =1|2|3y y dy -=1(2)3y y dy -． 于是所求面积为211(2)3A y y dy =-⎰=52． 例42 抛物线22y x =把圆228x y +=分成两部分，求这两部分面积之比．解 抛物线22y x =与圆228x y +=的交点分别为(2,2)与(2,2)-，如图所示5－2所示，抛物线将圆分成两个部分1A ，2A ，记它们的面积分别为1S ，2S ，则有图5－21S =2222(8)2y y dy ---⎰=24488cos 3d ππθθ--⎰=423π+，218S A π=-=463π-，于是12S S =423463ππ+-=3292ππ+-． 例43 求心形线1cos ρθ=+与圆3cos ρθ=所围公共部分的面积．分析 心形线1cos ρθ=+与圆3cos ρθ=的图形如图5－3所示．由图形的对称性，只需计算上半部分的面积即可． 解 求得心形线1cos ρθ=+与圆3cos ρθ=的交点为(,)ρθ=3(,)23π±，由图形的对称性得心形线1cos ρθ=+与圆3cos ρθ=所围公共部分的面积为图5－3A =223203112[(1cos )(3cos )]22d d πππθθθθ++⎰⎰=54π． 3πθ=3cos ρθ=3211-xoy121-2A 1A 12(2,2)-oxy22y x=228x y +=2-1-121-2-2x y =1y =3y x =o 1-3-321211-2-xy2y =图5－1342-1cos ρθ=+例44 求曲线ln y x =在区间(2,6)内的一条切线，使得该切线与直线2x =，6x =和曲线ln y x =所围成平面图形的面积最小（如图5－4所示）．分析 要求平面图形的面积的最小值，必须先求出面积的表达式．解 设所求切线与曲线ln y x =相切于点(,ln )c c ，则切线方程为1ln ()y c x c c-=-．又切线与直线2x =，6x =和曲线ln y x =所围成的平面图形的面积为图5－4A =621[()ln ln ]x c c x dx c -+-⎰=44(1)4ln 46ln 62ln 2c c-++-+．由于dA dc =2164c c-+=24(4)c c --，令0dA dc =，解得驻点4c =．当4c <时0dA dc<，而当4c >时0dAdc >．故当4c =时，A 取得极小值．由于驻点唯一．故当4c =时，A 取得最小值．此时切线方程为：11ln 44y x =-+． 例45 求圆域222()x y b a +-≤（其中b a >）绕x 轴旋转而成的立体的体积．解 如图5－5所示，选取x 为积分变量，得上半圆周的方程为222y b a x =+-，下半圆周的方程为221y b a x =--．图5－5则体积元素为dV =2221()y y dx ππ-=224b a x dx π-．于是所求旋转体的体积为 V =224aab a x dx π--⎰=228ab a x dx π-⎰=284a b ππ⋅=222a b π．注 可考虑选取y 为积分变量，请读者自行完成．例46（03研） 过坐标原点作曲线ln y x =的切线，该切线与曲线ln y x =及x 轴围成平面图形D ．（1）求D 的面积A ；（2）求D 绕直线x e =旋转一周所得旋转体的体积V ． 分析 先求出切点坐标及切线方程，再用定积分求面积A ，旋转体积可用大的立体体积减去小的立体体积进行图5－6计算，如图5－6所示．ln y x=ln y x=y xo12311y xe=(0,)b o222()(0)x y b a b a +-=>>xy1xo y23121-45673ln y x=2x =6x =(,ln )c c解 （1）设切点横坐标为0x ，则曲线ln y x =在点00(,ln )x x 处的切线方程是0001ln ()y x x x x =+-． 由该切线过原点知0ln 10x -=，从而0x e =，所以该切线的方程是1y x e=．从而D 的面积10()12y eA e ey dy =-=-⎰． （2）切线1y x e =与x 轴及直线x e =围成的三角形绕直线x e =旋转所得的旋转体积为2113V e π=，曲线ln y x =与x 轴及直线x e =围成的图形绕直线x e =旋转所得的旋转体积为1222011()(2)22y V e e dy e e ππ=-=-+-⎰．因此，所求体积为212(5123)6V V V e e π=-=-+．例47 有一立体以抛物线22y x =与直线2x =所围成的图形为底，而垂直于抛物线的轴的截面都是等边三角形，如图5－7所示．求其体积．解 选x 为积分变量且[0,2]x ∈．过x 轴上坐标为x 的点作垂直于x 轴的平面，与立体相截的截面为等边三角形，其底边长为得等边三角形的面积为图5－7()A x 2=． 于是所求体积为 V =2()A x dx ⎰=2⎰=例48（03研） 某建筑工程打地基时，需用汽锤将桩打进土层，汽锤每次击打，都将克服土层对桩的阻力而作功，设土层对桩的阻力的大小与桩被打进地下的深度成正比（比例系数为k ，0k >），汽锤第一次击打进地下a （m ），根据设计方案，要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数r （01r <<）．问： （1）汽锤打桩3次后，可将桩打进地下多深？（2）若击打次数不限，汽锤至多能将桩打进地下多深？（注：m 表示长度单位米） 分析 本题属于变力作功问题，可用定积分来求．解 （1）设第n 次击打后，桩被打进地下n x ，第n 次击打时，汽锤所作的功为n W （1n =，2，）．由题设，当桩被打进地下的深度为x 时，土层对桩的阻力的大小为kx ，所以12211022x k k W kxdx x a ===⎰，2122222211()()22x x k kW kxdx x x x a ==-=-⎰．由21W rW =得22221x x ra -=，即 222(1)x r a =+，3222223323()[(1)]22x x k kW kxdx x x x r a ==-=-+⎰．由2321W rW r W == 得22223(1)x r a r a -+=，即 2223(1)x r r a =++．从而汽锤击打3次后，可将桩打进地下3x =m ）． （2）问题是要求lim n n x →∞，为此先用归纳法证明：1n n x r +=++．假设1n n x r a -=++，则12211()2n nx n n n x k W kxdx x x +++==-⎰2121[(1...)]2n n kx r r a -+=-+++． 由2111...n n n n W rW r W r W +-====，得21221(1...)n n n x r r a r a -+-+++=．从而 1n n x r a +=++.于是1lim n n n x +→∞==． ()m ．例49 有一等腰梯形水闸．上底为6米，下底为2米，高为10米．试求当水面与上底相接时闸门所受的水压力．解 建立如图5－8所示的坐标系，选取x 为积分变量．则过点(0,3)A ，(10,1)B 的直线方程为135y x =-+．于是闸门上对应小区间[,]x x dx +的窄条所承受的水压力为2dF xy gdx ρ=．故闸门所受水压力为F =10012(3)5g x x dx ρ-+⎰=5003g ρ，其中ρ为水密度，g 为重力加速度．图5－8。

1. 曲边梯形的面积设在区间上，则由直线、、及曲线所围成的图形称为曲边梯形，下面求这个曲边梯形的面积分割求近似：在区间中任意插入若干个分点将分成n 个小区间，小区间的长度在每个小区间上任取一点作乘积，求和取极限：则面积取极限其中，即小区间长度最大者趋于零。

2.变速直线运动的路程设某物体作变速直线运动，速度是上的连续函数，且，求在这段时间内物体所经过的路程。

分割求近似：在内插入若干分点将其分成n 个小区间，小区间长度，。

任取，做求和取极限：则路程取极限定义设函数在上有界，在中任意插入若干个分点将分成n 个小区间，其长度为，在每个小区间上任取一点，作乘积，并求和，记，如果不论对怎样分法，也不论小区间上的点怎样取法，只要当时，和总趋于确定的极限，则称这个极限为函数在区间上的定积分，记作，即，（*）其中叫被积函数，叫被积表达式，叫积分变量，叫积分下限，叫积分上限，叫积分区间。

叫积分和式。

说明：1.如果（*）式右边极限存在，称在区间可积，下面两类函数在区间可积，（1）在区间上连续，则在可积。

（2）在区间上有界且只有有限个间断点，则在上可积。

2.由定义可知，定积分的值只与被积函数和积分区间有关，而与积分变量无关，所以3.规定时 ,在上时, 表示曲线、两条直线、与轴所围成的曲边梯形的面积；在上时, 表示曲线、两条直线、与轴所围成的曲边梯形的面积（此时，曲边梯形在轴的下方）；例1 利用定积分的几何意义写出下列积分值（1）（三角形面积）（2）（半圆面积）设可积性质1性质2性质3 （定积分对区间的可加性）对任何三个不同的数，有性质4性质5 如果在区间上，，则推论性质6 （定积分的估值）设M 及m 分别是函数在区间上的最大值及最小值，则性质7 （定积分中值定理）如果函数在区间上连续，则在上至少有一点，使成立例2 比较下面两个积分的大小与解设，在（0，1）内，单调增当时，有，即由性质5，例3估计积分的值解只需求出在区间上的最大值、最小值即可。

积分的计算方法积分是数学中的一个重要概念，它在微积分中有着广泛的应用。

在实际问题中，我们经常需要计算曲线下的面积、求解定积分等，而这些都需要用到积分的计算方法。

接下来，我们将介绍一些常见的积分计算方法，希望能够对大家有所帮助。

首先，我们来介绍一下定积分的计算方法。

对于一个函数f(x)，如果我们需要求解其在区间[a, b]上的定积分，可以使用定积分的定义公式进行计算。

即∫[a, b]f(x)dx = lim(n→∞) Σf(xi)Δx，其中Δx = (b a)/n，xi为区间[a, b]上的任意取点。

这是定积分的最基本的计算方法，通过将区间[a, b]分成n个小区间，然后在每个小区间上取一个点，最后求和并取极限，即可得到定积分的近似值。

其次，我们来介绍一些常见的积分计算公式。

在实际计算中，我们经常会遇到一些常见函数的积分，比如幂函数、三角函数、指数函数等。

对于这些函数，我们可以利用它们的积分计算公式来进行计算，而不需要每次都使用定积分的定义公式。

比如，对于幂函数f(x) = x^n，其积分计算公式为∫x^n dx = x^(n+1)/(n+1) + C，其中C为积分常数。

对于三角函数sin(x)、cos(x)的积分计算公式也有相应的表达式，同样，指数函数e^x的积分计算公式也是已知的。

这些常见函数的积分计算公式在实际计算中有着重要的作用，能够大大简化计算过程。

另外，我们还可以利用一些积分的性质来简化积分的计算。

比如，积分的线性性质、积分的换元积分法、分部积分法等，都是在积分计算中常用的方法。

通过灵活运用这些性质和方法，我们可以将复杂的积分化简为简单的形式，从而更加方便地进行计算。

最后，我们还需要注意一些特殊函数的积分计算方法。

比如，有理函数的积分计算、反三角函数的积分计算、分段函数的积分计算等，都需要我们根据具体的函数形式来选择合适的计算方法。

对于一些特殊函数，我们可能需要利用部分分式分解、三角恒等变换等方法来进行积分计算，这就需要我们对这些特殊函数有一定的了解和掌握。