最新微专题训练9 “等时圆”模型资料

等时圆模型最GROUP systen. ofHce roon.GEIGEIHUA^H-GEIHUA GEIHU/栏等时模型的规律及应用一.等时圆模型（如图所示） B B 1、小球从圆的J 贝瑞沿比消弦轨道靜山渭卜，滑到弦轨道与圆的交点的时间相 等。

（如图a ）2、小球从圆上的各个位置沿光滑弦轨道静止滑下，滑到圆的底端的时间相等。

（如图b ）3、沿不同的弦轨道运动的时间相等，都等于小球沿竖直直径（〃）自由落体 的时间，即山=禺=黒=2耳 （式中R 为圆的半径。

）三、等时性的证明 设某一条弦与水平方向的夹角为圆的直径为〃图）。

根据物体沿光滑弦作初速度为零的匀加速直线运度为d = gsina,位移为s = 〃sina,所以运动时间为即沿各条弦运动具有等时性，运动时间与弦的倾角、长短无关。

等时圆规 A A（如右动，加速四、应用等时圆模型解典型例题例1：如图1,通过空间任一点A可作无限多个斜面，若将若干个小物体从点A 分别沿这些倾角各不相同的光滑斜面同时滑下，那么在同一时刻这些小物体所在位置所构成的面是（）A.球面B.抛物面C.水平面D.无法确定【解析】：由“等时圆”可知，同一时刻这些小物体应在同一“等时圆”上, 所以A正确。

例2：如图2,在斜坡上有一根旗杆长为L,现一个小环从旗杆顶部沿一根光滑钢丝AB 滑至斜坡底部，又知0B二L。

求小环从A滑到B的时间。

【解析】：可以以0为圆心，以L为半径画一圆。

根据“等时圆”的规律可知，从A滑到B的时等于从A点沿例3：如图5所示，在同一竖直线上有A、B两点，相距为h, B点离地高度为H,现在要在地面上寻找一点P,使得从A、B两点分别向点P安放的光滑木板，满足物体从静止开始分别由A和B沿木板下滑到P点的时间相等，求0、P两点之间的葩离OPo解析：由“等时圆”特征可知，当A、B处于等时圆周上，且P点处于等时圆的最低点时，即能满足题设要求。

如图6所示，此时等时圆的半径为:所以OP = AR 2H(H+h)光滑），使 例4：如图7, AB 是一倾角为。

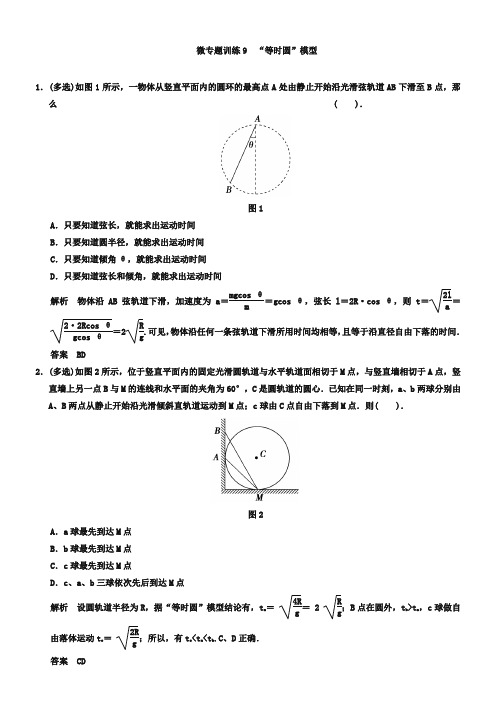
微专题训练9 “等时圆”模型1．(多选)如图1所示，一物体从竖直平面内的圆环的最高点A处由静止开始沿光滑弦轨道AB下滑至B点，那么( )．图1A．只要知道弦长，就能求出运动时间B．只要知道圆半径，就能求出运动时间C．只要知道倾角θ，就能求出运动时间D．只要知道弦长和倾角，就能求出运动时间解析物体沿AB弦轨道下滑，加速度为a＝mgcos θm＝gcos θ，弦长l＝2R·cos θ，则t＝2la＝2·2Rcos θgcos θ＝2Rg.可见，物体沿任何一条弦轨道下滑所用时间均相等，且等于沿直径自由下落的时间．答案BD2．(多选)如图2所示，位于竖直平面内的固定光滑圆轨道与水平轨道面相切于M点，与竖直墙相切于A点，竖直墙上另一点B与M的连线和水平面的夹角为60°，C是圆轨道的圆心．已知在同一时刻，a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道运动到M点；c球由C点自由下落到M点．则( )．图2A．a球最先到达M点B．b球最先到达M点C．c球最先到达M点D．c、a、b三球依次先后到达M点解析设圆轨道半径为R，据“等时圆”模型结论有，t a＝4Rg＝ 2Rg；B点在圆外，t b>t a，c球做自由落体运动t c＝2Rg；所以，有t c<t a<t b.C、D正确．答案CD3．(单选)如图3所示，AB 和CD 为两条光滑斜槽，它们各自的两个端点均分别位于半径为R 和r 的两个相切的圆上，且斜槽都通过切点P.设有一重物先后沿两个斜槽，从静止出发，由A 滑到B 和由C 滑到D ，所用的时间分别为t 1和t 2，则t 1与t 2之比为( )．图3A ．2∶1B ．1∶1 C.3∶1D ．1∶ 3解析 由“等时圆”模型结论有：t AP ＝t CP ＝ 2Rg，t PB ＝t PD ＝2 rg，所以t 1＝t AP ＋t PB ，t 2＝t CP ＋t PD ，知t 1＝t 2，B 项正确． 答案 B4．(单选)如图4所示，在倾角为θ的斜面上方的A 点处放置一光滑的木板AB ，B 端刚好在斜面上．木板与竖直方向AC 所成角度为α，一小物块自A 端沿木板由静止滑下，要使物块滑到斜面的时间最短，则α与θ角的大小关系应为( )．图4A ．α＝θB ．α＝θ2C ．α＝θ3D ．α＝2θ解析 如图所示，在竖直线AC 上选取一点O ，以适当的长度为半径画圆，使该圆过A 点，且与斜面相切于D 点．由等时圆知识可知，由A 沿斜面滑到D 所用时间比由A 到达斜面上其他各点所用时间都短．将木板下端与D 点重合即可，而∠COD ＝θ，则α＝θ2.答案 B5．(单选)如图5甲是某景点的山坡滑道图片，为了探究滑行者在滑道直线部分AE 滑行的时间，技术人员通过测量绘制出如图乙所示的示意图．AC 是滑道的竖直高度，D 点是AC 竖直线上的一点，且有AD ＝DE ＝10 m ，滑道AE 可视为光滑，滑行者从坡顶A 点由静止开始沿滑道AE 向下做直线滑动，g 取10 m/s 2，则滑行者在滑道AE 上滑行的时间为( )．甲 乙图5A. 2 s B ．2 s C. 3 sD ．2 2 s解析 A 、E 两点在以D 为圆心半径为R ＝10 m 的圆上，在AE 上的滑行时间与沿AD 所在的直径自由下落的时间相同，t ＝ 4R g＝ 4ADg＝2 s ，选B. 答案 B6．如图6所示，圆弧AB 是半径为R 的14圆弧，在AB 上放置一光滑木板BD ，一质量为m 的小物体在BD 板的D 端由静止下滑，然后冲向水平面BC ，在BC 上滑行L 后停下．不计小物体在B 点的能量损失，已知小物体与水平面BC 间的动摩擦因数为μ.求：小物体在BD 上下滑过程中，重力做功的平均功率．图6解析 由动能定理可知小物体从D 到C 有W G －μmgL ＝0，所以W G ＝μmgL由等时圆知识可知小物体从D 到B 的时间等于物体从圆周的最高点下落到B 点的时间，即为t ＝4Rg，所以小物体在木板BD 上下滑过程中，重力做功的平均功率为P ＝W G t ＝μmgL2g R. 答案 μmgL 2g R。

微专题训练9 “等时圆”模型i.（多选）如图i所示，一物体从竖直平面内的圆环的最高点A处由静止开始沿光滑弦轨道AB下滑至B点，那么（A •只要知道弦长，就能求出运动时间B •只要知道圆半径，就能求出运动时间C.只要知道倾角9，就能求出运动时间D .只要知道弦长和倾角，就能求出运动时间mg cos 92R cos =2 g.可见，物体沿任何一条弦解析物体沿AB弦轨道下滑，加速度为a二------------------------------------------------------二gcos 9,弦长1 =轨道下滑所用时间均相等，且等于沿直径自由下落的时间.答案BD2 .（多选）如图2所示，位于竖直平面内的固定光滑圆轨道与水平轨道面相切于M点，与竖直墙相切于A点，竖直墙上另一点B与M的连线和水平面的夹角为60 °,C是圆轨道的圆心.已知在同一时刻，a、b两球分别由A、B两点从静止开始沿光滑倾斜直轨道运动到M点；c图2球由C点自由下落到M点.则（）.A . a球最先到达M点B. b球最先到达M点C . c 球最先到达M 点D . c 、a 、b 三球依次先后到达 M 点g ； B 点在圆外，t b >t a , C 球做自由落体运动tt c <t a <t b .C 、D 正确.答案 CD3. （单选）如图3所示，AB 和CD 为两条光滑斜槽，它们各自的两个端点均分别位于半径为 R 和r 的两个相切的圆上，且斜槽都通过切点P.设有一重物先后沿两个斜槽，从 静止出发，由A 滑到B 和由C 滑到D ，所用的时间分别为t l 和t 2，则t l 与t 2之比为（）.所以 t l = t AP + t pB ， t 2 = t cP + t pD ，知 t l = t 2， B 项正确.答案 B 4. （单选）如图4所示，在倾角为B 的斜面上方的A 点处放 置一光滑的木板AB ，B 端刚好在斜面上.木板与竖直方 向AC所成角度为a 一小物块自A 端沿木板由静止滑下，A . 2 : 1B . 1 : 1 解析 由“等时圆”模型结论有:解析 设圆轨道半径为 R ,据“等时圆”模型结论有要使物块滑到斜面的时间最短，则a与B角的大小关系应为()•9A . a= 9 B. a=—29C. a= —D. a= 2 93解析如图所示，在竖直线AC上选取一点0,以适当的长度为半径画圆，使该圆过A点，且与斜面相切于D点.由等时圆知识可知，由A沿斜面滑到D所用时间比由A到达斜面上其他各点所用时间都短.将木板下端与D点重合即可，而/C0D二99，则a = _.2答案B5. (单选)如图5甲是某景点的山坡滑道图片，为了探究滑行者在滑道直线部分AE滑行的时间，技术人员通过测量绘制出如图乙所示的示意图. AC是滑道的竖直高度，D点是AC竖直线上的一点，且有AD = DE = 10 m，滑道AE 可视为光滑，滑行者从坡顶A点由静止开始沿滑道AE向下做直线滑动，g 取10 m/s 2，则滑行者在滑道AE上滑行的时间为甲A. ：'2 s B . 2 s C. ：' 3 s D . 2 12 s解析 A 、E 两点在以D 为圆心半径为R = 10 m 的圆上，在AE 上的滑行时 I4R I4AD 间与沿AD 所在的直径自由下落的时间相同，t = ・；-g~ = . ,； — = 2s ,选B.答案 B1 6 .如图6所示，圆弧AB 是半径为R 的■圆弧，在AB 上放置一光滑木板BD , 4一质量为m 的小物体在BD 板的D 端由静止下滑，然后冲向水平面 BC ，在 BC 上滑行L 后停下.不计小物体在B 点的能量损失，已知小物体与水平面 BC 间的动摩擦因数为仏求：小物体在BD 上下滑过程中，重力做功的平均功 率.解析 由动能定理可知小物体从 D 到C 有W G —卩mg A 0，所以W G =卩mgL 由等时圆知识可知小物体从 D 到B 的时间等于物体从圆周的最高点下落到 B点的时间, ，所以小物体在木板BD 上下滑过程中，重力做功 的平均功率为 W G P = t g (jmgL 答案-y。

动力学中的九类常见问题等时圆模型【模型解读】“等时圆”描述了一个物体沿着位于同一竖直圆上的所有光滑细杆 (或光滑斜面)由静止下滑，到达圆周的最低点(或从最高点到达同一圆周上各点)的时间相等，这个时间等于物体沿直径做自由落体运动所用的时间。

这个模型在物理计算中有着重要的应用，特别是在研究物体的运动轨迹和时间关系时。

由2R ·sin θ=12·g sin θ·t 2，可推得t 1=t 2=t 3。

“等时圆”模型的基本特性在于，它揭示了物体在不同路径上运动时，如果路径都在同一个竖直圆上，那么物体到达圆周最低点的时间是相等的。

这一特性不仅适用于光滑细杆，也适用于光滑斜面。

此外，如果物体的运动路径的端点在圆外，那么质点运动的时间会长一些；反之，如果端点在圆内，质点运动的时间则会短一些。

这个模型的应用不仅限于物理学科，它也体现了数学和物理之间的紧密联系。

通过“等时圆”模型，我们可以更好地理解物体在不同条件下的运动规律，以及这些规律如何影响物体的运动时间和路径。

物体在“两类”光滑斜面上的下滑时间的比较第一类：等高斜面(如图1所示)由L =12at 2，a =g sin θ，L =hsin θ可得t =1sin θ2h g ，可知倾角越小，时间越长，图1中t 1>t 2>t 3。

第二类：同底斜面(如图2所示)由L =12at 2，a =g sin θ，L =dcos θ可得t =4d g sin2θ，可见θ=45°时时间最短，图2中t 1=t 3>t 2。

【典例精析】1(2023年7月浙江宁波期末). 滑滑梯是小朋友们爱玩的游戏现有直滑梯AB 、AC 、AD 和BD ，A 、B 、C 、D 在竖直平面内的同一圆周上，且A 为圆周的最高点，D 为圆周的最低点，如图所示，已知圆周半径为R 。

在圆周所在的竖直平面内有一位置P ，距离A 点为3R ，且与A 等高。

物理等时圆模型讲解
物理学中的等时圆模型是一种用于描述和分析某些物理现象的理论模型。

它常用于处理具有周期性运动的系统，如简谐振动、电磁波传播等。

首先，我们来看简谐振动。

等时圆模型可以将简谐振动表示为一个在坐标平面上做圆周运动的矢量。

设想一个物体在沿着一条直线上做来回振动，当它靠近平衡位置时速度最大，远离平衡位置时速度最小。

根据简谐振动的特点，我们可以将振动物体的坐标和速度分别表示为水平和垂直方向上的矢量。

当振子在运动过程中，坐标和速度的矢量始终保持与圆的切线垂直的关系，因此可以用一个等时圆来表示。

对于电磁波传播，等时圆模型可以用来描述电场和磁场的变化规律。

在电磁波传播中，电场和磁场的振荡是相互垂直的，且它们的振幅和相位差随着时间的推移而变化。

通过等时圆模型，我们可以将电场和磁场的振荡表示为在一个垂直于传播方向的平面内的圆周运动。

等时圆模型的优点在于它直观地表示了振动的周期性和相位差的变化。

通过观察等时圆的形状和位置，我们可以推断出振动的特性和性质。

比如，对于简谐振动，圆的半径表示振幅的大小，圆的位置表示相位差的大小，而圆的旋转速度表示振动的频率。

需要注意的是，等时圆模型只是一种近似描述，它在一些特殊情况下可能不适用，或者需要结合其他模型和理论来进行更精确的分析。

但在许多情况下，等时圆模型提供了一个简单而直观的工具，帮助我们理解和解释物理现象。

等时圆模型(最新最全)(总9页)
等时圆模型，也称为基于等时线的圆形模型，是专为考量太阳系中行星运行速度变化而提出的天体运行模型。

它是建立在数量物理的理论框架上的，可以用来提供一种更加准确灵活的推进器性能预测方法。

简而言之，等时圆模型的主要思想是，当一个行星或小行星在恒星系的引力场中运行时，其运动速度受到重力场的抑制，由而产生一种抛物形线，即行星运动轨道形状具有椭圆或螺旋形，另外，它在运动过程中出现大量剧烈变化。

等时轨道模型是根据英国天文学家布洛克在1609年提出的费米力学原理而构建的。

他认为，行星的运行轨道具有椭圆的形状，靠近恒星的运动速度减慢，而离恒星的距离增加时，速度增加。

在这种做法下，行星在恒星系宇宙中运行时形成一种螺旋形轨道。

等时圆模型用一条。

等时圆问题模型总结等时圆问题模型是指在给定的一组点上，寻找一个圆，使得这个圆上的所有点到圆心的距离都相等。

这个问题在实际生活中有着广泛的应用，比如在无线传感器网络中，节点需要以某个节点为中心，以一定的范围进行通信，这就需要找到一个等时圆来满足通信需求。

在地理信息系统中，也经常需要寻找等时圆来确定某个地点的辐射范围。

因此，等时圆问题模型的研究具有重要的理论和实际意义。

在解决等时圆问题时，我们通常会采用数学建模的方法。

首先，我们需要确定给定点集上的一个圆心，然后确定这个圆心到各个点的距离，最后通过调整半径，使得这些距离相等。

这个过程可以用数学的方法来描述和求解。

在实际应用中，等时圆问题模型的解决往往需要考虑到一些实际情况的限制条件。

比如在无线传感器网络中，节点之间的通信范围可能受到地形、建筑物等因素的限制，这就需要在寻找等时圆的过程中考虑这些限制条件。

在地理信息系统中，地图的尺度、地形的复杂程度等因素也会对等时圆的确定产生影响。

因此，解决等时圆问题不仅需要数学方法，还需要考虑到实际应用中的各种因素。

近年来，随着计算机技术的发展，人们对等时圆问题的研究也取得了一些进展。

通过计算机模拟和优化算法，可以更快速、更精确地求解等时圆问题。

同时，人工智能、机器学习等技术的应用也为等时圆问题的求解提供了新的思路和方法。

总的来说，等时圆问题模型是一个具有理论和实际意义的重要问题。

在实际应用中，我们需要综合考虑数学建模、实际限制条件以及计算机技术等因素，来寻找等时圆的最优解。

希望在未来的研究中，我们可以进一步深化对等时圆问题的理解，为实际应用提供更加可靠、高效的解决方案。

等时圆模型 稷王中学 李王东一、等时圆模型1、物体沿着位于同一竖直圆上的所有光滑弦由静止下滑，到达圆周最低点时间均相等，且为g2t R= 2、物体沿着位于同一竖直圆上的所有过顶点的光滑弦由静止下滑，到达圆周低端时间相等为g2t R=说明：沿不同的弦轨道运动的时间相等，都等于小球沿竖直直径（d ）自由落体的时间，即g2g 4g d 2t 0RR ===（式中R 为圆的半径。

）二、等时性的证明设某一条弦与水平方向的夹角为α，圆的直径为d （如右图）。

根据物体沿光滑弦作初速度为零的匀加速直线运动，加速度为αgs in a =，位移为αg s i n a =，所以运动时间为gd2gsin dsin 2a s 2t 0===αα 即：沿各条弦运动具有等时性，运动时间与弦的倾角、长短无关。

说明：如果细杆是粗糙的，环与细杆间的动摩擦因数都为μ，由运动学公式有2t g c os -gs i n 21s i n 2）（θμθθ=R ，解得θμθμθgco t-g 2g c o s -gs i n s i n 2t RR ==，θ增大，时间t 减小，规律不成立.2004年高考试题：1、如图1所示，ad 、bd 、cd 是竖直面内三根固定的光滑细杆，a 、b 、c 、d 位于同一圆周上，a 点为圆周的最高点，d 点为最低点。

每根杆上都套有一个小滑环（图中未画出），三个滑环分别从a 、b 、c 处释放（初速为0），用t 1、t2、t 3依次表示各滑环到达d 所用的时间，则（ ）A.t 1<t 2<t 3B.t 1>t 2>t 3C.t 3>t 1>t 2D.t 1=t 2=t 3 解析：选任一杆上的环为研究对象，受力分析并建立坐标如图所示，设圆半径为R ，由牛顿第二定律得，ma mgcos =θ① 再由几何关系，细杆长度 θcos 2R L = ② 设下滑时间为t ，则 2at 21=L ③ 由以上三式得，g2t R=可见下滑时间与细杆倾角无关，所以D 正确。