安培环路定理解读

安培环路定理
安培环路定理，又称为安培定理或安培第二定理，是电磁学中的一条重要定理，描述了由电流所产生的磁场的性质。

它是由法国物理学家安德烈-玛丽·安培在19世纪初提出的。

安培环路定理是基于麦克斯韦方程组中的一个方程，可以用来计算磁场的强度。

根据该定理，通过电流所形成的磁场的磁感应强度H，沿着任意封闭曲线所围成的面积S的总磁通量Φ，与该封闭曲线所围成的电流之间的关系为：
∮H·dl = ∫∫S B·dS = Φ
其中，H是磁场的强度，dl是沿着闭合曲线的微元路径元素，B是磁感应强度，dS是平面面元素，Φ是通过该曲线所围成的面积的磁通量。

安培环路定理本质上是一个积分方程，可以通过对曲线的路径和曲面的选择来灵活地应用。

根据闭合曲线的选择不同，可以得到更方便的计算磁场的方法。

通常情况下，选择封闭曲线为简单的几何形状，例如圆形、矩形或直线，可以大大简化计算的过程。

安培环路定理的应用广泛，可以用于解决与电流所产生的磁场相关的问题。

例如，在电磁铁中，可以利用安培环路定理计算铁芯的磁场分布；在电感器中，可以通过该定理计算电感量。

此外，还可以利用安培环路定理推导出其他电磁学中的重要定理，如磁场的叠加定理和比奥-萨伐尔定律等。

综上所述，安培环路定理是电磁学中的一条基本定理，描述了电流所产生的磁场的性质。

通过应用安培环路定理，可以方便地计算出磁场的强度和分布，解决各种与电流和磁场相关的问题，为电磁学的研究和应用提供了重要的理论基础。

安培环路定理的表达式
安培环路定理：
1. 定义：安培环路定理是一种复杂的物理电路原理，它可以用来求出
一个电路中的特定电场和电势差之间的关系。

它表明，任意一个无逆
反元件的环路中，环路中的电势差与环路中的电流的乘积之和等于零。

2. 公式：安培环路定理表示为:ΣV=0，其中V表示环路中有电势差的元件/器件，负号表示电势差方向与电流方向相反，Σ符号表示环路中所
有器件的电势差求和。

3. 对它的解释：安培环路定理告诉我们，只要通过一个无逆反电路，
将环路中每个电子器件的电势差之和求出，就能够找出环路中的电流
是多少。

即在一个无逆反电路中，任意一连接线或分支的电势差与环
路中的电流的乘积之和等于零。

4. 安培环路定理的应用：安培环路定理涉及多个电路分析技术，广泛
应用于工程领域，如汽车电子、发电机、电源系统、电子设备等。

具
体来说，它可以用于计算电压和电流变化之间的关系。

同时，电路分
析问题的研究也是在安培环路定理的指导下进行的。

而安培环路定理
也利于我们更好地了解短路，而短路提供了进一步了解电路的方式。

安培环路定理静电场中的环路定理为，它说明静电场是保守场。

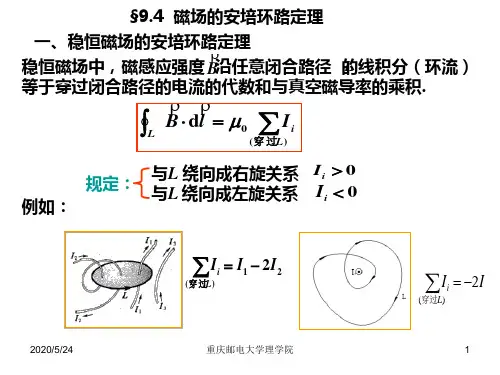
在稳恒磁场中，磁感应强度B 沿任意闭合环路的线积分（又称B 的环流）等于什么？磁场是否为保守场？安培环路定律回答了上述问题。

设在真空中有一无限长载流直导线，其电流为I 。

取一平面与电流垂直，平面与电流相交与O 点，在平面内取以O 为圆心、r 为半径的闭合回路L ，在圆周上各点磁感强度B 的大小为若B 的方向与积分的绕行路径L 上各处dl 的方向相同，即B 与dl 的夹角θ= 0，则B 的环流为若积分的绕行方向反向，即B 与dl 方向相反,,则B 的环流为0=∙⎰dl E Ldl B L∙⎰r I B πμ20=⎰⎰==∙L L Idl r Idl B 002μπμπθ=⎰⎰-=-=∙LLI dl r Idl B )(200μπμ可把上述结果推广到闭合回路为任意形状，而且回路中包围有任意电流（包括回路中不包围电流）的情况，因而，可得B 的环流为（9-9）上式为安培环路定理的表述式。

它表明，在稳恒磁场中，磁感强度B 沿任何闭合回路L 的线积分，等于穿过这个回路所围曲面的所有电流的代数和的μ0倍。

电流的正负规定如下：取右手螺旋的旋转方向（四指弯曲方向）为积分回路L 的绕行方向，与右螺旋前进方向（拇指指向）一致的电流为正，反之为负。

如图9-9所示，则式（9-9）右侧不计入I 3 。

在图9-9所示的情况下，安培环路定理表示为当闭合回路不包围电流，或虽包围电流，但所围电流的代数和为零时，B 的环路等于零。

安培环路定理表明稳恒磁场不是保守场。

一般称环流不等于零的场为蜗旋场。

稳恒磁场是蜗旋场，这时它不同于静电场的又一特征。

⎰∑=∙LL Idl B 内）(0μ()210I I dl B L-=∙⎰μ为了更好地理解安培环路定理，作如下说明：（1）式（9-9）右方的∑I 中只包括穿过闭合回路L 的电流；（2）回路L 的绕行方向与穿过回路L 的电流的正、负符号，遵从右手螺旋法则，而∑I 为所有正、负电流的代数和；（3）式（9-9）左端的B 是环路上的磁感强度，它是空间所有电流（包括穿过L 和不穿过L 的电流）共同产生的；（4）如果，他只说明B 沿L 的环流为零（此时，L 所围电流代数和等于零或不围电流）而不能理解为回路L 上各点的B 一定等于零。

安培环路定理和毕奥萨伐尔定律是电磁学中重要的定理和法则，它们在描述电路中电流和磁场的关系上起着关键作用。

下面将分别对这两个定理进行介绍和解析。

一、安培环路定理安培环路定理又称安培定律，是电磁学中重要的定理之一，它描述了磁场中闭合曲线上的磁场强度与该曲线所围成的电流的关系。

安培环路定理可以总结为以下几点：1. 磁场环路定理的表述在闭合曲线上的磁场强度的矢量和等于该曲线所围成的电流的矢量和乘以一个常数μ0，即ΣH·dl=μ0ΣI。

2. 安培环路定理的数学表达式安培环路定理的数学表达式为∮H·dl=μ0∑I，其中∮H·dl表示磁场强度矢量沿着曲线的积分，μ0为真空磁导率，∑I表示曲线所围成电流的代数和。

3. 安培环路定理的应用安培环路定理可以用于计算闭合曲线中的磁场强度，是电磁学中重要的工具之一。

通过安培环路定理，可以求解复杂电路中的磁场分布，为电磁学的研究和应用提供了重要的方法。

二、毕奥萨伐尔定律毕奥萨伐尔定律是电磁学中描述通过导体中电流产生的磁场的定律，它对于电路和电磁场的分析具有重要意义。

以下是毕奥萨伐尔定律的主要内容：1. 毕奥萨伐尔定律的表述毕奥萨伐尔定律指出，通过导体中电流产生的磁场的强度与导体上任意点到电流元素的距离成正比，在大小和方向上满足右手定则。

2. 毕奥萨伐尔定律的数学表达式毕奥萨伐尔定律的数学表达式为B=μ0/4π∫(Idl×r)/r^3，其中B表示磁场强度，μ0为真空磁导率，Idl表示电流元素，r为导体上任意点到电流元素的距离。

3. 毕奥萨伐尔定律的应用毕奥萨伐尔定律可用于计算导体中的磁场分布，也可以应用于分析电路中的电流产生的磁场对周围环境的影响。

在电磁学的理论研究和工程实践中，毕奥萨伐尔定律都具有重要的应用价值。

总结安培环路定理和毕奥萨伐尔定律是描述电流和磁场之间关系的重要定理，在电磁学的理论研究和工程应用中起着关键作用。

通过学习和理解这两个定律，可以更好地理解电磁学的基本原理，为电路和电磁场的分析提供重要的方法和工具。

磁介质中的安培环路定理
安培环路定理是描述电流在一个闭合环路内的磁场强度的定量关系的定理。

在磁介质中，安培环路定理可以表述为：闭合环路内的磁通量等于环路内电流所产生的磁场强度与环路中磁化强度的代数和。

换句话说，如果我们将一个磁介质的闭合环路划分成若干小段，对每一小段进行磁场分析，然后将它们按照一定的方向按顺序排列，就形成了一个完整的安培环路。

在磁介质中，该安培环路的总磁通量等于环路内任意一个小段上的磁场强度与该小段上的磁化强度的代数和。

这个定理主要用于计算磁介质中的磁场分布及其对电路的影响。

对于任意一个闭合环路，我们都可以通过安培环路定理求得环路内的磁通量，再根据法拉第电磁感应定律计算出环路内的感应电动势，从而分析电路中的电磁现象。

总之，安培环路定理是一种描述磁介质中电流与磁场强度之间关系的基本定理，是电磁学研究中不可或缺的重要工具。

安培环路定理的原理及应用1. 安培环路定理的原理安培环路定理是电磁学中的基本定理之一，它描述了电流通过一个封闭路径的总和等于该路径上环绕的总磁场的空间积分。

安培环路定理是麦克斯韦方程组中的一部分，对于理解和分析电路中的电磁现象非常重要。

根据安培环路定理，一个封闭路径上的环绕磁场的空间积分等于该路径上的电流的总和乘以真空中的磁导率常数，即：$$\\oint \\vec{B} \\cdot \\vec{dl} = \\mu_0 \\cdot I_{\\text{enc}}$$其中， - $\\vec{B}$ 表示磁场的矢量 - $\\vec{dl}$ 表示路径上的无穷小位移矢量 - $\\mu_0$ 是真空中的磁导率常数 - $I_{\\text{enc}}$ 表示通过封闭路径所包围的电流的总和2. 安培环路定理的应用2.1 电磁铁电磁铁是利用安培环路定理工作的重要装置之一。

在电磁铁中，通电线圈产生的磁场可以吸引或排斥物体，从而实现各种实际应用。

根据安培环路定理，我们可以通过改变通电线圈中的电流大小来控制磁场的强度，进而达到对物体的吸引或排斥。

2.2 变压器变压器也是应用安培环路定理的重要设备。

变压器是一种用于改变交流电压的装置，它由两个共用一个磁路的线圈构成。

输入线圈（原线圈）中的交流电流通过变压器的磁场感应出感应电动势，进而产生在输出线圈上的输出电压。

安培环路定理被用于分析和计算变压器中的磁场和电流之间的关系。

2.3 电感与电感耦合安培环路定理在电感和电感耦合的研究和应用中也起到了重要作用。

电感是一种储存电能的元件，当电流通过电感时，会在其周围产生磁场。

根据安培环路定理，我们可以得到电感中的磁场与电流的关系，从而进一步分析和设计电感相关的电路。

而电感耦合是指通过电感的互相感应，将两个或多个电路联系起来。

在电感耦合的应用中，安培环路定理可用于计算和描述各个电路之间的电磁相互作用，以及电感耦合的性能与参数之间的关系。

安培环路定理的三个公式安培环路定理是电磁学中的一个重要定理，它描述了磁场的环流与电流之间的关系。

在这个定理中，有三个常用的公式，下面咱们就来好好唠唠这三个公式。

咱们先来说说第一个公式，这个公式表述为：在真空中，磁感应强度 B 沿任何闭合回路的线积分，等于穿过该回路所包围面积的电流的代数和乘以真空磁导率μ₀。

这听起来可能有点绕，咱举个例子啊。

就比如说，你想象有一个环形的电线，电流在里面流动。

咱们把这个环形电线想象成一个跑道，而磁场呢，就像是在跑道上奔跑的运动员。

这个运动员沿着跑道跑一圈，他跑的路程就是磁感应强度 B 的线积分。

而跑道里面的电流，就决定了这个运动员跑得有多快、跑的路程有多长。

再来讲讲第二个公式。

这个公式在有介质存在的情况下适用。

啥是介质呢？简单说，就是除了真空以外的其他物质。

这时候，磁感应强度 B 沿闭合回路的线积分，等于穿过回路所包围面积的传导电流和磁化电流的代数和乘以真空磁导率μ₀。

咱还是举个例子。

假设你有一块磁铁，周围有一些铁粉。

这些铁粉会被磁铁吸引，形成特定的分布。

这个分布就相当于一种介质。

在这种情况下，磁场的环流就不仅仅取决于传导电流，还和磁化电流有关。

最后说说第三个公式。

这个公式是在时变电磁场中的情况。

它可就更复杂一点啦，磁感应强度 B 沿闭合回路的线积分，等于穿过回路所包围面积的全电流的代数和乘以真空磁导率μ₀。

这里的全电流包括传导电流、位移电流。

那啥是位移电流呢？想象一下，有一个电容器正在充电，虽然没有电荷在电容器极板之间流动，但是电场在变化，就好像有电流在流动一样，这就是位移电流。

我记得之前给学生们讲这部分内容的时候，有个小家伙瞪着大眼睛一脸懵地问我：“老师，这也太抽象了，到底有啥用啊？”我笑着跟他说：“孩子，你想想咱们家里用的电器，比如电灯泡能亮、风扇能转，这里面可都离不开这些知识呢。

”那孩子似懂非懂地点点头。

其实啊，安培环路定理的这三个公式虽然看起来复杂，但在实际的电磁学应用中可是非常重要的。

《大学物理》作业 No.6 磁场的安培环路定理班级 ___________ 学号 __________ 姓名 ____________ 成绩 __________说明：字母为黑体者表示矢量内容提要：安培环路定理 ∑⎰=⋅I l d B L0μ1. 安培环路定理的理解：①B是环路上各点的磁感应强度，是环路内外所有电流共同激发的磁场。

②∑I 只是被环路包围的电流的代数和。

③不被环路包围的电流在环路上激发的磁场在环路的线积分中抵消掉了。

④环路上各点0=B 时，必有0=∑I ；但0=∑I 时，未必环路上各点的B 一定都为零。

⑤对于电流的正负的规定：当电流的方向与环路积分的方向符合右手螺旋关系时，电流为正，否则为负。

⑥安培环路定理中的电流应该是闭合（或无限长）恒定电流，对于一段恒定电流的磁场，安培环路定理不成立。

2. 安培环路定理的应用：①只有在磁场具有较好的对称性时才能用安培环路定理求解B ，但安培环路定理是普遍成立的，不具有较好对称性的磁场不能用安培环路定理求解B ，但定理依然成立。

②利用安培环路定理求磁场分布一般包含两步：首先依据电流的对称性分析磁场分布的对称性，然后再利用安培环路定理计算磁感应强度的数值和方向。

此过程中决定性的技巧是选取合适的闭合路径L （环路），以便⎰⋅Ll d B 中的B 能以标量形式从积分号内提出来。

基本要求：1.掌握安培环路定理：2.掌握安培环路定理分析计算磁感应强度的条件和方法，并能熟练运用。

一、选择题1.如图6.1所示,有两根无限长直载流导线平行放置,电流分别为I 1和I 2, LI 1在L 内,I 2在L 外,P 是L 上的一点,今将I 2 在L 外向I 1移近时,则有 [ ] (A)l B d ⋅⎰L与B P同时改变. (B) l B d ⋅⎰L与B P都不改变. (C) l B d ⋅⎰L不变,B P改变.(D)l B d ⋅⎰L改变,BP不变.2.对于某一回路l ，积分l B d ⋅⎰l等于零，则可以断定I 图6.1[ ] (A) 回路l 内一定有电流. (B) 回路l 内可能有电流.(C) 回路l 内一定无电流. (D) 回路l 内可能有电流，但代数和为零.3. 如图6.2所示，两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上，稳恒电流I 从a 端流入而从d 端流出，则磁感应强度B 沿图中闭合路径L 的积分l B d ⋅⎰l等于[ ] (A) I u 0(B) I u 031(C)I u 041(D) I u 0324. 用相同细导线分别均匀密绕成两个单位长度匝数相等的半径为R 和r 的长直螺线管(R =2r )，螺线管长度远大于半径.今让两螺线管载有电流均为I ，则两螺线管中的磁感强度大小B R 和B r 应满足：[ ] (A) B R = 2B r . (B) B R = B r . (C) 2B R = B r . (D) B R = 4B r .二、填空题1.在安培环路定理中iLI∑=⋅⎰0d μl B , 其中∑I i 是指 ;B 是由 的电流产生的.2. 两根长直导线通有电流I ,图6.3所示有三种环路,对于环路a ,=⋅⎰a L l B d ;对于环路b , =⋅⎰b L l B d 。

磁场中的安培环路定理磁场中的安培环路定理是电磁学中的一条重要定律，描述了磁场中电流的产生和作用规律。

通过安培环路定理，我们可以更好地理解和分析电磁现象，并应用于实际问题的求解。

安培环路定理的核心思想是，磁场中的闭合回路上的环流等于该回路所包围的总电流的代数和的倍数。

换句话说，磁场中的环流产生的磁场强度与该环路所包围的电流有直接的关系。

为了更好地理解安培环路定理，我们可以通过一个简单的实例来说明。

想象一下，我们有一个长直导线，通过它有一定大小的电流流过。

我们用一张纸将导线覆盖起来，并在纸上标出一个闭合的任意形状。

随后，我们在导线周围放置一个磁场感应器，并记录下所测得的磁场强度。

根据安培环路定理，我们可以得出结论：所测得的磁场强度与所包围的电流有直接的关系。

也就是说，随着电流的增大，所测得的磁场强度也会增大；反之，随着电流的减小，磁场强度也会相应减小。

这一定律在电磁学中具有广泛的应用。

在实际应用中，安培环路定理可以帮助我们解决许多与磁场和电流有关的问题。

例如，在电动机的设计过程中，我们可以利用安培环路定理来计算电动机所需的磁场大小。

同样，在电磁铁的设计中，我们也可以通过安培环路定理来确定所需的电流大小。

除了上述的应用，安培环路定理还可以用于求解磁场的分布情况。

通过将闭合回路划分为许多小段，我们可以对每一小段的环流进行求和，并根据安培环路定理计算出整个回路上的环流。

进一步地，我们可以根据磁场的分布情况，推导出磁场强度在不同位置的数值。

需要注意的是，安培环路定理是基于一些假设的。

例如，假设所研究的磁场是稳定的，即磁场不随时间变化；同时，假设所研究的回路是理想的，即电阻为零。

虽然这些假设在实际中并不总是成立，但在许多情况下，它们可以作为近似的模型来使用，从而能够得到比较准确的结果。

磁场中的安培环路定理是电磁学中的一条重要定律，它描述了磁场中电流的产生和作用规律。

通过安培环路定理，我们可以更好地理解和分析电磁现象，并应用于实际问题的求解。

安培环路定理的表述和证明磁感应线是套连载闭合载流回路上的闭合线。

若取磁感应强线的环路积分，则因B与dL的夹角θ=0，cosθ=1,故在每条线上，从而。

安培环路定理就是反映磁感应这一特点的。

安培环路定理：磁感应强度沿任何闭合环路L的线积分，等于穿过这环路全部电流强度的代数和的μ0倍。

用公式表示有: 。

其中电流I的正负规定如下：当穿过回路L的电流方向与回路L的环绕方向听从右手法则时，I0,反之，I0。

假如电流不穿过回路L，则它对上式右端无贡献。

安培环路定理的证明,如图：dL是L上的线元，dL'代表载流回路L'上的线元。

根据毕奥-萨伐尔定律:其中代表dS对场点P所张的立体角dω,沿L'的积分代表整个载流回路作位移-dl时扫过的带状面对P点所张的立体角ω。

所以。

假设以L'为边界作一曲面S'，S'对P点也张有肯定的立体角Ω。

当L'平移时，Ω随之转变。

如上图L2'和L1'分别是L'沿-dl平移前后的新、旧位置，令S2'和S1'代表S'的相应位置，Ω2和Ω1代表相应的立体角。

因S2'和S1'和带状面组成闭合曲面，它对于外边的P点所张的总立体角Ω2-Ω1+ω=0，所以:由于dl是任意的，从而，即磁场正比于载流线圈对场点所张立体角的梯度。

假设场点P沿闭合的安培环路L移动一周，则环路积分将正比于立体角Ω在此过程中的总转变量ΔΩ。

假如L不与L'套连，则ΔΩ=0，于是: 但是，当L与L'套连时，ΔΩ=4π。

因此：。

所以安培环路定理得证。

留意：该定理表达式中各物理量的意义。

I只包括穿过闭合回路L的电流。

B代表空间全部电流产生的磁场强度的矢量和，其中也包括那些不穿过L的电流产生的磁场，只不过后者的磁场沿闭合环路积分后的总效果为0。

I只包括穿过闭合回路L的电流。

磁场安培环路定理一、引言磁场安培环路定理是电磁学中的重要定理之一，它描述了磁场沿闭合回路的环流与该回路所围面积上的磁通量之间的关系。

本文将从理论和应用两个方面对磁场安培环路定理进行探讨。

二、理论基础2.1 安培环路定理的表达方式磁场安培环路定理可以用数学方式表示为：∮B⃗ ⋅dl=μ0⋅I其中，左侧表示磁场矢量B⃗ 沿闭合回路的环流，右侧表示该回路所围面积上的磁通量，μ0为真空中的磁导率，I为通过该回路的电流。

2.2 安培环路定理的推导安培环路定理可以通过安培力定律和法拉第电磁感应定律的结合推导得到。

根据安培力定律，我们知道磁场对通过导线的电流会产生力。

根据法拉第电磁感应定律，我们知道变化的磁场会引起感应电动势。

结合这两个定律，可以得到磁通量与电流之间的关系，从而推导出安培环路定理。

三、应用实例磁场安培环路定理在电磁学中有着广泛的应用，下面将介绍一些实际应用的例子。

3.1 磁场的计算磁场安培环路定理可以用来计算磁场的大小和方向。

通过选择适当的闭合回路，可以测量电流所产生的磁场。

根据安培环路定理，可以将测得的环路上的环流与围绕该回路的面积上的磁通量相对应，从而计算得到磁场的大小。

3.2 电磁铁的设计电磁铁是一种利用电磁感应原理工作的装置，它可以产生强大的磁场。

在设计电磁铁时，可以利用安培环路定理来确定所需的电流和线圈的绕制方式。

通过测量所需磁场的大小和形状，可以确定合适的回路和线圈参数，从而实现对磁场的精确控制。

3.3 磁场的传感器磁场传感器是一种用于检测和测量磁场的设备，它在许多领域中都有广泛的应用，如导航、地质勘探等。

磁场安培环路定理可以用于传感器的设计和校准。

通过选择合适的回路和测量环路上的环流，可以将磁场的变化转化为电信号，并进行准确的测量和分析。

四、总结磁场安培环路定理是电磁学中的重要定理，它描述了磁场沿闭合回路的环流与该回路所围面积上的磁通量之间的关系。

本文从理论和应用两个方面对磁场安培环路定理进行了探讨。

安倍环路定理（Ampère's Circuital Law）是电磁学中的一个基本定律，描述了电流产生的磁场的特性。

它是法国物理学家安德烈-玛丽·安倍于1826年提出的，被广泛应用于电磁场的分析和计算中。

安倍环路定理陈述如下：通过任何闭合路径的磁场线积分等于该路径内所包围的电流总和的倍数，即：
∮B·dl = μ₀ΣI
其中，∮B·dl表示对磁场B沿闭合路径的环路积分，μ₀为真空磁导率（约等于4π×10⁻⁷特斯拉·米/安培），ΣI表示闭合路径内的电流总和。

换句话说，安倍环路定理指出了通过一个闭合路径所围绕的磁场总量与该路径内所包围的电流的关系。

安倍环路定理可以用于计算静态和稳恒电流产生的磁场分布。

它对于分析磁场的对称性和确定电流分布与磁场之间的关系非常有用。

需要注意的是，安倍环路定理适用于没有电场变化或电场变化非常缓慢的情况。

对于存在变化的电场或非静态情况，需要结合法拉第电磁感应定律等其他定律进行综合分析。

安培环路定理知识点安培环路定理（Kirchhoff's loop rule），又称为基尔霍夫环路定律，是电路分析中的重要基本原理。

它描述了在闭合电路中电流的流动规律，从而帮助我们理解和解决各种电路问题。

本文将介绍安培环路定理的定义、原理和应用。

一、安培环路定理的定义安培环路定理是基于电荷守恒定律和电场的环路定理推导而来的。

根据安培环路定理，在任何一个闭合电路中，电流的代数和必须等于零，即电流在电路中经过各分支的代数和等于电流离开电路的代数和。

二、安培环路定理的原理1. 闭合电路的特性安培环路定理适用于闭合电路，即电流可以通过一条回路从一个点流向另一个点。

闭合电路是电流分析的基本前提，只有满足闭合条件，安培环路定理才能有效地应用。

2. 电流的代数和为零根据安培环路定理，电流的代数和在闭合电路中必须等于零。

这是因为电流在电路中没有被消耗或产生，而是通过各分支流动，因此电流的代数和保持平衡。

3. 方向与正负号在应用安培环路定理时，我们需要为电路中的每个分支选择一个参考方向，并赋予正负号。

一般来说，沿着参考方向流动的电流取正号，相反方向流动的电流取负号。

4. 电阻和电动势根据欧姆定律，电阻中的电流与电压成正比。

在安培环路定理中，我们可以使用电阻和电动势（如电池或电源）来描述电路中的元件。

电动势提供了驱动电流流动的能量。

三、安培环路定理的应用1. 电路分析安培环路定理是电路分析中常用的工具，特别适用于复杂电路的分析。

通过将电路划分为多个闭合回路，并应用安培环路定理，我们可以解析电流和电压的分布，找到各个分支中的电流大小和方向。

2. 电源电流计算在电路中，电源提供了电流的驱动力。

应用安培环路定理，我们可以通过计算各个分支中的电流来确定电源的输出电流。

这对于设计电路和选择合适的电源非常重要。

3. 电感和电容的分析除了电阻和电源外，安培环路定理也适用于电感和电容。

在交流电路中，电感和电容的特性可以通过安培环路定理来分析，并计算它们在电路中的作用。