【物理】2010届高考物理专题复习课件:运动和力11
- 格式:ppt
- 大小:887.50 KB
- 文档页数:56
第三课时专题:运动图象追及相遇问题•一、对直线运动的s-t图象的认识•1.物理意义:反映了做直线运动的物体位移随时间变化的规律.•2.图线斜率的意义•(1)图线上某点切线的斜率大小表示物体速度的大小.•(2)图线上某点切线的斜率正负表示物体速度的方向.•1.图线与横轴和纵轴的截距,各表示什么物理意义?•2.物体沿x轴运动,观察者在O点,在x轴上有A、B、C三个点,它们到观察者的距离分别为4 m、4 m、8 m,如下图甲所示.请在下图乙中做出观察者看到的下列物体运动的位移—时间图象.•(1)物体甲从O点开始以1 m/s的速度沿x轴正方向运动;•(2)物体乙在B点静止;•(3)物体丙从A点开始以1 m/s的速度沿x轴正方向运动;•(4)物体丁从C点开始以2 m/s的速度沿x轴负方向运动.•二、对直线运动的v-t图象的理解•1.物理意义:反映了做直线运动的物体速度随时间变化的关系.•2.图线斜率的意义•(1)图线上某点切线的斜率大小表示物体运动的加速度的大小.•(2)图线上某点切线的斜率正负表示运动的加速度的方向.•3.图象与坐标轴围成的“面积”的意义•(1)图象与坐标轴围成的面积表示相应时间内的位移.•(2)若此面积在时间轴的上方,表示这段时间内的位移方向为正方向;若此面积在时间轴的下方,表示这段时间内的位移方向为负方向.•3.图线与横轴和纵轴的截距,各表示什么物理意义?•4.物体沿x轴运动,请在右图中做出物体运动的速度—时间图象.•(1)物体甲以2 m/s的速度,沿x轴正方向做匀速运动;• (2)物体乙以2 m/s 的速度,沿x 轴负方向匀速运动;• (3)物体丙由静止以1 m/s 2的加速度沿x 轴正方向运动;• (4)物体丁以4 m/s 的初速度,1 m/s 2的加速度沿x 轴正方向做匀减速运动.• 【轻轻告诉你】• 思考1.图线在横轴上的截距表示物体从记时开始过一段时间从参考点出发.图线与纵轴的截距表示开始计时时物体相对于参考点的位移.•思考2.如图所示;图线在横轴t上的截距表示物体从记时开始过一段时间才开始运动.•思考3.图线在纵轴上的截距表示运动物体的初速度v•思考4.如下图•三、根据v-t图象的形状判断物体的运动性质•1.图线是直线:表示物体做匀变速直线运动(一条倾斜的直线)或匀速直线运动(一条平行于t轴的直线).•2.图线是曲线:表示物体做变加速直线运动,图线上某点切线的斜率表示该点对应时刻的加速度,如图所示表示a、b、c、d四个物体的v-t图线.•a表示物体在做加速度减小的加速运动•b表示物体在做加速度减小的减速运动•c表示物体在做加速度增大的减速运动•d表示物体在做加速度增大的加速运动••(1)v-t图象斜率为正(即向上倾斜)不一定做加速运动,斜率为负(即向下倾斜)不一定做减速运动.•(2)无论是v-t图象还是s-t图象都不表示物体的运动轨迹.•四、追及、相遇•1.追上与追不上的临界条件•追和被追的两者的速度相等时常是能追上、追不上、二者距离有极值的临界条件.•2.追及、相遇的特征•两物体在同一直线上运动,他们之间的距离发生变化时,可能出现最大距离、最小距离或者是距离为零的情况,这类问题称为追及、相遇问题.•(1)速度大者减速(如匀减速直线运动)追速度小者(如匀速运动)•①两者速度相等时,追者位移仍小于被追者位移与初始间距之和,则永远追不上,此时二者间有最小距离.•②若速度相等时,若追者位移恰等于被追者位移与初始间距之和,则刚好追上,也是二者相遇时避免碰撞的临界条件.•③若相遇时追者速度仍大于被追者的速度,则被追者还能再一次追上追者,二者速度相等时,二者间距离有一个较大值.•(2)速度小者加速(如初速度为零的匀加速直线运动)追速度大者(如匀速运动)•①当两者速度相等时二者间有最大距离.•②当追者位移等于被追者位移与初始间距之和时,即后者追上前者(两物体从同一位置开始运动)即相遇.•列车以72 km/h的速度行驶,司机突然发现同一平直铁路上前方500 m处,一货车正以36 km/h的速度同向行驶,为避免撞车,列车司机立即刹车,求列车刹车时加速度的最小值.• 【解析】 设列车刹车的加速度大小为a ,刹车后经时间t ,列车速度与货车速度相等,这段时间内货车、列车的位移分别为s 1、s 2,如图所示,则不撞车的条件是• s 1+500≥s 2 ①• 且有s 1=v 1t• 根据匀变速运动规律有 ②• s 2=v 2t - at 2③• v 2-at =v 1 ④ • 由④得t =•代入②、③,结合①得:•a≥=0.1 m/s 2(s=500 m)•即最小加速度为0.1 m/s 2 .•【答案】0.1 m/s 2•如下图所示,甲、乙、丙、丁是以时间为横轴的匀变速直线运动的图象,下列说法正确的是()•A.甲是a-t图象B.乙是s-t图象•C.丙是s-t图象D.丁是v-t图象•【解析】匀变速直线运动的加速度恒定,其速度随时间均匀变化,故A、D错;匀变速直线运动的位移—时间关系为s=v0t+at2,图象丙是v=0时的位移—时间图象,故C对B错.•1-1:某人骑自行车在平直道路上行进,右图中的实线记录了自行车开始一段时间内的v-t图象.某同学为了简化计算,用虚线作近似处理,下列说法正确的是()•A.在t1时刻,虚线反映的加速度比实际的大•B.在0~t1时间内,由虚线计算出的平均速度比实际的大•C.在t1~t2时间内,由虚线计算出的位移比实际的大•D.在t3~t4时间内,虚线反映的是匀速直线运动•【解析】如图所示,t1时刻,实线上A点的切线为AB,实际加速度为AB的斜率,由图可知虚线反映的加速度小于实际加速度,故选项A错误;在v-t图象中,位移等于所对应图线与坐标轴所包围的面积,0~t1时间内,虚线所对应的位移大于实线所对应的位移,由知,由虚线计算出的平均速度比实际的大,故选项B正确;在t1~t2时间内,虚线计算出的位移比实际小,故选项C错误;t3~t4时间内虚线为平行于时间轴的直线,此线反映的运动为匀速直线运动,故选项D正确.•【答案】BD•如图所示,甲、乙两运动物体相对同一原点的位移—时间图象,下面有关说法中正确的是() •A.甲和乙都做匀速直线运动•B.甲、乙运动的出发点相距s•C.乙运动的速率大于甲运动的速率•D.乙比甲早出发t1时间•【解析】图中表示s-t图象都是直线,所以甲、乙均是做匀速直线运动,故A正确;因t=0,甲图象在s轴的截距为s,而乙图象表示乙在原点,所以出发点相距s.故B正确;因乙图象的斜率大于甲图象斜率的绝对值,所以乙运动速率大于甲运动速率,故C正确;从图象中可以看出甲比乙早出发t1的时间,故D错.•运用图象时的注意问题•(1)首先明确所给的图象是什么图象.即认清图象中横纵轴所代表的物理量及它们的函数关系.•(2)要清楚地理解图象中的“点”、“线”、“斜率”、“截距”、“面积”的物理意义.•①点:图线上的每一个点对应研究对象的一个状态,特别要注意“起点”、“终点”、“拐点”,它们往往对应一个特殊状态.•②线:表示研究对象的变化过程和规律,如v-t图象中图线若为倾斜直线,则表示物体做匀变速直线运动.•③斜率:表示横、纵坐标上两物理量的比值,常有一个重要的物理量与之对应.•④面积:图线与坐标轴围成的面积常与某一表示过程的物理量相对应.•⑤截距:表示横、纵坐标两物理量在“边界”条件下的大小.由此往往能得到一个很有意义的物理量.•2-1:右图是甲、乙两物体做直线运动的v-t图象.下列表述正确的是()•A.0~1 s内甲和乙的位移相等•B.乙做匀加速直线运动•C.甲和乙的加速度方向相同•D.甲的加速度比乙的小•【解析】v-t图象的斜率代表加速度,所以B正确.两图象斜率的正、负不同,因此C错误.甲图象的斜率大于乙图象的斜率,所以D错误.图象下的面积表示位移,0~1 s内甲、乙图象下的面积不等,所以A错误.•【答案】B• 在水平轨道上有两列火车A 和B 相距s ,A 车在后面做初速度为v 0、加速度大小为2a 的匀减速直线运动,而B 车同时做初速度为零、加速度为a 的匀加速直线运动,两车运动方向相同.要使两车不相撞,求A 车的初速度v 0满足什么条件.• 【思路点拨】• 【解析】 解法一 (物理分析法)A 、B 车的运动过程(如图甲) • 利用位移公式、速度公式求解. • 对A 车有s A =v 0t + ×(-2a )×t 2• v A =v 0+(-2a )×t• 对B 车有s B = at 2,v B=at•两车有s=sA-sB•追上时,两车不相撞的临界条件是vA =vB•联立以上各式解得v=•故要使两车不相撞,A车的初速度v0应满足的条件是v≤.解法二 (极值法)利用判别式求解,由解法一可知 s A =s +s B ,即v 0t +12×(-2a )×t 2=s +12at 2整理得3at 2-2v 0t +2s =0这是一个关于时间t 的一元二次方程,当根的判别式 Δ=(2v 0)2-4×3a ×2s <0时,t 无实数解,即两车不相撞,所以要使两车不相撞,A 车的初速度v 0应满足的条件是v 0≤6as .解法三(图象法)利用速度—时间图象求解,先作A、B两车的速度—时间图象,其图象如图乙所示,设经过t时间两车刚好不相撞,则对A车有v A=v=v0-2at对B车有v B=v=at以上两式联立解得t=v0 3a经t时间两车发生的位移之差,即为原来两车间的距离s,它可用图中的阴影面积表示,由图象可知s=12v0·t=12v0·v03a=v206a所以要使两车不相撞,A车的初速度v0应满足的条件是v0≤6as.•对追及问题的一般分析思路•(1)根据追赶和被追赶的两个物体的运动性质,列出两个物体的位移方程,并注意两物体运动时间之间的关系.•(2)通过对运动过程的分析,画出简单的运动示意图,找出两物体的运动位移间的关系式,追及的主要条件是两个物体在追上时位置坐标相同.• 3-1:一辆值勤的警车停在公路边,当警员发现从他旁边以10 m/s 的速度匀速行驶的货车严重超载时,决定前去追赶,经过5.5 s 后警车发动起来,并以2.5 m/s 2的加速度做匀加速运动,但警车的行驶速度必须控制在90 km/h 以内.问: • (1)警车在追赶货车的过程中,两车间的最大距离是多少? • (2)警车发动后要多长时间才能追上货车?• 【解析】 (1)警车在追赶货车的过程中, 当两车速度相等时.它们间的距离最大,设警车发动后经过t 1时间两车的速度相等.则t 1=102.5s =4 ss 货=(5.5+4)×10 m =95 m s 警=12at 21=12×2.5×42 m =20 m所以两车间的最大距离Δs =s 货-s 警=75 m(2)v0=90 km/h=25 m/s,当警车刚达到最大速度时,运动时间t2=252.5s=10 ss′货=(5.5+10)×10 m=155 ms′警=12at22=12×2.5×102 m=125 m因为s′货>s′警,故此时警车尚未赶上货车,且此时两车距离Δs′=s′货-s′警=30 m•警车达到最大速度后做匀速运动,设再经过Δt时间追赶上货车,则Δt==2 s•所以警车发动后要经过t=t2+Δt=12 s才能追上货车•【答案】(1)75 m(2)12 s•1.某质点做直线运动的位移s和时间t的关系如图所示,那么该质点在3 s内通过的路程是()•A.2 m B.3 m•C.1 m D.0.5 m•【解析】由题图可知,在0~1 s内质点静止在位移为1 m的地方;1~2 s内质点从位移为1 m的地方匀速运动到位移为2 m的地方;在2~3 s内质点静止在位移为2 m的地方,因而质点在3 s内的路程即为在1~2 s内通过的路程,应为1 m.•【答案】C•2.(2009年广东卷)某物体运动的速度图象如图所示,根据图象可知()2•A.0~2 s内的加速度为1 m/s•B.0~5 s内的位移为10 m•C.第1 s末与第3 s末的速度方向相同•D.第1 s末与第5 s末加速度方向相同• 【解析】 0~2 s 内的加速度(即图象的斜率)a ==1 m/s 2,故A 对;0~5 s 内的位移为x = (2+5) ×2 m =7 m ,故B 错;从图象可以看出,第1 s 末与第3 s 末物体的速度都为正值,即都与所设的正方向相同,故C 对;而在第5 s 末的加速度为负,所以D 错误. • 【答案】 AC• 3.如下图所示s -t 图象和v -t 图象中,给出四条曲线1、2、3、4代表四个不同物体的运动情况,关于它们的物理意义,下列描述正确的是( )• A .图线1表示物体做曲线运动 • B .s -t 图象中t 1时刻v 1>v 2•C.v-t图象中0至t3时间内4的平均速度大于3的平均速度•D.两图象中,t2、t4时刻分别表示2、4开始反向运动•【答案】BC•4.在2008年北京奥运会上,两艘赛艇a、b在两条平行的直赛道上行驶.t=0时两艘赛艇处在同一计时位置,此时比赛开始.它们在四次比赛中的v-t图象如下图所示,其中能够表示其所对应的比赛中有一艘赛艇始终没有追上另一艘的图象是()•【解析】从图上可以看出A图中加速度一样,但a赛艇有初速度,所以b赛艇始终追不上;B图中a、b均做匀速运动,但速度不一样,所以速度小的始终追不上;D图中a在前15 s内没有追上b,15 s后a的速度又小于b,因此始终追不上;从C图中可以看出经过20 s b追上a.•【答案】ABD•5.甲车以10 m/s的速度在平直的公路上匀速行驶,乙车以4 m/s的速度与甲车平行同向做匀速直线运动,甲车经过乙车旁边时开始以0.5 m/s 2的加速度刹车,从甲车刹车开始计时,求:•(1)乙车在追上甲车前,两车相距的最大距离;•(2)乙车追上甲车所用的时间.• 【解析】 (1)当甲车速度减至等于乙车速度时两车的距离最大,设该减速过程时间为t ,则 • v 乙=v 甲-at • 解得:t =12 s.• 此时甲、乙间距离为• v 甲t - at 2-v 乙t• =10×12 m - ×0.5×122 m -4×12 m =36 m.(2)设甲车减速到零所需时间为t1,则有:t1=v甲a=20 s.t1时间内,x甲=v甲2t1=102×20 m=100 m,x乙=v乙t1=4×20 m=80 m.此后乙车运动时间t2=x甲-x乙v乙=204s=5 s,故乙车追上甲车需t1+t2=25 s.【答案】(1)36 m(2)25 s。

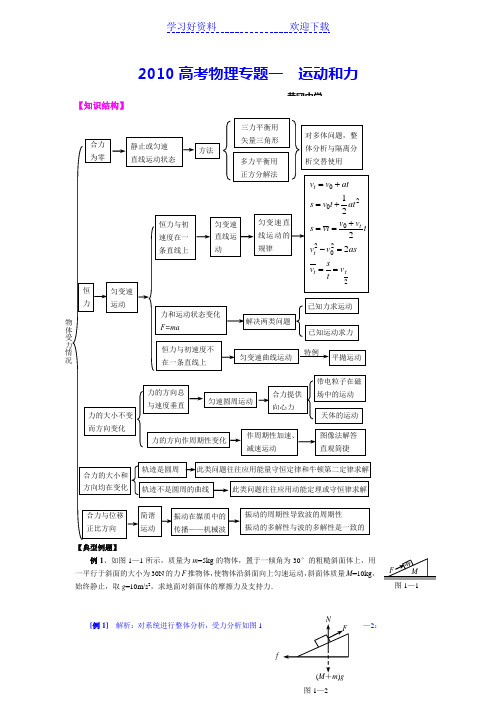
2010高考物理专题一 运动和力【知识结构】【典型例题】例1、如图1—1所示,质量为m =5kg 的物体,置于一倾角为30°的粗糙斜面体上,用一平行于斜面的大小为30N 的力F 推物体,使物体沿斜面向上匀速运动,斜面体质量M =10kg ,始终静止,取g =10m/s 2,求地面对斜面体的摩擦力及支持力.[例1] 解析:对系统进行整体分析,受力分析如图1—2:图1—1f图1—2黄冈中学由平衡条件有:cos30F f ︒=sin30()N F M m g +︒=+由此解得f =()sin30135N N M m g F =+-︒=例2 、如图1—3所示,声源S 和观察者A 都沿x 轴正方向运动,相对于地面的速率分别为v S 和v A ,空气中声音传播的速率为P v ,设,S P A P v v v v <<,空气相对于地面没有流动.(1)若声源相继发出两个声信号,时间间隔为△t ,请根据发出的这两个声信号从声源传播到观察者的过程,确定观察者接收到这两个声信号的时间间隔△t ′.(2)利用(1)的结果,推导此情形下观察者接收到的声源频率与声源发出的声波频率间的关系式.[例2] 解析: (1)设t 1、t 2为声源S 发出两个信号的时刻,12、t t ''为观察者接收到两个信号的时刻.则第一个信号经过11()t t '-时间被观察者A 接收到,第二个信号经过(22t t '-)时刻被观察者A 接收到,且 2121t t t t t t '''∆=-∆=-设声源发出第一个信号时,S 、A 两点间的距离为L ,两个声信号从声源传播到观察者的过程中,它们的运动的距离关系如图所示,可得11112221()()()()P A P A S v t t L v t t v t t L v t t v t ''''-=+--=+--∆ 由以上各式解得P SP Av v t t v v -'∆=∆-(2)设声源发出声波的振动周期为T ,这样,由以上结论,观察者接收到的声波振动的周期T ′,P SP Av v T T v v -'=-.由此可得,观察者接收到的声波频率与声源发出声波频率间的关系为P AP Sv v f f v v -'=-.例3、假设有两个天体,质量分别为m 1和m 2,它们相距r ;其他天体离它们很远,可以认为这两个天体除相互吸引作用外,不受其他外力作用.这两个天体之所以能保持距离.............r .不变,完全是由于它们绕着共.............同“中心”(质心)做匀速圆周运动,它们之间.....................的万有引力作为做圆周运动的向心力................,“中心”O 位于两个天体的连线上,与两个天体的距离分别为r 1和r 2.(1)r 1、r 2各多大?(2)两天体绕质心O 转动的角速度、线速度、周期各多大? [例3] 解答:根据题意作图1—4.对这两个天体而言,它们的运动方程分别为212112m m Gm r rω= ①v A图1—31 t 't 1 v A1 t 'v S212222m m Gm r r ω= ②以及12r r r += ③由以上三式解得21121212;m m r r r r m m m m ==++.将r 1和r 2的表达式分别代①和②式, 可得12()1G m m r rω+=.2121121212112221121212()()()()22()m G m m Gv r m m m r m m r m G m m Gv r m m m r m m rrT rG m m ωωππω+===+++===++==+例4、A 、B 两个小球由柔软的细线相连,线长l =6m ;将A 、B 球先后以相同的初速度v 0=4.5m/s ,从同一点水平抛出(先A 、后B )相隔时间△t =0.8s .(1)A 球抛出后经多少时间,细线刚好被拉直?(2)细线刚被拉直时,A 、B 球的水平位移(相对于抛出点)各多大?(取g =10m/s 2)[例4] 解答:(1)A 、B 两球以相同的初速度v 0,从同一点水平抛出,可以肯定它们沿同一轨道运动. 作细线刚被拉直时刻A 、B 球位置示意图1—5. 根据题意可知:022224.50.8 3.6(m)6 3.6 4.8(m)x v t y l x ∆=∆=⨯=∆=-∆=-=设A 球运动时间为t ,则B 球运动时间为t -0.8,由于A 、B 球在竖直方向上均作自由落体运动,所以有2211(0.8)22y gt g t ∆=--. 由此解得t =1s . (2)细线刚被拉直时,A 、B 球的水平位移分别为004.5m (0.8)0.9m A B x v t x v t ===-=例5、内壁光滑的环形细圆管,位于竖直平面内,环的半径为R (比细管的半径大得多).在细圆管中有两个直径略小于细圆管管径的小球(可视为质点)A 和B ,质量分别为m 1和m 2,它们沿环形圆管(在竖直平面内)顺时针方向运动,经过最低点时的速度都是v 0;设A 球通过最低点时B 球恰好通过最高点,此时两球作用于环形圆管的合力为零,那么m 1、m 2、R 和v 0应满足的关系式是____________.r 2r 1m 1m 2O图1—4xy图1—5[例5] 解答:(1)A 球通过最低点时,作用于环形圆管的压力竖直向下,根据牛顿第三定律,A 球受到竖直向上的支持力N 1,由牛顿第二定律,有:2111v N m g m g-= ①由题意知,A 球通过最低点时,B 球恰好通过最高点,而且该时刻A 、B 两球作用于圆管的合力为零;可见B 球作用于圆管的压力肯定竖直向上,根据牛顿第三定律,圆管对B 球的反作用力N 2竖直向下;假设B 球通过最高点时的速度为v ,则B 球在该时刻的运动方程为2222v N m g m R+= ②由题意N 1=N 2 ③∴2210212m v m v m g m g R R+=-④ 对B 球运用机械能守恒定律22202211222m v m v m gR =+ ⑤ 解得2204v v gR =- ⑥⑥式代入④式可得:21212(5)()0v m m g m m R++-=.例6、有两架走时准确的摆钟,一架放在地面上,另一架放入探空火箭中.假若火箭以加速度a =8g 竖直向上发射,在升高时h =64km 时,发动机熄火而停止工作.试分析计算:火箭上升到最高点时,两架摆钟的读数差是多少?(不考虑g 随高度的变化,取g =10m/s 2)[例6] 解答:火箭上升到最高点的运动分为两个阶段:匀加速上升阶段和竖直上抛阶段.地面上的摆钟对两个阶段的计时为140(s)t == 1218320(s)at t t g=== 即总的读数(计时)为t =t 1+t 2=360(s ) 放在火箭中的摆钟也分两个阶段计时.第一阶段匀加速上升,a =8g ,钟摆周期112233T T '=== 其钟面指示时间113120s t t '== 第二阶段竖直上抛,为匀减速直线运动,加速度竖直向下,a =g ,完全失重,摆钟不“走”,计时20t '=.可见放在火箭中的摆钟总计时为12120s t t t '''=+=. 综上所述,火箭中的摆钟比地面上的摆钟读数少了240s t t t '∆=-=.例7、光滑的水平桌面上,放着质量M =1kg 的木板,木板上放着一个装有小马达的滑块,它们的质量m =0.1kg .马达转动时可以使细线卷在轴筒上,从而使滑块获得v 0=0.1m/s 的运动速度(如图1—6),滑块与木板之间的动摩擦因数μ=0.02.开始时我们用手抓住木板使它不动,开启小马达,让滑块以速度v 0运动起来,当滑块与木板右端相距l =0.5m 时立即放开木板.试描述下列两种不同情形中木板与滑块的运动情况,并计算滑块运动到木板右端所花的时间.图1—6(1)线的另一端拴在固定在桌面上的小柱上.如图(a ). (2)线的另一端拴在固定在木板右端的小柱上.如图(b ). 线足够长,线保持与水平桌面平行,g =10m/s 2.[例7] 解答:在情形(1)中,滑块相对于桌面以速度v 0=0.1m/s 向右做匀速运动,放手后,木板由静止开始向右做匀加速运动.20.02m/s mga Mμ==经时间t ,木板的速度增大到v 0=0.1m/s ,05s v t a==. 在5s 内滑块相对于桌面向右的位移大小为S 1=v 0t =0.5m . 而木板向右相对于桌面的位移为2210.25m 2S at ==. 可见,滑块在木板上向右只滑行了S 1-S 2=0.25m ,即达到相对静止状态,随后,它们一起以共同速度v 0向右做匀速直线运动.只要线足够长,桌上的柱子不阻挡它们运动,滑块就到不了木板的右端.在情形(2)中,滑块与木板组成一个系统,放手后滑块相树于木板的速度仍为v 0,滑块到达木板右端历时05s lt v '==.例8、相隔一定距离的A 、B 两球,质量相等,假定它们之间存在着恒定的斥力作用.原来两球被按住,处在静止状态.现突然松开,同时给A 球以初速度v 0,使之沿两球连线射向B 球,B 球初速度为零.若两球间的距离从最小值(两球未接触)在刚恢复到原始值所经历的时间为t 0,求B 球在斥力作用下的加速度.(本题是2000年春季招生,北京、安徽地区试卷第24题)[例8] 解答:以m 表示球的质量,F 表示两球相互作用的恒定斥力,l 表示两球间的原始距离.A 球作初速度为v 0的匀减速运动,B 球作初速度为零的匀加速运动.在两球间距由l 先减小,到又恢复到l 的过程中,A 球的运动路程为l 1,B 球运动路程为l 2,间距恢复到l 时,A 球速度为v 1,B 球速度为v 2.由动量守恒,有012mv mv mv =+ 由功能关系:A 球221011122Fl mv mv =- B 球:22212Fl mv =根据题意可知l 1=l 2,由上三式可得22222220120220022()22v v v v v v v v v v =+=-+=-+得v 2=v 0、v 1=0 即两球交换速度.当两球速度相同时,两球间距最小,设两球速度相等时的速度为v , 则00(),2v mv m m v v =+= B 球的速度由02v v =增加到v 0花时间t 0,即00002vv v at at =+=+ 得02v a t =.解二:用牛顿第二定律和运动学公式.(略)【跟踪练习】1、如图1—7所示,A 、B 两球完全相同,质量为m ,用两根等长的细线悬挂在O 点,两球之间夹着一根劲度系数为k 的轻弹簧,静止不动时,弹簧位于水平方向,两根细线之间的夹角为θ.则弹簧的长度被压缩了( )A .tan mg k θ B .2tan mg kθC .(tan )2mg k θD .2tan()2mg kθ2、如图1—8所示,半径为R 、圆心为O 的大圆环固定在竖直平面内,两个轻质小圆环套在大圆环上,一根轻质长绳穿过两个小圆环,它的两端都系上质量为m 的重物,忽略小圆环的大小.(1)将两个小圆环固定在大圆环竖直对称轴的两侧θ=30°的位置上(如图),在两个小圆环间绳子的中点C 处,挂上一个质量2M m =的重物,使两个小圆环间的绳子水平,然后无初速释放重物M ,设绳子与大、小圆环间的摩擦均可忽略,求重物M 下降的最大距离.(2)若不挂重物M ,小圆环可以在大圆环上自由移动,且绳子与大、小圆环间及大、小圆环之间的摩擦均可以忽略,问两个小圆环分别在哪些位置时,系统可处于平衡状态?3、图1—9中的A 是在高速公路上用超声测速仪测量车速的示意图,测速仪发出并接收超声波脉冲信号.根据发出和接收到的信号间的时间差,测出被测物体的速度,图B 中P 1、P 2是测速仪发出的超声波信号,n 1、n 2分别是P 1、P 2由汽车反射回来的信号,设测速仪匀速扫描,P 1、P 2之间的时间间隔△t =1.0s ,超声波在空气中传播的速度v =340m/s ,若汽车是匀速行驶的,则根据图中可知,汽车在接收到P 1、P 2两个信号之间的时间内前进的距离是_________m ,汽车的速度是________m/s .图1—94、利用超声波遇到物体发生反射,可测定物体运动的有关参量,图1—10(a )中仪器A 和B 通过电缆线连接,B 为超声波发射与接收一体化装置,仪器A 和B 提供超声波信号源而且能将B 接收到的超声波图1—7图1—8信号进行处理并在屏幕上显示其波形.现固定装置B ,并将它对准匀速行驶的小车C ,使其每隔固定时间T 0发射一短促的超声波脉冲,如图1—10(b )中幅度较大的波形,反射波滞后的时间已在图中标出,其中T 和△T 为已知量,另外还知道该测定条件下超声波在空气中的速度为v 0,根据所给信息求小车的运动方向和速度大小.图1—105、关于绕地球匀速圆周运动的人造地球卫星,下列说法中,正确的是( ) A .卫星的轨道面肯定通过地心B .卫星的运动速度肯定大于第一宇宙速度C .卫星的轨道半径越大、周期越大、速度越小D .任何卫星的轨道半径的三次方跟周期的平方比都相等6、某人造地球卫星质量为m ,其绕地球运动的轨道为椭圆.已知它在近地点时距离地面高度为h 1,速率为v 1,加速度为a 1,在远地点时距离地面高度为h 2,速率为v 2,设地球半径为R ,则该卫星.(1)由近地点到远地点过程中地球对它的万有引力所做的功是多少? (2)在远地点运动的加速度a 2多大?7、从倾角为θ的斜面上的A 点,以水平初速度v 0抛出一个小球.问: (1)抛出后小球到斜面的最大(垂直)距离多大? (2)小球落在斜面上B 点与A 点相距多远?8、滑雪者从A 点由静止沿斜面滑下,经一平台后水平飞离B 点,地面上紧靠平台有一个水平台阶,空间几何尺度如图1—12所示.斜面、平台与滑雪板之间的动摩擦因数为μ,假设滑雪者由斜面底端进入平台后立即沿水平方向运动,且速度大小不变.求:(1)滑雪者离开B 点时的速度大小;(2)滑雪者从B 点开始做平抛运动的水平距离.9、如图1—13所示,悬挂在小车支架上的摆长为l 的摆,小车与摆球一起以速度v 0匀速向右运动.小车与矮墙相碰后立即停止(不弹回),则下列关于摆球上升能够达到的最大高度H 的说法中,正确的是( )A .若02v gl =,则H =lB .若04v gl =,则H =2lC .不论v 0多大,可以肯定H ≤22v g总是成立的D .上述说法都正确BAθ图1—11图1—12v 0图1—13AB(a )10、水平放置的木柱,横截面为边长等于a 的正四边形ABCD ;摆长l =4a 的摆,悬挂在A 点(如图1—14所示),开始时质量为m 的摆球处在与A 等高的P 点,这时摆线沿水平方向伸直;已知摆线能承受的最大拉力为7mg ;若以初速度.....v .0.竖直向下将摆球从........P .点抛出,为使摆球能始终沿圆弧运动,并最后击中......................A .点..求v 0的许可值范围(不计空气阻力).11、已知单摆a 完成10次全振动的时间内,单摆b 完成6次全振动,两摆长之差为1.6m ,则两摆长a l 与b l 分别为( )A . 2.5m,0.9m a b l l ==B .0.9m, 2.5m a b l l ==C . 2.4m, 4.0m a b l l ==D . 4.0m, 2.4m a b l l ==12、一列简谐横波沿直线传播,传到P 点时开始计时,在t =4s 时,P 点恰好完成了6次全振动,而在同一直线上的Q 点完成了124次全振动,已知波长为113m 3.试求P 、Q 间的距离和波速各多大.13、如图1—15所示,小车板面上的物体质量为m =8kg ,它被一根水平方向上拉伸了的弹簧拉住而静止在小车上,这时弹簧的弹力为6N .现沿水平向右的方向对小车施以作用力,使小车由静止开始运动起来,运动中加速度由零逐渐增大到1m/s 2,随即以1m/s 2的加速度做匀加速直线运动.以下说法中,正确的是( )A .物体与小车始终保持相对静止,弹簧对物体的作用力始终没有发生变化B .物体受到的摩擦力先减小、后增大、先向左、后向右C .当小车加速度(向右)为0.75m/s 2时,物体不受摩擦力作用D .小车以1m/s 2的加速度向右做匀加速直线运动时,物体受到的摩擦力为8N14、如图1—16所示,一块质量为M ,长为L 的均质板放在很长的光滑水平桌面上,板的左端有一质量为m 的小物体(可视为质点),物体上连接一根很长的细绳,细绳跨过位于桌边的定滑轮.某人以恒定的速率v 向下拉绳,物体最多只能到达板的中点,而板的右端尚未到达桌边定滑轮处.试求:(1)物体刚达板中点时板的位移.(2)若板与桌面之间有摩擦,为使物体能达到板的右端,板与桌面之间的动摩擦因数的范围是多少.15、在水平地面上有一质量为2kg 的物体,物体在水平拉力F 的作用下由静止开始运动,10s 后拉力大小减为3F,该物体的运动速度随时间变化的图像如图1—17所示,求:(1)物体受到的拉力F 的大小;(2)物体与地面之间的动摩擦因数(g 取10m/s 2).16、如图所示,一高度为h =0.8m 粗糙的水平面在B 点处与一倾角为θ=30°的斜面BC 连接,一小滑块从水平面上的A 点以v 0=3m/s 的速度在粗糙的水平面上向右运动.运动到B 点时小滑块恰能沿光滑斜面下滑.已知AB 间的距离S =5m ,求:图1—14图1—15vMm图1—16v /m ·s -1/s46 868101214O图1—17(1)小滑块与水平面间的动摩擦因数. (2)小滑块从A 点运动到地面所需的时间.(3)若小滑块从水平面上的A 点以v 1=5m/s 的速度在粗糙的水平面上向右运动,运动到B 点时小滑块将做什么运动?并求出小滑块从A 点运动到地面所需时间(取g =10m/s 2).跟踪练习1.C 提示:利用平衡条件.2.(1)重物先向下做加速运动,后做减速运动,当重物速度为零时,下降的距离最大,设下降的最大距离为h ,由机械能守恒定律得222((sin )sin )Mgh mg h R R θθ=+- 解得2h R =.(2)系统处于平衡状态时,两小环的可能位置为 a .两小环同时位于大圆环的底端 b .两小环同时位于大圆环的顶端c .两小环一个位于大圆环的顶端,另一个位于大圆环的底端d .除上述三种情况外,根据对称性可知,系统如能平衡,则小圆环的位置一定关于大圆环竖直对称轴对称.设平衡时,两小圆环在大圆环竖直对称轴两侧α角的位置上(如图).对于重物m ,受绳的拉力T 与重力mg 作用,有T =mg .对于小圆环,受到三个力的作用,水平绳的拉力T ,竖直绳的拉力T ,大圆环的支持力N .两绳的拉力沿大圆环切向的分力大小相等,方向相反sin sin T T αα'=.得,90,45ααααα''=+=︒=︒而∴.3.设测速仪扫描速度为v ′,因P 1、P 2在标尺上对应间隔为30小格,所以3030v t'==∆格/s . 测速仪发出超声波信号P 1到接收P 1的反射信号n 1.从图B 上可以看出,测速仪扫描12小格,所以测速仪从发出信号P 1到接收其反射信号n 1所经历时间120.4s t v '=='. 汽车接收到P 1信号时与测速仪相距1168m 2t S v ==声. 同理,测速仪从发出信号P 2到接收到其反射信号n 2,测速仪扫描9小格,故所经历时间290.3s t v =='.汽车在接收到P 2信号时与测速仪相距2251m 2t S v ==声. 所以,汽车在接收到P 1、P 2两个信号的时间内前进的距离△S =S 1-S 2=17m .从图B 可以看出,n 1与P 2之间有18小格,所以,测速仪从接收反射信号n 1到超声信号P 2的时间间隔3180.6s t v =='. 所以汽车接收P 1、P 2两个信号之间的时间间隔为1230.95s 22t tt t ∆=++=. Tα' αNα m 1m mgThA BCθ 图1—18∴汽车速度17.9Sv t∆==∆m/s . 4.从B 发出第一个超声波开始计时,经2T被C 车接收.故C 车第一次接收超声波时与B 距离102T S v =.第二个超声波从发出至接收,经T +△T 时间,C 车第二车接收超声波时距B 为202T TS v +∆=,C 车从接收第一个超声波到接收第二个超声波内前进S 2-S 1,接收第一个超声波时刻12Tt =,接收第二个超声波时刻为202T Tt T +∆=+. 所以接收第一和第二个超声波的时间间距为2102Tt t t T ∆∆=-=+. 故车速0021002222C v TTv S S v T T tT T ∆∆-===+∆∆+∆.车向右运动. 5.ACD6.(1)根据动能定理,可求出卫星由近地点到远地点运动过程中,地球引力对卫星的功为22211122W mv mv =-. (2)由牛顿第二定律知1222112()()GM GM a a R h R h ==++ ∴21212()R h a a R h +=+ 7.(1)建立如图所示坐标系,将v 0与g 进行正交分解.0000cos ,sin sin ,cos x y x y v v v v g g g g θθθθ====-在x 方向,小球以0x v 为初速度作匀加速运动. 在y 方向,小球以0y v 为初速度,作类竖直上抛运动.当y 方向的速度为零时,小球离斜面最远,由运动学公式02220sin |2|2cos y y v v H g g θθ==.小球经时间t 上升到最大高度,由0y y v g t =得000sin tan cos g yv v v t g g gθθθ===.(2)02220000221sin 1sin 2(2)2cos sin 42cos 2cos ABx x v v Sv t g t v v g g θθθθθθ=+=+2202sin (1tan )v gθθ=+8.(1)设滑雪者质量为m ,斜面与水平面夹角为θ,滑雪者滑行过程中克服摩擦力做功cos (cos )W mg S mg L S mgL μθμθμ=+-= ①y由动能定理21()2mg H h mgL mv μ--= ② 离开B点时的速度v ③(2)设滑雪者离开B点后落在台阶上2111122h gt S vt ==<可解得1S =④ 此时必须满足2H L h μ-< ⑤当2H L h μ->时,滑雪者直接落到地面上,222221,2h gt S v t ==,可解得2S = 9.AC10.摆球先后以正方形的顶点为圆心,半径分别为R 1=4a ,R 2=3a ,R 3=2a ,R 4=a 为半径各作四分之一圆周的圆运动.当摆球从P 点开始,沿半径R 1=4a 运动到最低点时的速度v 1, 根据动量定理221011422mv mv mga -= ① 当摆球开始以v 1绕B 点以半径R 2=3a 作圆周运动时,摆线拉力最大,为T max =7mg ,这时摆球的运动方程为21max3mv T mg a-= ② 由此求得v 0的最大许可值为0v当摆球绕C 点以半径R 3=2a 运动到最高点时,为确保沿圆周运动,到达最高点时的速度3v由动能定理223001122mv mv mga v -=-=得0v 11.B12.由题意知,周期为42s 63T ==.波速40320m/s 23v T λ===.P 、Q 两点距离相差9(6)4-次全振动所需时间即9235(6)4s.4322t ∆=-⨯=-= ∴50m PQ v t =∆=.13.ABC 开始时小车上的物体受弹簧水平向右的拉力为6N ,水平向左的静摩擦力也为6N ,合力为零.沿水平向右方向对小车施加以作用力,小车向右做加速运动时,车上的物体沿水平向右方向上的合力(F =ma )逐渐增大到8N 后恒定.在此过程中向左的静摩擦力先减小,改变方向后逐渐增大到(向右的)2N 而保持恒定;弹簧的拉力(大小、方向)始终没有变,物体与小车保持相对静止,小车上的物体不受摩擦力作用时,向右的加速度由弹簧的拉力提供:260.75m/s 8T a m ===. 14.(1)设物体与板的位移分别为S 物、S 板,则由题意有2LS S -=物板 ① 212S S vt a t =物板板∶∶ ② 解得:,2L S L S ==物板.(2)由22112,,mgMv v a S a M mgLμμ===板板板得.212,21,,2,(),2S S L S S S L S L mg M m g Ma v a S μμ''''''-===='''-+==物板物板板物板板板∶∶得由得222()Mv M m gL μ=+,故板与桌面之间的动摩擦因数222()Mv M m gLμ+≥.15.在0~10s 内,物体的加速度210.8m/s va t∆==∆(正向) 在10~14s 内,物体的加速度222m/s va t∆==∆ (反向) 由牛顿第二定律1F mg ma μ-= ① 23Fmg ma μ-=- ② 由此解得F =8.4Nμ=0.3416.(1)依题意得1B v =0,设小滑块在水平面上运动的加速度大小为a ,由牛顿第二定律,f mg ma μ==,由运动学公式202v gS μ=,解得0.09μ=.(2)滑块在水平面上运动时间为t 1,由01110, 3.3s 23v S t t ===得.在斜面上运动的时间2120.8s 4.1s t t t t ==+=∴(3)若滑块在A 点速度为v 1=5m/s ,则运动到B点的速度4m/s B v .即运动到B 点后,小滑块将做平抛运动.假设小滑块不会落到斜面上,则经过30.4s t =落到水平面上, 则水平位移3 1.67m tan30B hx v t ==>︒.所以假设正确,即小滑块从A 点运动到地面所需时间为312 1.5s BSt t v v '=+=+.。



2010年高考物理二轮考点典型例题解析专题辅导2[高三]高考二轮复习-02力和运动考点11.运动和力的关系,力是矢量,力的合成与分解。
1.力的概念:力是物体对物体的作用。
是物体发生形变和物体运动状态变化的原因。
(1)力的基本特征:①力的物质性:力不能脱离物体而独立存在。
②力的相互性:力的作用是相互的。
③力的矢量性:力是矢量,既有大小,又有方向。
④力的独立性:力具有独立作用性,用牛顿第二定律表示时,则有合力产生的加速度等于几个分力产生的加速度的矢量和。
(2)力的分类:①按力的性质分类:如重力、电场力、磁场力、弹力、摩擦力、分子力、核力等②按力的效果分类:如拉力、推力、支持力、压力、动力、阻力、向心力、回复力等.2. 力的合成与分解合力和力的合成:一个力产生的效果如果能跟原来几个力共同作用产生的效果相同,这个力就叫那几个力的合力,求几个力的合力叫力的合成.力的平行四边形定则:求两个互成角度的共点力的合力,可以用表示这两个力的线段为邻边作平行四边形,合力的大小和方向就可以用这个平行四边形的对角线表示出来。
分力与力的分解:如果几个力的作用效果跟原来一个力的作用效果相同,这几个力叫原来那个力的分力.求一个力的分力叫做力的分解.分解原则:平行四边形定则.将一个已知力F进行分解,其解是不唯一的。
要得到唯一的解,必须另外考虑唯一性条件,常见的唯一性条件有:已知两个不平行分力的方向,已知一个分力的大小和方向。
44.如图,将力F分解为F1 和F2 两个分力,若已知F1的大小及F与F2 间的夹角α,且α为锐角,则下列说法中错误的是()A.当F1 > F sin α时有两个解B.当F > F1 > F sin α时有两个解C.当F1 = F sin α时有唯一解D.当F1 < F sin α时无解考点12.万有引力定律。
重力,重心。
1.万有引力定律。
2. 重力,重心。
(1)重力:重力是由于地球的吸引而使物体受到的力。