第24届全国中学生物理竞赛复赛试题参考解答

第十九届全国中学生物理竞赛复赛试题一、（20分）某甲设计了1个如图复19-1所示的“自动喷泉”装置，其中A 、B 、C 为3个容器，D 、E 、F 为3根细管，管栓K 是关闭的．A 、B 、C 及细管D 、E中均盛有水，容器水面的高度差分别为1h 和1h 如图所示．A 、B 、C 的截面半径为12cm ，D 的半径为0.2cm ．甲向同伴乙说：“我若拧开管栓K ，会有水从细管口喷出．”乙认为不可能．理由是：“低处的水自动走向高外，能量从哪儿来？”甲当即拧开K ，果然见到有水喷出，乙哑口无言，但不明白自己的错误所在．甲又进一步演示．在拧开管栓K 前，先将喷管D 的上端加长到足够长，然后拧开K ，管中水面即上升，最后水面静止于某个高度处． (1)．论证拧开K 后水柱上升的原因．(2)．当D 管上端足够长时，求拧开K 后D 中静止水面与A 中水面的高度差．(3)．论证水柱上升所需能量的来源．二、 (18 分) 在图复19-2中，半径为R 的圆柱形区域内有匀强磁场，磁场方向垂直纸面指向纸外，磁感应强度B 随时间均匀变化，变化率/B t K ∆∆=(K 为一正值常量),圆柱形区外空间没有磁场，沿图中AC 弦的方向画一直线，并向外延长，弦AC 与半径OA 的夹角/4απ=．直线上有一任意点，设该点与A 点的距离为x ，求从A 沿直线到该点的电动势的大小．三、（18分）如图复19-3所示，在水平光滑绝缘的桌面上，有三个带正电的质点1、2、3，位于边长为l 的等边三角形的三个顶点处。

C 为三角形的中心，三个质点的质量皆为m ，带电量皆为q 。

质点 1、3之间和2、3之间用绝缘的轻而细的刚性杆相连，在3的连接处为无摩擦的铰链。

已知开始时三个质点的速度为零，在此后运动过程中，当质点3运动到C 处时，其速度大小为多少？ 四、（18分）有人设计了下述装置用以测量线圈的自感系数．在图复19-4-1中，E 为电压可调的直流电源。

第26届全国中学生物理竞赛复赛试卷一、填空（问答）题（每题5分，共25分）有人假想了一种静电场：电场的方向都垂直于纸面并指向纸里，电场强度的大小自左向右慢慢增大，如下图。

这种散布的静电场是不是可能存在？试述理由。

2．海尔-波普彗星轨道是长轴超级大的椭圆，近日点到太阳中心的距离为天文单位（1天文单位等于地日间的平均距离），那么其近日点速度的上限与地球公转（轨道可视为圆周）速度之比约为（保留2位有效数字） 。

用测电笔接触市电相线，即便赤脚站在地上也可不能触电，缘故是；另一方面，即便穿绝缘性能良好的电工鞋操作，测电笔仍会发亮，缘故是 。

4．在图示的复杂网络中，所有电源的电动势均为E 0，所有电阻器的电阻值均为R 0，所有电容器的电容均为C 0，那么图示电容器A 极板上的电荷量为 。

5．如图，给静止在水平粗糙地面上的木块一初速度，使之开始运动。

一学生利用角动量定理来考察此木块以后的运动进程：“把参考点设于如下图的地面上一点O ，现在摩擦力f 的力矩为0，从而地面木块的角动量将守恒，如此木块将不减速而作匀速运动。

”请指出上述推理的错误，并给出正确的说明： 。

二、（20分）图示正方形轻质刚性水平桌面由四条完全相同的轻质细桌腿一、二、3、4支撑于桌角A 、B 、C 、D 处，桌腿竖直立在水平粗糙刚性地面上。

已知桌腿受力后将产生弹性微小形变。

现于桌面中心点O 至角A 的连线OA 上某点P 施加一竖直向下的力F ，令c OAOP，求桌面对桌腿1的压力F 1。

三、（15分）1．一质量为m 的小球与一劲度系数为k 的弹簧相连组成一体系，置于滑腻水平桌面上，弹簧的另一端与固定墙面相连，小球做一维自由振动。

试问在一沿此弹簧长度方向以速度u 作匀速运动的参考系里观看，此体系的机械能是不是守恒，并说明理由。

2．假设不考虑太阳和其他星体的作用，那么地球-月球系统可看成孤立系统。

假设把地球和月球都看做是质量均匀散布的球体，它们的质量别离为M 和m ，月心-地心间的距离为R ，万有引力恒量为G 。

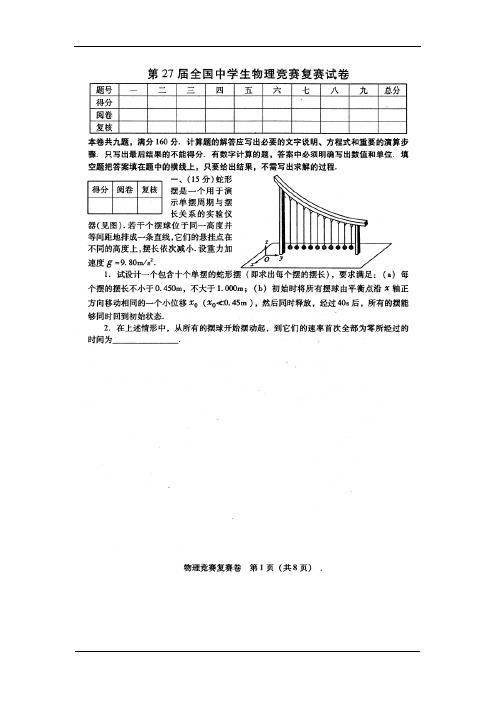
解答一、参考解答： 1．以i l 表示第i 个单摆的摆长，由条件（b ）可知每个摆的周期必须是40s 的整数分之一，即i i402T N == （N i 为正整数） （1） [(1)式以及下面的有关各式都是在采用题给单位条件下的数值关系.]由(1)可得，各单摆的摆长i 22i400πg l N = （2） 依题意，i 0.450m 1.000m l ≤≤，由此可得i N << （3） 即i 2029N ≤≤ （4） 因此，第i 个摆的摆长为i 22400π(19i)g l =+ (i 1,2,,10)= （5） 2．20s评分标准：本题15分．第1小问11分．（2）式4分，（4）式4分，10个摆长共3分．第2小问4分．二、参考解答：设该恒星中心到恒星－行星系统质心的距离为d ，根据题意有2L d θ∆= （1） 将有关数据代入（1）式，得AU 1053-⨯=d ．又根据质心的定义有Md r d m-= （2） 式中r 为行星绕恒星做圆周运动的轨道半径，即行星与恒星之间的距离.根据万有引力定律有222πMm G Md r T ⎛⎫= ⎪⎝⎭（3） 由（2）、（3）两式得()23224π1md G TM m =+ （4） [若考生用r 表示行星到恒星行星系统质心的距离，从而把(2)式写为Md r m =，把(3)式写为()222πMmG Md T r d ⎛⎫= ⎪⎝⎭+，则同样可得到(4)式，这也是正确的.] 利用（1）式，可得 ()()3222π21L m GT Mm θ∆=+ （5） （5）式就是行星质量m 所满足的方程．可以把(5)试改写成下面的形式()()()33222π21m M L GMT m M θ∆=+ （6）因地球绕太阳作圆周运动，根据万有引力定律可得3S 22(1AU)(1y)4πGM = （7）注意到S M M =，由（6）和（7）式并代入有关数据得()()310S 8.6101S m M mM -=⨯+ (8) 由（8）式可知 S1m M << 由近似计算可得3S 110m M -≈⨯ （9）由于m M 小于1/1000，可近似使用开普勒第三定律，即3322(1AU)(1y)r T =（10） 代入有关数据得5AU r ≈ （11）评分标准：本题20分．（1）式2分，（2）式3分，（3）式4分，（5）式3分，（9）式4分，（11）式4分．三、参考解答：解法一一倾角为θ的直角三角形薄片(如图1所示)紧贴于半径为R 的圆柱面，圆柱面的轴线与直角三角形薄片的沿竖直方向的直角边平行，若把此三角形薄片卷绕在柱面上，则三角形薄片的斜边就相当于题中的螺线环．根据题意有π1tan 2π2R R θ== （1） 可得：sin 5θ=，cos 5θ= （2） 设在所考察的时刻，螺旋环绕其转轴的角速度为ω，则环上每一质量为i m ∆的小质元绕转轴转动线速度的大小都相同，用u 表示，u R ω= （3） 该小质元对转轴的角动量2i i i L m uR m R ω∆=∆=∆整个螺旋环对转轴的角动量22i i L L m R mR ωω=∆=∆=∑∑ （4）小球沿螺旋环的运动可视为在水平面内的圆周运动和沿竖直方向的直线运动的合成．在螺旋环的角速度为ω时，设小球相对螺旋环的速度为'v ，则小球在水平面内作圆周运动的速度为cos Rθω'=-v v（5）沿竖直方向的速度sin ⊥'=v v θ （6）对由小球和螺旋环组成的系绕，外力对转轴的力矩为0，系统对转轴的角动量守恒，故有0m R L=-v（7）由（4）、（5）、（7）三式得：'v cos θ-ωωR =R （8）在小球沿螺旋环运动的过程中，系统的机械能守恒，有()222i 1122mgh m m u ⊥=++∆∑v v（9） 由（3）、（5）、（6）、（9）四式得：()2222sin gh =R R θ-ωθω2''++v v 2cos（10）解（8）、（10）二式，并利用（2）式得ω=（11）'v =（12） 由（6）、（12）以及（2）式得⊥=v（13） 或有2123gh ⊥=v（14）（14）式表明，小球在竖直方向的运动是匀加速直线运动，其加速度13⊥=a g（15） 若小球自静止开始运动到所考察时刻经历时间为t ，则有212⊥h =a t （16） 由（11）和（16）式得3=ωgt R（17） （17）式表明，螺旋环的运动是匀加速转动，其角加速度3=βgR（18）小球对螺旋环的作用力有：小球对螺旋环的正压力1N ，在图1所示的薄片平面内，方向垂直于薄片的斜边；螺旋环迫使小球在水平面内作圆周运动的向心力2N '的反作用力2N ．向心力2N '在水平面内，方向指向转轴C ，如图2所示．1N 、2N 两力中只有1N 对螺旋环的转轴有力矩，由角动量定理有1sin ∆=∆N R t L θ （19）由（4）、（18）式并注意到∆=∆ωβt得13sin mg N θ==（20） 而222N N m R '==v（21）图2由以上有关各式得22 3 =hN mgR（22）小球对螺旋环的作用力13N==（23）评分标准：本题22分．（1）、（2）式共3分，（7）式1分，（9）式1分，求得（11）式给6分，（20）式5分，（22）式4分，（23）式2分．解法二一倾角为θ的直角三角形薄片(如图1所示)紧贴于半径为R的圆柱面，圆柱面的轴线与直角三角形薄片的沿竖直方向的直角边平行，若把此三角形薄片卷绕在柱面上，则三角形薄片的斜边就相当于题中的螺线环．根据题意有：π1tan2π2RRθ==（1）可得：sinθ=cosθ=（2）螺旋环绕其对称轴无摩擦地转动时，环上每点线速度的大小等于直角三角形薄片在光滑水平地面上向左移动的速度．小球沿螺旋环的运动可视为在竖直方向的直线运动和在水平面内的圆周运动的合成．在考察圆周运动的速率时可以把圆周运动看做沿水平方向的直线运动，结果小球的运动等价于小球沿直角三角形斜边的运动．小球自静止开始沿螺旋环运动到在竖直方向离初始位置的距离为h的位置时，设小球相对薄片斜边的速度为'v，沿薄片斜边的加速度为'a．薄片相对地面向左移动的速度为u，向左移动的加速度为a．u就是螺旋环上每一质元绕转轴转动的线速度，若此时螺旋环转动的角速度为ω，则有u Rω=（3）而a就是螺旋环上每一质元绕转轴转动的切向加速度，若此时螺旋环转动的角加速度为β，则有=a Rβ（4）小球位于斜面上的受力情况如图2所示：图1a 图2重力mg ，方向竖直向下，斜面的支持力N ，方向与斜面垂直，以薄片为参考系时的惯性力f *，方向水平向右，其大小0*=f ma （5）由牛顿定律有cos sin mg θN f θ*--=0 （6） sin cos *'+=mg f ma θθ （7） 0sin =N ma θ （8）解（5）、（6）、（7）、（8）四式得2sin sin '1+2a =g θθ （9） 2cos =1sin +N mg θθ （10）02sin cos 1+sin =a g θθθ （11）利用（2）式可得'a =g（12） 3N =mg （13） 013=a g （14） 由（4）式和（14）式，可得螺旋环的角加速度1=3βg R（15） 若小球自静止开始运动到所考察时刻经历时间为t ，则此时螺旋环的角速度=ωβt （16）因小球沿螺旋环的运动可视为在水平面内的圆周运动和沿竖直方向的直线运动的合成，而小球沿竖直方向的加速度sin ⊥⊥''==a a a θ（17） 故有212⊥h =a t （18） 由（15）、（16）、（17）、（18）、以及（2）式得=ω （19）小球在水平面内作圆周运动的向心力由螺旋环提供，向心力位于水平面内，方向指向转轴，故向心力与图2中的纸面垂直，亦即与N 垂直．向心力的大小21N mR=v （20）式中v 是小球相对地面的速度在水平面内的分量.若a 为小球相对地面的加速度在水平面内的分量，则有a t =v （21）令a '为a '在水平面内的分量，有00cos a a a a a θ''=-=- （22）由以上有关各式得123=hN mg R（23） 小球作用于螺旋环的力的大小0N =（24）由（13）、（23）和（24）式得0N = （25）评分标准：本题22分．（1）、（2）式共3分，（9）或（12）式1分，（10）或（13）式5分，（11）或（14）式1分，（19）式6分，（23）式4分，（25）式2分．四、参考解答：而R ω=v （2）由（1）、（2）两式得m B q ω=（3）如图建立坐标系，则粒子在时刻t 的位置()cos x t R t ω=，()sin y t R t ω= （4）取电流的正方向与y 轴的正向一致，设时刻t 长直导线上的电流为()i t ，它产生的磁场在粒子所在处磁感应强度大小为()()i t B kd x t =+ （5） 方向垂直圆周所在的平面.由（4）、（5）式，可得()(cos )m i t k d R t q ωω=+（6）评分标准：本题12分．（3）式4分，（4）式2分，（5）式4分，（6）式2分．五、参考解答：1．质点在A B →应作减速运动（参看图1）．设质点在A 点的最小初动能为k0E ，则根据能量守恒，可得质点刚好能到达B 点的条件为 k03/225/2kqQ kqQ kqQ kqQmgR E R R R R -+=+-（1） 由此可得:k0730kqQE mgR R=+（2） 2． 质点在B O →的运动有三种可能情况：i ．质点在B O →作加速运动（参看图1），对应条件为249kqQmg R≤ （3） 此时只要质点能过B 点，也必然能到达O 点，因此质点能到达O 点所需的最小初动能由（2）式给出，即k0730kqQE mgR R =+（4） 若（3）式中取等号，则最小初动能应比（4）式给出的k0E 略大一点．ii ．质点在B O →作减速运动（参看图1），对应条件为 24kqQmg R ≥ （5） 此时质点刚好能到达O 点的条件为图1k0(2)/225/2kqQ kqQ kqQ kqQmg R E R R R R -+=+-（6） 由此可得k011210kqQE mgR R=-（7） iii ．质点在B O →之间存在一平衡点D （参看图2），在B D →质点作减速运动，在D O →质点作加速运动，对应条件为22449kqQ kqQmg R R <<（8） 设D 到O 点的距离为x ，则()2(/2)kqQ mg R x =+ （9）即2R x =（10）根据能量守恒，质点刚好能到达D 点的条件为()k0(2)/225/2kqQ kqQ kqQ kqQ mg R x E R R xR R -+-=+-+ （11）由（10）、（11）两式可得质点能到达D 点的最小初动能为k059210kqQ E mgR R=+- （12）只要质点能过D 点也必然能到达O 点，所以，质点能到达O 点的最小初动能也就是（12）式（严格讲应比（12）式给出的k0E 略大一点．）评分标准：本题20分．第1小问5分．求得（2）式给5分．第2小问15分．算出第i 种情况下的初动能给2分；算出第ii 种情况下的初动能给5分；算出第iii 种情况下的初动能给8分，其中（10）式占3分．六、参考解答：1n =时，A 、B 间等效电路如图1所示， A 、B 间的电阻rLAB图 1图211(2)2R rL rL == （1）2n =时，A 、B 间等效电路如图2所示，A 、B 间的电阻21141233R rL R ⎛⎫=+ ⎪⎝⎭（2） 由（1）、（2）两式得256R rL = (3)3n =时，A 、B 间等效电路如图3所示，A 、B 间的电阻3211331233229443R rL R ⎡⎤⎛⎫=++++++ ⎪⎢⎥⎝⎭⎣⎦（4） 由（3）、（4）式得379R rL =（5）评分标准：本题20分．（1）式4分，（3）式6分，（5）式10分．七、参考解答：１．根据题意，太阳辐射的总功率24S S S 4πP R T σ=．太阳辐射各向同性地向外传播．设地球半径为E r ，可以认为地球所在处的太阳辐射是均匀的，故地球接收太阳辐射的总功率AB图321rL1211rL 1rL 9rL9rL11R 2rL 2rL23rL113R23rL图2为242S I S E πR P T r d σ⎛⎫= ⎪⎝⎭（1）地球表面反射太阳辐射的总功率为I P α．设地球表面的温度为E T ，则地球的热辐射总功率为24E E E 4πP r T σ= （2）考虑到温室气体向地球表面释放的热辐射，则输入地球表面的总功率为I E P P β+．当达到热平衡时，输入的能量与输出的能量相等，有I E I E P P P P βα+=+ （3）由以上各式得1/41/2S E S 121R T T d αβ⎫-⎛⎫=⎪⎪-⎝⎭⎝⎭（4）代入数值，有E 287K T = （5）2．当地球表面一部分被冰雪覆盖后，以α'表示地球表面对太阳辐射的平均反射率，根据题意这时地球表面的平均温度为E 273K T =．利用（4）式，可求得0.43α'= （6）设冰雪覆盖的地表面积与总面积之比为x ，则12(1)x x ααα'=+- （7）由（6）、（7）两式并代入数据得%30=x （8）评分标准：本题15分．第1小问11分．（1）式3分，（2）式1分，（3）式4分，（4）式2分，（5）式1分．第2小问4分．（6）式2分，（8）式2分．八、参考解答：方案一：采光装置由平面镜M 和两个凸透镜L 1、L 2组成．透镜组置于平面镜M 后面，装置中各元件的相对方位及光路图如图1所示．L 1、L 2的直径分别用D 1、D 2表示，其焦距的大小分别为f 1 、f 2．两透镜的距离12d f f =+ （1）直径与焦距应满足关系1212f fD D = （2） 设射入透镜L 1的光强为10I '，透过透镜L 1的光强为1I '，考虑到透镜L 1对光的吸收有 1100.70I I ''=（3） 从透镜L 1透出的光通量等于进入L 2的光通量，对应的光强与透镜的直径平方成反比，进入L 2的光强用20I 表示，即2220112122I D f I f D ⎛⎫== ⎪'⎝⎭故有212012f I I f ⎛⎫'= ⎪⎝⎭（4）透过L 2的光强2200.70I I '=，考虑到（3）式，得 2121020.49f I I f ⎛⎫''= ⎪⎝⎭（5） 由于进入透镜L 1的光强10I '是平面镜M 的反射光的光强，反射光是入射光的80%，设射入装置的太阳光光强为0I ，则1000.80I I '= L 22.5图1代入（5）式有212020.39f I I f ⎛⎫'= ⎪⎝⎭（6）按题设要求202I I '= 代入（6）式得2100220.39f I I f ⎛⎫= ⎪⎝⎭从而可求得两透镜的焦距比为122.26f f = （7） L 2的直径应等于圆形窗户的直径W ，即210cm D =，由（2）式得112222.6cm f D D f == （8） 由图可知，平面镜M 参与有效反光的部分为一椭圆，其半短轴长度为1/211.3cm b D == （9）半长轴长度为1(2sin 22.5)29.5cm a D == （10）根据装置图的结构，可知透镜组的光轴离地应与平面镜M 的中心等高，高度为H ． 评分标准：本题20分．作图8分（含元件及其相对方位，光路），求得（7）、（8）两式共10分，（9）、（10）式共2分．方案二：采光装置由平面镜M 和两个凸透镜L 1、L 2组成，透镜组置于平面镜M 前面，装置中各元件的相对方位及光路图如图2所示．对透镜的参数要求与方案一相同．但反射镜M 的半短轴、半长轴的长度分别为2/2 5.0cm b D == 和2(2sin 22.5)13.1cm a D ==评分标准：参照方案一．方案三、采光装置由平面镜M 和一个凸透镜L 1、一个凹透镜L 2组成，透镜组置于平面镜M 后面（也可在M 前面），装置中各元件的相对方位及光路图如图3所示．有关参数与方案一相同，但两透镜的距离12d f f =-如果平面镜放在透镜组之前，平面镜的尺寸和方案一相同；如果平面镜放在透镜组之后，平面镜的尺寸和方案二相同． 评分标准：参照方案一．九、参考解答：1．假设碰撞后球1和球2的速度方向之间的夹角为α（见图），1L 22.5图 322.5图2W则由能量守恒和动量守恒可得22220000102m c m c m c m c γγγ+=+ （1）()()()()()2220000110220110222cos m m m m m γγγγγα=++v v v v v（2）其中0γ=，1γ=，2γ=．由（1）、（2）式得2101γγγ+=+ （3）2222012121212(/)cos c γγγγγα+=++v v （4）由（3）、（4）式得222220121212121212111cos 02()()()c c γγγγγαγγγγ+-+--==>v v v v （5）π2α<（6） 即为锐角．在非相对论情况下，根据能量守恒和动量守恒可得2202100212121v v v m m m +=20 （7） ()()()()()22200010201022cos m m m m m α=++v v v v v（8）对斜碰，1v 的方向与2v 的方向不同，要同时满足（1）和（2）式，则两者方向的夹角π2α=（9） 即为直角．2．根据能量守恒和动量守恒可得22220m c +=+（10）1=+（11）令0γ=，1γ=，2γ=则有：0=v1=v2=v 代入（10）、（11）式得2101γγγ+=+ （12）111222120-+-=-γγγ（13）解（12）、（13）两式得11=γ 02γγ= （14）或01γγ= 21γ= （15）即10=v ， 20=v v （16）（或10=v v ，20=v ，不合题意）评分标准：本题16分．第1小问10分．（1）、（2）式各2分，（6）式4分，（9）式2分． 第2小问6分．（10）、（11）式各1分，（16）式4分．第32届全国中学生物理竞赛复赛理论考试试题及答案2015年9月19日说明：所有解答必须写在答题纸上，写在试题纸上无效。

第28届全国中学生物理竞赛复赛试题一、（20分）如图所示，哈雷彗星绕太阳S 沿椭圆轨道逆时针方向运动，其周期T 为76.1年，1986年它过近日点P 0时与太阳S 的距离r 0=0.590AU ，AU 是天文单位，它等于地球与太阳的平均距离，经过一段时间，彗星到达轨道上的P 点，SP 与SP 0的夹角θP =72.0°。

已知：1AU=1.50×1011m ，引力常量G=6.67×10－11Nm 2/kg 2，太阳质量m S =1.99×1030kg ，试求P 到太阳S 的距离r P 及彗星过P 点时速度的大小及方向（用速度方向与SP 0的夹角表示）。

二、（20分）质量均匀分布的刚性杆AB 、CD 如图放置，A 点与水平地面接触，与地面间的静摩擦系数为μA ，B 、D 两点与光滑竖直墙面接触，杆AB 和CD 接触处的静摩擦系数为μC ，两杆的质量均为m ，长度均为l 。

1、已知系统平衡时AB 杆与墙面夹角为θ，求CD 杆与墙面夹角α应该满足的条件（用α及已知量满足的方程式表示）。

2、若μA =1.00，μC =0.866，θ=60.0°。

求系统平衡时α的取值范围（用数值计算求出）。

三、（25分）在人造卫星绕星球运行的过程中，为了保持其对称转轴稳定在规定指向，一种最简单的办法就是让卫星在其运行过程中同时绕自身的对称轴转，但有时为了改变卫星的指向，又要求减慢或者消除卫星的旋转，减慢或者消除卫星旋转的一种方法就是所谓消旋法，其原理如图所示。

一半径为R ，质量为M 的薄壁圆筒，，其横截面如图所示，图中O 是圆筒的对称轴，两条足够长的不可伸长的结实的长度相等的轻绳的一端分别固定在圆筒表面上的Q 、Q ′（位于圆筒直径两端）处，另一端各拴有一个质量为2m的小球，正常情况下，绳绕在圆筒外表面上，两小球用插销分别锁定在圆筒表面上的P 0、P 0′处，与卫星形成一体，绕卫星的对称轴旋转，卫星自转的角速度为ω0。

第23届全国中学生物理竞赛复赛试卷一、（23分）有一竖直放置、两端封闭的长玻璃管，管内为真空，管内有一小球自某处自由下落（初速度为零），落到玻璃管底部时与底部发生弹性碰撞．以后小球将在玻璃管内不停地上下跳动。

现用支架固定一照相机，用以拍摄小球在空间的位置。

每隔一相等的确定的时间间隔T拍摄一张照片，照相机的曝光时间极短，可忽略不计。

从所拍到的照片发现，每张照片上小球都处于同一位置。

求小球开始下落处离玻璃管底部距离（用H表示）的可能值以及与各H值相应的照片中小球位置离玻璃管底部距离的可能值。

二、（25分）如图所示，一根质量可以忽略的细杆，长为2l，两端和中心处分别固连着质量为m的小球B、D和C，开始时静止在光滑的水平桌面上。

桌面上另有一质量为M的小球A，以一给定速度v沿垂直于杆DB的方间与右端小球B作弹性碰撞。

求刚碰后小球A,B,C,D的速度，并详细讨论以0后可能发生的运动情况。

三、（23分）有一带活塞的气缸，如图1所示。

缸内盛有一定质量的气体。

缸内还有一可随轴转动的叶片，转轴伸到气缸外，外界可使轴和叶片一起转动，叶片和轴以及气缸壁和活塞都是 绝热的，它们的热容量都不计。

轴穿过气缸处不漏气。

如果叶片和轴不转动，而令活塞缓慢移动，则在这种过程中，由实验测得，气体的压强p 和体积V 遵从以下的过程方程式k pVa=其中a ,k 均为常量, a ＞1（其值已知）。

可以由上式导出，在此过程中外界对气体做的功为 ⎥⎦⎤⎢⎣⎡--=--1112111a a V V a k W 式中2V 和1V ,分别表示末态和初态的体积。

如果保持活塞固定不动，而使叶片以角速度ω做匀角速转动，已知在这种过程中，气体的压强的改变量p ∆和经过的时间t ∆遵从以下的关系式ω⋅-=∆∆L Va t p 1 式中V 为气体的体积，L 表示气体对叶片阻力的力矩的大小。

上面并没有说气体是理想气体，现要求你不用理想气体的状态方程和理想气体的内能只与温度有关的知识，求出图2中气体原来所处的状态A 与另一已知状态B 之间的内能之差（结果要用状态A 、B 的压强A p 、B p 和体积A V 、B V 及常量a 表示）四、（25分）图1所示的电路具有把输人的交变电压变成直流电压并加以升压、输出的功能，称为整流倍压电路。

第28届全国中学生物理竞赛复赛试题（2011）一、（20分）如图所示，哈雷彗星绕太阳S 沿椭圆轨道逆时针方向运动，其周期T 为76.1年，1986年它过近日点P 0时与太阳S 的距离r 0=0.590AU ，AU 是天文单位，它等于地球与太阳的平均距离，经过一段时间，彗星到达轨道上的P 点，SP 与SP 0的夹角θP =72.0°。

已知：1AU=1.50×1011m ，引力常量G=6.67×10－11Nm 2/kg 2，太阳质量m S =1.99×1030kg ，试求P 到太阳S 的距离r P 及彗星过P 点时速度的大小及方向（用速度方向与SP 0的夹角表示）。

二、（20分）质量均匀分布的刚性杆AB 、CD如图放置，A 点与水平地面接触，与地面间的静摩擦系数为μA ，B 、D 两点与光滑竖直墙面接触，杆AB 和CD 接触处的静摩擦系数为μC ，两杆的质量均为m ，长度均为l 。

1、已知系统平衡时AB 杆与墙面夹角为θ，求CD 杆与墙面夹角α应该满足的条件（用α及已知量满足的方程式表示）。

2、若μA =1.00，μC =0.866，θ=60.0°。

求系统平衡时α的取值范围（用数值计算求出）。

三、（25分）在人造卫星绕星球运行的过程中，为了保持其对称转轴稳定在规定指向，一种最简单的办法就是让卫星在其运行过程中同时绕自身的对称轴转，但有时为了改变卫星的指向，又要求减慢或者消除卫星的旋转，减慢或者消除卫星旋转的一种方法就是所谓消旋法，其原理如图所示。

一半径为R ，质量为M 的薄壁圆筒，，其横截面如图所示，图中O 是圆筒的对称轴，两条足够长的不可伸长的结实的长度相等的轻绳的一端分别固定在圆筒表面上的Q 、Q ′（位于圆筒直径两端）处，另一端各拴有一个质量为2m的小球，正常情况下，绳绕在圆筒外表面上，两小球用插销分别锁定在圆筒表面上的P 0、P 0′处，与卫星形成一体，绕卫星的对称轴旋转，卫星自转的角速度为ω0。

第十三届全国物理竞赛复赛试题解答一、在各段电路上，感应电流的大小和方向如图复解13 - 1所示电流的分布，已考虑到电路的对称性，根据法拉第电磁感应定律和欧姆定律，对半径为α的圆电路，可得 π2a k = 21r 1I + 1r 1I ' 对等边三角形三个边组成的电路，可得332a k / 4 = 22r 2I + 22r 2I '对由弦AB 和弧AB 构成的回路，可得（π2a -332a / 4）k / 3 = 1r 1I - 2r 2I考虑到，流进B 点的电流之和等于流出B 点电流之和，有1I + 2I =1I ' + 2I ' 由含源电路欧姆定律可得A U -B U = π2a k /3 - 1I 1r由以上各式及题给出的 2r = 21r / 3可解得A U -B U = - 32a k / 32二、解法一：1、分析和等效处理根据棱镜玻璃的折射率，棱镜斜面上的全反射临界角为c α= arcsin ( 1 / n ) ≈ 42 注意到物长为4mm ，由光路可估算，进入棱镜的近轴光线在斜面上的入射角大多在 45左右，大于临界角，发生全反射。

所以对这些光线而言，棱镜斜面可看成是反射镜。

本题光路可按反射镜成像的考虑方法，把光路“拉直”如图复解13 – 2 - 1所示。

现在，问题转化为正立物体经过一块垂直于光轴、厚度为6cm 的平玻璃板及其后的会聚透镜、发散透镜成像的问题。

2、求像的位置；厚平玻璃板将使物的近轴光线产生一个向右侧移动一定距离的像，它成为光学系统后面部分光路的物，故可称为侧移的物。

利用沿光轴的光线和与光轴成α角的光线来讨论就可求出这个移动的距离。

设轴上的物点为B 。

由于厚平玻璃板的作用（即侧移的物点）为B ′（如图复解13 – 2 - 2所示）。

画出厚平玻图复解13 - 111I图复解13 - 2 - 2图复解13 - 2 - 1璃板对光线的折射，由图可知 Δl = d （ctg α） 而 d = D （tg α- tg β） 所以 Δl = D （1 – tg α/ tg β） 当α为小角度时 tg β/ tg α≈sin β/ sin α= 1/n 故得 Δl = D （1 – 1 / n ）= 2 cm这也就是物AB 与它通过厚玻璃板所成的像之间的距离。

2024年第41届全国中学生物理竞赛预赛试卷一、单选题：本大题共3小题，共36分。

1.n mol理想气体经过一个缓慢的过程，从状态P沿抛物线到达状态Q，其体积绝对温度图如图所示。

已知此过程中当时，温度达到最大值其中和分别是状态P的压强和体积，R是普适气体常量。

若状态P和Q的温度和都等于，则该过程的压强图为()A. B.C. D.2.一个动能为的电子从很远处向一个固定的质子飞去。

电子接近质子时被俘获，同时放出一个光子，电子和质子形成一个处于基态的静止氢原子。

已知氢原子的基态能量为，光在真空中的速度为，电子电量的大小和普朗克常量分别为和。

所放出的光子的波长最接近的值是()A.79nmB.91nmC.107nmD.620nm3.某人心跳为60次每分钟，每次心跳心脏泵出60mL血液，泵出血液的血压为100mmHg。

已知。

该人的心脏向外泵血输出的机械功率最接近的值为()A. B. C. D.二、多选题：本大题共2小题，共24分。

4.一边长为a的正方形处于水平面上，其四个顶点各固定一个正电子。

一个电子在该正方形的中心点O的正上方、P两点的距离远小于处自静止释放。

不考虑空气阻力、重力、电磁辐射、量子效应和其他任何扰动。

该电子()A.会运动到无穷远处B.与正电子构成的系统的能量守恒C.会在过O点的竖直线上做周期运动D.会在正方形上方振荡5.如图，两竖直墙面的间距为l，一个质量为m、边长为d的正方形木块被一轻直弹簧顶在左侧墙面上，弹簧右端固定在右侧墙面上，且弹簧与墙面垂直。

已知木块与墙面之间的静摩擦因数为，弹簧原长为l，劲度系数为k，重力加速度大小为g。

下列说法正确的是()A.如果，则木块不处于平衡状态B.如果，则墙面对木块的正压力为C.如果，则木块受到的静摩擦力大小为D.为使木块在此位置保持平衡状态，k最小为三、填空题：本大题共5小题，共100分。

6.时间、长度、质量、电荷的单位通常和单位制有关。

量子论的提出者普朗克发现利用真空中的光速c、万有引力常量G、普朗克常量h、真空介电常量可以组合出与单位制无关的质量单位、长度单位、时间单位、电荷单位，这些量分别称为普朗克质量、普朗克长度、普朗克时间、普朗克电量。

第38届全国中学生物理竞赛复赛试题（2021年9月19日上午9:00-12:00）考生必读1、考生考试前请务必认真阅读本须知。

2、本试题共4页，每大题40分，总分为320分。

3、如遇试题印刷不清楚情况，请务必向监考老师提出。

4、需要阅卷老师评阅的内容一定要写在答题纸上；写在试题纸和草稿纸上的解答一律不能得分。

一、（1）一宽束平行光正入射到折射率为n 的平凸透镜左侧平面上，会聚于透镜主轴上的点F ，系统过主轴的截面如图1a 所示。

已知凸透镜顶点O 到F 点的距离为0r 。

试在极坐标系中求所示平凸透镜的凸面形状，并表示成直角坐标系中的标准形式。

（2）在如图1a 所示的光学系统中，共轴地插入一个折射率为n '的平凹透镜（平凹透镜的平面在凹面的右侧，顶点在O 、F 点之间的光轴上，到F 的距离为0r '，00r r '<），使原来汇聚到F 点的光线经平凹透镜的凹面折射后平行向右射出。

（i ）在极坐标系中求所插入的平凹透镜的凹面形状，并表示成直角坐标系中的标准形式；（ii ）已知通过平凸透镜后的汇聚光线与主轴的夹角θ的最大值为max θ，求入射平行圆光束与出射平行圆光束的横截面半径之比。

二、如图2a ，一端开口的薄壁玻璃管竖直放置，开口朝上，玻璃管总长75.0 cm l =，横截面积210.0 cm S =，玻璃管内用水银封闭一段理想气体，水银和理想气体之间有一薄而轻的绝热光滑活塞，气柱高度与水银柱高度均为25.0 cm h =。

已知该理想气体初始温度0400 K T =，定体摩尔热容52V CR=，其中8.31 J/(mol K)R =⋅为普适气体常量；水银密度3313.610 kg/m ρ=⨯，大气压强075.0 cmHg p =，重力加速度大小29.80 m/s g =。

（1）过程A ：对封闭的气体缓慢加热，使水银上液面恰好到达玻璃管开口处，求过程A 中封闭气体对外所做的功；（2）过程B ：继续对封闭气体缓慢加热，直至水银恰好全部流出为止（薄活塞恰好与玻璃管开口平齐），通过计算说明过程B 能否缓慢稳定地发生？计算过程B 中封闭气体所吸收的热量。