2017-2018届广东省海珠区等四区高三联考理科数学试题及答案

试卷类型：A 2017-2018年广州市普通高中毕业班综合测试（二）数学（理科）4 本试卷共4页，21小题，满分150分.考试用时120分钟.注意事项：1．答卷前，考生务必用黑色字迹钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上.用2B铅笔将试卷类型（A）填涂在答题卡相应位置上.2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上.3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答的答案无效.4．作答选做题时，请先用2B铅笔填涂选做题的题号对应的信息点，再作答.漏涂、错涂、多涂的，答案无效.5．考生必须保持答题卡的整洁.考试结束后，将试卷和答题卡一并交回.参考公式：锥体的体积公式是13V Sh =,其中S 是锥体的底面积,h 是锥体的高.一、选择题：本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1. 若复数z 满足 i 2z =，其中i 为虚数单位，则z 的虚部为A ．2-B ．2C ．2-iD ．2i2．若函数()y f x =是函数3x y =的反函数，则12f ⎛⎫⎪⎝⎭的值为A ．2log 3-B ．3log 2-C ．19D 3．命题“对任意x ∈R ，都有32x x >”的否定是A ．存在0x ∈R ，使得3200x x >B ．不存在0x ∈R ，使得3200x x >C ．存在0x ∈R ，使得3200x x ≤ D ．对任意x ∈R ，都有32x x ≤4. 将函数()2cos 2(f x x x x =+∈R )的图象向左平移6π个单位长度后得到函数()y g x =，则函数()y g x =A ．是奇函数B ．是偶函数C ．既是奇函数又是偶函数D ．既不是奇函数，也不是偶函数5．有两张卡片，一张的正反面分别写着数字0与1，另一张的正反面分别写着数字2与3，将两张卡片排在一起组成两位数，则所组成的两位数为奇数的概率是A ．16B ．13C ．12D ．38图1俯视图侧视图正视图6．设12,F F 分别是椭圆()2222:10x y C a b a b+=>>的左、右焦点，点P 在椭圆C 上，线段1PF的中点在y 轴上，若1230PF F ︒∠=，则椭圆C A ．16 B ．13C7．一个几何体的三视图如图1，则该几何体 的体积为A ．6π4+B ．12π4+C ．6π12+D ．12π12+ 8．将正偶数2,4,6,8, 按表1的方式进行排列，记ij a 表示第i 行第j 列的数，若2014ij a =，则i j +的值为A ．257 B ．256C ．254D ．253表1 二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．（一）必做题（9～13题）9．不等式2210x x --<的解集为 .10．已知312nx x ⎛⎫- ⎪⎝⎭的展开式的常数项是第7项，则正整数n 的值为 .11．已知四边形ABCD 是边长为a 的正方形，若2,2DE EC CF FB == ，则AE AF ⋅的值为 .12．设,x y 满足约束条件 220,840,0,0.x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩若目标函数()0,0z ax by a b =+>>的最大值为8，则ab 的最大值为 .13．已知[]x 表示不超过x 的最大整数，例如[][]1.52,1.51-=-=.设函数()[]f x x x ⎡⎤=⎣⎦，当[)0,(x n n ∈∈N *)时，函数()f x 的值域为集合A ，则A 中的元素个数为 .（二）选做题（14～15题，考生从中选做一题）14．（坐标系与参数方程选做题）在平面直角坐标系xOy 中，直线,(x a t t y t =-⎧⎨=⎩为参数)与 圆1cos ,(sin x y θθθ=+⎧⎨=⎩为参数)相切，切点在第一象限，则实数a 的值为 .DCBA15．（几何证明选讲选做题）在平行四边形ABCD 中，点E 在线段AB 上，且12AE EB =，连接,DE AC ，AC 与DE 相交于点F ，若△AEF 的面积为1 cm 2，则△AFD 的面积为 cm 2.三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16.（本小题满分12分）如图2，在△ABC 中，D 是边AC 的中点， 且1AB AD ==，3BD =. (1) 求cos A 的值； （2）求sin C 的值.图217．（本小题满分12分）一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取50个作为样本，称出它们的重量（单位：克），重量分组区间为(]5,15，(]15,25，(]25,35，(]35,45，由此得到样本的重量频率分布直方图，如图3. （1）求a 的值；（2）根据样本数据，试估计盒子中小球重量的平均值；CBa 图3重量/克0.0320.02452515O （注：设样本数据第i 组的频率为i p ，第i 组区间的中点值为i x ()1,2,3,,i n = ，则样本数据的平均值为112233X x p x p x p =+++ （3）从盒子中随机抽取3个小球，其中重量在的小球个数为ξ，求ξ18．（本小题满分14分）如图4，在五面体ABCDEF 中，四边形ABCD 是边长为2的正方形，EF ∥平面ABCD ，1EF =，,90FB FC BFC ︒=∠=，AE =（1）求证：AB ⊥平面BCF ；（2）求直线AE 与平面BDE 所成角的正切值.图419．（本小题满分14分）已知数列{}n a 的前n 项和为n S ，且10a =，对任意n ∈N *，都有()11n n na S n n +=++.（1）求数列{}n a 的通项公式；（2）若数列{}n b 满足22log log n n a n b +=，求数列{}n b 的前n 项和n T .20．（本小题满分14分）已知定点()0,1F 和直线:1l y =-，过点F 且与直线l 相切的动圆圆心为点M ，记点M 的轨迹为曲线E . (1) 求曲线E 的方程;(2) 若点A 的坐标为()2,1, 直线1:1(l y kx k =+∈R ，且0)k ≠与曲线E 相交于,B C 两点，直线,AB AC 分别交直线l 于点,S T . 试判断以线段ST 为直径的圆是否恒过两个定点? 若是，求这两个定点的坐标；若不是，说明理由.21．（本小题满分14分）已知函数()ln (,f x a x bx a b =+∈R )在点()()1,1f 处的切线方程为220x y --=.（1）求,a b 的值；（2）当1x >时，()0kf x x+<恒成立，求实数k 的取值范围；（3）证明：当n ∈N *，且2n ≥时，22111322ln 23ln 3ln 22n n n n n n--+++>+ .2017-2018年广州市普通高中毕业班综合测试（二）数学（理科）试题参考答案及评分标准说明：1．参考答案与评分标准指出了每道题要考查的主要知识和能力，并给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力对照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．一、选择题：本大题考查基本知识和基本运算．共8小题，每小题5分，满分40分．二、填空题：本大题考查基本知识和基本运算，体现选择性．共7小题，每小题5分，满分30分．其中14~15题是选做题，考生只能选做一题．9．1,12⎛⎫- ⎪⎝⎭10．8 11．2a 12．4 13．222n n -+141 15．3三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤． 16．（本小题满分12分）（1）解：在△ABD 中，1AB AD ==，BD =， ∴222cos 2AB AD BD A AB AD+-=⋅⋅2221112113+-⎝⎭==⨯⨯. ……………4分（2）解：由（1）知，1cos 3A =，且0A <<π，∴sin 3A ==. ……………6分∵D 是边AC 的中点，∴22AC AD ==. 在△ABC中，222222121cos 22123AB AC BC BC A AB AC +-+-===⋅⋅⨯⨯，………8分解得BC =……………10分 由正弦定理得，sin sin BC ABA C=， ……………11分∴1sin sin AB AC BC⋅===. ……………12分17．（本小题满分12分） (1)解：由题意，得()0.020.0320.018101x +++⨯=， ……………1分解得0.03x =. ……………2分（2）解：50个样本小球重量的平均值为0.2100.32200.3300.184024.6X =⨯+⨯+⨯+⨯=（克）. ……………3分由样本估计总体，可估计盒子中小球重量的平均值约为24.6克. ……………4分（3）解：利用样本估计总体，该盒子中小球重量在(]5,15内的概率为0.2，则13,5B ξ⎛⎫⎪⎝⎭.……………5分 ξ的取值为0,1,2,3，……………6分 ()30346405125P C ξ⎛⎫=== ⎪⎝⎭，()2131448155125P C ξ⎛⎫⎛⎫==⨯= ⎪ ⎪⎝⎭⎝⎭， ()2231412255125P C ξ⎛⎫⎛⎫==⨯=⎪ ⎪⎝⎭⎝⎭，()3331135125P C ξ⎛⎫===⎪⎝⎭. ……………10分 为：∴ξ的分布列……………11分 ∴6448121301231251251251255E ξ=⨯+⨯+⨯+⨯=. ……………12分（或者13355E ξ=⨯=） 18．（本小题满分14分）（1）证明：取AB的中点M，连接EM，则1==，AM MB∵EF∥平面ABCD，EF⊂平面ABFE，平面ABCD 平面=，ABFE AB∴EF∥AB，即EF∥MB. ……………1分∵EF=MB1=∴四边形EMBF是平行四边形. ……………2分∴EM∥FB，EM FB=.在Rt△BFC中，2224=，得FB=+==，又FB FCFB FC BC∴EM=……………3分在△AME中，AE=1AM=，EM=∴222+==，3AM EM AE∴⊥. AM EM……………4分∴AM FB⊥.⊥，即AB FB∵四边形ABCD是正方形，∴⊥. AB BCMO HFEDCB……………5分∵FB BC B = ，FB ⊂平面BCF ，BC ⊂平面BCF ， ∴AB ⊥平面BCF . ……………6分（2）证法1：连接AC ，AC 与BD 相交于点O ，则点O 是AC 的中点， 取BC 的中点H ，连接,OH EO ，FH ， 则OH ∥AB ，112OH AB ==.由（1）知EF ∥AB ，且12EF AB =，∴EF ∥OH ，且EF OH =. ∴四边形EOHF 是平行四边形. ∴EO∥FH，且1EO FH == .……………7分由（1）知AB ⊥平面BCF ，又FH ⊂平面BCF ， ∴FH AB ⊥. ……………8分∵FH BC ⊥，,AB BC B AB =⊂ 平面ABCD ，BC ⊂平面ABCD ， ∴FH ⊥平面ABCD . (9)分∴EO ⊥平面ABCD .∵AO⊂平面ABCD，∴EO⊥AO. ……………10分∵AO BD⊥，,EO BD O EO=⊂平面EBD，BD⊂平面EBD，∴AO⊥平面EBD. (11)分∴AEO∠是直线AE与平面BDE所成的角. ……………12分在Rt△AOE中，tanAOAEOEO∠==……………13分∴直线AE与平面BDE所成角的正切值为……………14分证法2：连接AC，AC与BD相交于点O取BC的中点H，连接,OH EO，则OH∥AB，112OH AB==.由（1）知EF∥AB，且12EF AB=∴EF∥OH，且EF OH=.∴四边形EOHF是平行四边形.∴EO∥FH，且1EO FH==. ……………7分由（1）知AB ⊥平面BCF ，又FH ⊂平面BCF ， ∴FH AB ⊥.∵FH BC ⊥，,AB BC B AB =⊂ 平面ABCD ，BC ⊂平面ABCD ， ∴FH ⊥平面ABCD . ∴EO ⊥平面ABCD . (8)分以H 为坐标原点，BC 所在直线为x 轴，OH 所在直线为y 轴，HF 所在直线为z 轴，建立空间直角坐标系H xyz -，则()1,2,0A -，()1,0,0B ，()1,2,0D --，()0,1,1E -.∴()1,1,1AE =-，()2,2,0BD =--，()1,1,1BE =--. ……………9分设平面BDE 的法向量为=n (),,x y z ，由n 0BD ⋅= ，n 0BE ⋅=，得220x y --=，0x y z --+=，得0,z x y ==-. 令1x =，则平面BDE的一个法向量为=n ()1,1,0-. ……………10分设直线AE 与平面BDE 所成角为θ， 则sin θ=cos , n AE ⋅=n AE n AE3=. ……………11分∴cos 3θ==，sintan cos θθθ==……………13分 ∴直线AE 与平面BDE 所成角的正切值为……………14分19．（本小题满分14分）（1）解法1：当2n ≥时，()11n n na S n n +=++，()()111n n n a S n n --=+-，……1分 两式相减得()()()11111n n n n na n a S S n n n n +---=-++--， ……………3分即()112n n n na n a a n+--=+，得12n n a a +-=. ……………5分当1n =时，21112a S ⨯=+⨯，即212a a -=. ……………6分∴数列{}n a 是以10a =为首项，公差为2的等差数列. ∴()2122n a n n =-=-. ……………7分 解法2：由()11n n na S n n +=++，得()()11n n n n S S S n n +-=++， ……………1分整理得，()()111n n nS n S n n +=+++， ……………2分两边同除以()1n n +得，111n nS S n n+-=+. ……………3分 ∴数列n S n ⎧⎫⎨⎬⎩⎭是以101S =为首项，公差为1的等差数列. ∴011nS n n n=+-=-. ∴()1n S n n =-. ……………4分 当2n ≥时，()()()111222n n n a S S n n n n n -=-=----=-. ……………5分又10a =适合上式， ……………6分 ∴数列{}n a 的通项公式为22n a n =-. ……………7分（2）解法1：∵22log log n n a n b +=， ∴221224n a n n n b n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++ ()0122142434144n n n n --=+⨯+⨯++-⋅+⋅ ，①()1231442434144n nn T n n -=+⨯+⨯++-⋅+⋅ ，② ……………11分①-②得0121344444n nn T n --=++++-⋅ 14414n nn -=-⋅-()13413n n -⋅-=. ……………13分 ∴()131419nn T n ⎡⎤=-⋅+⎣⎦. ……………14分解法2：∵22log log n n a n b +=， ∴221224n a n n n b n n n --=⋅=⋅=⋅. ……………9分∴1231n n n T b b b b b -=+++++ ()0122142434144n n n n --=+⨯+⨯++-⋅+⋅ . 由()12311n nx x x x x x x x+-++++=≠- ， ……………11分 两边对x取导数得，12123n x x x nx-++++=()()12111n n nx n x x +-++-. ………12分令4x =，得()()0122114243414431419n n nn n n --⎡⎤+⨯+⨯++-⋅+⋅=-⋅+⎣⎦ .……………13分 ∴()131419n n T n ⎡⎤=-⋅+⎣⎦. ……………14分20．（本小题满分14分）（1）解法1：由题意, 点M 到点F 的距离等于它到直线l 的距离,故点M 的轨迹是以点F 为焦点, l 为准线的抛物线. ……………1分 ∴曲线E的方程为24x y =. ……………2分解法2：设点M 的坐标为(),x y ,依题意, 得1MF y =+, 即1y =+, ……………1分化简得24x y =. ∴曲线E的方程为24x y =. ……………2分(2) 解法1: 设点,B C 的坐标分别为()()1122,,,x y x y ，依题意得，2211224,4x y x y ==.由21,4,y kx x y =+⎧⎨=⎩消去y 得2440x kx --=，解得1,22x k ==±.∴12124,4x x k x x +==-. ……………3分直线AB 的斜率2111111124224AB x y x k x x --+===--， 故直线AB的方程为()12124x y x +-=-. ……………4分 令1y =-，得1822x x =-+， ∴点S的坐标为182,12x ⎛⎫-- ⎪+⎝⎭. ……………5分 同理可得点T的坐标为282,12x ⎛⎫-- ⎪+⎝⎭. ……………6分 ∴()()()121212888222222x x ST x x x x -⎛⎫=---= ⎪++++⎝⎭()()()121212121288248x x x x x x x x x x k k---===+++. ……………7分∴2ST =()()()2221212122221614k x x x x x x k k k +-+-==. ……………8分设线段ST 的中点坐标为()0,1x -，则()()()12012124418822222222x x x x x x x ++⎛⎫=-+-=-⎪++++⎝⎭()()()1212444444222248k k x x x x k k++=-=-=-+++. ……………9分∴以线段ST 为直径的圆的方程为()2222114x y ST k ⎛⎫+++= ⎪⎝⎭()2241k k +=. ……………10分 展开得()()22222414414k x x y k k k++++=-=. ……………11分 令x =，得()214y +=，解得1y =或3y =-. ……………12分∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分解法2：由（1）得抛物线E 的方程为24x y =.设直线AB 的方程为()112y k x -=-，点B 的坐标为()11,x y ，由()112,1,y k x y ⎧-=-⎨=-⎩解得122,1.x k y ⎧=-⎪⎨⎪=-⎩∴点S 的坐标为122,1k ⎛⎫-- ⎪⎝⎭. …………3分 由()1212,4,y k x x y ⎧-=-⎨=⎩消去y ，得2114840x k x k -+-=， 即()()12420x x k --+=，解得2x =或142x k =-. ……………4分∴1142x k =-，22111114414y x k k ==-+. ∴点B的坐标为()211142,441kk k --+. ……………5分同理，设直线AC 的方程为()212y k x -=-，则点T 的坐标为222,1k⎛⎫-- ⎪⎝⎭，点C 的坐标为()222242,441kk k --+. …………6分∵点,B C 在直线1:1l y kx =+上，∴()()()()()()22222211212121214414414242k k k k k k k k k k k k k -+--+---==----121k k =+-.∴121k k k +=+. ……………7分又()211144142k k k k -+=-1+，得()21111214442412k k kk k k k k k -=-=+--， 化简得122kk k =. ……………8分设点(),P x y 是以线段ST 为直径的圆上任意一点，则0SP TP ⋅=， ……………9分得()()122222110x x y y k k ⎛⎫⎛⎫-+-++++= ⎪⎪⎝⎭⎝⎭， ……………10分 整理得，()224410x x y k+-++=. ……………11分 令x =，得()214y +=，解得1y =或3y =-. ……………12分∴以线段ST 为直径的圆恒过两个定点()()0,1,0,3-. ……………14分21．（本小题满分14分）（1）解：∵()ln f x a x bx =+， ∴()a f x b x'=+. ∵直线220x y --=的斜率为12，且过点11,2⎛⎫- ⎪⎝⎭， ……………1分 ∴()()11,211,2f f ⎧=-⎪⎪⎨⎪'=⎪⎩即1,21,2b a b ⎧=-⎪⎪⎨⎪+=⎪⎩解得11,2a b ==-. ……………3分（2）解法1：由（1）得()ln 2xf x x =-.当1x >时，()0k f x x +<恒成立，即ln 02x kx x-+<，等价于2ln 2x k x x <-.……………4分令()2ln 2x g x x x=-，则()()ln 11ln g x x x x x '=-+=--. ……………5分令()1ln h x x x =--，则()111x h x x x-'=-=. 当1x >时，()0h x '>，函数()h x 在()1,+∞上单调递增，故()()10h x h >=.……………6分从而，当1x >时，()0g x '>，即函数()g x 在()1,+∞上单调递增， 故()()112g x g >=. ……………7分因此，当1x >时，2ln 2x k x x <-恒成立，则12k ≤. ……………8分 ∴所求k的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分 解法2：由（1）得()ln 2xf x x =-.当1x >时，()0k f x x +<恒成立，即ln 02x kx x-+<恒成立. ……………4分令()ln 2x k g x x x =-+，则()222112222k x x kg x x x x -+'=--=-.方程2220x x k -+=（﹡）的判别式48k ∆=-.（ⅰ）当0∆<，即12k >时，则1x >时，2220x x k -+>，得()0g x '<， 故函数()g x 在()1,+∞上单调递减.由于()()110,2ln 21022k g k g =-+>=-+>，则当()1,2x ∈时，()0g x >，即ln 02x k x x-+>，与题设矛盾. …………5分（ⅱ）当0∆=，即12k =时，则1x >时，()()2222121022x x x g x x x --+'=-=-<. 故函数()g x 在()1,+∞上单调递减，则()()10g x g <=，符合题意. ………6分(ⅲ) 当0∆>，即12k <时，方程（﹡）的两根为1211,11x x =<=>，则()21,x x ∈时，()0g x '>，()2,x x ∈+∞时，()0g x '<. 故函数()g x 在()21,x 上单调递增，在()2,x +∞上单调递减， 从而，函数()g x 在()1,+∞上的最大值为()2222ln 2x kg x x x =-+. ………7分 而()2222ln 2x k g x x x =-+2221ln 22x x x <-+， 由（ⅱ）知，当1x >时，1ln 022xx x-+<， 得2221ln 022x x x -+<，从而()20g x <. 故当1x >时，()()20g x g x ≤<，符合题意. ……………8分 综上所述，k的取值范围是1,2⎛⎤-∞ ⎥⎝⎦. ……………9分（3）证明：由（2）得，当1x >时，1ln 022x x x -+<，可化为21ln 2x x x -<， …10分又ln 0x x >， 从而，21211ln 111x x x x x >=---+. ……………11分 把2,3,4,,x n = 分别代入上面不等式，并相加得，11111111111112ln 23ln 3ln 32435211n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++>-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪--+⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭……………12分111121n n =+--+ ……………13分223222n n n n--=+. ……………14分。

2017-2018学年第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项 是符合题目要求的.1.若集合{|(1)(5)0}M x x x =--<，集合{|N x y =，则M N 等于（ ）A ．(1,4]B ．(1,4)C ．[4,5)D ．(4,5) 2.设复数z 为纯虚数，a R ∈，且1013x a i+=-，则a 的值为（ ） A ． 3 B ． -3 C ．1 D ．-13.下面是2010年3月安徽省芜湖楼市商品住宅板块销售对比饼状图，由图可知，戈江区3月销售套数为（ ）A ．350B ．340C ．330D ． 306 4.若sin cos tan 390αα+=，则sin 2α等于（ ） A. 23-B.34-C. 23D. 345.如图所示的五边形是由一个矩形截去一个角而得，且1BC =，2DE =，3AE =，4AB =，则CD 等于（ ）A ．1223AB AE + B ．1223AB AE -C. 1223AB AE -+ D ．1223AB AE -- 6.直线2y b =与双曲线22221(0,0)x y a b a b-=>>的左支、右支分别交于A B 、两点，O 为坐标原点，且AOB ∆为等腰直角三角形，则该双曲线的离心率为（ ）A ．2．32 C. 5 D ．57.某几何体的三视图如图所示，则该几何体的体积为（ ）A ． 40B ．48 C. 56 D ．928.执行如图所示的程序框图，若输入的2x =，4n =，则输出的s 等于（ ）A ．94B ． 99 C. 45 D ．2039.飞机的航线和山顶在同一个铅垂平面内，已知飞机的高度为海拔15000m ，速度为1000/km h ，飞行员先看到山顶的俯角为18，经过108s 后又看到山顶的俯角为78，则山顶的海拔高度为（ ）A．(15cos78)km - B．(15sin78)km -C. (15cos78)km - D．(15sin78)km - 10.已知抛物线2:2(04)C y px p =<<的焦点为F ，点P 为C 上一动点，(4,0)A，()B p ,且||PA||BF 等于（ ）A ． 4B ．92C. 5 D ．11211.已知函数()sin (0)f x x x ωωω=>在区间(0,)π上存在3个不同的0x ，使得0()1f x =，则ω的取值范围为（ ）A ．523(,]26 B ．523(,)26 C. 319(,)26 D ．319(,]2612.已知函数3,1()2,1x x x f x x x ⎧->=⎨+≤⎩，若关于x 的方程(())f f x a =存在2个实数根，则a 的取值范围为（ ）A ．[24,0)-B ．(,24)[0,2)-∞-C.(24,3)- D ．(,24][0,2]-∞-第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.设x y ，满足约束条件802020x y x y x +-≤⎧⎪--≤⎨⎪-≥⎩，则2z x y =-的最小值为_________.14.函数()426xxf x =--的零点为___________.15.设32340123455(12)2481632x a a x a x a x a x a x -=+++++，则12345a a a a a ++++=_____________.16.已知四面体ABCD 的每个顶点都在球O 的表面上，5AB AC ==，8BC =，AD ⊥底面ABC ，G 为ABC ∆的重心，且直线DG 与底面ABC 所成角的正切值为12，则球O 的表面积为____________.三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.（本小题满分12分）已知等差数列{}n a 的公差0d >，且1611a a =，3412a a +=. （1）求数列{}n a 的通项公式； （2）求数列112{}2n nn a a ++-的前n 项和n T .18. （本小题满分12分）为调查了解某高等院校毕业生参加工作后，从事的工作与大学所学专业是否专业对口，该校随机调查了80位该校2015年毕业的大学生，得到具体数据如下表：（1）能否在犯错误的概率不超过5%的前提下，认为“毕业生从事的工作与大学所学专业对口与性别有关”？参考公式：22()()()()()n ad bc k a b c d a c b d -=++++（n a b c d =+++）．附表：（2）求这80位毕业生从事的工作与大学所学专业对口的频率；（3）以（2）中的频率作为概率.该校近几年毕业的2000名大学生中随机选取4名，记这4名毕业生从事的工作与大学所学专业对口的人数为X ，求X 的数学期望()E X . 19. （本小题满分12分）在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAB ⊥平面ABCD ，3AB AP ==，2AD PB ==，E 为线段AB 上一点，且:7:2AE EB =，点F G M ，，分别为线段PA PD BC 、、的中点.（1）求证：PE ⊥平面ABCD ；（2）若平面EFG 与直线CD 交于点N ，求二面角P MN A --的余弦值. 20. （本小题满分12分）如图，已知椭圆2221(1)x y a a+=>的长轴长是短轴长的2倍，右焦点为F ，点,B C 分别是该椭圆的上、下顶点，点P 是直线:2l y =-上的一个动点（与y 轴交点除外），直线PC 交椭圆于另一点M ，记直线BM ，BP 的斜率分别为12k k ，.（1）当直线PM 过点F 时，求PB PM 的值；（2）求12||||k k +的最小值，并确定此时直线PM 的方程. 21. （本小题满分12分）设函数()2cos (1)ln(1)f x x x x x =--+++，22()()g x k x x=+.其中0k ≠.（1）讨论函数()g x 的单调区间；（2）若存在1(1,1]x ∈-，对任意21(,2]2x ∈，使得12()()6f x g x k -<-成立，求k 的取值范围.请考生在22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分.22.（本小题满分10分）选修4-1：几何证明选讲如图，过点A 分别作O 的切线AP 与割线AC ，P 为切点，AC 与O 交于B C 、两点，圆心O 在PAC ∠的内部，//BD AP ，PC 与BD 交于点N .（1）在线段BC 上是否存在一点M ，使A P O M 、、、四点共圆？若存在，请确定点M 的位置；若不存在，请说明理由. （2）若CP CD =，证明：CB CN =.23. （本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，圆C 的方程为22((1)9x y ++=，以O 为极点，x 轴的非负半轴为极轴建立极坐标系. （1）求圆C 的极坐标方程； （2）直线:6OP πθ=()p R ∈与圆C 交于点M N ，，求线段MN 的长.24. （本小题满分10分）选修4-5：不等式选讲已知()|2||21|f x x x =+--，M 为不等式()0f x >的解集. （1）求M ；（2）求证：当,x y M ∈时，||15x y xy ++<.高三数学试卷参考答案（理科）一、选择题1-5: ACDAC 6-10:BCADB 11、12：AB 二、填空题13.-2 14. 2log 3 15. 1- 16.6349π三、解答题17.解：（1）∵163412a a a a +=+=，………………1分∴16,a a 是2212110x x -+=方程的两根，且16a a <，………………2分 解得11a =，611a =，………………4分∴61510a a d -==，即2d =，………………5分 ∴21n a n =-.………………6分280(3053510)80 2.051 3.8414040651539k ⨯⨯-⨯==≈<⨯⨯⨯，故不能在犯错误的概率不超过5%的前提下，认为“毕业生从事的工作与大学所学专业对口与性别有关”.………5分（2）这80位毕业生从事的工作与大学所学专业对口的频率为65138016=.………………7分 （3）由题意可得13~(4,)16X B ，………………9分 ∴1313()4164E x =⨯=.……………………12分 19.（1）证明：在等腰APB ∆中，112cos 3PBABP AB ∠==，则由余弦定理可得22222132()2223339PE =+-⨯⨯⨯=，∴3PE =.………………2分 ∴2224PE BE PB +==，∴PE AB ⊥.………………3分∵平面PAB ⊥平面ABCD ，平面PAB 平面ABCD AB =，∴PE ⊥平面ABCD .………………4分（2）解：由已知可得//EN AD ，………………5分以E 为坐标原点，EP EB EN 、、分别为x 轴，y 轴，z 轴，建立空间直角坐标系如图所示，则2((0,,1)(0,0,2)33P M N ，，，从而2(,1)33PM =-，2(0,,1)3MN =-.………………7分设平面PMN 的法向量为(,,)n x y z =，则0n PM =，0n MN =，即2033x y z -++=，203y z -+=，令3y =，可得平面PMN的一个法向量为2)n =.………………9分 由（1）知平面AMN的一个法向量为4(3EP =，………………10分cos ,n EP ==，………………11分 由图可知二面角P MN A --的平面角为锐角， 故二面角P MN A --.………………12分20.解：（1）由椭圆2221(1)x y a a+=>的长轴长是短轴长的2倍得2a =.………………1分由题意(0,1)B ，(0,1)C -，焦点F ，当直线PM 过点F 时，则直线PM 的方程为11y =-，即1y x =-，令2y =-得x=(2)P -.………………3分联立22141x y y x ⎧+=⎪⎪⎨⎪=-⎪⎩解得717x y ⎧=⎪⎪⎨⎪=⎪⎩或01x y =⎧⎨=-⎩（舍），即1)7M .………………4分 因为(3,3)PB =，15()77PM =，………………5分 所以454590777PB PM =+=.………………6分 （2）设(,2)P m -，且0m ≠，则直线PM 的斜率为1(2)10k m m---==--，则直线PM 的方程为11y x m=--，………………7分 联立221114y x m x y ⎧=--⎪⎪⎨⎪+=⎪⎩化简得2248(1)0x x m m ++=，解得22284(,)44m m M m m --++，………………8分所以22212412148844m m m k m m m m ---+===--+，21(2)30k m m --==--，………………10分则1231||||||||4k k m m +=-+≥=31||||4m m -=，即m =±时取等号.所以12||||k k +此时直线PM 的方程为1y x =-.………………12分 21.解：（1）32222(1)'()2k k x g x kx x x -=-=，………………1分当0k >时，令'()0g x >，得1x >，∴()g x 的递增区间为(1,)+∞.………………2分令'()0g x <，得1x <，0x ≠，∴()g x 的递减区间为(,0)(0,1)-∞，...................3分 0k <当时，同理得()g x 的递增区间为(,0)(0,1)-∞，；递减区间为(1,)+∞. (5)分（2）'()2sin 1ln(1)12sin ln(1)f x x x x x =-+++=++，………………6分 ∵当(1,1]x ∈-时，2sin y x =及ln(1)y x =+均为增函数， ∴'()f x 在(1,1]-为增函数，又'(0)0f =，………………7分 ∴当(1,0)x ∈-时，'()0f x <；当(0,1]x ∈时，'()0f x >. 从而，()f x 在(1,0)-上递减，在(0,1]上递增，………………8分 ∴()f x 在(1,1]-上的最小值为(0)2f =-.………………9分 ∵12()()6f x g x k -<-，∴12()6()f x k g x <-+，∴min min ()6()f x k g x <-+，当0k >时，∴min ()(1)3g x g k ==，∴462k ->-，∴1k >.当0k <时，min ()(2)5g x g k ==，∴662k ->-，∴23k >， 又0k <，∴0k <时不合题意. 综上，(1,)k ∈+∞.………………12分22.（1）解：当点M 为BC 中点时，A P O M 、、、四点，证明如下： ∵M 为BC 的中点，故OM BC ⊥，即90OMA ∠=. 又∵OP AP ⊥，∴90OPA ∠=，∴OMA ∠与OPA ∠互补，∴A P O M 、、、四点共圆.………………5分 （2）证明：∵//BD AP ，∴CNB CPA ∠=∠， 连接PD ，∵AP 为切线，∴PDC CPA ∠=∠，∴CNB PDC ∠=∠，∵CP CD =，∴CPD PDC ∠=∠，又∵CBN CPD ∠=∠，∴CBN CNB ∠=∠，∴CB CN =.………………10分23.解：（1）22((1)9x y ++=可化为22250x y y +-+-=，故其极坐标方程为2cos 2sin 50ρθρθ-+-=.………………5分（2）将6πθ=代入2cos 2sin 50ρθρθ-+-=，得2250ρρ--=，∴122ρρ+=，125ρρ=-，∴12||||MN ρρ=-==.………………10分 24.解：（1）3,2,1()31,2,213,2x x f x x x x x ⎧⎪-<-⎪⎪=+-≤≤⎨⎪⎪-+>⎪⎩， 当2x <-时，由30x ->得，3x >，舍去； 当122x -≤≤时，由310x +>得，13x >-，即1132x -<≤； 当12x >时，由30x -+>得，3x <，即132x <<. 综上，1(,3)3M =-.………………6分 （2）∵,x y M ∈，∴||3x <，||3y <，∴||||||||||||||||||||333315x y xy x y xy x y xy x y x y ++≤++≤++=++<++⨯=.………………10分。

海珠区2017-2018学年第一学期高三综合测试（一）理科数学注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．答题前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答第Ⅰ卷时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮搽干净后，再选涂其他答案标号，写在本试卷上无效. 3．回答第Ⅱ卷时，将答案写在答题卡上，答在本试题上无效． 4．考试结束，将答题卡一并交回．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每个小题给出的四个选项中，只有一项是符合题目要求的．（1）若复数z 满足(1i)2z +=,则z 的虚部为（A ）1-（B ）i -（C ）i （D ）1（2）已知集合2{|16},{|}A x x B x x m =<=<，若A B A =，则实数m 的取值范围是（A ）[)4,-+∞ （B ）[)4,+∞ （C ）(,4]-∞- （D ）(,4]-∞ （3）设偶函数()f x 的定义域为R ，当[)0,x ∈+∞时，()f x 是增函数，则 ()()()2,,3f f f π--的大小关系是 （A ）()()()23f ff π-<<- （B ）()()()23f f f π<-<-（C ）()()()23f f f π-<-< （D ）()()()32f f f π-<-<（4） 双曲线E 的中心在原点，离心率等于2，若它的一个顶点恰好是抛物线28y x =的焦点，则双曲线E 的虚轴长等于（A ）4 （B （C ） （D ）（5）某食品厂为了促销，制作了3种不同的精美卡片，每袋食品中随机装入一张卡片，集齐3种卡片可获奖，现购买该食品4袋，能获奖的概率为（A ）427 （B ）827 （C ）49（D ）89 （6）在ABC ∆中，内角,,A B C 的对边分别是,,a b c ，若12,s i n s i n s i n 2c a b B a A a C =-=，则sin B 为（A ）4 （B ）34 （C ）3（D ）13（7）公差不为0的等差数列{}n a 的部分项123,,k k k a a a ,…构成等比数列{}n k a ，且121,2,6k k k ===231,2,6k k k ===，则4k 为 （A ）20 （B ）22 （C ）24 （D ）28 （8）已知函数()ln f x x x =-，则()f x 的图像大致为（A ） （B ） （C ） （D ）（9）若,x y 满足20400x y x y y -+≥⎧⎪+-≤⎨⎪>⎩，则2z y x =-的最大值为（A ）8- （B ）4- （C ）1 （D ）2 （10）执行如图所示的程序框图，则输出的结果为（A ）1- （B ）1 （C ）2- （D ）2 （11）过抛物线)0(22>=p px y 的焦点F 且倾斜角为60°的直线l与抛物线在第一、四象限分别交于A 、B 两点，则||||BF AF 的值等于（A ）5 （B ）4（C ）3 （D ）2（12）已知函数()cos sin f x x x =，给出下列四个说法：①函数()f x 的周期为π；②若12()()f x f x =，则Z k k x x ∈+=,21π；③()f x 在区间,44ππ⎡⎤-⎢⎥⎣⎦上单调递增；④()f x 的图象关于点,02π⎛⎫- ⎪⎝⎭中心对称．其中正确说法的个数是（A ）3个 （B ）2个 （C ）1个 （D ）0个第Ⅱ卷本卷包括必考题和选考题两个部分．第（13）题～第（21）题为必考题，每个试题考生都必须作答．第（22）题～第（24）题为选考题，考生根据要求作答． 二、填空题：本大题共４小题，每小题5分． （13）二项式6(2x 的展开式中常数项为_______．（14）已知4cos()35πα-=，则7sin()6πα+的值是_______． （15）如图所示是一个几何体的三视图，则这个几何体外接球的表面积为 ． （16）已知△ABC 的外接圆的圆心为O ，若2A B A CA O +=，且AC A O =，则AB 与BC的夹角为 .三、解答题：解答应写出文字说明，证明过程或演算步骤． （17）(本小题满分12分)已知数列{n a }的前n 项和为n S ，1a =1，0n a ≠，141n n n a a S +=-． （Ⅰ）求{}n a 的通项公式； （Ⅱ）证明: 12111...2nS S S +++<．（18）（本小题满分12分）社区服务是综合实践活动课程的重要内容.某市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[)75,80,[)80,85,[)85,90,[)90,95,[]95,100（单位：小时）进行统计,其频率分布直方图如图所示．（Ⅰ）求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率； （Ⅱ）从全市高中学生（人数很多）中任意选取3位学生,记X 为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量X 的分布列和数学期望EX ．（19）（本小题满分12分）如图，四棱锥S ABCD -中，//AB CD ，BC CD ⊥，2AB BC ==，1CD SD ==，侧面SAB 为等边三角形． （Ⅰ）证明：AB SD ⊥；（Ⅱ）求二面角A SB C --的正弦值．（20）（本小题满分12分）设椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ，点(A 在椭圆上，且满足2120AF F F ⋅=． （Ⅰ）求椭圆C 的标准方程；（Ⅱ）动直线:l y kx m =+与椭圆C 交于,P Q 两点，且OP OQ ⊥，是否存在圆222x y r +=使得l 恰好是该圆的切线，若存在，求出r ；若不存在，说明理由．（21）(本小题满分12分) 已知函数()2ln (2a f x x x x x a a=--+ （Ⅰ）求a 的取值范围；（Ⅱ）设两个极值点分别为12,x x ，证明:212x x e ⋅>．请考生从第（22）、（23）、（24）三题中任选一题作答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分．作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑． （22）（本小题满分10分）选修4—1：几何证明选讲如图，在ABC ∆中，CD 是ACB ∠的平分线，ACD ∆的外接圆交BC 于点E ， 2AB AC =． （Ⅰ）求证：2BE AD =；（Ⅱ）当1AC =，2EC =时，求AD 的长．（23）（本小题满分10分）选修4-4：坐标系与参数方程已知在直角坐标系xoy 中，曲线C 的参数方程为()22cos ,2sin ,x y θθθ=+⎧⎨=⎩为参数，在极坐标系（与直角坐标系xoy 取相同的长度单位，且以原点O 为极点，以x 轴正半轴为极轴）中，直线l 的方程为sin 4πρθ⎛⎫+= ⎪⎝⎭（Ⅰ）求曲线C 在极坐标系中的方程；（Ⅱ）求直线l 被曲线C 截得的弦长．（24）（本小题满分10分）选修4-5：不等式选讲已知函数212)(--+=x x x f . （Ⅰ）解不等式0)(≥x f ；（Ⅱ）若存在实数x ，使得a x x f +≤)(，求实数a 的取值范围．海珠区2017-2018学年第一学期高三综合测试（一）第22题图 E D C BA理科数学试题答案及评分参考说明：1．参考答案与评分标准给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考查的知识点和能力比照评分标准给以相应的分数．2．对解答题中的计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的得分，但所给分数不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，选择题和填空题不给中间分．一、选择题（每小题5分，共12小题，共60分）二、填空题（每小题5分，共6小题，共20分） （13）60. （14）45- （15）32π （16）56π 三、解答题（共6小题，共70分.解答应写出文字说明、证明过程或演算步骤） （17）（本小题满分12分）解:（I ）由题设,112141,4 1.n n n n n n a a S a a S ++++=-=- 两式相减得121()4.n n n a a a a +++-= ………………1分由于10n a +≠,所以2 4.n n a a +-= ………………2分由题设,11a =,12141a a S =-,可得2 3.a = ………………3分故可得{}21n a -是首项为1,公差为4的等差数列,()2143=2211n a n n -=---；………………4分{}2n a 是首项为3,公差为4的等差数列,241=221n a n n =-⋅-. ………………5分所以()21n a n n N *=-∈. (6)分（Ⅱ）()21212n n n S n +-==，………………7分 当1n >时()2111111n n n n n<=---. ………………9分 2222121111111......123n S S S n+++=++++ 11111111...2112231n n n<+-+-++-=-- ………………11分121112nS S S ∴+++< ………………12分（18）（本小题满分12分） （1）根据题意,参加社区服务在时间段[)90,95的学生人数为2000.06560⨯⨯=（人）； ………………1分参加社区服务在时间段[)95,100的学生人数为2000.02520⨯⨯=（人）． ………………2分∴抽取的200位学生中,参加社区服务时间不少于90小时的学生人数为80人． ……………3分∴从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率为8022005P ==．……4分 （2）由（1）可知,从全市高中生中任意选取1人,其参加社区服务时间不少于90小时的概率为25． 由已知得,随机变量X 的可能取值为0,1,2,3, ………………5分则()03032327055125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭；()12132354155125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭； ()21232336255125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭；()333238355125P X C ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭．（每个等式给1分）……9分随机变量X 的分布列为………………10分（19）（本小题满分12分）解：（1）取AB 的中点E ，连接DE ，则四边形BCDE 为矩形， ∴BE DE ⊥， ………………1分 ∵SAB ∆为等边三角形，∴AB SE ⊥. ………………2分 ∵SEDE E =， ………………3分∴AB ⊥平面SED ， ………………4分SD ⊂平面SED ，AB SD⊥. ………………5分（2）由（1）知，DE DC ⊥，过D 作DF ⊥平面ABCD ，则,,DE DC DF 两两垂直，分别以,,DE DC DF 的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系D xyz -，………………6分则(0,0,0),(2,1,0),(2,1,0),(0,1,0)D A B C -， ………………7分 ∵1,2,SD DE SE===∴SD SE ⊥，∴SD ⊥平面SAB ， ∴1(2S ，1(2DS =. ………………8分 设平面SBC 的法向量为(,,)n x y z =. ∵1(,1,2SC =-，(2,0,0)BC =-， ∴20102n SC x n BC x y ⎧∙=-=⎪⎨∙=-+=⎪⎩，∴0x y =⎧⎪⎨=⎪⎩.取1z =，则3(0,,1)n =， ………………9分 设二面角A SB C --为θ，则32|cos |||7||||7DS n DS n θ∙=== ………………11分∴二面角A SB C --的正弦值sin θ. ………………12分 （20）（本小题满分12分）解:（1）∵2120AF F F ⋅=∴212AF F F ⊥， ∵A 在椭圆上，∴220221y c a b +=，解得20b y a=. ………………1分∴22222c ba ab c=⎧⎪⎪=⎨⎪=+⎪⎩，解得228,4,a b ==. ………………3分 ∴椭圆22:184x y C +=. ………………4分（2）设1122(,),(,)P x y Q x y ，将:l y kx m =+代入22:184x y C +=得 222(12)4280k x kmx m +++-=， ………………5分∵0∆>，∴22840k m -+>， ………………6分且122412km x x k +=-+，21222812m x x k -=-+，∴22221212121228()()()12m k y y kx m kx m k x x km x x m k -=++=+++=+，………………7分∵OP OQ ⊥，∴12120x x y y +=，即2222228801212m m k k k--+=++， ∴22388m k -=， ………………8分由23808m -≥和2840k m -+>，得283m ≥即可. ………………9分因为l 与圆222x y r +=相切，∴222||813m r k ==+， ………………11分 存在圆2283x y +=符合题意. ………………12分（21）(本小题满分12分) 解：(Ⅰ)依题，函数错误！未找到引用源。

2017-2018学年广东省三（上）12月联考试卷（理科数学）一、选择题1．（6分）设复数z满足z﹣3i=3+zi，则z=（）A．3 B．﹣3 C．3i D．﹣3i2．（6分）求值=（）A．1 B．2 C．D．3．（6分）“a≤﹣3”是“f（x）=﹣|x+a|在[3，+∞）上为减函数”的什么条件（）A．充分不必要B．必要不充分C．充要 D．不充分不必要4．（6分）将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（）A．12种B．10种C．9种D．8种5．（6分）设F1，F2分别是双曲线的左、右焦点．若双曲线上存在点A，使∠F1AF2=90°，且|AF1|=3|AF2|，则双曲线离心率为（）A．B．C．D．6．（6分）如图是一个水平放置的透明无盖的正方体容器，高12cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为8cm，如果不计容器的厚度，则球的体积为（）A．cm3B．cm3C．cm3D．cm37．（6分）如图，在△ABC中，D、E分别是AB和BC的三等分点，若=，=，则=（）A．=+B．=+C．=+D．=+8．（6分）已知函数f（x）=，则y=f（x）的图象大致为（）A．B．C．D．9．（6分）如果执行右边的程序框图，输入正整数N（N≥2）和实数a1，a2，…，a n，输出A，B，则（）A．A+B为a1，a2，…，a n的和B．为a1，a2，…，a n的算术平均数C．A和B分别是a1，a2，…，a n中最大的数和最小的数D．A和B分别是a1，a2，…，a n中最小的数和最大的数10．（6分）（x+）（2x﹣）5的展开式中各项系数的和为2，则该展开式中含x2项为（）A．0 B．﹣80x2C．80x2D．160x211．（6分）如图是一个圆柱被一个平面截去一部分后与半球（半径r=3）组成一个几何体，该几何图体三视中的正视图和俯视图如图所示，则该几何体的表面积为（）A．63πB．80πC．36+27πD．36+45π12．（6分）设函数f（x）=（x﹣2）lnx﹣ax+1，若存在唯一的整数x0，使得f（x0）＜0，则a的取值范围是（）A．（0，）B．（，] C．（，1）D．[，1）二、填空题13．（8分）若函数f（x）=为奇函数．则a=．14．（8分）经过双曲线的左顶点、虚轴上端点、右焦点的圆的方程是．15．（8分）若x，y满足约束条件，则的最小值为．16．（8分）已知a，b，c分别为△ABC的三个内角A，B，C的对边，a=2且（2+b）（sinA﹣sinB）=（c ﹣b）sinC，则△ABC面积的最大值为．三、解答题17．（12分）已知S n为数列{a n}的前n项和，+++…+=a n﹣2（n≥2），且a1=2．（1）求{a n}的通项公式；（2）设b n=，求数列{b n}的前n项和B n．18．（12分）人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标，常用区间[0，10]内的一个数来表示，该数越接近10表示满意度越高．为了解某地区居民的幸福感情况，（Ⅰ）在图中绘出频率分布直方图，并估算该地区居民幸福感指数的平均值；（Ⅱ）如果居民幸福感指数不小于6，则认为其幸福．为了进一步了解居民的幸福满意度，调查组又在该地区随机抽取4对夫妻进行调查，用X表示他们之中幸福夫妻（夫妻二人都感到幸福）的对数，求X的分布列及期望（以样本的频率作为总体的概率）．19．如图是某直四棱柱被平面α所截得的部分，底面ABCD是矩形，侧棱GC、ED、FB都垂直于底面ABCD，GC=3，AB=2，BC=．四边形AEGF为菱形，经过C且垂直于AG的平面与EG、AG、FG分别交于点M、H、N；（1）求证：CN⊥BH；（2）求面AFGE与底面ABCD所成二面角的余弦值．20．椭圆C：+=1（a＞b＞0）的上顶点为A，P（，）是C上的一点，以AP为直径的圆经过椭圆C的右焦点F．（1）求椭圆C的方程；（2）设过点M（2，0）的动直线l与椭圆C相交于D、E两点，求△ODE面积的最大值．21．（12分）已知函数f（x）=（2﹣a）x﹣2lnx+a﹣2，g（x）=xe1﹣x（1）若函数f（x）在区间（0，）无零点，求实数a的最小值（2）若对任意给定的x0∈（0，e]，方程f（x）=g（x0）在（0，e]上总存在两个不等的实根，求实数a的取值范围．请在22、23、24、题中任选一题作答.选修4-1：几何证明选讲22．（10分）如图，已知PA与圆O相切于点A，经过点O的割线PBC交圆O于点B，C，∠APC的平分线分别交AB，AC于点D，E．（Ⅰ）证明：∠ADE=∠AED；（Ⅱ）若AC=AP，求的值．选修4-4：坐标系与参数方程23．在直角坐标系中，以原点O为极点，x轴为正半轴为极轴，建立极坐标系，已知曲线C1：（t为参数），C2：（θ为参数）．（1）过C1，C2的方程为普通方程，并说明它们分别表示什么曲线？（2）若C1上的点P对应的参数为t=π，Q为C2上的动点，求PQ中点M到直线C3：ρ（cosθ﹣2sinθ）=7距离的最大值．选修4-5：不等式选讲24．已知函数f（x）=|x﹣a|．（1）若f（x）＞m（m＞0）的解集为x∈（﹣∞，1）∪（7，+∞），求实数a，m的值；（2）当a=﹣1时，当x≤﹣2时，不等式f（x）+t≥f（x+2）恒成立，求t的取值范围．2017-2018学年广东省三（上）12月联考试卷（理科数学）参考答案与试题解析一、选择题1．（6分）（2016•北海一模）设复数z满足z﹣3i=3+zi，则z=（）A．3 B．﹣3 C．3i D．﹣3i【分析】设出z=a+bi，代入z﹣3i=3+zi，得到关于a，b的方程组，解出即可．【解答】解：设z=a+bi，∵z﹣3i=3+zi，∴（a+bi）﹣3i=3+（a+bi）i，∴a+b﹣3+（b﹣a﹣3）i=0，∴，解得：，则z=﹣3，故选：B．【点评】本题考查了复数的运算性质，考查计算能力，是一道基础题．2．（6分）（2015秋•凯里市校级期末）求值=（）A．1 B．2 C．D．【分析】需利用公式1﹣sin2α=（sinα﹣cosα）2、cos2α=cos2α﹣sin2α、cosαcosβ+sinαsinβ=cos（α﹣β）解决．【解答】解：原式=======．故选C．【点评】本题主要考查三角函数的倍角公式及和（差）角公式．3．（6分）（2015秋•广东校级月考）“a≤﹣3”是“f（x）=﹣|x+a|在[3，+∞）上为减函数”的什么条件（）A．充分不必要B．必要不充分C．充要 D．不充分不必要【分析】根据充分条件和必要条件的定义结合绝对值的性质，进行判断即可．【解答】解：∵f（x）=﹣|x+a|在[3，+∞）上为减函数，∴﹣a≤3，∴a≥﹣3，∴“a≤﹣3”是“f（x）=﹣|x+a|在[3，+∞）上为减函数”的，不充分不必要故选：D．【点评】本题考查充要条件的判断和已知函数单调性求参数范围问题，对函数f（x）=﹣|x﹣a|的图象要熟练掌握4．（6分）（2012•新课标）将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有（）A．12种B．10种C．9种D．8种【分析】将任务分三步完成，在每步中利用排列和组合的方法计数，最后利用分步计数原理，将各步结果相乘即可得结果【解答】解：第一步，为甲地选一名老师，有=2种选法；第二步，为甲地选两个学生，有=6种选法；第三步，为乙地选1名教师和2名学生，有1种选法故不同的安排方案共有2×6×1=12种故选A【点评】本题主要考查了分步计数原理的应用，排列组合计数的方法，理解题意，恰当分步是解决本题的关键，属基础题5．（6分）（2013•三门峡模拟）设F1，F2分别是双曲线的左、右焦点．若双曲线上存在点A，使∠F1AF2=90°，且|AF1|=3|AF2|，则双曲线离心率为（）A．B．C．D．【分析】由题设条件设|AF2|=1，|AF1|=3，双曲线中2a=|AF1|﹣|AF2|=2，，由此可以求出双曲线的离心率．【解答】解：设F1，F2分别是双曲线的左、右焦点．若双曲线上存在点A，使∠F1AF2=90°，且|AF1|=3|AF2|，设|AF2|=t，|AF1|=3t，（t＞0）双曲线中2a=|AF1|﹣|AF2|=2t，t，∴离心率，故选B．【点评】挖掘题设条件，合理运用双曲线的性质能够准确求解．6．（6分）（2015秋•广东校级月考）如图是一个水平放置的透明无盖的正方体容器，高12cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为8cm，如果不计容器的厚度，则球的体积为（）A．cm3B．cm3C．cm3D．cm3【分析】根据图形的性质，求出截面圆的半径，即而求出求出球的半径，得出体积．【解答】解：根据几何意义得出：边长为12的正方形，球的截面圆为正方形的内切圆，∴圆的半径为：6，∵球面恰好接触水面时测得水深为8cm，∴d=12﹣8=4，∴球的半径为：R=，R=∴球的体积为π×（）3=cm3故选D．【点评】本题考查了球的几何性质，运用求解体积面积，属于中档题．7．（6分）（2015秋•广东校级月考）如图，在△ABC中，D、E分别是AB和BC的三等分点，若=，=，则=（）A．=+B．=+C．=+D．=+【分析】根据平面向量的线性表示与运算性质，利用与表示出即可．【解答】解：△ABC中，D、E分别是AB和BC的三等分点，∴==，==（﹣）=（﹣），∴=+=+（﹣）=+．故选：A．【点评】本题考查了平面向量的线性表示与运算问题，是基础题目．8．（6分）（2012•新课标）已知函数f（x）=，则y=f（x）的图象大致为（）A．B．C．D．【分析】考虑函数f（x）的分母的函数值恒小于零，即可排除A，C，由f（x）的定义域能排除D，这一性质可利用导数加以证明【解答】解：设则g′（x）=∴g（x）在（﹣1，0）上为增函数，在（0，+∞）上为减函数∴g（x）＜g（0）=0∴f（x）=＜0得：x＞0或﹣1＜x＜0均有f（x）＜0排除A，C，又f（x）=中，，能排除D．故选B【点评】本题主要考查了函数解析式与函数图象间的关系，利用导数研究函数性质的应用，排除法解图象选择题，属基础题9．（6分）（2012•新课标）如果执行右边的程序框图，输入正整数N（N≥2）和实数a1，a2，…，a n，输出A，B，则（）A．A+B为a1，a2，…，a n的和B．为a1，a2，…，a n的算术平均数C．A和B分别是a1，a2，…，a n中最大的数和最小的数D．A和B分别是a1，a2，…，a n中最小的数和最大的数【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是求出a1，a2，…，a n中最大的数和最小的数．【解答】解：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知，该程序的作用是：求出a1，a2，…，a n中最大的数和最小的数其中A为a1，a2，…，a n中最大的数，B为a1，a2，…，a n中最小的数故选：C．【点评】本题主要考查了循环结构，解题的关键是建立数学模型，根据每一步分析的结果，选择恰当的数学模型，属于中档题．10．（6分）（2015秋•运城期末）（x+）（2x﹣）5的展开式中各项系数的和为2，则该展开式中含x2项为（）A．0 B．﹣80x2C．80x2D．160x2【分析】由于二项式展开式中各项的系数的和为2，故可以令x=1，建立a的方程，解出a的值，然后写出（2x﹣）5 的展开式的通项，进一步求得展开式中含x2项．【解答】解：令x=1，则有1+a=2，得a=1，故二项式为（x+）（2x﹣）5 ，（2x﹣）5 的展开式的通项为=，则展开式（x+）（2x﹣）5 中含x2项为．故选：A．【点评】本题考查二项式系数的性质，解题关键是掌握二项式系数的公式，以及根据二项式的形式判断出含x2项，是中档题．11．（6分）（2015秋•广东校级月考）如图是一个圆柱被一个平面截去一部分后与半球（半径r=3）组成一个几何体，该几何图体三视中的正视图和俯视图如图所示，则该几何体的表面积为（）A．63πB．80πC．36+27πD．36+45π【分析】由已知可得该几何图体是一个半圆柱与半球的组合体，半球和圆柱的底面半径r=3，半圆柱的高为2r=6，累加各个面的面积，可得答案．【解答】解：由已知可得该几何图体是一个半圆柱与半球的组合体，半球和圆柱的底面半径r=3，半圆柱的高为2r=6，故该几何体的表面积S=×4πr2+2××πr2+×2πr×2r+2r×2r=5πr2+4r2=36+45π，故选：D．【点评】本题考查的知识点是圆柱的体积和表面积，球的体积和表面积，简单几何体的三视图，难度中档．12．（6分）（2015秋•广东校级月考）设函数f（x）=（x﹣2）lnx﹣ax+1，若存在唯一的整数x0，使得f（x0）＜0，则a的取值范围是（）A．（0，）B．（，] C．（，1）D．[，1）【分析】设g（x）=（x﹣2）lnx，h（x）=ax﹣1，问题转化为存在唯一的整数x0使得g（x0）在直线y=ax ﹣1的下方，求导数判断单调性，数形结合可得g（1）≥h（1）=a﹣1且h（3）=3a﹣1≤g（3）=ln3，h （2）＞g（2），解关于a的不等式组可得．【解答】解：设g（x）=（x﹣2）lnx，h（x）=ax﹣1，由题意知存在唯一的整数x0使得g（x0）在直线y=h（x）=ax﹣1的下方，∵g′（x）=lnx+1﹣，∴当x≥2时，g′（x）＞0，当0＜x≤1时，g′（x）＜0，当x=1时，g（1）=0，当x=1时，h（1）=a﹣1＜0，即a≤1．直线y=ax﹣1恒过定点（0，﹣1）且斜率为a，由题意结合图象可知，存在唯一的整数x0=2，f（x0）＜0，故h（2）=2a﹣1＞g（2）=0，h（3）=3a﹣1≤g（3）=ln3，解得＜a≤．故选：B．【点评】本题考查导数的运用：判断单调性，涉及数形结合和转化的思想，属中档题．二、填空题13．（8分）（2015秋•广东校级月考）若函数f（x）=为奇函数．则a=±2．【分析】由函数f（x）=为奇函数，可知：f（﹣x）=﹣f（x）在[﹣2，2]上恒成立，进而解得a值．【解答】解：∵函数f（x）=为奇函数．∴f（﹣x）=﹣f（x）在[﹣2，2]上恒成立，即=﹣在[﹣2，2]上恒成立，解得：a=±2，故答案为：±2【点评】本题考查的知识点是函数奇偶性的性质，熟练掌握函数奇偶性的性质，是解答的关键．14．（8分）（2015秋•深圳校级期末）经过双曲线的左顶点、虚轴上端点、右焦点的圆的方程是x2+y2﹣2x+y﹣15=0．【分析】求出双曲线的左顶点、虚轴上端点、右焦点的坐标，利用待定系数法进行求解即可．【解答】解：双曲线的左顶点A（﹣3，0）、虚轴上端点B（0，4）、右焦点F（5，0），设圆的一般方程为x2+y2+Dx+Ey+F=0，则，得D=﹣2，E=，F=﹣15，即圆的一般方程为x2+y2﹣2x+y﹣15=0，故答案为：x2+y2﹣2x+y﹣15=0【点评】本题主要考查双曲线的图象和性质以及圆的方程的求解，利用待定系数法是解决本题的关键．15．（8分）（2016•河南二模）若x，y满足约束条件，则的最小值为．【分析】做出不等式表示的平面区域，将化成1+，即求过点（1，﹣1）的直线斜率的最小值问题．【解答】解：=1+，做出平面区域如图：有图可知当过点（1，﹣1）的直线经过点C（4，0）时，斜率最小为，∴的最小值为1+=．故答案为．【点评】本题考查了简单的线性规划，是基础题．16．（8分）（2014•新课标I）已知a，b，c分别为△ABC的三个内角A，B，C的对边，a=2且（2+b）（sinA﹣sinB）=（c﹣b）sinC，则△ABC面积的最大值为．【分析】由正弦定理化简已知可得2a﹣b2=c2﹣bc，结合余弦定理可求A的值，由基本不等式可求bc≤4，再利用三角形面积公式即可计算得解．【解答】解：因为：（2+b）（sinA﹣sinB）=（c﹣b）sinC⇒（2+b）（a﹣b）=（c﹣b）c⇒2a﹣b2=c2﹣bc，又因为：a=2，所以：，△ABC面积，而b2+c2﹣a2=bc⇒b2+c2﹣bc=a2⇒b2+c2﹣bc=4⇒bc≤4所以：，即△ABC面积的最大值为．故答案为：．【点评】本题主要考查了正弦定理，余弦定理，基本不等式，三角形面积公式在解三角形中的应用，考查了计算能力和转化思想，属于中档题．三、解答题17．（12分）（2015秋•广东校级月考）已知S n为数列{a n}的前n项和，+++…+=a n﹣2（n≥2），且a1=2．（1）求{a n}的通项公式；（2）设b n=，求数列{b n}的前n项和B n．【分析】（1）利用递推关系与“累乘求积”方法即可得出；（2）利用“裂项求和”方法即可得出．【解答】解：（1）∵+++…+=a n﹣2（n≥2），∴+++…++=a n+1﹣2，∴=a n+1﹣a n，化为=，∴a n=••…••a1=•…••2=n+1，∴a n=n+1．（2）b n====，∴数列{b n}的前n项和B n=+…+==．【点评】本题考查了递推关系与“累乘求积”方法、“裂项求和”，考查了推理能力与计算能力，属于中档题．18．（12分）（2016•白银模拟）人们常说的“幸福感指数”就是指某个人主观地评价他对自己目前生活状态的满意程度的指标，常用区间[0，10]内的一个数来表示，该数越接近10表示满意度越高．为了解某地区（Ⅰ）在图中绘出频率分布直方图，并估算该地区居民幸福感指数的平均值；（Ⅱ）如果居民幸福感指数不小于6，则认为其幸福．为了进一步了解居民的幸福满意度，调查组又在该地区随机抽取4对夫妻进行调查，用X表示他们之中幸福夫妻（夫妻二人都感到幸福）的对数，求X的分布列及期望（以样本的频率作为总体的概率）．【分析】（1）由调查数据能作出频率分布直方图，并能求出该地区居民幸福感指数的平均值．（2）由已知条件得到X的可能取值为0，1，2，3，4，且X～B（4，0.3），由此能求出X的分布列和期望．【解答】（本小题满分12分）解：（1）频率分布直方图如右图．…（3分）所求的平均值为0.01×2×1+0.015×2×3+0.2×2×5+0.15×2×7+0.125×2×9=6.46…（5分）（2）男居民幸福的概率为：=0.5．女居民幸福的概率为：=0.6，故一对夫妻都幸福的概率为：0.5×0.6=0.3…（7分）因此X的可能取值为0，1，2，3，4，且X～B（4，0.3）于是…（9分）∴E（X）=np=4×0.3=1.2…（12分）【点评】本题考查频率直方图的应用，考查离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意排列组合知识的合理运用．19．（2015秋•广东校级月考）如图是某直四棱柱被平面α所截得的部分，底面ABCD是矩形，侧棱GC、ED、FB都垂直于底面ABCD，GC=3，AB=2，BC=．四边形AEGF为菱形，经过C且垂直于AG的平面与EG、AG、FG分别交于点M、H、N；（1）求证：CN⊥BH；（2）求面AFGE与底面ABCD所成二面角的余弦值．【分析】（1）根据线面垂直的性质定理证明CN⊥面BAH即可证明CN⊥BH；（2）建立坐标系求出平面的法向量，利用向量法进行求解即可．【解答】（1）证明：连结BH，由题知AB⊥面BCGF又∵CN⊂面BCGF，∴AB⊥CN∵AG⊥面CMN，∴AG⊥CN又∵AG∩AB=A，AG、AB⊂面BAH，∴CN⊥面BAH又∵BH⊂面BAH，∴CN⊥BH（2）解：以DA、DC、DE为x、y、z轴，建立空间直角坐标系∵四边形AEFG为菱形，可设AE=EG=a，DE=b由AE2=AD2+DE2，得a2=5+b2，①由EG2=（GC﹣DE）2+DC2，得a2=（3﹣b）2+8，②以上面两式解得：a=3，b=2∴E（0，0，2）、A（，0，0）、G（0，2，3）∴=（﹣，0，2）、=（﹣，2.3），设=（x，y，z）为面AFGE的一个法向量，则由，解得=（8，﹣，4）为面AFGE的一个法向量由题知=（0，0，1）为面ABCD的一个法向量∴cos＜，＞==，∴所求二面角的余弦值为．【点评】本题综合考查空间中线线垂直和空间角的计算，涉及二面角的平面角，利用向量法是解决空间角常用的方法，考查的知识面较广，难度中等．20．（2015秋•广东校级月考）椭圆C：+=1（a＞b＞0）的上顶点为A，P（，）是C上的一点，以AP为直径的圆经过椭圆C的右焦点F．（1）求椭圆C的方程；（2）设过点M（2，0）的动直线l与椭圆C相交于D、E两点，求△ODE面积的最大值．【分析】（1）由于以AP为直径的圆经过椭圆C的右焦点F，可得=+=0．把点P（，）代入椭圆C的方程为：+=1，与b2+c2=a2联立解出即可得出．（2）设my=x﹣2，D（x1，y1），E（x2，y2）．与椭圆方程联立化为：（2+m2）y2+4my+2=0，△＞0，再利用弦长公式与点到直线的距离公式即可得出．【解答】解：（1）A（0，b）．∵以AP为直径的圆经过椭圆C的右焦点F，∴PF⊥AF，∴=•（c，﹣b）=+=0．把点P（，）代入椭圆C：+=1的方程为：+=1，解得a2=2，∴b2+c2=2，可得b2=2﹣c2，代入+=0，解得c=1，b=1．∴椭圆C的方程为+y2=1．（2）设my=x﹣2，D（x1，y1），E（x2，y2）．联立，化为：（2+m2）y2+4my+2=0，△=16m2﹣8（2+m2）＞0，解得或m．∴y1+y2=，y1y2=．∴|DE|===．原点O到直线DE的距离d=．∴S△ODE=d|DE|=××=．设=t＞0，则m2=t2+2．∴S△ODE==≤，当且仅当t=2时取等号．∴m=，满足△＞0．∴当m=时，△ODE面积的最大值为．【点评】本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题、点到直线的距离公式、基本不等式的性质，考查了推理能力与计算能力，属于难题．21．（12分）（2015秋•运城期末）已知函数f（x）=（2﹣a）x﹣2lnx+a﹣2，g（x）=xe1﹣x（1）若函数f（x）在区间（0，）无零点，求实数a的最小值（2）若对任意给定的x0∈（0，e]，方程f（x）=g（x0）在（0，e]上总存在两个不等的实根，求实数a 的取值范围．【分析】（1）f（x）＜0时不可能恒成立，所以要使函数在（0，）上无零点，只需要对x∈（0，）时f（x）＞0恒成立，列出不等式解出a大于一个函数，利用导数得到函数的单调性，根据函数的增减性得到这个函数的最大值即可得到a的最小值；（2）求出g′（x），根据导函数的正负得到函数的单调区间，即可求出g（x）的值域，而当a=2时不合题意；当a≠2时，求出f′（x）=0时x的值，根据x∈（0，e]列出关于a的不等式得到①，并根据此时的x 的值讨论导函数的正负得到函数f（x）的单调区间，根据单调区间得到②和③，令②中不等式的坐标为一个函数，求出此函数的导函数，讨论导函数的正负得到函数的单调区间，根据函数的增减性得到此函数的最大值，即可解出②恒成立和解出③得到④，联立①和④即可解出满足题意a的取值范围．【解答】解：（1）因为f（x）＜0在区间（0，）上恒成立不可能，故要使函数f（x）在（0，）上无零点，只要对任意的x∈（0，），f（x）＞0恒成立，即对x∈（0，），a＞2﹣恒成立．令l（x）=2﹣，x∈（0，），则l（x）=，再令m（x）=2lnx+﹣2，x∈（0，），则m′（x）=＜0，故m（x）在（0，）上为减函数，于是m（x）＞m（）=2﹣2ln2＞0，从而，l（x）＞0，于是l（x）在（0，）上为增函数，所以l（x）＜l（）=2﹣4ln2，故要使a＞2﹣恒成立，只要a∈[2﹣4ln2，+∞），综上，若函数f（x）在（0，）上无零点，则a的最小值为2﹣4ln2；（2）g′（x）=e1﹣x﹣xe1﹣x=（1﹣x）e1﹣x，当x∈（0，1）时，g′（x）＞0，函数g（x）单调递增；当x∈（1，e]时，g′（x）＜0，函数g（x）单调递减．又因为g（0）=0，g（1）=1，g（e）=e•e1﹣e＞0，所以，函数g（x）在（0，e]上的值域为（0，1]．当a=2时，不合题意；当a≠2时，f′（x）=2﹣a﹣=，x∈（0，e]当x=时，f′（x）=0．由题意得，f（x）在（0，e]上不单调，故0＜＜e，即a＜2﹣①，f（）=a﹣2ln，f（e）=（2﹣a）（e﹣1）﹣2，所以，对任意给定的x0∈（0，e]，在（0，e]上总存在两个不等的实根，使得f（x）=g（x0）成立，当且仅当a满足下列条件：即，令h（a）=a﹣2ln，a∈（﹣∞，2﹣），则h′（a）=1﹣2[ln2﹣ln（2﹣a）]′=1﹣=，令h′（a）=0，得a=0或a=2，故当a∈（﹣∞，0）时，h′（a）＞0，函数h（a）单调递增；当a∈（0，2﹣）时，h′（a）＜0，函数h（a）单调递减．所以，对任意a∈（﹣∞，2﹣），有h（a）≤h（0）=0，即②对任意a∈（﹣∞，2﹣）恒成立．由③式解得：a≤2﹣．④综合①④可知，当a∈（﹣∞，2﹣]时，对任意给定的x0∈（0，e]，在（0，e]上总存在两个不同的两个不等的实根使f（x）=g（x0）成立．【点评】此题考查学生会利用导函数的正负确定函数的单调性，会根据函数的增减性求出闭区间上函数的最值，掌握不等式恒成立时所满足的条件，是一道压轴题．请在22、23、24、题中任选一题作答.选修4-1：几何证明选讲22．（10分）（2016•榆林一模）如图，已知PA与圆O相切于点A，经过点O的割线PBC交圆O于点B，C，∠APC的平分线分别交AB，AC于点D，E．（Ⅰ）证明：∠ADE=∠AED；（Ⅱ）若AC=AP，求的值．【分析】（Ⅰ）根据弦切角定理，得到∠BAP=∠C，结合PE平分∠APC，可得∠BAP+∠APD=∠C+∠CPE，最后用三角形的外角可得∠ADE=∠AED；（Ⅱ）根据AC=AP得到∠APC=∠C，结合（I）中的结论可得∠APC=∠C=∠BAP，再在△APC中根据直径BC得到∠PAC=90°+∠BAP，利用三角形内角和定理可得．利用直角三角形中正切的定义，得到，最后通过内角相等证明出△APC∽△BPA，从而．【解答】解：（Ⅰ）∵PA是切线，AB是弦，∴∠BAP=∠C．又∵∠APD=∠CPE，∴∠BAP+∠APD=∠C+∠CPE．∵∠ADE=∠BAP+∠APD，∠AED=∠C+∠CPE，∴∠ADE=∠AED．…（5分）（Ⅱ）由（Ⅰ）知∠BAP=∠C，∵∠APC=∠BPA，∵AC=AP，∴∠APC=∠C∴∠APC=∠C=∠BAP．由三角形内角和定理可知，∠APC+∠C+∠CAP=180°．∵BC是圆O的直径，∴∠BAC=90°．∴∠APC+∠C+∠BAP=180°﹣90°=90°．∴．在Rt△ABC中，，即，∴．∵在△APC与△BPA中∠BAP=∠C，∠APB=∠CPA，∴△APC∽△BPA．∴．∴．…（10分）【点评】本题综合考查了弦切角、三角形的外角定理、直角三角形中三角函数的定义和相似三角形的性质等知识点，属于中档题．找到题中角的等量关系，计算出Rt△ABC是含有30度的直角三角形，是解决本题的关键所在．选修4-4：坐标系与参数方程23．（2015秋•广东校级月考）在直角坐标系中，以原点O为极点，x轴为正半轴为极轴，建立极坐标系，已知曲线C1：（t为参数），C2：（θ为参数）．（1）过C1，C2的方程为普通方程，并说明它们分别表示什么曲线？（2）若C1上的点P对应的参数为t=π，Q为C2上的动点，求PQ中点M到直线C3：ρ（cosθ﹣2sinθ）=7距离的最大值．【分析】（1）消去参数，求出C1，C2的普通方程即可；（2）求出P的坐标，设出Q的坐标，表示出M的坐标，代入点到直线的距离公式即可．【解答】解：（1）∵C1：（t为参数），∴C1：（x﹣3）2+（y﹣2）2=1，表示以（3，2）为圆心，1为半径的圆；∵C2：（θ为参数），∴C2：+=1，表示以长轴是8，短轴是6的椭圆；（2）t=π时，P（2，2），设Q（4cosθ，3sinθ），则M（2cosθ+1，sinθ+1），而C3：ρ（cosθ﹣2sinθ）=7，即：x﹣2y﹣7=0，故M到C3的距离是：d==≤．（其中sinβ=，cosβ=，当且仅当sin（β﹣α）=﹣1时“=”成立．【点评】本题考查了求曲线的普通方程，考查点到直线的距离公式以及三角函数的最值问题，是一道中档题．选修4-5：不等式选讲24．（2015秋•广东校级月考）已知函数f（x）=|x﹣a|．（1）若f（x）＞m（m＞0）的解集为x∈（﹣∞，1）∪（7，+∞），求实数a，m的值；（2）当a=﹣1时，当x≤﹣2时，不等式f（x）+t≥f（x+2）恒成立，求t的取值范围．【分析】（1）先求出不等式的解集，再根据f（x）＞m（m＞0）的解集为x∈（﹣∞，1）∪（7，+∞），即可求出a，m的值，（2）f（x）+t≥f（x+2）恒成立，得到f（x）min+t≥f（x+2）max，分别根据函数的性质求出最值即可．【解答】解：（1）f（x）=|x﹣a|=当x≥a时，x﹣a＞m，即x＞a+m，当x＜a时，﹣x+a＞m，即x＜a﹣m，∵f（x）＞m（m＞0）的解集为x∈（﹣∞，1）∪（7，+∞），∴，解得a=4，m=3，（2）当a=﹣1时，f（x）=，当x≤﹣2时，f（x）=﹣x﹣1，函数为减函数，故f（x）min=f（﹣2）=2﹣1=1，当x≤﹣2时，则（x+2）≤0，∴f（x+2）=，由于当﹣3≤x≤﹣2时，函数f（x+2）为增函数，故f（x+2）max=f（﹣2）=1，由于当x＜3时，函数f（x+2）为减函数，故f（x+2）max=f（﹣3）=0，故函数f（x+2）max=1，∵不等式f（x）+t≥f（x+2）恒成立，∴1+t≥1，解得t≥0，故t的取值范围为[0，+∞）．【点评】本题考查了绝对值不等式的解法以及求能成立问题参数范围；关键是转化的思想应用．。

x 二项式定理1.【来源】浙江省 2017 届高三“超级全能生”3 月联考数学试题 在二项式(2x - 1)6的展开式中，常数项是（ C ）xA ．-240B ．240C ．-160D ．160答案及解析：2.【来源】安徽省黄山市 2019 届高三第一次质量检测（一模）数学（理）试题在(1+x )6(1－2x )展开式中，含 x 5 的项的系数是( D ) A. 36B. 24C. －36D. －243.【来源】新疆维吾尔自治区 2018 届高三第二次适应性（模拟）检测数学（理）试题若⎛ 2 1 ⎫n- x ⎪ 展开式中含 x 项的系数为-80，则 n 等于（ A ）⎝ ⎭A ．5B ．6 C.7 D ．84.【来源】浙江省金丽衢十二校联考 2017 届高考二模数学试题在（1+x 3）（1﹣x ）8 的展开式中，x 5 的系数是（ A ） A ．﹣28B ．﹣84C ．28D ．84答案及解析：【考点】二项式定理的应用．【分析】利用二项式定理的通项公式求解即可．【解答】解：由（1+x 3）展开可知含有 x 3 与（1﹣x ）8 展开的 x 2 可得 x 5 的系数； 由（1+x 3）展开可知常数项与（1﹣x ）8 展开的 x 5，同样可得 x 5 的系数； ∴含 x 5 的项+=28x 5﹣56x 5=﹣28x 5；∴x 5 的系数为﹣28， 故选 A【点评】本题主要考查二项式定理的应用，求展开式的系数把含有 x 5 的项找到．从而可以利用通项求解．属于中档题5.【来源】北京东城景山学校 2016-2017 学年高二下学期期中考试数学（理）试题设(3x -1)4 = a + a x + a x 2 + a x 3 + a x 4 ，则 a + a + a + a的值为（ A ）．12341234A ．15B ．16C ．1D ．－15答案及解析： 在(3x -1)4= a + a x + a x 2 + a x 3 + a x 4 中，令 x = 0 ，可得 a = 1 ，1234再令 x = 1可得 a 0 + a 1 + a 2 + a 3 + a 4 = 16 ， 所以 a 1 + a 2 + a 3 + a 4 = 15 ．n 7 7 7 故选 A ．6.【来源】北京西城八中少年班 2016-2017 学年高一下学期期末考试数学试题在(x + y )n的展开式中，若第七项系数最大，则 n 的值可能等于（ D ）．A ．13，14B ．14，15C ．12，13D ．11，12，13答案及解析：(x + y )n 的展开式第七项系数为 C 6 ，且最大，可知此为展开式中间项，当展开式为奇数项时： n= 6 ， n = 12 ，2当有偶数项时 n + 1= 6 ， n = 11， 2 或 n + 1 = 7 ， n = 13 ，2故 n = 11，12 ，13 ． 选 D ．7.【来源】广东省广州市海珠区 2018 届高三综合测试（一）数学（理）试题(x + y )(2x - y )6 的展开式中 x 4 y 3 的系数为（ D ）A ．－80B ．－40C. 40D ．808.【来源】广东省潮州市 2017 届高三数学二模试卷数学（理）试题 在（1﹣2x ）7（1+x ）的展开式中，含 x 2 项的系数为（ B ） A ．71 B ．70 C ．21 D ．49答案及解析：【分析】先将问题转化为二项式（1﹣2x ）7 的系数问题，利用二项展开式的通项公式求出展开式的第 r+1 项，令 x 的指数分别等于 1，2 求出特定项的系数【解答】解：（1﹣2x ）7（1+x ）的展开式中 x 2 的系数等于（1﹣2x ）7 展开式的 x 的系数+（1﹣2x ）7 展开式的 x 2 的系数，（x+1）7 展开式的通项为 T r+1=（﹣2）r C r x r ，故展开式中 x 2 的系数是（﹣2）2C 2+（﹣2）•C 1=84﹣14=60，故选：B ．9.【来源】浙江省新高考研究联盟 2017 届第四次联考数学试题 在二项式(x 2- 1)5 的展开式中，含 x 7的项的系数是（ C ）xA ． -10B. 10C. -5D. 510.【来源】辽宁省重点高中协作校 2016-2017 学年高二下学期期末考试数学（理）试题 已知(1 + x )n的展开式中只有第 6 项的二项式系数最大，则展开式奇数项的二项式系数和为( D ) A ．212B ．211C.210D ．2911.【来源】上海市浦东新区 2018 届高三上学期期中考试数学试卷展开式中的常数项为（ C ）x -A.-1320B.1320C.-220D.22012.【来源】浙江省绍兴一中2017 届高三上学期期末数学试题在（x﹣y）10 的展开式中，系数最小的项是（C ）A．第4 项B．第5 项C．第6 项D．第7 项答案及解析：【考点】二项式定理的应用．【分析】由二项展开式可得出系数最小的项系数一定为负，再结合组合数的性质即可判断出系数最小的项．【解答】解：展开式共有11 项，奇数项为正，偶数项为负，且第6 项的二项式系数最大，则展开式中系数最小的项第 6项．故选C．13.【来源】浙江省金华十校联考2017 届高三上学期期末数学试题在（1﹣x）n=a0+a1x+a2x2+a3x3+…+a n x n中，若2a2+a n﹣5=0，则自然数n的值是（B）A．7 B．8 C．9 D．10答案及解析：【考点】二项式定理的应用．【分析】由二项展开式的通项公式T r+1=•（﹣1）r x r可得a r=（﹣1）r•，于是有2（﹣1）2+（﹣1）n﹣5=0，由此可解得自然数n 的值．【解答】解：由题意得，该二项展开式的通项公式•（﹣1）r x r，∴该项的系数，∵2a2+a n﹣5=0，∴2（﹣1）2+（﹣1）n﹣5=0，即+（﹣1）n﹣5•=0，∴n﹣5 为奇数，∴2==，∴2×=，∴（n﹣2）（n﹣3）（n﹣4）=120．∴n=8．故答案为：8．14.【来源】浙江省重点中学2019 届高三上学期期末热身联考数学试题⎛ 2 ⎫5 1⎪1展开式中，x2的系数是( B )⎝⎭A、80B、－80C、40D、－4015.【来源】山东省德州市2016-2017 学年高二下学期期末考试数学（理）试题a 2 4如果x + x - 的展开式中各项系数之和为2，则展开式中x 的系数是( C ) x xA．8 B．－8 C.16 D．－1616.【来源】云南省昆明市第一中学2018 届高三第八次月考数学（理）试题x x2 ⎪ ⎛1- 1 ⎫ (1+ x )6x 3⎝ ⎭ 展开式中 x 的系数为（B ）A ．－14B ．14C. 15D ．3017.【来源】安徽省安庆一中、山西省太原五中等五省六校（K12 联盟）2018 届高三上学期期末联考数学（理）试题在二项式(x - 1)n 的展开式中恰好第 5 项的二项式系数最大，则展开式中含有 x 2项的系数是（ C ）xA ．35B ．－35C ．－56D ．56答案及解析：第五项的二项式系数最大，则，通项，令，故系数.18.【来源】辽宁省实验中学、沈阳市东北育才学校等五校 2016-2017 学年高二下学期期末联考数学（理）试题 在( - 2)n 的展开式中，各项的二项式系数之和为 64，则展开式中常数项为（ A ）xA ．60B ．45C ． 30D ．1519.【来源】湖北省武汉市 2018 届高三四月调研测试数学理试题 在(x + 1-1)6 的展开式中，含 x 5项的系数为（ B ）xA ．6B ．－6C ．24D ．－24答案及解析：的展开式的通项 ．的展开式的通项=． 由 6﹣r ﹣2s=5，得 r+2s=1，∵r ，s ∈N ，∴r=1，s=0． ∴的展开式中，含 x 5 项的系数为 ． 故选：B ．20.【来源】辽宁省抚顺市 2018 届高三 3 月高考模拟考试数学（理）试题在(2 -1)6 的展开式中，含 1项的系数为( C )xA. －60B. 160C. 60D. 6421.【来源】2018 年高考真题——数学理（全国卷Ⅲ）(x 2+ 2)5 的展开式中 x 4 的系数为( C )xA ．10B ．20C ．40D ．80答案及解析：由题可得 令 ,则所以x2× 4x9 n故选 C.22.【来源】浙江省金华市十校联考 2016-2017 学年高二下学期期末数学试卷在（x 2﹣4）5 的展开式中，含 x 6 的项的系数为（ D ） A ．20 B ．40 C ．80 D ．160答案及解析：【分析】=（﹣4）r，令 10﹣2r=6，解得 r=2，由此能求出含 x 6 的项的系数．【解答】解：∵（x 2﹣4）5， ∴T r+1==（﹣4）r，令 10﹣2r=6，解得 r=2， ∴含 x 6 的项的系数为=160． 故选：D ．23.【来源】浙江省诸暨市牌头中学 2018 届高三 1 月月考数学试题 在⎛x 2 - ⎝2 ⎫6的展开式中，常数项为（ D ）⎪⎭ A ．-240 B ．-60 C ．60 D ．24024.【来源】浙江省湖州市 2017 届高三上学期期末数学试题在（1﹣x ）5+（1﹣x ）6+（1﹣x ）7+（1﹣x ）8 的展开式中，含 x 3 的项的系数是（ D ） A ．121 B ．﹣74C ．74D ．﹣121答案及解析：【考点】二项式定理的应用．【分析】利用等比数列的前 n 项公式化简代数式；利用二项展开式的通项公式求出含 x 4 的项的系数，即是代数式的含 x 3 的项的系数．【解答】解：（1﹣x ）5+（1﹣x ）6+（1﹣x ）7+（1﹣x ）8 ==，（1﹣x ）5 中 x 4 的系数 ，﹣（1﹣x ）9 中 x 4 的系数为﹣C 4=﹣126，﹣126+5=﹣121． 故选：D25.【来源】甘肃省兰州市第一中学 2018 届高三上学期期中考试数学（理）试题在(x 2-1)(x +1)4 的展开式中，x 3 的系数是（ A ） A ．0B ．10C ．－10D ．20答案及解析：(x +1)4 的展开式的通项, 因此在(x 2-1)(x +1)4 的展开式中,x 3 的系数是26.【来源】山西重点中学协作体 2017 届高三暑期联考数学（理）试题在二项式 + 1的展开式中，前三项的系数成等差数列，把展开式中所有的项重新排成一列，有理项都互 x xx 1 ⎝ ⎭不相邻的概率为( D ) A ． 16B ． 14C. 1 3D ． 51227.【来源】湖北省孝感市八校 2017-2018 学年高二上学期期末考试数学（理）试题已知C 0- 4C 1+ 42C 2- 43C 3+ + (-1)n 4nC n= 729 ，则C 1+ C 2+ + C n的值等于（ C ）nnnnnA ．64B ．32 C.63 D ．31答案及解析：nnn因为 ，所因，选 C. 28.【来源】辽宁省重点高中协作校 2016-2017 学年高二下学期期末考试数学（理）试题若òn(2x -1)dx = 6 ，则二项式(1 - 2x )n的展开式各项系数和为( A ) A ．－1 B ．26 C ．1 D ． 2n29.【来源】浙江省金华十校 2017 届高三数学模拟试卷（4 月份）数学试题若(x －1)8=1+a 1x +a 2x 2+…+a 8x 8，则 a 5=（ B ） A ．56B ．﹣56C ．35D ．﹣35答案及解析：利用通项公式即可得出． 解：通项公式 T r+1=（﹣1）8﹣r x r ，令 r=5，则（﹣1）3=﹣56．故选：B ．30.【来源】广东省茂名市五大联盟学校 2018 届高三 3 月联考数学（理）试题6⎛ 1 ⎫ x 4在( + x ) 1+ y ⎪ 的展开式中， y 2 项的系数为（ C ）A ．200B ．180 C. 150 D ．120答案及解析：展开式的通项公式，令可得：，，展开式的通项公式 ，令可得，据此可得： 项的系数为 .本题选择 C 选项.31.【来源】吉林省长春外国语学校 2019 届高三上学期期末考试数学（理）试题 (2－x )(1+2x )5 展开式中，含 x 2 项的系数为（ B ）x x 0 1 2 2017 3n nx A ． 30 B ． 70 C ．90 D ．－15032.【来源】浙江省新高考研究联盟 2017 届第三次联考数学试题若(1 + x )3 + (1 + x )4 + (1 + x )5 + + (1 + x )2017 = a + a x + a x 2 + + a x 2017 ，则 a 的值为（ D ）3 2017 32018 420174201833.【来源】广东省肇庆市 2017 届高考二模数学（理）试题若（x 6+ 1 ）n的展开式中含有常数项，则 n 的最小值等于（ C ）A ．3B ．4C ．5D ．6答案及解析：【分析】二项式的通项公式 T r+1=C ）r ，对其进行整理，令 x 的指数为 0，建立方程求出 n 的最小值．【解答】解：由题意 ）n 的展开式的项为）r =C n r=C r令r=0，得 r ，当 r=4 时，n 取到最小值 5故选：C ．【点评】本题考查二项式的性质，解题的关键是熟练掌握二项式的项，且能根据指数的形式及题设中有常数的条 件转化成指数为 0，得到 n 的表达式，推测出它的值．34.【来源】上海市金山中学 2017-2018 学年高二下学期期中考试数学试题 设(3x -1)6= a x 6+ a x 5+ + a x + a ，则| a | + | a | + | a | + + | a| 的值为…（ B ）651126(A) 26(B) 46(C) 56(D) 26+ 4635.【来源】浙江省台州市 2016-2017 学年高二下学期期末数学试题x -已知在（ 2 1 ）n的展开式中，第 6 项为常数项，则 n =（ D ）A ．9B ．8C ．7D ．6答案及解析：【考点】二项式系数的性质． 【分析】利用通项公式即可得出． 【解答】解：∵第 6 项为常数项，由 =﹣ •x n ﹣6，可得 n ﹣6=0．解得 n=6． 故选：D ．36.【来源】山东省潍坊寿光市 2016-2017 学年高二下学期期末考试数学（理）试题⎛ 1 ⎫6+ 2x ⎪ ⎝ ⎭的展开式中常数项为（ B ） A ．120B ．160C. 200D ．24037.【来源】北京西城八中少年班 2016-2017 学年高一下学期期末考试数学试题 (2x + 3)4 = a + a x + a x 2 + a x 3 + a x 4(a + a + a )2 - (a + a )2若0 1 2 3 4，则 0 2 41 3 的值为（ A ）． 5 x A ． C B ． C C ． C D ． Cx x A ．1 B ．－1 C ．0 D ．2答案及解析：令 x = 1， a + a + + a = (2 + 3)4 ，1 4令 x = -1， a - a + a - a + a= (-2 + 3)4 ，1234而 (a + a + a )2 - (a + a )22413= (a 0 + a 2 + a 4 + a 1 + a 3 )(a 0 - a 1 + a 2 - a 3 + a 4 )= (2 + 选 A ．3)4 (-2 + 3)4 = (3 - 4)4 = 1． 38.【来源】云南省曲靖市第一中学 2018 届高三 4 月高考复习质量监测卷（七）数学（理）试题设 i 是虚数单位，a 是(x + i )6的展开式的各项系数和，则 a 的共轭复数 a 的值是（ B ） A ． －8iB ． 8iC ． 8D ．-8答案及解析：由题意，不妨令 ，则，将转化为三角函数形式，，由复数三角形式的乘方法则，，则，故正确答案为 B.39.【来源】福建省三明市 2016-2017 学年高二下学期普通高中期末数学（理）试题 a 2 52x + x - 的展开式中各项系数的和为－1，则该展开式中常数项为( A ) x xA ．－200B ．－120 C.120 D ．20040.【来源】甘肃省天水一中 2018 届高三上学期第四次阶段（期末）数学（理）试题已知（1+ax ）(1+x )5 的展开式中 x 2 的系数为 5，则 a =( D )A.-4B.-3C.-2D.-141.【来源】广东省深圳市宝安区 2018 届高三 9 月调研测数学（理）试题(1 + 1)(1 + x )5 展开式中 x 2 的系数为 ( A )xA ．20B ．15C ．6D ．142.【来源】甘肃省民乐一中、张掖二中 2019 届高三上学期第一次调研考试（12 月）数学（理）试题⎛ a ⎫ ⎛1 ⎫5x + ⎪ 2x - ⎪ ⎝ ⎭ ⎝⎭ 的展开式中各项系数的和为 2，则该展开式中常数项为( D )A ．-40B ．-20C ．20D ．4043.【来源】浙江省名校协作体 2018 届高三上学期考试数学试题⎛ 1+ 2⎫(1- x )4 展开式中 x 2 的系数为（ C ） x ⎪ ⎝ ⎭A .16B .12C .8D .444.【来源】山西省太原市 2018 届高三第三次模拟考试数学（理）试题已知(x -1)(ax +1)6展开式中 x 2 的系数为 0，则正实数a = （ B ） 22 A ．1B ．C.53D ． 2x 4 5 5 答案及解析：的展开式的通项公式为.令 得 ；令得.展开式 为. 由题意知，解得（舍）.故选 B. 45.【来源】吉林省松原市实验高级中学、长春市第十一高中、东北师范大学附属中学 2016 届高三下学期三校联合模拟考试数学（理）试题(x +1)2 (x - 2)4的展开式中含 x 3 项的系数为( D )A ．16B ．40 C.－40 D ．846.【来源】海南省天一大联考 2018 届高三毕业班阶段性测试（三）数学（理）试题若(2x - 3)2018= a + a x + a x 2 + L + ax 2018 ，则 a + 2a + 3a + L + 2018a= （ D ）122018A ．4036B ．2018C ．-2018D ．-4036123201847.【来源】湖北省天门、仙桃、潜江 2018 届高三上学期期末联考数学（理）试题(1 + x )8 (1 + y )4 的展开式中 x 2y 2 的系数是 ( D )A ．56B ．84C ．112D ．168答案及解析：因的展开式 的系数 ，的展开式 的系数 ，所的系数.故选 D.48.【来源】北京西城八中 2016-2017 学年高一下学期期末考试数学试题 ⎛ x 2 - 在二项式⎝ 1 ⎫5⎪⎭ 的展开式中，含 x 的项的系数是（ C ）． A ．－10B ．－5C ．10D ．5答案及解析：解： ⎛ x 2 - 1 ⎫5⎪ 的展开项T = C k (x 2 )k (-x -1 )5-k = (-1)5-k C k x 3k -5 ，令3k - 5 = 4 ，可得 k = 3， ⎝x ⎭ k +1 5 5∴ (-1)5-k C k = (-1)5-3 C 3= 10 ． 故选 C ．49.【来源】广东省化州市 2019 届高三上学期第二次模拟考生数学（理）试题 已知(x +1)(ax - 1)5的展开式中常数项为－40，则 a 的值为（ C ）xA. 2B. －2C. ±2D. 450.【来源】福建省“华安一中、长泰一中、南靖一中、平和一中”四校联考 2017-2018 学年高二下学期第二次联考试题（5 月）数学（理）试题若(1 - 2 x )n(n ∈ N *) 的展开式中 x 4的系数为 80，则(1 - 2 x )n的展开式中各项系数的绝对值之和为( C ) A ．32B ．81C ．243D ．256。

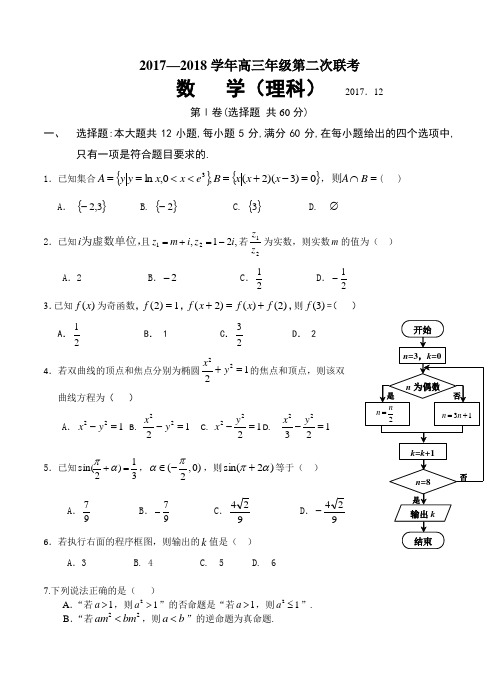
2017—2018学年高三年级第二次联考数 学（理科） 2017．12第Ⅰ卷(选择题 共60分)一、 选择题:本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1．已知集合{}{}0)3)(2(,0,ln 3=-+=<<==x x x B e x x y y A ，=⋂B A 则( ) A ． {}3,2- B. {}2- C. {}3 D. ∅ 2．已知为虚数单位，i 且,21,21i z i m z -=+=若21z z 为实数，则实数m 的值为（ ） A ．2 B ．2- C ．21 D ．21- 3．已知)(x f 为奇函数，1)2(=f ，)2()()2(f x f x f +=+，则)3(f =（ ） A ．21 B ． 1 C ．23D ． 2 4．若双曲线的顶点和焦点分别为椭圆2212x y +=的焦点和顶点，则该双 曲线方程为（ ）A ．221x y -= B. 2212x y -= C. 2212y x -= D. 22132x y -= 5．已知31)2sin(=+απ，(,0)2πα∈-，则)2sin(απ+等于（ ）A ．97B ．97-C ．924 D ．924-6．若执行右面的程序框图，则输出的k 值是（ ）A ．3 B. 4 C. 5 D. 67.下列说法正确的是（ ） A ．“若1a >，则21a >”的否命题是“若1a >，则21a ≤”.B ．“若22am bm <，则a b <”的逆命题为真命题.C ．)0(0，－∞∈∃x ，使0034x x <成立. D ．“若tan 3α≠，则3πα≠”是真命题.8.若函数)(x f y =)1,0(≠>a a 且的图象如右图所示，则下列函数图象正确的是（ ）A B C D 9. 已知实数a 、b 满足4)2()2(22=-+-b a ， 则使02≤-+b a 的 概率为（ ） A.ππ42- B.43 C.41 D.ππ423+ 10. 如图，网格纸上小正方形的边长为l ，粗实线画出的是某几何体的三视 图，该几何体是由一个三棱柱切割得到的，则该几何体外接球的表面积 为（ ） A.π20B. π18C. π16D. π811. P ､Q 为三角形ABC 中不同的两点,若PA PB PC AB ++=u u u r u u u r u u u r u u u r ,053=++QC QB QA ,则:PAB QAB S S △△为（ ）A ．31 B ．53 C ．75 D ． 97 12.设定义在R 上的函数()x f ，对任意的R x ∈，都有())1(1x f x f --=+， 且()02=f ，当1>x 时，()()0>+'x f x f ，则不等式()01ln <-⋅x x f 的解集为（ ）A. ()()1,00,Y ∞-B.()()+∞-,10,1YC. ()()1,,1-∞-+∞YD.()()1,00,1Y -第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13～21题为必考题,每个试题考生都必须作答.第22～23为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,满分20分.13. 在△ABC 中，a ＝3，b ＝7，c ＝2，那么∠B 等于_______.14. 《九章算术》是我国古代的数学名著，书中有如下问题：“今有五人分五钱，令上二人所得与下三人等．问各得几何．”其意思为“已知甲、乙、丙、丁、戊五人分5钱，甲、乙两人所得与丙、丁、戊三人所得相同，且甲、乙、丙、丁、戊所得依次成等差数列．问五人各得多少钱？”（“钱”是古代的一种重量单位）．这个问题中，乙所得为_______钱. 15.已知函数()24sin x x x f -+=，则()________11=⎰-dx x f16.已知()102sin 226k f x x k π⎛⎫>=++⎪⎝⎭，函数与函数4)3cos()(+-=πx k x g若⎥⎦⎤⎢⎣⎡∈∃⎥⎦⎤⎢⎣⎡∈∀32,6,34,3ππππs t 都，使得等式)()(s g t f =成立，则实数k 的取值集合是________. 三、解答题:本大题共7小题,共70分,解答须写出必要的文字说明、证明过程或演算步骤.17.(本小题满分12分)设数列{n a }满足n a n a a a n 2)12(53321=-++++Λ （1）求{n a }的通项公式；（2）数列{}n b 满足231)1(log 2+=-n n a b ，求数列{}n b 的前n 项和n S 18．（本小题满分12分）网上购物逐步走进大学生活，某大学学生宿舍4人积极参加网购，大家约定：每个人通过掷一枚质地均匀的骰子决定自己去哪家购物，掷出点数为5或6的人去淘宝网购物，掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物。

七校联合体2017-2018学年高三第一次联考试卷理科数学一、选择题：（本大题共8小题，每小题5分，满分40分）1．已知全集I ＝R ，集合A ＝{x |y ＝1－x }，集合B ＝{x |0≤x ≤2}，则(∁I A )∪B 等于( ) A ．[1，＋∞) B ．(1，＋∞) C ．[0，＋∞)D ．(0，＋∞)2．设{a n }是公比为q 的等比数列，则“q >1”是“{a n }为递增数列”的( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 3．根据如下样本数据得到的线性回归方程为y ＝b x ＋a ，则( )A.a ^>0，b ^>0 B.a ^>0，b ^<0 C.a ^<0，b ^>0 D.a ^<0，b ^<0 4．某几何体的三视图如图所示,则该几何体的体积为( )A ．168π+B ．88π+C ．1616π+D ．816π+5．执行上边的程序框图，若p ＝0.8，则输出的n ＝( ) A 3 B 4 C 5 D 6 6．由不等式组⎩⎪⎨⎪⎧x ≤0，y ≥0，y －x －2≤0确定的平面区域记为Ω1，不等式组⎩⎪⎨⎪⎧x ＋y ≤1，x ＋y ≥－2确定的平面区域为Ω2，在Ω1中随机取一点，则该点恰好在Ω2内的概率为( ) A.18 B.14 C.34 D.787．函数f (x )＝sin(2x ＋φ)⎝⎛⎭⎫|φ|＜π2的图像向左平移π6个单位后关于原点对称，则函数f (x )在区间⎣⎡⎦⎤0，π2上的最小值为( )A ．－32B ．－12C ．12D ．328．设函数)(x f 在其定义域D 上的导函数为)(/x f ，如果存在实数a 和函数)(x h ，其中)(x h 对任意的D x ∈，都有0)(>x h ，使得),1-)(()(2/+=ax x x h x f 则称函数)(x f 具有性质)(a ω，给出下列四个函数：①131)(23++=x x x x f -； ②14ln )(++=x x x f ；③xe x x xf )54()(2+=-； ④12)(2++=x xx x f其中具有性质)2(ω的函数为( )A ① ② ③B ① ② ④C ② ③ ④D ① ③ ④ 二、填空题：本题共6小题，考生作答6小题，每小题5分，共30分 9．已知复数z ＝(5＋2i)2(i 为虚数单位)，则z 的实部为________． 10．若偶函数()f x 的定义域为[,]p q ，则p q += 11．已知函数()3xf x =的反函数是1()fx -且1(18)23a f a -=+则=______________12．从编号为0,1,2，…，79的80件产品中，采用系统抽样的方法抽取容量为5的一个样本，若编号为42的产品在样本中，则该样本中产品的最小编号为13．2521(2)(1)x x+-的展开式的常数项是 14．设点()0,1M x ，若在圆22:+1O x y =上存在点N ，使得45OMN ∠=︒，则0x 的取值范围是________．三、解答题：本大题共6小题，满分80分，解答应写出文字说明，证明过程或演算步骤． 15．（本题满分12分）已知△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且2cos 2B2＝3sin B ，b ＝1．(1)若A ＝5π12，求边c ；(2)若a ＝2c ，求△ABC 的面积．16.（本小题满分13分）某企业招聘工作人员，设置A 、B 、C 三组测试项目供参考人员选择，甲、乙、丙、丁、戊五人参加招聘，其中甲、乙两人各自独立参加A 组测试，丙、丁两人各自独立参加B 组测试．已知甲、乙两人各自通过测试的概率均为13，丙、丁两人各自通过测试的概率均为12．戊参加C 组测试，C 组共有6道试题，戊会其中4题.戊只能且必须选择4题作答，至少答对3题则竞聘成功. （Ⅰ）求戊竞聘成功的概率；（Ⅱ）求参加A 组测试通过的人数多于参加B 组测试通过的人数的概率； （Ⅲ）记A 、B 组测试通过的总人数为ξ，求ξ的分布列和期望. 17．（本题满分13分）如图, 在直四棱柱ABCD －A 1B 1C 1D 1中，AB ＝AD ＝2，3321==AA DC ，， AD ⊥DC ，AC ⊥BD, 垂足为E ，（I ）求证：BD ⊥A 1C ；（II ）求二面角A 1－BD －C 1的大小；18．（本题满分14分）已知正项数列{}n a 的前n 项和为n S ，且(2)4n n n a a S += *()n ∈N . （1）求1a 的值及数列{}n a 的通项公式； （2）是否存在非零整数λ，使不等式112111(1)(1)(1)cos 2n n a a a a πλ+--⋅⋅-< 对一切*n ∈N 都成立？若存在，求出λ的值；若不存在，说明理由.19．（本小题满分14分）如图所示，椭圆C 1：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，x 轴被曲线C 2：y ＝x 2－b 截得的线段长等于C 1的短轴长．C 2与y 轴的交点为M ，过坐标原点O 的直线l 与C 2相交于点A ，B ，直线MA ，MB 分别与C 1相交于点D ，E . (1)求C 1，C 2的方程；(2)求证：MA ⊥MB ；(3)记△MAB ，△MDE 的面积分别为S 1，S 2，若S 1S 2＝λ，求λ的取值范围．20．（本小题满分14分） 设函数f (x )＝e x －ax －2． (1)求f (x )的单调区间；(2)若a ＝1，k 为整数，且当x ＞0时，(x －k )f ′(x )＋x ＋1＞0恒成立，求k 的最大值． 2016届七校高三摸底考答案 2015.8一、选择题：1C 2D 3B 4A 5B 6D 7A 8 A二、填空题：本题共7小题，考生作答6小题，每小题5分，共30分 (一)必做题(9～13题)9．答案 21 10．答案：0 11答案2 12．答案 10 13答案3 14．答案：011x -≤≤ （答案格式不唯一）三、解答题：15．解：(1)由已知可得1＋cos B ＝3sin B …………2分∴sin ⎝⎛⎭⎪⎫B －π6＝12．…………3分 又0<B<π，∴B ＝π3，∴C ＝π－A －B ＝π4，…………5分 ∴c ＝b sin B ·sin C ＝63．…………6分(2)由(1)知B ＝π3，…………7分∴由余弦定理得b 2＝a 2＋c 2－2accos B ．…………8分又a ＝2c ，∴c 2＝13，…………10分∴△ABC 的面积S ＝12acsin B ＝36．…………12分16、解： (I) 设戊竞聘成功为A 事件，则 …………1分()43144246+=C C C P A C 1+83==155 …………2分（Ⅱ）设“参加A 组测试通过的人数多于参加B 组测试通过的人数”为B 事件………3分()21211137233233436p B ⎛⎫=⨯⨯⨯+⨯⨯=⎪⎝⎭ …………5分（Ⅲ）ξ可能取0，1，2，3，4 …………6分364)21()32()0(22=⨯==ξP …………7分3612)21()32()21(3231)1(2212212=⨯+⨯⨯==C C P ξ …………8分3613)21()32()31()21()32()21()31()2(212122222=⨯⨯+⨯+⨯==C C P ξ …………9分 366)21()31()21(3231)3(2212212=⨯+⨯⨯==C C P ξ …………10分 361)21()31()4(22=⨯==ξP …………11分…………12分∴53E ξ=……13分17．解析：解法一：（I ）在直四棱柱1111ABCD A BC D -中,1A A ⊥ 底面ABCDAC ∴是1AC 在平面ABCD 上的射影. , ……2分,BD AC ⊥ 1.BD AC ∴⊥ ……4分（II ）连结1111,,.A E C E AC与（I ）同理可证11,,BD A E BD C E ⊥⊥ ……6分11A EC ∴∠为二面角11A BD C --的平面角. ……7分,AD DC ⊥11190,oA DC ADC ∴∠=∠= ……8分又111112,A D AD DC DC AA ====且,AC BD ⊥ ……9分11114,1,3,2,AC AE EC A E C E ∴===∴== ……11分在11A EC ∆中,222111111,90,oAC A E C E A EC =+∴∠= ……12分 即二面角11A BD C --的大小为90o . ……13分解法二：（I ）同解法一.（II ）,以D 为坐标原点,1,,DA DC DD 所在直线分别为x 轴,y 轴,z 轴,建立空间 直角坐标系, ……5分连结1111,,.A E C E AC 与（I ）同理可证,11,,BD A E BD C E ⊥⊥ ……7分11A EC ∴∠为二面角11A BD C --的平面角. ……8分113(2A C E 由 ……9分得1113(,(22EA EC →→==-……10分11111139.30.,.44EA EC EA EC EA EC →→→→∴=--+=∴⊥⊥即 ……12分∴二面角11A BD C --的大小为90o. ……13分18解．（1）由(2)4n n n a a S +=.当1n =时，1111(2)4a a a S +==，解得12a =或10a =（舍去）． ……2分当2n ≥时，由111(2)(2)44n n n n n n n a a a a a S S ---++=-=-22112()n n n n a a a a --⇒-=+，……………4分 ∵0n a >，∴10n n a a -+≠，则12n n a a --=，……………5分∴{}n a 是首项为2，公差为2的等差数列，故2n a n =．……………6分另法：易得1232,4,6a a a ===，猜想2n a n =，再用数学归纳法证明(略)．（2）由2n a n =，得11coscos(1)(1)2n n a n ππ++=+=-，……………7分设n b =1(1)n n b λ+-<.……………8分1n n b b +===1=>，……10分 ∵n b >，∴1n nb b +>，数列{}n b 单调递增. ……………… 11分假设存在这样的实数λ，使得不等式1(1)n n b λ+-<对一切*n ∈N 都成立，则① 当n为奇数时，得min 1()n b b λ<==； ……11分……………12分② 当n为偶数时，得min 2()n b b λ-<==，即λ>. ……13分综上，(λ∈，由λ是非零整数，知存在1λ=±满足条件．…… 14分19 (1)解 由题意，知c a ＝22，所以a 2＝2b 2. ……1分又2b ＝2b ，得b ＝1. ……2分所以曲线C 2的方程：y ＝x 2－1，椭圆C 1的方程：x 22＋y 2＝1. ……3分(2)证明 设直线AB ：y ＝kx ，A(x 1，y 1)，B(x 2，y 2)， 由题意，知M(0，－1)．则⎩⎪⎨⎪⎧y ＝kx ，y ＝x 2－1⇒x 2－kx －1＝0， ……4分解得x 1＝k ＋k 2＋42， x 2＝k －k 2＋42，……5分则x 1·x 2＝－1，x 1＋x 2＝k ， ·＝(x 1，y 1＋1)·(x 2，y 2＋1)＝(k 2＋1)x 1x 2＋k(x 1＋x 2)＋1＝－(1＋k 2)＋k 2＋1＝0， 所以MA ⊥MB. ……7分(3)解 设直线MA 的方程：y ＝k 1x －1，直线MB 的方程：y ＝k 2x －1，……8分由(2)知k 1k 2＝－1，M(0，－1)，由⎩⎪⎨⎪⎧y ＝k 1x －1，y ＝x 2－1，解得⎩⎪⎨⎪⎧x ＝0，y ＝－1，或⎩⎪⎨⎪⎧x ＝k 1，y ＝k 21－1， ……9分所以A(k 1，k 21－1)．同理，可得B(k 2，k 22－1)．……10分故S 1＝12|MA|·|MB|＝121＋k 21·1＋k 22|k 1||k 2|.由⎩⎪⎨⎪⎧y ＝k 1x －1，x 22＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝0，y ＝－1或⎩⎪⎨⎪⎧x ＝4k11＋2k 21，y ＝2k 21－11＋2k 21，所以D(4k 11＋2k 21，2k 21－11＋2k 21)．同理，可得E(4k 21＋2k 22，2k 22－11＋2k 22)．……11分故S 2＝12|MD|·|ME|＝121＋k 21·1＋k 22|16k 1k 2|(1＋2k 21)(1＋2k 22)， S 1S 2＝λ＝(1＋2k 21)(1＋2k 22)16＝5＋2(1k 21＋k 21)16≥916，……13分 则λ的取值范围是[916，＋∞)．……14分20解： (1)函数f(x)的定义域为(－∞，＋∞)，f ′(x)＝e x－a ．……1分 当a ≤0时，f ′(x)＞0，所以f(x)在区间(－∞，＋∞)上单调递增； ……………………………………3分当a ＞0时，若x ∈(－∞，ln a)，则f ′(x)＜0，若x ∈(ln a ，＋∞)，则f ′(x)＞0， 所以f(x)在区间(－∞，ln a)上单调递减，在区间(ln a ，＋∞)上单调递增． ……………………………………5分综上可知，当a ≤0时，f(x)的单调递增区间为(－∞，＋∞)；当a>0时，f(x)的单调递减区间为(－∞，ln a)，单调递增区间为(ln a ，＋∞) ……………………………………6分 (2)由于a ＝1，所以(x －k)f ′(x)＋x ＋1＝(x －k)(e x－1)＋x ＋1．设g(x)＝(x －k)(e x －1)＋x ＋1，则g ′(x)＝e x(x －k ＋1)． ……………………………………7分(i)若k ≤1，则当x ＞0时，g ′(x)＞0，所以g(x)在区间(0，＋∞)上单调递增，而g(0)＝1， 故当x ＞0时，g(x)＞1＞0，即有(x －k)f ′(x)＋x ＋1＞0恒成立． ……………………………………9分(ii)若k ＞1，则当x ∈(0，k －1)时，g ′(x)＜0；当x ∈(k －1，＋∞)时，g ′(x)＞0．所以g(x)在区间(0，＋∞)内的最小值为g(k －1)＝k －e k －1＋1． ……………………………………11分令h(k)＝k －e k －1＋1，则h ′(k)＝1－e k －1，因为k>1，所以h ′(k)<0，故h(k)在区间(1，＋∞)上单调递减．而h(2)＞0，h(3)＜0，所以当1＜k ≤2时，h(k)＞0，即g(k －1)＞0，从而当x ＞0时，g(x)＞0，即(x －k)f ′(x)＋x ＋1＞0恒成立；当k ≥3时，h(k)<0，即g(k －1)<0，故g(x)＞0在区间(0，＋∞)内不恒成立．……………………………………13分综上所述，整数k的最大值为2……………………………………14分。

文案秘密★启用前试卷类型： A2018届市高三年级调研测试 理科数学2017．12本试卷共5 页，23 小题，满分150 分，考试用时120 分钟.注意事项：1．本试卷分第1卷（选择题）和第2卷（非选择题）两部分。

答卷前，考生务必将自己的和考生号、试室号、座位号填写在答题卡上，并用2B 铅笔在答题卡的相应位置填涂考生号。

2．作答第1卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

写在本试卷上无效.3．第2卷必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液.不按以上要求作答无效。

4．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.设集合{}1,0,1,2,3A =-，{}230B x x x =->，则AB =（）A.{}1-B.{}1,0-C.{}1,3-D.{}1,0,3- 2.若复数z 满足()121i z i +=-，则z =（） A.25B.35C.53.在等差数列{}n a 中，已知22a =，前7项和756S =，则公差d =（） A.2 B.3 C.2- D.3-4.已知变量x 、y 满足202300x y x y y -≤⎧⎪-+≥⎨⎪≥⎩，则2z x y =+的最大值为（）A.0B.4C.5D.65.912x x ⎛⎫- ⎪⎝⎭的展开式中3x 的系数为（）文案A.212-B.92-C.92D.2126.在如图所示的程序框图中，()i f x '是()i f x 的导函数，若()0sin f x x =，则输出的结果是（） A.sin x - B.cos x C.sin x D.cos x -7.正方体1111ABCD A B C D -的棱长为2，点M 为1CC 的中点，点N 为线段1DD 上靠近1D 的三等分点，平面BMN 交1AA 于点Q ，则AQ 的长为（） A.23 B.12 C.16 D.138.已知直线2y kx =-与曲线ln y x x =相切，则实数k 的值为（） A.ln 2 B.1 C.1ln2- D.1ln2+9.某学校获得5个高校自主招生推荐名额，其中甲大学2名，乙大学2名，丙大学1名，并且甲大学和乙大学都要求必须有男生参加，学校通过选拔定下3男2女共5个推荐对象，则不同的推荐方法共有（） A.36种B.24种 C.22种 D.20种 10.将函数2sin sin 36y x x ππ⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭的图象向左平移()0ϕϕ>个单位，所得图象对应的函数恰为奇函数，则ϕ的最小值为（）文案A.6π B.12π C.4π D.3π11.在直角坐标系xOy 中，设F 为双曲线()2222:10,0x y C a b a b-=>>的右焦点，P 为双曲线C 右支上一点，且OPF ∆为正三角形，则双曲线C 的离心率为（）B.3C.12 12.对于定义域为R 的函数()f x ，若满足①()00f =；②当x R ∈，且0x ≠时，都有()0xf x '>；③当120x x <<，且12x x =时，都有()()12f x f x <，则称()f x 为“偏对称函数”.现给出四个函数：()32132f x x x =-+；()21x f x e x =--；()()3ln 1,02,0x x f x x x -+≤⎧⎪=⎨>⎪⎩；()411,02120,0xx x f x x ⎧⎛⎫+≠⎪ ⎪=-⎝⎭⎨⎪=⎩.则其中是“偏对称函数”的函数个数为（） A.0 B.1 C.2 D.3二、填空题：本题共 4 小题，每小题 5 分，共 20 分.13.已知向量(),2a x x =-，()3,4b =，若//a b ，则向量a 的模为. 14.在各项都为正数的等比数列{}n a中，若2018a =2017201912a a +的最小值为.15.过抛物线()2:20C y px p =>的焦点F 的直线交抛物线C 于A 、B 两点，若6AF =，3BF =，则p 的值为.16.如图，网格纸上正方形小格的边长为1，图中粗线画出的是某三棱锥的三视图，则该三棱锥的外接球的表面积为________．三、解答题：共70分．解答应写出文字说明、证明过程和演算步骤．第 17～21 题为必考题，每个试题考生都必须做答．第 22、23 题为选考题，考生根据要求做答. （一）必考题：共 60 分.文案17．（本小题满分 12 分）ABC ∆的角A 、B 、C 的对边分别为a 、b 、c ，且满足2a =，()cos 2cos a B c b A =-.（1）求角A 的大小； （2）求ABC ∆周长的最大值.18.（本小题满分 12 分）如图，已知多面体PABCDE 的底面ABCD 是边长为2的菱形，PA ⊥底面ABCD ，//ED PA ，且PA =22ED =.文案（1）证明：平面PAC ⊥平面PCE ；（2）若直线PC 与平面ABCD 所成的角为45，求二面角P CE D --的余弦值.19.（本小题满分 12 分）某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示，该地周光照量X （小时）都在30小时以上，其中不足50小时的周数有5周，不低于50小时且不超过70小时的周数有35周，超过EDCBAP文案70小时的周数有10周．根据统计，该基地的西红柿增加量y （百斤）与使用某种液体肥料x （千克）之间对应数据为如图所示的折线图.（1）依据数据的折线图，是否可用线性回归模型拟合y 与x 的关系？请计算相关系数r 并加以说明（精确到0.01）.（若0.75r >，则线性相关程度很高，可用线性回归模型拟合）（2）蔬菜大棚对光照要求较大，某光照控制仪商家为该基地提供了部分光照控制仪，但每周光照控制仪最多可运行台数受周光照量X 限制，并有如下关系：制仪周亏损1000元.以过去50周的周光照量的频率作为周光照量发生的概率，商家欲使周总利润的均值达到最大，应安装光照控制仪多少台？附：相关系数公式()()niix x y y r --=∑0.55≈0.95≈.20.（本小题满分 12 分）文案如图，在直角坐标系xOy 中，椭圆()2222:10y x C a b a b +=>>的上焦点为1F ，椭圆C 的离心率为12，且过点1,3⎛⎫⎪ ⎪⎝⎭.（1）求椭圆C 的方程；（2）设过椭圆C 的上顶点A 的直线l 与椭圆C 交于点B （B 不在y 轴上），垂直于l 的直线与l 交于点M ，与x 轴交于点H ，若110F B F H ⋅=，且MO MA =，求直线l 的方程.21.（本小题满分 12 分）文案已知函数()()ln 0bf x a x xa =+≠.（1）当2b =时，若函数()f x 恰有一个零点，数a 的取值围；（2）当0a b +=，0b >时，对任意1x 、21,x e e ⎡⎤∈⎢⎥⎣⎦，有()()122f x f x e -≤-成立，数b 的取值围.（二）选考题：共 10 分．请考生在第 22、23 题中任选一题做答，如果多做，则按所做的第一题计分． 22．（本小题满分 10 分）选修 4－4：坐标系与参数方程文案在直角坐标系xOy 中，曲线1C 的参数方程为cos 2sin x y αα=⎧⎨=⎩（α为参数），将曲线1C 经过伸缩变换2x xy y'=⎧⎨'=⎩后得到曲线2C ，在以原点为极点，x 轴正半轴为极轴的极坐标系中，直线l 的极坐标方程为cos ρθ-sin 100ρθ-=.（1）说明曲线2C 是哪一种曲线，并将曲线2C 的方程化为极坐标方程；（2）已知点M 是曲线2C 上任意一点，求点M 到直线l 的距离的最大值和最小值.23．（本小题满分 10 分）选修 4－5：不等式选讲 已知函数()f x x a =+.文案（1）当1a =时，求不等式()211f x x ≤+-的解集；（2）若函数()()3g x f x x =-+的值域为A ，[]2,1A -⊆，求a 的取值围.。

2017-2018 学年广州市一般高中毕业班综合测试（一）理科数学一、选择题（本大题共12 个小题，每题 5 分，共 60 分. 在每题给出的四个选项中，只有一项为哪一项切合题目要求的. ）（ 1）已知会合A x x 1 ， B x x2x0，则 A B （）（ A）x 1 x 1（ B）x 0 x 1（ C）x 0 x 1（ D）x 0 x 1【答案】 D【分析】试题剖析：A x1x1， B x 0x 1 ， A B x 0x 1，应选 D.考点：会合的交集 .（ 2）已知复数z3i，此中 i 为虚数单位，则复数z 的共轭复数z 所对应的点在（）1i（ A）第一象限（ B）第二象限（C）第三象限（ D）第四象限【答案】 D【分析】试题剖析：z 3i1i14i12i， z 1 2i，即 z 对应点在第四象限，1i1i22应选 D.考点： 1、复数的观点；2、复数的运算 .（ 3）履行如下图的程序框图，假如输入x 3，则输出 k 的值为（）k0x2x3k k 2x100?是开始输入 x输出 k结束否（A）6（B）8（C）10（ D）12【答案】 C【分析】试题剖析：第一循环 x233 9, k 2 ；第二循环 x 2 9321,k 4 ；第三循环x 2 21 3 45, k 6 ；第四循环x 2 45 3 93, k8 ；第五循环x 2 93 3 189, k 10 ，189100结束循环，输出k 10，应选 C.考点 :程序框图及循环结构 .（ 4）假如函数 f x sin x60 的相邻两个零点之间的距离为，则的值为6（）（A）3（B）6（C）12（D） 24【答案】 B【分析】试题剖析：函数 f x sin x0的相邻两个零点之间的距离为函数的半个周6期，T, 6 ，应选B.26考点：三角函数的图象和周期 .（ 5）设等差数列a n的前 n 项和为 S n，且 a2a7a1224 ，则 S13（）（A）52（B）78（ C） 104（ D） 208【答案】 C【分析】a2a7a1224 ，3a724 ，即 a7 8 ，13 a1a1313a7104 ，试题剖析：S132应选 C.考点：等差数列的性质及前n 项和公式.（ 6）假如P1，P2， , ，P n是抛物线C：y24x 上的点，它们的横坐标挨次为x1， x2，,，x n，F 是抛物线 C 的焦点，若x1x2x n10 ，则 PF P F P F （）12n（ A）n 10（ B）n 20（ C）2n 10（ D）2n 20【答案】 A【分析】试题剖析：y 24x,p 1 ，由抛物线定义可知 PF 11 x 1 , P2 F2 x 2 ， ，2P n F 1 x n ，12nx 2 x nn10 ，应选 A.PF PF P F n x 1 考点： 1、抛物线的标准方程； 2、抛物线的定义及简单几何性质 .（ 7）在梯形 ABCD 中，ADBC ，已知 AD 4 ，BC6 ，若 CD mBA nBCm,nR ，则m（）n（A ） 3（ B ）11（D ） 3（ C ）33【答案】 A【分析】试题剖析： 过 A 作 AECD 交BG 于E ，则CD EA EB BA1BC BA ，即 m 1，31 m3 ，应选 A.n，3n考点 : 1 、平面向量基本观点定理；2、向量的运算 .x y 1 0,2（ 8）设实数 x ， y 知足拘束条件xy1 0, 则 x 2y 2的取值范围是（）x，1（A ） 1,17（B ） 1,17（C ） 1, 17（D ）2 , 17 22【答案】 A【分析】试题剖析：画出拘束条件所表示的可行域，如图，A1,2 , D 0.2 ，由可行域知z x y 222y1 0 的距离的平方为 1 ，的最大值是 AD17 ，最小值为 D 到直线 x2应选 A.y3A2x+y- 1= 01x= -1C-4-3-2-1O1234x-1x-y- 1=0-2DB-3考点 : 利用可行域求目标函数的最值 .（ 9）一个六棱柱的底面是正六边形，侧棱垂直于底面，全部棱的长都为1，极点都在同一个球面上，则该球的体积为（）（ A）（B）20 5（C）5（D）5 536【答案】 D 【分析】125， R545试题剖析：由题意知，R212, V球=R3 5 ，应选 D.24236考点 : 1 、棱柱的性质；2、球的体积公式 .（ 10）已知以下四个：p1：若直线l和平面内的无数条直线垂直，则l；p2：若 f x2x 2 x，则x R，f x f x ；p3：若 f x x 1，则x00,， f x0 1 ；x 1p4：在△ABC中，若A B ，则 sin A sin B ．此中真的个数是（）（A）1（B）2（C） 3（ D）4【答案】 B【分析】试题剖析：假如l 与内无数条平行线垂直，则l 与不必定垂直，因此p1错误；f x2x 2 x，f x 2 x2x f x，故 p2正确；f x1, 只有一个根x0 ，x 0 时，f x1无解，故p3错误；因为在ABC中A B 必定有 a b ，再由正弦定理可得sin A sin B ，故p4正确；应选 B.考点： 1、直线与平面垂直的判断；2、正弦定理及函数的奇偶性.（11）如图，网格纸上小正方形的边长为 1，粗线画出的是某个四周体的三视图，则该四周体的表面积为（）（A）882 46（B）882 26（C）2 2 26（D）126224【答案】 A【分析】试题剖析：由三视图可知，几何体是以P 为极点，以ABC 为底面，以 PC 为高的三棱锥，如图 . 由三视图可知PC4, BC 2 ，可求得AB PB 2 5,AC 4 2, AP 4 3，因此S表SABCSBCSPACSPAB 88 246 ，应选 A.BCAP考点： 1、几何体的三视图；2、几何体的表面积.（12）以下数表的结构思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉三角形”．12 3 4 5,2013 20142015 20163579,,,,4027 4029 403181216,,,,,,,805680602028,,,,,,,,,,16116,,,,,,,,,,,,,,,,该表由若干行数字构成，从第二行起，每一行中的数字均等于其“肩上”两数之和，表中最后一行仅有一个数，则这个数为（）（ A）201722015（ B）2017 22014（ C）201622015（D）201622014【答案】 B【分析】试题剖析：第一行为1、 2 、 3 的三角形，最后一行的数为3121；第一行为1、2、 3、4 的三角形，最后一行的数为 4 122；第一行为1、2、 3、4 、 5的三角形最后一行的数为，5123,可猜想第一行为1、 2、3,2016 最后一行的数为2016 122014201722014，应选 B.考点：概括推理及不完整概括法.第Ⅱ卷（非选择题共90 分）二、填空题（本大题共 4 小题，每题 5 分，满分20 分．）（ 13）一个整体中有 60 个个体，随机编号 0， 1， 2，, ，59，依编号次序均匀分红 6 个小组，组号挨次为 1， 2，3，, ， 6．现用系统抽样方法抽取一个容量为 6 的样本，若在第 1 组随机抽取的号码为3，则在第 5 组中抽取的号码是．【答案】43【分析】试题剖析：整体 60 个个体，依编号次序分红 6 个小组，则间隔编号为6010 ，因此在第 5 组6中抽取的号码为 3 10443 ，故答案为43 .考点：系统抽样方法 .（ 14）已知双曲线C：x2y 2 1 a0,b0的左极点为 A ，右焦点为 F ，点B 0,b，a2b2且BA BF0 ，则双曲线C的离心率为．【答案】512【分析】试题剖析：BA BF 0,AB BF ，又BO AF，因此由射影定理知OB2OAOF，即 b 2ac c22， e2e10, e5151 a2，故答案为2考点:1、向量垂直与向量数目积之间的关系；2、双曲线的几何性质及离心率 .（ 15）x2x4x3的系数为2的睁开式中，．（用数字填写答案）【答案】40【分析】试题剖析： x2x4x2x24x 24C43 x2 x3中含 x3项其2睁开后只有与2系数和为C4123C43C312240，故答案为40 .考点：二项睁开式定理 .（ 16）已知函数f x 1x 1 ,x1,则函数 g x 2 x f x 2 的零点个数为2x，x4x 2,1个．【答案】 2考点 :函数的零点和图象交点的关系.三、解答题（本大题共 6 小题，共70 分 . 解答应写出文字说明、证明过程或演算步骤. ）（ 17）（本小题满分12 分）如图，在△ABC 中，点 D 在边 AB 上， CD BC ，AC 5 3 ，CD5, BD 2AD .（Ⅰ）求 AD 的长；（Ⅱ）求△ABC 的面积．CA D B75 3【答案】（Ⅰ） 5 ；（Ⅱ）.【分析】试题剖析：( Ⅰ ) 设 AD x x 0 ，则 BD 2 x ．因为 CD BC ， CD 5 ， BD 2 x ，因此cos CDB CD5，由余弦定理得BD2xcos ADC AD 2CD 2AC 2x252(53) 2．因为 cos ADC cos CDB ，即2AD CD2x 5x252(53) 25．解得 x 5 ．因此AD的长为 5 ；（Ⅱ）由 ( Ⅰ )AB 3 x15，所2x 52x以S ABC 1BC sin CBA可得正确答案 .AB2试题分析： ( Ⅰ )在ABC 中，因为BD 2AD，设 AD x x 0 ，则 BD 2 x ．在 BCD 中，因为CD BC，CD 5 ， BD 2x ，因此 cos CDB CDBD5．在 ACD 中，因为 AD x ， CD5，AC 5 3 ，2x由余弦定理得 cos ADC AD 2CD 2AC 2x252(5 3)2．因为2AD CD 2 x5CDB ADC，因此 cos ADC cos CDB ，即 x252(5 3)25．解得 x 5 ．因此AD的长为 5 .2x 5 2 x（Ⅱ）由（Ⅰ）求得AB3x 15 ， BC225 5 3 ．因此cos CBD BC34 xBD，2从而 sin1,因此S ABC1sin115 51753 CBD AB BC CBA34．2222考点：余弦定理及三角形面积公式.（ 18）（本小题满分12 分）从某公司生产的某种产品中抽取100件，丈量这些产品的质量指标值，由丈量结果获得如图所示的频次散布直方图，质量指标值落在区间55,65 ，65,75，75,85内的频次之比为4:2:1 ．（Ⅰ）求这些产质量量指标值落在区间75,85内的频次；（Ⅱ）若将频次视为概率，从该公司生产的这类产品中随机抽取 3 件，记这 3 件产品中质量指标值位于区间45,75 内的产品件数为X，求X的散布列与数学希望．频次组距0.0300.0190.0120.004015 25 35 45 55 65 75 85质量指标值【答案】（Ⅰ） 0.05 ；（Ⅱ） 1.8 .【分析】试题剖析：（Ⅰ）先依据比率设出质量指标值落在区间55,65 ， 65,75 , 75,85 内的频次，再依据各个矩形面积和为1可求得质量指标值落在区间75,85 内的频次；（Ⅱ）从该公司生产的该种产品中随机抽取 3 件，相当于进行了 3 次独立重复试验，因此X听从二项散布 B n, p ，此中 n 3 ，依据独立重复试验概率公式求概率，依据二项散布希望公式求希望.试题分析：（Ⅰ）设区间75,85 内的频次为 x ，则区间55,65 ， 65,75 内的频次分别为4x 和 2x ．依题意得0.004 0.012 0.019 0.03 10 4x 2 x x 1 ，解得x0.05 .因此区间75,85 内的频次为0.05．（Ⅱ）从该公司生产的该种产品中随机抽取3件，相当于进行了3次独立重复试验，因此 X 听从二项散布B n, p ，此中n 3．由（Ⅰ）得，区间45,75 内的频次为0.3 0.2+0.1=0.6 ，将频次视为概率得p 0.6 ．因为X的全部可能取值为0、1、 2、 3，且 P(X 0)C300.600.430.064， P(X1)C13 0.610.420.288 ，P( X2)C320.620.410.432 ，P( X3) C330.630.400.216．因此 X 的散布列为：X0123P0.0640.2880.4320.216 X 听从二项散布B n, p，因此 X 的数学希望为EX 3 0.6 1.8 ．考点： 1、频次散布直方图； 2、失散型随机变量的均值希望 .（ 19）（本小题满分12 分）如图，四棱柱 ABCD A1 BC1 1D1的底面ABCD是菱形，AC BD O，AO1底面ABCD ，AB AA1 2．（Ⅰ）证明：平面ACO1平面 BB1D1 D ；（Ⅱ）若 BAD60 ，求二面角 B OB1 C 的余弦值．【答案】（Ⅰ）证明看法析；（Ⅱ）6 4.【分析】试题剖析：（Ⅰ）先证AO BD，CO BD 可得BD平面ACO ，从而得平面BB1D1D平11面ACO1；（Ⅱ）以 O 为原点，OB，OC，OA1方向为x，y，z轴正方向成立如下图空间直角坐标系．分别求出平面OBB1的法向量，平面OCB1的法向量，利用空间向量夹角公式即可求得二面角 B OB1 C的余弦值 .试题分析：（Ⅰ）证明：因为 AO平面 ABCD，1BD 平面ABCD，因此AO BD．因为 ABCD 是菱形，1因此 CO BD ．因为AO1CO O ，因此 BD平面 ACO．因为BD 平面BB1 D1D，1因此平面BB1 D1 D 平面 ACO1．（Ⅱ）解：因为1平面 ABCD ，CO BD ，以 O 为原点，OB，OC，OA1方AO向为 x ，y， z 轴正方向成立如下图空间直角坐标系．因为 AB AA1 2 ，BAD60，因此 OB OD1，OA OC3，OA1AA12OA21．则B 1,0,0，C0, 3,0 ，A 0,3,0，A10,0,1 ，因此 BB1AA10, 3,1 ，OB1OB+ BB11, 3,1 ．设平面OBB1的法向量为n x, y, z ，因为 OB1,0,0， OB11, 3,1 ，因此x0,x3y z 0.令 y1，得 n0,1, 3．同理可求得平面OCB1的法向量为m1,0,1．因此 cos n,m36B OB1C 的平面角为钝角，22．因为二面角4因此二面角 B OB1 C 的余弦值为 6 ．4z D1C1A1B1DCyOA Bx考点： 1、线面及面面垂直的判断定理；2、利用法向量夹角公式求二面角的余弦.（ 20）（本小题满分12 分）已知椭圆 C 的中心在座标原点，焦点在x 轴上，左极点为 A ，左焦点为F12，0，点B2, 2在椭圆 C 上，直线y kx k 0 与椭圆C交于E，F两点，直线AE ， AF 分别与 y 轴交于点M ，N．（Ⅰ）求椭圆 C 的方程；（Ⅱ）以 MN 为直径的圆能否经过定点？若经过，求出定点的坐标；若不经过，请说明原因．【答案】（Ⅰ）x2y21；（Ⅱ）经过两定点P12,0， P22,0 . 84【分析】试题剖析：（Ⅰ）椭圆的左焦点为 F12，0 ，因此a2b24．由点 B 2, 2 在椭圆 C上，得421，从而解出 a, b 获得椭圆 C 的方程；（Ⅱ）直线 y kx (k 0) 与椭圆x2y21 a2b284联立，解得 E, F 的坐标（用 k 表示），设出 AE ， AF 的方程，解出 M , N 的坐标，圆方程用k 表示，最后可求得MN 为直径的圆经过两定点.试题分析：（Ⅰ）设椭圆 C 的方程为x2y2 1 (a b 0) ，a2b2因为椭圆的左焦点为F12，0 ，因此a2b2 4 ．因为点 B 2,2在椭圆 C421 ．上，因此2b2a由①②解得， a2 2 ，b 2 ．因此椭圆 C 的方程为x 2y 2 1．84（Ⅱ）因为椭圆 C 的左极点为 A ，则点 A 的坐标为 2 2,0 ．因为直线 ykx ( k 0) 与椭圆x 2y 21交于两点 E ，F ，84设点 E x 0 , y 0 （不如设 x 00 ），则点 F x 0 , y 0 ．y kx, 2 8联立方程组x 2 y 2 1消去 y 得 x 12 ．8 42k因此 2 2 ，则 y 02 2k ．x 02k 2 1 2k 21因此直线 AE 的方程为 ykx2 2 ．1 12k2因为直线 AE ， AF 分别与 y 轴交于点 M ， N ，令 x0 得 y2 2k，即点 M 0,2 2k．112k 22k 211同理可得点 N0,2 2k．11 2k 2因此 MN2 2k2 2k2 2 1 2k 2．11 2k2112k2k设 MN 的中点为 P ，则点 P 的坐标为 P 0,2 ．k222 1 2k2则以 MN 为直径的圆的方程为x2y2 ，kk即 x 2y 2 2 2 y 4 ．k令 y0 ，得 x 24 ，即 x2 或 x 2 ．故以 MN 为直径的圆经过两定点P 1 2,0 ， P 2 2,0 ．考点： 1、 待定系数法求椭圆；2、圆的方程及几何意义 .（ 21）（本小题满分 12 分）已知函数 f ( x) e x+mx 3 , g xln x1 2 ．（Ⅰ）若曲线yf x 在点0 f 0 处的切线斜率为 1，务实数 m 的值；，（Ⅱ）当 m 1时，证明： f xg(x)x 3 .【答案】（Ⅰ） m 0 ；（Ⅱ）证明看法析 .【分析】试题剖析：（Ⅰ）先求出 f ( x) ，再令fe m，可解得m 的值；（Ⅱ） f xg( x) x31等价于 ex+ mln x 1 20 ，当 m1时，只要证明 e x1ln( x1) 2 0 ，设h xe x 1ln x 12 ，则 h xe x 1x 1 ，利用 hx 的单一性， 能够证明 h x 的1最小值 hx 0 为正，从而 f xg( x)x 3 .试题分析： （Ⅰ）因为f ( x)e x+ mx 3 ，因此 f (x)e x+m3x 2 . 因为曲线yf x 在点0 f 0处的切线斜率为 1，因此 fe m1，解得 m0 .，（Ⅱ）因为 f ( x) e x+m x 3 , g xln x12 ，因此 fxg( x) x 3 等价于 e x+m ln x 12 0．当 m 1时， e x+m ln x 1 2 e x 1 ln x 1 2 ．要证 e x+mln x 12 0 ，只要证明 e x 1 ln( x 1)20设 h x e x 1 ln x 12 ，则 h x e x 1x 1 .1设 p x ex 11x 110 ．x ，则 p x ex211因此函数 p xh xe x11 1 在 1，+ 上单一递加．x1 1因为 he 2 2 0 ， h 0 e 10，2因此函数 h xe x11 在 1，+上有独一零点x 0 ，且 x 01 ,0x 12因为 h x0，因此e x0 +11，即 ln x1x 1 .0x0100当 x1, x 时， h x0 ；当 x x,时， h x 0 ，00因此当 x x0时， h x 获得最小值 h x0.因此 h x h x0 = e x01ln x0 1 2x01x0120.1综上可知，当 m 1时，f x g( x)x3.考点： 1、利用导数求切线斜率；2、利用导数研究函数的单一性及最值 .请考生在第22、 23、 24 三题中任选一题作答，假如多做，则按所做的第一题记分. 解答时请写清题号 .（ 22）（本小题满分10 分）选修4－1：几何证明选讲如下图，△ABC 内接于⊙ O ，直线 AD 与⊙ O 相切于点 A ，交 BC 的延伸线于点 D ，过点D 作DE CA 交BA 的延伸线于点 E ．（Ⅰ）求证：（Ⅱ）若直线DE2AE BE ；EF 与⊙ O 相切于点F，且EF4，EA 2 ，求线段AC的长．FB．OE ACD【答案】（Ⅰ）证明看法析；（Ⅱ） 3 .考点： 1、三角形相像；2、切割线定理 .（ 23）（本小题满分10 分）选修4－4：坐标系与参数方程在平面直角坐标系xOy 中，以坐标原点O为极点，x轴正半轴为极轴成立极坐标系，曲线C 的极坐标方程为 2 sin ，0,2 .（Ⅰ）求曲线 C 的直角坐标方程；（Ⅱ）在曲线 C 上求一点 D ，使它到直线 l ：x3t3,（ t 为参数，t R ）的距离最y3t2短，并求出点D 的直角坐标.【答案】（Ⅰ） x2y2 2 y33 0 ；（Ⅱ）， .22【分析】试题剖析：（Ⅰ）利用极坐标方程与直角坐标的互化公式可得：（Ⅱ）参数方程化为一般方程，利用圆心到直线的距离减半径最小可知，过圆心与直线垂直的直线与圆的交点之一获得最小值，依据几何意义清除一个即可.试题分析：（Ⅰ）解：由 2 sin ，0,2 ，可得2 2 sin ．因为2x 2 y 2 ，siny ，因此曲线 C 的一般方程为 x 2y 2 2y0 （或 x 221）．y 1 （Ⅱ） 解： 因为直线的参数方程为x 3t 3,（ t 为参数， tR ），y3t2消去 t 得直线 l 的一般方程为 y3x 5 ．因为曲线 C ： x 2y 1 21是以 G0,1 为圆心， 1 为半径的圆，设点 Dx 0 , y 0 ，且点 D 到直线 l ： y3x 5 的距离最短，因此曲线 C 在点 D 处的切线与直线 l ： y3x 5平行．即直线 GD 与 l 的斜率的乘积等于1，即y 0131．x 02 y 0 1233因为x 01，解得 x 0或 x 0 2．2 因此点 D 的坐标为3 1或3 32，2 ， ．22因为点 D 到直线 y3x 5 的距离最短，因此点 D 的坐标为332 ， ．2考点： 1、极坐标方程与直角坐标的方程互化； 2、参数方程与一般方程的互化 .（ 24）（本小题满分 10 分）选修 4－5：不等式选讲设函数 f xx ax 1 a ． （Ⅰ）当 a1 时，求不等式f x1的解集；2（Ⅱ）若对随意【答案】（Ⅰ）a0,1 ，不等式1,；（Ⅱ）4f xb 的解集为空集，务实数 b 的取值范围．2，+ .【分析】试题剖析：（Ⅰ）议论三种状况x 1 ， 1 x 0 ， x 0 ，最后找并集即可； （Ⅱ）不等式f xb 的解集为空集，只要 bf x，利用基本不等式可得f xa 1 a ，max从而转变为ba1 a，最后运用三角换元法或平方后联合基本不等式求出maxa1 a.max试题分析：（Ⅰ） 解： 当 a 1 时， fx1 x 1 x1等价于．1 22①当 x1时，不等式化为 x 1 x，无解；21 1②当 1x 0 时，不等式化为 x1 xx 0 ；，解得41 2③当 x0 时，不等式化为 x1 x0 ．，解得 x2综上所述，不等式f x1的解集为1 , .4（Ⅱ）因为不等式f xb 的解集为空集，因此 bf x．max因为 f x x a x1 ax a x1 aa 1 aa 1 a ，当且仅当 x1 a 时取等号． 因此 f xmaxa1 a ．因为对随意 a0,1 ，不等式f xb 的解集为空集，因此 ba1 a, 令 gaa1 a ，max因此 g 2a12 a1 a1a21a22 ．当且仅当a1 a ，即 a12时等号成立．因此 g amax2 ．因此 b 的取值范围为2，+ ．考点： 1、绝对值不等式的解法； 2、利用基本不等式求最值.。

广东省珠海市2018届高三3月质量检测数学（理）试题含答案珠海市2017～2018学年度第二学期普通高中学业质量监测高三理科数学试题 第Ⅰ卷 选择题一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.请在答题卡上填涂相应选项.1.复数2ii-=（ ） A ．12i +B ．12i -C ．12i -+D ．12i --2.命题“0x N +∃∈，使得002(1)1xx +>”的否定是（ ） A ．x N +∀∈，都有2(1)1xx +> B ．x N +∀∉，都有2(1)1x x +≤C ．0x N +∀∉，都有002(1)1xx +≤D ．x N +∀∈，都有2(1)1xx +≤3.n S 是正项等比数列{}n a 的前n 项和，318a =，326S =，则1a =（ ）A ．2B ．3C ．1D ．64.将一个长、宽、高分别为3、4、5的长方体截去一部分后，得到的几何体的三视图如图所示，则该几何体的体积为（ ）A ．24B ．48C ．30D ．605.设变量x ，y 满足约束条件22020440x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩，则2z x y =-的最小值为（ ）A ．4B ．6-C ．6D ．4-6.进位制转换：(3)13___=（ ） A ．101B ．110C ．111 D ．1217.将5个不同的球放入4个不同的盒子中，每个盒子至少放一个球，则不同放法共有（ ）种 A ．480 B ．360 C ．240D ．1208.执行如图的程序框图，如果输入1a =，则输出的s =（ ）A ．23-B ．191-C ．23D ．1919.已知双曲线M ：22221x y a b-=(0,0)a b >>，其焦点(,0)(0)F c c ±>，右顶点(,0)A a 到双曲线M 的一条渐近线距离为125，以点A 为圆心，c 为半径的圆在y 轴所截弦长为8，则双曲线M 的方程为（ ） A ．221916x y -= B ．221169x y -= C ．229x y -= D ．2216x y -=10.如图，在直四棱柱1111ABCD A BC D -中，四边形ABCD 为梯形，//AD BC ，13AA =，AB BC CD ==120BCD ∠= ，则直线1A B 与1B C 所成的角的余弦值为（ ）A ．78B ．58C ．8D ．811.定义在R 上的连续函数()f x ，其导函数'()f x 为奇函数，且(2)1f =，()0f x ≥；当0x >时，'()()0xf x f x +<恒成立，则满足不等式(2)1f x -≤的解集为（ ）A ．[2,2]-B ．[0,4]C ．(,2][2,)-∞-+∞D ．(,0][4,)-∞+∞12.函数()sin cos f x a x b x ωω=+sin()A x ωϕ=+(,,0,0,)2a b R A πωϕ∈>><的一个对称中心为(,0)6π-，且'()f x 的一条对称轴为3x π=，当ω取得最小值时，22aba b=+（ ） A ．1 B．4 D．2第Ⅱ卷非选择题二、填空题：本大题共4小题，每小题5分，满分20分.请将答案填在答题卡相应位置. 13.设向量(1,3)a m = ，(2,)b m =- ，满足()()0a b a b +⋅-=，则m =．14.已知α，β均为锐角，cos β=，1cos()2αβ+=，则cos α=．15.过点(1,1)M 作斜率为13-的直线l 与椭圆C ：22221x y a b+=(0)a b >>相交于A ，B 两点，若M 是线段AB 的中点，则椭圆C 的离心率为．16.在ABC ∆中，角A 、B 、C 所对边的边长分别为a 、b 、c ，若3CA CB -=，6CA CB ⋅= ，则ABC ∆面积的最大值为．三、解答题：本题共有5个小题，满分60分.解答应写出文字说明、证明过程. 17.已知数列{}n a 的前n 项和为n S ，满足12a =，122n n S S +-=.（1）求数列{}n a 的通项n a ； （2）令2n n nb S =+，求数列{}n b 的前n 项和n T .18.某兴趣小组进行“野岛生存”实践活动，他们设置了200个取水敞口箱.其中100个采用A 种取水法，100个采用B 种取水法.如图甲为A 种方法一个夜晚操作一次100个水箱积取淡水量频率分布直方图，图乙为B 种方法一个夜晚操作一次100个水箱积取淡水量频率分布直方图.（1）设两种取水方法互不影响，设M 表示事件“A 法取水箱水量不低于1.0kg ，B 法取水箱水量不低于1.1kg ”，以样本估计总体，以频率分布直方图中的频率为概率，估计M 的概率；附：2K 2()()()()()n ad bc a b c d a c b d -=++++19.如图，四棱锥P ABCD -中，//CD AB ，2CD AB =，16AB =，10PA PB ==，AD BD ==PD =点E 为PD 中点.（1）求证：PD CD ⊥；（2）求直线BE 与平面PCD 所成角的正弦值. 20.已知抛物线1C ：22(0)y px p =>，圆2C ：224x y +=，直线l ：y kx b =+与抛物线1C 相切于点M ，与圆2C 相切于点N .（1）若直线l 的斜率1k =，求直线l 和抛物线1C 的方程；（2）设F 为抛物线1C 的焦点，设FMN ∆，FON ∆的面积分别为1s ，2s ，若12s s λ=，求λ的取值范围.21.函数()ln ()x f x axe x x a R =++∈.（1）若0a ≥，试讨论函数()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围.选考题：共10分.请考生在22、23题中任选一题作答.如果多做，则按所做的第一题计分. 22.选修4-4：极坐标与参数方程在平面直角坐标系xoy 中，直线l的参数方程为42x y ⎧=-+⎪⎪⎨⎪=⎪⎩（t 为参数）.若以原点O 为极点，x 轴的非负半轴为极轴建立极坐标系，则曲线C 的极坐标方程为2222cos 3ρθρ=-.（1）写出曲线C 和直线l 的直角坐标方程； （2）求曲线C 上的点到直线l 距离的最大值. 23.选修4-5：不等式选讲 已知函数()1f x x =+.（1）解不等式2()42f x x <--；（2）已知2(0,0)m n m n +=>>，若不等式11()x a f x m n--≤+恒成立，求实数a 的取值范围.高三理科数学试题参考答案一、选择题1-5: DDABB 6-10: CCBAA 11、12：DC 二、填空题13. 4±14. 3615. 34三、解答题17.解：（1）∵122n n S S +-=……①，∴2122n n S S ++-=……②，②-①得212n n a a ++=，∵12a =，∴2112122S S a a a -=+-222a =-=，∴24a =，∴n N +∈时，212a a =，212n n a a ++=，即n N +∈时，12n n a a +=， ∴数列{}n a 是2为首项，2为公比的等比数列，∴2n na =.（2）2(21)21n n S -=-122n +-，则12n n nb +=， ∴123nn T b b b b =+++⋅⋅⋅+23411232222n n +=+++⋅⋅⋅+……③， ∴2n T 231232222n n=+++⋅⋅⋅+……④， ④-③得n T 231111122222n n n+=+++⋅⋅⋅+-111(1)221212n n n +---1212n n ++=-.18. 解：（1）设“A 法取水箱水量不低于1.0kg ”为事件E ，“B 法取水箱水量不低于1.1kg ”为事件F ，()(210.3)0.10.33P E =++⨯=，()(530.20.1)0.10.83P F =+++⨯=， ()()()()P M P EF P E P F ==⨯0.330.830.2739=⨯=，故M 发生的概率为0.2739. （2）22⨯列联表：2K 2()()()()()n ad bc a b c d a c b d -=++++2200(87831317)(8717)(1383)(6717)(3383)⨯⨯-⨯=++++98.157 6.635≈>， ∴2(98.157 6.635)0.01P K=><，∴有99%的把握认为箱积水量与取水方法有关. 19.（1）证明：取AB 中点F ，连接PF 、FD ， ∵10PA PB ==，AD BD ==∴AB PF ⊥，AB FD ⊥， ∵PF FD F = ，∴AB ⊥平面PFD ，PD ⊂平面PFD ， ∴AB PD ⊥，又∵//CD AB ， ∴PD CD ⊥.（2）解：过P 做PO FD ⊥于O ， ∵AB ⊥平面PFD ，PO ⊂平面PFD ，∴AB PO ⊥，∵AB FD F = ，∴PO ⊥平面ABCD . 过O 做//OG AB 交BC 于G ，则PO 、OF 、OG 两两垂直，以OF 、OG 、OP 分别为x 、y 、z 轴建立如图所示空间直角坐标系o xyz -， ∵16AB =，10PA PB ==，AD BD ==PD =E 为PD 中点，∴6PF =，12FD =， ∴222PF PD FD +=， ∴PF PD ⊥，∴PO =3OF =，9OD =.∵//CD AB ，12CD AB =， ∴////CD OG FB ，CD FB =，∴四边形FBCD 是矩形，8CD OG FB ===，∴P ，(9,0,0)D -，(3,8,0)B ，(9,8,0)C -，∵E 为PD 中点，∴9(2E -，∴15(,8,2EB =，(9,0,PD =-- ，(0,8,0)CD =- .设平面PCD 的法向量000(,,)n x y z = ，由0009080n PD x n CD y ⎧⋅=--=⎪⎨⋅=-=⎪⎩，得0000z y ⎧=⎪⎨=⎪⎩，令01x =，得0z =则(1,0,n =，则n 与EB所成角设为α，其余角就是直线BE 与平面PCD 所成角，设为β，sin cos βα=n EB n EB⋅==⋅∴直线BE 与平面PCD所成角的正弦值为127.20. 解：（1）由题设知l ：0x y b -+=，且0b >，由l 与2C 相切知，2(0,0)C 到l的距离2d==，得b = ∴l：0x y -+=.将l 与1C 的方程联立消x得2240y py -+=，其240p ∆=-=得p =∴1C：2y =.综上，l：0x y -+=，1C：2y =.（2）不妨设0k >，根据对称性，0k >得到的结论与0k <得到的结论相同. 此时0b >，又知0p >，设11(,)M x y ，22(,)N x y ，由22y kx by px=+⎧⎨=⎩消y 得2222()0kx kb p x b +-+=，其2224()40kb p k b ∆=--=得2p kb =，从而解得2(,)2p p M k k， 由l 与2C 切于点N 知2(0,0)C 到l ：0kx y b -+=的距离2d ==，得b =4p =M .由224y kx b x y =+⎧⎨+=⎩得(N ，故M NMN x =-=242k k +=. (,0)2p F 到l ：0kx y b -+=的距离为0pkbd +222k =+， ∴1012FMNs s MN d ∆==222(21)(1)k k k ++=， 又2122FON N s s OF y k ∆==⋅=， ∴22122(21)(1)s k k s kλ++==221(2)(1)k k =++221233k k =++≥. 当且仅当2212k k =即k =时取等号，与上同理可得，0k <时亦是同上结论. 综上，λ的取值范围是[3)++∞.21.解：(1)(1)'()x x axe f x x++=(0)x >.（1）若0a ≥，则'()0f x >在0x >时恒成立， ∴()f x 的增区间是(0,)+∞.（2）①若0a ≥，由（1）知()f x 在(0,)+∞上单增， 故()f x 不可能有两个零点.②若0a <，令()1(0)xg x axe x =+>，则'()(1)0x g x a x e =+<，∴()g x 在(0,)+∞上单减，∵(0)10g =>，11()10a g e a--=-+<，∴01(0,)x a∃∈-，使得000()10x g x ax e=+=，即001x ax e =-，当00x x <<时，()0g x >，即'()0f x >；当0x x >时，()0g x <，即'()0f x <. 故()f x 在0(0,)x 上单增，在0(,)x +∞上单减， ∴max 0()()f x f x =0000ln x ax e x x =++00ln 1x x =+-.若()f x 有两个零点，首先须max 0()()f x f x =0000ln x ax e x x =++00ln 10x x =+->，令()ln 1h x x x =+-1(0)x a<<-，则()h x 在(0,)a1-上单增，∵(1)0h =，∴须011x a <<-即01x ae e e -<<，∴001x e x e a <=-11a e a-<-且11a <-，得到10a e-<<， 此时，1）0101a x e<-<<<，∴ln()1a -<-， ∴2()ln()a f a a e a --=-+-210a a a e a --<---<.2）取0b x >且2ln()b a>-，则0b e b x >>， ()bbb e bf e ae e b e =++2()2b ba e e <+(2)bbe ae =+2ln()(2)0bae ae-<+=，∴()f x 在0(0,)x 和0(,)x +∞各一个零点， 综上，()f x 有两个零点，a 的取值范围是1(,0)e-. 22.解：（1）直线l 的直角坐标方程为40x y -+=，曲线C 的直角坐标方程为2213y x +=. （2）设曲线C上的任一点(cos )P θθ，P 到直线l的距离为d==，当sin()16πθ-=-时，d 得到最大值∴曲线C 上的点到直线l 距离的最大值为23.解：（1）2()42f x x <--等价于2124x x ++-<，当2x ≥时原不等式转化为2(1)(2)4x x ++-<，即43x <，此时空集； 当12x -<<时原不等式转化为2(1)(2)4x x +--<，即0x <，此时10x -<<； 当1x ≤-时原不等式转化为2(1)(2)4x x -+--<，即43x >-，此时413x -<≤-. 综上可得，原不等式解集为4{|0}3x x -<<. （2）()x a f x --1x a x =--+1a ≤+.又2(0,0)m n m n +=>>由柯西不等式，得111()()2m n m n ++21(11)22≥+=， 由题意知12a +≤，解得31a -≤≤.。