七年级数学下册82角的比较同步训练题青岛版!

青岛版七年级数学下册第8章角同步训练考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、已知 '13836,238.36,338.6∠∠∠===， 则下列说法正确的是（ ）A ．12∠=∠B ．23∠∠=C ．13∠=∠D ．123∠∠∠、、互不相等2、如图，△ABC 中，∠C ＝90°，AB ＝8，∠B ＝30°，点P 是BC 边上的动点，则AP 长不可能是( )A ．3.5B ．4.2C ．5.8D ．7.33、如图，直线AB 和CD 相交于点O ，下列选项中与∠AOC 互为邻补角的是（ ）A ．∠BOCB ．∠BODC ．∠DOED ．∠AOE4、如图，90AOB ∠=︒，直线b 经过点O ．在下面的五个式子中：①1802︒-∠；②3∠；③212∠+∠；④23212∠-∠-∠；⑤1801︒-∠，等于2∠的补角的式子的个数是（ ）A ．2B ．3C ．4D ．55、已知70A ∠=︒，则A ∠的补角的度数为（ ）A ．20︒B ．30C ．110︒D ．130︒6、将一副直角三角尺按如图所示的不同方式摆放，则图中∠α与∠β相等的是（） A ． B ．C ．D ．7、如图，90ACB ∠=︒，CD AB ⊥，垂足为点D ，则点C 到直线AB 的距离是（）A ．线段AC 的长度B ．线段CB 的长度C ．线段CD 的长度 D ．线段AD 的长度8、如图，点O 在直线AB 上，OD 平分COB ∠，3AOE EOC ∠=∠，50EOD ∠=︒，则BOD ∠=（ ）A ．10°B ．20°C ．30°D ．40°9、下列说法中，正确的是（ ）A ．一个锐角的补角大于这个角的余角B ．一对互补的角中，一定有一个角是锐角C ．锐角的余角一定是钝角D ．锐角的补角一定是锐角10、如图，OA 表示北偏东20°方向的一条射线，OB 表示南偏西50°方向的一条射线，则∠AOB 的度数是（ ）A ．110°B ．120°C ．140°D ．150°第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、南偏西25°：_________北偏西70°：_________南偏东60°：_________2、冬至是地球赤道以北地区白昼最短、黑夜最长的一天，在苏州有“冬至大如年”的说法．苏州冬至日正午太阳高度角是3524'︒，3524'︒的余角为__________︒．3、如图，上午8：30时，时针和分针所夹锐角的度数是___．4、如图，∠AOB =60°，∠AOC =40°，OD 、OE 分别平分AOB ∠和AOC ∠，则DOE ∠=______°．5、如图，直线AB ，CD 相交于点O ，31DOE BOE ∠=∠=︒，则1∠=__°．三、解答题（5小题，每小题10分，共计50分）1、已知∠AOB 是直角，∠AOC 是锐角，OC 在∠AOB 的内部，OD 平分∠AOC ，OE 平分∠BOC ．(1)根据题意画出图形；(2)求出∠DOE 的度数；(3)若将条件“∠AOB 是直角”改为“∠AOB 为锐角，且∠AOB ＝n °”，其它条件不变，请直接写出∠DOE 的度数．2、如图，直线AB 、CD 相交于点O ，70AOC ∠=︒，射线OE 把BOD ∠分成两个角，且:3:4BOE EOD ∠∠=．(1)求EOD ∠的度数．(2)过点O 作射线OF OE ⊥，求DOF ∠的度数．3、如图1，AOC ∠和BOD ∠都是直角．(1)如果35DOC ∠=︒，则AOB ∠=______；(2)找出图1中一组相等的锐角为：______；(3)若DOC ∠变小，AOB ∠将______；（填变大、变小、或不变）(4)在图2中，利用能够画直角的工具在图2上再画一个与BOC ∠相等的角．4、如图，在高速公路l的同一侧有A、B两座城市．(1)现在要以最低成本在A、B两座城市之间修建一条公路，假设每公里修建的成本相同，试在图中画出这条公路的位置，并简要说明你的依据；(2)若要在高速公路l边建一个停靠站C，使得A城市的人到该停靠点最方便（即距离最近），请在图中标出C的位置，并简要说明你的依据．5、如图，已知P，A，B三点，按下列要求完成画图和解答．(1)作直线AB；(2)连接PA，PB，用量角器测量∠APB＝．(3)用刻度尺取AB中点C，连接PC；(4)过点P画PD⊥AB于点D；(5)根据图形回答：在线段PA，PB，PC，PD中，最短的是线段的长度．理由：．-参考答案-一、单选题1、C【解析】【分析】先换算单位，再比较大小即可．【详解】解：1383638.6∠=︒'=︒，238.36∠=︒，338.6∠=︒，13∠∠∴=．故选：C ．【点睛】考查了度分秒的换算，解题的关键是将单位换算一致．2、A【解析】【分析】根据直角三角形30°角所对的直角边等于斜边的一半求出AC ，再根据垂线段最短求出AP 的最小值，然后得到AP 的取值范围，从而得解．【详解】解：∵∠C =90°，AB =8，∠B =30°，∴AC =12AB =12×8=4，∵点P 是BC 边上的动点，∴4＜AP ＜8，∴AP 的值不可能是3.5．故选：A ．【点睛】本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质，垂线段最短，熟记性质并求出AP 的取值范围是解题的关键．3、A【详解】解：图中与AOC ∠互为邻补角的是BOC ∠和AOD ∠，故选：A ．【点睛】本题考查了邻补角，熟练掌握邻补角的定义（两个角有一条公共边，且它们的另一边互为反向延长线，具有这种关系的两个角互为邻补角）是解题关键．4、C【解析】【分析】根据已知条件得到∠1+∠2=90°，∠2+∠3=180°，利用补角定义依次判断即可．【详解】解：∵90AOB ∠=︒，∴∠1+∠2=90°，∵直线b 经过点O ，∴∠2+∠3=180°，①1802︒-∠；②3∠是等于2∠的补角的式子，∵2（∠1+∠2）=180°，∴∠2=180°-（212∠+∠），故③符合题意；∵∠3=180°-∠2，∠1=90°-∠2，∴23212∠-∠-∠=2（180°-∠2）-2（90°-∠2）-∠2=1802︒-∠，故④符合题意；∵18012180︒-∠+∠≠︒，∴⑤不符合题意，【点睛】此题考查了补角的定义：相加得180度的两个角叫互为补角，根据图形对角度进行和差计算是解题的关键．5、C【解析】【分析】两个角的和为180,︒ 则这两个角互补，利用补角的含义直接列式计算即可.【详解】 解： 70A ∠=︒，∴ A ∠的补角18070110,故选C【点睛】本题考查的是互为补角的含义，掌握“两个角的和为180,︒ 则这两个角互补”是解本题的关键.6、C【解析】【分析】A 、由图形可得两角互余，不合题意；B 、由图形得出两角的关系，即可做出判断；C 、根据图形可得出两角都为45°的邻补角，可得出两角相等；D 、由图形得出两角的关系，即可做出判断．【详解】解：A 、由图形得：α+β＝90°，不合题意；B、由图形得：β+γ＝90°，α+γ＝60°，可得β﹣α＝30°，不合题意；C、由图形可得：α＝β＝180°﹣45°＝135°，符合题意；D、由图形得：α+45°＝90°，β+30°＝90°，可得α＝45°，β＝60°，不合题意．故选：C．【点睛】本题考查了等角的余角相等，三角尺中角度的计算，掌握三角尺中各角的度数是解题的关键．7、C【解析】【分析】直线外一点到直线的垂线段的长度，叫做点到直线的距离，根据点到直线的距离的定义解答即可．【详解】于D，∵CD AB∴点C到直线AB的距离是指线段CD的长度．故选：C．【点睛】本题考查了点到直线的距离的定义，点到直线的距离是一个长度，而不是一个图形，也就是垂线段的长度，而不是垂线段．8、A【解析】【分析】设∠BOD=x，分别表示出∠COD，∠COE，根据∠EOD=50°得出方程，解之即可．【详解】解：设∠BOD=x，∵OD平分∠COB，∴∠BOD=∠COD=x，∴∠AOC=180°-2x，∵∠AOE=3∠EOC，∴∠EOC=14∠AOC=18024x︒-=902x︒-，∵∠EOD=50°，∴90502xx︒-+=︒，解得：x=10，故选A．【点睛】本题考查角平分线的意义，通过图形表示出各个角，是正确计算的前提．9、A【解析】【分析】依据余角和补角的定义可作出判断．【详解】解：选项A ：一个锐角的补角为钝角，它的余角为锐角，故其补角大于其余角，选项A 正确； 选项B ：一对互补的角中，也可以两个角是直角，故B 错误；选项C ：锐角的余角一定是锐角，故C 错误；选项D ：锐角的补角一定是钝角，故D 错误．故选：A ．【点睛】本题主要考查的是补角和余角的定义，掌握补角和余角的定义是解题的关键．10、D【解析】【分析】首先根据已知的方向角的度数，得到余角的度数，然后再根据所求得的余角的度数即可得到AOB ∠的度数．【详解】解：标定字母如图所示：∵OA 表示北偏东20°方向的一条射线，OB 表示南偏西50°方向的一条射线，∴20EOA ∠=︒，50FOB ∠=︒，∴40DOB ∠=︒，∴209040150∠=∠+∠+∠=︒+︒+︒=︒AOB EOA EOD DOB ，故选：D ．【点睛】本题主要考查的是方向角及其计算的知识，熟练掌握余角的定义是解题的关键．二、填空题1、 射线OA 射线OB 射线OC【解析】略2、5436'︒【解析】【分析】两个角的和为直角，则称这两个角互为余角，简称互余，根据余角的概念即可求得结果．【详解】9035245436''︒-︒=︒故答案为：5436'︒【点睛】本题主要考查了余角的计算，掌握余角的概念是关键．3、75゜【解析】【分析】时针、分针转一小格转了30゜，转半格则旋转了15゜，分针要旋转2小格再加半格才能与时针重合，从而可求得时针和分针所夹锐角的度数．【详解】由图知，分针旋转一小格旋转30゜，分针要旋转2小格再加半格才能与时针重合，则时针和分针所夹锐角的度数是2×30゜+15゜=75゜；故答案为：75゜【点睛】本题考查了钟面角、角的度量与运算，掌握钟面角的特征是关键．4、50【解析】【分析】由OD 、OE 分别平分∠AOB 、∠AOC ．可得出∠AOE =∠EOC =12∠AOC ，∠DOB =∠AOD =12∠AOB ，进一步求出∠DOE 即可．【详解】解：∵OD 、OE 分别平分∠AOB 、∠AOC ，∠AOB =60°，∠AOC =40°，∴∠AOE =∠EOC =12∠AOC =20°，∠DOB =∠AOD =12∠AOB =30°，∴∠DOE =∠AOD +∠AOE =30°+20°=50°；故答案为：50．【点睛】本题考查了角平分线的意义，角的和与差，熟记各图形的性质并准确识图是解题的关键． 5、62【解析】【分析】先求出∠DOB 的值，然后根据对顶角相等求解即可．【详解】解：31DOE BOE ∠=∠=︒，313162∴∠=∠+∠=︒+︒=︒，DOB DOE BOD∠=∠，1DOB∴∠=︒，162故答案为62．【点睛】本题考查了角的和差，对顶角相等，正确识图是解答本题的关键．三、解答题1、 (1)见解析(2)45°n°(3)12【解析】【分析】（1）根据要求画出图形即可；（2）利用角平分线的定义计算即可；（3）利用（2）中，结论解决问题即可．(1)解：图形如图所示．，(2)解：∵OD平分∠AOC，OE平分∠BOC，∴∠DOC=12∠AOC，∠EOC=12∠BOC，∴∠DOE=12（∠AOC+∠BOC）=12∠AOB，∵∠AOB=90°，∴∠DOE=45°；(3)解：当∠AOB为锐角，且∠AOB=n°时，由（2）可知∠DOE=12 n°．【点睛】本题考查作图-复杂作图，角平分线的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题．2、(1)40°(2)50°或130°【解析】【分析】（1）根据对顶角相等可得∠BOD=∠AOC=70°，然后根据比例求解即可；（2）先求出∠DOE，再分OF在∠AOD的内部时，∠DOF=∠EOF-∠DOE，OF在∠BOC的内部时，∠DOF=∠EOF+∠DOE进行计算即可得解．(1)∵∠AOC=70°，∠BOD=∠AOC，∴∠BOD=70°，∵∠BOE：∠EOD=3：4，∴∠EOD=70°×434=40°；(2)如图：∵OF⊥OE，∴∠EOF=90°，当OF在∠AOD的内部时，∠DOF=∠EOF-∠DOE=90°-40°=50°，当OF在∠BOC的内部时，∠DOF=∠EOF+∠DOE=90°+40°=130°，综上所述∠DOF=50°或130°．【点睛】本题考查了对顶角相等的性质，角的计算，熟记概念并准确识图是解题的关键．3、 (1)145°(2)AOD BOC ∠=∠(3)变大(4)作图见解析【解析】【分析】（1）90AOC BOD ∠=∠=︒，9055BOC DOC ∠=︒-∠=︒，对AOB AOC BOC ∠=∠+∠计算求解即可；（2）由AOD AOC DOC ∠=∠-∠，=BOC BOD DOC ∠∠-∠，AOC BOD ∠=∠即可得到结果；（3）180AOB BOD AOD BOD AOC DOC DOC ∠=∠+∠=∠+∠-∠=︒-∠，可对DOC ∠变小时，AOB ∠的变化进行判断；（4）根据同角的余角相等，作∠COE =∠BOF =90°，则∠EOF 就是所求的角．(1)解：由题意知90AOC BOD ∠=∠=︒∵35DOC ∠=︒∴9055BOC DOC ∠=︒-∠=︒∴145AOB AOC BOC ∠=∠+∠=︒故答案为：145°．(2)解：AOD BOC ∠=∠∵AOC BOD ∠=∠∴AOD AOC DOC BOD DOC BOC ∠=∠-∠=∠-∠=∠故答案为：AOD BOC ∠=∠．(3)解：变大∵180AOB BOD AOD BOD AOC DOC DOC ∠=∠+∠=∠+∠-∠=︒-∠∴当DOC ∠变小，AOB ∠将变大故答案为：变大．(4)如图：作∠COE =∠BOF =90°，则∠EOF 即为所求．【点睛】本题考查了角的计算，余角的性质等知识．解题的关键在于正确的表示角的数量关系．4、 (1)图见解析，两点之间，线段最短(2)图见解析，垂线段最短【解析】【分析】（1）根据两点之间，线段最短画图解答即可；（2）根据垂线段最短画图解答即可．(1)这条公路的位置如图所示，我的依据是“两点之间，线段最短”．(2)点C的位置如图所示，我的依据是“垂线段最短”．【点睛】本题考查最短路径问题及垂线段最短，解题关键是掌握两点之间，线段最短及垂线段最短．5、 (1)见解析(2)90°(3)见解析(4)见解析(5)PD，垂线段最短【解析】【分析】（1）根据直线的特点画图即可；（2）用量角器量取即可；（3）根据中点的定义解答；（4）用三角板的两条直角边画图即可；（5）根据垂线段最短解答．(1)如图，直线AB即为所求作．(2)测量可知，∠APB＝90°．故答案为：90°．(3)如图，线段PC即为所求作．(4)如图，线段PD即为所求作．(5)根据垂线段最短可知，线段PD最短，故答案为：PD，垂线段最短．【点睛】本题考查了直线，射线，线段等知识，以及线段的中点，垂线的性质，解题的关键是理解题意，灵活运用所学知识解决问题．。

8.2角的比较一．选择题（共10小题）1．（2014秋•故城县校级月考）如图，如果∠CAE＞∠BAD，那么下列说法中一定正确的是（）A．∠BAC＞∠CAD B．∠DAE＞∠CADC．∠CAE＜∠BAC+∠DAE D．∠BAC＜∠DAE（1题图）（7题图）（8题图）（10题图）2．（2014秋•故城县校级月考）将∠1、∠2的顶点和其中一边重合，另一边都落在重合边的同侧，且∠1＞∠2，那么∠1的另一边落在∠2的（）A．另一边上B．内部C．外部D．无法判断3．（2015•江东区模拟）下列角度中，比20°小的是（）A．19°38′B．20°50′C．36.2°D．56°4．（2014秋•潜山县期末）在∠AOB的内部任取一点C，作射线OC，则一定存在（）A．∠AOB＞∠AOC B．∠AOB＜∠BOC C．∠BOC＞∠AOC D．∠AOC＞∠BOC5．比较∠CAB与∠DAB时，把它们的顶点A和边AB重合，把∠CAB和∠DAB放在AB的同一侧，若∠CAB＞∠DAB，则（）A．AD落在∠CAB的内部B．AD落在∠CAB的外部C．AC和AD重合D．不能确定AD的位置6．（2014秋•太谷县校级期末）若∠1=40.4°，∠2=40°4′，则∠1与∠2的关系是（）A．∠1=∠2B．∠1＞∠2C．∠1＜∠2D．以上都不对7．如图，小于平角的角共有（）A．10个B．9个C．8个D．4个8．如图．∠AOB=∠COD，则（）A．∠1＞∠2B．∠1=∠2C．∠1＜∠2D．∠1与∠2的大小无法比较9．下列说法错误的是（）A．角的大小与角的边的长短无关B．角的大小和它们的度数大小是一致的C．角的平分线是一条直线D．如果C点在∠AOB的内部，那么射线OC上所有的点都在∠AOB的内部10．（2014秋•定兴县期末）如图，射线OB、OC将∠AOD分成三部分，下列判断错误的是（）A．如果∠AOB=∠COD，那么∠AOC=∠BODB．如果∠AOB＞∠COD，那么∠AOC＞∠BODC．如果∠AOB＜∠COD，那么∠AOC＜∠BODD．如果∠AOB=∠BOC，那么∠AOC=∠BOD二．填空题（共10小题）11．（2014秋•开封期末）如图所示，其中最大的角是，∠DOC，∠DOB，∠DOA 的大小关系是．（11题图）（14题图）（15题图）（16题图）12．（2014秋•晋安区期末）比较两个角度的大小：35.30°35°30′（用“＞”，“＜”或“=”填空）13．（2014秋•云南校级月考）若∠A=∠B，∠B=2∠C，则∠A2∠C（填＜，＞或=）．14．（2014秋•厦门月考）如图，∠AOB、∠COD都是直角，那么∠DOB与∠AOC的大小关系是∠DOB∠AOC．15．如图，∠AOB=90°，OD平分∠BOC，∠DOE=45°，则∠AOE∠COE（填“＜”“＞”或“=”号）16．如图，图中小于平角的角共有个，其中能用一个大写字母表示的角是．17．如图，小于平角的角有个，最大的一个角是．（17题图）（18题图）（20题图）18．如图，AOB为一直线，OC，OD，OE是射线，则图中大于0°小于180°的角有个．19．已知∠α是直角，∠β是钝角，∠γ是锐角，则用“＜”号将三个角连接起来是．20．如图，AOE是一条直线，∠AOC＞∠COE，OB是∠AOC的角平分线，OD是∠COB的角平分线，则图中的钝角共有个．三．解答题（共2小题）21．（2014秋•郯城县期末）如图，将两块三角板的顶点重合．（1）请写出图中所有以O点为顶点且小于平角的角；（2）你写出的角中相等的角有；（3）若∠DOC=53°，试求∠AOB的度数；（4）当三角板AOC绕点O适当旋转（保持两三角板有重合部分）时，∠AOB与∠DOC之间具有怎样的数量关系？22．如图，∠BOD=90°，∠COE=90°，解答下列问题：（1）图中有哪些小于平角的角？用适当的方法表示出它们．（2）比较∠AOC、∠AOD、∠AOE、∠AOB的大小，并指出其中的锐角、钝角、直角、平角．（3）找出图中所有相等的角．23、如图，AO⊥OC，解答下列问题：①比较∠AOB、∠AOC、∠AOD、∠A OE的大小，并指明其中的锐角、直角、钝角及平角；②写出∠AOB、∠AOC、∠BOC、∠AOE中某些角之间的两个等量关系．24、（2014秋•甘州区校级月考）把一副三角尺如图所示拼在一起．（1）写出图中∠A、∠B、∠BCD、∠D、∠AED的度数；（2）用小于号“＜”将上述各角连接起来．25、（2014秋•钟山区期末）观察、探究与思考．根据图，求解下列问题：（1）比较∠AOB、∠AOC、∠AOD、∠AOE、的大小，并指出其中的锐角、直角、钝角、平角．（2）写出∠AOB、∠AOC、∠BOC、∠AOE中某些角之间的两个等量关系．青岛版七年级数学下册第8章8.2角的比较同步训练题参考答案一．选择题（共10小题）1．D 2．C 3．A 4．A 5．A 6．B 7．B 8．B 9．C 10．D 二．填空题（共10小题）11．∠AOD∠DOA＞∠DOB＞∠DOC12．＜13．= 14．=15．= 16．7∠B，∠C17．7∠ACB18．9 19．∠γ＜∠α＜∠β20．3三．解答题（共2小题）21．解：（1）图中所有以O点为顶点且小于平角的角有∠AOD，∠AOC，∠AOB，∠DOC，∠DOB，∠COB．（2）图中相等的角有∠AOC=∠DOB，∠AOD=∠COB，故答案为：∠AOC=∠DOB，∠AOD=∠COB．（3）∵∠DOC=53°，∠AOC=90°，∴∠AOD=90°﹣53°=37°，∵∠DOB=90°，∴∠AOB=∠AOD+∠DOB=90°+37°=127°．（4）∠AOB=180°﹣∠DOC，理由是：∵∠AOC=90°，∴∠AOD=90°﹣∠DOC，∵∠DOB=90°，∴∠AOB=∠AOD+∠DOB=90°﹣∠DOC+90°=180°﹣∠DOC，即∠AOB=180°﹣∠DOC．22．解：（1）图中小于平角的角有∠AOC、∠AOD、∠AOE、∠COD、∠COE、∠DOE、∠DOB、∠EOB；（2）由图可知，∠AOC＜∠AOD＜∠AOE＜∠AOB，其中∠AOC为锐角，∠AOD为直角，∠AOE为钝角，∠AOB为平角；（3）∠AOC=∠DOE，∠COD=∠BOE，∠AOD=∠BOD=∠COE．23、解：（1）∠AOB＜∠AOC＜∠AOD＜∠AOE，∵AE⊥OC，∴∠AOC=90°，∴∠AOB是锐角，∠AOC是直角，∠AOD是钝角，∠AOE是平角；（2）∠AOB+∠BOC=∠AOC，∠AOB+∠BOC+∠AOC=∠AOE．24、解：（1）∠A=30°，∠B=90°，∠BCD=150°，∠D=45°，∠AED=135°；（2）∠A＜∠D＜∠B＜∠AED＜∠BCD．25、解：（1）根据图形可得：∠AOB＜∠AOC＜∠AOD＜∠AOE；锐角的是∠AOB，直角的是∠AOC，钝角的是∠AOD，平角的是∠AOE；（2）根据图形可得：∠AOB=∠AOC﹣∠BOC；∠AOB+∠BOC+∠AOC=∠AOE；。

初中数学青岛版七年级下册第8章8.2角的比较练习题（无答案）一、选择题1.已知射线OC在∠AOB的内部，下列4个表述中：①∠AOC=12∠AOB ②∠AOC=∠BOC③∠AOB=2∠BOC④∠AOC+∠BOC=∠AOB，能表示射线OC是∠AOB的角平分线的有()．A. 1个B. 2个C. 3个D. 4个2.下列说法中，正确的个数有()①过两点有且只有一条直线；②连接两点的线段叫做两点间的距离；③两点之间，线段最短；④若∠AOC=2∠BOC，则OB是∠AOC的平分线．A. 1个B. 2个C. 3个D. 4个3.如图∠AOB=60°，射线OC平分∠AOB，以OC为一边作∠COP=15°，则∠BOP=()A. 15°B. 45°C. 15°或30°D. 15°或45°4.如图所示，已知∠AOB=90°，∠BOC=30°，OM平分∠AOC，ON平分∠BOC，则∠MON的度数为()A. 30°B. 45°C. 60°D. 75°5.射线OC在∠AOB内部，下列条件不能说明OC是∠AOB的平分线的是()A. ∠AOC=12AOB B. ∠BOC=12∠AOBC. ∠AOC+∠BOC=∠AOBD. ∠AOC=∠BOC6.如图，∠AOB=∠COD，则()第1页，共6页A. ∠1>∠2B. ∠1=∠2C. ∠1<∠2D. ∠1与∠2的大小无法比较7.从点O引出三条射线OA，OB，OC，已知∠AOB=30°，在这三条射线中，当其中一条射线是另两条射线所组成角的平分线时，则∠AOC=()A. 30°B. 60°C. 15°或30°或60°D. 15°或30°或45°或60°8.已知三条不同的射线OA、OB、OC，有下列条件，其中能确定OC平分∠AOB的有()①∠AOC=∠BOC②∠AOB=2∠AOC③∠AOC+∠COB=∠AOB④∠BOC=12∠AOBA. 1个B. 2个C. 3个D. 4个9.如图，直线AB、CD相交于点O，射线OM平分∠AOC，∠MON=90∘.若∠MOC=35∘，则∠BON的度数为()A. 35∘B. 45∘C. 55∘D. 64∘10.下列说法正确的个数有①两点之间，直线最短.②直线AB可以写成直线BA.③如果AC=BC，那么C是线段AB的中点．④从一个顶点引出三条射线，形成的角有3个．⑤在∠AOB的内部，射线OC分得∠AOC=∠BOC，那么OC是∠AOB的平分线．A. 1个B. 2个C. 3个D. 4个二、填空题11.如图，点A、O、B在一条直线上，∠AOC=130°，OD是∠BOC的平分线，则∠COD=______度．12.如图，点O是直线AD上一点，射线OC，OE分别平分∠AOB、∠BOD.若∠AOC=28°，则∠BOE=______．13.如图，OM，ON平分∠AOB和∠BOC，∠MON=60°，那么∠AOC=______．14.如图，已知O是直线AB上一点，∠1=40°，OD平分∠BOC，则∠2的度数是______．三、解答题15.如图①，已知线段AB=12cm，点C为AB上的一个动点，点D、E分别是AC和BC的中点．(1)若点C恰好是AB中点，则DE=______ cm；(2)若AC=4cm，求DE的长；(3)若AC的长表示为a cm，试说明不论a为何值(不超过12cm)，DE的长不变；(4)知识迁移：如图②，已知∠AOB=120°，过角的内部任一点C画射线OC，若OD、OE分别平分∠AOC和∠BOC，试说明∠DOE=60°与射线OC的位置无关．第3页，共6页16.如图，射线OA的方向是北偏东15°，射线OB的方向是北偏西40°，OA是∠BOC的平分线，射线OD是OB的反向延长线．(1)射线OD的方向是______；(2)在图中画出表示南偏东75°的射线OE；(3)在(2)的条件下，求∠COE的度数．17.如图，在△ABC 中，．(1)尺规作图：作的平分线交BC于点D.(不写作法，保留作图痕迹)；(2)已知，求的度数．18.如图，已知∠AOB=108°，OE是∠AOB的平分线，OC在∠AOE内．∠AOE，求∠AOC的度数；(1)若∠COE=13(2)若∠BOC−∠AOC=72°，则OB与OC有怎样的位置关系？为什么？第5页，共6页。

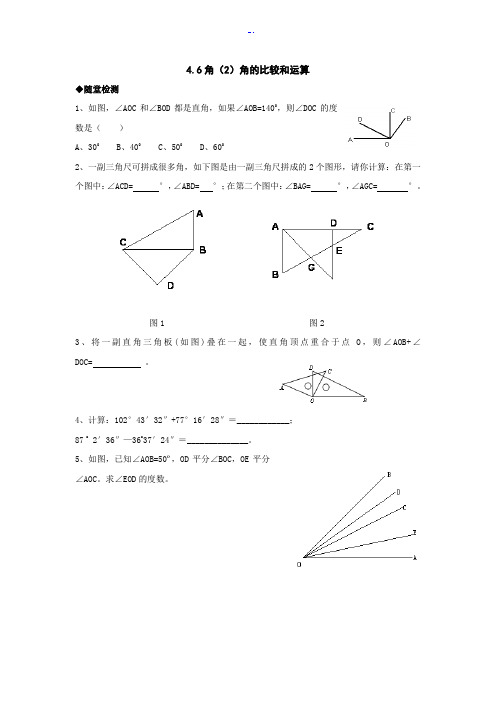
4.6角（2）角的比较和运算◆随堂检测1、如图，∠AOC和∠BOD都是直角，如果∠AOB=1400，则∠DOC的度数是（）A、300B、400C、500D、6002、一副三角尺可拼成很多角，如下图是由一副三角尺拼成的2个图形，请你计算：在第一个图中：∠ACD= °，∠ABD= °；在第二个图中：∠BAG= °，∠AGC= °。

图1 图23、将一副直角三角板(如图)叠在一起，使直角顶点重合于点O，则∠AOB+∠DOC= 。

4、计算：102°43′32″+77°16′28″＝____________；87 o2′36″—36o37′24″＝______________。

5、如图，已知∠AOB=50º，OD平分∠BOC，OE平分∠AOC。

求∠EOD的度数。

◆典例分析例：如图，（1）已知∠AOB 是直角，∠BOC=30°，OM 平分∠AOC ，ON 平分∠BOC ，求∠MON 般性的规律。

◆课下作业●拓展提高1、平面内两个角∠AOB=60°，∠AOC=20°，OA 为两角的公共边，则∠BOC 为（ ） A 、40° B、80° C、40°或80° D、无法确定2、下面一些角中，可以只用一副三角尺（不用量角器）画出来的角是（ ） （1）150的角 （2）650的角 （3）750的角 （4）1350的角 （5）1450的角 A 、（1）（3）（4） B 、（1）（3）（5） C 、（1）（2）（4） D 、（2）（4）（5） 3、已知：∠A=50º24’，∠B=50.24º，∠C =50º14’24”，那么下列各式正确的是（ ） A 、∠A>∠B>∠C B 、∠A>∠B=∠C C 、∠B>∠C>∠A D 、∠B=∠C>∠A 4、如图，BO 、CO 分别平分∠ABC 和∠ACB ，已知任意三角形的3个内角的和都是180°，若∠A ＝80°，你能求出∠BOC 的度数吗？试试看。

七年级数学《角的比较》同步练习题一、填空:1.如图1,∠AOB______∠AOC,∠AOB_______∠BOC(填>,=,<); 用量角器度量∠BOC=____°,∠AOC=______°,∠AOC______∠BOC.OC(1)AB O DC(2)ABOD C (3)A B2.如图2,∠AOC=______+______=______-______;∠BOC=______-______= _____-________.3.OC 是∠AOB 内部的一条射线,若∠AOC=12________,则OC 平分∠AOB;若OC 是∠AOB 的角平分线,则_________=2∠AOC. 二、选择：4.下列说法错误的是( )A.角的大小与角的边画出部分的长短没有关系；B.角的大小与它们的度数大小是一致的；C.角的和差倍分的度数等于它们的度数的和差倍分；D.若∠A+∠B>∠C,那么∠A 一定大于∠C 。

5.用一副三角板不能画出( )A.75°角B.135°角C.160°角D.105°角 6.如图3,若∠AOC=∠BOD,那么∠AOD 与∠BOC 的关系是( )A.∠AOD>∠BOCB.∠AOD<∠BOC;C.∠AOD=∠BOCD.无法确定 7.如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是( ) A.∠3>∠4 B.∠3=∠4; C.∠3<∠4 D.不确定8.OC 是从∠AOB 的顶点O 引出的一条射线,若∠AOB=90°,∠AOB= 2∠BOC, 求∠AOC 的度数.9.如图,把∠AOB 绕着O 点按逆时针方向旋转一个角度, 得∠A ′OB ′,指出图中所有相等的角,并简要说明理由.OABB 'A '10.如图,BD 平分∠ABC,BE 分∠ABC 分2:5两部分,∠DBE=21°,求∠ABC 的度数.D CAE11.如图,已知∠α、∠β ,画一个角∠γ，使∠γ=3∠β-12∠α.βα12.如图,A 、B 两地隔着湖水,从C 地测得CA=50m,CB=60m,∠ACB=145°,用1 厘米代表10米(就是1:1000的比例尺)画出如图的图形.量出AB 的长(精确到1毫米), 再换算出A 、B 间的实际距离.AB13.如图,∠AOB 是平角,OD 、OC 、OE 是三条射线,OD 是∠AOC 的平分线, 请你补充一个条件,使∠DOE=90°,并说明你的理由.OD CAE B答案: 1．略。

青岛版七年级数学下册第8章角同步训练考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、如图，已知AO⊥OC，OB⊥OD，∠COD=38°，则∠AOB的度数是（）A．30ºB．145ºC．150ºD．142º2、如图，BD在∠ABC的内部，∠ABD＝13∠CBD，如果∠ABC＝80°，则∠ABD＝（）A ．80()3︒B ．20°C ．60°D ．160()3︒ 3、小光准备从A 地去往B 地，打开导航显示两地距离为39.6km ，但导航提供的三条可选路线长却分别为52km ，53km ，56km （如图）．能解释这一现象的数学知识是（ ）A ．两点之间，线段最短B ．两点确定一条直线C ．垂线段最短D ．过一点有且只有一条直线与已知直线垂直4、下列说法：①射线AB 与射线BA 是同一条射线；②两点确定一条直线；③把一个角分成两个角的射线叫角的平分线；④若线段AM 等于线段BM ，则点M 是线段AB 的中点；⑤连接两点的线段叫做这两点之间的距离．其中正确的个数为（ ）A ．1个B ．2个C ．3个D ．4个5、如图所示，AOB ∠是平角，OC 是射线，OD 、OE 分别是AOC ∠、BOC ∠的角平分线，若28COE ∠=︒，则AOD ∠的度数为（ ）A ．56°B ．62°C ．72°D ．124°6、已知α与β互为余角，若20α=︒，则β的补角的大小为（ ）A ．70︒B ．110︒C ．140︒D ．160︒7、如图，直线AB 与CD 相交于点O ，若1280∠+∠=︒，则1∠等于（ ）A ．40°B ．60°C ．70°D ．80°8、如图，AC BC ⊥，直线EF 经过点C ，若134∠=︒，则2∠的大小为（ ）A ．56°B ．66°C ．54°D ．46°9、如图，∠AOC 和∠BOD 都是直角，如果∠DOC ＝38°，那么∠AOB 的度数是（）A ．128°B ．142°C ．38°D ．152°10、下列说法正确的是（ ）A ．锐角的补角不一定是钝角B ．一个角的补角一定大于这个角C ．直角和它的的补角相等D ．锐角和钝角互补第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、如图，上午8：30时，时针和分针所夹锐角的度数是___．2、一个角比它的补角的3倍多40°，则这个角的度数为______．3、如图，将三个形状、大小完全一样的正方形的一个顶点重合放置，若4126GAF '∠=︒，2524BAC '∠=︒，则DAE =∠_____．4、已知∠α和∠β互为补角，并且∠β的一半比∠α小30°，则∠α＝_____，∠β＝_____．5、已知α∠的补角是13739'︒，则α∠的余角度数是______°．（结果用度表示）三、解答题（5小题，每小题10分，共计50分）1、已知∠AOB 是直角，∠AOC 是锐角，OC 在∠AOB 的内部，OD 平分∠AOC ，OE 平分∠BOC ．(1)根据题意画出图形；(2)求出∠DOE 的度数；(3)若将条件“∠AOB 是直角”改为“∠AOB 为锐角，且∠AOB ＝n °”，其它条件不变，请直接写出∠DOE 的度数．2、如图，已知90AOB ∠=︒，60EOF ∠=︒，OE 平分AOB ∠，OF 平分BOC ∠，求AOC ∠的度数．3、如图，将两块三角板的直角顶点重合．(1)写出以C为顶点相等的角；(2)若∠ACB＝150°，求∠DCE的度数．4、如图，点O是直线AB上的一点，∠COD是直角，OE平分∠BOC．(1)如图（1），若∠AOC=40°，求∠DOE的度数；(2)如图（2），若∠COE=∠DOB，求∠AOC的度数．5、如图，直线AB和直线CD交于O点，EO AB，(1)若2EOC COB∠=∠，求AOD∠的度数．(2)作OF CD⊥，证明：EOF COB∠=∠．-参考答案-一、单选题1、D【解析】【分析】根据垂直的定义得到∠AOC=∠DOB=90°，由互余关系得到∠BOC=52°，然后计算∠AOC+∠BOC即可．【详解】解：∵AO⊥OC，OB⊥OD，∴∠AOC=∠DOB=90°，而∠COD=38°，∴∠BOC=90°-∠COD=90°-38°=52°，∴∠AOB=∠AOC+∠BOC=90°+52°=142°．故选：D．【点睛】本题考查了余角的概念：若两个，角的和为90°，那么这两个角互余．2、B【解析】【分析】根据角的和差与倍分得出∠ABC=4∠ABD，列方程求解即可．【详解】解：∵∠ABD＝13∠CBD，∴∠CBD=3∠ABD，∵∠ABC=∠CBD+∠ABD=3∠ABD+∠ABD=4∠ABD=80°，∴ABD=20°．故选择B．【点睛】本题考查角的倍分，角的和差，一元一次方程，掌握角的倍分关系，角的和差计算，解一元一次方程是解题关键．3、A【解析】【分析】根据线段的性质可得答案．【详解】解：打开导航显示两地距离为39.6km，但导航提供的三条可选路线长却分别为52km，53km，56km （如图）．能解释这一现象的数学知识是两点之间，线段最短．A、故选项正确，符合题意；B、故选项错误，不符合题意；C、故选项错误，不符合题意；D、故选项错误，不符合题意．故选：A．【点睛】此题考查了线段的性质，解题的关键是熟记线段的性质并应用．4、A【解析】【分析】根据射线定义可判断①，根据直线公理可判断②，根据角平分线的定义可判断③，根据线段中点定义可判断④，根据两点之间距离定义可判断⑤．【详解】解：射线AB与射线BA的起点不同方向不同，不是同一条射线，故①不正确；经过两点，有且只有一条直线，两点确定一条直线，故②正确；把一个角分成两个相等的角的射线叫角的平分线，故③不正确；若线段AM等于线段BM，当点A、M、B三点共线时，点M是线段AB的中点，当A、M、B三点不一定在一条直线上，则点M不一定是线段AB的中点，故④不正确；连接两点的线段的长度叫做这两点之间的距离，线段即有形状又有数量，而两点之间的距离只有数量，故⑤不正确．所以正确的说法有1个．故选A．【点睛】本题考查射线识别，直线公理，角平分线的定义，线段中点，两点之间距离，掌握射线定义与特征，直线公理，角平分线的定义，线段中点，两点之间距离是解题关键．5、B【解析】【分析】根据OE 平分BOC ∠可求得∠BOC 的度数，由∠AOC 与∠BOC 互补即可得到∠AOC 的度数，由OD 平分∠AOC ， 即可求得∠AOD 的度数．【详解】∵OE 平分BOC ∠∴∠BOC =2∠COE =2×28°=56°∵∠AOC +∠BOC =180°∴∠AOC =180°−∠BOC =124°∵OD 平分AOC ∠ ∴111246222AOD AOC ∠=∠=⨯︒=︒故选：B【点睛】本题考查了角平分线的性质、互补等知识，角平分线的性质熟练掌握相关知识点是关键．6、B【解析】【分析】根据90βα=︒-求得β，根据180β︒-求得β的补角【详解】解：∵α与β互为余角，若20α=︒，∴9070βα=︒-=︒∴180β︒-110=︒故选B【点睛】本题考查了求一个角的余角、补角，解题的关键是理解互为余角的两角之和为90︒，互为补角的两角之和为180︒．7、A【解析】【分析】根据对顶角的性质，可得∠1的度数．【详解】解：由对顶角相等，得∠1=∠2，又∠1+∠2=80°，∴∠1=40°．故选：A ．【点睛】本题考查的是对顶角，掌握对顶角相等这一性质是解决此题关键．8、A【解析】【分析】根据，∠1，∠2，和∠ACB 为180°，且∠ACB 为90°，所以∠1和∠2互余，由∠1度数可求出∠2度数．【详解】解：∵AC BC ⊥，∴90ACB ∠=︒，∵由图可知12180ACB ∠+∠+∠=︒，且90ACB ∠=︒，∴1290∠+∠=︒，∴2901903456∠=︒-∠=︒-︒=︒，故选：A ．【点睛】本题考查，补角与余角的概念，能够根据图形中的角的位置关系求出角的度数关系式解决本题的关键．9、B【解析】【分析】首先根据题意求出52AOD ∠=︒，然后根据AOB AOD BOD ∠=∠+∠求解即可．【详解】解：∵∠AOC 和∠BOD 都是直角，∠DOC ＝38°，∴903852AOD AOC DOC ∠=∠-∠=︒-︒=︒，∴5290142AOB AOD BOD ∠=∠+∠=︒+︒=︒．故选：B ．【点睛】此题考查了角度之间的和差运算，直角的性质，解题的关键是根据直角的性质求出AOD ∠的度数．10、C【解析】【分析】根据余角和补角的概念判断即可．解：A、因为锐角的补角与锐角之和为180°，所以锐角的补角一定是钝角，所以本说法不符合题意；B、当这个角为120°时，120°的补角是60°，所以本说法不符合题意；C、根据直角的补角是直角．所以本说法符合题意；D、锐角和钝角的度数不确定，不能确定锐角和钝角是否互补，所以本说法不符合题意；故选：C．【点睛】本题考查的是余角和补角的概，如果两个角的和等于90°，就说这两个角互为余角；如果两个角的和等于180°，就说这两个角互为补角．二、填空题1、75゜【解析】【分析】时针、分针转一小格转了30゜，转半格则旋转了15゜，分针要旋转2小格再加半格才能与时针重合，从而可求得时针和分针所夹锐角的度数．【详解】由图知，分针旋转一小格旋转30゜，分针要旋转2小格再加半格才能与时针重合，则时针和分针所夹锐角的度数是2×30゜+15゜=75゜；故答案为：75゜【点睛】本题考查了钟面角、角的度量与运算，掌握钟面角的特征是关键．2、145 ##145度【解析】设这个角的补角的度数为x ，则这个角的度数为180x ︒- ，根据“一个角比它的补角的3倍多40°，”列出方程，即可求解．【详解】解：设这个角的补角的度数为x ，则这个角的度数为180x ︒- ，根据题意得：180340x x ︒--=︒ ，解得：35x =︒ ，∴这个角的度数为180145x ︒-=︒．故答案为：145︒【点睛】本题主要考查了补角的性质，一元一次方程的应用，利用方程思想解答是解题的关键．3、2310'︒【解析】【分析】首先求得DAF ∠和∠EAC ，然后根据90DAEDAF EAC 即可求解．【详解】解：∵将三个形状、大小完全一样的正方形的一个顶点重合放置，∴ FAC ∠=∠GAD =∠EAB =90°， 4126GAF '∠=︒，2524BAC '∠=︒，∴909041264834,DAF GAF 909025246436,EAC BAC ∴90483464369011310902310,DAE DAF EAC 故答案为：2310'︒本题考查的是角的和差关系，角度的加法运算，掌握“角的和差关系与角度的加法运算”是解本题的关键.4、 80°##80度 100°##100度【解析】【分析】根据互为补角的和等于180°，得到α=180°-β，然后根据题意列出关于β的一元一次方程，求解即可．【详解】解：∵∠α和∠β互为补角，∴α=180°-β，根据题意得，180°-β-12β=30°，解得β=100°， α=180°-β=80°，故答案为：80°，100°．【点睛】本题考查了互为补角的和等于180°的性质，根据题意列出一元一次方程是解题的关键． 5、47.65【解析】【分析】根据180°-13739'︒求得α∠，根据90α︒-∠即可求得答案【详解】解：∵α∠的补角是13739'︒，∴α∠18013739'=︒-︒∴α∠的余角为90α︒-∠()9018013739'=︒-︒-︒1373990'=︒-︒4739'=︒ 3939=0.6560'=︒ ∴4739'︒47.65=︒故答案为：47.65【点睛】本题考查了求一个角的补角和余角，角度进制转换，正确的计算是解题的关键．三、解答题1、 (1)见解析(2)45°(3)12n °【解析】【分析】（1）根据要求画出图形即可；（2）利用角平分线的定义计算即可；（3）利用（2）中，结论解决问题即可．(1)解：图形如图所示．，(2)解：∵OD平分∠AOC，OE平分∠BOC，∴∠DOC=12∠AOC，∠EOC=12∠BOC，∴∠DOE=12（∠AOC+∠BOC）=12∠AOB，∵∠AOB=90°，∴∠DOE=45°；(3)解：当∠AOB为锐角，且∠AOB=n°时，由（2）可知∠DOE=12 n°．【点睛】本题考查作图-复杂作图，角平分线的定义等知识，解题的关键是理解题意，灵活运用所学知识解决问题．2、120°【解析】【分析】根据角平分线的定义得到∠BOE=12∠AOB=45°，∠BOC=2∠BOF，再计算出∠BOF=∠EOF-∠BOE=15°，然后根据∠BOC=2∠BOF，∠AOC=∠BOC+∠AOB进行计算．【详解】解：∵OE平分∠AOB，OF平分∠BOC，∴∠BOE=12∠AOB=12×90°=45°，∠BOC=2∠BOF，∵∠BOF=∠EOF-∠BOE=60°-45°=15°，∴∠BOC=2∠BOF=30°；∠AOC=∠BOC+∠AOB=30°+90°=120°．【点睛】本题主要考查了角的计算以及角平分线的定义，正确应用角平分线的定义是解题关键．3、(1)∠ACE=∠BCD，∠ACD=∠ECB(2)30°【解析】【分析】（1）根据余角的性质即可得到结论；（2）根据角的和差即可得到结论．(1)∵∠ACD=∠BCE=90°，∴∠ACE+∠DCE=∠BCD+∠DCE=90°，∴∠ACE=∠BCD；∠ACD=∠ECB=90°(2)∵∠ACB=150°，∠BCE=90°，∴∠ACE=150°－90°=60°.∴∠DCE=90°－∠ACE=90°－60°=30°【点睛】本题考查了余角和补角，关键是熟练掌握余角的性质，角的和差关系．4、(1)∠DOE的度数为20°；(2)∠AOC的度数为120°．【解析】【分析】（1）先求得∠BOC，再根据角平分线的性质得出∠COE，根据余角的性质得出∠DOE的度数；（2）根据角平分线的定义得到∠COE=∠BOE，于是得到∠COE=∠BOE=∠DOB=30°，然后根据平角的定义即可得到结论．(1)解：∵∠AOC+∠BOC=180°，∴∠BOC=180°-∠AOC=180°-40°=140°，∵OE平分∠BOC，∴∠COE=12∠BOC=12×140°=70°，∵∠COD是直角，∴∠COE+∠DOE=90°，∴∠DOE=90°-∠COE=90°-70°=20°；(2)解：∵OE平分∠BOC，∴∠COE=∠BOE，∵∠COE=∠BOD，∴∠COE=∠BOE=∠DOB，∵∠COD=90°，∴∠COE=∠BOE=13×90°=30°，∴∠AOC=180°-30°-30°=120°．【点睛】本题考查了角平分线的定义，是基础题，难度不大，掌握各角之间的关系是解题的关键．5、 (1)见解析(2)见解析【解析】【分析】（1）根据EO⊥AB，可得∠EOB=∠EOC+∠COB=90°，再根据2∠EOC=∠COB，即可求出AOD的度数．（2）根据EO⊥AB，FO⊥CD，可得∠EOC+∠COB=∠EOF+∠EOC=90°，即可得证∠COB=∠EOF．(1)解：∵EO⊥AB∴∠EOB=∠EOC+∠COB=90°∵2∠EOC=∠COB∴3∠EOC=90°∴∠EOC=30°∴∠AOD=∠COB=2∠EOC=60°(2)证明：∵EO⊥AB，FO⊥CD∴∠EOC+∠COB=∠EOF+∠EOC=90°∴∠COB=∠EOF【点睛】此题考查了角度的计算以及证明，解题的关键是掌握垂直的定义以及性质、对顶角相等．。

青岛版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！青岛版初中数学和你一起共同进步学业有成！8.2 角的比较 同步练习1．下列说法错误的是（ ）A ．角的大小与角的两边的长短无关B ．角的大小与它们的度数的大小是一致的C ．角的平分线是一条直线D ．角的和、差、倍、分的度数，等于它的度数的和、差、倍分2．已知是从顶点O 引出的一条射线，若，则OC AOB ,60︒=∠︒=∠20BOC 的度数为（ ）AOC ∠ A ．40° B ．80° C ．20°或80° D ．40°或80°3．已知平分，且，则与的关系为OC AOB ,3α∠=∠AOB ∠︒=∠60αAOC ∠α∠（ ）A ．B ． α∠=∠3AOB α∠=∠2AOC C ．D ． α∠=∠23AOC α∠=∠34AOC 4．如图，已知，射线OE 、OF 分别平分4:3:2::=∠∠∠COD BOC AOB AOB ∠和，且，则的度数为（ ）COD ∠︒=∠90EOF AOB ∠A ．20°B ．30°C ．40°D ．45°5．如图，已知，则等于βα∠=∠∠=∠︒=∠=∠BOC AOD COD AOB ,,90βα+（ ）A ．180°B ．120°C ．90°D ．不能确定6．如图，OC 是的平分线，OB 是的平分线，且，则BOD ∠AOD ∠ 30=∠COD 等于（ ）AOC ∠A ．60°B ．80°C ．90°D ．120°填空题：1．如图所示，则．________________∠-∠=∠+∠=∠AOC2．如图所示，已知，则，又如果，则322,221∠=∠∠=∠3____1∠=∠43∠=∠．2____4∠=∠3．已知是的平分线，OF 为的平分OE BOC AOB ,40,60︒=∠︒=∠AOB ∠BOC ∠线，则． ____=∠EOF 解答题：1．如图，是∠BOD 的平分线，OD 平分∠AOC ，请你观察图OC BOD ,90︒=∠中相等的角有几对？2．若＝25°12′，＝25.12°，＝25.2°，试比较的大小． αβγγβα,,3．已知，你知道∠AOC 的度数是多少吗？ ︒=∠︒=∠30,45BOC AOB 4．如图，OC 平分∠AOB ，OD 是∠BOC 内的一条射线，且BOD COD ∠=∠21，试判断∠AOB 是∠COD 的几倍？参考答案： 选择题：1．C 2．D 3．C 4．B 5．A 6．C 填空题：1．COD AOD BOC AOB ∠∠∠∠,,,2．4，213．10°或50° 解答题：1．，AOB COD AOD COD BOD AOB AOC BOC ∠-∠-∠=∠-∠=∠-∠=∠COD AOD BOC AOB AOC ∠-∠=∠+∠=∠2．3对3．βγα∠>∠=∠4．75°或15°相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

青岛版七年级数学下册第8章角同步测试考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I 卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。

第I 卷（选择题 30分）一、单选题（10小题，每小题3分，共计30分）1、已知 '13836,238.36,338.6∠∠∠===， 则下列说法正确的是（ ）A ．12∠=∠B ．23∠∠=C ．13∠=∠D ．123∠∠∠、、互不相等 2、如图，∠AOB ，以OA 为边作∠AOC ，使∠BOC =12∠AOB ，则下列结论成立的是（ ）A ．AOC BOC ∠=∠B ．AOC AOB ∠<∠ C ．AOC BOC ∠=∠或2AOC BOC ∠=∠D ．AOC BOC ∠=∠或3AOC BOC ∠=∠3、如图所示，∠1和∠2是对顶角的图形共有（ ）A ．0个B ．1个C ．2个D ．3个4、钟表10点30分时，时针与分针所成的角是（ ）A ．120︒B ．135︒C ．150︒D ．225︒5、已知∠α＝125°19′，则∠α的补角等于（ ）A ．144°41′B ．144°81′C ．54°41′D ．54°81′6、若36A ∠=︒，则A ∠的余角大小是（ ）A ．54°B ．64°C ．134°D ．144°7、如图，AB CD ⊥于点O ，OE 平分AOC ∠，若18BOF ∠=︒，则EOF ∠的度数为（ ）．A ．116°B ．117°C ．118°D ．127°8、如图，AB 与CD 交于点O ，AOE ∠与AOC ∠互余，20AOE ∠=︒，则BOD ∠的度数为（ ）A ．20︒B ．70︒C ．90︒D ．110︒9、如图，将一副三角板重叠放在一起，使直角顶点重合于点O ．若125AOC ∠=︒，则BOD ∠=（ ）A ．45°B ．50°C ．55°D ．60°10、计算：600″＝（ ）A ．6′B ．10′C ．36′D ．60′第Ⅱ卷（非选择题 70分）二、填空题（5小题，每小题4分，共计20分）1、已知α∠的补角是13739'︒，则α∠的余角度数是______°．（结果用度表示）2、9点30分时，钟表上时针与分针所组成的角为____度．3、如图，直线AB 与直线CD 相交于点O ，OE AB ⊥，已知30BOD ∠=︒，则COE ∠=______________．4、已知∠α与∠β互余，且∠α=35°30′，则∠β=______度．5、如图，将一副三角尺的直角顶点O 重合在一起．若∠COB 与∠DOA 的比是2：7，OP 平分∠DOA ，则∠POC ＝_________度．三、解答题（5小题，每小题10分，共计50分）1、如图，直线AB 、CD 相交于点O ，70AOC ∠=︒，射线OE 把BOD ∠分成两个角，且:3:4BOE EOD ∠∠=．(1)求EOD ∠的度数．(2)过点O 作射线OF OE ⊥，求DOF ∠的度数．2、如图，OD 平分BOC ∠，OE 平分AOC ∠．若35BOD ∠=︒，50AOC ∠=︒．(1)求出AOB ∠的度数；(2)求出DOE ∠的度数，并判断DOE ∠与AOB ∠的数量关系是互补还是互余．3、如图（1），直线AB 、CD 相交于点O ，直角三角板EOF 边OF 落在射线OB 上，将三角板EOF 绕点O 逆时针旋转180°．(1)如图（2），设AOE n ∠=︒，当OF 平分BOD ∠时，求DOF ∠（用n 表示）(2)若40AOC ∠=︒，①如图（3），将三角板EOF 旋转，使OE 落在AOC ∠内部，试确定COE ∠与BOF ∠的数量关系，并说明理由．②若三角板EOF 从初始位置开始，每秒旋转5°，旋转时间为t ，当AOE ∠与DOF ∠互余时，求t 的值．4、如图，直线AB 和CD 相交于点O ，若40BOD ∠=︒，OA 平分EOC ∠，求EOD ∠的度数．5、如图，点O 是直线AB 上的一点，∠COD 是直角，OE 平分∠BOC ．(1)如图（1），若∠AOC =40°，求∠DOE 的度数；(2)如图（2），若∠COE =∠DOB ，求∠AOC 的度数．-参考答案-一、单选题1、C【解析】【分析】先换算单位，再比较大小即可．【详解】解：1383638.6∠=︒'=︒，238.36∠=︒，338.6∠=︒，13∠∠∴=．故选：C ．【点睛】考查了度分秒的换算，解题的关键是将单位换算一致．2、D【解析】【分析】分OC 在∠AOB 内部和OC 在∠AOB 外部两种情况讨论，画出图形即可得出结论．【详解】解：当OC 在∠AOB 内部时，∵∠BOC=12∠AOB，即∠AOB=2∠BOC，∴∠AOC=∠BOC；当OC在∠AOB外部时，∵∠BOC=12∠AOB，即∠AOB=2∠BOC，∴∠AOC=3∠BOC；综上，∠AOC=∠BOC或∠AOC=3∠BOC；故选：D．【点睛】本题考查了角平分线的定义，熟练掌握角平分线的定义，数形结合解题是关键．3、B【解析】【分析】对顶角：有公共的顶点，角的两边互为反向延长线，根据定义逐一判断即可．【详解】只有（3）中的∠1与∠2是对顶角．故选B【点睛】本题考查了对顶角的定义，理解对顶角的定义是解题的关键．4、B【解析】【分析】根据时针与分针相距的份数乘以每份的度数，可得答案．【详解】解：10点30分时的时针和分针相距的份数是4.5，10点30分时的时针和分针所成的角的度数为30°×4.5=135°，故选：B.【点睛】本题考查的知识点是钟面角，解题关键是求出时针和分针之间的格子数，再根据每个格子对应的圆心角的度数，列式解答．5、C【解析】【分析】两个角的和为180,︒则这两个角互为补角，根据互为补角的含义列式计算即可.【详解】解：∠α＝125°19′，∴∠α的补角等于180125195441故选C【点睛】本题考查的是互补的含义，掌握“两个角的和为180,︒则这两个角互为补角”是解本题的关键.6、A【解析】【分析】根据余角的意义：两个角的和为90°，则这两个角互余，由此求得∠A的余角度数即可．【详解】解：∵∠A=36°，∴∠A的余角=90°﹣∠A=90°﹣36°=54°．故选A．【点睛】本题考查的是余角的定义，即如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角，解题关键是掌握余角的定义．7、B【解析】【分析】根据垂线的定义，即可得到∠AOC的度数，依据角平分线的定义，即可得到∠AOE的度数，由平角定义即可求解.【详解】解：∵AB CD⊥于点O，∴∠AOC＝90°，∵OE平分∠AOC，∴∠AOE＝12∠AOC＝12×90°＝45°，∴∠EOF ＝180°−∠AOE −∠BOF ＝180°−45°−18°＝117°．故选：B【点睛】本题考查了垂线的定义，角平分线的定义，熟记概念并准确识图是解题的关键．8、B【解析】【分析】先由AOE ∠与AOC ∠互余，求解70,AOC 再利用对顶角相等可得答案.【详解】解：AOE ∠与AOC ∠互余，90AOE AOC ∴∠+∠=︒，20AOE ∠=︒，70AOC ∴∠=︒，70BOD AOC ∴∠=∠=︒，故选：B ．【点睛】本题考查的是互余的含义，角的和差关系，对顶角的性质，掌握“两个角互余的含义”是解本题的关键.9、C【解析】【分析】结合题意，根据三角板的性质，得90AOB COD ∠=∠=︒；根据角度和差性质运算，得AOD ∠，再根据余角的性质计算，即可得到答案．根据题意，得：90AOB COD ∠=∠=︒∵125AOC ∠=︒∴35AOD AOC COD ∠=∠-∠=︒∴903555BOD AOB AOD ∠=∠-∠=︒-︒=︒故选：C ．【点睛】本题考查了角的知识；解题的关键是熟练掌握角度和差运算、余角的性质，从而完成求解．10、B【解析】【分析】根据160'︒=，160'''=计算即可得．【详解】 解：600600()1060''''==， 故选：B【点睛】题目主要考查角度各单位间的换算，熟练掌握角度单位之间的进率是解题关键．二、填空题1、47.65【解析】【分析】根据180°-13739'︒求得α∠，根据90α︒-∠即可求得答案解：∵α∠的补角是13739'︒，∴α∠18013739'=︒-︒∴α∠的余角为90α︒-∠()9018013739'=︒-︒-︒1373990'=︒-︒4739'=︒ 3939=0.6560'=︒ ∴4739'︒47.65=︒故答案为：47.65【点睛】本题考查了求一个角的补角和余角，角度进制转换，正确的计算是解题的关键．2、105°【解析】【分析】根据题意画出图形，可得∠AOC =∠COD =∠DOE =30° ，15BOE ∠=︒ ，即可求解．【详解】解：如图，根据题意得：∠AOC =∠COD =∠DOE =13603012︒⨯=︒ ，30301560BOE ∠=︒⨯=︒ ，∴∠AOB=30°×3+15°=105°．故答案为：105°【点睛】本题主要考查了钟面角的计算；熟练掌握钟面上每2个数字之间相隔30度；时针1分钟走0.5度是解题的关键．3、120°##120度【解析】【分析】根据垂直定义求出∠AOE，根据对顶角求出∠AOC，相加即可．【详解】解：∵OE⊥AB，∴∠AOE＝90°，∵∠AOC＝∠BOD＝30°，∴∠COE＝∠AOE＋∠AOC＝90°＋30°＝120°．故答案是：120°．【点睛】本题考查了垂直，对顶角的应用，主要考查学生的计算能力．4、54.5【解析】【分析】∠的值．根据90°－∠α即可求得β【详解】解：∵∠α与∠β互余，且∠α=35°30′，∴∠β903530'=︒-︒896035305430'''=︒-︒=︒ 30300.560'==︒ 54.5β∴∠=︒故答案为：54.5【点睛】本题考查了求一个角的余角，角度进制的转化，正确的计算是解题的关键．5、20【解析】【分析】根据条件可知90AOB COD ∠=∠=︒，并且180COB DOA AOB COD ∠+∠=∠+∠=︒，再根据COB ∠与DOA ∠的比是2:7，可求DOA ∠，再根据角平分线的定义和角的和差关系即可求解．【详解】解：180COB DOA COB COA COB DOB AOB COD ∠+∠=∠+∠+∠+∠=∠+∠=︒，又COB ∠与DOA ∠的比是2:7，718014027DOA ∴∠=︒⨯=︒+， OP 平分DOA ∠，70DOP ∴∠=︒，20POC ∴∠=︒．故答案为：20．【点睛】本题考查了余角与补角，角平分线的定义，正确认识COB DOA ∠+∠AOB COD =∠+∠ 180=︒ 这一个关系是解题的关键，这是一个常用的关系，需熟记．三、解答题1、(1)40°(2)50°或130°【解析】【分析】（1）根据对顶角相等可得∠BOD=∠AOC=70°，然后根据比例求解即可；（2）先求出∠DOE，再分OF在∠AOD的内部时，∠DOF=∠EOF-∠DOE，OF在∠BOC的内部时，∠DOF=∠EOF+∠DOE进行计算即可得解．(1)∵∠AOC=70°，∠BOD=∠AOC，∴∠BOD=70°，∵∠BOE：∠EOD=3：4，∴∠EOD=70°×434=40°；(2)如图：∵OF⊥OE，∴∠EOF=90°，当OF在∠AOD的内部时，∠DOF =∠EOF -∠DOE=90°-40°=50°，当OF 在∠BOC 的内部时，∠DOF =∠EOF +∠DOE=90°+40°=130°，综上所述∠DOF =50°或130°．【点睛】本题考查了对顶角相等的性质，角的计算，熟记概念并准确识图是解题的关键．2、 (1)120︒(2)60︒，互补【解析】【分析】（1）先根据角平分线的定义求出∠BOC 的度数，然后可求AOB ∠的度数；（2）先根据角平分线的定义求出∠COD、∠COE 的度数，然后可求DOE ∠的度数，进而可判断DOE ∠与AOB ∠的数量关系．(1)解：∵OD 平分BOC ∠，35BOD ∠=︒，∴270BOC BOD ∠=∠=︒，又∵50AOC ∠=︒，∴7050120AOB BOC AOC ∠=∠+∠=︒+︒=︒；(2)解：∵OD 平分BOC ∠，OE 平分AOC ∠，50AOC ∠=︒，∴35COD BOD ∠=∠=︒，1252COE AOC ∠=∠=︒，∴352560DOE COD COE ∠=∠+∠=︒+︒=︒，∴60120180DOE AOB ∠+∠=︒+︒=︒，∴DOE ∠与AOB ∠的数量关系是互补．【点睛】本题主要考查角平分线的定义和补角的定义，关键是根据补角的定义解答．如果两个角的和等于90°，那么这两个角互为余角，其中一个角叫做另一个角的余角；如果两个角的和等于180°，那么这两个角互为补角，其中一个角叫做另一个角的补角．3、 (1)90DOF n ∠=︒-︒(2)①130COE BOF ∠+∠=︒，理由见解析；②4秒或22秒【解析】【分析】（1）利用角的和差关系求解,BOF ∠ 再利用角平分线的含义求解DOF ∠即可；（2）①设∠=COE β，再利用角的和差关系依次求解40AOE β∠=︒-， 50AOF β∠=︒+，130BOF β∠=︒-， 从而可得答案；②由题意得：OE 与OA 重合是第18秒，OF 与OD 重合是第8秒，停止是36秒．再分三种情况讨论：如图，当08t <<时 905AOE t ∠=︒-，405DOF t ∠=︒-，如图，当818t <<时 905AOE t ∠=︒-，540DOF t ∠=-︒，如图，当1836t <<时，590AOE t ∠=-︒，540DOF t ∠=-︒，再利用互余列方程解方程即可.(1)解：180,90,,AOB EOF AOE n∴ 18090BOF EOF AOE n ∠=︒-∠-∠=︒-︒∵OF 平分BOD ∠∴90DOF BOF n ∠=∠=︒-︒(2)解：①设∠=COE β，则40AOE β∠=︒-，∴()904050AOF ββ∠=︒-︒-=︒+∴()180********BOF AOF ββ∠=︒-∠=︒-︒+=︒-，∴130COE BOF ∠+∠=︒②由题意得：OE 与OA 重合是第18秒，OF 与OD 重合是第8秒，停止是36秒．如图，当08t <<时 905AOE t ∠=︒-，405DOF t ∠=︒-，则90540590t t -+-=，∴4t =如图，当818t <<时 905AOE t ∠=︒-，540DOF t ∠=-︒，则90554090t t -+-=，方程无解，不成立如图，当1836t <<时，590AOE t ∠=-︒，540DOF t ∠=-︒，则59054090t t -+-=，∴22t =综上所述4t =秒或22秒【点睛】本题考查的是角的和差运算，角平分线的定义，角的动态定义的理解，互为余角的含义，清晰的分类讨论是解本题的关键.4、100°【解析】【分析】根据对顶角相等以及角平分线的性质可得出∠AOE 的度数，再根据平角的定义即可得出∠EOD 的度数．【详解】解：∵∠BOD =40°，∴∠AOC =∠BOD =40°.∵OA 平分∠EOC ，∴∠AOE =∠AOC =40°，∴1801804040100EOD AOE BOD ∠=︒-∠-∠=︒-︒-︒=︒.【点睛】本题主要考查了角平分线的性质以及对顶角、邻补角的性质，难度不大．5、 (1)∠DOE 的度数为20°；(2)∠AOC 的度数为120°．【解析】【分析】（1）先求得∠BOC ，再根据角平分线的性质得出∠COE ，根据余角的性质得出∠DOE 的度数；（2）根据角平分线的定义得到∠COE =∠BOE ，于是得到∠COE =∠BOE =∠DOB =30°，然后根据平角的定义即可得到结论．(1)解：∵∠AOC +∠BOC =180°，∴∠BOC =180°-∠AOC =180°-40°=140°，∵OE 平分∠BOC ，∴∠COE =12∠BOC =12×140°=70°，∵∠COD 是直角，∴∠COE+∠DOE=90°，∴∠DOE=90°-∠COE=90°-70°=20°；(2)解：∵OE平分∠BOC，∴∠COE=∠BOE，∵∠COE=∠BOD，∴∠COE=∠BOE=∠DOB，∵∠COD=90°，∴∠COE=∠BOE=13×90°=30°，∴∠AOC=180°-30°-30°=120°．【点睛】本题考查了角平分线的定义，是基础题，难度不大，掌握各角之间的关系是解题的关键．。

2019年精选数学七年级下册8.2 角的比较青岛版课后练习【含答案解析】九十九第1题【单选题】若∠1=50^05"∠2=50.5^0则∠1与∠2的大小关系是( )A、∠1=∠2B、∠1＞∠2C、∠1＜∠2D、无法确定【答案】：【解析】：第2题【单选题】两个锐角的和( )A、一定是锐角B、一定是钝角C、一定是直角D、可能是钝角，直角或锐角【答案】：【解析】：第3题【单选题】已知∠α=18°18′，∠β=18.18°，∠γ=18.3°，下列结论正确的是( )A、∠α=∠βB、∠α＜∠βC、∠α=∠γD、∠β＞∠γ【答案】：【解析】：第4题【单选题】如图，将一副三角板如图放置，∠COD=20°，则∠AOB的度数为( )A、140°B、150°C、160°D、170°【答案】：【解析】：第5题【单选题】已知∠α=39°18′，∠β=39.18°，∠γ=39.3°，下面结论正确的是( )A、<!--{cke_protected}{C}%3C!%2D%2D%5Bif%20gte%20mso%209%5D%3E%3Cxml%3E%0A%20%3Cw%3 AWordDocument%3E%0A%20%20%3Cw%3AView%3ENormal%3C%2Fw%3AView%3E%0A%20%20%3 Cw%3AZoom%3E0%3C%2Fw%3AZoom%3E%0A%20%20%3Cw%3ATrackMoves%2F%3E%0A%20%20% 3Cw%3ATrackFormatting%2F%3E%0A%20%20%3Cw%3APunctuationKerning%2F%3E%0A%20%20%3 Cw%3ADrawingGridVerticalSpacing%3E7.8%20%E7%A3%85%3C%2Fw%3ADrawingGridVerticalSpacin g%3E%0A%20%20%3Cw%3ADisplayHorizontalDrawingGridEvery%3E0%3C%2Fw%3ADisplayHorizontal DrawingGridEvery%3E%0A%20%20%3Cw%3ADisplayVerticalDrawingGridEvery%3E2%3C%2Fw%3ADis playVerticalDrawingGridEvery%3E%0A%20%20%3Cw%3AValidateAgainstSchemas%2F%3E%0A%20%2 0%3Cw%3ASaveIfXMLInvalid%3Efalse%3C%2Fw%3ASaveIfXMLInvalid%3E%0A%20%20%3Cw%3AIgnor eMixedContent%3Efalse%3C%2Fw%3AIgnoreMixedContent%3E%0A%20%20%3Cw%3AAlwaysShowPl aceholderText%3Efalse%3C%2Fw%3AAlwaysShowPlaceholderText%3E%0A%20%20%3Cw%3ADoNotP romoteQF%2F%3E%0A%20%20%3Cw%3ALidThemeOther%3EEN-US%3C%2Fw%3ALidThemeOther%3 E%0A%20%20%3Cw%3ALidThemeAsian%3EZH-CN%3C%2Fw%3ALidThemeAsian%3E%0A%20%20%3C w%3ALidThemeComplexScript%3EX-NONE%3C%2Fw%3ALidThemeComplexScript%3E%0A%20%20%3 Cw%3ACompatibility%3E%0A%20%20%20%3Cw%3ASpaceForUL%2F%3E%0A%20%20%20%3Cw%3AB alanceSingleByteDoubleByteWidth%2F%3E%0A%20%20%20%3Cw%3ADoNotLeaveBackslashAlone%2 F%3E%0A%20%20%20%3Cw%3AULTrailSpace%2F%3E%0A%20%20%20%3Cw%3ADoNotExpandShiftR eturn%2F%3E%0A%20%20%20%3Cw%3AAdjustLineHeightInTable%2F%3E%0A%20%20%20%3Cw%3A BreakWrappedTables%2F%3E%0A%20%20%20%3Cw%3ASnapToGridInCell%2F%3E%0A%20%20%20% 3Cw%3AWrapTextWithPunct%2F%3E%0A%20%20%20%3Cw%3AUseAsianBreakRules%2F%3E%0A%2 0%20%20%3Cw%3ADontGrowAutofit%2F%3E%0A%20%20%20%3Cw%3ASplitPgBreakAndParaMark% 2F%3E%0A%20%20%20%3Cw%3ADontVertAlignCellWithSp%2F%3E%0A%20%20%20%3Cw%3ADontB reakConstrainedForcedTables%2F%3E%0A%20%20%20%3Cw%3ADontVertAlignInTxbx%2F%3E%0A%2 0%20%20%3Cw%3AWord11KerningPairs%2F%3E%0A%20%20%20%3Cw%3ACachedColBalance%2F% 3E%0A%20%20%20%3Cw%3AUseFELayout%2F%3E%0A%20%20%3C%2Fw%3ACompatibility%3E%0A %20%20%3Cw%3ADoNotOptimizeForBrowser%2F%3E%0A%20%20%3Cm%3AmathPr%3E%0A%20%2 0%20%3Cm%3AmathFont%20m%3Aval%3D%22Cambria%20Math%22%2F%3E%0A%20%20%20%3Cm %3AbrkBin%20m%3Aval%3D%22before%22%2F%3E%0A%20%20%20%3Cm%3AbrkBinSub%20m%3Av al%3D%22%26%2345%3B-%22%2F%3E%0A%20%20%20%3Cm%3AsmallFrac%20m%3Aval%3D%22off %22%2F%3E%0A%20%20%20%3Cm%3AdispDef%2F%3E%0A%20%20%20%3Cm%3AlMargin%20m%3 Aval%3D%220%22%2F%3E%0A%20%20%20%3Cm%3ArMargin%20m%3Aval%3D%220%22%2F%3E%0 A%20%20%20%3Cm%3AdefJc%20m%3Aval%3D%22centerGroup%22%2F%3E%0A%20%20%20%3Cm %3AwrapIndent%20m%3Aval%3D%221440%22%2F%3E%0A%20%20%20%3Cm%3AintLim%20m%3Av al%3D%22subSup%22%2F%3E%0A%20%20%20%3Cm%3AnaryLim%20m%3Aval%3D%22undOvr%22% 2F%3E%0A%20%20%3C%2Fm%3AmathPr%3E%3C%2Fw%3AWordDocument%3E%0A%3C%2Fxml%3E %3C!%5Bendif%5D%2D%2D%3E--><!--{cke_protected}{C}%3C!%2D%2D%5Bif%20gte%20mso%209%5D%3E%3Cxml%3E%0A%20%3Cw%3ALatentStyles%20DefLockedState%3D%22false%22%20DefUnhide WhenUsed%3D%22true%22%0A%20%20DefSemiHidden%3D%22true%22%20DefQFormat%3D%22fal se%22%20DefPriority%3D%2299%22%0A%20%20LatentStyleCount%3D%22267%22%3E%0A%20%20 %3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%220%22%20SemiHidden%3D%2 2false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20QFormat%3D%22true%22%20Na me%3D%22Normal%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20 Priority%3D%229%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22fa lse%22%20QFormat%3D%22true%22%20Name%3D%22heading%201%22%2F%3E%0A%20%20%3Cw %3ALsdException%20Locked%3D%22false%22%20Priority%3D%229%22%20QFormat%3D%22true%2 2%20Name%3D%22heading%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%2 2false%22%20Priority%3D%229%22%20QFormat%3D%22true%22%20Name%3D%22heading%203%2 2%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%229%22 %20QFormat%3D%22true%22%20Name%3D%22heading%204%22%2F%3E%0A%20%20%3Cw%3ALsd Exception%20Locked%3D%22false%22%20Priority%3D%229%22%20QFormat%3D%22true%22%20Na me%3D%22heading%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%2 2%20Priority%3D%229%22%20QFormat%3D%22true%22%20Name%3D%22heading%206%22%2F%3 E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%229%22%20QFor mat%3D%22true%22%20Name%3D%22heading%207%22%2F%3E%0A%20%20%3Cw%3ALsdExceptio n%20Locked%3D%22false%22%20Priority%3D%229%22%20QFormat%3D%22true%22%20Name%3D %22heading%208%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Pr iority%3D%229%22%20QFormat%3D%22true%22%20Name%3D%22heading%209%22%2F%3E%0A% 20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2239%22%20Name%3D %22toc%201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priorit y%3D%2239%22%20Name%3D%22toc%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Lock ed%3D%22false%22%20Priority%3D%2239%22%20Name%3D%22toc%203%22%2F%3E%0A%20%20% 3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2239%22%20Name%3D%22toc% 204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%22 39%22%20Name%3D%22toc%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%2 2false%22%20Priority%3D%2239%22%20Name%3D%22toc%206%22%2F%3E%0A%20%20%3Cw%3AL sdException%20Locked%3D%22false%22%20Priority%3D%2239%22%20Name%3D%22toc%207%22% 2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2239%22%2 0Name%3D%22toc%208%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%2 2%20Priority%3D%2239%22%20Name%3D%22toc%209%22%2F%3E%0A%20%20%3Cw%3ALsdExcept ion%20Locked%3D%22false%22%20Priority%3D%2235%22%20QFormat%3D%22true%22%20Name% 3D%22caption%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priori ty%3D%2210%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false% 22%20QFormat%3D%22true%22%20Name%3D%22Title%22%2F%3E%0A%20%20%3Cw%3ALsdExcept ion%20Locked%3D%22false%22%20Priority%3D%221%22%20Name%3D%22Default%20Paragraph%2 0Font%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D% 2211%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20 QFormat%3D%22true%22%20Name%3D%22Subtitle%22%2F%3E%0A%20%20%3Cw%3ALsdException %20Locked%3D%22false%22%20Priority%3D%2222%22%20SemiHidden%3D%22false%22%0A%20%2 0%20UnhideWhenUsed%3D%22false%22%20QFormat%3D%22true%22%20Name%3D%22Strong%22 %2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2220%22 %20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20QFormat% 3D%22true%22%20Name%3D%22Emphasis%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Lock ed%3D%22false%22%20Priority%3D%2259%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Table%20Grid%22%2F%3E%0A%20%20%3Cw%3A LsdException%20Locked%3D%22false%22%20UnhideWhenUsed%3D%22false%22%20Name%3D%22 Placeholder%20Text%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%2 0Priority%3D%221%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22f alse%22%20QFormat%3D%22true%22%20Name%3D%22No%20Spacing%22%2F%3E%0A%20%20%3C w%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2260%22%20SemiHidden%3D%22f alse%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Shading%22 %2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2261%22 %20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D %22Light%20List%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Pri ority%3D%2262%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22fals e%22%20Name%3D%22Light%20Grid%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3 D%22false%22%20Priority%3D%2263%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhide WhenUsed%3D%22false%22%20Name%3D%22Medium%20Shading%201%22%2F%3E%0A%20%20% 3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2264%22%20SemiHidden%3D%2 2false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Shadin g%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D %2265%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%2 0Name%3D%22Medium%20List%201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3 D%22false%22%20Priority%3D%2266%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhide WhenUsed%3D%22false%22%20Name%3D%22Medium%20List%202%22%2F%3E%0A%20%20%3Cw %3ALsdException%20Locked%3D%22false%22%20Priority%3D%2267%22%20SemiHidden%3D%22fals e%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%201% 22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2268%2 2%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3 D%22Medium%20Grid%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false %22%20Priority%3D%2269%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed %3D%22false%22%20Name%3D%22Medium%20Grid%203%22%2F%3E%0A%20%20%3Cw%3ALsdExc eption%20Locked%3D%22false%22%20Priority%3D%2270%22%20SemiHidden%3D%22false%22%0A %20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Dark%20List%22%2F%3E%0A%20 %20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2271%22%20SemiHidden% 3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Colorful%20S hading%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D %2272%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%2 0Name%3D%22Colorful%20List%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22f alse%22%20Priority%3D%2273%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUs ed%3D%22false%22%20Name%3D%22Colorful%20Grid%22%2F%3E%0A%20%20%3Cw%3ALsdExcepti on%20Locked%3D%22false%22%20Priority%3D%2260%22%20SemiHidden%3D%22false%22%0A%20 %20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Shading%20Accent%201%22 %2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2261%22 %20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D %22Light%20List%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%2 2false%22%20Priority%3D%2262%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhen Used%3D%22false%22%20Name%3D%22Light%20Grid%20Accent%201%22%2F%3E%0A%20%20%3C w%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2263%22%20SemiHidden%3D%22f alse%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Shading %201%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2264%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D% 22false%22%20Name%3D%22Medium%20Shading%202%20Accent%201%22%2F%3E%0A%20%20%3 Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2265%22%20SemiHidden%3D%22 false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20List%20 1%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20U nhideWhenUsed%3D%22false%22%20Name%3D%22Revision%22%2F%3E%0A%20%20%3Cw%3ALsdE xception%20Locked%3D%22false%22%20Priority%3D%2234%22%20SemiHidden%3D%22false%22%0 A%20%20%20UnhideWhenUsed%3D%22false%22%20QFormat%3D%22true%22%20Name%3D%22Lis t%20Paragraph%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Prio rity%3D%2229%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false %22%20QFormat%3D%22true%22%20Name%3D%22Quote%22%2F%3E%0A%20%20%3Cw%3ALsdEx ception%20Locked%3D%22false%22%20Priority%3D%2230%22%20SemiHidden%3D%22false%22%0A %20%20%20UnhideWhenUsed%3D%22false%22%20QFormat%3D%22true%22%20Name%3D%22Inte nse%20Quote%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priori ty%3D%2266%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false% 22%20Name%3D%22Medium%20List%202%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdExc eption%20Locked%3D%22false%22%20Priority%3D%2267%22%20SemiHidden%3D%22false%22%0A %20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%201%20Accent %201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D% 2268%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20N ame%3D%22Medium%20Grid%202%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdException %20Locked%3D%22false%22%20Priority%3D%2269%22%20SemiHidden%3D%22false%22%0A%20%2 0%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%203%20Accent%201% 22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2270%2 2%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3 D%22Dark%20List%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D% 22false%22%20Priority%3D%2271%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhe nUsed%3D%22false%22%20Name%3D%22Colorful%20Shading%20Accent%201%22%2F%3E%0A%20 %20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2272%22%20SemiHidden% 3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Colorful%20Li st%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20P riority%3D%2273%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22fa lse%22%20Name%3D%22Colorful%20Grid%20Accent%201%22%2F%3E%0A%20%20%3Cw%3ALsdExc eption%20Locked%3D%22false%22%20Priority%3D%2260%22%20SemiHidden%3D%22false%22%0A %20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Shading%20Accent%202 %22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2261 %22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name %3D%22Light%20List%20Accent%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3 D%22false%22%20Priority%3D%2262%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhide WhenUsed%3D%22false%22%20Name%3D%22Light%20Grid%20Accent%202%22%2F%3E%0A%20%2 0%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2263%22%20SemiHidden%3D %22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Sha ding%201%20Accent%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false% 22%20Priority%3D%2264%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3 D%22false%22%20Name%3D%22Medium%20Shading%202%20Accent%202%22%2F%3E%0A%20%20 %3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2265%22%20SemiHidden%3D% 22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20List%201%20Accent%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%2 0Priority%3D%2266%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%2 2false%22%20Name%3D%22Medium%20List%202%20Accent%202%22%2F%3E%0A%20%20%3Cw%3 ALsdException%20Locked%3D%22false%22%20Priority%3D%2267%22%20SemiHidden%3D%22false% 22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%201%20 Accent%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority %3D%2268%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%2 2%20Name%3D%22Medium%20Grid%202%20Accent%202%22%2F%3E%0A%20%20%3Cw%3ALsdExc eption%20Locked%3D%22false%22%20Priority%3D%2269%22%20SemiHidden%3D%22false%22%0A %20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%203%20Accent %202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D% 2270%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20N ame%3D%22Dark%20List%20Accent%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locke d%3D%22false%22%20Priority%3D%2271%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhi deWhenUsed%3D%22false%22%20Name%3D%22Colorful%20Shading%20Accent%202%22%2F%3E% 0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2272%22%20SemiHi dden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Colorfu l%20List%20Accent%202%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%2 2%20Priority%3D%2273%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3 D%22false%22%20Name%3D%22Colorful%20Grid%20Accent%202%22%2F%3E%0A%20%20%3Cw%3 ALsdException%20Locked%3D%22false%22%20Priority%3D%2260%22%20SemiHidden%3D%22false% 22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Shading%20Accen t%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D% 2261%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20N ame%3D%22Light%20List%20Accent%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locke d%3D%22false%22%20Priority%3D%2262%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhi deWhenUsed%3D%22false%22%20Name%3D%22Light%20Grid%20Accent%203%22%2F%3E%0A%20 %20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2263%22%20SemiHidden% 3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20S hading%201%20Accent%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22fals e%22%20Priority%3D%2264%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed %3D%22false%22%20Name%3D%22Medium%20Shading%202%20Accent%203%22%2F%3E%0A%20 %20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2265%22%20SemiHidden% 3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20L ist%201%20Accent%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%2 2%20Priority%3D%2266%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3 D%22false%22%20Name%3D%22Medium%20List%202%20Accent%203%22%2F%3E%0A%20%20%3C w%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2267%22%20SemiHidden%3D%22f alse%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%20 1%20Accent%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Pr iority%3D%2268%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22fal se%22%20Name%3D%22Medium%20Grid%202%20Accent%203%22%2F%3E%0A%20%20%3Cw%3AL sdException%20Locked%3D%22false%22%20Priority%3D%2269%22%20SemiHidden%3D%22false%22 %0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%203%20Ac cent%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority% 3D%2270%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22 %20Name%3D%22Dark%20List%20Accent%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2271%22%20SemiHidden%3D%22false%22%0A%20%20%20 UnhideWhenUsed%3D%22false%22%20Name%3D%22Colorful%20Shading%20Accent%203%22%2F% 3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2272%22%20Se miHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Co lorful%20List%20Accent%203%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22fals e%22%20Priority%3D%2273%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed %3D%22false%22%20Name%3D%22Colorful%20Grid%20Accent%203%22%2F%3E%0A%20%20%3Cw %3ALsdException%20Locked%3D%22false%22%20Priority%3D%2260%22%20SemiHidden%3D%22fals e%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Shading%20Ac cent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority% 3D%2261%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22 %20Name%3D%22Light%20List%20Accent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20 Locked%3D%22false%22%20Priority%3D%2262%22%20SemiHidden%3D%22false%22%0A%20%20%2 0UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Grid%20Accent%204%22%2F%3E%0 A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2263%22%20SemiHid den%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium %20Shading%201%20Accent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%2 2false%22%20Priority%3D%2264%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhen Used%3D%22false%22%20Name%3D%22Medium%20Shading%202%20Accent%204%22%2F%3E%0A %20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2265%22%20SemiHidd en%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium %20List%201%20Accent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22fals e%22%20Priority%3D%2266%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed %3D%22false%22%20Name%3D%22Medium%20List%202%20Accent%204%22%2F%3E%0A%20%20% 3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2267%22%20SemiHidden%3D%2 2false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%2 01%20Accent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20 Priority%3D%2268%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22f alse%22%20Name%3D%22Medium%20Grid%202%20Accent%204%22%2F%3E%0A%20%20%3Cw%3A LsdException%20Locked%3D%22false%22%20Priority%3D%2269%22%20SemiHidden%3D%22false%2 2%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%203%20A ccent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority %3D%2270%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%2 2%20Name%3D%22Dark%20List%20Accent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%2 0Locked%3D%22false%22%20Priority%3D%2271%22%20SemiHidden%3D%22false%22%0A%20%20% 20UnhideWhenUsed%3D%22false%22%20Name%3D%22Colorful%20Shading%20Accent%204%22%2 F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2272%22%20 SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22 Colorful%20List%20Accent%204%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22f alse%22%20Priority%3D%2273%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUs ed%3D%22false%22%20Name%3D%22Colorful%20Grid%20Accent%204%22%2F%3E%0A%20%20%3C w%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2260%22%20SemiHidden%3D%22f alse%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Shading%20 Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority %3D%2261%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%2 2%20Name%3D%22Light%20List%20Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%2 0Locked%3D%22false%22%20Priority%3D%2262%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Grid%20Accent%205%22%2F%3E% 0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2263%22%20SemiHi dden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Mediu m%20Shading%201%20Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D %22false%22%20Priority%3D%2264%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWh enUsed%3D%22false%22%20Name%3D%22Medium%20Shading%202%20Accent%205%22%2F%3E% 0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2265%22%20SemiHi dden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Mediu m%20List%201%20Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22f alse%22%20Priority%3D%2266%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUs ed%3D%22false%22%20Name%3D%22Medium%20List%202%20Accent%205%22%2F%3E%0A%20%2 0%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2267%22%20SemiHidden%3D %22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid %201%20Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22% 20Priority%3D%2268%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D% 22false%22%20Name%3D%22Medium%20Grid%202%20Accent%205%22%2F%3E%0A%20%20%3Cw %3ALsdException%20Locked%3D%22false%22%20Priority%3D%2269%22%20SemiHidden%3D%22fals e%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%203% 20Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Prior ity%3D%2270%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false %22%20Name%3D%22Dark%20List%20Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException %20Locked%3D%22false%22%20Priority%3D%2271%22%20SemiHidden%3D%22false%22%0A%20%2 0%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Colorful%20Shading%20Accent%205%22 %2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2272%22 %20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D %22Colorful%20List%20Accent%205%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D %22false%22%20Priority%3D%2273%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWh enUsed%3D%22false%22%20Name%3D%22Colorful%20Grid%20Accent%205%22%2F%3E%0A%20%2 0%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2260%22%20SemiHidden%3D %22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Shadin g%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Pr iority%3D%2261%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22fal se%22%20Name%3D%22Light%20List%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdExcepti on%20Locked%3D%22false%22%20Priority%3D%2262%22%20SemiHidden%3D%22false%22%0A%20 %20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Light%20Grid%20Accent%206%22%2F %3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2263%22%20S emiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22 Medium%20Shading%201%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locke d%3D%22false%22%20Priority%3D%2264%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhi deWhenUsed%3D%22false%22%20Name%3D%22Medium%20Shading%202%20Accent%206%22%2F %3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2265%22%20S emiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22 Medium%20List%201%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3 D%22false%22%20Priority%3D%2266%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhide WhenUsed%3D%22false%22%20Name%3D%22Medium%20List%202%20Accent%206%22%2F%3E%0 A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2267%22%20SemiHid den%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid%201%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22fal se%22%20Priority%3D%2268%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUse d%3D%22false%22%20Name%3D%22Medium%20Grid%202%20Accent%206%22%2F%3E%0A%20%2 0%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2269%22%20SemiHidden%3D %22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Medium%20Grid %203%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22% 20Priority%3D%2270%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D% 22false%22%20Name%3D%22Dark%20List%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdExc eption%20Locked%3D%22false%22%20Priority%3D%2271%22%20SemiHidden%3D%22false%22%0A %20%20%20UnhideWhenUsed%3D%22false%22%20Name%3D%22Colorful%20Shading%20Accent%2 06%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%227 2%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20Nam e%3D%22Colorful%20List%20Accent%206%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locke d%3D%22false%22%20Priority%3D%2273%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhi deWhenUsed%3D%22false%22%20Name%3D%22Colorful%20Grid%20Accent%206%22%2F%3E%0A% 20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2219%22%20SemiHidde n%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20QFormat%3D%22true%2 2%20Name%3D%22Subtle%20Emphasis%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked %3D%22false%22%20Priority%3D%2221%22%20SemiHidden%3D%22false%22%0A%20%20%20Unhid eWhenUsed%3D%22false%22%20QFormat%3D%22true%22%20Name%3D%22Intense%20Emphasis% 22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2231%2 2%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false%22%20QFormat %3D%22true%22%20Name%3D%22Subtle%20Reference%22%2F%3E%0A%20%20%3Cw%3ALsdExcep tion%20Locked%3D%22false%22%20Priority%3D%2232%22%20SemiHidden%3D%22false%22%0A%2 0%20%20UnhideWhenUsed%3D%22false%22%20QFormat%3D%22true%22%20Name%3D%22Intens e%20Reference%22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Prio rity%3D%2233%22%20SemiHidden%3D%22false%22%0A%20%20%20UnhideWhenUsed%3D%22false %22%20QFormat%3D%22true%22%20Name%3D%22Book%20Title%22%2F%3E%0A%20%20%3Cw%3 ALsdException%20Locked%3D%22false%22%20Priority%3D%2237%22%20Name%3D%22Bibliography %22%2F%3E%0A%20%20%3Cw%3ALsdException%20Locked%3D%22false%22%20Priority%3D%2239 %22%20QFormat%3D%22true%22%20Name%3D%22TOC%20Heading%22%2F%3E%0A%20%3C%2Fw %3ALatentStyles%3E%0A%3C%2Fxml%3E%3C!%5Bendif%5D%2D%2D%3E--><!--{cke_protected}{C}%3 C!%2D%2D%5Bif%20gte%20mso%2010%5D%3E%0A%3Cstyle%3E%0A%20%2F*%20Style%20Definitio ns%20*%2F%0A%20table.MsoNormalTable%0A%09%7Bmso-style-name%3A%E6%99%AE%E9%80%9 A%E8%A1%A8%E6%A0%BC%3B%0A%09mso-tstyle-rowband-size%3A0%3B%0A%09mso-tstyle-colban d-size%3A0%3B%0A%09mso-style-noshow%3Ayes%3B%0A%09mso-style-priority%3A99%3B%0A%09 mso-style-qformat%3Ayes%3B%0A%09mso-style-parent%3A%22%22%3B%0A%09mso-padding-alt%3 A0cm%205.4pt%200cm%205.4pt%3B%0A%09mso-para-margin%3A0cm%3B%0A%09mso-para-margi n-bottom%3A.0001pt%3B%0A%09mso-pagination%3Awidow-orphan%3B%0A%09font-size%3A10.5pt %3B%0A%09mso-bidi-font-size%3A11.0pt%3B%0A%09font-family%3A%22Calibri%22%2C%22sans-ser if%22%3B%0A%09mso-ascii-font-family%3ACalibri%3B%0A%09mso-ascii-theme-font%3Aminor-latin% 3B%0A%09mso-fareast-font-family%3A%E5%AE%8B%E4%BD%93%3B%0A%09mso-fareast-theme-fon t%3Aminor-fareast%3B%0A%09mso-hansi-font-family%3ACalibri%3B%0A%09mso-hansi-theme-font% 3Aminor-latin%3B%0A%09mso-bidi-font-family%3A%22Times%20New%20Roman%22%3B%0A%09ms o-bidi-theme-font%3Aminor-bidi%3B%0A%09mso-font-kerning%3A1.0pt%3B%7D%0A%3C%2Fstyle% 3E%0A%3C!%5Bendif%5D%2D%2D%3E-->∠α＜∠γ＜∠βB、∠γ＞∠α=∠β。

角的比较例1如图：（1）以B 为顶点的角有几个：把它们表示出来；（2）指出以射线BA 为边的角；（3）以D 为顶点，DC 为一边的角有几个？分别表示出来。

解：（1）以B 为顶点的角有3个，分别是ABD ∠、ABC ∠、DBC ∠。

（2）以射线BA 为边的角有2个，分别是ABD ∠和ABC ∠。

（3）以D 为顶点，DC 为一边的角有2个，分别是BDC ∠和CDE ∠。

说明：（1）以D 为顶点的角在图形中只有4个，因为除非特别注明，所说的角都是指小于平角的角。

再加上右边DC 的限制，所以以D 为顶点，DC 为一边的角只有两个角。

例2如例 根据图，回答下列问题（1）AOC ∠是哪两个角的和？（2）AOB ∠是哪两个角的差？（3）如果COD AOB ∠=∠，那么AOC ∠与DOB ∠的大小关系如何？解：（1）AOC ∠是AOB ∠与BOC ∠的和.（2）AOB ∠是AOC ∠与BOC ∠的差，或AOB ∠是AOD ∠与BOD ∠的差.（3）因为COD AOB ∠=∠，所以BOC COD BOC AOB ∠+∠=∠+∠，即DOB AOC ∠=∠.说明：等式的性质也适用于几何中的量，如长度、角度等等.下图，从直线AB 上任一点引一条射线，已知OD 平分BOC ∠，若,90=∠EOD 那么OE 一定是AOC ∠的平分线，请说明理由。

解 ∵AB 是直线，.1804321 =∠+∠+∠+∠∴OD 平分.43,∠=∠∴∠BOC由已知得,9032 =∠+∠.21,9041∠=∠∴=∠+∠∴即OE 平分.AOC ∠说明 本题考查角平分线的判定，解题时要注意平分线的性质与平角性质的应用。

例3（1）如下图，已知OM BOC AOB ,30,90 =∠=∠平分ON AOC ,∠平分BOC ∠，求MON ∠度数。

（2）如果（1）中α=∠AOB ，其他条件不变，求MON ∠的度数。

（3）如果（1）中β=∠BOC （β为锐角），其他条件不变，求MON ∠的度数。