无向图的传递闭包
- 格式:ppt
- 大小:152.00 KB
- 文档页数:22

摘要本次课程设计主要核心为利用迪杰斯特拉算法和Floyd算法实现无向图的最短路径的计算和求解。
要求理解算法的具体实现流程、学会正确使用该算法求解实际问题。
本次课程设计具体内容是:通过对两个算法的理解与应用来比较两个算法的优缺点。
本程序要求结合最短路算法以及相应的数据结构的定义和使用,实现一个最短路径算法的简单应用。
本课程设计是对书本知识的简单应用,以此培养大家用书本知识解决实际问题的能力;培养实际工作所需要的动手能力;培养以科学理论和工程上能力的技术,规范地开发大型、复杂、高质量的应用软件和系统软件。
关键字:迪杰斯特拉算法,Floyd算法,最短路径,算法设计,数据结构目录摘要 --------------------------------------------------------------- 1一、Dijkstra算法--------------------------------------------------- 31.1定义概览 ---------------------------------------------------- 31.2算法描述 ---------------------------------------------------- 31.2.1算法思想:--------------------------------------------- 31.1.2算法步骤----------------------------------------------- 31.3算法代码实现 ------------------------------------------------ 41.4算法实例 ---------------------------------------------------- 5二、Floyd算法------------------------------------------------------ 72.1定义概览 ---------------------------------------------------- 72.2算法描述 ---------------------------------------------------- 72.2.1算法思想原理------------------------------------------- 72.3算法代码实现 ----------------------------------------------- 10三、结论 ---------------------------------------------------------- 11四、参考文献 ------------------------------------------------------ 12一、Dijkstra算法1.1定义概览Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。

路径规划的主要算法与展望-应用数学论文-数学论文——文章均为WORD文档,下载后可直接编辑使用亦可打印——摘要:路径规划算法是智能领域中一项新兴的关键支撑技术;依据路径规划算法的实现原理,将其分为进化型算法与非进化型算法;再依据数学特征将非进化型算法细分为经典数学与几何图论两类;针对每类算法,分别从发展背景、设计思想、优缺点、改进与发展等方面简要归纳分析;最后对路径规划算法的未来发展趋势进行展望。
关键词:路径规划; 进化型算法; 非进化型算法; 未来展望;Summary of Path Planning AlgorithmsLIANG Xiao-hui MU Yong-hui WU Bei-hua JIANG YuShijiazhuang Campus of Army Engineering UniversityAbstract:Path planning algorithm is an emerging key supporting technology in the field of intelligence; According to the implementation principle of path planning algorithm, it is divided into evolutionary algorithm and non-evolutionary algorithm; Then based on the mathematical characteristics, the non-evolutionary algorithm can be divided into two types: classical mathematics and geometric graph theory; For each type of algorithm, the paper will give a brief summary and analysis from some aspects: the background of development,design ideas, advantages and disadvantages, improvement. Finally the future development trend of the path planning algorithm is forecasted.0 引言路径规划(Path Planning)[1]是智能技术中的热点研究问题,已在多领域有所突破并成功得以应用。

Dijkstra算法1.定义概览Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。
主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
注意该算法要求图中不存在负权边。
问题描述:在无向图G=(V,E) 中,假设每条边E[i] 的长度为w[i],找到由顶点V0 到其余各点的最短路径。
(单源最短路径)2.算法描述1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径, 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S 中。
在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U 中任何顶点的最短路径长度。
此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤: a.初始时,S只包含源点,即S={v},v的距离为0。
U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
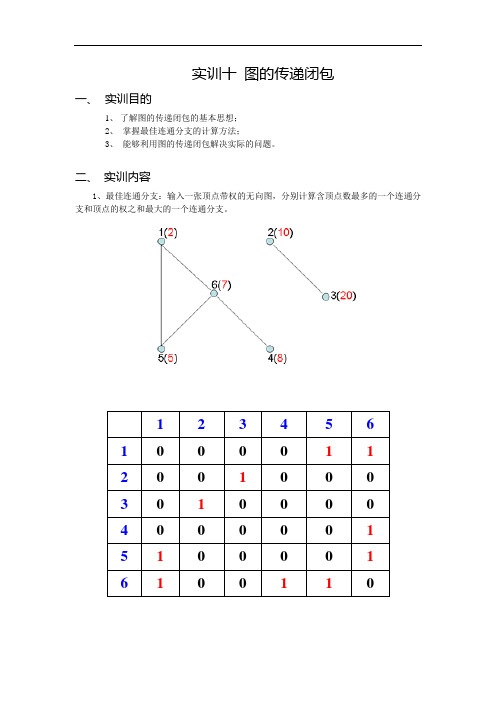
实训十图的传递闭包一、实训目的1、了解图的传递闭包的基本思想;2、掌握最佳连通分支的计算方法;3、能够利用图的传递闭包解决实际的问题。
二、实训内容1、最佳连通分支:输入一张顶点带权的无向图,分别计算含顶点数最多的一个连通分支和顶点的权之和最大的一个连通分支。
[输入]:第1行为顶点数n(1<=n<=20),随后的n行,依次表示顶点1 ~ 顶点n上的权。
第n+2行为边数e(1<=e<=210),随后的e行中每行为有边连接的一对顶点。
[输出]:两行。
第一行为含顶点数最多的一个连通分支,第二行为顶点的权之和最大的一个连通分支。
(输出时按顶点编号从小到大输出)【解题思路】:1、我们可以先通过传递闭包的longlink,计算出每个顶点所在的连通分支,然后在所有可能的连通分支中找出满足条件的解即可。
2、至于计算连通分支的顶点方案,只要分别从连通分支中任选一个代表顶点,由此出发,通过深度优先搜索即可得到顶点方案。
设:1)best,besti分别存放含顶点数最多的连通分支中的顶点数和代表顶点;2)max,maxk分别存放顶点的权之和最大的连通分支的顶点权之和和代表顶点。
3、计算best,besti,max,maxk的过程如下:1)读入无向图的信息;2)计算传递闭包longlink;3)穷举每一个顶点;4)dfs(besti); {从代表顶点besti出发,深度优先搜索含顶点数最多的连通分支}5)dfs(maxk); {从代表顶点maxk出发,深度优先搜索顶点的权之和最大的连通分支}【核心代码】:1、传递闭包longlink 的计算过程如下:3三、课后作业1、一笔画问题。
[问题描述] 编程对给定的一个图,判断能否一笔画出,若能请输出一笔画的先后顺序,否则输出“No Solution !”。
[输入格式]输入文件共n+1行,第1行为图的顶点数n ,接下来的n 行(每行n 个数据)为图的邻接矩阵,G[i,j]=1表示顶点i 和顶点j 有边相连,G[i,j]=0表示顶点i 和顶点j 无边相连。

传递闭包、即在数学中,在集合X上的二元关系R的传递闭包是包含R的X上的最小的传递关系。
例如,如果X是(生或死)人的集合而R是关系“为父子”,则R 的传递闭包是关系“x是y的祖先”。
再比如,如果X是空港的集合而关系xRy为“从空港x到空港y有直航”,则R的传递闭包是“可能经一次或多次航行从x飞到y”。
存在性和描述对于任何关系R,R 的传递闭包总是存在的。
传递关系的任何家族的交集也是传递的。
进一步的,至少存在一个包含R 的传递关系,也就是平凡的: X × X。
R 传递闭包给出自包含R 的所有传递关系的交集。
我们可以用更具体术语来描述R 的传递闭包如下。
定义在X 上的一个关系T,称xTy 当且仅当存在有限的元素(xi)序列,使得x = x0 并且x0Rx1, x1Rx2, …, xn−1Rxn 和xnRy形式上写为容易检查出关系T 是传递的并且包含R。
进一步的,任何包含R 的传递关系也包含T,所以T 是R 的传递闭包。
证实T 是包含R 的最小传递关系设A 是任何元素的集合。
假定: GA 传递关系RAGA TAGA。
所以(a,b)GA(a,b)TA. 所以,特定的(a,b)RA。
现在通过T 的定义,我们知道了n (a,b)RnA。
接着,i, in eiA。
所以,有从a 到b 路径如下: aRAe1RA...RAe(n-1)RAb。
但是,通过GA 在RA 上的传递性,i, in (a,ei)GA,所以,(a,e(n-1))GA (e(n-1),b)GA,所以通过GA 的传递性,我们得到了(a,b)GA。
矛盾于(a,b)GA。
因此,(a,b)AA, (a,b)TA (a,b)GA。
这意味着TG,对于任何包含R 的传递的G。
所以,T 是包含R 的最小传递闭包。
推论如果R 是传递的,则R = T。
用途注意两个传递关系的并集不必须是传递的。
为了保持传递性,必须采用传递闭包。
例如,这出现在取两个等价关系或预序的并的时候。

一、计算( 每题参考分值5分)1、设有向图D=<V,E>,V={v1,v2,v3,v4,v5,v6},E={(v1,v1),(v2,v1),(v2,v1),(v2,v3),(v3,v1),(v3,v4),(v3,v4) ,(v4,v1)},请画出图G的图形,并写出邻接矩阵。
正确答案:2、若马会飞或羊吃草,则母鸡就是会是飞鸟;如果母鸡是飞鸟,那么烤熟的鸭子还会跑;烤熟的鸭子不会跑;所以,羊不吃草。
正确答案:解:(1)将简单陈述句符号化p: 马会飞;q: 羊吃草;r: 母鸡是飞鸟;s: 烤熟的鸭子会跑。
(2)写出前提和结论前提: p∨q→r ;r →s;��s;结论:��q(3)自然构造法证明①r →s 前提引入②��s 前提引入③�� r ①②拒取式④ p∨q→r 前提引入⑤��(p∨q) ③④拒取式⑥�� p∧�� q ⑤等值演算⑦�� q ⑥化简规则3、设A = {1, 2, 3}, R = {<x,y> | x, yÎA且x+2y £ 6 },S = {<1,2>, <1,3>,<2,2>}, 求: (1) R的集合表达式;(2) R-1(3) RoS, R3正确答案:解:解:(1) R = {<1,1>, <1,2>, <2,1>, <2,2>, <3,1>}(2) R 1 = {<1,1>, <2,1>, <1,2>, <2,2>, <1,3 >}(3) R S = {<1,2>, <1,3>, <2,2>, <2,3>, <3,2>, <3,3>}R3 = {<1,1>, <1,2>, <2,1>, <2,2>, <3,1>, <3,2>}4、设集合A={a, b, c, d}上的关系R={<a, a>, <a,b>,<b, c>, <b, b>,<c,c>,<c,a>, <c, d>},试画出它的关系图及关系矩阵。
中山大学本科教学大纲Undergraduate Course Syllabus学院(系):数据科学与计算机学院School (Department):School of Data and Computer Science课程名称:离散数学基础Course Title:Discrete Mathematics二〇二〇年离散数学教学大纲Course Syllabus: Discreate Mathematics(编写日期:2020 年12 月)(Date: 19/12/2020)一、课程基本说明I. Basic Information二、课程基本内容 II. Course Content(一)课程内容i. Course Content1、逻辑与证明(22学时) Logic and Proofs (22 hours)1.1 命题逻辑的语法和语义(4学时) Propositional Logic (4 hours)命题的概念、命题逻辑联结词和复合命题,命题的真值表和命题运算的优先级,自然语言命题的符号化Propositional Logic, logic operators (negation, conjunction, disjunction, implication, bicondition), compound propositions, truth table, translating sentences into logic expressions1.2 命题公式等值演算(2学时) Logical Equivalences (2 hours)命题之间的关系、逻辑等值和逻辑蕴含,基本等值式,等值演算Logical equivalence, basic laws of logical equivalences, constructing new logical equivalences1.3 命题逻辑的推理理论(2学时)论断模式,论断的有效性及其证明,推理规则,命题逻辑中的基本推理规则(假言推理、假言易位、假言三段论、析取三段论、附加律、化简律、合取律),构造推理有效性的形式证明方法Argument forms, validity of arguments, inference rules, formal proofs1.4 谓词逻辑的语法和语义 (4学时) Predicates and Quantifiers (4 hours)命题逻辑的局限,个体与谓词、量词、全程量词与存在量词,自由变量与约束变量,谓词公式的真值,带量词的自然语言命题的符号化Limitations of propositional logic, individuals and predicates, quantifiers, the universal quantification and conjunction, the existential quantification and disjunction, free variables and bound variables, logic equivalences involving quantifiers, translating sentences into quantified expressions.1.4 谓词公式等值演算(2学时) Nested Quantifiers (2 hours)谓词公式之间的逻辑蕴含与逻辑等值,带嵌套量词的自然语言命题的符号化,嵌套量词与逻辑等值Understanding statements involving nested quantifiers, the order of quantifiers, translating sentences into logical expressions involving nested quantifiers, logical equivalences involving nested quantifiers.1.5谓词逻辑的推理规则和有效推理(4学时) Rules of Inference (4 hours)证明的基本含和证明的形式结构,带量词公式的推理规则(全程量词实例化、全程量词一般化、存在量词实例化、存在量词一般化),证明的构造Arguments, argument forms, validity of arguments, rules of inference for propositional logic (modus ponens, modus tollens, hypothetical syllogism, disjunctive syllogism, addition, simplication, conjunction), using rules of inference to build arguments, rules of inference for quantified statements (universal instantiation, universal generalization, existential instantiation, existential generalization)1.6 数学证明简介(2学时) Introduction to Proofs (2 hours)数学证明的相关术语、直接证明、通过逆反命题证明、反证法、证明中常见的错误Terminology of proofs, direct proofs, proof by contraposition, proof by contradiction, mistakes in proofs1.7 数学证明方法与策略初步(2学时) Proof Methods and Strategy (2 hours)穷举法、分情况证明、存在命题的证明、证明策略(前向与后向推理)Exhaustive proof, proof by cases, existence proofs, proof strategies (forward and backward reasoning)2、集合、函数和关系(18学时)Sets, Functions and Relations(18 hours)2.1 集合及其运算(3学时) Sets (3 hours)集合与元素、集合的表示、集合相等、文氏图、子集、幂集、笛卡尔积Set and its elements, set representations, set identities, Venn diagrams, subsets, power sets, Cartesian products.集合基本运算(并、交、补)、广义并与广义交、集合基本恒等式Unions, intersections, differences, complements, generalized unions and intersections, basic laws for set identities.2.2函数(3学时) Functions (3 hours)函数的定义、域和共域、像和原像、函数相等、单函数与满函数、函数逆与函数复合、函数图像Functions, domains and codomains, images and pre-images, function identity, one-to-one and onto functions, inverse functions and compositions of functions.2.3. 集合的基数(1学时)集合等势、有穷集、无穷集、可数集和不可数集Set equinumerous, finite set, infinite set, countable set, uncountable set.2.4 集合的归纳定义、归纳法和递归(3学时)Inductive sets, inductions and recursions (3 hours)自然数的归纳定义,自然数上的归纳法和递归函数;数学归纳法(第一数学归纳法)及应用举例、强归纳法(第二数学归纳法)及应用举例;集合一般归纳定义模式、结构归纳法和递归函数。
图论中有向图的矩阵方法方冬云【摘要】图论中的有向图应用较广,而有向图本身具有一些性质.文章利用高等代数中的矩阵来研究有向图的关系传递闭包问题和有向图中的回路类型问题.当然矩阵来还可以解决图论中的其它问题,解决中学数学中的一些问题,也能解决生活中的一些问题.【期刊名称】《榆林学院学报》【年(卷),期】2018(028)006【总页数】4页(P79-82)【关键词】矩阵;关系图;关系闭包;有向图;回路【作者】方冬云【作者单位】莆田学院数学与金融学院,福建莆田 351100【正文语种】中文【中图分类】O157.51 引言高等代数或线性代数中的矩阵除了研究自身的性质外,更重要的是它在其它领域上的应用,如:在高代或线代中解线性方程组的应用;在中学数学中解三角形面积的应用;在高等数学中对隐函数求导的应用;在密码学中的应用;社会生产管理问题;锁具装箱问题;商人过河问题;选址问题;配电网络问题等,下面就是利用矩阵来研究有向图的相关问题。
2 相关概念图论中的图分为无向图和有向图,它们由顶点集合和边的集合构成的,顶点之间有关系称为边,可以用线段或弧线来连结,当边有方向则就变为有向图,否则就是无向图。
有向图中因顶点与边的关系存在通路和回路,有向图中的通路:从顶点vi到vj存在这样的交替序列viei0vi1ei1…eijvj,则称为顶点vi到vj的通路。
有向图的回路:顶点vi到vj的通路上,如果vi= vj,则称之为回路。
回路类型可分为复杂回路、简单回路及初级回路(也称为圈),复杂回路:回路中边可以重复,顶点也可重复;简单回路:回路中各条边不能相同,但顶点可以重复;初级回路:回路中各条边不能相同且各个顶点也不能相同。
有向图中的边因顶点之间之间的关系而决定的,这样的有向图称为关系图,关系图与关系是一一对应的,所以有必要了解关系的相关概念。
已知集合A,集合A 上的二元关系(简称关系)是可定义为:R = {<x,y>x,y ∈ A},集合A×B上的二元关系可定义为: R = { <x,y>x ∈A,y ∈ B}。