当前位置：文档之家 › 第三章紊流模型

第三章紊流模型

  • 格式：ppt
  • 大小：445.50 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

中科大FLUENT讲稿_第三章_湍流模型

中科大FLUENT讲稿_第三章_湍流模型

第三章，湍流模型第一节， 前言湍流流动模型很多，但大致可以归纳为以下三类：第一类是湍流输运系数模型，是Boussinesq 于1877年针对二维流动提出的，将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。

即：2121x u u u t ∂∂=''-μρ 3－1 推广到三维问题，若用笛卡儿张量表示，即有：ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3－2 模型的任务就是给出计算湍流粘性系数t μ的方法。

根据建立模型所需要的微分方程的数目，可以分为零方程模型（代数方程模型），单方程模型和双方程模型。

第二类是抛弃了湍流输运系数的概念，直接建立湍流应力和其它二阶关联量的输运方程。

第三类是大涡模拟。

前两类是以湍流的统计结构为基础，对所有涡旋进行统计平均。

大涡模拟把湍流分成大尺度湍流和小尺度湍流，通过求解三维经过修正的Navier-Stokes 方程，得到大涡旋的运动特性，而对小涡旋运动还采用上述的模型。

实际求解中，选用什么模型要根据具体问题的特点来决定。

选择的一般原则是精度要高，应用简单，节省计算时间，同时也具有通用性。

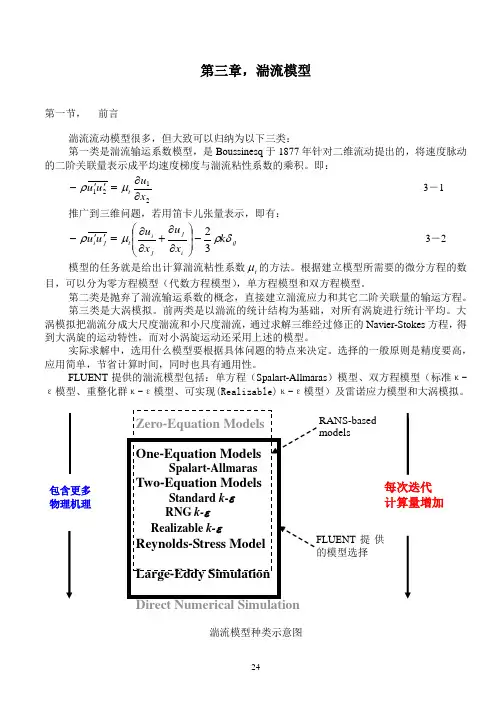
FLUENT 提供的湍流模型包括：单方程（Spalart-Allmaras ）模型、双方程模型（标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型）及雷诺应力模型和大涡模拟。

湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提供RANS-based models第二节，平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。

对于速度，有：i i i u u u '+= 3－3其中，i u 和i u '分别是平均速度和脉动速度（i=1,2,3）类似地，对于压力等其它标量，我们也有：φφφ'+= 3－4 其中，φ表示标量，如压力、能量、组分浓度等。

钻井液工艺学-第三章

钻井液工艺学-第三章

第二节
数学表达式：
钻井液的基本流型及特点
y
第二节
钻井液的基本流型及特点
流型判断（作图法）
（1）多点测试（τ，γ ） （2）分别以τ和γ为坐标轴绘图 （3）结合标准流变曲线进行判断
第三节
流变参数测量与计算
一.测量仪器及原理
1、漏斗粘度计
漏斗粘度 Funnel Viscosity 定 单 类 义：定体积泄流时间。 位：秒；s 型：
第四节 钻井液流变性与钻井作业的关系
三.钻井液流变性与井壁稳定的关系
流态对井壁稳定的影响：层流比紊流有利于井壁稳定。
第四节 钻井液流变性与钻井作业的关系
四.钻井液流变性与钻速的关系
第四节 钻井液流变性与钻井作业的关系
五.钻井液流变性与井内压力激动的关系
下钻: 当钻头在井内向下运动时，钻井液被推动着向上流动。这时钻头 处的压力等于钻头以上钻井液的流动阻力与该段钻井液的静液柱压力 。超出静液柱压力的部分被称为“激动压力”。这是造成井漏的原因之 一。 起钻:相反，当钻头在井内向上运动时，钻井液向下流动。这时钻头处 的压力等于钻头以上钻井液的静液柱压力减去该段钻井液的流动阻力 。低于静液柱压力的部分被称为“抽吸压力”。这是诱发井喷、井塌的 原因之一。 主要控制措施： 控制起下钻速度； 降低钻井液粘切。
μ a=τ/γ ，mPa· s
第三节
流变参数测量与计算
某一剪切速率下的表观粘度可用下式表示：
μ a=（300ѲN）/N
N—表示转速，单位为r/min； ѲN—表示转速为N时的刻度盘读数。 在评价钻井液的性能时，为便于比较，如果没有特别注明某一剪切速率， 一般是指测定600r/min时的表观粘度，即：
μp

第三章(第三次课) 两相流动模型(飘)

第三章(第三次课) 两相流动模型(飘)

1 x 1 1 K 2 x
3
1 2
式中
K2
l v
Jl
0 .5
exp 1 . 72 10

6
q


环形通道下求得的值与Marchaterre（泡状流）、 Cook（泡状流）、Egen（泡状流）以及Hoglund （泡状流）等的数据相比较，符合得很好。对于棒 束通道，当由泡状流过渡到弹状流时，观察到空泡 份额有一个峰值，这可能是由于邻近子通道间存在 紊流交混和横向流动影响的缘故；在弹状流与环状 流区，具有较大的扰动波。4根棒束的值比圆管与 同心环形通道下的值要低约5；7根棒束时，则 要低约10。
Zuber-Findlay方法 弹状流

x
1 2 x 1 x 0 . 35 g l v D v C 0 l G l v
搅拌流

x
1 4 x 1 x 1 . 18 g l v v C 0 2 l G l v

模型的建立
考察一维稳态流动，对每一相写出力平衡方
程（忽略壁面剪切力），则： 对液相，有
dp
对气相，有
dz
lg
F 1
0
dp dz
gg
F

0
这里，F为单位容积混合物的某一相对另一相
拖曳力。将上两式中的
F 1

dp dz
消去，有
l
2 l
C0
Biblioteka 1 4 u vj
g l v 1 . 18 2 l

紊流力学1

紊流力学1

紊流数值计算基础理论紊流运动的数值模拟，主要包括两方面，一是建立紊流数学模型，二是进行数值计算。

紊流数学模型主要包括零方程模型，单方程模型，双方程模型，雷诺应力模型（微分、代数）和近壁区模拟等，本文主要就最近所学内容，介绍紊流数值计算的相关基础理论。

一、 紊流数值计算概述一般情况下，紊流数学模型是一组偏微分方程。

方程中的自变量包括三个空间坐标和时间坐标，微分方程的最高阶数为二阶，所以属于四元二阶偏微分方程。

方程组中偏微分方程的个数，即基本待求变量的个数，少的有五个，如二元ε-K 模型（连续方程，两个方向的动量方程，K 的方程及ε的方程），多的从八九个到十六七个不等，视具体问题而定。

待求变量的个数总是和方程式的个数相一致的。

除基本变量外，方程式中还会有其它非独立变量，它们一般通过代数关系式和基本变量联系起来。

实际应用中计算最多的是二元问题，空间一维非恒定流实际也是二元问题：二元问题 ⎪⎪⎩⎪⎪⎨⎧恒定流沿宽度平均的立面二维恒定流沿水深平均的平面二维立面二维恒定流平面二维恒定流三元问题 ⎩⎨⎧空间三维恒定流空间二维非恒定流三元问题已有了不少工程算例，而三维空间的非恒定流，除少量理论性研究外，工程应用算例很少。

流体运动微分方程仅能描述流体运动的一般规律，还不能确定运动的具体状态，因此称为泛定方程，确定具体的运动状态，还需根据运动方程的类型给出定解条件，即初始条件和边界条件。

给定的条件适当，方程才有解，才能保证解是存在的，唯一的和连续的。

求解微分方程，首先要给定定解条件，紊流模拟的定解条件多数是在建立紊流模型的同时，结合流体运动的物理边界条件提出处理办法，有些要在数值计算中结合计算方法来解决。

二、 偏微分方程的性质及其分类微分方程转化为差分方程进行数值求解时，对于不同类型的方程，其求解方法不同。

流体力学中的微分方程通常分为双曲型、抛物型和椭圆型三类。

不同类型方程在数学上具有不同的特点，反映了物理上不同的流动特征。

第三章(第三次课) 两相流动模型(飘)

第三章(第三次课) 两相流动模型(飘)

1. Zuber-Findlay方法 弹状流
α=
x ⎧ ⎡ x 1 − x ⎤ 0.35 ⎡ g ( ρ − ρ )D ⎤ 1 2 ⎫ ⎪ ⎪ l v ρ v ⎨C 0 ⎢ + ⎥+ ⎢ ⎥ ⎬ ρl ⎦ G ⎣ ρl ⎪ ⎣ ρv ⎦ ⎪ ⎭ ⎩
搅拌流
α=
x ⎧ ⎡ x 1 − x ⎤ 1.18 ⎡ gσ ( ρ − ρ ) ⎤ 1 4 ⎫ ⎪ ⎪ l v ρ v ⎨C 0 ⎢ + + ⎢ ⎥ ⎬ ⎥ 2 ρl ⎦ G ⎣ ρl ⎪ ⎣ ρv ⎦ ⎪ ⎭ ⎩
第三课 两相流漂移流模型
上海交通大学 核工系
一、漂移流模型
漂移流（Drift Flux）模型主要是由Zuber等人 提出的。它是在热力学平衡的假设下，建立 在两相平均速度场基础上的一种模型。 漂移流模型的建立是将观察者建立在两相流 动的两相混合物上，认为观察者随着混合物 一起流动来观察气、液相的流动情况。
式中的C0是这个公式的精华所在,它是考虑了 流速与空泡份额的不均匀分布的影响，称为 分布参数
(1 A)∫AαJdA αJ C0 = = α J (1 A)∫ αdA ⋅ (1 A)∫ JdA
A A
Lahey给出了各种不同 空泡份额分布情况下的 变化，如图所示
Wallis对孤立小气泡垂直上升流道的泡状流型 （α < 0.2 ），建议 C 0 = 1.0 Zuber-Staub等对垂直上升流动的搅拌流型， p 建议则取决于流道直径与对比态压力 p cr （p为系统压力，pcr为临界压力） 关于C0的具体计算公式可以看教材表3-2
本次课结束！
⎛ ρv 其中 b = ⎜ ⎜ρ ⎝ l
⎞ ⎟ ⎟ ⎠
0.1

流体力学5.1紊流汇编

流体力学5.1紊流汇编
北京工业大学市政学科部——马长明 高等流体(水）力学讲稿
边界层中能量 各项平衡图示
15
第四讲
紊（湍）流运动基础
三、紊流统计理论与模式理论简介
紊流的研究主围绕对雷诺应力或各阶相关量的确定展开。 一百多年理论研究沿着两条不同的路线进行： 一种采用统计方法，侧重研究紊流机理，称为紊流统计理论； 另一种引入不同的经验假设，侧重解决工程实际问题，称为紊流模式理论。 1980年以后，随着计算计术的发展，N-S方程的直接数值模拟（DNS）及大 涡模拟（LES）得到蓬勃发展。
可得紊流动能方程
ui k k uj u u i j t x j x j x j Ck Pk
式中： Ck：紊动动能的随体导数，称为传输项； Pk：雷诺应力与平均流速梯度的乘积，称为产生项； Dk：是一种梯度表示，称为扩散项； ε：是速度脉动量的平均值，称为耗散项。
Qij ( x, r )
2 2 u ( x ) u i j ( x r)
北京工业大学市政学科部——马长明
高等流体(水）力学讲稿
10
第四讲
紊（湍）流运动基础
2、紊流时均运动方程（对不可压流动）
（1）连续方程 ui 0 x i 时均运算：
ui ( ui u i ) 0 x i x i
北京工业大学市政学科部——马长明
高等流体(水）力学讲稿
4
第四讲
紊（湍）流运动基础
（4）充分发展的紊流研究 紊流的发生：剪切层的存在—产生涡。（剪切层的类型图示）
对充分发展的紊流研究分类： 1）自由剪切紊流：剪切层由流速间断面引起，紊动发展 不受边壁的限制； 2）边壁剪切紊流：剪切层由边壁附着引起，紊动发展受 边壁限制。 3）均匀各向同性紊流：作为理论研究的假想模型。流动 中无速度梯度，也无剪切应力。

von karman模型三维大气紊流仿真理论与方法

von karman模型三维大气紊流仿真理论与方法

von karman模型三维大气紊流仿真理论与方法
维尔•凯尔曼模型（Von Karman Model）是一种模拟大气紊流的仿真理论和方法。

该
模型以把紊流进行粗略的三维仿真为特色，被广泛应用在大气科学、气象学等领域。

凯尔
曼模型将大气中受湍流影响的气流运动描述为平均流与湍流流之间的相互作用，折射率参
数描述了湍流对平均流的影响。

通过这种方式，可以更清楚地观察到扰动流的变化的过程，从而更好地理解湍流流动过程中的细节。

凯尔曼模型在仿真三维大气紊流方面有着重要意义。

它基于传统气体理论提出了湍流
模型，并将一般动量方程积分一般化，反映了空间和时间尺度上湍流流动的影响。

它模拟
了湍流流动过程中的紊流特性，如湍流衰减、发展之间的关系，以及空间结构尺度和混合
尺度的影响。

此外，凯尔曼模型还能够处理不同空间尺度上的湍流，并且可以模拟平流流
的稳定性。

凯尔曼模型对于仿真三维大气紊流有着许多优势，它可以快速、准确地模拟空间参量
分布，进而精确模拟出高度不稳定流态，使研究者能够进行更多的控制参数分析，准确掌
握大气紊流参数，为研究者提供更多的实际帮助。

在科研应用方面，凯尔曼模型的参数分
析可以更好地理解湍流流动的规律性，为全局模型分析提供参考，还为天气预测提供更准
确的模型数据。

因此，维尔•凯尔曼模型为仿真三维大气紊流仿真提供了一种令人信服的
仿真技术，在气象科学等领域有大量应用。

几种紊流模型比较

几种紊流模型比较

文章 编 号 ：００ ８３ （０ ０１— １６ ０ １０ ～ １然和水利： 中， 程 紊流现象随处 可见 。从原则上说 ， 求解 上 述 问题 以及 各 种 复 杂 的紊 流 问题 并 无 理论 上 的 困 难 。 因为 这 方面， 描述紊流运动的精确的微分方程已经给出 ， 即纳维 一斯 托 克斯 方 程 ； 数 学 的 观 念来 看 ， 流 就 是 纳 维 一斯 托 克 斯 方 程 从 紊 的通解 ， 求解紊流问题与求解层流 问题并无本质上的差别 。另一 方面， 数值计算方法的发展 ， 以足 以求解纳维 一斯 托克斯方程１ ” 。 但 是 ，现 代 计 算 机 的 储 存 能 力 和 运 算 速 度 尚不 足 以 不 做 任 何 假 设 的求解实际紊流问题 ， 因为紊流运动所包 含的单元 ， 比流动区 域 的尺度要小得多 ， 典型的数量级是流动区域尺度 的 １。倍 。为 ０ 了用数值计算方法求解紊动单元的运动要素 ，数值计 算的 网格
这类模型发展中的重要一步就是放弃速度比尺和时均速度梯度之间的直接联系转而根据微分输运方程确定速度比尺构成单方程紊流模精确的k方程在紊流模型中无法使用因为扩散项和耗散项中出现了新的紊动相关关系为了得到封闭的方程组必须提出假设对这两项进行模拟与标量扩散的表达式314相似可假设k的扩散通量与k的梯度成正比
塞 弗 曼 在 １７ 年 曾经 预 言 ， ２ ９７ 在 ０世 纪 末 ， 算 机 将 有 足 够 的 能 计
对于避免确定 １，冯 ・ 卡门曾建议将 与时均流速分布按照 下式建立关系 ：
Ｏ／ Ｏ ｕ ｙ （） ３
力 用 数 值计 算 方 法 求 解 紊 流 的精 确 控 制 方 程 。近十 年 中 ， 够 在 能
科 学 之友
Ｆｅｄ ｆｃ ｎｅ ｍ ｔ ｒ ｒｎ ｉ ｃＡ ａ ｕ ｉ ｏＳ ｅ ｅ ｓ

层流与紊流

层流与紊流

层流与紊流层流科技名词定义中文名称:层流英文名称:laminar flow定义1:流体中液体质点彼此互不混杂，质点运动轨迹呈有条不紊的线状形态的流动。

在河渠流动中当雷诺数小于500,2 000时出现，而在多孔介质中流动时，在当雷诺数小于1,10时出现。

应用学科:地理学(一级学科);水文学(二级学科)定义2:黏性流体低速运动时质点的层状流动。

应用学科:电力(一级学科);通论(二级学科)定义3:黏性流体质点互不掺混，迹线有条不紊、层次分明的流动。

应用学科:航空科技(一级学科);飞行原理(二级学科)定义4:黏性流体的互不混掺的层状运动。

应用学科:水利科技(一级学科);水力学、河流动力学、海岸动力学(二级学科);水力学(水利)(三级学科)本内容由全国科学技术名词审定委员会审定公布求助编辑百科名片层流层流是流体的一种流动状态。

流体在管内流动时，其质点沿着与管轴平行的方向作平滑直线运动。

此种流动称为层流或滞流，亦有称为直线流动的。

流体的流速在管中心处最大，其近壁处最小。

管内流体的平均流速与最大流速之比等于0.5，根据雷诺实验，当雷诺准数引Re<2320时，流体的流动状态为层流。

粘性流体的层状运动。

在这种流动中，流体微团的轨迹没有明显的不规则脉动。

相邻流体层间只有分子热运动造成的动量交换。

常见的层流有毛细管或多孔介质中的流动、轴承润滑膜中的流动、绕流物体表面边界层中的流动等。

目录相关计算举例说明编辑本段相关计算层流只出现在雷诺数Re(Re,ρUL,μ)较小的情况中，即流体密度ρ、特征速度U和物体特征长度L都很小，或流体粘度μ很大的情况中。

当Re超过某一临界雷诺数Recr时，层流因受扰动开始向不规则的湍流过渡，同时运动阻力急剧增大。

临界雷诺数主要取决于流动形式。

对于圆管，Recr?2000，这里特征速度是圆管横截面上的平均速度，特征长度是圆管内径。

层流远比湍流简单，其流动方程大多有精确解、近似解和数值解。

第三章 流体动力学.

第三章 流体动力学.

二. 伯努利方程的应用 ❖ 流速计原理——根据压强和流速的关系
ρgh
pA

pO

1 2
vO2
vO 2gh
❖ 流量计
1 2
1 2
v12

P1

1 2
v22

p2
Q=S1 v1= S2 v2
2gh Q S1S2 S12 S22
体位对血压的影响---压强和高度的关系
案例 患者，男，18岁，患鼻咽纤维血管瘤入院，全身麻醉下施
▪ 熟悉黏性流体层流 和湍流的特点、雷 诺数的意义。
❖ 物态 物体根据存在的形态分为固态、液态和气态.
❖ 流体(fluid) 气体与液体没有一定的形状,各部分之间极易发 生相对运动,具有流动性,因而被统称为流体.
❖ 流体动力学(hydrodynamics) 研究流体运动规律及其与边界相互作用的学科.

1 2
vB2
pB

p0

1 2
vB2
根据连续性方程可知,均匀虹吸管内,水的速率处
处相等,vB=vD.
对于同一流线上的B、C两点,应用伯努利方程有
pC

1 2
vC2

ghC

pB

1 2
vB2

ghB
均匀虹吸管内,水的速率处处相等,vC=vB ,整理得
pC pB g(hB hC )

1 2
v2A

pA

ghD

1 2
vD2

pD
vD 2g(hA hD )
QD SD vD
结果表明,通过改变D点距水面的垂直距离和虹 吸管内径,可以改变虹吸管流出水的体积流量.

第三章 层流流动及湍流流动

第三章 层流流动及湍流流动

3.4 管路计算
并联管路
指管路先出现分支而后又汇合
的管路。
图示为三管并联，各支管中流量 A
B
互相影响和制约，其流动情况比
较复杂，但仍然遵循质量和能量
守恒原则。特点是：
1.总管流量等于各支管流量之和：
qv ＝
＋ q q v1
v2
＋qv3
＋······
(2)各支管中的能量损失相同： ∑h失１＝∑h失２＝∑h失３＝∑h失ＡＢ
第三章 层流流动及湍流流动
3.1 流体的流动状态 3.2 管道中的流动 3.3 流动阻力与能量损失 3.4 管路计算 小结
3.1 流体的流动状态
雷诺实验
（Reynold，英国物理学家，1883年） •层流：流速较小时，流体迹线呈平行 于管轴的线簇或层状。 •过渡流：流速增大，层状或线簇状流 动模式被扰动，流体迹线开始摆动， 弯曲。 •紊流（湍流）：流速进一步增大，流 体质点开始搅混，交叉，并形成漩 涡，出现脉动。
复杂管路
并联管路 分支管路 汇合管路
3.4 管路计算
•计算内容： 1)已知：管径d、管长l、管件阀门设置∑le、流体输送量，求：输送设 备所加外功We，设备内压力p，设备相对位置ΔZ。 2)已知：d、l＋∑le求：ub或Vs(W) 3)已知： l＋∑le、 Vs求：d •试差法 •ub或d未知→Re未知→λ不能确定→无法用柏努利方程求解 •试差法方法： 1.设λ′=(0.02～0.03) → 由柏努利方程计算ub→计算Re →根据e/d 查摩擦系数图得λ，若λ′ = λ(相对误差≤3%)，则假设正确，否则 重新假设 2.设ub′ →由柏努利方程及阻力方程计算λ→据 e/d 查摩擦系数图得 Re→反算ub，若ub′=ub(相对误差≤3%)，则假设正确，否则重新假设。

室内空调环境紊流模型数值试验分析

室内空调环境紊流模型数值试验分析

比分 析 三 种 紊 流 模 型 的 流 场 与 实验 流 场 的 吻 合 度 ， 验 证 了 ＲＮ Ｇｋ 一￡ 模 型 对 实验 流 场 的 相 对 适 应 性 ， 为相 关流场 的
数值计算提供参考 。
关键词 ： 实验台； 流场 ； 速 度； 紊流模型 ； 数 值 计 算
中图分类号 ： ＴＥ ６ ８ ４
某些 流动 参数 ， 并需 要 对 建 立 的数 学模 型进 行 验 证
来确 定湍 流 模 型 是 否 适 用 。本 文 主 要 是 针 对 普 通
办公 室 流场 的研究 ， 先 建 立 与普 通 办 公 室流 场 相 似 的试 验 台 ， 通 过 实 验 与数 值 模 拟相 互 对 照 ， 对 比分 析 三种紊 流模 型对 试 验 流场 的吻 合度 ， 寻找 实 验 流 场 匹配 的紊流 模型 ， 为 普 通 办公 室 流 场 的数 值 模 拟 提供 参考 。
第３ ２ 卷第 １ 期
２ ０１ ４年 １ 月
西 安 航 空 学 院 学 报
Ｊ ｏ ｕ ｒ ｎ ａ ｌ ｏ ｆ Ｘｉ ’ ａ ｎ Ａｅ ｒ ｏ ｎ ａ ｕ ｔ ｉ ｃ ａ ｌ Ｕｎ ｉ ｖ ｅ ｒ ｓ ｉ ｔ ｙ
Ｖ０ １ ． ３ ２ ＮＯ ． １
Ｊ ａ ｎ．２ ０１ ４
２ 三 维 紊 流 实验
２ ． １ 实验 台的搭 建 实 验 台为一抽 象 的空 调 房 间 ， 该 房 间 的长 ×宽
图 １ 实 验 台
×高为 １ ． ６ ｍ×０ ． ８ ｍ×１ ． ５ ５ ｍ。空 调 系统 采 用 上
收 稿 日期 ： ２ ０ １ ３ 一 ｌ Ｏ 一 ２ ２
作者简 介： 李异（ １ ９ ８ ２ 一） ， 男， 湖南岳阳人 ， 讲师 ， 从 事暖通空调工程的教学和研究 。

3种紊流数值模型模拟明渠丁坝三维水流初探

3种紊流数值模型模拟明渠丁坝三维水流初探

Ｐ Ｐ 、 Ｐ Ｐ Ｐ 为流体 内应 力张量 的分 ｗ Ｐ
量。
维 丁坝水流的数值模拟还有待于进一步研究 ；并且 以前有关丁坝绕流的研究基本上都是基于 １ 紊 种 流模 型（ 标准 ， 模 型、ｋ ６ 模 型或者 Ｒ Ｍ模 ｃ — 一０ Ｓ 型等 ） ，对于这 ３种 紊流模 型在 同一个实 验条件 下还没有做过探索 。本文采用 ３种不 同的紊 流模 型模拟丁坝绕流流场 ，把数值计算 成果与实验成
中图分类号 ：Ｔ ８ ３ Ｖ ２ Ｖ ６ ；Ｔ ３ ２ 文献标志码 ：Ｂ 文章编号 ：１０ — １３ ２ １ ） ５０ ５ — ３ ０ ７ ０ ３ （ ０ １ ０－ ０ ６ ０
０ 概 述
丁坝 是水 利工 程 中被广 泛应用 的一种水 工 建筑
１ 数 值 方 法
比较 ３种数值紊流模型 ：标准 — 模型、ｋ 一
模 型 、Ｒ ｙｏｄ ｅｎｌｓ—Ｓｒｓ 型 （ Ｓ 模 型 ） ｔ ｓ模 ｅ ＲＭ 。这 里 为 了节 省文 章 的篇 幅只是把 ３种 紊流 数值模 型 的基
物 ，在航道整治、防洪护岸 、促淤保滩等工程中发 挥着 重要 的作 用 。修 建 丁 坝后 ，它 可 以束 窄 河 床 、 调整水流 ，使局部水流结构发生剧烈的改变 ，从而 打破了原有的水沙平衡 ，引起河床冲刷。因此对坝 后下游形成的漩涡区的大小 、水流对河床底的冲刷 程度等的研究是非常重要的。 到 目前 为止 ，国内外 的许 多学者做 了很多研 究 ，包括 实验 、理论 和数 值模 拟 。例 如 Ｆｊ ａ ｕｗ ｒ ｉ ａ 等 Ｊ ｏ ｎｇ ＿ 、Ｓｉａ３等 对 丁 坝 周 围 的 水 流 、Ｔｍｉａａ２ ｈｂ ｌ ｊ 流场的变化 以及紊流特性 做了实验研究 ；１７ ９８年 窦 国仁根据丁坝压缩水流的动量方程推导出了矩形

紊流基础

紊流基础

度长得多，但是又要比平均流动的非恒定时间尺度（波浪或者潮汐波动）短很多。
时均速度:
T
1
u
u t dt
T
N
1 u
N
(2)
连续记录
离散等间距点
紊流脉动: (3)
u t u t u 连续记录
u
u u 离散点
紊动强度:
u
ut
N
离散等间距点
相对紊动强度:
u /u
5
下标“rms”代表“均方根”。你应该看出（4）式给出的 urms 定义就是“随机”速度脉动集 合 u ′的标准差。类似的定义应用到横向和垂向速度 v（t）和 w（t）。大些的 urms 表示一 个更高程度的紊动。在下面的图中，两个记录具有相同的时均速度，但是左边的记录具有更 高些的紊动程度。
同的特征，在那里紊动控制着动量的垂直输运。非常靠近边界的区域称为层流次层，因为在
这个区域内，紊动被粘性抑制着。在这个区域中，速度剖面通过式（7）中给出的应力－应
变关系定义。我们将（6）式中给出的定义代入到（7）式中，并且使用近似∂u/ ∂y 求解速度剖面
u/y 来
层流次层
y δ 5ν/u :
u y u y/ν
什么这样，回忆（10）式中的层流次层的厚度δ ＝5ν/u 。所以尼古拉兹的结论简单地说就
是，当表面不平整度要低于层流次层厚度时（ε 5ν/u ），那么在层流次层以上的流动是感 觉不到边界表面的不平整程度的。我们称这个体系为光滑紊流。当粗糙度变得比层流次层高，
具体就是 ε 70 至 100 ν/u ＝14 到 20δ ，那么在层流次层以上的流动就能感觉到边界表 面的粗糙程度。在这些条件下 y0 = ε/30，也就是特征粗糙度是真实粗糙度尺度的函数，并且 通过 y0，对数剖面受边界表面粗糙度的影响而改变。我们称这个体系为粗糙紊流。

3-钻井液流变性

3-钻井液流变性
流变曲线： γ1/2-τ1/2 作图，为一条直线。
r1/2
γ -τ作图，为直线与曲线之和。
模式讨论 τ1/2 = τc1/2 + η1/2 γ1/2
0 r τ c1/2 τ 1/2
γ 0， τ τc 能够反映多数钻井液 具有内部结构情况。 γ ，η 能够反映多数钻井液 的剪切稀释性。 γ，η η 极限粘度。 能够反映出钻井液的
降τs—— 与上相反。
1 27
静切力的实际应用
（1）悬浮岩屑和加重材料
悬浮岩屑（球形）所需静切力为： τs（dyn/cm2) = d(岩- 浆）/6 τs(mg/cm2) = 1000 d(岩- 浆）/6 经验数据： 初切力 = 2～6 Pa时，可达到良好的悬浮能力。
τs
终切力 = 2初切力，属于良好型触变体。
模式讨论
τ- τ0 = ηp γ
或者 η= ηp + τ0/ γ
γ 0， τ τ0
能够反映多数钻井液具有内部结构情况。
γ ，η
γ， η ηp
能够反映多数钻井液的剪切稀释性。
能够反映出钻井液的极限粘度。
低剪切速率下： τ实> τ宾 表明模型拟合实际曲线有较大偏差.
1 13
真实泥浆与不同流型的比较
液 -液分子间内摩擦阻力；
特点： ηp不随dv/dr变化而变化。
1 34
影响因素：
固相含量：固含 ηp ； 分散度：分散度 ηp ； 液相粘度：液相粘度 ηp ；
它直接反映了钻井液中固相含量的高低及分散程度。
调整ηp 的方法：
根据影响因素升、降ηp 。
1 35
作用：衡量判断钻井液中固相含量的高低及分散程度。 高则有害，低则有利。

几种主要紊流模型的应用特性比较

几种主要紊流模型的应用特性比较
杂， 常与流 动的类 型有关 。但必须 指出混合 长度 理论是基 于紊流 局部 平衡 的假定 基础 上 的 ，在物 理概 念上 有一定
的不足 。
融
ａ ＝
吉＋ １ 一］［ ＇ Ｄ 妄票 ｌ ｌｌ一］ 罢 ［一 ＋ 雾 ＋Ｔ 一 ∽ｍｍ 暑 ｌ ］ ｜ ｎ １ 昙罢ｔ ∞∞ｄ １＇ Ｗ １
后， 计算紊流流动 的关键 就在于如何确定 。所谓紊 流模
型也就是把 与紊流 时均参数联 系起来 的关系式 。 根据
确定 方法 的不 同 ， 以将紊流模 型区分 为所谓 的零方程 可
模型、 一方程模 型及 两方程模 型等。
２１１ 方 程 模 型 零
所谓零 方程 模型 ，是指不需 要微分方程而是用 代数关
上式 中 为紊 流粘性 系数 。引入 Ｂ ｕｓ ｅｑ假 设 以 ｏｓｉ ｓ ｎ
值计算 ， 必须采用很小 的时 间与空 间步长 ， 才能分辨出紊流 中详细的空间结 构及变化 剧烈 的特 性。现代计算 机的存储 能力和运算 速度 尚不足求解 任何一个 实际的紊 流问题 ， 应
用 时甚为 困难。 求取流场内所有 尺度 涡的细节对 于水力学工程应用 而 言， 往往是不经济的 ， 大部分情况下 只关心 流场 内运 动要 素
维普资讯
。 淮水科研院办 科 论 】 萎利学究协 ｌ 技 坛 【 ｌ
几种主要紊流模型响应用特性比较
施 奇
（ 安徽省水利水资源重点实验室
【 摘
安徽省水利科学研究院
蚌埠
２ ３０ ） ３ ００
要】 紊流的数值模拟始 于上世 纪 ５ 年代 ， ０ 先后发展 了 ｋ －￡模型 、 二阶矩模型和代数 应力模型 ， 在工程 实际中得 到 了 紊流模型 二阶矩模 型 代 数应力模型
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2、紊流的基本特性
不规则性 或者叫随机性，由于这个特性，我们只
能应用统计的方法对紊流进行研究。
扩散特性 一个随机流动，如果不具有把速度的脉
动（或热、质量等）扩散到整个流场的特性，它不能 称作是紊流运动。
高雷诺数 紊流总是高雷诺数的流动。随着雷诺数的
增大，原来为层流的流动产生不稳定而转变成紊流。
涡度脉动的三维性 紊流是涡度的脉动强度很大的有
时均流方程
UUui pppi
代入精确方程，得时均值方程：
连续性方程
U i 0 xi
N-S方程
U ti U j U xji 1 x p i1 xj U xjiu iu j fi
温度和浓度 方程
t Uj x j xi xi uiS
1、紊动粘性概念 鲍辛涅斯克假设：
④溢流坝反弧段的高速水流有可 能在反弧段末端引起空蚀破坏， 如何计算反弧段紊流的速度场。 压力场，预测空泡在水中的发生、 发展和溃灭，从而寻求减免空蚀 破坏的合理措施。
三、研究方法
l）经验资料相关法
2）用解析方法求解 简化的方程
3）数值求解时间平均 的纳维埃－斯托克斯方Fra bibliotek程（即雷诺方程）
这类方法借助于因次分析， 将实验资料浓缩成许多经验 公式。只能描述一些最简单 的水流现象。
2、紊流模型的发展
普朗特（IJPrandtl）于1925年提出的混合长假设，是最早 把紊动输运项与时均流的当地量建立联系的紊流模型。应 用范围窄，通用性差。
从20世纪40年代开始，采用一些紊动量的微分输运方程，例如 紊动动能的输运方程、雷诺应力的输运方程等。这类模型的特 点是理论严谨、概念完整，其中某些模型中提出的基本概念仍 作为目前最先进的紊流模型的理论基础。
势流理论就是这类方法的典型例 子，由于实际流体现象复杂，古 典的势流理论已不能全面满足水 利工程发展的实际需要。
作为紊流的通解，纳维埃－斯 托克斯方程描述了流体运动的 一切细节
四、紊流模型
作为紊流的通解，N－S方程描述了流体运动的一 切细节
U ti Uj U xji fi 1 xpi x2 jU xij
t
l
2 m
U y
适用：简单的剪力层流动
局限性： 1、混合长理论忽略了紊动量的扩散输运 2、混合长理论忽略了紊动量的对流输运 3、混合长模型缺少通用性
但是，取平均的过程中方程中包含一些新未知项， 表示紊动引起的平均动量的输运以及热和物质的输运。 这使时均过程所得的方程组不再构成封闭系统，只有 借助于经验公式，才能使这些方程构成封闭系统，各 种类型的紊流模型应运而生。
1、紊流模型定义 紊流模型可定义为一组方程（代数方程或微分方
程），这组方程确定时均流方程中的紊动输运项，从 而封闭时均流方程组。
但在实际工程中具有重要意义的并不是紊流的一切细节，而 是紊流对于时间的平均效应。雷诺（Osborne Reynolds）第 一个建议用统计方法将N－S方程对某一时间比尺取平均，所 得到的方程描述水流的时均流速、时均压力分布以及其它物 理量（温度、浓度等）的时均分布。
UUU ppp
U ti U j U xjifi1 x p i xj U xji U iU j
一、紊流及其特性 1、紊流的定义
◆雷诺实验（1883年）：紊流中各层流体互相混掺， 流体质点作不规则运动。将紊流视为一种蜿蜒曲折、起 伏不定的流动。
◆泰勒（1937年）：流体流过固体表面或者相同流 体的分层流动中出现的一种不规则流动。
◆ Dryden(1939)：紊流是一种不规则的随机运动，随 时间作不易为普通量测仪器所察觉的振荡，这种振荡可 以认为是叠加在一种恒定运动之上的。
二、紊流现象及相应的研究课题
②河流中的淡水注人海洋，与 咸水混合，在河口区域内，水 中含盐量的分布规律如何？是 否影响水中动植物的生长？
①热电厂的废气排人大气层中，这 些废气在风的作用下如何运动？是 否有可能触及地面，地面上废气的 浓度如何？
③管流中的突然放大段，通常 在突然放大处形成涡旋，使流 态复杂，涡旋的尺寸和流速分 布如何确定？局部阻力系数如 何计算？
◆ Hinze(1975) ：紊流运动是一种不规则的流动状 态，它的流动参数随时间和空间随机变化，所以， 只能根据这些参数的统计平均值来区别各种紊流流 态。
可见，“不规则”是紊流的一个最重要的特 征。而这种不规则既是时间上的概念，同时也是 空间上的概念。仅仅从时间的概念上谈紊流的不 规则性，或仅仅从空间的概念上谈紊流的不规则 性都是不完整的。
uiuj tU xji U xij 3 2kij
紊动动能
k12u12u22u32
与气体分子运动 类似
tVL
2、紊动扩散概念
假设
ui
xi
紊动扩散系数
t t
普朗特数 施密特数
六、零方程模型
1、 t 和 为常数的模型
适用：大体积水体的流动，紊动粘性项对计算影响很小；温度场
的远区。 2、混合长模型
旋三维运动。
耗散性 紊动动能通过粘性切应力的作用不
断转化成流体的内能，如果紊动的能量得不到 连续的补充，紊动会迅速衰减。
连续性 在每个涡旋的尺度范围内，单位时
间分子的碰撞次数是如此之多，至使动量的传 递和调整时间短到可以看作是瞬时反应，因此 可以认为，紊流运动仍然符合连续性的条件。
紊动只是流体流动的一种特性，而不是流体 的特征。所以，紊流的许多动力特性对一切流 体（液体和气体）流动都相同。
在20世纪60年代中期，计算机的威力已足够强大，才有可能 求解时均流偏微分方程，也才有可能检验、应用和发展这一 类紊流模型。
3、紊流模型分类
①零方程模型：常系数模型，混合长模型，剪力模型等 ②单方程模型：k方程模型
③双方程模型：k- 模型
4、评价紊流模型优劣的标准
①适用于多种类型的水流现象； ②具有足够的精度； ③人力和计算机费用适度； ④复杂程度适当。
五、 紊流的数学描述
紊流是满足连续性条件的，因此对于连续介质流体所导出的连续 性方程和Navier-Stokes方程组可以用于描述紊流的瞬时流态。
张量表达式：
连续性方程
精 确
N-S方程
方
程
温度和浓度 方程
U i 0 xi
U ti Uj U xji 1 x pi x2 jU xij fi
t Uj x j xj2 xj S