紊流理论(紊流模型)-文档资料
- 格式：ppt
- 大小：1.99 MB
- 文档页数：19
下载文档原格式
合集下载
第四章紊流流动
式中：
R2
Fk R 2 P P2 1 —管道横截面积。
4 1
13
对于层流，可通过动量传输原理严格地解出管道 中的速度分布函数vx(r)，并由牛顿粘性定律： dv 0 x r R dr 准确地推导出在管壁处的粘性切应力 0 。但是由于 紊流很复杂，不易推导出严格的管中流体的速度分布， 因而也无法计算管中的流量Q及阻力Fk等。 处理管中紊流流动及摩擦阻力Fk的方法是假定存 在一无量纲的参数—摩擦系数f ，且紊流对管道的摩 擦阻力可表示为：
212kvv243122kffak?frl?v?????????????????15如果已知某紊流流体在一定的管道中的流动摩擦系数f就可由上式算出管道中的平均速度
第四章 流体的紊流流动
Chapter 4 Turbu动值
2
3
速度的时均值和脉动值
紊流时，各质点的运动复杂，没有一定的规律和方向。 但可以认为有一个平均度，附加一个脉动速度。这一脉动 速度的大小和方向变化很快。
v x v x v x 1 t v x v x dt t 0 t 1 vx 0 vx dt 0 t
4
v 式中： x —X轴方向上的平均速度； v x —是 v x 中围绕 v x 的脉动变化量。称为脉动速 度。v x 的大小和快慢由流体的紊流状态决定。且具有如
(v (强 ) ) 2 (vx ) 2 x
5
6
7
8
9
4.2 沿平板的紊流速度边界层
有一时均速度为 vx v 的束流紊流流体沿水平方向 流过一大平板，如图所示：
10
与平板接触后，由于流体的粘性作用，在平板附近 产生一很大的速度梯度(粘性应力很大)，首先产生一 层流的速度边界层。在层流边界层区，粘性应力为主。 随着沿平板流动，粘性动量传输作用。有所下降， 但很大，会产生不稳定的扰动。在边界层上都会产生 局部紊流，即，速度边界层发生分支。此过程为边界 层从层流边界层向紊流边界层过渡，称“过渡区”。
总结紊流模型
总结紊流模型引言紊流模型是研究流体力学中的一种重要模型。
紊流是流体运动中的一种不规则且无序的状态，其对流体的输运和混合过程具有重要影响。
紊流模型是为了研究和描述紊流行为而开发的一套数学模型和数值方法。
在本文中，我们将对紊流模型进行总结和介绍。
紊流模型的背景紊流是指流体运动中出现的一种混乱、不规则且无序的状态。
紊流行为对于理解和描述自然界中很多现象具有重要意义。
例如，在地球大气层中，气象学家需要研究和预测风场的紊流行为，以便预测天气和气候变化。
此外，在工程领域中，了解和控制液体和气体的紊流行为对于设计有效的流体输运系统和减小能量损耗也是至关重要的。
紊流模型的发展可以追溯到19世纪。
著名的物理学家奥斯特里奇尔首先提出了紊流的描述方法，他认为紊流是由无数个不同尺度的涡旋组合而成的。
随后，许多学者对紊流进行了深入研究，并提出了不同的理论和模型。
这些模型主要包括雷诺平均纳维-斯托克斯（RANS）方程模型、大涡模拟（LES）模型和直接数值模拟（DNS）模型等。
雷诺平均纳维-斯托克斯方程模型雷诺平均纳维-斯托克斯方程模型是最常用的紊流模型之一。
该模型基于平均流动场的假设，将流场分解为平均部分和涨落部分。
该模型利用雷诺应力项来描述涨落部分的影响，并采用一系列经验公式来计算涨落部分的动力学行为。
尽管RANS 模型已经广泛应用于各个领域，但由于其对涡旋的统计特性进行了平均化处理，因此无法准确描述流体中小尺度涡旋的空间和时间演化。
大涡模拟模型大涡模拟模型是一种介于RANS模型和DNS模型之间的紊流模型。
该模型利用滤波方法将流体运动分解为大尺度运动和小尺度运动，并采用过滤后的雷诺平均纳维-斯托克斯方程对大尺度运动进行求解，对小尺度运动进行模型化处理。
大涡模拟模型具有较好的精度和计算效率，因此在工程领域中得到了广泛应用。
直接数值模拟模型直接数值模拟模型是对紊流行为进行最准确描述的一种模型。
该模型通过离散化流体运动方程，并采用数值方法对其进行求解，可以直接获得流体中各个尺度的涡旋的空间和时间演化。
冯卡门大气紊流模型推导
冯卡门大气紊流模型推导介绍大气紊流是指地球大气中的湍流现象。
冯卡门大气紊流模型是描述大气中的湍流现象的模型。
冯卡门方程冯卡门方程是描述大气紊流的微分方程组。
它包括三个方程：连续性方程、Navier-Stokes方程和状态方程。
连续性方程连续性方程描述了质量守恒的原则，可以表示为：∂ρ∂t+∇⋅(ρu)=0其中，ρ是空气密度，u是速度矢量。
Navier-Stokes方程Navier-Stokes方程描述了动量守恒的原则，可以表示为：∂u ∂t +u⋅∇u=−1ρ∇P+ν∇2u+g其中，P是压力，ν是动力粘性系数，g是重力加速度。
状态方程状态方程描述了气体物理性质与状态之间的关系，通常可以表示为：P=ρRT其中，R是气体常数，T是温度。
大气边界层大气边界层是指大气中靠近地表的一层区域，受到地表摩擦力和大气条件的影响。
在大气边界层中，湍流是主要的运动形式。
大气边界层可以分为三个不同的区域：大气表面层、颠簸层和波动层。
大气表面层大气表面层是距离地表几百米的一层区域。
在大气表面层中，湍流强度较大，主要受到地表摩擦力的影响。
这个区域的湍流可以通过冯卡门大气紊流模型来描述。
颠簸层颠簸层是距离地表几百米到几千米的一层区域。
在颠簸层中，湍流强度逐渐减弱，主要受到大气条件的影响。
波动层波动层是距离地表几千米以上的一层区域。
在波动层中，湍流强度较小，主要受到大气条件和地形等因素的影响。
大气紊流模拟方法大气紊流模拟是通过数值模拟方法来研究大气中的湍流现象。
目前常用的大气紊流模拟方法包括直接数值模拟（DNS）、大涡模拟（LES）和雷诺平均Navier-Stokes 方程模拟（RANS）等。
直接数值模拟（DNS）直接数值模拟是一种通过求解Navier-Stokes方程来模拟湍流的方法。
它可以精确地模拟湍流的细节，但需要消耗大量的计算资源。
大涡模拟（LES）大涡模拟是一种通过分解湍流流场为尺度较大的大涡和尺度较小的小涡来模拟湍流的方法。
火电厂集控运行专业《紊流》
圆管内流动规律
二、紊流流动规律
紊流结构 1—层流底层；2—过渡区；3—紊流核心
层流底层虽然很薄，但是它对紊流流动的能量损失以及流体与管壁之间 的热交换起着重要的影响。 例如层流底层的厚度越薄，换热就越强，流动阻力也越大。
圆管内流动规律
紊流流动速度分布
层流低层δ 过渡区 紊流核心区
层流低层δ
c (0.75 ~ 0.9)umax
混乱程度越大，速度分布越趋近于一致 。
பைடு நூலகம்
圆管内流动规律
二、紊流流动规律
水力光滑管与水力粗糙管 壁面的绝对粗糙度ε：管壁起伏高度的平均值 水力光滑管—— δ＞ε
特点：壁面粗糙对流动阻力的影响可忽略 水力粗糙管——δ＜ ε
特点：壁面粗糙对流动阻力的影响不可忽略 水力光滑与粗糙是相对的
原因：δ是可以改变的？ 思考：当qv增大时，δ如何变化
二、紊流流动规律
紊流结构 1—层流底层；2—过渡区；3—紊流核心
层流底层虽然很薄，但是它对紊流流动的能量损失以及流体与管壁之间 的热交换起着重要的影响。 例如层流底层的厚度越薄，换热就越强，流动阻力也越大。
圆管内流动规律
紊流流动速度分布
层流低层δ 过渡区 紊流核心区
层流低层δ
c (0.75 ~ 0.9)umax
混乱程度越大，速度分布越趋近于一致 。
பைடு நூலகம்
圆管内流动规律
二、紊流流动规律
水力光滑管与水力粗糙管 壁面的绝对粗糙度ε：管壁起伏高度的平均值 水力光滑管—— δ＞ε
特点：壁面粗糙对流动阻力的影响可忽略 水力粗糙管——δ＜ ε
特点：壁面粗糙对流动阻力的影响不可忽略 水力光滑与粗糙是相对的
原因：δ是可以改变的？ 思考：当qv增大时，δ如何变化
4.5 紊流运动——学习材料
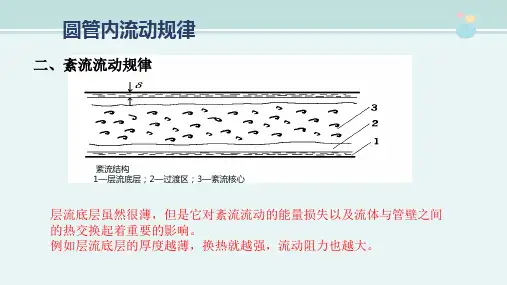
学习单元五、紊流运动运动要素的脉动和时均化研究方法紊流是自然界与工程中最常见的流动现象，研究其流动中的水头损失具有更重要的实际工程意义。
紊流比层流更复杂，目前的理论并不完善，主要从半理论半经验的角度介绍紊流的特征及其能量损失的实验研究和计算方法。
紊流流动中流体质点相互掺混，做无定向、无规则的运动，这种不规则性主要体现在紊流的脉动现象。
所谓脉动现象，就是诸如速度、压强等空间点上的物理量随时间的变化做无规则的即随机的变动。
在做相同条件下的重复试验时，所得的瞬时值不相同，但多次重复实验的结果的算术平均值趋于一致，具有规律性。
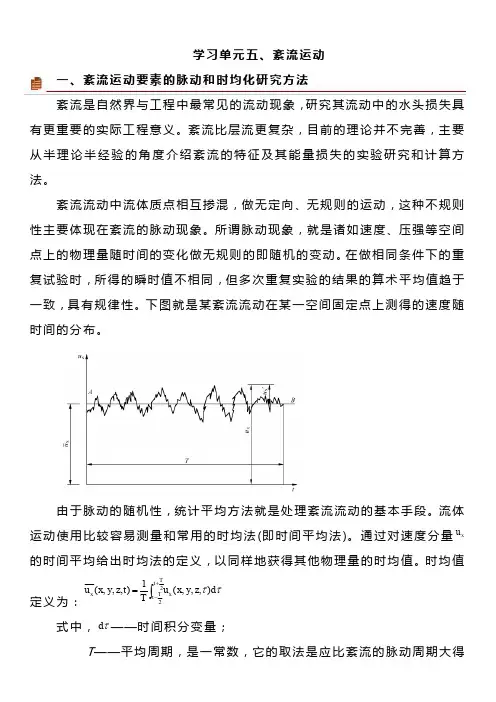
下图就是某紊流流动在某一空间固定点上测得的速度随时间的分布。
由于脉动的随机性，统计平均方法就是处理紊流流动的基本手段。
流体运动使用比较容易测量和常用的时均法(即时间平均法)。
通过对速度分量x u 的时间平均给出时均法的定义，以同样地获得其他物理量的时均值。
时均值定义为：⎰+-=22),,,(1),,,(TtTtxxdzyxuTt zyxuττ式中，τd——时间积分变量；T——平均周期，是一常数，它的取法是应比紊流的脉动周期大得多，而比流动的不恒定性的特征时间又小得多，随具体的流动而定。
瞬时值与平均值之差即为脉动值，脉动速度为：x x x u u u -=';y y y u u u -='。
如果紊流流动中，速度等各物理量的时均值不随时间而变，仅仅是空间点的函数，即称时均流动是恒定流动。
紊流的瞬时运动总是非恒定的，而平均运动可能是非恒定的，也可能是恒定的。
工程上关注的总是时均流动，一般仪器和仪表测量的也是时均值。
对紊流运动参数采用时均化后，前面所述的连续性方程、伯努利方程及动量方程等仍将适用。
在管流、射流和物体绕流等紊流流动中，初始来流的紊流度的强弱将影响到流动的发展。
紊流可分为以下3 种。
(1) 均匀各向同性紊流：在流场中，不同点以及同一点在不同方向上的紊流特性都相同。
紊流理论(紊流模型)
切细节，但在实际工程中具有重要意义的并不是紊 流的一切细节，而是紊流对于时间的平均效应。 – 雷诺（Osborne Reynolds）建议用统计方法将N －S方程取时间平均。但取平均的过程产生了新问 题：方程增加了新未知项，时均方程组不再封闭， 因此各种类型的紊流模型应运而生。 – 紊流模型可定义为一组方程，这组方程确定时均流 方程中的紊动输运项，从而封闭时均流动方程组（ 零方程、单方程、双方程）。
雷诺方程数值模拟（RANS）
• 单方程模型
– 将上式i方向乘以u’j，j方向乘以u’i，然后相加， 进行时间平均得
雷诺方程数值模拟（RANS）
• 单方程模型
雷诺方程数值模拟（RANS）
• 单方程模型
– 令i=j，将k带入，可得
雷诺方程数值模拟（RANS）
• 单方程模型
– 可见二者相同。
雷诺方程数值模拟（RANS）
紊流理论(紊流模型)
概述
• 紊流运动的瞬时连续方程和运动方程 • 连续方程 • 运动方程
概述
• 直接求解连续方程和运动方程，即 DNS(Direct Numerical Simulation)。
• 原则上讲，DNS并无理论上的困难。
– 一方面，描述紊流运动的精确的微分方程已经得出 ，即N－S方程；从数学观点看来，紊流就是N－S 方程的通解。
概述
• 紊流模型分类
– 直接数值模拟（DNS）。直接求解N－S方程，必 须采用很小的时间步长与空间步长。
– 大涡模拟（LES）。 DNS模拟大尺度运动，亚网格 上模拟小尺度运动。
– Reynolds时均方程法（RANS）。将N－S方程对 时间平均，并通过一些假定建立模型，是目前工程 中所采用的基本方法。根据对雷诺应力的处理方式 不同，分为基于涡粘性假设的模型和应力输运模型 两类，根据引入方程的数量，前者又分为零方程、 单方程和双方程模型。
雷诺方程数值模拟（RANS）
• 单方程模型
– 将上式i方向乘以u’j，j方向乘以u’i，然后相加， 进行时间平均得
雷诺方程数值模拟（RANS）
• 单方程模型
雷诺方程数值模拟（RANS）
• 单方程模型
– 令i=j，将k带入，可得
雷诺方程数值模拟（RANS）
• 单方程模型
– 可见二者相同。
雷诺方程数值模拟（RANS）
紊流理论(紊流模型)
概述
• 紊流运动的瞬时连续方程和运动方程 • 连续方程 • 运动方程
概述
• 直接求解连续方程和运动方程，即 DNS(Direct Numerical Simulation)。
• 原则上讲，DNS并无理论上的困难。
– 一方面，描述紊流运动的精确的微分方程已经得出 ，即N－S方程；从数学观点看来，紊流就是N－S 方程的通解。
概述
• 紊流模型分类
– 直接数值模拟（DNS）。直接求解N－S方程，必 须采用很小的时间步长与空间步长。
– 大涡模拟（LES）。 DNS模拟大尺度运动，亚网格 上模拟小尺度运动。
– Reynolds时均方程法（RANS）。将N－S方程对 时间平均，并通过一些假定建立模型，是目前工程 中所采用的基本方法。根据对雷诺应力的处理方式 不同，分为基于涡粘性假设的模型和应力输运模型 两类，根据引入方程的数量，前者又分为零方程、 单方程和双方程模型。
紊流理论(紊流模型)
ui 0 – 根据 xi
u v 0 x y
2
– v’与u’具有相同量级，且符号相反，则有
– 考虑紊动应力与粘性应力符号的一致性有
du u v l dy
' ' 2
du 2 du du l t u v l dy dy dy
' '
d ( u) 2 du t m ,m l l u2 dy dy
雷诺方程数值模拟（RANS）
• 零方程模型——混掺长度模型
– 普朗特假定l与从固体壁面算起的法向距离y成正比： l ky ，k=0.4（平板紊流边界层l~y 分布图） – 对于自由剪切紊流，混掺长度与断面混掺区宽度成 正比
带入可得12121212121412ckkcck57ransu方向v方向58rans对于k方程如果第一内结点设臵在粘性底层内贴近壁面的地方k0但按壁面函数法的要求将第一内结点布臵在对数规律层那里k的产生与耗散都比向壁面的扩散大得多取壁面上k1153020040059rans为了克服壁面函数法和低re数模型的缺陷近年来发展了区域模型法
• 零方程模型——混掺长度模型
– 卡门相似理论。上式每一项都有长度的尺度，假定 与混掺长度成比例，即
du dy
d u d u l, 2 2 dy 1 dy
2
1
2
d u 1 l 3 dy 2
2
3
– 卡门在分析时只取上式的第一项
du l dy
d u dy 2
概述
• 雷诺时均方程模型发展史
– 1942年，Kolmogorov提出了第一个完整的紊流模 型，除了k方程，还引入了另外一个参数ε，能量耗 散率，得到了双方程模型，即k-ε模型。70年代得 到应用。 – 他们的共同贡献是指出了封闭 Reynolds 方程或 Reynolds 应力的封闭表达式应从湍流脉动场的性 质去寻找。称为一阶封闭格式。 – 周培源（1945）和Rotta（1951），绕过 Boussinesq 涡粘性假定，提出了一个描述紊流切 应力张量演化的微分方程，即雷诺应力张量，得到 了应力输运模型，也称为二阶封闭或者二阶矩封闭 模型。70年代得到应用。
u v 0 x y
2
– v’与u’具有相同量级，且符号相反，则有
– 考虑紊动应力与粘性应力符号的一致性有
du u v l dy
' ' 2
du 2 du du l t u v l dy dy dy
' '
d ( u) 2 du t m ,m l l u2 dy dy
雷诺方程数值模拟（RANS）
• 零方程模型——混掺长度模型
– 普朗特假定l与从固体壁面算起的法向距离y成正比： l ky ，k=0.4（平板紊流边界层l~y 分布图） – 对于自由剪切紊流，混掺长度与断面混掺区宽度成 正比
带入可得12121212121412ckkcck57ransu方向v方向58rans对于k方程如果第一内结点设臵在粘性底层内贴近壁面的地方k0但按壁面函数法的要求将第一内结点布臵在对数规律层那里k的产生与耗散都比向壁面的扩散大得多取壁面上k1153020040059rans为了克服壁面函数法和低re数模型的缺陷近年来发展了区域模型法
• 零方程模型——混掺长度模型
– 卡门相似理论。上式每一项都有长度的尺度，假定 与混掺长度成比例，即
du dy
d u d u l, 2 2 dy 1 dy
2
1
2
d u 1 l 3 dy 2
2
3
– 卡门在分析时只取上式的第一项
du l dy
d u dy 2
概述
• 雷诺时均方程模型发展史
– 1942年，Kolmogorov提出了第一个完整的紊流模 型，除了k方程，还引入了另外一个参数ε，能量耗 散率，得到了双方程模型，即k-ε模型。70年代得 到应用。 – 他们的共同贡献是指出了封闭 Reynolds 方程或 Reynolds 应力的封闭表达式应从湍流脉动场的性 质去寻找。称为一阶封闭格式。 – 周培源（1945）和Rotta（1951），绕过 Boussinesq 涡粘性假定，提出了一个描述紊流切 应力张量演化的微分方程，即雷诺应力张量，得到 了应力输运模型，也称为二阶封闭或者二阶矩封闭 模型。70年代得到应用。
紊流力学1
紊流数值计算基础理论紊流运动的数值模拟，主要包括两方面，一是建立紊流数学模型，二是进行数值计算。
紊流数学模型主要包括零方程模型，单方程模型，双方程模型，雷诺应力模型（微分、代数）和近壁区模拟等，本文主要就最近所学内容，介绍紊流数值计算的相关基础理论。
一、 紊流数值计算概述一般情况下，紊流数学模型是一组偏微分方程。
方程中的自变量包括三个空间坐标和时间坐标，微分方程的最高阶数为二阶，所以属于四元二阶偏微分方程。
方程组中偏微分方程的个数，即基本待求变量的个数，少的有五个，如二元ε-K 模型（连续方程，两个方向的动量方程，K 的方程及ε的方程），多的从八九个到十六七个不等，视具体问题而定。
待求变量的个数总是和方程式的个数相一致的。
除基本变量外，方程式中还会有其它非独立变量，它们一般通过代数关系式和基本变量联系起来。
实际应用中计算最多的是二元问题，空间一维非恒定流实际也是二元问题：二元问题 ⎪⎪⎩⎪⎪⎨⎧恒定流沿宽度平均的立面二维恒定流沿水深平均的平面二维立面二维恒定流平面二维恒定流三元问题 ⎩⎨⎧空间三维恒定流空间二维非恒定流三元问题已有了不少工程算例，而三维空间的非恒定流，除少量理论性研究外，工程应用算例很少。
流体运动微分方程仅能描述流体运动的一般规律，还不能确定运动的具体状态，因此称为泛定方程，确定具体的运动状态，还需根据运动方程的类型给出定解条件，即初始条件和边界条件。
给定的条件适当，方程才有解，才能保证解是存在的，唯一的和连续的。
求解微分方程，首先要给定定解条件，紊流模拟的定解条件多数是在建立紊流模型的同时，结合流体运动的物理边界条件提出处理办法，有些要在数值计算中结合计算方法来解决。
二、 偏微分方程的性质及其分类微分方程转化为差分方程进行数值求解时，对于不同类型的方程，其求解方法不同。
流体力学中的微分方程通常分为双曲型、抛物型和椭圆型三类。
不同类型方程在数学上具有不同的特点，反映了物理上不同的流动特征。
紊流理论基础
紊流理论基础一、紊流的特点无序性：流体质点相互混掺，运动无序，运动要素具有随机性。
耗能性：除了粘性耗能外，还有更主要的由于紊动产生附加切应力引起的耗能。
扩散性：除分子扩散外，还有质点紊动引起的传质、传热和传递动量等扩散性能。
二、紊流切应力表达式1.紊流运动要素的脉动及其时均化时间平均流速：流体质点的瞬时速度始终围绕着某一平均值而不断跳动（即脉动），这一平均值就称作时间平均流速（图6-7）。
（6-14）或图6-7 紊流度N 可以表示紊动的程度：§ 脉动量的特点：脉动量的时均值为零，即。
各脉动量的均方值不等于零，即2.紊流切应力紊流流态下，紊流切应力：。
（6-15）矩形断面风洞中测得的切应力数据如图6-8：图6-8 说明：1）在雷诺数较小时，脉动较弱，粘性切应力占主要地位。
2）雷诺数较大时，脉动程度加剧，紊流附加切应力加大，在已充分发展的紊流中，粘性切应力与紊流附加切应力相比忽略不计。
3）沿断面切应力分布不同，近壁处以粘性切应力为主（称粘性底层）。
a.粘性切应力τv：从时均紊流的概念出发，各液层之间存在着粘性切应力：式中: b.紊流附加切力τt: ——时均流速梯度。
液体质点的脉动导致了质量交换，形成了动量交换和质点混掺，从而在液层交界面上产生了紊流附加切应力τt：的推导观看动画>> 由动量定律可知：动量增量等于紊流附加切应力△T 产生的冲量（图6-9），即：由质量守恒定律得：符号相反图6-9 由此可得二元紊流切应力表达式（6-16）注意：紊流附加切应力是由微团惯性引起的，只与流体密度和脉动强弱有关，而与流体粘性无直接关系。
3.紊流动量传递理论——普兰特混合长度理论紊流附加切应力中，脉动流速均为随机量，不能直接计算，无法求解切应力。
所以1925 年德国力学家普兰特比拟气体分子自由程的概念，提出了混合长理论。
a.普兰特假设：（1）不可压缩流体质点在从某流速的流层因脉动uy'进入另一流速的流层时，在运动的距离L（普1 兰特称此为混合长度）内，微团保持其本来的流动特征不变。
09_TurbFlow
23
水流运动基本方程的守恒形式
抖 u + 抖 x
抖 u + 抖 t 抖 v + 抖 t 抖 w + 抖 t
v + y
w = 0 z
2 骣 2u 抖u uw 1抖 p = fx + nç 2 + + ç 2 ç x z r 抖 x 抖 y 桫 2 骣 2v vw 1抖 p 抖v = fy + nç 2 + + ç 2 ç x z r 抖 y 抖 y 桫 2 骣 2w 抖w ww 1抖 p = fz + nç 2 + + ç 2 ç x z r 抖 z 抖 y 桫
¶ R yx u 鼢 1 骣 R xx 抖 + + + 鼢 2鼢 z r 桫抖 x y
2
R zx z
1 骣 s xx ç抖 + ¶ t yx + ç rç抖 y 桫x
¶u ¶x u÷ ÷ y÷ u÷ ÷ z÷
t zx ÷ ÷ z ÷
¶u ¶x u÷ ÷ y÷ u÷ ÷ z÷
s xx = 2r n t yx
ò
DW
r r r ⅱ ( r - r ) dW B (r )G
描述大涡运动的物理量
39
箱式滤波
ì 1 ï ï 3 ï r ¢- r ) = ï D G (r í ï ï 0 ï ï î
when x i¢- x i ot herwise
D 2
40
高斯滤波
r G (r ⅱ r ) = -
2 6 骣 6 r Exp ç- 2 r - r ÷ ÷ 3 ç D 桫 pD
R xx = 2r ne R yx
骣v 抖 = rnç + ç ç抖 桫x
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
– 对应层流中切应力与流速梯度关系的公式： d u dy
– 引入一个涡粘度 t ，将紊流中的雷诺应力与流场 中的时均流速梯度建立下述关系：
t uvt dduyt dduy
t
-uiuj
t
xuij
uj xi
11
雷诺方程数值模拟（RANS）
• 涡粘性假设（紊动粘性）
– 当i=j时，假设不合理，引入湍流脉动所产生的压力
续方程和运动方程，并对方程两边取平均：
ux uy uz 0 x y z
u ti uj x uij fi 1 x pi xj x uij uiuj
– 引入数学方程或者代数公式，确定所产生的新未知
项雷诺应力 u iu j ，而不引入新的变量。
10
雷诺方程数值模拟（RANS）
• 涡粘性假设（紊动粘性）
– 周培源（1945）和Rotta（1951），绕过 Boussinesq 涡粘性假定，提出了一个描述紊流切 应力张量演化的微分方程，即雷诺应力张量，得到 了应力输运模型，也称为二阶封闭或者二阶矩封闭 9 模型。70年代得到应用。
雷诺方程数值模拟（RANS）
• 雷诺时均方程的封闭问题
– 将瞬时值写成时均值+脉动值uu u，代入连
– 他们都没有尝试对雷诺方程进行系统的求解，许多 粘性流动的机理尚未清楚。
– 1925年，Prandtl 提出了混合长度理论来计算涡粘 性，为早期的研究奠定了基础。早期贡献最为显著 的还有von Karman，1930 年提出相似性假定。此 类模型并没有引入微分方程，称为零方程或者代数 模型。
– 1945年，Prandtl 提出一个涡粘性依赖于紊动能k 的模型，建议使用一个偏微分方程的模型对精确的 k方程进行近似，得到了单方程模型，即k方程模型。8
t
-uiuj
t xuji
uj xi
ptij
– 紊流涡粘度与层流中的粘度相对应，也可称为表观
粘度。粘度是流体本身的物理特性，与流动情况无
关。但是涡粘度则不是流体的物理性质，而是紊流
的一种流动特性，决定于流动的时均流速场和边界
条件。
– 引入涡粘性假设并未构成紊流模型，只是提供了构
造紊流模型的基础，但使模拟紊动应力问题转化为
– 紊流模型可定义为一组方程，这组方程确定时均流
方程中的紊动输运项，从而封闭时均流动方程组
（零方程、单方程、双方程）。
5
概述
• DNS之外的其他方法
– 大涡模拟LES。 – DNS可以获得尺度大于网格尺度的紊流结构，但却
无法模拟小于该网格尺度的紊动结构。 – 大涡模拟的思路是： DNS模拟大尺度紊流运动，而
概述
• 雷诺时均方程模型发展史
– 1942年，Kolmogorov提出了第一个完整的紊流模 型，除了k方程，还引入了另外一个参数ε，能量耗 散率，得到了双方程模型，即k-ε模型。70年代得 到应用。
– 他们的共同贡献是指出了封闭 Reynolds 方程或 Reynolds 应力的封闭表达式应从湍流脉动场的性 质去寻找。称为一阶封闭格式。
– 作为紊流的通解， N－S方程描述了流体运动的一 切细节，但在实际工程中具有重要意义的并不是紊 流的一切细节，而是紊流对于时间的平均效应。
– 雷诺（Osborne Reynolds）建议用统计方法将N －S方程取时间平均。但取平均的过程产生了新问 题：方程增加了新未知项，时均方程组不再封闭， 因此各种类型的紊流模型应运而生。
– Reynolds时均方程法（RANS）。将N－S方程对 时间平均，并通过一些假定建立模型，是目前工程 中所采用的基本方法。根据对雷诺应力的处理方式 不同，分为基于涡粘性假设的模型和应力输运模型 两类，根据引入方程的数量，前者又分为零方程、 单方程和双方程模型。
7
概述
• 雷诺时均方程模型发展史
– 1895年，Reynolds发表对紊流研究结果的文章。 – 1897年，Boussinesq((布辛涅司克))涡粘性假定。
二、紊流模型
• 1、概述 • 2、雷诺方程数值模拟（RANS） • 3、大涡模拟（LES） • 4、直接数值模拟（DNS）
1
概述
• 紊流运动的瞬时连续方程和运动方程
• 连续方程 • 运动方程
u 0，ui 0 xi
du f 1 p 2u
dt
ui t
uj
ui xj
fi
1 p
xi
2ui
xjxj
确定的分布。
12
雷诺方程数值模拟（RANS）
• 紊动扩散概念
– 将紊动热(或质量)输运与紊动动量输运直接类比， 假设热(或质量)输运与被输运的量有关：
ui'
xi
t /t
– 对于热输运问题,称为紊动普朗特数；对于质量输 运问题，称为紊动施密特(Schmidt)数。实验表明, 在流场中各点，甚至在不同型式的水流中，紊动普 朗特数几乎不变。
– 但是，现代计算机的储存的能力和运算速度尚不足 以求解任何一个实际的紊流问题。
3
概述
• DNS实际应用中的困难
– 紊流运动所包含的单元，比流动区域的尺度要小得 多。为了用数值计算方法求解紊动单元的运动要素， 数值计算的网格必须比紊动单元的尺度更小。如此 之多的网格点贮存各种变量，远远超过了现代计算 机的内存容量，而且，随着网格点的增加，算术运 算的次数显著增多，所需计算的时间令人望而却步。
– 塞弗曼（P G Saffmann）在1977年曾经预言，大 约在本世纪末，高度发展的计算机将有足够的能力 用数值计算方法求解紊流的精确方程，但在较近的 未来，精确地求解紊流问题无疑是不可能的。
– 到现在，DNS算法已有很大发展。
4
概述
• DNS之外的其他方法
– 求解时均N－S方程（即雷诺方程）。
2
概述
• 直接求解连续方程和运动方程，即 DNS(Direct Numerical Simulation)。
• 原则上讲，DNS并无理论上的困难。
– 一方面，描述紊流运动的精确的微分方程已经得出， 即N－S方程；从数学观点看来，紊流就是N－S方 程的通解。
– 另一方面，数值计算方法的发展，已足以求解 Nhomakorabea－S 方程。
利用亚网格尺度模型模拟小尺度紊流运动对大尺度 紊流运动的影响。 – LES较DNS拟占计算机的内存小，模拟需要的时间 也短，并且能够得到较雷诺平均模型更多的信息。
6
概述
• 紊流模型分类
– 直接数值模拟（DNS）。直接求解N－S方程，必 须采用很小的时间步长与空间步长。
– 大涡模拟（LES）。 DNS模拟大尺度运动，亚网格 上模拟小尺度运动。
– 引入一个涡粘度 t ，将紊流中的雷诺应力与流场 中的时均流速梯度建立下述关系：
t uvt dduyt dduy
t
-uiuj
t
xuij
uj xi
11
雷诺方程数值模拟（RANS）
• 涡粘性假设（紊动粘性）
– 当i=j时，假设不合理，引入湍流脉动所产生的压力
续方程和运动方程，并对方程两边取平均：
ux uy uz 0 x y z
u ti uj x uij fi 1 x pi xj x uij uiuj
– 引入数学方程或者代数公式，确定所产生的新未知
项雷诺应力 u iu j ，而不引入新的变量。
10
雷诺方程数值模拟（RANS）
• 涡粘性假设（紊动粘性）
– 周培源（1945）和Rotta（1951），绕过 Boussinesq 涡粘性假定，提出了一个描述紊流切 应力张量演化的微分方程，即雷诺应力张量，得到 了应力输运模型，也称为二阶封闭或者二阶矩封闭 9 模型。70年代得到应用。
雷诺方程数值模拟（RANS）
• 雷诺时均方程的封闭问题
– 将瞬时值写成时均值+脉动值uu u，代入连
– 他们都没有尝试对雷诺方程进行系统的求解，许多 粘性流动的机理尚未清楚。
– 1925年，Prandtl 提出了混合长度理论来计算涡粘 性，为早期的研究奠定了基础。早期贡献最为显著 的还有von Karman，1930 年提出相似性假定。此 类模型并没有引入微分方程，称为零方程或者代数 模型。
– 1945年，Prandtl 提出一个涡粘性依赖于紊动能k 的模型，建议使用一个偏微分方程的模型对精确的 k方程进行近似，得到了单方程模型，即k方程模型。8
t
-uiuj
t xuji
uj xi
ptij
– 紊流涡粘度与层流中的粘度相对应，也可称为表观
粘度。粘度是流体本身的物理特性，与流动情况无
关。但是涡粘度则不是流体的物理性质，而是紊流
的一种流动特性，决定于流动的时均流速场和边界
条件。
– 引入涡粘性假设并未构成紊流模型，只是提供了构
造紊流模型的基础，但使模拟紊动应力问题转化为
– 紊流模型可定义为一组方程，这组方程确定时均流
方程中的紊动输运项，从而封闭时均流动方程组
（零方程、单方程、双方程）。
5
概述
• DNS之外的其他方法
– 大涡模拟LES。 – DNS可以获得尺度大于网格尺度的紊流结构，但却
无法模拟小于该网格尺度的紊动结构。 – 大涡模拟的思路是： DNS模拟大尺度紊流运动，而
概述
• 雷诺时均方程模型发展史
– 1942年，Kolmogorov提出了第一个完整的紊流模 型，除了k方程，还引入了另外一个参数ε，能量耗 散率，得到了双方程模型，即k-ε模型。70年代得 到应用。
– 他们的共同贡献是指出了封闭 Reynolds 方程或 Reynolds 应力的封闭表达式应从湍流脉动场的性 质去寻找。称为一阶封闭格式。
– 作为紊流的通解， N－S方程描述了流体运动的一 切细节，但在实际工程中具有重要意义的并不是紊 流的一切细节，而是紊流对于时间的平均效应。
– 雷诺（Osborne Reynolds）建议用统计方法将N －S方程取时间平均。但取平均的过程产生了新问 题：方程增加了新未知项，时均方程组不再封闭， 因此各种类型的紊流模型应运而生。
– Reynolds时均方程法（RANS）。将N－S方程对 时间平均，并通过一些假定建立模型，是目前工程 中所采用的基本方法。根据对雷诺应力的处理方式 不同，分为基于涡粘性假设的模型和应力输运模型 两类，根据引入方程的数量，前者又分为零方程、 单方程和双方程模型。
7
概述
• 雷诺时均方程模型发展史
– 1895年，Reynolds发表对紊流研究结果的文章。 – 1897年，Boussinesq((布辛涅司克))涡粘性假定。
二、紊流模型
• 1、概述 • 2、雷诺方程数值模拟（RANS） • 3、大涡模拟（LES） • 4、直接数值模拟（DNS）
1
概述
• 紊流运动的瞬时连续方程和运动方程
• 连续方程 • 运动方程
u 0，ui 0 xi
du f 1 p 2u
dt
ui t
uj
ui xj
fi
1 p
xi
2ui
xjxj
确定的分布。
12
雷诺方程数值模拟（RANS）
• 紊动扩散概念
– 将紊动热(或质量)输运与紊动动量输运直接类比， 假设热(或质量)输运与被输运的量有关：
ui'
xi
t /t
– 对于热输运问题,称为紊动普朗特数；对于质量输 运问题，称为紊动施密特(Schmidt)数。实验表明, 在流场中各点，甚至在不同型式的水流中，紊动普 朗特数几乎不变。
– 但是，现代计算机的储存的能力和运算速度尚不足 以求解任何一个实际的紊流问题。
3
概述
• DNS实际应用中的困难
– 紊流运动所包含的单元，比流动区域的尺度要小得 多。为了用数值计算方法求解紊动单元的运动要素， 数值计算的网格必须比紊动单元的尺度更小。如此 之多的网格点贮存各种变量，远远超过了现代计算 机的内存容量，而且，随着网格点的增加，算术运 算的次数显著增多，所需计算的时间令人望而却步。
– 塞弗曼（P G Saffmann）在1977年曾经预言，大 约在本世纪末，高度发展的计算机将有足够的能力 用数值计算方法求解紊流的精确方程，但在较近的 未来，精确地求解紊流问题无疑是不可能的。
– 到现在，DNS算法已有很大发展。
4
概述
• DNS之外的其他方法
– 求解时均N－S方程（即雷诺方程）。
2
概述
• 直接求解连续方程和运动方程，即 DNS(Direct Numerical Simulation)。
• 原则上讲，DNS并无理论上的困难。
– 一方面，描述紊流运动的精确的微分方程已经得出， 即N－S方程；从数学观点看来，紊流就是N－S方 程的通解。
– 另一方面，数值计算方法的发展，已足以求解 Nhomakorabea－S 方程。
利用亚网格尺度模型模拟小尺度紊流运动对大尺度 紊流运动的影响。 – LES较DNS拟占计算机的内存小，模拟需要的时间 也短，并且能够得到较雷诺平均模型更多的信息。
6
概述
• 紊流模型分类
– 直接数值模拟（DNS）。直接求解N－S方程，必 须采用很小的时间步长与空间步长。
– 大涡模拟（LES）。 DNS模拟大尺度运动，亚网格 上模拟小尺度运动。