龙格库塔法RKF45Matlab实现

matlab龙格库塔方法求解二元二阶常微分方程组文章标题：深入探讨matlab中的龙格库塔方法及其在求解二元二阶常微分方程组中的应用摘要：在科学与工程领域，常常需要求解复杂的微分方程组，而matlab作为一种强大的数学工具，提供了许多求解微分方程组的方法。

本文将深入探讨matlab中的龙格库塔方法及其在求解二元二阶常微分方程组中的应用，以便读者全面理解该方法并能灵活应用于实际问题中。

正文：一、介绍龙格库塔方法龙格-库塔法（Runge-Kutta methods）是一种数值求解常微分方程的方法，通过将微分方程的解进行离散化，将微分方程转化为差分方程，从而进行数值求解。

龙格库塔方法通过迭代计算，能够得到微分方程的数值解，广泛应用于科学计算和工程技术领域。

二、matlab中的龙格库塔方法在matlab中，龙格库塔方法通过ode45函数实现，该函数能够对一阶或高阶常微分方程进行数值求解。

用户可以通过设定初始条件、微分方程表达式，以及积分区间等参数，快速得到微分方程的数值解。

ode45函数采用自适应步长的方式进行求解，能够有效解决微分方程解的数值稳定性和精确度问题。

三、龙格库塔方法在求解二元二阶常微分方程组中的应用考虑如下形式的二元二阶常微分方程组：$$\begin{cases}y_1' = f_1(t, y_1, y_2) \\y_2' = f_2(t, y_1, y_2)\end{cases}$$其中，$y_1(t)$和$y_2(t)$是未知函数，$f_1(t, y_1, y_2)$和$f_2(t,y_1, y_2)$分别表示其对应的函数表达式。

通过matlab中的ode45函数，可以将该二元二阶常微分方程组转化为一阶常微分方程组的形式，然后利用龙格库塔方法进行数值求解。

设定初始条件$y_1(0) = y1_0, y_2(0) = y2_0$，对应的一阶方程组为：$$\begin{cases}u_1' = u_3 \\u_2' = u_4 \\u_3' = f_1(t, u_1, u_2) \\u_4' = f_2(t, u_1, u_2)\end{cases}$$其中，$u_1(t) = y_1(t), u_2(t) = y_2(t), u_3(t) = y_1'(t), u_4(t) =y_2'(t)$，通过ode45函数求解该一阶常微分方程组即可得到原二元二阶常微分方程组的数值解。

常微分方程组的四阶Runge-Kutta方法1.问题：1.1若用普通方法-----仅适用于两个方程组成的方程组编程实现：创建M 文件：function R = rk4(f,g,a,b,xa,ya,N)%UNTITLED2 Summary of this function goes here% Detailed explanation goes here%x'=f(t,x,y) y'=g(t,x,y)%N为迭代次数%h为步长%ya,xa为初值f=@(t,x,y)(2*x-0.02*x*y);g=@(t,x,y)(0.0002*x*y-0.8*y);h=(b-a)/N;T=zeros(1,N+1);X=zeros(1,N+1);Y=zeros(1,N+1);T=a:h:b;X(1)=xa;Y(1)=ya;for j=1:Nf1=feval(f,T(j),X(j),Y(j));g1=feval(g,T(j),X(j),Y(j));f2=feval(f,T(j)+h/2,X(j)+h/2*f1,Y(j)+g1/2);g2=feval(g,T(j)+h/2,X(j)+h/2*f1,Y(j)+h/2*g1); f3=feval(f,T(j)+h/2,X(j)+h/2*f2,Y(j)+h*g2/2); g3=feval(g,T(j)+h/2,X(j)+h/2*f2,Y(j)+h/2*g2); f4=feval(f,T(j)+h,X(j)+h*f3,Y(j)+h*g3);g4=feval(g,T(j)+h,X(j)+h*f3,Y(j)+h*g3);X(j+1)=X(j)+h*(f1+2*f2+2*f3+f4)/6;Y(j+1)=Y(j)+h*(g1+2*g2+2*g3+g4)/6;R=[T' X' Y'];end情况一：对于x0=3000，y0=120控制台中输入：>> rk4('f','g',0,10,3000,120,10)运行结果：ans =1.0e+003 *0 3.0000 0.12000.0010 2.6637 0.09260.0020 3.7120 0.07740.0030 5.5033 0.08860.0040 4.9866 0.11930.0050 3.1930 0.11950.0060 2.7665 0.09510.0070 3.6543 0.07990.0080 5.2582 0.08840.0090 4.9942 0.11570.0100 3.3541 0.1185数据:情况二：对于x0=5000，y0=100命令行中输入：>> rk4('f','g',0,10,5000,100,10)运行结果：ans =1.0e+003 *0 5.0000 0.10000.0010 4.1883 0.11440.0020 3.2978 0.10720.0030 3.3468 0.09220.0040 4.2020 0.08760.0050 4.8807 0.09950.0060 4.2090 0.11260.0070 3.3874 0.10690.0080 3.4011 0.09340.0090 4.1568 0.08890.0100 4.7753 0.0991数据：结论：无论取得初值是哪一组，捕食者与被捕食者的数量总是一个增长另一个减少，并且是以T=5 为周期交替增长或减少的。

% [x0 xn]是计算范围
% hh 是步长
%% ===输入判断===
if (4 == nargin) % == 当没有给步长的时候使用默认步长==
h = 0.1 ;
elseif (5 == nargin)
h = hh ;
end
%% ===参数初始化(可以修改，可从网上找相关参数的值)，以下是通用参数===
废话不多说直接复制就可以运行文章底部有参考例子不明白就看看
四阶龙格库塔法matlab实现
% 废话不多说，直接复制就可以运行，文章底部有参考例子，不明白就看看
function [ yy ] = R_K_4( f , y0 , x0 , xn , hh )
% f 是inline function的句柄
% y0 是初始值
end
elseif (1 == nargout)
yy = y ;
else
disp('error : please check your input') ;
return ;
end
end
%% === 例子=======
%
% === input =========
% f = inline('x+y'') ;
% x: 0.800000 y: 2.651042
% x: 1.000000 y: 3.436502
y(k+1) = y(k) + h* ( c(1)*kk(1) + c(2)*kk(2) + c(3)*kk(3) + c(4)*kk(4) ) ;
end
%% ===输出处理===
if (0 == nargout)

MATLAB是一种用于算法开发、数据分析、可视化和数值计算的高级技术计算语言和交互式环境。

作为一个强大的工具，MATLAB提供了许多数值计算方法，其中4级4阶Runge-Kutta方法就是其中之一。

1. Runge-Kutta方法简介Runge-Kutta方法是求解常微分方程（ODE）的数值方法之一。

在MATLAB中，用户可以使用内置的ode45函数来调用4级4阶Runge-Kutta方法。

具体来说，4级4阶Runge-Kutta方法是一种单步迭代方法，通过在每个步骤中计算斜率来逐步逼近解析解。

它的优点是数值稳定性好，适用于多种类型的微分方程。

2. Runge-Kutta方法的公式4级4阶Runge-Kutta方法的一般形式如下：$$k_1 = hf(t_n, y_n)$$$$k_2 = hf(t_n + \frac{1}{2}h, y_n + \frac{1}{2}k_1)$$$$k_3 = hf(t_n + \frac{1}{2}h, y_n + \frac{1}{2}k_2)$$$$k_4 = hf(t_n + h, y_n + k_3)$$$$y_{n+1} = y_n + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)$$其中，$t_n$是当前的独立变量值，$y_n$是当前的解向量，h是步长，$f(t_n, y_n)$是给定点$(t_n, y_n)$处的斜率。

通过不断迭代上述公式，可以逐步求解微分方程的数值解。

3. MATLAB中的4级4阶Runge-Kutta方法的应用在MATLAB中，用户可以使用ode45函数调用4级4阶Runge-Kutta方法来求解常微分方程。

使用ode45函数的基本语法如下：```matlab[t, y] = ode45(odefun, tspan, y0)```其中，odefun是用户定义的ODE函数句柄，tspan指定了求解的时间范围，y0是初始条件。

龙格库塔法RKF45的Matlab实现2007-08-16 14:03:32| 分类：MatLab/Maple/Mat|字号订阅4阶5级龙格库塔法用于解一阶微分方程（组），对于高阶微分方程，可以将其转换为一阶微分方程组求解。

原程序由John.H.Mathews编写（数值方法matlab版），但只能解微分方程，不能解微分方程组。

由LiuLiu@uestc修改，使之能够解微分方程组。

该程序精度比matlab自带的ode45更高。

rkf45.m:function [Rt Rx]=rkf45(f,tspan,ya,m,tol)% Input:% - f function column vector% - tspan[a,b] left & right point of [a,b]% - ya initial value column vector% -m initial guess for number of steps% -tol tolerance% Output:% - Rt solution: vector of abscissas% - Rx solution: vector of ordinates% Program by John.Mathews, improved by liuliu@uestcif length(tspan)~=2error('length of vector tspan must be 2.');endif ~isnumeric(tspan)error('TSPAN should be a vector of integration steps.');endif ~isnumeric(ya)error('Ya should be a vector of initial conditions.');endh = diff(tspan);if any(sign(h(1))*h <= 0)error('Entries of TSPAN are not in order.') ;enda=tspan(1);b=tspan(2);ya=ya(:);a2 = 1/4; b2 = 1/4; a3 = 3/8; b3 = 3/32; c3 = 9/32; a4 = 12/13;b4 = 1932/2197; c4 = -7200/2197; d4 = 7296/2197; a5 = 1;b5 = 439/216; c5 = -8; d5 = 3680/513; e5 = -845/4104; a6 = 1/2;b6 = -8/27; c6 = 2; d6 = -3544/2565; e6 = 1859/4104; f6 = -11/40;r1 = 1/360; r3 = -128/4275; r4 = -2197/75240; r5 = 1/50;r6 = 2/55; n1 = 25/216; n3 = 1408/2565; n4 = 2197/4104; n5 = -1/5;big = 1e15;h = (b-a)/m;hmin = h/64;% 步长自适应范围下限hmax = 64*h;% 步长自适应范围上限max1 = 200;% 迭代次数上限Y(1,:) = ya;T(1) = a;j = 1;% tj = T(1);br = b - 0.00001*abs(b);while (T(j)<b),if ((T(j)+h)>br), h = b - T(j); end%caculate values of k1...k6,y1...y6tj = T(j);yj = Y(j,:);y1 = yj;k1 = h*feval(f,tj,y1);y2 = yj+b2*k1;if big<abs(max(y2)) return, endk2 = h*feval(f,tj+a2*h,y2);y3 = yj+b3*k1+c3*k2; if big<abs(max(y3)) return, endk3 = h*feval(f,tj+a3*h,y3);y4 = yj+b4*k1+c4*k2+d4*k3; if big<abs(max(y4)) return, endk4 = h*feval(f,tj+a4*h,y4);y5 = yj+b5*k1+c5.*k2+d5*k3+e5*k4; if big<abs(max(y5)) return, end k5 = h*feval(f,tj+a5*h,y5);y6 = yj+b6*k1+c6.*k2+d6*k3+e6*k4+f6*k5; if big<abs(max(y6)) return, endk6 = h*feval(f,tj+a6*h,y6);err = abs(r1*k1+r3*k3+r4*k4+r5*k5+r6*k6);ynew = yj+n1*k1+n3*k3+n4*k4+n5*k5;% error and step size controlif ( (err<tol) | (h<2*hmin) ),Y(j+1,:) = ynew;if ((tj+h)>br),T(j+1) = b;elseT(j+1) = tj + h;endj = j+1;tj = T(j);endif (max(err)==0),s = 0;elses1 = 0.84*(tol.*h./err).^(0.25);% 最佳步长值s=min(s1);endif ((s<0.75)&(h>2*hmin)), h = h/2; endif ((s>1.50)&(2*h<hmax)), h = 2*h; endif ( (big<abs(Y(j,:))) | (max1==j) ), return, endend% [Rt Rx]=[T' Y];Rt=T';Rx=Y;使用方法：首先编写方程（组）文件（注意与ode45不同，这儿方程组为1Xn数组：function dx= fun(t,x)dx=zeros(1,2);dx(1)=x(1)+x(2)*2+0*t;dx(2)=3*x(1)+x(2)*2+0*t;然后使用：[Rt,Rx]=rkf45(@fun,[0,0.2],[6;4],100,1e-7)。

T
t
1.0e+003 *
1.4
0
0.989
5
0.787
10
0.663
15
0.5788
20
0.5187
25
0.474
30
0.4401
35
0.4139
40
0.3935
45
0.3773
50
0.3644
55
0.3541
60
0.3458
65
0.3391
70
0.3337Leabharlann 750.329380
0.3258
85
0.3229
喃喃喔开3有一初始温度为1400k的铁球投入到无限大的水池中水温为310k假设铁球温度随时间的变化规律为下列表达式试用四五阶rk龙格库塔方法计算铁球在35min95min的温度
3、有一初始温度为1400K的铁球投入到无限大的水池中，水温为310K，假设铁球温度随时间的变化规律为下列表达式，试用四五阶 R-K（龙格-库塔）方法计算铁球在35min，95min的温度。
90
0.3205
95
步骤1：重新打开或直接输入clear
步骤2：创建m文件左上角File>>New>>M-File
步骤3：
在m文件编辑器里输入function temp =temp1(t,T)
temp=-0.04*exp(0.001*(T-310))*(T-310)
步骤4：保存m文件，注意文件名是函数名.mFile>>Save Workspace As
步骤5：保存m文件，注意文件名是<函数名>.m不然等会调不出来函数。
步骤6：在matlab 右边命令栏输入

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载龙格库塔方法及其matlab实现地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容龙格-库塔方法及其matlab实现摘要：本文的目的数值求解微分方程精确解，通过龙格-库塔法，加以利用matlab为工具达到求解目的。

龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法，用于数值求解微分方程。

MatLab软件是由美国Mathworks公司推出的用于数值计算和图形处理的科学计算系统环境。

MatLab 是英文MATrix LABoratory（矩阵实验室）的缩写。

在MratLab环境下，用户可以集成地进行程序设计、数值计算、图形绘制、输入输出、文件管理等各项操作。

关键词：龙格-库塔 matlab 微分方程前言1.1：知识背景龙格－库塔法（Runge-Kutta）是用于非线性常微分方程的解的重要的一类隐式或显式迭代法。

这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。

通常所说的龙格库塔方法是相对四阶龙格库塔而言的，成为经典四阶龙格库塔法。

该方法具有精度高，收敛，稳定，计算过程中可以改变步长不需要计算高阶导数等优点，但是仍需计算在一些点上的值，比如四阶龙格-库塔法没计算一步需要计算四步，在实际运用中是有一定复杂性的。

Matlab是在20世纪七十年代后期的事：时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授出于减轻学生编程负担的动机，为学生设计了一组调用LINPACK和EISPACK库程序的“通俗易用”的接口，此即用FORTRAN编写的萌芽状态的MATLAB。

经几年的校际流传，在Little的推动下，由Little、Moler、Steve Bangert合作，于1984年成立了MathWorks公司，并把MATLAB正式推向市场。

函数功能编辑本段回目录ode是专门用于解微分方程的功能函数，他有ode23,ode45,ode23s等等，采用的是Runge-Kutta算法。

ode45表示采用四阶，五阶runge-kutta单步算法,截断误差为(Δx)³。

解决的是Nonstiff(非刚性)的常微分方程.是解决数值解问题的首选方法,若长时间没结果,应该就是刚性的,换用ode23来解.使用方法编辑本段回目录[T,Y] = ode45(odefun,tspan,y0)odefun 是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名tspan 是区间[t0 tf] 或者一系列散点[t0,t1,...,tf]y0 是初始值向量T 返回列向量的时间点Y 返回对应T的求解列向量[T,Y] = ode45(odefun,tspan,y0,options)options 是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等[T,Y,TE,YE,IE] =ode45(odefun,tspan,y0,options)在设置了事件参数后的对应输出TE 事件发生时间YE 事件解决时间IE 事件消失时间sol =ode45(odefun,[t0 tf],y0...)sol 结构体输出结果应用举例编辑本段回目录1 求解一阶常微分方程程序:一阶常微分方程odefun=@(t,y) (y+3*t)/t^2; %定义函数tspan=[1 4]; %求解区间y0=-2; %初值[t,y]=ode45(odefun,tspan,y0);plot(t,y) %作图title('t^2y''=y+3t,y(1)=-2,1<t<4')legend('t^2y''=y+3t')xlabel('t')ylabel('y')% 精确解% dsolve('t^2*Dy=y+3*t','y(1)=-2')% ans =一阶求解结果图% (3*Ei(1) - 2*exp(1))/exp(1/t) - (3*Ei(1/t))/exp(1/t)2 求解高阶常微分方程关键是将高阶转为一阶,odefun的书写.F(y,y',y''...y(n-1),t)=0用变量替换,y1=y,y2=y'...注意odefun方程定义为列向量dxdy=[y(1),y(2)....]程序:function Testode45tspan=[3.9 4.0]; %求解区间y0=[2 8]; %初值[t,x]=ode45(@odefun,tspan,y0);plot(t,x(:,1),'-o',t,x(:,2),'-*')legend('y1','y2')title('y'' ''=-t*y + e^t*y'' +3sin2t')xlabel('t')ylabel('y')function y=odefun(t,x)y=zeros(2,1); % 列向量y(1)=x(2);y(2)=-t*x(1)+exp(t)*x(2)+3*sin(2*t);endend高阶求解结果图相关函数编辑本段回目录ode23, ode45, ode113, ode15s, ode23s, ode23t, ode23tbMatlab中龙格-库塔(Runge-Kutta)方法原理及实现(自己写的，非直接调用)龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。

matlab runge-kutta-fehlberg method1. 引言1.1 概述本文旨在介绍Matlab Runge-Kutta-Fehlberg方法，这是一种常用的数值解法，用于求解常微分方程组。

该方法结合了Runge-Kutta方法和Fehlberg方法的优点，具有较高的精度和稳定性。

1.2 文章结构本文首先介绍Matlab Runge-Kutta-Fehlberg方法的原理和实现步骤。

接着，我们将通过一个应用案例研究来验证该方法的有效性，并对结果进行详细分析。

然后，我们将与其他数值方法进行比较，评估其精度和速度。

最后，根据研究成果进行总结，并提出存在的问题及改进方向。

1.3 目的本文旨在全面了解Matlab Runge-Kutta-Fehlberg方法的原理和实现步骤，并通过应用案例研究来验证其有效性。

我们希望通过对不同数值算法结果的比较以及对结果解释与分析，评估该方法在求解常微分方程组中的优势，并提出改进方向以扩展其应用范围。

这将为科学研究和工程实践提供有力支持。

2. Matlab Runge-Kutta-Fehlberg Method2.1 方法介绍Matlab Runge-Kutta-Fehlberg方法（简称RKF方法）是一种高精度的数值积分方法，用于求解常微分方程（ODEs）初值问题。

该方法采用了经典的龙格-库塔（Runge-Kutta）方法和Fehlberg算法的组合，以提供更高的精度和稳定性。

RKF方法是一类自适应步长控制的显式算法，其基本思想是通过计算不同阶数下的两个解并利用它们之间的差异来评估误差。

该方法根据所需精度自动调整步长，确保求解结果具有较高的准确性。

2.2 方法实现步骤以下是Matlab中执行RKF方法的基本步骤：1. 定义初值问题：确定ODEs以及初始条件。

2. 设定积分区间和初始步长。

3. 使用RKF公式计算当前时间点处的解，并得到不同阶数下的两个解。

这就是改进的欧拉公式，通常写成 h y = y + ( K1 + K2 ) i i+1 2 K1 = f ( x i , y i ) K2 = f (xi + h, yi + hK1) 由此可见，为了提高精度，可以多取几点的斜率值作加权平均当作平均斜 率kave，这就是龙格库塔法基本思想. 一般的显式龙格库塔方法可以写成
2. 二阶龙格――库塔法
在改进的欧拉公式中将xi+1替换为区间中的任意一点 xi+p = xi + ph (0 < p ≤ 1)
将它的斜率记为K2。利用欧拉公式得y (xi+p)的预报值 y i+p = yi + phK1 求得 K2 = f (xi+p, y i+p) 平均斜率则取 Keve ≈ λ1K1 + λ2K2 其中λ1, λ2是待定的系数。
(h)
y (xi+1) − yi+1 由此可得下列事后估计式
2 y (xi+1) − yi+1 ≈
(h)
≈
1 16
(h)
1 (h (h) 2) (yi+1 − yi+1) 15
这样，可以通过检查步长折半前后两次计算结果的偏差 ∆=
(h 2) |yi+1
− yi+1|
(j )
来判断所选取的步长是否合适。具体可分以下两种情况： 1. 对于给定的精度 ,如果∆ > ，就反复将步长折半计算，直至∆ < 为 (h 2) 止，这时取步长折半后的“新值”yi+1 作为结果。 2. 如果∆ < ，就反复将步长加倍，直至∆ > 为止，这时取步长加倍前 的“旧值”作为结果。 这种通过步长折半或加倍的计算的方法就叫变步长方法。表面上看，为了 选择步长，每一步的计算量似乎增加了，但从总体上考虑往往是合算的。

matlab四阶龙格库塔法解方程组摘要：一、引言二、龙格库塔法介绍1.龙格库塔法的基本原理2.龙格库塔法的发展历程三、MATLAB 实现四阶龙格库塔法1.MATLAB 中龙格库塔法的函数2.四阶龙格库塔法的MATLAB 实现四、龙格库塔法解方程组的应用1.线性方程组的求解2.非线性方程组的求解五、结论正文：一、引言在数学领域，求解方程组是一项基本任务。

龙格库塔法作为高效数值求解线性方程组的方法，被广泛应用于各个领域。

MATLAB 作为一款强大的数学软件，可以方便地实现龙格库塔法求解方程组。

本文将介绍MATLAB 中四阶龙格库塔法解方程组的原理、实现与应用。

二、龙格库塔法介绍1.龙格库塔法的基本原理龙格库塔法（Runge-Kutta method）是一种求解常微分方程初值问题的数值方法。

它通过求解一组线性方程来逼近微分方程的解，具有较高的数值稳定性和精度。

龙格库塔法可以分为四阶、五阶等多种形式，其中四阶龙格库塔法是较为常用的一种。

2.龙格库塔法的发展历程龙格库塔法由德国数学家卡尔·龙格（Carl Runge）和英国数学家詹姆斯·库塔（James Kutta）分别在1900 年和1901 年独立发现。

自那时以来，龙格库塔法在数学、物理、工程等领域得到了广泛应用，并发展出了多种改进和扩展。

三、MATLAB 实现四阶龙格库塔法1.MATLAB 中龙格库塔法的函数在MATLAB 中，可以使用内置函数ode45、ode23、ode113 等实现龙格库塔法求解常微分方程。

这些函数分别对应四阶、五阶和三阶龙格库塔法。

2.四阶龙格库塔法的MATLAB 实现以下是一个使用MATLAB 实现四阶龙格库塔法求解方程组的示例：```matlabfunction [x, status] = solve_system_with_ode45(A, B, x0)% 定义方程组func = @(t, x) A * x + B;% 初始条件x0 = [1; 2];% 时间区间tspan = [0, 10];% 求解[x, status] = ode45(func, tspan, x0);end```四、龙格库塔法解方程组的应用1.线性方程组的求解线性方程组在数学、物理、工程等领域具有广泛应用。

matlab, 求解时延方程, 龙格库塔方法【主题】MATLAB中的龙格库塔方法求解时延方程一、引言时延方程是一类具有时滞效应的微分方程，其求解对于许多实际问题具有非常重要的意义。

在MATLAB中，我们可以利用龙格库塔方法来高效地求解时延方程，本篇文章将深入探讨这一方法的原理、实现步骤以及实际应用。

二、时延方程的概念和应用时延方程是一种描述系统动力学行为的微分方程，其中包含了自变量的延迟项。

时延方程的求解在控制系统、生态学、神经科学等领域有着广泛的应用，例如在控制系统中常用于描述时滞控制器，生态学中用于描述种群动力学的迟滞效应，神经科学中用于描述神经元之间的传导时延等。

三、龙格库塔方法的原理龙格库塔方法是一种常用的数值求解方法，特别适用于求解微分方程。

其基本思想是通过递推的方式，利用前一步的计算结果来近似下一步的解，并通过不断迭代来逼近精确解。

在求解时延方程时，我们可以利用龙格库塔方法对时滞项进行适当的处理，并结合数值积分技巧来求得方程的近似解。

四、龙格库塔方法的实现步骤1. 制定数值积分网格：在MATLAB中，我们首先需要制定适当的数值积分网格，将时延方程离散化为一系列常微分方程。

2. 利用龙格库塔方法进行迭代求解：我们可以编写MATLAB代码，利用龙格库塔方法对时延方程进行迭代求解，其中需要注意时滞项的处理和数值积分的精度控制。

3. 可视化结果：我们可以利用MATLAB绘图工具对求解结果进行可视化展示，从而直观地观察系统的动力学行为和时滞效应对系统响应的影响。

五、实际应用案例分析以某控制系统中的时滞控制器设计为例，我们可以利用MATLAB中的龙格库塔方法对时延方程进行求解，并结合控制理论进行系统设计和分析。

通过该案例，我们不仅可以初步了解龙格库塔方法在控制系统中的应用，还可以深入思考时滞效应对系统稳定性和性能的影响。

六、个人观点和总结从个人角度而言，我认为MATLAB中的龙格库塔方法对时延方程的求解提供了一种高效、灵活和可靠的数值计算工具。

m a t l a b四阶龙格-库塔法求微分方程Matlab 实现四阶龙格-库塔发求解微分方程从理论上讲，只要函数在某区间上充分光滑，那么它可以展开为泰勒级数，因此在该区间上的函数值可用各阶导数值近似地表示出来，反之其各阶导数值也可用某些函数值的线性组合近似地表示出来。

龙格-库塔法就是将待求函数)(t y 展开为泰勒级数，并用方程函数),(y f t 近似其各阶导数，从而迭代得到)(t y 的数值解。

具体来说，四阶龙格-库塔迭代公式为)22(6143211k k k k h n n ++++=+y y ),(1n n t k y f =)2/,2/(12hk h t k n n ++=y f)2/,2/(23hk h t k n n ++=y f),(33hk h t k n n ++=y f实验内容：已知二阶系统21x x= ，u x x x 5.02.04.0212+--= ，0)0()0(21==x x ，u 为单位阶跃信号。

用四阶龙格-库塔法求数值解。

分析步长对结果的影响。

实验总结：实验报告要求简要的说明实验原理；简明扼要地总结实验内容；编制m 文件，并给出运行结果。

报告格式请按实验报告模板编写。

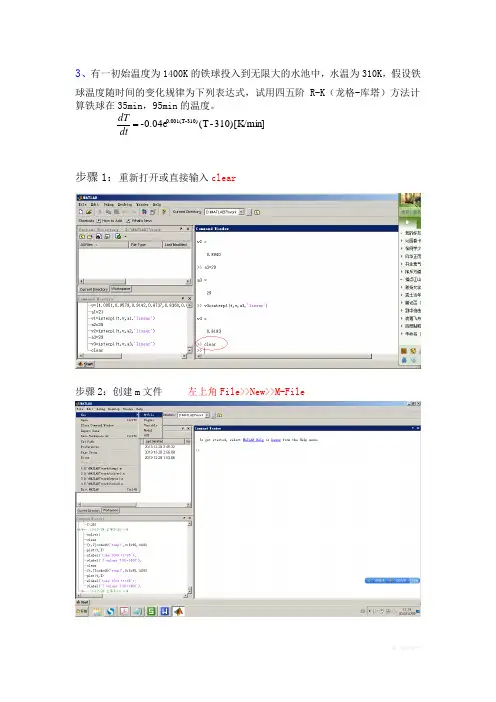
进入matlab ，Step1：choose way1 or way2way1）：可以选择直接加载M 文件（函数M 文件）。

way2）：点击new ——function ，先将shier （函数1文本文件）复制运行;点击new——function，再将RK（函数2文本文件）运行;点击new——function，再将finiRK（函数3文本文件）运行;Step2：回到command页面输入下面四句。

[t,k]=finiRK45([0;0],150);%迭代150次，步长=20/150[t1 k1]=ode45(@shier,[0 -10],[0 0]);%调用matlab自带四阶龙格-库塔，对比结果[t2 k2]=ode45(@shier,[0 10],[0 0]);plot(t,k(1,:),'-',t1,k1(:,1),'*',t2,k2(:,1),'^')%在图形上表示出来补充：改变步长影响数据的准确性。

matlab中rungekutta方法的用法在MATLAB中，Runge-Kutta方法可以通过ode45函数实现。

ode45函数是用于求解初值问题的常微分方程组的函数，它使用了4阶和5阶的Runge-Kutta方法来计算微分方程的数值解。

下面是在MATLAB中使用ode45函数的基本语法：[t,y] = ode45(odefun,tspan,y0)其中：* odefun：函数句柄，它描述了微分方程组。

odefun应该接受两个输入参数（t和y），并返回一个列向量，该列向量包含y的每个分量的导数。

* tspan：时间跨度，它是一个包含起始时间和结束时间的向量，例如[t0 tf]。

如果省略tf，则默认为Inf。

tspan也可以是一个包含多个时间点的向量，例如[t0,t1,...,tf]。

在这种情况下，ode45将在指定的时间点返回解。

* y0：初始条件向量，它包含了在tspan起始时间点的y的值。

ode45函数返回两个输出：* t：一个列向量，包含了ode45计算解的时间点。

* y：一个矩阵，每一行包含了对应时间点t的y的值。

例如，如果我们有一个简单的微分方程组 dy/dt = -2.3y，我们可以使用以下代码在MATLAB中使用ode45函数求解：首先定义odefun函数：function dy = odefun(t,y)dy = -2.3 * y;end然后在MATLAB命令窗口中输入以下代码：tspan = [0 10]; % 时间跨度为0到10y0 = 1; % 初始条件为1[t,y] = ode45(@odefun,tspan,y0); % 使用ode45函数求解微分方程组。

一、介绍Matlab作为一种强大的科学计算软件，提供了众多函数和工具来解决微分方程组。

其中，四阶龙格库塔函数是一种常用的数值方法，用于求解常微分方程组。

本文将介绍如何使用Matlab中的四阶龙格库塔函数来求解微分方程组，并对该方法的原理和实现进行详细说明。

二、四阶龙格库塔方法四阶龙格库塔方法是一种常用的数值方法，用于求解常微分方程组。

它是一种显式的Runge-Kutta方法，通过逐步逼近微分方程的解，在每一步使用多个中间值来计算下一步的解。

该方法通过四个中间值来计算下一步的状态，并且具有较高的精度和稳定性。

三、在Matlab中使用四阶龙格库塔方法求解微分方程组在Matlab中，可以使用ode45函数来调用四阶龙格库塔方法来解决微分方程组的问题。

ode45函数是Matlab提供的用于求解常微分方程组的函数，可以通过指定微分方程组以及初值条件来调用四阶龙格库塔方法来进行求解。

1. 定义微分方程组我们需要定义要求解的微分方程组。

可以使用Matlab中的匿名函数来定义微分方程组，例如：```matlabf = (t, y) [y(2); -sin(y(1))];```其中，f是一个匿名函数，用于表示微分方程组。

在这个例子中，微分方程组是y' = y2, y2' = -sin(y1)。

2. 指定初值条件和求解区间接下来，我们需要指定微分方程组的初值条件和求解区间。

初值条件可以通过指定一个初始时刻的状态向量来完成，例如：```matlabtspan = [0, 10];y0 = [0, 1];```其中，tspan表示求解区间，y0表示初值条件。

3. 调用ode45函数进行求解我们可以通过调用ode45函数来求解微分方程组的数值解。

具体的调用方式如下：```matlab[t, y] = ode45(f, tspan, y0);```其中，t和y分别表示求解的时间点和对应的状态值。

四、示例下面我们通过一个具体的例子来演示如何使用Matlab中的四阶龙格库塔方法来求解微分方程组。

matlab龙格库塔法解微分方程组
一、引言
龙格库塔法是数值计算中常用的一种求解微分方程的方法，其具有较高的精度和稳定性。

在MATLAB中，可以使用ode45函数来实现龙格库塔法求解微分方程组。

二、龙格库塔法简介
龙格库塔法是一种常用的数值积分方法，也可用于求解微分方程。

该方法将微分方程转化为一个初值问题，并采用逐步逼近的方式计算出数值解。

三、使用ode45函数求解微分方程组
在MATLAB中，可以使用ode45函数来求解微分方程组。

该函数使用了龙格库塔法进行数值计算，并提供了较高的精度和稳定性。

四、MATLAB代码实现
以下是一个使用ode45函数求解微分方程组的示例代码：
function dydt = myfun(t,y)
dydt = zeros(2,1);
dydt(1) = y(2);
dydt(2) = -sin(y(1));
end
[t,y] = ode45(@myfun,[0 10],[0;1]);
plot(t,y(:,1),'-o',t,y(:,2),'-o')
xlabel('Time')
ylabel('Solution')
legend('y_1','y_2')
五、总结
龙格库塔法是一种常用的数值计算方法，可以用于求解微分方程。

在MATLAB中，可以使用ode45函数来实现龙格库塔法求解微分方程组。

通过以上示例代码，我们可以看到MATLAB提供了较为简单的方式来实现龙格库塔法求解微分方程组，并且具有较高的精度和稳定性。

matlab用四阶龙格库塔法解二阶常微分方程在数学和工程中，常微分方程是描述自然界中各种物理现象和过程的常见数学模型。

常微分方程通常包含未知函数及其导数的方程。

在求解常微分方程时，人们通常使用数值方法来近似求解，其中一种常见的方法是使用龙格-库塔方法。

四阶龙格-库塔方法是一种常用的数值方法，用于求解二阶常微分方程。

它是通过在每个步骤中估计未知函数的导数来数值求解方程。

它的精度比较高，通常被认为是最常用的龙格-库塔方法。

对于一个二阶常微分方程：y''(t) = f(t, y(t), y'(t))其中y(t)是未知函数，f(t, y(t), y'(t))是已知的函数。

我们可以将这个二阶微分方程转化为两个一阶微分方程：y'(t) = u(t)u'(t) = f(t, y(t), u(t))其中u(t)是y'(t)的一个替代函数。

为了使用四阶龙格-库塔方法求解这个方程，我们需要将时间区间[t0, tn]分割为等距的n个子区间，每个子区间的长度为h = (tn - t0)/n。

我们从初始点t0开始，通过多个步骤来逼近解直到tn。

每一步我们使用以下递推公式来估计y(t)和u(t)的值：k1 = h * u(t)l1 = h * f(t, y(t), u(t))k2 = h * (u(t) + l1/2)l2 = h * f(t + h/2, y(t) + k1/2, u(t) + l1/2)k3 = h * (u(t) + l2/2)l3 = h * f(t + h/2, y(t) + k2/2, u(t) + l2/2)k4 = h * (u(t) + l3)l4 = h * f(t + h, y(t) + k3, u(t) + l3)然后我们可以使用以下公式来更新y(t)和u(t)的值：y(t + h) = y(t) + (k1 + 2k2 + 2k3 + k4)/6u(t + h) = u(t) + (l1 + 2l2 + 2l3 + l4)/6这个过程重复n次，直到达到结束时间tn。