当前位置：文档之家 › 3特殊锐角的三角函数

3特殊锐角的三角函数

  • 格式：ppt
  • 大小：948.50 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

特殊锐角三角函数

特殊锐角三角函数

三角 函数 锐角α
30°45°6来自°sinαcosα
tanα
特殊角的三角函数应用：
（1）利用锐角度数求其对应的三角函数值； 利用三角函数值求唯一对应的锐角。 （2）变化趋势： 正弦值随锐角的增大而（ ）, 始终小于1； 余弦值随锐角的增大而（ )，始终大于0； 正切值随锐角的增大而（ ）。 （3）互余角之间关系： sin30°=( ) cos30°=( ) sin45°=( ) tan30°tan60°=( ) tan45°tan45°=( （4）同锐角之间关系： sin²30°+cos²30°=( ) sin²45°+sin²45°=( sin²60°+cos²60°=( )
特殊锐角三角函数
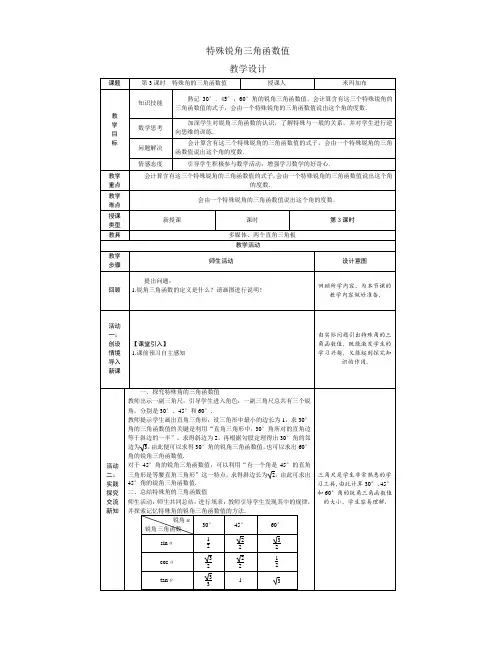
• 学习目标： • 1:掌握特殊锐角三角函数值； • 2:利用锐角度数求其对应三角函数值； • 3:利用三角函数值求唯一对应锐角。 • 自学指导： • 1:完成课本79页探究，熟记特殊锐角三角函 数值； • 2:自学例3，完成课后练习1； • 3:自学例4，完成课后练习2.
探究30°,45°,60°角的正弦值,余弦值,正切值:
1 2.已知：∠A,∠B,∠C都是锐角，sinA= 2
tanB= 3
）。
cosC=
2 2
,则∠A+∠B+∠C=（
3.已知：∠A为锐角，且cos(90°-∠A)=0.5，则∠A
的度数为（ ）。
日清：练习册49页第14,15题。
作业：课本82页第3题。
) )
当堂训练（一）
1.自学例3独立完成课本80页练习1（1）（2）.
2.sin60°的相反数是（
2
）
3.在△ABC中，若|sinA-0.5|+(cosB-0.5)²=0,
特殊锐角三角函数

特殊锐角三角函数


4．当锐角A>45°时，sinA的值（ A．小于 C．小于 B2 ．大于 D．大于
）
B
2
2 2
3 2
5．当锐角A>30°时，cotA的值（ A．小于 C．小于 ）
3 2
C
1 B．大于 2
3 2
D．大于
1 2
3 2
6．计算：
(1) 2sin30°+3cos30°+cot45°
3 3 2 2
3 3 4 2
解：
2 2
3 2 5 (1)cos 30 sin 45 ; 2 2 4
cos 30 3 3 (2) cot 45 1 0. sin60 2 2
例3
求下列各式的值 : cos 450 0 (2) tan 45 sin 450
a
b
C
课堂小结
1．锐角∠A的正弦、余弦、正切、余切函数，统称为 锐角∠A的三角 函数． 2．30°、45°、60°角的三角函数值． 3．锐角α的三角函数值的取值范围 ． 正弦 余弦 0＜ sinα＜1 0＜ cosα＜1 正切 余切 tanα>0 cotα>0
4．三角函数的增减性： sinα、tanα随着自变量α的增大而增大 cosα、cotα随着自变量α的增大而减小
5．三角函数的几个重要关系式
tanα•cot（90°-α） =1 sin2 α +cos2 （90°-α） =1 sinα= cos（90°-α） cosα= sin（90°-α） tanα= cot（90°-α） cotα = tan（90°-α）
随堂练习
1．当∠A为锐角，且tanA的值大于 时，∠A（ ） D
锐角三角函数---特殊角的三角函数值

锐角三角函数---特殊角的三角函数值


5分钟后比谁能正确做出检测题
例1 求下列各式的值： （1）cos260°＋sin260°
1 2 3 2 解：原式 ( ) ( ) 2 2
2 sin 2 60表示（sin 60） ，
即(sin 60) (sin 60).
1 cos 45 （ 2） tan45 sin 45
1
1
2
2
3
1、这两块三角尺各有几个锐角？它们分别等于多少度？ 30° 60° 45° 45° 2、每块三角尺的三边之间有怎样的特殊关系？如 果设每块三角尺较短的边长为1，请你说出未知边 的长度。
*请你根据得出的三角尺各边的长度，探索 sin30°、cos30°、tan3o°、sin45°、 cos45°、tan45°、sin60°、cos600、 tan600这些特殊角的三角函数值 *请你观察特殊角的三角函数值探索锐角三角 函数的增减性
A
D B
C
1如图，在△ABC中，∠A=30度， 求AB。 解：过点C作CD⊥AB于点D ∠A=30度， AC 2 3
1 CD 1 CD 2 3 3 sin A 2 AC 2
A
3 tanB , AC 2 3, 2
C
D
B
3 AD 3 AD 2 3 3 cos A 2 AC 2 CD 3 BD 3 2 2 tan B 3 BD 2
2 2 解：原式 1 2 2
0
求下列各式的值：
（ 1 ） 1 2 sin 30 cos 30；
（2） 3 tan 30 tan 45 2 sin 60； cos 60 1 （3） ； 1 sin 60 tan 30
B
特殊锐角三角函数值

特殊锐角三角函数值

④[习题反思]
好题题号
错题题号
反思教学过程和教师表现，进一步提升操作流程和自身素质.
授课
类型
新授课
课时
第3课时
教具
多媒体、两个直角三角板
教学活动
教学
步骤
师生活动
设计意图
回顾
提出问题：
1.锐角三角函数的定义是什么？请画图进行说明！
回顾所学内容，为本节课的教学内容做好准备.
活动
一：
创设
情境
导入
新课
【课堂引入】
1.课前预习自主感知
由实际问题引出特殊角的三角函数值，既能激发学生的学习兴趣，又能起到探究知识的作用.
对于45°角的锐角三角函数值，可以利用“有一个角是45°的直角三角形是等腰直角三角形”这一特点，求得斜边长为 ，由此可求出45°角的锐角三角函数值.
二、总结特殊角的三角函数值
师生活动：师生共同总结，进行填表：教师引导学生发现其中的规律，并探索记忆特殊角的锐角三角函数值的方法.
锐角α
锐角三角函数
30°
2.学生不断质疑、解惑，不但完善了思维也锻炼了能力，使学生形成对知识的总体把握.
活动
三：
开放
训练
体现
应用
【拓展提升】
【达标测评】
通过设置达标测评，进一步巩固所学新知，同时检测学习效果，做到“堂堂清”.
活动
四：
课堂
总结
反思
1.课堂总结：
请同学们回顾30°，45°，60°角的锐角三角函数值分别是多少？
2.布置作业：
45°
60°
sinα
cosα
tanα
1
三角尺是学生非常熟悉的学习工具，由此计算30°、45°和60°角的锐角三角函数值的大小，学生容易理解.
3.28.1 第3课时 特殊角的三角函数值

3.28.1 第3课时 特殊角的三角函数值


特殊角的三角函数值
1 3 3 解： (1)2－2sin30°cos30°＝2－2× × ＝2－ . 2 2 2 3 2 2 (2) cos60°－sin45°＋ tan 30°＋cos 30°－sin30 ° 4
1 2 3 2 3 2 3 2 1 ＝ － ＋ × ＋ － ＝1－ . 2 2 4 3 2 2 2
sin30° 1 (3) ＋ ＝ 1＋sin60° tan 30°
1 2＋ 3 ＝ ÷ ＋ 3 ＝ 2. 2 2
＋ 3 3 1＋ 2 3
1 2
1
第3课时
特殊角的三角函数值
[ 归纳总结 ] 方法一： (1) 将各角的函数值代入； (2)化简计 算．
方法二：根据代数式的特点，化简整理后再代入求值．
第3课时
特殊角的三角函数值
探究问题二
例2
由特殊角的三角函数值求角的度数
[教材例 4 变式题] 在 Rt△ ABC 中， ∠C＝90°， BC＝ 7 ，
AC＝ 21 ，求∠A，∠B 的度数．
第3课时
特殊角的三角函数值
解： ∵BC＝ 7 ，AC＝ 21 ， BC 7 3 ∴tanA＝ ＝ ＝ ， AC 21 3 AC 21 tanB＝ ＝ ＝ 3， BC 7 ∴∠A ＝30°，∠B ＝60°.
tan60°＝____．
第3课时
特殊角的三角函数值
图28－1－39
第3课时
特殊角的三角函数值
2．如图 28－ 1－40，在 Rt△ABC 中，∠ C＝90°，∠A ＝∠B＝ 45°，设 BC＝1，则 AC＝1，AB＝ 2(为什么)．于是有 sin45°＝
2 2 1 2 2 ______，cos45°＝_______，tan45°＝______．
28.1 第3课时 特殊角的三角函数值

28.1 第3课时 特殊角的三角函数值

328．1锐角三角函数 第3课时 特殊角的三角函数姓名： 评价：【学习目标】⑴: 能推导并熟记30°、45°、60°角的三角函数值，并能根据这些值说出对应锐角度数。

⑵: 能熟练计算含有30°、45°、60°角的三角函数的运算式。

【学习重点】熟记30°、45°、60°角的三角函数值，能熟练计算含有30°、45°、60°角的三角函数的运算式。

【学习难点】30°、45°、60°角的三角函数值的推导过程。

【导学过程】 一、自学提纲：一个直角三角形中，一个锐角正弦是怎么定义的？一个锐角余弦是怎么定义的？一个锐角正切是怎么定义的？二、合作交流：思考：两块三角尺中有几个不同的锐角？是多少度？你能分别求出这几个锐角的正弦值、余弦值和正切值码？．例3：求下列各式的值．（1）cos 260°+sin 260°． （2）cos 45sin 45︒︒-tan45°．例4：（1）如图（1），在Rt △ABC 中，∠C=90，，，求∠A 的度数．（2）如图（2），已知圆锥的高AO等于圆锥的底面半径OB倍，求a．四、训练：一）、选择题：1．已知：Rt△ABC中，∠C=90°，cosA=35，AB=15，则AC的长是（）．A．3 B．6 C．9 D．12 2．下列各式中不正确的是（）．A．sin260°+cos260°=1 B．sin30°+cos30°=1 C．sin35°=cos55° D．tan45°>sin45°3．计算2sin30°-2cos60°+tan45°的结果是（）．A．2 B．14．已知∠A为锐角，且cosA≤12，那么（）。

锐角三角函数3——特殊角的三角函数值

锐角三角函数3——特殊角的三角函数值


3、思考 P83 第 9、10 题
忻州市十二中学
九年级 （数学）导学案 （教师版）
主备人：王小平 审核人：刘文华
授课人： 学生姓名：
授课时间： 小组： 课时
班级： 得分： 备注 （教师复备栏及学 生笔记）
课题 ：28．1 锐角三角函数（3） 【学习目标】
1、 能推导并熟记 30°、45°、60°角的三角函数值，并能根据这 些值说出对应锐角度数。 2、 能熟练计算含有 30°、45°、60°角的三角函数的运算式。 【重点】熟记 30°、45°、60°角的三角函数值，能熟练计算含有 30°、45°、60°角的三角函数的运算式 【难点】30°、45°、60°角的三角函数值的推导过程。 【自学指导】仔细看：课本 P79—P80 例 4 结束。 想一想：1、30°、45°、60°角的三角函数值的推导过程。测】 课本 P80 练习 1、2。
【合作探究】
忻州市十二中学
九年级 （数学）导学案 （教师版）
【总结反思】
【当堂训练】 1、课本 P82 第 3 题
2、若（ 3 tanA-3）2+│2cosB- 3 │=0，则△ABC（ ） ． A．是直角三角形 B．是等边三角形 C． 是含有 60°的任意三角形 D． 是顶角为钝角的等腰三角形
第二十八章 锐角三角函数 第3课时 特殊角的三角函数值 《全品学练考》九年级下数学

第二十八章 锐角三角函数 第3课时 特殊角的三角函数值 《全品学练考》九年级下数学

解： (1)按键顺序： cos 6 3 ° ′ ″ 1 7 ° ′ ″ ＝ ， 得到结果：cos63°17′＝0.44957885. (2)按键顺序： tan 2 7 ·3 5 ＝ ， 得到结果：tan27.35°＝0.517244127. (3)按键顺序： sin 3 9 ° ′ ″ 5 7 ° ′ ″ 6 ° ′ ″ ＝ ， 得到结果：sin39°57′6″＝0.642141164.
∴∠A＝30°，∠B＝60°.
第3课时 特殊角的三角函数值
【归纳总结】由特殊角的三角函数值确定角的度数的一般步骤： (1)通过边之间的关系或者其他关系得到三角函数值； (2)根据特殊角的三角函数值确定角的度数．
第3课时 特殊角的三角函数值
目标三 会用计算器求锐角的三角函数值或由三角函数值求角度
例 3 教材补充例题 用计算器求下列锐角三角函数值： (1)cos63°17′；(2)tan27.35°；(3)sin39°57′6″.
第3课时 特殊角的三角函数值
例4 教材补充例题 已知下列锐角三角函数值，用计算器求其 相应锐角A的度数： (1)sinA＝0.9816； (2)cosA＝0.8067； (3)tanA＝0.189.
[解析] 首先选择第二功能键 2nd F ，转换功能后再按其他键．
第3课时 特殊角的三角函数值
解： (1)按键顺序： 2nd F sin 0 ·9 8 1 6 ＝ ，得到结果：∠A＝78.99184039°. (2)按键顺序： 2nd F cos 0 ·8 0 6 7 ＝ ， 得到结果：∠A＝36.22524578°. (3)按键顺序： 2nd F tan 0 ·1 8 9 ＝ ， 得到结果：∠A＝10.70265749°.
余弦值为
23，
人教九年级数学下28锐角三角函数第三课时特殊三角函数值(共22张PPT)

人教九年级数学下28锐角三角函数第三课时特殊三角函数值(共22张PPT)

tan 30 a 3 3 3a
新人教九年级数学下
两块三角 60° 尺中有几个不同的锐角？ 分别求出这几个锐角的正 弦值、余弦值和正切值．
30°
45°
45°
设30°所对的直角边长为a，那么斜边长为2a 另一条直角边长＝ 2a a 2 3a
2
sin 60
a 1 cos 60 2a 2
1
3
的锐角三角函数值 之间也是有规律的， 互余的两个锐角的 正弦值的平方和为1， 互余的两个锐角的 余弦值的平方和为1， 它们的正切值的积 为1。
新人教九年级数学下
1、(2014·天津)cos60°的值等于(
A
)
3 1 2 A. B. C. D. 3 2 2 2 2、（2013天津）tan60°的值等于（ C
2 2 2 2
45°
a tan 45 1 a
新人教九年级数学下
30°、45°、60°角的正弦值、 余弦值和正切值如下表： 锐角a 30° 三角函数 sin a cos a tan a
1 2
仔细观察,说 说你发现这张表 有哪些规律?
点拨：这些常用
45°
2 2
60°
3 2
3 2
3 3
2 2
1 2
cos 45 (2) tan 45 sin 45
cos 45 (2) tan 450 sin 45
12 3 2 ( ) ( ) 2 2
＝1
2 2 1 2 2
＝0
新人教九年级数学下 B
例2
（1）如图1，在Rt△ABC中，∠C＝90°，
6
A
3
C
AB 6, BC 3 ，求∠A的度数．
锐角三角函数特殊角

锐角三角函数特殊角

锐角三角函数特殊角导言三角函数是数学中一门重要的分支，它们在几何、物理、工程等领域发挥着重要作用。

在三角函数中，有一类特殊的角度被称为锐角。

本文将详细介绍锐角三角函数的特殊角，包括定义、性质以及相关应用。

一、锐角三角函数的定义锐角指的是角度大小在0°和90°之间的角。

在三角函数中，主要涉及的三个函数是正弦函数（sin）、余弦函数（cos）和正切函数（tan）。

它们的定义如下：•正弦函数（sin）：在锐角ABC中，∠ABC的顶点位于单位圆的圆心O上，点A位于单位圆上，点C位于x轴上。

正弦函数sinA的值等于A点在单位圆上的y坐标值，即sinA=y。

•余弦函数（cos）：在锐角ABC中，∠ABC的顶点位于单位圆的圆心O上，点A位于单位圆上，点C位于x轴上。

余弦函数cosA的值等于A点在单位圆上的x坐标值，即cosA=x。

•正切函数（tan）：在锐角ABC中，∠ABC的顶点位于单位圆的圆心O上，点A位于单位圆上，点C位于x轴上。

正切函数tanA的值等于A点在单位圆上的y坐标值除以A点在单位圆上的x坐标值，即tanA=y/x。

二、锐角三角函数特殊角的定义在锐角三角函数中，存在一些特殊角，它们的值可以用简单的形式表示。

这些特殊角包括以下几个：1.0°：对应的三角函数值为sin0°=0，cos0°=1，tan0°=0。

2.30°：对应的三角函数值为sin30°=1/2，cos30°=√3/2，tan30°=√3/3。

3.45°：对应的三角函数值为sin45°=√2/2，cos45°=√2/2，tan45°=1。

4.60°：对应的三角函数值为sin60°=√3/2，cos60°=1/2，tan60°=√3。

5.90°：对应的三角函数值为sin90°=1，cos90°=0（定义无意义），tan90°=无穷（定义无意义）。

人教版初三数学下册《特殊角的锐角三角函数》

人教版初三数学下册《特殊角的锐角三角函数》

“315”教学模式导学案1•掌握30°、45°、60°角的三角函数值，能够用它们进行计算、学习重难点二握学习重难点30°角的三角函数值，能够用它们进行计算2•能够根据30°、45°、60。

角的三角函数值，说出相应锐角的大小三、学习方法自主学习、合作探究（一）自主学习阅读教材P65-67页，自习“探究”、“例3 ”与“例4” •学生独立完成后 集体订正、学习内容① sin30° =，cos30° = =（一），自主学习，ta n45 cos60° = ， tan60° =② Sin a 的值随着角a 的增大而 而，tan a 的值随着角a 的增大而 教师归纳：这些常用的锐角三角函数值之间也是有规律的， 互余的两个锐角的正弦值的平方和为1，互余的两个锐角的余弦值的平方和为1,它们的正切值 的积为1. （二）合作探究例1求下列各式的值：2 2 cos45① cos 30 ° +sin 30。

：② ----- 7 -tan60 ° .-二 si n45例（二如图合作探究2 m ，斜坡面与地平面夹角为 a 的楼梯表面铺地毯，楼梯宽2 m ，共需地毯的面积为（4 、. 3 +4）m 2,则a 为多少度？课题：《特殊角的锐角三角函数 》执笔:聂志平审核人： _________个性化设计:学习学习目标2•能够根据30°、45 60°角的三角函数值，说出相应锐角的大小,tan30° = , sin45 ° ______ , sin60 ° = ___________ ,cos a 的值随着角a 的增大1•计算:① |3-屁 1+( "6 )°+COS 230 ° -4sin60°;2+>}2② 2 (2cos45° -sin60 ° ) + 丄 4 ，③ （sin30 ° ）-1-2 010°+|-4 ”3|-tan60 ° .12•直线y=kx-4与y 轴相交所成的锐角的正切值为，则k 的值为 ____________ 3.已知a 为锐角，则 m=sin a +COS a 的值() A.m>1 B.m=1C.m<14. 求下列锐角a 的大小： ① 4cos 2a -3 2 sin45 ° =0;② tan 2 a -（+1）tan a + 3 =0.5. 在△ ABC 中，/ C=90。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2 2 2 2
－1
＝ 1
＝ 1 －1
＝ 0
2、求满足下列条件的锐角α .
1 ① sinα ＝ 2
3 ② cosα ＝ 2
解：α ＝30° ③ 2sinα ＝ 3 解：sinα ＝
3 2
解：α ＝30° ④ 3 tan(80°－α )－1＝0 解： 3tan (80－α )＝ 1
α ＝60°
3 tan (80－α )＝ 3 80°－α ＝30°
第一轮
课本
P80
练习：1、2
第二轮
课本
P82
练习：3
你对本节课所学的内容存在疑问吗？欢迎提出来，共同讨论！
锐角α 三角函数
30°
1 2
3 2 3 3
45°
60°
sinα cosα tanα
2 2 2 2
1
3 2
1 2
3
1、求下列各式的值. ① sin260°＋cos260°
1 3 2 ) ＋ ( )2 2 2 3 1 ＝ ＋ 4 4
cos 45 ② sin 45 －tan 45
解：原式＝ (
解：原式＝
α ＝50°
3、（1）如图，在Rt△ABC中，∠C＝90°，AB＝ 6 ， BC＝ 3 ，求∠A的度数.
（2）如图，已知圆锥的高AO是它的地面半径OB 的 3 倍，求α . B
6 3
A
(1)
C
(2)
1 2
BC 3 解：(1)∵sinA＝ AB ＝ 6 ＝ ∴∠A＝45° AO (2)∵tanα ＝ ＝ 3 OB ∴∠α ＝60°
1、尽最大的努力，做最好的自己。
2、不叫一日闲过，坚持就有收获。
30°
1
1
45°
3
2
45°
60°
2
两个三角板中所含的锐角（30°. 45°.60°）是非常特殊的锐角,本节 课我们系统的归纳一下它们的三角函并熟记30°、45°、60°角的三角函数值，并 能根据这些值说出对应的锐角的度数. 2、能熟练计算含有30°、45°、60°角的三角函数的运 算式.
＝
2 2
4、在△ABC中，若 2sin 2 A－1＋(tan C－ 3 ) 2＝0，求∠B的度数. 解： 2sin2A－1＝0
tan C－ 3＝0
2sin 2 A＝ 1 1 2 sin A＝ 2 2 sin A＝ 2 A＝45
tanC＝ 3
C＝60
∴∠B＝180°－∠A－∠C ＝180°－45°－60° ＝75°