锐角三角函数;特殊值
- 格式:pdf
- 大小:2.01 MB
- 文档页数:19
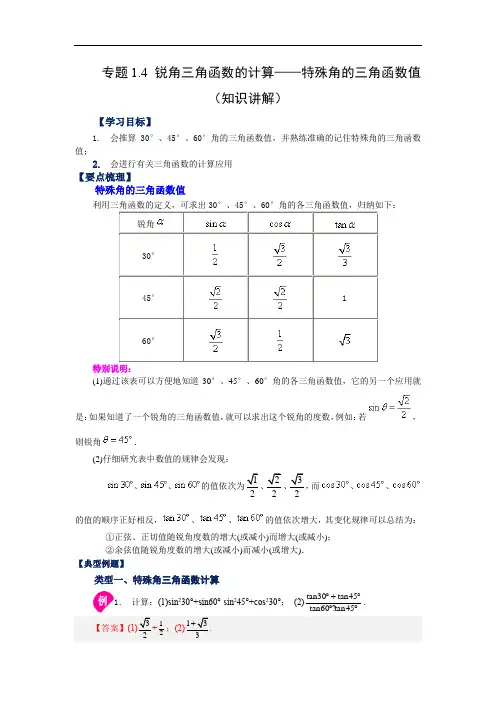
专题1.4 锐角三角函数的计算——特殊角的三角函数值(知识讲解)【学习目标】1.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值;2.会进行有关三角函数的计算应用【要点梳理】特殊角的三角函数值锐角30°45° 160°特别说明:(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为12、22、32,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小);②余弦值随锐角度数的增大(或减小)而减小(或增大).【典型例题】类型一、特殊角三角函数计算1.计算:(1)sin230°+sin60°-sin245°+cos230°;(2)tan30tan45 tan60?tan45︒+︒︒︒.【答案】(1)32+12;(2)133+.【分析】(1)将特殊角的三角函数值代入求解;(2)将特殊角的三角函数值代入求解.特殊值:sin 30° =12;sin 60° = 32;sin 45° = 22;cos 30° = 32;tan 60° = 3;tan 45° = 1解:(1)原式=1342+-12+34=32 + 12; 3133?1+(2)原式= =133+. 【点拨】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.举一反三:【变式1】计算:222sin 60cos 60︒︒︒︒-﹣sin45°•tan45° 【答案】3232+ 【分析】把特殊角的三角函数值代入计算即可.解:222sin 60cos 60tan 604cos 45︒︒︒︒--﹣sin45°•tan45° ()22312222122342⎛⎫⨯- ⎪⎝⎭=-⨯-⨯ 122322=-- 23222=+-=3232+. 【点拨】本题考查了特殊角的三角函数值及分母有理化、二次根式的化简,牢记特殊角的三角函数值,是解决本题的关键.【变式2】计算:2cos45°﹣tan60°+sin30°﹣12tan45°【答案】2-3【分析】将各特殊角的三角函数值代入即可得出答案.解:原式=2×22﹣3+12﹣12×1 =2-3【点拨】此题考查特殊角的三角函数值,属于基础题,熟练记忆一些特殊角的三角函数值是关键.类型二、特殊角三角函数计算2.计算:()2012sin 451220202π-︒⎛⎫----+- ⎪⎝⎭ 【答案】-2【分析】直接利用特殊角的三角函数值、绝对值的性质、零指数幂的性质、负整数指数幂的性质分别代入化简即可.解:原式=24121-+-+=-2【点拨】此题主要考查了实数运算,正确化简各数是解题关键.举一反三:【变式1】计算:0113tan 30(2014π)32()3-︒---. 【答案】-2试题分析:分别计算033tan3033=⨯,(2014-π)0=1,32-=2﹣11333-⎛⎫= ⎪⎝⎭,,再用实数的混合运算法则计算.解:原式=3×33﹣1+2﹣3﹣3=﹣2. 【变式2】计算:()()2(31)3tan3052522sin60+--++. 【答案】3试题分析:用完全平方公式、平方差公式去括号,计算出特殊角三角函数值,再进行乘法运算,最后进行加减运算即可.解:(3-1)2+3tan 30°-(5-2)( 5+2)+2sin 60°=4-23+3×33-(5-4)+2×32=4-23+3-1+3=3.【点拨】掌握二次根式的加减乘除运算法则.类型三、三角函数计算3. 已知A ∠为锐角,且24sin 30A -=,则A ∠=______. 【答案】60︒【分析】计算,并结合A ∠是个锐角,即可求解.解:∵24sin 30A -=,∵23sin 4A =, ∵3sin 2A =±, ∵A ∠为锐角,∵3sin 2A =, ∵60A ∠=︒故答案是:60°【点拨】本题主要考察计算和锐角三角函数与角度关系,属于基础的计算题,难度不大.解题的关键是结合角度范围确定三角函数值范围.举一反三:【变式1】已知矩形ABCD 的周长为()232cm ,对角线2cm AC =,求BAC ∠与DAC ∠的度数. 【答案】30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒.【分析】设AB=x,将BC 表示出来,再利用勾股定理可求出x=1或x=3,再利用三角函数求出一个角为30°,另一个角为60°.解:∵矩形ABCD 的周长为232+,∵AB+BC= 3+1,∵对角线AC=2,∵设AB=x,则BC=3+1-x,∵AB 2+BA 2=AC 2,∵x 2+(3+1-x)2=22,解得:x 1=1,x 2=3,∵当AB=1,则BC=3,∵tan∵BAC=3,∵∵BAC=60°,∵DAC=30°,当AB=3,则BC=1,∵tan∵BAC= 33, ∵∵BAC=30°,∵DAC=60°,故30BAC ∠=︒,60=︒∠DAC 或60BAC ∠=︒,30DAC ∠=︒. 【点拨】此题主要考查了勾股定理和特殊角的三角函数值,解答本题的关键是掌握特殊角的三角函数值.【变式2】计算(1)23602cos 30tan 45︒-︒+︒(2)已知α是锐角,且()1sin 152α-︒=84cos α的值. 【答案】(1)1 (2)0【分析】(1)把特殊角的三角函数值代入代数式进行计算即可;(2)先利用锐角的正弦求解α的大小,再代入代数式进行计算即可.(1)解:23sin 602cos 30tan 45︒-︒+︒ 23332122331122(2) α是锐角,且()1sin 152α-︒=,1530,=45,∴ 84cos α-2224222220=-=【点拨】本题考查的是特殊角的三角函数值的混合运算,已知三角函数值求解锐角的大小,熟记特殊角的三角函数值是解本题的关键.类型四、三角函数计算4.(1)计算:21122cos453-⎛⎫--︒+-⎪⎝⎭.(2)如图,在△ABC中,∵ACB=90°,角平分线AE与高CD交于点F,求证:CE=CF.【答案】(1)8;(2)见分析【分析】(1)计算绝对值、特殊角的三角函数值、负整数指数幂,再合并即可;(2)根据直角三角形两锐角互余求得∵B=∵ACD,然后根据三角形外角的性质求得∵CEF=∵CFE,根据等角对等边求得CE=CF.(1)解:21 122cos453-⎛⎫--︒+-⎪⎝⎭221292=--⨯+2129=--+=8;(2)证明:∵在△ABC中,∵ACB=90°,∵∵B+∵BAC=90°,∵CD是AB边上的高,∵∵ACD+∵BAC=90°,∵∵B=∵ACD,∵AE是∵BAC的角平分线,∵∵BAE=∵EAC,∵∵B +∵BAE =∵ACD +∵EAC ,即∵CEF =∵CFE ,∵CE =CF .【点拨】本题考查了特殊角的三角函数值,负整数指数幂,直角三角形的性质,三角形外角的性质,等腰三角形的判定等,熟练掌握性质定理是解题的关键.举一反三:【变式1】如图,将∵ABC 沿射线AB 平移4cm 后能与∵BDE 完全重合,连接CE 、CD 交BE 于点O ,OB =OC .(1)求证:四边形CBDE 为矩形;(2)若S △BOC 432,求∵ACD 的度数. 【答案】(1)见分析(2)120°【分析】(1)由平移的性质及ASA判定定理可证得OCE ODB ≌,根据全等三角形的性质即可求证结论.(2)根据矩形的性质及面积公式即可求得BC ,进而可利用特殊三角函数值可求得60BCD ∠=︒,根据垂直平分线的性质即可求解.(1)证明:由题意可知:△BDE 由△ABC 平移后得到,∵//BC DE ,且BC DE =,∵四边形CBDE 是平行四边形,∵//CE BD ,且CE BD =,∵ECD CDB ∠=∠,CEB EBD ∠=∠,在OCE 和ODB △中 ECD CDB CE BDCEB EBD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∵ ()OCE ODB ASA ≌∵OC OD =,OB OE =,又∵OB OC =,∵CD BE =,∵ 平行四边形CBDE 为矩形.(2)由(1)可知四边形CBDE 为矩形,∵90CBD ∠=︒,且4BD =cm ,在OBC 中过点O 作BC 的垂线,垂足为F ,则2OF =,∵143223BOC S BC =⨯⨯=,∵433BC =cm , ∵在Rt CBD △,43433BD tan BCD CB ∠===,∵60BCD ∠=︒,又∵在△ACD 中,BC 是AD 的垂直平分线,∵60ACB BCD ∠=∠=︒,∵120ACD ∠=︒,∴∵ACD 的度数为120︒.【点拨】本题考查了平移的性质、全等三角形的判定及性质、矩形的判定及性质、特殊三角函数值求角度,熟练掌握相关性质及判定定理是解题的关键.【变式2】将矩形ABCD 对折,使AD 与BC 重合,得到折痕EF ,展开后再一次折叠,使点A 落在EF 上的点A '处,并使得折痕经过点B ,得到折痕BG ,连接AA ',如图1,问题解决:(1)试判断图1中ABA '△是什么特殊的三角形?并说明理由;(2)如图2,在图1的基础上,AA '与BG 相交于点N ,点P 是BN 的中点,连接AP 并延长交BA '于点Q ,求BQ BA '的值.【答案】(1)ABA '△是等边三角形,理由见分析(2)13BQ BA =' 【分析】(1)等边三角形,解法一利用垂直平分线性质得出AA ′=BA ′,利用折叠得出BA BA '=即可,解法二:根据折叠得出12BE BA =,BA BA '=,90A EB '∠=︒然后利用锐角三角函数定义得出1cos 2BE A BE BA '∠==' ,求出60A BE '∠=︒即可; (2)解法一:过点N 作NH A B '∥交AP 于H ,先证PHN PQB ≌△△(AAS ),再证AHN AQA '∽△△,得出12BQ QA =' 即可 解法二:由折叠可知A N AN '=,由点P 是BN 的中点 ,得出BP PN =,利用平行线等分性质得出1A M A N QM AN ''==,1BQ BP QM PN ==,证出BQ QM A M '==即可.(1)解:ABA '△是等边三角形.解法一:理由是:由折叠可知EF 垂直平分AB ;∵AA ′=BA ′,∵∵ABG 折叠得△A ′BG ,∵BA BA '=,∵AA BA BA ''==;∵ABA '△是等边三角形;解法二:理由是:由折叠可知12BE BA =,BA BA '=,90A EB '∠=︒, ∵1cos 2BE A BE BA '∠==' , ∵60A BE '∠=︒,∵ABA '△是等边三角形;(2)解法一:过点N 作NH A B '∥交AP 于H ,∵HNP QBP ∠=∠,NHP BOP ∠=∠, 又∵点P 是BN 的中点 , ∵BP NP =,在△PHN 和△PQB 中, HNP QBP NHP BQP PN PB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∵PHN PQB ≌△△(AAS ), ∵HN BQ =,又∵NH A B '∥,∵ANH AA Q '∠=∠,AHN AQA '∠=∠, ∵AHN AQA '∽△△, 由折叠可知12A N AN AA ''==, ∵12HN AN QA AA =='' , ∵12BQ QA =', ∵13BQ BA ='; 解法二:由折叠可知A N AN '=, 又∵点P 是BN 的中点 , ∵BP PN =,过点N 作NM AQ ∥交BA '于M , ∵1A M A N QM AN''==,1BQ BP QM PN ==, ∵BQ QM A M '==, ∵13BQ BA ='.【点拨】本题考查一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质,锐角三角函数值求角,掌握一题多解,等边三角形的判定,折叠性质,线段垂直平分线性质,平行线等分线段定理,三角形相似判定与性质是解题关键.。

特殊锐角三角函数值三角函数是一种重要的函数,可用来描述任意角度的实际运动、振动,以及各种复杂的数学关系。
它是一种多用途函数,能够把圆周运动变成直线运动,也可以用来求解振动、空气流动、电磁波传播等问题。
它也可以用来描述三角形的形状,以及多边形的形状。
三角函数在运算中有一个重要的性质,就是它可以在锐角处有很好的表达能力。
锐角是指两个直线之间较小的夹角,一般被划分为45°、30°、60°。
三角函数的特殊锐角值是指三角函数在特殊锐角(45°、30°、60°)处的值,它们出现的频率非常高。
下面是特殊锐角的三角函数值表:45°:sin45°=0.707,cos45°=0.707,tan45°=130°:sin30°=0.500,cos30°=0.866,tan30°=0.57760°:sin60°=0.866,cos60°=0.500,tan60°=1.732 这些特殊锐角三角函数值在数学中有着广泛的应用,它们可用于解决各种复杂的数学关系和运算问题。
例如,有一个包含60°锐角的三角形,那么它的两条直角边的边长比例可以用特殊锐角的三角函数值求出来,即a:b=sin60°:cos60°,即a:b=0.866:0.500。
此外,这些特殊锐角三角函数值还可用于求解另一个角度,例如给出一个等腰三角形的其中一个边长为a,另外一条边长为b,此时可以用特殊锐角三角函数值来求出它们之间的夹角,即tanα=a/b。
另外,特殊锐角三角函数值也可以用来求解特殊三角形,例如等腰直角三角形,它的两个直角的锐角值均为45°,然后可以利用三角函数特殊锐角值来求出等腰直角三角形的边长等相关数据。
总之,特殊锐角三角函数值对于数学的应用非常重要,它们既可以用来求解复杂的数学关系,也可以在求解三角形等几何问题时产生相当大的帮助,是数学中一种重要的参考值。

特殊角的锐角三角函数值三角函数是数学中最主要的函数之一,了解它们对我们日常学习和工作都有很大的帮助。
三角函数的定义指出,三角函数是由采用角度作为自变量的函数表示的。
此外还有正弦、余弦和正割三角函数,它们的变化规律是周期性的。
其中正、余弦和正割的值,当角大于360°时,会出现周期性变化的现象。
特殊角也就是角的大小大于360°的角,也就是弧度的值大于2π的角度。
这些特殊角的锐角三角函数值在数学中有很多应用。
比如说,科学计算中有时需要使用这些特殊角,以求出曲线在特定点处切向线的斜率。
弧度的值和角的余弦值也有一定的关系,因此经常需要用到特殊角的锐角三角函数值。
正弦、余弦和正割的特殊角值,由于角的大小大于360°,其函数值也就不是个位数。
需要进行进一步的计算,以求出特殊角的锐角三角函数值。
例如,正弦函数sin(x)当x=390°时,此时角大于360°,因此特殊角的正弦值就不是个位数。
角度的大小可以转换为弧度,即x=390°可以转换成弧度,即x=6.8Rad,此时正弦函数值sin(x)=sin(6.8)=0.851。
余弦函数cos(x)当x=400°时,其值也是特殊角,角度可以转换成6.9Rad,余弦函数值cos(x)=cos(6.9)=-0.228。
正割函数tan(x)当x=450°时,此时正割值也是特殊角,角度可以转换成7.85Rad,此时正割函数值tan(x)=tan(7.85)=4.16。
特殊角的锐角三角函数值不仅在科学计算中有用,还有一些工程学中的应用,比如说在机械设计中,当制作一个机器的齿轮的时候,也会使用特殊角的锐角三角函数值。
此外,特殊角的锐角三角函数值也可以用于研究建筑物的强度和结构的实际情况,可以用于绘制平面图,也可以用于解决导航、地理学和气象学等科学问题。
总之,特殊角的锐角三角函数值在数学中有着重要的作用,它们不仅在科学计算中有用,而且在机械设计、建筑物的强度和结构分析及各种科学问题解决等领域也有重要的意义。


三角函数值大全(1)特殊角三角函数值sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0cos0=1cos30= 二分之根号3cos45= 二分之根号2cos60=cos90=0tan0=0tan30= 三分之根号3tan45=1tan60= 根号3tan90=无cot0=无cot30= 根号3cot45=1cot60= 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°< α<90°间变化时,tanα>0, cotα>0.附:三角函数值表sin1= sin2= sin3=sin4= sin5= sin6=sin7= sin8= sin9=sin10= sin11= sin12=sin13= sin14= sin15=sin16= sin17= sin18=sin19=0. sin20=0. sin21=sin22= sin23= sin24=sin25= sin26= sin27=sin28= sin29= sin30=sin31= sin32= sin33=sin34= sin35= sin36=0.sin37= sin38= sin39=0.sin40=0. sin41=0. sin42=sin43= sin44= sin45=sin46= sin47= sin48=sin52= sin53= sin54=sin55= sin56=0. sin57=0. sin58= sin59= sin60=0.sin61= sin62=0. sin63=sin64= sin65=0. sin66=sin67=0. sin68= sin69=0. sin70= sin71= sin72=sin73=0. sin74= sin75=0. sin76=0. sin77=0. sin78= sin79= sin80= sin81=sin82=0. sin83= sin84=sin85= sin86= sin87=0.sin88=0. sin89=0.sin90=1cos1=0. cos2=0. cos3=0. cos4= cos5= cos6=cos7= cos8=0. cos9=cos10= cos11= cos12=cos13=0. cos14=0. cos15=0.cos19= cos20= cos21=0. cos22= cos23=0. cos24= cos25=0. cos26= cos27= cos28= cos29= cos30=0. cos31= cos32= cos33=cos34=0. cos35= cos36= cos37= cos38= cos39=cos40= cos41= cos42=cos43= cos44= cos45=cos46= cos47= cos48=cos49=0. cos50=0. cos51=0. cos52= cos53= cos54=0. cos55=0. cos56= cos57=0. cos58= cos59= cos60=cos61= cos62= cos63=0. cos64= cos65= cos66=0. cos67= cos68=0. cos69= cos70=0. cos71= cos72= cos73= cos74= cos75=cos79= cos80= cos81=cos82= cos83= cos84=cos85= cos86= cos87=cos88= cos89=cos90=0tan1= tan2= tan3=tan4= tan5= tan6=tan7= tan8= tan9=tan10= tan11= tan12=tan13=0. tan14= tan15=0. tan16=0. tan17= tan18= tan19= tan20= tan21=0. tan22=0. tan23=0. tan24=0. tan25=0. tan26=0. tan27=0. tan28= tan29= tan30=0. tan31=0. tan32=0. tan33=0. tan34=0. tan35=0. tan36=0. tan37= tan38= tan39=0. tan40=0. tan41=0. tan42=0.tan43= tan44=0. tan45=0. tan46= tan47= tan48=tan49= tan50= tan51=tan52= tan53=1. tan54= tan55= tan56=1. tan57=1. tan58=1. tan59=1. tan60=1. tan61=1. tan62=1. tan63= tan64= tan65= tan66=tan67= tan68=2. tan69=2. tan70=2. tan71= tan72= tan73=3. tan74= tan75=3. tan76= tan77= tan78=tan79= tan80= tan81=tan82= tan83= tan84=tan85= tan86= tan87=tan88= tan89=tan90=无取值。

第2节 特殊角三角函数值及锐角三角函数性质※知识要点1.,的增大而 , c osα 随着α 的增大而 ;(4)商数关系: ; (5)平方关系: ; ※题型讲练【例1】已知如图,△ABC 是等腰三角形,AB =AC ,CD ⊥AB ,若顶角∠A =45°. (1)求∠BCD 的度数; (2)利用图像求tan 22.5°的值. 变式训练1:1.试设计图形求75°角的三角函数值. 【例2】计算下列各式的值:(1) tan 30°-sin 60°·sin 30° (2) 2sin 60°-cos 30°·tan 45° (3)变式训练2:1.计算:2-1-3tan 30°+(2-1)0+12+cos 60°2.在△ABC 中,|tanA -1|+(cosB - )2=0,BC =4cm , (1)求∠C 的度数; (2)求AC 和AB 的长. 【例3】计算下列各题: (1)sin 35°cos 55°十cos 35°sin 55° (2)sin 18°+tan 53°tan 37°-tan 45°cos 72° 变式训练3:1.若sin (90°-α)=0.618,则cos α= ;2.若12 < cosα <32,则锐角α的取值范围是 ;3.将下列三角函数用“>”连接起来: (1)sin 42°、cos 42°、sin 64°、cos 50°; (2)sin 53°、cos 53°、tan 53°、tan 62°;【例4】已知锐角α满足tanα=2,求下列各式的值:(1) (2)变式训练4:1.已知α为锐角,且sinα-cosα= ,求sinαcosα的值.2.已知锐角α满足sinα=1-m ,cosα=2m ,求m 的值.※课后练习1.|-cos 30°|的相反数是( )A .12B .-22C .-32 D . 32.计算2sin 60°-cos 30°·tan 45°的结果为( ) A . 3 B .32 C .-32D .0 3.如果△ABC 中,sin A =cos B =22,下列说法正确是( ) A .△ABC 是直角三角形 B .△ABC 是等腰三角形 C .△ABC 是等腰直角三角形 D .△ABC 是锐角三角形 4.如图所示,在数轴上点A 所表示的数x 的范围是( ) A .32sin 30°<x <sin 60° B .cos 30°<x <32cos 45°C . 32tan 30°<x <tan 45°D .32tan 45°<x <tan 60°5.在△ABC 中,若∠A 、∠B 满足|cosA -12|+(1-tanB )2=0,则∠C 的度数是( )A .45°B .60°C .75°D .105° 6.在Rt △ABC 中,∠C =60°,下列说法错误的是( ) A .sinA =cosB B .tanA ·tanB =1 C .cosB =tanA ·sinA D .cosA =tanB ·cosB7.在Rt △ABC 中,∠C =90°,若∠A =30°,则∠B =______, sinA =_________,cosA =_________,tanA =_________, sinB =_________,cosB =_________,tanB =_________. 8.比较下列各组数的大小:(1)sin 26° cos 26°; (2)cos 74° tan 50°. 9.当锐角α满足下列条件时,分别求角α的取值范围: (1)若cosα<12,则角α 的取值范围是 ;(2)若sin α<12,则角α 的取值范围是 ;(3)若1<tan α<3,则角α 的取值范围是 . 10.计算下列各题: (1)2cos 30°-tan 45°--2(2)|-2|+2sin 30°-(-3)2+(tan 45°)-1 11.计算下列各题:(1)tan 36°tan 54°-cos 72°+sin 18°(2)46sin 46tan ·sin4480cos 10sin 2- 12.已知:如图 ,在△ABC 中,BC =8,∠B =60°,∠C =45°, 求BC 边上的高AD 的长.13.已知锐角α满足sinα=4m ,cosα=1-2m ,求tanα 的值. 14.经查,三角函数公式:sin (α+β)=sin αcos β+cos αsin β; 请利用公式计算sin 75°的值.15.已知:如图,Rt △ABC 中,∠C =90°,∠BAC =30°,延长CA 至D 点,使AD =AB .求:(1)∠D 及∠DBC ; (2)tanD 及tan ∠DBC ; (3)请用类似的方法求tan 22.5°.ααααcos sin 2cos 2sin -+αααααcos sin sin 2cos sin 222+-51( )。


三角函数值大全(1)特殊角三角函数值sin0=0,sin15=(√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=(√6-√2)/4sin180=0sin270=-1sin360=0cos0=1cos30= 二分之根号3cos45= 二分之根号2cos60=cos90=0tan0=0tan30= 三分之根号3tan45=1tan60= 根号3tan90=无cot0=无cot30= 根号3cot45=1cot60= 三分之根号3cot90=0(2)0°~90°的任意角的三角函数值,查三角函数表。
(3)锐角三角函数值的变化情况(i)锐角三角函数值都是正值(ii)当角度在0°~90°间变化时,正弦值随着角度的增大(或减小)而增大(或减小)余弦值随着角度的增大(或减小)而减小(或增大)正切值随着角度的增大(或减小)而增大(或减小)余切值随着角度的增大(或减小)而减小(或增大)(iii)当角度在0°≤α≤90°间变化时,0≤sinα≤1, 1≥cosα≥0,当角度在0°< α<90°间变化时,tanα>0, cotα>0.附:三角函数值表sin1= sin2= sin3=sin4= sin5= sin6=sin7= sin8= sin9=sin10= sin11= sin12=sin13= sin14= sin15=sin16= sin17= sin18=sin19= sin20= sin21=sin22= sin23= sin24=sin25= sin26= sin27=sin28= sin29= sin30=sin31= sin32= sin33=sin34= sin35= sin36=sin37= sin38= sin39=sin40= sin41= sin42=sin43= sin44= sin45=sin46= sin47= sin48=sin52= sin53= sin54= sin55= sin56= sin57= sin58= sin59= sin60= sin61= sin62= sin63= sin64= sin65= sin66= sin67= sin68= sin69= sin70= sin71= sin72= sin73= sin74= sin75= sin76= sin77= sin78= sin79= sin80= sin81= sin82= sin83= sin84= sin85= sin86= sin87= sin88= sin89=sin90=1cos1= cos2= cos3= cos4= cos5= cos6= cos7= cos8= cos9= cos10= cos11= cos12= cos13= cos14= cos15=cos19= cos20= cos21= cos22= cos23= cos24= cos25= cos26= cos27= cos28= cos29= cos30= cos31= cos32= cos33= cos34= cos35= cos36= cos37= cos38= cos39= cos40= cos41= cos42= cos43= cos44= cos45= cos46= cos47= cos48= cos49= cos50= cos51= cos52= cos53= cos54= cos55= cos56= cos57= cos58= cos59= cos60= cos61= cos62= cos63= cos64= cos65= cos66= cos67= cos68= cos69= cos70= cos71= cos72= cos73= cos74= cos75=cos79= cos80= cos81= cos82= cos83= cos84= cos85= cos86= cos87= cos88= cos89=cos90=0tan1= tan2= tan3= tan4= tan5= tan6= tan7= tan8= tan9= tan10= tan11= tan12= tan13= tan14= tan15= tan16= tan17= tan18= tan19= tan20= tan21= tan22= tan23= tan24= tan25= tan26= tan27= tan28= tan29= tan30= tan31= tan32= tan33= tan34= tan35= tan36= tan37= tan38= tan39= tan40= tan41= tan42=tan43= tan44= tan45= tan46= tan47= tan48= tan49= tan50= tan51= tan52= tan53= tan54= tan55= tan56= tan57= tan58= tan59= tan60= tan61= tan62= tan63= tan64= tan65= tan66= tan67= tan68= tan69= tan70= tan71= tan72= tan73= tan74= tan75= tan76= tan77= tan78= tan79= tan80= tan81= tan82= tan83= tan84= tan85= tan86= tan87= tan88= tan89=tan90=无取值。



锐角三角函数及特殊角的三角函数值【教学建议】本节内容较简单,把定义讲透,加强对复杂图形中的三角函数问题的解题示范。
1.正切、正弦、余弦:如下图所示,在Rt △ABC 中,∠C =90°,①正弦:锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即sinA=A ac ∠的对边斜边.②余弦:锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cosA=A bc ∠的邻边斜边.③正切:锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即tanA =A aA b∠的对边∠的邻边.2.坡度:如图:AB 表示水平面,BC 表示坡面,我们把水平面AB 与坡面BC 所形成的ABC 称为坡角.教学过程一、导入 二、知识讲解知识点1 正切、正弦、余弦一般地,线段BE 的长度称为斜坡BC 的水平宽度,线段CE 的长度称为斜坡BC 的铅垂高度。
如图;坡面的铅垂高度h 和水平宽度l 的比叫做坡面的坡度(或坡比),用ι表示,记作=ιh:l,坡度通常写成1:m 的形式(m 可为小数)。
坡面与水平面的夹角叫做坡角,记作α。
于是tan hi lα==,显然,坡度越大,α越大,坡面就越陡.三角函数︒30 ︒452.运算的顺序:先乘方,再乘除,后加减;同级运算从左到右依次进行.3.强调:(sin 60°)2用sin 260°表示,即为(sin 60°)·(sin 60°).【题干】若△ABC 在正方形网格纸中的位置如图所示,则tan α的值是( )知识点2 30°、45°、60°角的三角函数值及其运算 三、例题精析例题1A .2B .12CD .1【答案】D【解析】根据图形可知∠α的对边及邻边的值,再根据锐角三角函数的定义求解即可. 解:根据图形可知:△ABC 是直角三角形,且AC =3,BC =3. 根据勾股定理得到AB , 则tan α=ACBC=1. 故选D .【题干】如图,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD ,使点B 落在AD 边上的点F 处,若AB =4,BC =5,则tan ∠AFE 的值为( )A .43B .35C .34D .45【答案】C【解析】由四边形ABCD 是矩形,可得:∠A =∠B =∠D =90°,CD =AB =4,AD =BC =5,由折叠的性质可得:∠EFC =∠B =90°,CF =BC =5,由同角的余角相等,即可得∠DCF =∠AFE ,然后在Rt △DCF 中,即可求得答案.解:∵四边形ABCD 是矩形,∴∠A =∠B =∠D =90°,CD =AB =4,AD =BC =5, 由题意得:∠EFC =∠B =90°,CF =BC =5, ∴∠AFE +∠DFC =90°,∠DFC +∠FCD =90°,例题2∴∠DCF =∠AFE ,∵在Rt △DCF 中,CF =5,CD =4, ∴DF =3,∴tan ∠AFE =tan ∠DCF =DF DC =34. 故选C .【题干】如图,菱形ABCD 的对角线AC =6,BD =8,∠ABD =α,则下列结论正确的是( )A .sin α=45B .cos α=35C .tan α=43D .tan α=34【答案】D【解析】根据菱形的性质及勾股定理可求得AB 的长,从而可表示出不同的三角函数从而验证得到正确的那个选项.解:菱形ABCD 的对角线AC =6,BD =8, 则AC ⊥BD ,且OA =3,OB =4.在直角△ABO 中,根据勾股定理得到:AB =5, 则sin α=35,cos α=45,tan α=34, 故选D .【题干】如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m .如果在坡度为0.75的山坡上种树,也要求株距为4m ,那么相邻两树间的坡面距离为( )A .5mB .6mC .7mD .8m例题3例题4【答案】A【解析】解:由题知:tan A =0.75,此时坡上株距是4m ,设相邻两树间的坡面距离为xm 所以满足sin A =0.8=4x解得x =5 故选A .【题干】如图,修建抽水站时,沿着坡度为i =1A 处铅垂高度为6m ,则所铺设水管AC 的长度为( )A .8mB .10mC .12mD .18m 【答案】C【解析】∵该斜坡的坡度为i =1 ∴AB :BC =1 ∵AB =6m , ∴BC m , 则AC 12==(m ). 故选C .【题干】1.下列各式正确的是( ) A . cos 600<sin 450<tan 45B . sin 450<cos 600<tan 450C . cos 600<tan 450<sin 450D . tan 450<cos 600<sin 450【答案】A【解析】根据特殊角的锐角三角函数值依次分析各选项即可作出判断.例题5例题6∵2160cos =︒,2245sin =︒,145tan =︒∴<︒60cos <︒45sin ︒45tan 故选A .【题干】2.已知α为锐角,sin (α﹣20°),则α=( ) A .20°B .40°C .60°D .80°【答案】D【解析】∵α为锐角,sin (α﹣20°)=2, ∴α﹣20°=60°, ∴α=80°, 故选D .【题干】3.计算5sin 30°+2cos 245°-tan 260°的值是( ) AB .12C .-12D .1 【答案】B【解析】根据特殊角的锐角三角函数值计算即可得到结果. 5sin 30°+2cos 245°-tan 260°21321225)3()22(221522=−⨯+=−⨯+⨯= 故选B .【题干】4.在△ABC中,若1|sin ||cos |022A B −+−=,则C ∠=_______. 【答案】120°【解析】因为||0a ≥,且1|sin ||cos |022A B −+−=,所以11sin 0sin 22cos 0cos 22A AB B ⎧⎧−==⎪⎪⎪⎪∴⎨⎪−==⎪⎪⎩⎩,又因为13sin 30,cos303012022A B C ==∴∠=∠=∴∠=。
28.1锐角三角函数 ——特殊角三角函数值(第3课时)年级:九年级:九年级 学科:数学:数学班级: 姓名:【学习目标】⑴: 能推导并熟记3030°°、4545°°、6060°角的三角函数值,并能根据这些值说出对应锐角度数。
°角的三角函数值,并能根据这些值说出对应锐角度数。
⑵: 能熟练计算含有3030°°、4545°°、6060°角的三角函数的运算式°角的三角函数的运算式°角的三角函数的运算式【导学过程】一、自学提纲:一个直角三角形中,一个直角三角形中,一个锐角正弦是怎么定义的?一个锐角正弦是怎么定义的?一个锐角余弦是怎么定义的?一个锐角余弦是怎么定义的?一个锐角正切是怎么定义的?一个锐角正切是怎么定义的?二、合作交流:思考:两块三角尺中有几个不同的锐角?两块三角尺中有几个不同的锐角? 是多少度?是多少度? 你能分别求出这几个锐角的正弦值、余弦值和正切值码?.你能分别求出这几个锐角的正弦值、余弦值和正切值码?.三、教师点拨:归纳结果3030°° 4545°° 6060°° siaAcosAtanA例3:求下列各式的值.:求下列各式的值.(1)cos 260°60°+sin +sin 260°. (2)cos 45sin 45°°-tan45°.°. 例4:(1)如图()如图(11),在Rt Rt△△ABC 中,∠中,∠C=90C=90C=90,,AB=6,BC=3,求∠,求∠A A 的度数.的度数.(2)如图()如图(22),已知圆锥的高AO 等于圆锥的底面半径OB 的3倍,求a .四、学生展示:1.已知:.已知:Rt Rt Rt△△ABC 中,∠中,∠C=90C=90C=90°,°,°,cosA=cosA=35 ,AB=15AB=15,则,则AC 的长是(的长是( )). A A..3 B 3 B..6 C 6 C..9 D9 D..12 2.下列各式中不正确的是(.下列各式中不正确的是( )). A A..sin 260°+cos 26060°°=1 B =1 B..sin30sin30°°+cos30+cos30°°=1C C..sin35sin35°°=cos55=cos55°°D D..tan45tan45°°>sin45>sin45°°3.计算2sin302sin30°°-2cos60-2cos60°°+tan45+tan45°的结果是(°的结果是(°的结果是( )). A A..2 B 2 B..3 C C..2 D D..14.已知∠.已知∠A A 为锐角,且cosA cosA≤≤12 ,那么(,那么( ))A A..0°<∠A ≤6060°°B .6060°≤∠°≤∠°≤∠A<90A<90A<90°°C C..0°<∠A ≤3030°°D .3030°≤∠°≤∠°≤∠A<90A<90A<90°°5.在△.在△ABC ABC 中,∠中,∠A A 、∠、∠B B 都是锐角,且sinA=12, cosB=3 2 ,则△,则△ABC ABC 的形状是(的形状是()) A A.直角三角形.直角三角形.直角三角形 B B B.钝角三角形.钝角三角形C .锐角三角形.锐角三角形 D D D.不能.不能确定确定6.如图Rt Rt△△ABC 中,∠中,∠ACB=90ACB=90ACB=90°,°,°,CD CD CD⊥⊥AB 于D ,BC=3BC=3,,AC=4AC=4,设∠,设∠,设∠BCD=a BCD=a BCD=a,则,则tana•tana•的值为的值为( )). A .34 B B..43 C C..35 D D..457.当锐角a>60a>60°时,°时,°时,cosa cosa 的值(的值( )). A A.小于.小于12 B B.大于.大于12 C C.大于.大于3 2 D D.大于.大于1 8.在△.在△ABC ABC 中,三边之比为a :b :c=1c=1::3:2,则sinA+tanA 等于(等于( )). A .32313331.3..6222B C D +++9.已知梯形ABCD 中,腰BC 长为2,梯形对角线BD 垂直平分AC AC,若梯形的高是,若梯形的高是3,•则∠CAB 等于(等于( ))A A..3030°°B B..6060°°C C..4545°°D D.以上都不对.以上都不对.以上都不对1010..sin 272°+sin 21818°的值是(°的值是(°的值是( )). A A..1 B 1 B..0 C 0 C..12 D D..3 2 1111.若(.若(3 tanA-3tanA-3))2+│2cosB-3 │=0=0,则△,则△,则△ABC ABC ABC(( )). A A.是直角三角形.是直角三角形.是直角三角形 B B B.是等边三角形.是等边三角形.是等边三角形C C.是含有.是含有6060°的任意三角形°的任意三角形°的任意三角形D D D.是顶角为钝角的等腰三角形.是顶角为钝角的等腰三角形.是顶角为钝角的等腰三角形三、填空题.三、填空题.1212.设.设α、β均为锐角,且sin α-cos β=0=0,则,则α+β=_______=_______..1313..cos 45sin 301cos60tan 452°-°°+°的值是的值是_____________________..1414..已知,等腰△等腰△ABC•ABC•ABC•的腰长为的腰长为43 ,•底为30•30•°,°,•则底边上的高为则底边上的高为__________________,,•周长为周长为__________________..1515.在.在Rt Rt△△ABC 中,∠中,∠C=90C=90C=90°,已知°,已知tanB=5 2,则cosA=________cosA=________..。
三角函数特殊角值表1、图示法:借助于下面三个图形来记忆,即使有所遗忘也可根据图形重新推出:in30°=co60°=12in45°=co45°=22tan30°=cot60°=221tan45°=cot45°=132213451601说明:正弦值随角度变化,即030456090变化;值从031变化,其余类似记忆.23、规律记忆法:观察表中的数值特征,可总结为下列记忆规律:①有界性:(锐角三角函数值都是正值)即当0°<<90°时,则0<in<1;0<co<1;tan>0;cot>0。
②增减性:(锐角的正弦、正切值随角度的增大而增大;余弦、余切值随角度的增大而减小),即当0<A<B<90°时,则inA<inB;tanA<tanB;coA>coB;cotA>cotB;特别地:若0°<<45°,则inA<coA;tanA<cotA若45°<A<90°,则inA>coA;tanA>cotA.4、口决记忆法:观察表中的数值特征正弦、余弦值可表示为m形式,正切、余切值可表示为形式,有关m的值可归纳成23顺口溜:一、二、三;三、二、一;三九二十七.巧记特殊角的三角函数值初学三角函数,记忆特殊角三角函数值易错易混。
若在理解掌握的基础上,经过变形,使其呈现某种规律,再配以歌诀,则可浅显易记,触目成诵。
仔细观察表1,你会发现重要的规律。
表1中,三角函数值的前三行,分子被开方数排列特征依次为“1,2,3,3,2,1,3,9,27”。
“一二三,三二一,三九二十七”。
记此歌诀即可。
观察表2也可发现重要的规律。
表2中,弦函数分子被开方数分别为1,2,3,3,2,1,分母都是2;切函数分子的幂指数分别是1,2,3,3,2,1,分母都是3。
据此概括歌诀为:“一二三,三二一,弦内切外莫忘记。
《锐角的三角函数》知识清单一、锐角三角函数的定义在直角三角形中,我们把锐角的对边与斜边的比叫做正弦(sin),锐角的邻边与斜边的比叫做余弦(cos),锐角的对边与邻边的比叫做正切(tan)。
以一个锐角为∠A 的直角三角形为例。
假设∠C = 90°,∠A 所对的边为 a,∠A 的邻边为 b,斜边为 c。
那么正弦 sinA =对边/斜边= a/c;余弦 cosA =邻边/斜边= b/c;正切 tanA =对边/邻边= a/b。
需要注意的是,三角函数的值只与角的大小有关,而与三角形的大小无关。
二、特殊锐角的三角函数值我们需要牢记一些特殊锐角(30°、45°、60°)的三角函数值。
当∠A = 30°时,sinA = 1/2,cosA =√3/2,tanA =√3/3;当∠A = 45°时,sinA = cosA =√2/2,tanA = 1;当∠A = 60°时,sinA =√3/2,cosA = 1/2,tanA =√3。
这些特殊值在解题中经常会用到,所以一定要熟练记忆。
三、锐角三角函数的关系1、平方关系sin²A + cos²A = 1这意味着,如果已知一个锐角的正弦值,可以通过这个关系式求出它的余弦值;反之亦然。
2、商数关系tanA = sinA / cosA这个关系常用于将正切转化为正弦和余弦的形式进行计算。
四、锐角三角函数的应用锐角三角函数在实际生活中有广泛的应用,比如:1、测量物体的高度如果知道一个物体与观测点的水平距离以及观测点看物体顶部的仰角,就可以利用正切函数求出物体的高度。
2、测量河流的宽度在河的一岸选择一个观测点,测出对岸某一点的俯角以及观测点到对岸的距离,通过三角函数可以计算出河流的宽度。
3、计算斜坡的坡度坡度是斜坡的垂直高度与水平距离的比值,通常用正切值来表示。
五、解直角三角形解直角三角形是指在直角三角形中,由已知元素求出未知元素的过程。
锐角三角函数的特殊值。
锐角三角函数是数学中常见的一类函数,它们在三角学和解析几何中有着重要的应用。
这些函数的特殊值在计算和解题中起着重要的作用,下面我们将详细介绍锐角三角函数的特殊值。
一、正弦函数的特殊值正弦函数是最基本的三角函数之一,它表示一个角的对边与斜边的比值。
在锐角三角函数中,正弦函数的特殊值主要集中在0°、30°、45°、60°和90°五个角度上。
1. 当角度为0°时,正弦函数的值为0。
这是因为0°角的对边为0,所以正弦函数的值也为0。
2. 当角度为30°时,正弦函数的值为1/2。
这是因为30°角的对边等于斜边的一半,所以正弦函数的值为1/2。
3. 当角度为45°时,正弦函数的值为√2/2。
这是因为45°角的对边等于斜边的一半,所以正弦函数的值为√2/2。
4. 当角度为60°时,正弦函数的值为√3/2。
这是因为60°角的对边等于斜边的一半,所以正弦函数的值为√3/2。
5. 当角度为90°时,正弦函数的值为1。
这是因为90°角的对边等于斜边,所以正弦函数的值为1。
二、余弦函数的特殊值余弦函数是三角函数中的另一个重要函数,它表示一个角的邻边与斜边的比值。
在锐角三角函数中,余弦函数的特殊值也主要集中在0°、30°、45°、60°和90°五个角度上。
1. 当角度为0°时,余弦函数的值为1。
这是因为0°角的邻边等于斜边,所以余弦函数的值为1。
2. 当角度为30°时,余弦函数的值为√3/2。
这是因为30°角的邻边等于斜边的一半,所以余弦函数的值为√3/2。
3. 当角度为45°时,余弦函数的值为√2/2。
这是因为45°角的邻边等于斜边的一半,所以余弦函数的值为√2/2。