人教版全国数学中考复习方案第17讲几何初步及平行线、相交线
- 格式:ppt
- 大小:488.50 KB
- 文档页数:23
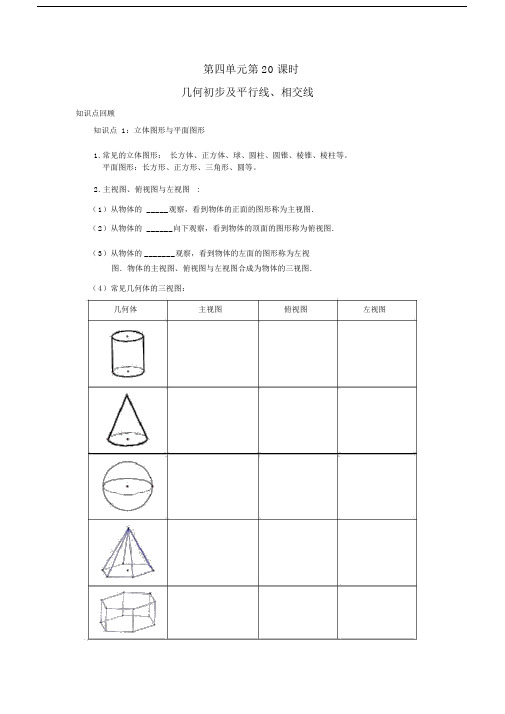
第四单元第 20 课时几何初步及平行线、相交线知识点回顾知识点 1:立体图形与平面图形1.常见的立体图形:长方体、正方体、球、圆柱、圆锥、棱锥、棱柱等。
平面图形:长方形、正方形、三角形、圆等。
2.主视图、俯视图与左视图 :(1)从物体的 _____观察,看到物体的正面的图形称为主视图.(2)从物体的 ______向下观察,看到物体的顶面的图形称为俯视图.(3)从物体的 _______观察,看到物体的左面的图形称为左视图.物体的主视图、俯视图与左视图合成为物体的三视图.(4)常见几何体的三视图:几何体主视图俯视图左视图3.几种常见几何体的展开图:1.圆柱展开图:上、下底面为________,侧面是 ________ ,长方形的长是圆柱的底面周长,宽是圆柱的高。
2.圆锥展开图:底面是_______,侧面是 ________,扇形的弧长是底面圆的周长。
3.棱柱展开图:上、下底面是_____________ ,侧面都是 _________。
4.棱锥展开图:底面是__________,侧面都是 ________,这些三角形的公共顶点就是棱锥的顶点。
4.正方体的表面展开图 :把正方体的表面展开成平面图形后,有很多种形状,如果将经过平移、旋转等变化后可以重合的两个图形看成是同一图形,那么正方体的表面展开图共有11 种不同的情况。
我们可以将则11 种图形分类:( 1)“一·四·一”型,中间一行 4 个作侧面,两边各 1 个分别作上下底面,?共有 6种.如图( 1)——( 6).( 2)“二·三·一” (或一·三·二)型,中间 3 个作侧面,上(或下)边2?个那行,相连的正方形作底面,不相连的再下折作另一个侧面,共 3 种.如图( 7)——( 9).( 3)“二·二·二”型,成阶梯状.如图(10).( 4)“三·三”型,两行只能有 1 个正方形相连.如图(11).(1)( 2)( 3)( 5)( 4)( 6)(7)(8)(9)(10)(11)例 1、( 2009 年内蒙古包头)将一个正方体沿某些棱展开后,能够得到的平面图形是()A.B.C.D.【解析】本题考查图形的展开与折叠中,正方体的常见的十余种展开图有关内容,可将这四个图折叠后,看能否组成正方形,显然只有 C 符合要求。


课时教案课题线、角、平行线与相交线(含命题)课型复习教材分析教学目标1、掌握直线、射线、线段的概念与区别2、掌握平行线的性质与判断定理3、掌握并会运用平行线的性质与判断定理解决相关问题教学重点平行线的性质与判断定理教学难点运用平行线的性质与判断定理解决问题教法学法讲授法、讨论法、练习法步骤设计意图(目的)教师活动/方法学生活动/方法时间12梳理本章知识结构,构建知识整体。
通过回顾知识点,使学生掌握各知识点之间的联系。
从性质与判定两个角度研究平行线与相交线一、科学备考学生用自己的方式总结本章知识点,并画出关系图,课堂上先交流讨论。
以小组为单位,进行交流讨论,共同回顾本章知识点,进行查漏补缺。
教师巡视、指导,发3min103 4复习命题与反证法重难点选讲:平行线的性质与判定真假命题讲解变式训练及时强化重难点通过练习,体验中考,加深对相关知识的二、重难点选讲三、变式训练四、随堂练习(深圳五年中考)现问题后,及时纠正学生的问题,培养学生的总结归纳能力,同时培养学生观察力。
让学生先独立完成,而后将不会的问题各小组交流讨论得出结果.养成学以致用的好习惯.教师将课堂还给学生,争取让学生自主复习。
教师巡视,适时点拨.学生完成后及时点min5min5min15Min应用.通过老师的辅导,帮助学生对本节内容进行查漏补缺。
总结本节课的内容,建构知识整体.五、本章小结评,借助多媒体展示学生出现的问题进行矫正。
此环节让学生独立完成,教师进行巡视指导,针对学生出现的问题再进行强调,先小组内交流本节课的收获和感想,然后以小组为单位派代表进行总结.教师进行补充。
2min作业布置直击中考P75-78(64选做)板书设计线、角、平行线与相交线一、线段与角二、平行线与相交线三、命题与反证法教学反思这堂课是复习课,容量较大。
线段、角、相交线与平行线是几何知识的基础内容,在平面几何计算和证明中,应用十分广泛。
课前我要求学生归纳整理了有关线段、角、相交线与平行线的知识点,这样不仅复习了所学知识,而且可以使学生逐渐学会反思、总结,提高自主学习的能力;在教学活动中教师是学生学习的组织者、引导者与合。
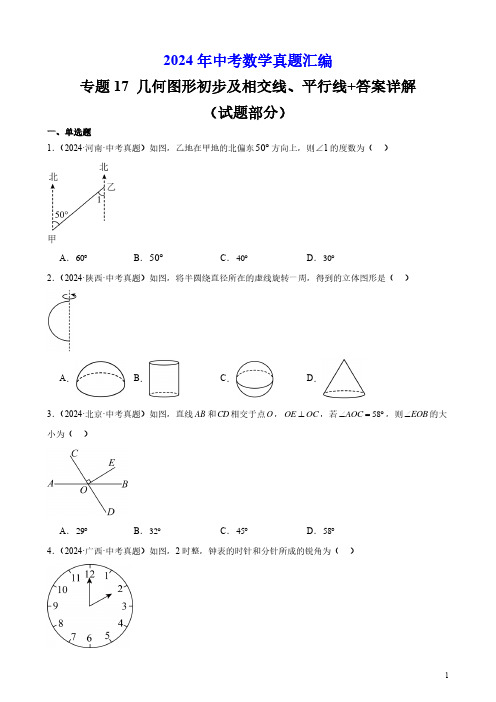
2024年中考数学真题汇编专题17 几何图形初步及相交线、平行线+答案详解(试题部分)一、单选题1.(2024·河南·中考真题)如图,乙地在甲地的北偏东50︒方向上,则∠1的度数为()A.60︒B.50︒C.40︒D.30︒2.(2024·陕西·中考真题)如图,将半圆绕直径所在的虚线旋转一周,得到的立体图形是()A.B.C.D.∠的大3.(2024·北京·中考真题)如图,直线AB和CD相交于点O,OE OC∠=︒,则EOBAOC⊥,若58小为()A.29︒B.32︒C.45︒D.58︒4.(2024·广西·中考真题)如图,2时整,钟表的时针和分针所成的锐角为()A .20︒B .40︒C .60︒D .80︒5.(2024·四川内江·中考真题)如图,AB CD ∥,直线EF 分别交AB 、CD 于点E 、F ,若64EFD ∠=︒,则BEF ∠的大小是( )A .136︒B .64︒C .116︒D .128︒6.(2024·湖北·中考真题)如图,直线AB CD ∥,已知1120∠=︒,则2∠=( )A .50︒B .60︒C .70︒D .80︒7.(2024·陕西·中考真题)如图,AB DC ∥,BC DE ∥,145B ∠=︒,则D ∠的度数为( )A .25︒B .35︒C .45︒D .55︒8.(2024·黑龙江齐齐哈尔·中考真题)将一个含30︒角的三角尺和直尺如图放置,若150∠=︒,则2∠的度数是( )A .30︒B .40︒C .50︒D .60︒9.(2024·广东·中考真题)如图,一把直尺、两个含30︒的三角尺拼接在一起,则ACE ∠的度数为( )A .120︒B .90︒C .60︒D .30︒10.(2024·青海·中考真题)生活中常见的路障锥通常是圆锥的形状,它的侧面展开图是( )A.B.C.D.11.(2024·四川德阳·中考真题)走马灯,又称仙音烛,据史料记载,走马灯的历史起源于隋唐时期,盛行于宋代,是中国特色工艺品,常见于除夕、元宵、中秋等节日,在一次综合实践活动中,一同学用如图所示的纸片,沿折痕折合成一个棱锥形的“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯旋转时,正好看到“吉祥如意”的字样.则在A、B、C处依次写上的字可以是()A.吉如意B.意吉如C.吉意如D.意如吉12.(2024·四川广安·中考真题)将“共建平安校园”六个汉字分别写在某正方体的表面上,下图是它的一种展开图,则在原正方体上,与“共”)A.校B.安C.平D.园13.(2024·江苏盐城·中考真题)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是()A.湿B.地C.之D.都14.(2024·江西·中考真题)如图是43的正方形网格,选择一空白小正方形,能与阴影部分组成正方体展开图的方法有( )A .1种B .2种C .3种D .4种15.(2024·江苏扬州·中考真题)如图是某几何体的表面展开后得到的平面图形,则该几何体是( )A .三棱锥B .圆锥C .三棱柱D .长方体16.(2024·河北·中考真题)如图,AD 与BC 交于点O ,ABO 和CDO 关于直线PQ 对称,点A ,B 的对称点分别是点C ,D .下列不一定正确的是( )A .AD BC ⊥B .AC PQ ⊥ C .ABO CDO △≌△D .AC BD ∥17.(2024·福建·中考真题)在同一平面内,将直尺、含30︒角的三角尺和木工角尺(CD ⊥DE )按如图方式摆放,若AB CD ,则1∠的大小为( )A .30︒B .45︒C .60︒D .75︒18.(2024·江苏苏州·中考真题)如图,AB CD ,若165∠=︒,2120∠=︒,则3∠的度数为( )A .45︒B .55︒C .60︒D .65︒19.(2024·内蒙古包头·中考真题)如图,直线AB CD ∥,点E 在直线AB 上,射线EF 交直线CD 于点G ,则图中与AEF ∠互补的角有( )A .1个B .2个C .3个D .4个20.(2024·广东深圳·中考真题)如图,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角150∠=︒,则反射光线与平面镜夹角4∠的度数为( )A .40︒B .50︒C .60︒D .70︒21.(2024·吉林·中考真题)如图,四边形ABCD 内接于O ,过点B 作BE AD ∥,交CD 于点E .若50BEC ∠=︒,则ABC ∠的度数是( )A .50︒B .100︒C .130︒D .150︒22.(2024·重庆·中考真题)如图,AB CD ∥,若1125∠=︒,则2∠的度数为( )A .35︒B .45︒C .55︒D .125︒23.(2024·吉林长春·中考真题)如图,在ABC 中,O 是边AB 的中点.按下列要求作图:①以点B 为圆心、适当长为半径画弧,交线段BO 于点D ,交BC 于点E ;②以点O 为圆心、BD 长为半径画弧,交线段OA 于点F ;③以点F 为圆心、DE 长为半径画弧,交前一条弧于点G ,点G 与点C 在直线AB 同侧;④作直线OG ,交AC 于点M .下列结论不一定成立的是( )A .AOMB ∠=∠B .180OMC C ∠+∠= C .AM CM =D .12OM AB = 24.(2024·青海·中考真题)如图,一个弯曲管道AB CD ,120ABC ∠=︒,则BCD ∠的度数是( )A .120︒B .30︒C .60︒D .150︒25.(2024·吉林长春·中考真题)在剪纸活动中,小花同学想用一张矩形纸片剪出一个正五边形,其中正五边形的一条边与矩形的边重合,如图所示,则α∠的大小为( )A .54oB .60C .70D .7226.(2024·内蒙古赤峰·中考真题)将一副三角尺如图摆放,使有刻度的两条边互相平行,则1∠的大小为( )A .100︒B .105︒C .115︒D .120︒27.(2024·四川达州·中考真题)如图,正方体的表面展开图上写有“我们热爱中国”六个字,还原成正方体后“我”的对面的字是( )A .热B .爱C .中D .国28.(2024·四川宜宾·中考真题)如图是正方体表面展开图.将其折叠成正方体后,距顶点A 最远的点是( )A .B 点 B .C 点 C .D 点 D .E 点29.(2024·四川泸州·中考真题)把一块含30︒角的直角三角板按如图方式放置于两条平行线间,若145∠=︒,则2∠=( )A .10︒B .15︒C .20︒D .30︒30.(2024·江苏盐城·中考真题)小明将一块直角三角板摆放在直尺上,如图,若155∠=︒,则2∠的度数为( )A .25︒B .35︒C .45︒D .55︒31.(2024·甘肃·中考真题)若55A ∠=︒,则A ∠的补角为( )A .35︒B .45︒C .115︒D .125︒32.(2024·内蒙古呼伦贝尔·中考真题)如图,,AD BC AB AC ⊥∥,若135.8∠=,则B ∠的度数是( )A .3548'︒B .5512'︒C .5412'︒D .5452'︒二、填空题33.(2024·吉林·中考真题)如图,从长春站去往胜利公园,与其它道路相比,走人民大街路程最近,其蕴含的数学道理是 .34.(2024·广西·中考真题)已知1∠与2∠为对顶角,135∠=︒,则2∠= °.35.(2024·广东广州·中考真题)如图,直线l 分别与直线a ,b 相交,a b ,若171∠=︒,则2∠的度数为 .36.(2024·四川乐山·中考真题)如图,两条平行线a 、b 被第三条直线c 所截.若160∠=︒,那么2∠= .37.(2024·黑龙江绥化·中考真题)如图,AB CD ∥,33C ∠=︒,OC OE =.则A ∠= ︒.38.(2024·山东威海·中考真题)如图,在正六边形ABCDEF 中,AH FG ∥,BI AH ⊥,垂足为点I .若20EFG ∠=︒,则ABI ∠= .39.(2024·河北·中考真题)如图,ABC 的面积为2,AD 为BC 边上的中线,点A ,1C ,2C ,3C 是线段4CC 的五等分点,点A ,1D ,2D 是线段3DD 的四等分点,点A 是线段1BB 的中点.(1)11AC D △的面积为 ;(2)143B C D △的面积为 .三、解答题40.(2024·福建·中考真题)在手工制作课上,老师提供了如图1所示的矩形卡纸ABCD ,要求大家利用它制作一个底面为正方形的礼品盒.小明按照图2的方式裁剪(其中AE FB =),恰好得到纸盒的展开图,并利用该展开图折成一个礼品盒,如图3所示.图1 图2 图3(1)直接写出AD AB的值; (2)如果要求折成的礼品盒的两个相对的面上分别印有“吉祥”和“如意”,如图4所示,那么应选择的纸盒展开图图样是( )图4A.B.C.D.(3)现以小明设计的纸盒展开图(图2)为基本样式,适当调整AE,EF的比例,制作棱长为10cm的正方体礼品盒,如果要制作27个这样的礼品盒,请你合理选择上述卡纸(包括卡纸的型号及相应型号卡纸的张数),并在卡纸上画出设计示意图(包括一张卡纸可制作几个礼品盒,其展开图在卡纸上的分布情况),给出所用卡纸的总费用.(要求:①同一型号的卡纸如果需要不止一张,只要在一张卡纸上画出设计方案;②没有用到的卡纸,不要在该型号的卡纸上作任何设计;③所用卡纸的数量及总费用直接填在答题卡的表格上;④本题将综合考虑“利用卡纸的合理性”和“所用卡纸的总费用”给分,总费用最低的才能得满分;⑤试卷上的卡纸仅供作草稿用)2024年中考数学真题汇编专题17 几何图形初步及相交线、平行线+答案详解(答案详解)一、单选题1.(2024·河南·中考真题)如图,乙地在甲地的北偏东50︒方向上,则∠1的度数为( )A .60︒B .50︒C .40︒D .30︒ 【答案】B 【分析】本题主要考查了方向角,平行线的性质,利用平行线的性质直接可得答案.【详解】解:如图,由题意得,50BAC ∠=︒,AB CD ∥,∴150BAC ∠=∠=︒,故选:B .2.(2024·陕西·中考真题)如图,将半圆绕直径所在的虚线旋转一周,得到的立体图形是( )A .B .C .D .【答案】C【分析】本题主要考查了点、线、面、体问题.根据旋转体的特征判断即可.【详解】解:将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球,故选:C .3.(2024·北京·中考真题)如图,直线AB 和CD 相交于点O ,OE OC ⊥,若58AOC ∠=︒,则EOB ∠的大小为( )A .29︒B .32︒C .45︒D .58︒ 【答案】B 【分析】本题考查了垂直的定义,平角的定义,熟练掌握知识点,是解题的关键.根据OE OC ⊥得到90COE ∠=︒,再由平角180AOB ∠=︒即可求解.【详解】解:∵OE OC ⊥,∴90COE ∠=︒,∵180AOC COE BOE ∠+∠+∠=︒,58AOC ∠=︒,∴180905832EOB ∠=︒−︒−=︒,故选:B .4.(2024·广西·中考真题)如图,2时整,钟表的时针和分针所成的锐角为( )A .20︒B .40︒C .60︒D .80︒【答案】C 【分析】本题考查了钟面角,用30︒乘以两针相距的份数是解题关键.根据钟面的特点,钟面平均分成12份,每份是30︒,根据时针与分针相距的份数,可得答案.【详解】解:2时整,钟表的时针和分针所成的锐角是30260︒⨯=︒,故选:C .5.(2024·四川内江·中考真题)如图,AB CD ∥,直线EF 分别交AB 、CD 于点E 、F ,若64EFD ∠=︒,则BEF ∠的大小是( )A .136︒B .64︒C .116︒D .128︒ 【答案】C 【分析】本题考查了平行线的性质,根据两直线平行,同旁内角互补求解即可.【详解】解:∵AB CD ∥,∴180BEF EFD ∠+∠=︒,∵64EFD ∠=︒,∴116180EFD BEF ∠︒∠==︒−,故选:C .6.(2024·湖北·中考真题)如图,直线AB CD ∥,已知1120∠=︒,则2∠=( )A .50︒B .60︒C .70︒D .80︒ 【答案】B 【分析】本题主要考查了平行线的性质,解题的关键是熟练掌握平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.根据同旁内角互补,1120∠=︒,求出结果即可.【详解】解:∵AB CD ∥,∴12180∠+∠=︒,∵1120∠=︒,∴218012060∠=︒−︒=︒, 故选:B .7.(2024·陕西·中考真题)如图,AB DC ∥,BC DE ∥,145B ∠=︒,则D ∠的度数为( )A .25︒B .35︒C .45︒D .55︒【答案】B 【分析】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.先根据“两直线平行,同旁内角互补”,得到35C ∠=︒,再根据“两直线平行,内错角相等”,即可得到答案.【详解】AB DC ∥,180B C ∠+∠=︒∴,145B ∠=︒,18035C B ∴∠=︒−∠=︒,∥Q BC DE ,35D C ∴∠=∠=︒.故选B .8.(2024·黑龙江齐齐哈尔·中考真题)将一个含30︒角的三角尺和直尺如图放置,若150∠=︒,则2∠的度数是( )A .30︒B .40︒C .50︒D .60︒由题意得3150∠=∠=︒,590∠=∴2418090390∠=∠=︒−︒−∠=︒故选:B .9.(2024·广东·中考真题)如图,一把直尺、两个含30︒的三角尺拼接在一起,则ACE ∠的度数为( )A .120︒B .90︒C .60︒D .30︒【答案】C【分析】本题考查了平行线的性质.熟练掌握平行线的性质是解题的关键.由题意知,AC DE ∥,根据ACE E ∠=∠,求解作答即可.【详解】解:由题意知,AC DE ∥,∴60ACE E ∠=∠=︒,故选:C . 10.(2024·青海·中考真题)生活中常见的路障锥通常是圆锥的形状,它的侧面展开图是( )A .B .C .D .【答案】D【分析】本题考查了立体图形的侧面展开图.熟记常见立体图形的侧面展开图的特征是解决此类问题的关键.由圆锥的侧面展开图的特征知它的侧面展开图为扇形.【详解】解:圆锥的侧面展开图是扇形.故选:D .11.(2024·四川德阳·中考真题)走马灯,又称仙音烛,据史料记载,走马灯的历史起源于隋唐时期,盛行于宋代,是中国特色工艺品,常见于除夕、元宵、中秋等节日,在一次综合实践活动中,一同学用如图所示的纸片,沿折痕折合成一个棱锥形的“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯旋转时,正好看到“吉祥如意”的字样.则在A 、B 、C 处依次写上的字可以是( )A .吉 如 意B .意 吉 如C .吉 意 如D .意 如 吉【答案】A 【分析】本题考查的是简单几何体的展开图,利用四棱锥的展开图的特点可得答案.【详解】解:由题意可得:展开图是四棱锥,∴A、B、C处依次写上的字可以是吉,如,意;或如,吉,意;故选A12.(2024·四川广安·中考真题)将“共建平安校园”六个汉字分别写在某正方体的表面上,下图是它的一种展开图,则在原正方体上,与“共”字所在面相对的面上的汉字是()A.校B.安C.平D.园【答案】A【分析】此题考查正方体相对面上的字.根据正方体相对面之间间隔一个正方形解答.【详解】解:与“共”字所在面相对面上的汉字是“校”,故选:A.13.(2024·江苏盐城·中考真题)正方体的每个面上都有一个汉字,如图是它的一种平面展开图,那么在原正方体中,与“盐”字所在面相对的面上的汉字是()A.湿B.地C.之D.都【答案】C【分析】本题主要考查了正方体相对两个面上的文字,对于正方体的平面展开图中相对的面一定相隔一个小正方形,由此可解.【详解】解:由正方体表面展开图的特征可得:“盐”的对面是“之”,“地”的对面是“都”,“湿”的对面是“城”,故选C.14.(2024·江西·中考真题)如图是43的正方形网格,选择一空白小正方形,能与阴影部分组成正方体展开图的方法有()A.1种B.2种C.3种D.4种【答案】B【分析】此题主要考查了几何体的展开图,关键是掌握正方体展开图的特点.依据正方体的展开图的结构特征进行判断,即可得出结论.【详解】解:如图所示:共有2种方法,故选:B.15.(2024·江苏扬州·中考真题)如图是某几何体的表面展开后得到的平面图形,则该几何体是()A.三棱锥B.圆锥C.三棱柱D.长方体【答案】C【分析】本题考查了常见几何体的展开图,掌握常见几何体展开图的特点是解题的关键.根据平面图形的特点,结合立体图形的特点即可求解.【详解】解:根据图示,上下是两个三角形,中间是长方形,∴该几何体是三棱柱,故选:C .16.(2024·河北·中考真题)如图,AD与BC交于点O,ABO和CDO关于直线PQ对称,点A,B的对称点分别是点C,D.下列不一定正确的是()A .AD BC ⊥B .AC PQ ⊥ C .ABO CDO △≌△D .AC BD ∥ 【答案】A 【分析】本题考查了轴对称图形的性质,平行线的判定,熟练掌握知识点是解题的关键.根据轴对称图形的性质即可判断B 、C 选项,再根据垂直于同一条直线的两条直线平行即可判断选项D .【详解】解:由轴对称图形的性质得到ABO CDO △≌△,,AC PQ BD PQ ⊥⊥,∴AC BD ∥,∴B 、C 、D 选项不符合题意,故选:A .17.(2024·福建·中考真题)在同一平面内,将直尺、含30︒角的三角尺和木工角尺(CD ⊥DE )按如图方式摆放,若AB CD ,则1∠的大小为( )A .30︒B .45︒C .60︒D .75︒ 【答案】A【分析】本题考查了平行线的性质,由ABCD ,可得60CDB ∠=︒,即可求解.【详解】∵AB CD , ∴60CDB ∠=︒, ∵CD ⊥DE ,则90CDE ∠=︒,∴118030CDB CDE ∠=︒−∠−∠=︒,故选:A .18.(2024·江苏苏州·中考真题)如图,AB CD ,若165∠=︒,2120∠=︒,则3∠的度数为( )A .45︒B .55︒C .60︒D .65︒ 【答案】B 【分析】题目主要考查根据平行线的性质求角度,根据题意得出60BAD ∠=︒,再由平角即可得出结果,熟练掌握平行线的性质是解题关键【详解】解:∵AB CD ,2120∠=︒,∴2180BAD ∠+∠=︒,∴60BAD ∠=︒,∵165∠=︒,∴3180155BAD ∠=︒−∠−∠=︒,故选:B19.(2024·内蒙古包头·中考真题)如图,直线AB CD ∥,点E 在直线AB 上,射线EF 交直线CD 于点G ,则图中与AEF ∠互补的角有( )A .1个B .2个C .3个D .4个 【答案】C 【分析】本题考查了平行线的性质,对顶角的性质,补角的定义等知识,利用平行线的性质得出180AEF CGE +∠=︒∠,得出结合对顶角的性质180AEF DGF ∠+∠=︒,根据邻补角的定义得出180AEF BEG ∠+∠=︒,即可求出中与AEF ∠互补的角,即可求解.【详解】解∶∵AB CD ∥,∴180AEF CGE +∠=︒∠,∵CGE DGF ∠=∠,∴180AEF DGF ∠+∠=︒,又180AEF BEG ∠+∠=︒,∴图中与AEF ∠互补的角有CGE ∠,DGF ∠,BEG ∠,共3个.故选∶C .20.(2024·广东深圳·中考真题)如图,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角150∠=︒,则反射光线与平面镜夹角4∠的度数为( )A .40︒B .50︒C .60︒D .70︒ DE GF ,450=∠=︒故选:B .21.(2024·吉林·中考真题)如图,四边形ABCD 内接于O ,过点B 作BE AD ∥,交CD 于点E .若50BEC ∠=︒,则ABC ∠的度数是( )A .50︒B .100︒C .130︒D .150︒【答案】C【分析】本题考查了平行线的性质,圆的内接四边形的性质,熟练掌握知识点是解题的关键.先根据BE AD ∥得到50D BEC ∠=∠=︒,再由四边形ABCD 内接于O 得到180ABC D ∠+∠=︒,即可求解.【详解】解:∵BE AD ∥,50BEC ∠=︒,∴50D BEC ∠=∠=︒,∵四边形ABCD 内接于O ,∴180ABC D ∠+∠=︒,∴18050130ABC ∠=︒−︒=︒,故选:C .22.(2024·重庆·中考真题)如图,AB CD ∥,若1125∠=︒,则2∠的度数为( )A .35︒B .45︒C .55︒D .125︒【答案】C 【分析】本题考查了平行线的性质,邻补角的定义,根据邻补角的定义求出3∠,然后根据平行线的性质求解即可.【详解】解:如图,∵1125∠=︒,∴3180155∠=︒−∠=︒,∵AB CD ∥,∴2355∠=∠=︒,故选:C .23.(2024·吉林长春·中考真题)如图,在ABC 中,O 是边AB 的中点.按下列要求作图:①以点B 为圆心、适当长为半径画弧,交线段BO 于点D ,交BC 于点E ;②以点O 为圆心、BD 长为半径画弧,交线段OA 于点F ;③以点F 为圆心、DE 长为半径画弧,交前一条弧于点G ,点G 与点C 在直线AB 同侧;④作直线OG ,交AC 于点M .下列结论不一定成立的是( )A .AOMB ∠=∠B .180OMC C ∠+∠= C .AM CM =D .12OM AB = 180,根据平行线分线段成比例得出AOM ∠180一定成立,故的中点,24.(2024·青海·中考真题)如图,一个弯曲管道AB CD ,120ABC ∠=︒,则BCD ∠的度数是( )A .120︒B .30︒C .60︒D .150︒【答案】C 【分析】本题考查平行线的性质,熟练掌握平行线的性质是解题的关键.根据两直线平行,同旁内角互补即可得出结果.【详解】AB CD180ABC BCD ∴∠+∠=︒120ABC ∠=︒60BCD ∴∠=︒ 故选:C25.(2024·吉林长春·中考真题)在剪纸活动中,小花同学想用一张矩形纸片剪出一个正五边形,其中正五边形的一条边与矩形的边重合,如图所示,则α∠的大小为( )A .54oB .60C .70D .7226.(2024·内蒙古赤峰·中考真题)将一副三角尺如图摆放,使有刻度的两条边互相平行,则1∠的大小为( )A .100︒B .105︒C .115︒D .120︒【答案】B 【分析】本题考查了三角板中角度计算问题,由题意得3230∠=∠=︒,根据1180345∠=︒−∠−︒即可求解.【详解】解:如图所示:∠=∠=︒由题意得:3230∠=︒−∠−︒=︒∴1180345105故选:B.27.(2024·四川达州·中考真题)如图,正方体的表面展开图上写有“我们热爱中国”六个字,还原成正方体后“我”的对面的字是()A.热B.爱C.中D.国28.(2024·四川宜宾·中考真题)如图是正方体表面展开图.将其折叠成正方体后,距顶点A最远的点是()A.B点B.C点C.D点D.E点【答案】B【分析】本题考查了平面图形和立体图形,把图形围成立体图形求解.【详解】解:把图形围成立方体如图所示:所以与顶点A距离最远的顶点是C,故选:B.29.(2024·四川泸州·中考真题)把一块含30︒角的直角三角板按如图方式放置于两条平行线间,若145∠=︒,则2∠=()A.10︒B.15︒C.20︒D.30︒【答案】B【分析】本题考查了平行线的性质,三角板中角的运算,熟练掌握相关性质是解题的关键.利用平行线性∠=︒,再根据平角的定义求解,即可解题.质得到3135【详解】解:如图,∠=︒,直角三角板位于两条平行线间且145∴∠=︒,3135又直角三角板含30︒角,∴︒−∠−∠=︒,1802330∴∠=︒,215故选:B.30.(2024·江苏盐城·中考真题)小明将一块直角三角板摆放在直尺上,如图,若155∠=︒,则2∠的度数为()A .25︒B .35︒C .45︒D .55︒ 【答案】B 【分析】此题考查了平行线的性质,根据平行线的性质得到3155∠=∠=︒,再利用平角的定义即可求出2∠的度数.【详解】解:如图,∵155∠=︒,ABCD∴3155∠=∠=︒, ∴21802335∠=︒−∠−∠=︒,故选:B31.(2024·甘肃·中考真题)若55A ∠=︒,则A ∠的补角为( )A .35︒B .45︒C .115︒D .125︒32.(2024·内蒙古呼伦贝尔·中考真题)如图,,AD BC AB AC ⊥∥,若135.8∠=,则B ∠的度数是( )A .3548'︒B .5512'︒C .5412'︒D .5452'︒【答案】C 【分析】本题考查了平行线的性质,垂直的定义,度分秒的计算等,先利用垂直定义结合已知条件求出125.8BAD ∠=︒,然后利用平行线的性质以及度分秒的换算求解即可.【详解】解∶∵AB AC ⊥,135.8∠=,∴19035.8125.8BAD BAC ∠=∠+∠=︒+︒=︒,∵AD BC ∥,∴180B BAD ∠+∠=°,∴18054.25412B BAD '∠=︒−∠=︒=︒,故选∶C .二、填空题33.(2024·吉林·中考真题)如图,从长春站去往胜利公园,与其它道路相比,走人民大街路程最近,其蕴含的数学道理是 .【答案】两点之间,线段最短【分析】本题考查了两点之间线段最短,熟记相关结论即可.【详解】从长春站去往胜利公园,走人民大街路程最近,其蕴含的数学道理是:两点之间,线段最短故答案为:两点之间,线段最短.34.(2024·广西·中考真题)已知1∠与2∠为对顶角,135∠=︒,则2∠= °. 【答案】35【分析】本题主要考查了对顶角性质,根据对顶角相等,得出答案即可.【详解】解:∵1∠与2∠为对顶角,135∠=︒, ∴2135∠=∠=︒.故答案为:35.35.(2024·广东广州·中考真题)如图,直线l 分别与直线a ,b 相交,a b ,若171∠=︒,则2∠的度数为 .∵a b ,171∠=︒,∴1371∠=∠=︒,∴21803109∠=︒−∠=︒;故答案为:109︒36.(2024·四川乐山·中考真题)如图,两条平行线a 、b 被第三条直线c 所截.若160∠=︒,那么2∠= .【答案】120︒/120度【分析】本题考查了直线平行的性质:两直线平行同位角相等.也考查了平角的定义.根据两直线平行同位角相等得到1360∠=∠=︒,再根据平角的定义得到23180∠+∠=︒,从而可计算出2∠.【详解】解:如图,a b ∥,1360∴∠=∠=︒,而23180∠+∠=︒,218060120∴∠=︒−︒=︒,故答案为:120︒.37.(2024·黑龙江绥化·中考真题)如图,AB CD ∥,33C ∠=︒,OC OE =.则A ∠= ︒.【答案】66【分析】本题考查了平行线的性质,等边对等角,三角形外角的性质,根据等边对等角可得33E C ∠=∠=︒,根据三角形的外角的性质可得66DOE ∠=︒,根据平行线的性质,即可求解.【详解】解:∵OC OE =,33C ∠=︒,∴33E C ∠=∠=︒,∴66DOE E C ∠=∠+∠=︒,∵AB CD ∥,∴66A DOE =∠=︒∠,故答案为:66.38.(2024·山东威海·中考真题)如图,在正六边形ABCDEF 中,AH FG ∥,BI AH ⊥,垂足为点I .若20EFG ∠=︒,则ABI ∠= .【答案】50︒/50度【分析】本题考查了正六边形的内角和、平行线的性质及三角形内角和定理,先求出正六边形的每个内角为120︒,即120EFA FAB ∠=∠=︒,则可求得GFA ∠的度数,根据平行线的性质可求得FAH ∠的度数,进而可求出HAB ∠的度数,再根据三角形内角和定理即可求出ABI ∠的度数. 【详解】解:∵正六边形的内角和(62)180720=−⨯=︒, 每个内角为:7206120︒÷=︒,120EFA FAB ∴∠=∠=︒, 20EFG ∠=︒,12020100GFA ∴∠=︒−︒=︒, AH FG ∥,180G FAH FA ∠=︒∴∠+,180********GFA FAH =︒−∠=︒−︒=︒∴∠, 1208040HAB FA FAH B ∴∠=∠−︒−︒=︒∠=,BI AH ⊥,90BIA ∴∠=︒,904050ABI ∴∠=︒−︒=︒.故答案为:50︒.39.(2024·河北·中考真题)如图,ABC 的面积为2,AD 为BC 边上的中线,点A ,1C ,2C ,3C 是线段4CC 的五等分点,点A ,1D ,2D 是线段3DD 的四等分点,点A 是线段1BB 的中点.(1)11AC D △的面积为 ; (2)143B C D △的面积为 . ,证明()11SAS AC D ACD ≌)证明()11SAS AB D ABD ≌三点共线,得11112AB D AC D S △△+=,继而得出113AB D =△,证明3C AD △99CAD S ==△,推出S △【详解】解:(1)连接11B D 、1B ∵ABC 的面积为ABD S S △=∵点A ,1C ,1AC AC =和ACD 中,CAD , ∴()11SAS AC D ACD ≌111AC D ACD S S ==△△,∠11AC D △的面积为1,故答案为:1;)在11AB D 和△1AB AD BAD AD =∠∴()11SAS AB D ABD ≌111AB D ABD S S ==△△,∠180BDA CDA ∠+∠=︒1111180B D A C D A ∠+∠=和ACD 中,3AD AD,3C ∠CAD △,332233C AD CADS AC SAC ⎫==⎪⎭33C AD =△1AC C =【点睛】本题考查三角形中线的性质,全等三角形的判定与性质,相似三角形的判定与性质,等分点的意义,三角形的面积.掌握三角形中线的性质是解题的关键.三、解答题40.(2024·福建·中考真题)在手工制作课上,老师提供了如图1所示的矩形卡纸ABCD,要求大家利用它制作一个底面为正方形的礼品盒.小明按照图2的方式裁剪(其中AE FB=),恰好得到纸盒的展开图,并利用该展开图折成一个礼品盒,如图3所示.图1图2图3(1)直接写出ADAB的值;(2)如果要求折成的礼品盒的两个相对的面上分别印有“吉祥”和“如意”,如图4所示,那么应选择的纸盒展开图图样是()图4A.B.C.D.(3)现以小明设计的纸盒展开图(图2)为基本样式,适当调整AE,EF的比例,制作棱长为10cm的正方体礼品盒,如果要制作27个这样的礼品盒,请你合理选择上述卡纸(包括卡纸的型号及相应型号卡纸的张数),并在卡纸上画出设计示意图(包括一张卡纸可制作几个礼品盒,其展开图在卡纸上的分布情况),给出所用卡纸的总费用.(要求:①同一型号的卡纸如果需要不止一张,只要在一张卡纸上画出设计方案;②没有用到的卡纸,不要在该型号的卡纸上作任何设计;③所用卡纸的数量及总费用直接填在答题卡的表格上;④本题将综合考虑“利用卡纸的合理性”和“所用卡纸的总费用”给分,总费用最低的才能得满分;⑤试卷上的卡纸仅供作草稿用)【答案】(1)2;(2)C;∴所用卡纸总费用为:⨯+⨯+⨯=(元).202533158。


中考数学一轮复习第17讲几何初步及平行线相交线专题精练一、夯实基础1.如图1,已知a∥b,∠1=50°,则∠2=______度.(1)(2)(3)2.已知∠α与∠β互余,且∠α=40°,且∠β的补角为______度.3.时钟在4点整时,时针与分针的夹角为_______度.4.如图2,点A、B、C在直线L上,则图中共有______条线段.5.如图3,若AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD 的平分线与EP相交于点P,且∠BEP=40°,则∠EPF=_______度.6.如图4,•将一副三角板的直角顶点重合,•摆放在桌面上,•若∠AOD=145°,则∠BOC=_______度.7.如图5,AB∥CD,若∠ABE=120 °, ∠DCE= 35 °,•则有∠BEC=_______度.(4)(5)(6)二、能力提升8.如图6,是共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是()A.180° B.150° C.135° D.120°9.已知:如图7,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,在OB•上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB 的度数是()A.60° B.80° C.100° D.120°10.如图8,B是线段AC的中点,过点C的直线L与AC成60°的角,•在直线L上取一点P,使∠APB=30°,则满足条件的点P共有()A.1个 B.2个 C.3个 D.无数个三、课外拓展11.如图9,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF 的平分线交CD于点G,若∠EFG=72°,则∠EGF等于()A.36° B.54° C.72° D.108°(7)(8)(9)12.小颖在做下面的数学作业时,因钢笔漏墨水,•不小心将部分字迹污损了,作业过程如下(涂黑部分即污损部分);已知:如图所示,OP平分∠AOB,MN∥OB.求证:OM=NM.证明:因为OP平分∠AOB所以▅▅▅▅又因为MN∥OB所以▅▅▅▅故∠1=∠3所以OM=NM.小颖思考:污损部分应分别是以下四项中的两项:①∠1=∠2 ②∠2=∠3 ③∠3=∠4 ④∠1=∠4那么她补出来的结果应是()A.①④ B.②③ C.①② D.③④四、中考链接13.已知图中小方格的边长为1,求点C到线段AB的距离.14.如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.15.如图,已知AB⊥BC,DC⊥BC,BE∥CF,求证:∠1=∠2.参考答案一、夯实基础1.130°2.130°3.120°4.35.65°6.35°7.95°二、能力提升8.A9.B10.B三、课外拓展11.B12.C四、中考链接13.414.连结AF,则AF=FC,AF=BF,∴BF=2C F 1215.利用平行线内错角相等及等角的余角相等即可证明。
几何初步及平行线、相交线◆课前热身1.(2009年山东日照)如图所示,把一个长方形纸片沿EF 折叠后,点D ,C 分别落在D ′,C ′地位置.若∠EFB =65°,则∠AED ′等于 ( )A.70° B .65° C.50°D .25°2.(2009年福建福州)已知∠1=30°,则∠1地余角度数是( )A .160° B.150° C.70° D.60°3.(2009年江西省)如图,直线m n ∥,︒∠1=55,︒∠2=45, 则∠3地度数为( )A .80︒B .90︒C .100︒D .110︒4.(2009年重庆)如图,直线AB CD 、相交于点E ,DF AB ∥.若100AEC ∠=°, 则D ∠等于( )A .70°B .80°C .90°D .100°【参考答案】 1. C 2. D 3. C 4. B ◆考点聚焦CAE BF D 第4题EDBC′FCD ′A第1题〖知识点〗两点确定一条直线、相交线、线段、射线、线段地大小比较、线段地和与差、线段地中点、角、角地度量、角地平分线、锐角、直角、钝角、平角、周角、对顶角、邻角、余角、补角、点到直线地距离、同位角、内错角、同旁内角、平行线、平行线地性质及判定、命题、定义、公理、定理〖大纲要求〗1.了解直线、线段和射线等概概念地区别,两条相交直线确定一个交点,解线段和与差及线段地中点、两点间地距离、角、周角、平角、直角、锐角、钝角等概念,掌握两点确定一条直线地性质,角平分线地概念,度、分、秒地换算,几何图形地符号表示法,会根据几何语句准确、整洁地画出相应地图形;2.了解斜线、斜线段、命题、定义、公理、定理及平行线等概念,了解垂线段最短地性质,平行线地基本性质,理解对顶角、补角、邻补角地概念,理解对顶角地性质,同角或等角地补角相等地性质,掌握垂线、垂线段、点到直线地距离等概念,会识辨别同位角、内错角和同旁内角,会用一直线截两平行线所得地同位角相等、内错角相等、同旁内角互补等性质进行推理和计算,会用同位角相等、内错角相等、或同旁内角互补判定两条直线平行.考点提炼:1.运用两点确定一条直线解决实际问题.2.会比较角地大小,掌握角地表示法,能进行角地有关计算.3.明确线段、直线、射线地概念及区别与联系,线段地表示方法,•会进行有关线段地计算.4.掌握角平分线地定义及性质.5.掌握两角互余、互补地概念,并能进行有关计算.6.掌握对顶角、同位角、内错角、同旁内角等概念.7.掌握平行线地性质与判定,并能运用这些知识进行有关计算或推理.8.掌握两条直线垂直地概念.◆备考兵法1.能运用方程思想解决互余、互补、平行线地性质以及三角形内、•外角和等知识和一些有关计算线段、角地问题.2.在进行角地计算时,要注意单位地换算,即1°=60′,1′=60″.3.要注意区分平行线地判定与性质,不要混淆滥用.〖考查重点与常见题型〗1.求线段地长、角地度数等,多以选择题、填空题出现,如:已知∠а=112°,则∠а地补角地度数是_________.◆考点链接1. 两点确定一条直线,两点之间线段最短._______________叫两点间距离.2. 1周角=__________平角=_____________直角=____________.3. 如果两个角地和等于90度,就说这两个角互余,同角或等角地余角相等;如果_____________________互为补角,__________________地补角相等.4. ___________________________________叫对顶角,对顶角___________.5. 过直线外一点心___________条直线与这条直线平行.6. 平行线地性质:两直线平行,_________相等,________相等,________互补.7. 平行线地判定:________相等,或______相等,或______互补,两直线平行.8. 平面内,过一点有且只有_____条直线与已知直线垂直.◆典例精析例1 (2009年湖北黄冈)66°角地余角是_________.24【答案】︒24【解析】如果两个角地和等于90度,就说这两个角互余.由此可以得出答案为︒例2(2008年湖北孝感)如图,a∥b,点M,N分别在a,b上,P为两平行线间一点,•那么∠1+∠2+∠3=()A.180° B.270° C.360° D.540°【答案】C【解析】方法一:过点P作PE∥a(如图).∵a∥b,∴PE∥b.∴∠1+∠MPE=180°,∠3+∠NPE=180°,∴∠1+∠3+∠2=180°+180°=360°.方法二:过点P作PF∥a(如图),∵a∥b,∴PF∥b.∴∠1=∠MPF,∠3=∠NPF.∵∠2+∠MPF+∠NPF=360°,∴∠1+∠2+∠3=360°. 方法三:连结MN (如图). ∵a ∥b ,∴∠AMN+∠BNM=180°. 又∵△MPN 内角和为180°,∴∠1+∠2+∠3=180°+180°=360°. 方法四:延长MP 交直线b 于点D (如图). ∵a ∥b ,∴∠1=∠4.∵∠2,∠3,∠4是△DPN 地外角. ∴∠2+∠3+∠4=360°, ∴∠1+∠2+∠3=360°.点评 在数学学习与复习过程中,通过一题多解,从不同侧面复习数学知识,•使大学开阔视野,拓展思路,提高解题能力. 例3 已知n (n ≥2)个点P 1,P 2,P 3,……,P n 在同一个平面内,且其中没有任何三点在同一条直线上,设S n 表示过这n 个点中地任意两个点所作地直线条数,显然S 2=1,S 3=3,S 4=6,S 5=10,…,由此可推断S n =______. 【答案】S n =12n (n-1). 【解析】 方法一:∵n 个点中任意三点不在同一直线上. ∴其中这一点分别与其他(n-1)个点可作(n-1)条直线.这样共可作n (n-1)条直线,此时两点间地直线重复作了一次,故S n =12n (n-1). 方法二:因要探究S n 与n 地关系,可设S n 关于n 地二次函数关系,即S n =an 2+bn+c (a ,•b ,c 是常数),若是一次函数关系,则a=0,依题意,得421,933,164 6.a b c a b c a b c ++=⎧⎪++=⎨⎪++=⎩解得1,21,20.b a c =-=⎧=⎪⎪⎪⎨⎪⎪⎪⎩ 即S n =12n 2-12n .验证:当n=5时,S n =12×52-12×5=10. ∴S n =12n 2-12n=(1)2n n -.方法三:∵S 2=1,S 3=1+2,S 4=1+2+3,S 5=1+2+3+4,… ∴S n =1+2+3+…+n-1,∴S n =(1)2n n -. 答案 (1)2n n -点评 通过一题多解,让同学们从不同角度认识理解数学,拓展了解题思路,•提高了数学能力. ◆迎考精练 一、选择题1.(2009年重庆綦江)如图,直线EF 分别与直线AB 、CD 相交于点G 、H ,已知∠1=∠2= 90°,GM 平分∠HGB 交直线CD 于点M .则∠3=( )A .60°B .65°C .70°D .130°2.(2009年安徽)如图直线1l ∥2l ,则∠α为( ).A.150°B.140°C.130°D.120°3.(2009年辽宁朝阳)如图,已知AB ∥CD,若∠A =20°,∠E=35°,则∠C 等于( ).A.20° B. 35° C. 45° D.55°4.(2009年广东广州)如图,AB ∥CD ,直线l 分别与AB 、CD 相交,若∠1=130°,则∠2=( )A.40° B.50° C.130° D.140°AEB G CDM H F1 2 35.(2009年山东临沂)下列图形中,由AB CD ∥,能得到12∠=∠地是( )6.(2009年广东清远)如图,AB CD ∥,EF AB ⊥于E EF , 交CD 于F ,已知160∠=°,则2∠=( )A .20°B .60°C .30°D .45°eUts8。
17.几何初步及平行线、相交线【课前热身】1. 如图,延长线段AB 到C ,使BC=4,若AB=8,则线段AC 是BC 的____倍.2. 下列图形中,是正方体的平面展开图的是( )A B C D3.如图,已知直线a ∥b ,∠1=35°,则∠2的度数是______.4.如图,在不等边△ABC 中,DE ∥BC ,∠ADE=60°,图中等于60°的角还有____________.5.如图,直线a ∥b ,则∠A 的度数是( )A .28°B .31°C .39°D .42° 6.经过任意三点中的两点共可以画出的直线条数是( )A .一条或三条B .三条C .两条D .一条【学习目标】见《中考说明》本专题开头考点解读 【知识整理】1. 点、直线、平面、几何体等,是从客观物体抽象出来的几何元素,它们是几何学研究的对象. 点动成线,线动成面,面动成体.2. 常见的平面图形:三角形、长方形、正方形、圆等;常见的立体图形:长方体、正方体、球、圆柱、圆锥、棱锥、棱柱等.3. 两点确定____________,两点之间______最短,__________________叫两点之间的距离.4. 过直线外一点________________直线与这条直线平行.5. 平面内,过一点________________直线与已知直线垂直;直线外一点与直线上各点连接的线段中,垂线段最短.6. 1°=60′,1′=60″;1周角=_____平角=_____直角=_____.7. 如果两个角的和等于_____度,就说这两个角互为余角,同角或等角的余角相等;如果两个角的和等于_____度,就说这两个角互为补角,同角或等角的补角相等.8. 有公共顶点,两边互为反向延长线的两个角叫做对顶角,对顶角________.9. 平行线的性质:两直线平行,_________相等,________相等,__________互补.10. 平行线的判定:________相等,或________相等,或___________互补,两直线平行.11.点到直线的距离:从直线外一点向已知直线作垂线,这点和垂足之间的垂线段的长度,叫做点到这条直线的距离.12. 角平分线:一条射线把一个角分成相等的两个角,这条射线叫做这个角AB CAD B CE (第4题) a b c 1 2 (第3题)(第5题)图A D a b 70° 31°的平分线. 角平分线上的点到这个角的两边距离相等;到一个角两边距离相等的点在这个角的平分线上.13. 线段垂直平分线:垂直且平分一条线段的直线,叫做这条线段的垂直平分线(中垂线).线段垂直平分线上的点到这条线段两个端点的距离相等;到一条线段两个端点的距离相等的点在这条线段的垂直平分线上. 【典例精析】例1 如图:AB∥CD,直线EF 分别交AB 、CD 于E 、F ,EG 平分∠BEF, 若∠1=72°,则∠2等于多少度?例2 若一个角的余角与这个角的补角之比是2∶7,求这个角的邻补角. 例3 如图,DE ∥BC ,FG ⊥AB 于G ,∠1=∠2,求证:CD ⊥AB.【中考演练】1. 锯木头时,一般先在木板上画出两个点,然后过这两点弹出一条墨线,这种做法的理由是___________________.2. 如果一个角的补角是120°,那么这个角的余角是_______.3. 32.43°=_____度_____分_____秒. 4.如图,直线a 、b 被直线c 所截,若要a∥b,需增加条件 ___________.(填一个即可)5.如图,直线l 1∥l 2,AB⊥CD,∠1=34°,那么∠2的度数是________. 6. 如图,把一张长方形纸条ABCD 沿EF 折叠,若∠1=58°, 则∠AEG=________.7. 如图,直线AB ∥CD ,EF ⊥CD 于F ,如果∠GEF=20°,那么∠1的度数是________8. 如图,已知AB ∥CD ,直线MN 分别交AB 、CD 于E 、F ,∠MFD=50°,EG 平分∠MEB ,那么∠MEG 的大小是_____度.9. 如图,所示,AB ∥CD ,∠E=27°,∠C=52°,则∠EAB=_____度. 10. 如图,AB ∥CD ∥EF ,∠A=30°,∠1=80°,则∠E=______度.E C D G 1 2 FA B 第8题 第9题 第7题21D CB A l 2l 1第5题 第4题1A EC F G BD 'C '第6题 D11. 如图,射线OA 表示的方向是_________________.12. 如图,AC ⊥l 1,AB ⊥l 2,则点A 到直线l 2的距离是指线段________的长度.13. 下面图形中,不能折成正方体的是( )14. 已知某多面体的平面展开图如图所示,其中是三棱柱的有( ) A. 1个 B. 2个 C. 3个 D. 4个16. 一个四棱柱被一刀切去一部分,剩下的部分可能是( )A .四棱柱B .三棱柱C .五棱柱D .以上都有可能 17. 下列语句准确规范的是( )A. 直线a 、b 相交于一点mB. 延长直线ABC. 反向延长射线AO(O 是端点)D. 延长线段AB 到C ,使BC=AB 18. 下列四个图中的线段(或直线、射线)能相交的是( )A.(1)B.(2)C.(3)D.(4)19. 如图,从A 到B 有3条路径,最短的路径是③,理由是( )A. 因为③是直的B. 两点之间,线段最短C. 两点间距离的定义D. 两点确定一条直线20. 如图,是赛车跑道的一段示意图,其中AB ∥DE ,测得∠B=140°,∠D=120°,则∠C 的度数为( )A. 120°B. 100°C. 140°D. 90°东南西A北)30°O 第10题 第11题A BCl 1l 2第12题21. 如图,Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,若∠BCE=35°,则∠A的度数为( )A.35°B.45°C.55°D.65°22. 小明由A点出发向正东方向走10米到达B点,再由B点向东南方向走10米到达C点,则正确的是( )A.∠ABC=22.5° B.∠ABC=45°C.∠ABC=67.5° D.∠ABC=135°23. 如图,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=•15°30′,则下列结论中不正确的是( )A.∠2=45° B.∠1=∠3C.∠AOD与∠1互为补角 D.∠1的余角等于75°30′24. 已知:如图所示,直线AB、CD相交于O,已知∠AOC=75°,OE把∠BOD 分为两部分,且∠BOE:∠EOD=2:3,求∠AOE.25.如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.【课堂小结】对照学习目标进行总结【当堂检测】见《中考说明》。