当前位置：文档之家 › 【建筑制图】平面立体

【建筑制图】平面立体

  • 格式：ppt
  • 大小：405.00 KB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

《建筑制图与识图》第3章

《建筑制图与识图》第3章


3.2.3 曲面立体表面上点的投影
1．利用曲面投影的积聚性
例3-2 如图（a）所示，已知圆柱体表面上一点A的V面投影。 求点A的H面、W面投影。
3.2.3 曲面立体表面上点的投影
分析与作图： 因圆柱的轴线垂直于H面，故圆柱的水平投影有积聚性，又 因a′可见，表明点A位于圆柱的前半个表面上，因此过a′向下投 影，在圆柱水平投影的前半圆周上得点A的水平投影a。由a，a′ 可求出a″，如图3-9（b）所示。因a′位于V投影对称轴的右侧， 故a″为不可见，A点在圆柱体上的位置如图3-9（c）所示。
3.3.1 截切体
因为立体的形状都不一样，截平面与立体表面的相对位置 也各不相同，由此产生的截交线形状也千差万别，但所有的截交 线都具有以下基本性质：
① 共有性。截交线是截平面与立体表面的共有线，既在截 平面上，又在立体表面上，是截平面与立体表面共有点的集合。
② 封闭性。由于立体表面是有范围的，所以截交线一般是 封闭的平面图形。
第3章 立体的投影
目录
3.1
平面立体
曲面立体
3.2
3.3
截切体和相贯体
组合体
3.4
3.1 平面立体
3.1.1 常见平面立体的投影图
平面立体
3.1.2 平面立体的投影图的绘制
3.1.3 平面立体表面上点和直线的投影
3.1.1 常见平面立体的投影
3.1.1 常见平面立体的投影
3.1.1 常见平面立体的投影
3.1.2 平面立体图的绘制
绘制平面立体的三面投影图，首先要按正确位置将 形体放入三面投影体系中，让形体的表面和棱线与投影 面尽量平行或垂直。
绘制平面体的投影图实际上就是绘制平面体底面和 侧表面的投影，一般先画出反映底面实形的正投影图， 然后再根据投影规律画出其他两个投影。
《建筑制图与识图》经典教案第二章

《建筑制图与识图》经典教案第二章

《建筑制图与识图》经典教案第⼆章第⼆章平⾯⽴体⼀.教学⽬的了解空间形体的分类，掌握基本平⾯形体的投影特性及形体表⾯上求点的⽅法。

能够补绘由基本平⾯体演变的简单平⾯体组合体的第三⾯投影。

⼆.教学重点重点掌握基本形体的投影特性和形体表⾯上求点的⽅法。

三.教学难点根据形体的三⾯投影，正确建⽴形体的空间模型。

通过空间想象正确判断形体表⾯上点的投影的可见性。

四.布置作业习题集§2-1 2-2概述及平⾯体的投影在建筑⼯程中的建筑物及其构配件，如果从⼏何体型⾓度来分析，它们总可以看作由⼀些形状简单，形成也简单的⼏何体组合⽽成。

在制图中常把这些⼯程上经常使⽤的单⼀⼏何形体如棱柱、棱锥、圆柱、圆锥、球和圆环等称为基本⼏何体，简称基本体。

基本体有平⾯体和曲⾯体。

由平⾯围成的基本⼏何体称为平⾯体。

⼯程中常见的平⾯体主要有棱柱、棱锥和棱锥台。

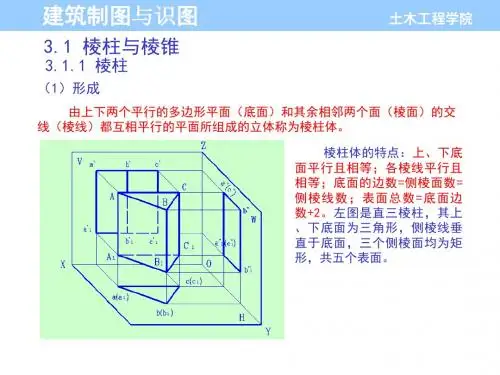
⼀、棱柱体棱柱由两个相互平⾏的底⾯和若⼲个侧棱⾯围成，相邻两侧棱⾯的交线称为侧棱线，简称棱线。

棱柱的棱线相互平⾏。

1.棱柱体的投影从三棱柱的投影图中可看到：其⽔平投影是⼀个三⾓形，它是三棱柱上、下底⾯的投影，三⾓形的三条边分别是左、右、后三个棱⾯的投影（有积聚性），三⾓形的三个顶点分别是三条棱线的⽔平投影；正⾯投影中两个并⽴的矩形是三棱柱左、右两个棱⾯的投影；正⾯投影的外形轮廓则是三棱柱后棱⾯的投影（反映实形）；正⾯投影中上、下两条⽔平线是三棱柱上、下底⾯的投影（有积聚性）；侧⾯投影只是⼀个矩形，左、右⼆棱⾯在此重影，上、下两条⽔平线仍是上、下底⾯有积聚性的投影，矩形的两条竖边中靠⾥⾯的⼀条还是三棱柱后棱⾯的投影（有积聚性）。

2.棱柱体表⾯上求点棱柱体表⾯上求点可以利⽤柱体表⾯的积聚投影来求得。

例1 已知三棱柱的三⾯投影及其表⾯上的点M和N的正⾯投影m'和n'，求作它们的另两个投影。

分析：根据已知条件，M点必在三棱柱前右侧的棱⾯上（因m'可见），⽽N 点必在三棱柱的后棱⾯上（因n'不可见）。

建筑形体的投影—基本几何体的投影(建筑制图)

建筑形体的投影—基本几何体的投影(建筑制图)

3.1.2曲面体的投影
2、球体的投影 球体的H投影是球面上最大的纬圆 (即上、下半球的分界线)的投影； 球体的V投影是球面上最左、最右 素线（即前、后半球的分界线)的 投影；球体的W投影是球面上最 前、最后素线（即左、右半球的 分界线基本几何体的投影
3.1.2曲面体的投影
2、圆锥体的投影 圆锥体的三个投影分别是：一个圆和两个全等的等腰三角形。
3.1 基本几何体的投影
3.1.2曲面体的投影
三、圆台体
1、圆台体的形成 圆台体由圆台面和上、下底面所围成。 如图所示，将圆锥用平行于底面的平面 切割，截面和底面之间的部分即为圆台， 截面和底面之间的距离即为圆台的高。
3.1 基本几何体的投影
3.1.1平面立体投影
六棱柱的投影
3.1 基本几何体的投影
3.1.1平面立体投影
六棱柱的投影
3.1 基本几何体的投影
3.1.1平面立体投影
棱柱体投影规律 棱柱的一个投影为多边形，另两个投影为一个或多个矩形； 反之，当一个形体的三面投影中有一个投影为多边形，另两个投影为一个或 多个矩形时，就可判定该形体为棱柱体，从多边形的边数可得出棱柱的棱数。
3.1 基本几何体的投影
3.1.1平面立体投影
四棱锥
3.1 基本几何体的投影
3.1.1平面立体投影
四棱锥投影图分析：
底面：水平面ABCD 四个侧面：
△SAB 一般位置平面 △SBC 一般位置平面 △SCD 一般位置平面 △SAD 一般位置平面
3.1 基本几何体的投影
3.1.1平面立体投影
棱锥体投影规律 棱锥的投影中有一个投影外轮廓为多边形，内部 是以该多边形的各边为底边的多个三角形，另两个 投影是有公共顶点的三角形。 反之，当一个形体的三个投影，其中一个投影外 轮廓为多边形，内部是以该多边形为底边的三角形， 另两个投影都是有公共顶点的三角形，则可以判断 该形体为棱锥体，多边形的边数为棱锥体的棱数。
土木工程制图_平面立体构形及轴测图画法PPT课件

土木工程制图_平面立体构形及轴测图画法PPT课件

土木工程制图（第四版）
第4章 平面立体构形及轴测图画法
目录
平面立体构形方式 §4.1 基本平面体的叠加 §4.2 基本平面体的切割 §4.3 基本平面体的交接 §4.4 简单平面立体的尺寸标注 §4.5 轴测投影原理及画法
2
平面立体构形方式
叠加
切割
交接
3
平面立体构形方式
叠加
切割
交接
4
§4.1 基本平面体的叠加 叠加是一种自然（无损伤）堆积，基本体之间只有简单的接触（叠合面），不另外产 生表面交线。
34 下页解答
§4.3 基本平面体的交接 例4-8 完成图示房屋模型的两面投影图.4 简单平面立体的尺寸标注
在投影图上标注尺寸的基本要求： （1）遵守制图标准的规定。 （2）尺寸必须齐全，应能完全确定形体的大小和形状，既不 能有遗漏，也不能有互相矛盾的多余尺寸。 （3）尺寸布置得当，标注清晰，便于看图。
25
§4.3 基本平面体的交接
求相贯线的步骤： 1. 分析相贯线的类型；
确定折线的条数、每条折线的边数或顶点数。 2. 求交线；或者 3. 求交点，连接成线；
某两点在第一个立体的同一表面上，又在第二个立体的 同一个表面上，这样的两点才可以相连。 4. 分清各边线的可见性； 产生该边线的两个表面的某个投影均都可见时，该边线 的相应投影才是可见的。 5. 整理修饰，描黑 。
5
§4.1 基本平面体的叠加 组成叠加立体的基本体表面间的关系
6
§4.1 基本平面体的叠加 叠加形成的立体，投影图上常有明显的分块痕迹。借助于 投影图上的分块线框便于分析形体的构成及其形状。
单击开始自动演播
7
§4.2 基本平面体的切割 立体被平面切割，也叫截切，形成截切体。切割平面称为截 平面，截平面与立体表面的交线称为截交线，截交线所围成的截 面图形称为截断面或断面。
建筑制图与识图第3章 立体(棱柱体与棱锥体)

建筑制图与识图第3章 立体(棱柱体与棱锥体)

建筑制图与识图
3.1 棱柱与棱锥
3.1.1 棱柱
（1）形成
土木工程学院
由上下两个平行的多边形平面（底面）和其余相邻两个面（棱面）的交 线（棱线）都互相平行的平面所组成的立体称为棱柱体。
棱柱体的特点：上、下底 面平行且相等；各棱线平行且 相等；底面的边数 = 侧棱面数 = 侧棱线数；表面总数 = 底面边 数 +2 。左图是直三棱柱，其上 、下底面为三角形，侧棱线垂 直于底面，三个侧棱面均为矩 形，共五个表面。
(1)形成
土木工程学院 由一个多边形平面（底面）和其 余相邻两个面（侧棱面）的交 线（棱线）都相交于一点 （顶点）的平面所围成的 立体称为棱锥体。 棱锥体的特点： 底面为多边 形；各侧棱线相 交于一点；底面 的边数=侧棱面 数=侧棱线数； 表面总数=底面 边数+1。
建筑制图与识图
s
(2) 投影
土木工程学院
b' c' b"
a"
(c")
b c a
B
A
C
建筑制图与识图
s′
土木工程学院
s〞
2´
( 2″) 3 4 a〞(c〞)
(3) 4 a′ a 3 (4) b b′ c′ c s
2
S
b〞
Ⅱ
A B
C
s
①. 安放位置：如上 页图所示，将三棱锥底面 平行于H 面，后棱面垂直 于W 面 ②. 投影分析
H 面投影：是三个
b
a
b
s
c （c） b y c
y
a
小三角形合成的一 个大三角形。
V 面投影：是两个
小三角形合成的一 个大三角形。
W 面投影：是一个
建筑识图-平面曲面立体

建筑识图-平面曲面立体


a
(b)
(a) b
b a
5
2. 棱 锥
(1) 棱锥的投影 s s
S
b’ b s
a’
c’ c b”(c”)
a”
B
A
C
a
(2) 棱锥表面上取点 s s 2 2 r 1
(3) a c
c
3
1 a
b
b r s 1
b(c)
3
2 a
作图规则小结
► 形体的三面投影图应该符合“长对正，高平
截交线的性质：
截交线是一个由直线组成的封闭的平面多边形，其 形状取决于平面体的形状及截平面对平面体的截切 位置。 截交线的每条边是截平面与棱面的交线－－即为两平 面共有。
求截交线的实质是求两平面的交线
截交线的求法
关键是正确地画出截交线的投影。
⒈ 求截交线的两种方法： ★ 求各棱线与截平面的交点→棱线法。 ★ 求各棱面与截平面的交线→棱面法。 ⒉ 求截交线的步骤：
3" 7" 2"
4 光滑且顺次地连接各点，作 出截交线，并且判别可见性； 5 整理轮廓线。
Ⅵ
Ⅰ
4
6 1
Ⅳ Ⅷ
Ⅴ
Ⅲ Ⅶ
7 3
5
Ⅱ
作图步骤： （1）根据截平面位置与曲面立体表面的性质、判别 截交线的形状和性质。 （2）求出截交线上的特殊点。 （3）根据需要求出若干个一般点。 （4）光滑且顺次地连接各点，作出截交线，并且判 别可见性。 （5）最后，补全可见与不可见部分的轮廓线或转向 轮廓素线，并擦除被切割掉的轮廓线或转向轮廓素线。 特殊点：是指绘制曲线时有影响的各种点。 极限位置点 曲线的最高、最低、最前、最后、最左和最右点。 转向轮廓点 曲线上处于曲面投影转向轮廓线上的点，它们是区 分曲线可见与不可见部分的分界点。 特征点 曲线本身具有特征的点，如椭圆长短轴上四个端点。 结合点 截交线由几部分不同线段组成时结合处的点。
建筑制图与识图3立体的投影

建筑制图与识图3立体的投影

3
3.3 切割体的投影
3.3.1 平面切割体的投影
（2）棱面法——面面交线法
将平面立体上参与相交的各棱面， 与截平面求交线，这些交线即围成所 求的平面立体截交线。
3.3 切割体的投影
3.3.1 平面切割体的投影
作图步骤：
1）空间分析及投影分析 a、截平面与立体的相对位置——确定截交线的形状 b、截平面，立体表面与投影面的相对位置——确定截交线的投影特性
PV2
6′ (7′) 7 ′′
例3-8：求作被截五棱柱的三面投影图
4′ (5′) 2′ ( 3′)
PV1
1′
5′′ 3 ′′
6′′
4′′ 2′′ 1′′
3 7(5)
1
2
6(4)
3.3 切割体的投影
3.3.2 曲面切割体的投影
截交线：一般为封闭的平面曲线，特殊情况为直线。 其形状取决于曲面立体的几何特征，以及截平面与曲面立体的相对位置。
c’ （2）绘出圆柱的顶面和底面。
（3）画出正面转向轮廓线和侧面转向轮廓线。
Z
a1’ c1’(d1’) d(d1)
a(a1) c(c1)
d1’
b1’
a1”(b1”) c1’’
c’d’ b’
V a’
D
A
d” B
a”b”
c”W
C
b(b1)
圆柱的投影
正面转向轮廓线 a1’
X
c1’d1’ A1 d(d1)
da11””(b1)”c1” C1b(b1)
曲面上可见与不可见的分界线称为回转面对该投影面的转向轮 廓线，在其他投影面不应画出。
圆柱体的投影
圆柱表面由圆柱面和上下两底面所组成。圆柱面是由一直母线绕与之 平行的轴线回转而成。圆柱上任意一条平行于轴线的直母线称之为素线。
平面立体棱台的投影

平面立体棱台的投影

《建筑制图基础》系列微课广播电视大学
重点难点
建筑制图基础
教 学 目 标
熟练掌握平面立体棱台的投影特征
沈阳广播电视大学
授课脉络
建筑制图基础
概念
沈阳广播电视大学
讲课内容
建筑制图基础
1 概念
用平行于棱锥底面的平面切割棱锥，底面和截面之间的部分称为棱台。
现在大家看到的棱台是由四棱锥切得的，所以称之为四棱台。
沈阳广播电视大学
讲课内容
建筑制图基础
1 概念
棱台的分类：按底面多边形的边数分为三棱台、四棱台、五棱台等；
沈阳广播电视大学
讲课内容
建筑制图基础
1 概念
正棱台：由正棱锥截得的棱台叫做正棱台。
正棱锥
沈阳广播电视大学
正四棱台
讲课内容
建筑制图基础
1 概念
如图所示，这是上下底面为矩形的正四棱台立体图和投影图，正四棱台上下底面为水平 面，左右侧面为正垂面，前后侧面为侧垂面。
分析其三面投影图。 H投影：为大小两个矩形。 V面投影、W面投影：都为等腰梯形。
沈阳广播电视大学
讲课内容
建筑制图基础
1 概念
棱台可用表示上、下底面的字母来命名，如可以记 作 棱 台ABCD－A’B’C’D’， 或 记 作 棱 台AC’.
D' A' D O A
沈阳广播电视大学
O' B'
C'
C
B
课程小结
建筑制图基础
课 程 小 结
熟练掌握棱台的投影特征
沈阳广播电视大学
课后内容
建筑制图基础
思考：一个投影外轮廓线为多边形，另两个投影 为一个或若干个有公共顶点的三角形，满足这样条 件的投影是哪种形体的投影？
房屋建筑工程图集-平面图立面图剖面图详图

房屋建筑工程图集-平面图立面图剖面图详图


结合实际看图。
1111
（二）、阅读房屋建筑工程图的方法 先读首页图 读总平面图 读建筑施工图 读结构施工图 读设备施工图 读图时注意工种之间的联系，前后照应。
1212
8.2 总平面图
一、总平面图的形成和用途及表示方法
总平面图的形成 将新建工程四周一定范围内的新建、拟建、原有和拆除的建筑物、
99
五、建筑设计总说明
设计依据：立项，规划许可证 建筑规模 占地面积——建筑物底层外墙皮以内所有面积之和 建筑面积——建筑物外墙皮以内各层面积之和 标高 相对标高———以建筑物底层室内地面为零的标高 绝对标高——以青岛黄海平均平面的高度为零点的标高 装修做法：地面、楼面、墙面的装修做法 施工要求 1)严格执行施工验收规范中规定 2)对图纸中不详之处的说明
2、建筑平面图表达的内容 建筑平面图反映新建建筑的平面形状、房间的位置、大小、相互关
系、墙体的位置、厚度、材料、柱的截面形状与尺寸大小，门窗的位 置及类型。 3、建筑平面图的用途
是施工放线、砌墙、安装门窗、室内外装修及编制工程预算的重要依 据，是建筑施工中的重要图纸。
2323
二、建筑平面图的图示方法
1818
5．等高线
1）地形——地面上高低起伏的形状，地形用等高线表示 2）等高线的绘制 假想用间隔相等的若干水平面把山头从某一高度顶一层一层地剖开， 在山头表面上便出现一条一条的截交线，把这些截交线投射到水平投影 面上，就得到一圈一圈的封闭曲线，即为等高线。 3）由等高线分析地形的高低起伏状况： A 等高线间距越大，地面越平坦，间距越小，地面越陡峭 B 数值由外圈向内圈增大，地形上凸；数值由外向内减小，地形下凹 6、 道路：标注道路中心控制点，道路的标高及平面位置
建筑图学立体的阴影平面立体PPT课件

建筑图学立体的阴影平面立体PPT课件


e
a(f)
第7页/共26页
靠在V面上的长方体在V面上的落影
第8页/共26页
位于H面且靠在V面上的长方体
为了作图清晰， 可将投影分开画
第9页/共26页
左右组合的长方体的落影
第10页/共26页
上下组合的长方体的落影
D A
CE B
第11页/共26页
l1=l2 如果l1>l2或者 l1<l2呢？
正三棱柱的落影
第4页/共26页
长方体在V 面上的落影
1.分别求阴线AB、BC、 CD、DE、EF、FA的落 影 2.用粗实线连接各影线 3.给落影上色
第5页/共26页
长方体在H 面上的落
影
第6页/共26页
3. 长方体在H面和V面上的落影
(c')
a'(b')
e'(d')
f' c'V
d'V
c(d)
eV
b
b'V
aV fV
GH
1.判断阴线为 ABCDEFGHIJ 2.求阴线的顶点的落影 3.连接各影线 4.给阴面和落影上色
第17页/共26页
二、 棱锥的阴影
1. 棱锥的变化引起阴影的变化 2. 判别立体（ a ）的阴阳面 3. 判别立体（ b）的阴阳面 4. 判别立体（ c）的阴阳面 5. 判别立体（ d）的阴阳面
第18页/共26页
Sh
，成为影线,
那么SE和SD
Dh
就是阴线
e
Bh
Ch
a
d
s
b
c
第22页/共26页
3. 判别立体（ b ）的阴阳面
s'
工程制图-体、平面立体、曲面立体

工程制图-体、平面立体、曲面立体


2" b"
1" a"
b 2
1 a
返回
返回
4.圆环体
(1)圆环体的组成
O
由圆环体组成。
(2)圆环体的形成
圆环体是由圆绕偏离圆心的中
心轴线旋转而成。这条运动的圆线称
为母线，圆环体上任一位置的母线圆 称为素线，母线上的各点绕轴线旋转
O1
时，形成回转面上垂直于轴线的纬圆。
返回
5.复合回转体
(1)复合回转体的组成
a'
c' (c"b) "
a"
b c
s
B
2'
a
2 C
A
返回
s'
三棱锥表面上取点3
s"
(3 ')
3"
b'
a' e’ c' (c") b"
a"
e
b
3
c
s
B
a
S 3
C
A
返回
s'
三棱锥表面上取线
s"
3’ 2’
1’
b'
a'
d’
b
d 1s 3 2
c' e’
c e
y3
y1 y2
a
(3”)
2” 1”
b"(c")
a"
返回
3.圆球体 (1)球体的组成
由球面组成。
(2)圆球面的形成
球面是由圆绕与它的中心轴线 OO1旋转而成。
这条运动的圆线称为母线。母线 上的各点绕轴线旋转时，形成回转面 上垂直于轴线的纬圆。

边做边学AutoCAD建筑制图立体化教程第3章绘制和编辑平面图形三

边做边学AutoCAD建筑制图立体化教程第3章绘制和编辑平面图形三contents目录01 /绘制建筑平面图02 /编辑建筑平面图03 /绘制和编辑建筑立面图04 /绘制和编辑建筑剖面图05 /绘制和编辑建筑详图绘制建筑平面图绘制建筑平面图的步骤01020304 05绘制完成后，保存并打印出图纸。

添加尺寸标注，确保图形的准确性和可读性。

使用偏移、修剪等编辑命令，对绘制的图形进行修改和完善。

使用直线、圆弧等基本绘图命令，绘制出建筑的墙体、门窗等基本结构。

打开A u t o C A D软件，新建文件并设置好单位和绘图比例。

绘制建筑平面图的基本命令•L I N E：绘制直线C I R C L E：绘制圆A R C：绘制弧线P L I N E：绘制多段线R E C T A N G L E：绘制矩形E L L I P S E：绘制椭圆P O L Y G O N：绘制多边形T E X T：添加文本D I ME N S I O N：添加尺寸标注B L OC K：创建和插入块H A T C H：填充图案S C A L E：调整图形比例M O V E：移动图形C O P Y：复制图形M I R R O R：镜像图形R O T A T E：旋转图形O F F S E T：偏移图形T R I M：修剪图形E X T E N D：延伸图形F I L L E T：倒角C H A M F E R：倒圆角E X P L O D E：分解块G R O U P：组合图形L A Y E R：管理图层C O L O R：设置颜色L I N E S T Y L E：设置线型L I N E W E I G H T：设置线宽Z O O M：缩放视图P A N：平移视图U N D O：撤销操作R E D O：恢复操作绘制建筑平面图的实例绘制墙体：使用直线工具绘制墙体，并设置墙体的厚度和材质。

绘制家具：使用矩形工具绘制家具，并设置家具的大小和位置。

建筑工程制图(第六章)


平面多边形
1、平面切割四棱锥
由于截平面P是正垂面，所以截交线的正面投影积聚成直线， 水平投影和侧面投影都是四边形 ( 类似形 )，只要求得四棱锥的 四条棱线与截平面的交点，依次连接即可完成作图，如图所示。
(a) 直观图
(b) 截交线的求法
2、平面切割四棱柱
截平面P与四棱柱的4个棱面及上底面相交，截交线是五边形， 如图所示。
(c) 两曲面体相贯
相交型建筑形体
1 两平面体的表面交线
2 平面体与曲面体的表面交线
3 两曲面体的表面交线
4 两曲面形体表面交线的特殊情况
1、两平面体的表面交线
如图所示为烟囱与坡屋面相交的形体，其形体可看成是由 四棱柱与五棱柱相贯，相贯线是封闭的空间折线，折线的每 一段分别属于两立体侧面的交线，折线上每个顶点都是一形 体上的棱线与另一形体侧面的交点。因此，求两平面体的相 贯线实际上是求两平面的交线或直线与平面的交点。
[例4.1] 如图所示，求作高低房屋相交的表面交线。
2、平面体与曲面体的表面交线 平面体与曲面体相交，其交线是由几段平面曲线组成的空 间曲线。
【例4.2】 如图4-11所示，求作圆锥形薄壳基础的表面交线。
(a) 求特殊点
(b) 求一般点
3、两曲面体的表面交线
两曲面体表面的相贯线，一般是空间曲线，特殊情况下 可能是平面曲线或直线。相贯线上的每个点都是两形体表 面的共有点，因此，求作两曲面体的相贯线时，通常是先 求出一系列共有点，然后依次光滑连接相邻各点。
第六章 立体表面的交线
第一节 立体表面上点的投影
第二节 立体表面截交线 第三节 立体表面相贯线
第一节 求立体表面上点、线的投影
1.1 平面立体上点和直线的投影

建筑工程制图 基本形体PPT课件

第40页/共68页
轴线 母线
底圆
圆锥体
2.圆锥的投影
H面投影是一个圆周。 V面、W投影是等腰三角形。
Z
X
O
YW
YH
第41页/共68页
圆锥体
3. 圆锥体的投影分析
s'
s"
S
b'
c' (d')
a'
D
d"
a"
(b") B
c"
A
C
d
b
s
a
c
s'
Z
s"
H面投影是一个圆周为锥
面和底面的重影。
V面投影是等腰三角形。
第47页/共68页
6. 圆环面
圆环体
第48页/共68页
曲面体截交线
截交线投影作法：
可以采用描点法来求。即先求出曲线上一些点，包括三类特殊 点和一些一般点。然后将这些点光滑连线。
特殊点包括： 1.确定曲线轮廓的点。如：最左点、最右点、最高点、最低点、 最前点、最后点。 2. 截交线上位于曲面体轮廓线上的点：轴线上的点、中心线 上的点、截交线本身固有的特殊点。 3.截交线每面投影可见与不可见的分界点。 在求每类点时，可以采用曲面体上求点的方法来求。如：素 线法、纬圆法等。
第4页/共68页
三视图的形成
第5页/共68页
平面体
平面体的投影 平面体表面的点和线 平面与平面体表面的交线 两平面体表面的交线
第6页/共68页
平面立体
平面立体：表面全是平面的立体。 有：棱面、棱线、底面、底边线、顶点。
平面立体的投影，实质上是
各棱面、各棱线及各顶点的投影。

建筑制图--第三章--立体投影参考课件

——如果点或直线在一般位置平面内，则需过已知点的一个投影作 辅助线，求出其它投影。
[例题1] 求立体的侧面投影
§3-2曲面立体的投影
基本要求 一、 概述 二、 圆柱的投影 三、 圆锥的投影 四、 圆球的投影 五、 圆环的投影
基本要求
本章学习的基本要求是: (1) 掌握曲面立体的投影特性及作图方法。 (2) 熟练掌握在曲面立体表面上取点和取
c' a"(c") b"
as
c
m
b
(a) 直观图
(b) 投影
小结
1.平面立体投影的作图可归结为绘制平面（立体表面）和（棱）线
投影的作图。
2.在立体表面上取点、取线的方法与在平面上取点、取线的方法 相同。
——如果点或直线在特殊位置平面内，则作图时，可充分利用平面 投影有积聚性的特点，由一个投影求出其另外两个投影；
判断可见性的方法，是对于可见位置的面和线用粗实线表示， 而对于不可见位置的面和线用虚线表示。
平面立体的投影特性：
⑴立体的三面投影图之间保持三等关系，适应整体和每一局部。 ⑵立体上各组成平面的投影，一般表现为一个封闭的线框，特殊积聚
为一直线。 ⑶投影图上各线框的分界线，表示物体表面发生变化（凹、凸或转折）
第三章 立体的投影
§3-1 平面立体的投影 §3-2 曲面立体的投影 §3-3 平面立体的截交线 §3-4 曲面立体的截交线 §3-5 立体的相贯线
§ 3-1 平面立体的投影 基本要求 一、 平面立体的投影特性 二、 平面立体表面上取点
基本要求
1. 掌握立体的投影特性和作图方法 2. 掌握在立体表面上取点、线的方法 3.掌握平面立体截交线的方法
3.1 平面立体的投影

建筑制图和识图第3章 立体-PPT文档资料

1
建筑制图与识图
(ห้องสมุดไป่ตู้)投影
土木工程学院
①.安放位置：为简 便作图，一般将圆柱 体的轴线垂直于某一 投影面。将圆柱体的 轴线（OO1）垂直于H 面，则圆柱面垂直于H 面，上、下底圆平行 于H面。 ②. 投影分析 H面投影:为一个圆。 它是可见的上底圆 和不可见的下底圆 V面投影:为一矩形。 它是可见的前半圆 柱的不可见的后半 圆柱投影的重合。 W面投影： 为一矩 形。它是可见的左 半圆柱和不可见的 右半圆柱投影的重 合。
建筑制图与识图
3.2.1 圆柱体
土木工程学院
由曲面围成或由曲面和平面围成的立体称为曲面立体。常见的 曲面立体有圆柱体、圆锥体、圆球体等，它们都是旋转体。
(1)形成：由矩形（AA1O1O）绕其边（OO1）为轴旋转运动的轨迹 称为圆柱体（右图)。 O 与 轴 垂 直 的 两 边 （ OA 和O1A1）的运动轨迹是上、 下 底 圆 ， 与轴 平 行 的 一 A 边（A A1）运动的轨迹是 圆柱面。A A1称为母线， 母 线 在 圆 柱面 上 任 一 位 置 称 为 素 线。 圆 柱 面 是 无 数 多 条 素线 的 集 合 。 圆 柱 体 由 上、 下 底 圆 和 A1 圆 柱 面 围 成。 上 、 下 底 圆 之 间 的 距离 称 为 圆 柱 O1 体的高。
W面投影：底边
8
建筑制图与识图
土木工程学院 (4) 圆锥体表面上取点
【例6-3】已知圆锥上1点
的V面投影（可见），求 另二投影。
m" '
9
建筑制图与识图
3.2.3 圆球体
（1）形成
土木工程学院
半圆面绕其直经（OO1）为轴旋转运动的轨迹称为圆球体。半圆线旋转运 动的轨迹是球面，即圆球的表面。

《土木工程制图》第04章 平面立体构形及轴测图画法

确定轴测图类型和投影方向 建立坐标系，确定坐标原点和坐标轴 绘制平面立体的轴测图 添加尺寸标注和文字说明 检查和完善轴测图
轴测图的作图技巧
确定轴测图类型和投影方向：根据物体的形状 和结构特点，选择合适的轴测图类型和投影方 向，以便更好地表达物体的形状和结构。
确定坐标系：在轴测图中建立合适的坐标系，以 便确定物体的位置和方向。
斜二轴测图与正等轴测图的比 较
05
平面立体构形的作图方法和技巧
平面立体构形的作图步骤
确定立体形状：根据题目要求，确定要绘制的立体形状。 绘制投影图：根据立体形状，绘制其正立面、侧立面和水平面的投影图。 绘制轴测图：根据投影图，绘制轴测图，注意轴测图的绘制方法和技巧。 标注尺寸：在轴测图上标注尺寸，注意尺寸的标注方法和技巧。 完善细节：根据题目要求，完善立体形状的细节部分，如孔洞、凹槽等。 检查并修改：最后检查并修改作图过程中可能出现的错误或遗漏。
常见错误分析
视图选择不当：选择不当的视图可能导致无法正确表达物体的形状和尺寸 投影关系错误：投影关系错误可能导致视图之间的尺寸关系不正确 线条绘制错误：线条绘制错误可能导致视图之间的连接关系不正确 尺寸标注错误：尺寸标注错误可能导致无法正确表达物体的尺寸和比例关系
06
轴测图的作图方法和技巧
轴测图的作图步骤
正二轴测图：将物体放置在两个互相垂直的投 影面上，分别沿两个投影面的坐标轴方向进行 等距离投影，得到的图形即为正二轴测图。
正等轴测图的画法
轴测图的基本概 念和分类
正等轴测图的投 影特性
正等轴测图的画 法步骤
注意事项和常见 错误分析
斜二轴测图的画法
斜二轴测图的基本概念
斜二轴测图的绘制技巧
斜二轴测图的画法步骤
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第八章 平面立体
§8－1 平面立体的投影 §8－2 平面和平面立体
相交 §8－3 直线和平面立体
相交
§8－1 平面立体的投影
由平面围合而成的具有长、宽、高三个方向 尺度的几何体称为平面立体。常见的平面立体有 棱柱、棱锥（台）。
平面立体的投影
棱柱体的投影特性 棱锥体的投影特性 平面立体表面上的点和直线
V X
棱柱体的投影特性
Z
在图示情况下，上、下底面
为水平面，两者的水平投影
重影且反映实形，正面投影
和侧面投影积聚为水平线。
前、后两棱面为正平面，两
者的正面投影重影且反映实
W 形，水平投影和侧面投影积
O
聚为垂直于OY轴的直线段。
左边的两个棱面和右边的两
个棱面均为铅垂面，其水平
投影积聚为等于底面边长的
线段，正面投影和侧面投影
s'
PV f'
1'
2'
3'
n'
e'
m'
a'
b'
c'
a
f n
1
s m
3c
e
2
b
截交线的求法
交点法：求出平面立体的棱线和截平面的交点。 交线法：求出平面立体的棱面和截平面的交线。
在实际作图时，常采用交点法。交点求出后 的连接原则是：位于同一棱面上的两个交点才能 连接。同时还要注意可见性：可见棱面上的两点 用实线连接，不可见棱面上的两点用虚线连接。
截交线的求法
例4、求作正 垂面截割三棱 锥S－ABC的 截交线。
H
均为矩形，但不反映实形。
Y
棱柱体的投影特性
45°
棱锥体的投影特性
V
a'
X
A
a
Z s'
S
s"
C a" c"
Bc s
H
b
在图示情况下，由于底 面为水平面，所以它的 水平投影反映实形，正 面投影和侧面投影积聚 为水平线。
W
后棱面SAC为侧垂面， 所以其侧面投影积聚为
一条斜线段，正面投影
和水平投影都是三角形。
平面立体的投影
例1、作出图示立体的三面投影图。
平面立体表面上的点和直线
要取得平面立体表面上的点和直线 的投影，可采用辅助线法（简单情况下可 直接根据点的投影规律获得）。由于立体 是不透明的，因此还要判断所求出的投影 的可见性。
平面立体表面上的点和直线
n'
n"
例2、
m'
( m")
nm
平面立体表面上的点和直线
s'
1' 2'
a'
b'
a 1 s
2
b
3' PV c'
3c
截交线的求法
例5、补出立体 被截割后的投影。
Ⅵ Ⅴ
Ⅳ Ⅲ
Ⅱ Ⅰ
1'
3 1
2
6' 4'（5'） 2（' 3'）
5 6
4
(6 ")
5"
4"
3" 1" 2 "
§5－3 直线和平面立体相交
M N
直线和平面立体 相交，在立体的表面 上可以得到两个交点。 这种交点叫做贯穿点。
贯穿点的求法
求平面立体的贯穿点，如同求直线和平面的交 点一样。步骤如下： 1、通过已知直线作一个辅助平面（通常选择投 影面垂直面作为辅助平面）。 2、求出辅助平面和平面立体的截交线。 3、确定截交线和已知直线的交点。这个交点即 为所求贯穿点。
贯穿点的求法
例6、求直线 EF和三棱锥S －ABC的贯穿 点。
s'
s"
例3、
2'
n'
k'
m'
2" n" (k")
m"
a'
3' b' 1' c' c" (1") a" 3" b"
c
a
2 n
sk 1
m
3b
§8－2 平面和平面立体相交
平面和平面立体相交，也叫做立体被平面截割。
截断面
截平面
截交线
截交线的性质
闭合性：截交线一定是闭合的平 面多边形。多边形的各顶点就是 平面立体的棱线和截平面的交点。 共有性：截交线即从属于截平面， 又从属于立面SAB、 SBC均为一般位置平面，
所以它们的三个投影均
Y 为三角形。
棱锥体的投影特性
s'
s"
a'
b'
a s
b
a" （c"） b" c'
45° c
平面立体的投影
由于点、线、面是构成平面立体表面的 几何元素，因此绘制平面立体的投影，归根 结底是绘制点、线、面的投影，且投影同样 遵循“长对正、高平齐、宽相等”的规律。