齿轮啮合动态接触过程仿真分析
- 格式:pdf
- 大小:562.92 KB
- 文档页数:4

基于ANSYS/LS 2DY NA 的直齿锥齿轮动力学接触仿真分析高 翔,程建平(江苏大学汽车与交通工程学院,江苏镇江 212013)摘要:针对直齿锥齿轮疲劳破坏中出现儿率最高的齿面接触疲劳强度问题,在UG 中建立齿轮几何模型,利用ANSYS/LS 2DY NA 对齿轮进行动力学接触仿真分析,计算了齿轮副在啮合过程中齿面接触应力、应变的变化情况及两对轮齿同时接触过程中接触压力的分布情况。
关键词:直齿锥齿轮;AN S YS /LS 2D Y NA;动力学;接触仿真分析中图分类号:TH132.421 文献标识码:A 文章编号:1006-0006(2008)02-0050-02Dynam ic Contact Emulate Analysis of Bevel Gear with ANSYS/LS 2DY NAGAO X iang,CHEN G J ian 2ping(School of Aut omotive and Traffic Engineering,J iangsu University,Zhenjiang 212013,China )Ab s tra c t:Geometrical model of a bevel gear is established and bevel gear dyna m ic emulati on analysis is operatedwith ANSYS/LS 2DY NA s oft w are f or that the fatigue failure p r obability of bevel gear is the highest in t ooth surfaces contact fatigue resistance .The contact stress and def or mati on during the meshing p r ocess are calculated .And the distributi on of contact f orce is calculated when t w o pairs of teeth contact si m ultaneously .Key wo rd s:Bevel gear;ANSYS/LS 2DY NA;Dyna m ic;Contact si m ulati on analysis 由于车用齿轮的传动比和传递功率大,加工难度与成本都相当高,所以如何提高车用齿轮的传动性能与使用寿命,近年来一直深受社会各界的广泛关注。



第1篇一、实验背景齿轮作为机械传动系统中的重要组成部分,其性能直接影响着整个系统的效率和寿命。
为了提高齿轮设计的准确性和可靠性,本研究采用有限元分析(FEA)和刚柔耦合动力学仿真(Rigid-Flexibility Coupling)方法,对齿轮进行仿真耦合实验,以评估齿轮在实际工作条件下的力学行为和性能。
二、实验目的1. 建立齿轮的有限元模型,并进行网格划分。
2. 通过有限元分析,计算齿轮在静态载荷作用下的应力分布和变形情况。
3. 利用刚柔耦合动力学仿真,模拟齿轮在实际工作条件下的动态响应。
4. 分析齿轮的疲劳寿命和强度性能,为齿轮设计和优化提供理论依据。
三、实验方法1. 有限元模型建立与网格划分首先,根据齿轮的实际尺寸和材料属性,建立齿轮的几何模型。
然后,采用四面体网格对齿轮进行网格划分,确保网格质量满足仿真要求。
2. 静态载荷下的有限元分析在有限元分析中,将齿轮置于静态载荷作用下,通过求解非线性方程组,得到齿轮的应力分布和变形情况。
主要关注齿轮的齿面接触应力、齿根应力、齿面磨损和齿面疲劳寿命。
3. 刚柔耦合动力学仿真为了模拟齿轮在实际工作条件下的动态响应,采用刚柔耦合动力学仿真方法。
将齿轮视为柔性体,同时考虑齿轮与轴承、轴等部件的相互作用。
通过施加转速和扭矩等激励,模拟齿轮在旋转过程中的动态响应。
4. 疲劳寿命和强度性能分析在仿真过程中,对齿轮的疲劳寿命和强度性能进行分析。
通过计算齿面接触应力、齿根应力等参数,评估齿轮的疲劳寿命和强度性能。
四、实验结果与分析1. 静态载荷下的应力分布和变形通过有限元分析,得到齿轮在静态载荷作用下的应力分布和变形情况。
结果表明,齿轮的齿面接触应力主要集中在齿根附近,齿根应力较大。
同时,齿轮的变形主要集中在齿面和齿根处。
2. 刚柔耦合动力学仿真结果通过刚柔耦合动力学仿真,模拟齿轮在实际工作条件下的动态响应。
结果表明,齿轮的齿面接触应力、齿根应力等参数在旋转过程中发生变化,但总体上满足设计要求。

根据图1可知赫兹接触理论模型的接触半宽为:式中,E1、E2为齿轮1、齿轮2、齿轮2的泊松比;L为接触面长度;最大值;F n为外力;R1为齿轮1的分度圆半径;的分度圆半径;b为接触面半宽。
赫兹接触理论模型的接触应力为:(考虑齿轮传动中小齿轮单对齿啮合系数Z B ;节点区域系数Z H ;弹性系数Z E ;重合度系数Z L ;螺旋角系数Z β;荷系数K ;太阳轮上转矩T 1;齿轮传动比i ,得到最大接触应力为:(由弹性理论可得内力与体积力的关系方程为:体内的应力与表面力存在的边界条件为:式中,F Sx 、F Sy 、F Sz 为表面力在x 为表面外法线方向余弦。
对于具有接触面的结构,在承受荷载的过程中,面的状态变化影响接触体的应力场,接触状态。
分析接触问题的常用方法有数学规划法、元法和有限元法,对复杂的接触问题常用有限元法。
有限接触点的柔度方程组为:式中,δi ,A 和C Aij 为物体A 在接触点子矩阵;δi ,B 和C Bij 为物体B 在接触点矩阵;m 1为外力作用点数;R Ak 为载荷向量。
由于两相互接触物体一般不会产生渗透,两接触面间的接触关系以阻止穿透的发生,表面接触,存在大变形的摩擦接触时可引入额外因子虽然拉朗格朗日乘子模型能够得到接近零的穿透量,但计算量较大。
当允许有较小的穿透量时可使得接触状态图1赫兹接触理论模型F nR 1σHmax2bR 2F n图2基于UG的齿轮对接触仿真模型图3基于UG的齿轮对接触分析位移云图得到齿轮对的应力云图如图4所示。
可知齿轮对在接触区的应力较大,且最大应力发生在齿轮对接触面上,与实际情况相符,齿轮对的最大应力为15.53MPa,远小于材料的屈服应力。
通过对齿轮对接触面处的接触分析可进一步了解齿轮对的传动性能情况。
图4基于UG的齿轮对接触分析应力云图得到齿轮对的接触力与接触压力云图如图5所示。
将视图进行局部选择,图5(a)为齿轮对接触面处接触力云图,图5(b)为齿轮对接触面处的接触压力云图。
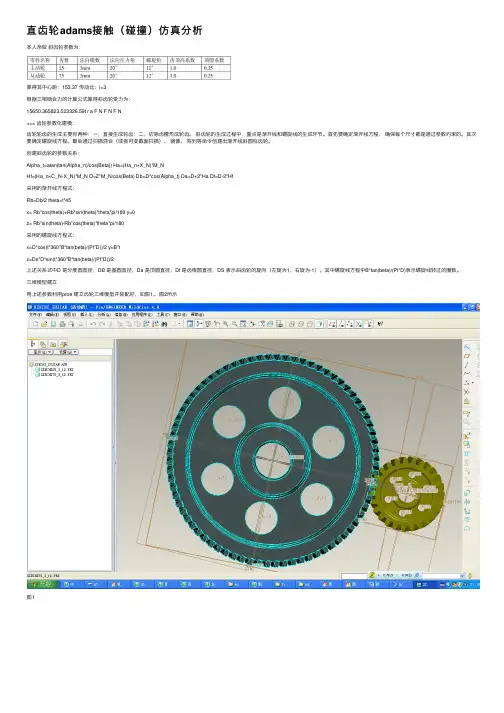
直齿轮adams接触(碰撞)仿真分析本⼈亲做斜齿轮参数为:算得其中⼼距:153.37 传动⽐:i=3根据三相啮合⼒的计算公式算得斜齿轮受⼒为:15650.365823.523326.59t r a F N F N F N=== 齿轮参数化建模:齿轮轮齿的⽣成主要有两种:⼀,直接⽣成轮齿;⼆,切除齿槽形成轮齿。
斜齿轮的⽣成过程中,重点是渐开线和螺旋线的⽣成环节。
⾸先要确定渐开线⽅程,确保每个尺⼨都是通过参数约束的。
其次要确定螺旋线⽅程。
最后通过扫描混合(或者可变截⾯扫描)、镜像、阵列等命令创建出渐开线斜圆柱齿轮。
创建斜齿轮的参数关系:Alpha_t=atan(tan(Alpha_n)/cos(Beta)) Ha=(Ha_n+X_N)*M_NHf=(Ha_n+C_N-X_N)*M_N D=Z*M_N/cos(Beta) Db=D*cos(Alpha_t) Da=D+2*Ha Df=D-2*Hf采⽤的渐开线⽅程式:Rb=Db/2 theta=t*45x= Rb*cos(theta)+Rb*sin(theta)*theta*pi/180 y=0z= Rb*sin(theta)-Rb*cos(theta)*theta*pi/180采⽤的螺旋线⽅程式:x=D*cos(t*360*B*tan(beta)/(PI*D))/2 y=B*tz=Ds*D*sin(t*360*B*tan(beta)/(PI*D))/2上述关系式中D 是分度圆直径,DB 是基圆直径,Da 是顶圆直径,Df 是齿根圆直径,DS 表⽰斜齿轮的旋向(左旋为1,右旋为-1)。
其中螺旋线⽅程中B*tan(beta)/(PI*D)表⽰螺旋线转过的圈数。
三维模型建⽴⽤上述参数利⽤proe 建⽴齿轮三维模型并装配好,如图1,、图2所⽰图1图2将三维模型导⼊adams定义导⼊模型后,逐步进⾏:材料属性定义,添加约束,添加驱动,添加负载,添加接触⼒,然后得到仿真处理前期⼯作,如图3,图4所⽰图3图4、仿真后处理仿真后处理得到斜齿轮三个⽅向上波动图和均值。





点线啮合齿轮动态接触应力仿真分析与齿廓修形刘梦蝶 罗齐汉 黄 海 杨 帆武汉理工大学工程学院 武汉 430063摘 要:针对DZLY180型硬齿面点线啮合齿轮减速器,利用SolidWorks建立其高速级齿轮副三维模型,采用Ansys Workbench对模型进行动态接触应力仿真分析,然后对其进行修形并重新建模、仿真,结果显示修形后点线啮合齿轮接触应力减小,啮入冲击得到明显改善。
关键词:点线啮合齿轮;瞬态动力学仿真;修形中图分类号:TH132.46 文献标识码:A 文章编号:1001-0785(2021)04-0058-05Abstract: A three-dimensional model of the high-speed gear pair of DZLY180 hard tooth surface point-line meshing gear reducer is established by using SolidWorks. The dynamic contact stress of the model is simulated and analyzed through Ansys Workbench, and then modified, re-modeled and simulated. Results show that the contact stress of the point-line meshing gear is reduced and the meshing impact is improved obviously after profile modification.Keywords: point-line meshing gear; transient dynamics simulation: profile modification0 引言点线啮合齿轮既具有渐开线齿轮加工方便、可分性的优点,又同时囊括了圆弧齿轮承载能力高的优点,有较好的发展前景。
兆瓦级风机增速器轮齿修形及载荷研究【摘要】齿轮在现代工业中得到了广泛的应用,特别是近年来在风力发电设备中的应用,对其性能要求更高,轮齿修形技术对提高齿轮传动性能具有重要意义。
本文以兆瓦级风电增速箱中的输出端大小齿轮为研究对象,基于渐开线齿轮啮合原理和振动冲击理论,从理论上分析了齿轮啮合载荷,完成了齿向、齿廓的修形设计,应用有限元软件对齿轮啮合运动进行了动态接触仿真,分析了啮合载荷分配与分布情况,比较了修形前后的压力分布和接触应力。
本文首先根据加工刀具齿廓方程推导了组成轮齿齿廓的各段曲线方程,以此为基础应用NX软件建立了精确的大小斜齿轮三维模型,并完成了齿轮副的装配,然后把分析模型导入到有限元软件中,并进行了网格划分。
其次,结合斜齿轮啮合变形协调条件和力平衡条件,建立了节点力和啮合变形的线性方程,并从理论上分析了斜齿轮的齿向载荷分布和齿间载荷分配。
应用有限元软件动态模拟了齿轮啮合过程,得出了齿面接触应力分布云图,同时探讨了对接触分析有重要影响的刚度系数和摩擦系数的选取问题。
然后,分析比较了三种齿向修形方法,提出了螺旋角修形的齿向修形方案,并通过对带轴齿轮的动态接触分析,确定了螺旋角修形量。
同时根据齿廓修形理论,确定了齿廓曲线的最... 更多还原【Abstract】 Gears are commonly used in industry, especiallyin the wind power generation equipment in the recent years, which requires better performance. Modification has a greatsignificance to improve the loading capacity of gears. Output gears of increasing gearbox of Megawatt Wind Accelerator were studied in this paper. Based on principles of involutes gears and vibration theory, the analysis of mesh load based on theoretical, completed helix angle modification and tooth profile modification was made. ... 更多还原【关键词】斜齿轮;有限元法;动态接触分析;啮合载荷;轮齿修形;【Key words】Helical Gear;FEM;Contact Analysis of Dynamic;Load of Meshing;Gear Modification;摘要5-6Abstract 6-7第一章绪论10-151.1 课题的背景和意义111.2 国内外研究现状和发展趋势11-131.2.1 国外的研究现状11-131.2.2 国内的研究现状131.3 课题的主要研究方法13-15第二章非线性接触有限元法15-192.1 有限元法解算的基本步骤15-162.2 非线性接触有限元法16-182.2.1 接触有限元法的基本概念16-172.2.2 接触问题求解的过程172.2.3 求解接触问题的罚函数法17-182.4 本章小结18-19第三章斜齿轮模型的建立及啮合载荷研究19-403.1 斜齿轮齿廓曲线方程的建立19-223.2 建立斜齿轮模型22-323.2.1 齿轮的基本参数22-233.2.2 NX建模23-273.2.3 斜齿轮模型的导入、参数设置及网格划分27-323.3 斜齿轮啮合载荷研究32-343.3.1 啮合载荷分配32-333.3.2 齿向载荷分布33-343.4 有限元法的啮合载荷研究34-373.4.1 有限元法研究齿间载荷分配的数学模型34-363.4.2 ANSYS/LS-DYNA分析轮齿接触应力分布36-373.5 主要接触参数的分析37-393.5.1 接触刚度系数的选取37-383.5.2 摩擦系数的选取38-393.6 本章小结39-40第四章轮齿修形研究40-604.1 齿向修形研究40-454.1.1 齿向修形技术40-414.1.2 螺旋角修形理论41-434.1.3 螺旋角修形量的确定43-454.2 齿廓修形研究45-514.2.1 齿轮的啮合传动分析45-484.2.2 齿廓修形方法48-494.2.3 齿顶修形量、修形长度和修形曲线的确定49-514.3 修形前后的结果分析51-584.3.1 修形前各齿接触应力和压力曲线51-544.3.2 修形后各齿接触应力和压力曲线54-574.3.3 修形前后结果比较57-584.4 本章小结58-60第五章结论60-625.1 结论605.2 展望60-62参考文献。
高强度轻型材料齿轮传动动态接触仿真研究第4期2006年8月中国鼋;珂躇q宪阪罾瓤JournalofCAEITV01.1No.4Aug.2006高强度轻型材料齿轮传动动态接触仿真研究马磊(中国电子科学研究院,北京100041)摘要:由于航空,航天,电子等领域对重量的严格要求,研究高强度轻型材料以取代钢材,是走上第四代齿轮的热点课题.但是由于在传动过程中相互啮合的齿面相对运动为滚动兼滑动,并且,在不同的啮合位置其相对滑动速度,接触应力不断变化,所以精确仿真计算某种材料齿轮啮合过程的接触应力变化.对研究齿轮材料特性十分必要.本文运用Ls—Dyna动态仿真软件,对尼龙66材料齿轮啮合过程进行了动态仿真计算并与试验结果进行了对比,此仿真方法可以运用到所有齿轮材料研究,为高强度轻型材料齿轮的进一步发展提供了新的有效途径.关键词:高强度;轻型;齿轮;动态;接触;仿真中图分类号:TP337文献标识码:A文章编号:1673—5692(2006)04—341—04 TheStudyofHighStrengthandLowWeightGear'SMesh PerformanceCharacteristicsDynamicContactSimulationMALeiAbstract:Duetothesternrequirementsinaviation,spaceflightandelectronics,thestudyofhi gh strengthandlowweightgearstosubstitutesteelgearsiscurrentlyahottopicalongtheprogress ionto—wardsthe4th—generationgears.However,gear'Smeshperformanceisslipandrol1.Suchparameters asrelativeslipvelocityandcontactstressarevariableatdifferentmeshlocations.SOitiSneces saryforgearmaterialcharacteristicsresearchthatacertainmaterial'Sprecisecontactstressissimulat edinthemeshprocess.Nylon66gear'Smeshperformancecharacteristicssimulationisstudiedbased onthead—vancedthree.dimensionaldynamiccontactFEAsoftwareLS—DYNA,andtheresultiscontrastedwiththetraditionalgeartestingoutcome.Itprovesthatthisnewmethodcanbeappliedtoallgearmat erialresearch,thusprovidinganupdated,effectiveapproachforthedevelopmentofhighstrengtha ndlowweightgears.Keywords:highstrength;lowweight;gear;dynamic;contact;simulation引随着材料工业及航空,航天,电子技术的迅速发展,高强度轻型材料齿轮在很多场合已经取代金属齿轮,并被越来越广泛地应用于运动及动力传动的场合.高强度轻型材料齿轮,如尼龙66齿轮可以采用注塑成型的方法制造,降低了制造成本,并且具有收稿日期:2006—07—24修订日期:2006—08—15重量轻,噪音低,抗化学腐蚀,可无润滑传动等优点.但同时也具有弹性模量低,机械强度低等缺点,这些限制了该齿轮的使用.近年来,国内外对各种高强度轻型材料齿轮的磨擦,磨损还有其失效形式,失效机理进行了大量的研究与探索.以渐开线直齿齿轮为例,发现在传动过程中相互啮合的齿面曲率不断变化,相对运动为滚动兼滑动;并且,在不同的啮合位置其相对滑动速言日342.fr橱雹;纠学研雹阪学极2006年第4期度,接触应力不断变化,这些都增加了对齿轮材料分析的复杂性.所以对齿轮啮合的全过程进行精确数值仿真是一个研究关键.2000年,林腾姣等_1]应用三维冲击一动力接触问题的有限元混合算法对齿轮传动的突加载荷冲击及啮入冲击,进行了冲击特性数值仿真.本文则运用LS—DYNA对齿轮啮合全过程接触应力变化进行了数值仿真.2建模根据齿轮材料的使用场合,结合变位系数选择原理和变位系数的计算公式(1),(2),(3)及《机械零部件手册:选型设计指南》中介绍的齿宽,模数选取方法_2J表1,表2,进行标准渐开线直齿齿轮设计, 然后再进行齿轮仿真建模.经过设计,齿轮几何模型如图1所示,具体参数如表3所示.minf(z)=印(1)式中,为变化后的小齿轮齿根应力;齿根应力计算公式为O"FvKF器FFt式中,KA为使用系数;Kv为动载系数;KF8为齿向载荷分布系数;K为齿问载荷分配系数;为齿形系数;Ys为应力修正系数;为弯曲强度计算的重合度系数,yE=0.25+0.75/e0=f(z1+z2),e0为重合度.表1(St)齿宽系数选择表齿轮相对于软齿面轴承的位置(硬度≤350HBS)硬齿面对称分布0.8~1.40.4~0.9非对称分布0.6~1.20.3~0.6悬臂布置0.3~0.40.2~O.25表1(b)齿宽系数=b/m的最大值J,l为模数结构特点重载精密传动,轴,轴承与箱体的刚度都很大:软齿面45~30硬齿面30~20减速器之类的独立传动装置,轴和轴承都有足够大的刚度:软齿面30~25硬齿面20~15变位系数的选择受以下条件限制.①齿轮齿顶变尖对变位系数的限制Sa=s2y(invaa-in式中,y0.5z,S丁7fTf/+2xmtan口表2渐开线圆柱齿轮模数选择表(2)第一系列第二系列44.555.56(6.5)8710912(11)②变位系数的重合度e=:[z(a口1一)]≥1.2(3)式中,a,aa2为齿轮的齿顶压力角;Ct"为齿轮传动的啮合角.表3齿轮副参数表参数小齿轮大齿轮材料尼龙66弹性模量E/Nm12.85×109淮松比(I.3齿数1741模数m/ram4变位系数z0.35—0.35齿宽B/mm57.557.5压力角a20齿顶高系数11弯曲强度/MPa510图1设计后变速齿轮对的几何模型在保证求解精度的前提下,为减小求解规模,采用参数化方法建立了四对齿啮合的齿轮轮齿几何模型,划分网格时,选取精度较高的六面体单元,并对沿齿形渐开线方向和齿根过渡圆弧方向的单元进行适当加密.得到的有限元模型图如图2所示.确定边界条件时,将齿轮轴径表面的节点通过2006年第4期马磊:高强度轻型材料齿轮传动动态接触仿真计算研究343 刚性面单元与转动中心固联,且将刚性面单元的质心定义在转动中心线上,并约束转动中心线,从而约束其周向和轴向位移,只释放沿轴向的转动位移,并在主动小齿轮上施加1500r/min的转速,在从动大齿轮上施加30Nm的扭矩.图2齿轮啮合三维有限元模型3设定参数时的注意事项因为是动态接触仿真,结果要真实可信的话,参数设置要注意如下几点.(1)网格的划分及单元类型的确定网格划分看似简单但却很有讲究,因为它直接影响着后面的运算能否进行下去.首先,在划分网格前要先对称划分好几个部分,然后去分别划分网格,每一部分的网格疏密必须调整合适,这对运算精度影响很大.必须选取正确部分单元类型,否则无法运算,比如齿轮固连的内表面必须选取为刚性面.(2)接触方法在接触分析中,由于问题的复杂性,判断接触发生的方向有时是很困难的,因此分析中应尽量使用自动接触(不需要人工干预接触方向).但当面的方向在整个分析过程中都能确定的情况下,下面的非自动接触类型是非常有效的.*Contact—Nodes_T—Surface*Contact—One_Way—Surface—To—Surface*Contact—Constraint—Nodes_To—Surface*Contact—Eroding—Nodes—To_Surface(3)材料在LS—DYNA定义材料单位时不需要每个都定义,但必须使约束材料的每个参数单位保持一致.(4)约束方法每个齿轮的转动中心的约束必须正确,否则的话,就会出现齿轮转偏无法仿真的现象.(5)加载方法在给大小齿轮加载初速度时,两个速度必须协调,否则会出现齿轮严重振荡及一侧轮齿穿透另一侧轮齿的现象.(6)局部坐标系的建立因为两个齿轮的中心不在一起,尽量将其中一个放在总体坐标系的原点,而在导入ANSYS的模型坐标比较难于确定,所以应建立一个局部坐标系, 令它的原点与另一个齿轮中心重合.(7)沙漏的控制有限单元单点积分方法可以大幅度降低计算成本,但是由此产生的沙漏问题如果不得到有效控制, 将使计算结果完全不可信.(8)K文件的修改LS-DYNA通常应用的是ANSYS工作环境.但在某些情况下两者兼容的并不是十分好,所以往往在生成K文件后,需要修改K文件.在LS—DYNA的使用过程中还有很多需要注意的地方,就不一一列举了,这需要在实际应用中不断积累和发现,还需要对所分析的模型特点十分熟悉. 4啮合过程仿真计算利用显式非线性动力分析通用有限元软件ANSYS/LS—DYNA,仿真计算过程如图3所示,应力结果如图4所示.(a)齿轮开始啮合(b)两对齿同时啮合+00:疆+004+000344.fr目1{}弓钶髫研宪阪瓤(c)单齿对啮合图3齿轮啮合过程V onMises应力云图6.00E+055.0OE+054.0OE+053.00E+05b2.00E+051.00E+050.00E+00图4啮合过程接触应力随时间变化图5与试验结果对比利用试验方法(转速在500~1500r/min,转矩在7~30Nm)再结合计算,得出在一般滑动速度下的极限接触应力_3如图5所示.根据仿真是设定的参数计算得知,齿轮相对滑动速度为0.2~0.41m/s.所以根据图5可知,接触极限应力为58~60MPa;而由图4可知,仿真计算所得接触极限应力53~56MPa,仿真结果可信. 6结语高强度轻型材料齿轮研究领域是个新兴的研究宴佳2006年第4期滑动速度V(m/s)图5在一定滑动速度下的极限接触应力领域,在材料优选,齿轮优化设计,传动失效规律等方面需要进一步研究,但是传统计算方法很不精确,试验测试数据耗费成本太高,所以齿轮啮合仿真计算具有一些实际意义,可以从建模乃至参数设定,边界条件选择方面进一步优化,使结果更加精确,以便对高强度轻型材料齿轮的研究提供更多帮助.参考文献1林腾姣,李润方,陶泽光.齿轮传动三维间隙非线性冲击一动力接触特性数值仿真.机械工程,2000,36(6).2余梦生,吴宗泽.机械零部件手册:选型设计指南.北京:机械工业出版社,1996:186—282.3孙晓伟,毛昆.塑料齿轮传动磨损特点.材料科学与工程,1999,17(3).作者简介一马磊(1980一),男,籍贯山西侯马,硕士,就职于中国电子科学研究院.。
基于虚拟样机齿轮啮合过程中啮合力动态仿真*许俊梅,苟向锋(兰州交通大学机电工程学院,兰州730070)摘要:基于多体动力学仿真软件ADAMS 建立了齿轮-转子系统扭转振动动力学模型。
该齿轮副模型包含传统齿轮副扭转振动模型的全部动力学内容。
对齿轮啮合过程进行了仿真分析。
分析了该模型中主要参数:扭转刚度、扭转阻尼、啮合刚度、啮合阻尼对齿轮啮合力的影响。
结果表明:提高啮合刚度、增大啮合阻尼、减小扭转刚度、增大扭转阻尼都能有效地降低齿轮传动时产生的振动和噪声。
为齿轮传动系统实现减振降噪提出了可行的优化措施。
关键词:ADAMS ;动力学仿真;啮合力中图分类号:TH132.413文献标识码:A文章编号:1007-4414(2012)06-0068-03Dynamic simulation of meshing force in gear meshing process based on virtual prototypingXu Jun-mei ,Gou Xiang-feng(College of engineering of Lanzhou Jiaotong university ,Lanzhou Gansu 730070,China )Abstract :The torsional vibration model of the gear-rotor system is set up based on ADAMS.The model includes all the ki-netic contents of a torsional vibration model.Dynamic simulation of meshing force in gear meshing process is completed.The main parameters are analyzed including torsional stiffness ,torsion damper ,mesh stiffness ,mesh damping ,which affecting gear meshing force ,.The results show that the vibration and noise problems in gear transmission can be effectively reduced by improving meshing stiffness ,increasing meshing damping ,reducing torsional stiffness and increasing torsion damper.Some op-timized solutions are provided for reducing the vibration and noise problems in gear transmission system.Key words :ADAMS ;dynamics simulation ;meshing force1引言齿轮是传递动力和运动的一种常用机构,在机械设备中占有重要地位。