基于Matlab求解建筑结构地震响应的时程分析法_孟宪萍 (1)
- 格式:pdf
- 大小:244.25 KB
- 文档页数:3

基于MATLAB的地震数据的分析地震是地球内部能量释放的结果,地震数据的分析对于理解地震活动的规律和预测地震发生的可能性具有重要意义。
MATLAB是一个功能强大的数值计算和数据可视化软件,可以用于地震数据的处理、分析和展示。
本文将介绍基于MATLAB的地震数据分析的方法和技巧。
对于地震数据的分析,可以从多个方面入手。
首先,可以对地震数据进行整体的统计分析。
可以统计地震事件的频率分布、震中位置的分布、地震震级的分布等等,这些统计信息对于理解地震活动的规律和特征非常重要。
MATLAB提供了丰富的统计工具,可以方便地进行数据的统计分析。
其次,可以对地震波形进行分析。
地震波形是地震能量沿时间传播的表现,可以通过地震仪器记录到。
地震波形可以用来研究地震波的传播规律、地震震源的机制等。
MATLAB提供了丰富的信号处理工具,可以对地震波形进行频谱分析、滤波、去噪等操作,从而揭示地震波的特征和信息。
此外,还可以对地震数据进行地震活动的空间分布分析。
地震活动具有明显的空间集聚性,可以通过空间统计方法研究地震活动的空间分布规律。
MATLAB提供了空间统计工具包,可以进行地震活动的聚类分析、空间插值分析等,以及地震活动与地球构造、地质灾害等的关联性研究。
另外,在地震数据的分析中还可以结合地震地质调查数据、地震前兆数据等多源数据进行综合分析。
地震地质调查数据包括断层观测数据、地震破裂带的研究等,可以用来研究地震发生的条件和机制。
地震前兆数据包括地震活动前的地形变、地磁变化、水质变化等,可以用来进行地震预测和预警。
MATLAB提供了数据处理和分析的综合环境,可以方便地进行多源数据的整合和分析。
在MATLAB中进行地震数据的分析和展示时,可以利用MATLAB自带的绘图函数进行数据的可视化展示。
MATLAB提供了各种绘图函数,包括曲线图、散点图、等值线图、三维图等,可以方便地进行数据可视化分析和结果展示。
同时,MATLAB还支持脚本编程和函数编程,可以编写自定义的算法和分析工具,以满足不同的地震数据分析需求。

Matlab技术在工程结构分析和振动控制中的应用随着科技的进步和工程技术的不断发展,结构分析和振动控制在工程领域中变得越来越重要。
尤其是在建筑物和桥梁等大型工程的设计和建设中,通过对结构的分析和控制,可以确保工程的安全性和稳定性。
而其中,Matlab技术作为一种强大的计算工具,为工程结构分析和振动控制提供了全面的解决方案。
一、结构分析1.1 结构模型在进行结构分析之前,首先需要建立准确的结构模型。
Matlab提供了丰富的建模和仿真工具,可以方便地构建各种结构模型。
通过Matlab中的有限元分析工具,可以将实际结构转化为有限元模型,并进行静力学和动力学分析。
同时,Matlab还提供了各种材料和截面的库,使得分析过程更加快捷和精确。
1.2 静力学分析静力学分析是结构分析的基础,用于计算结构受力情况和位移响应。
Matlab中的强大计算能力和矩阵运算功能,可以快速、准确地完成静力学分析。
通过建立结构模型,采用适当的边界条件和加载方式,可以计算结构的内力、位移、应力等参数,以评估结构的强度和刚度。
1.3 动力学分析动力学分析是研究结构在外界激励作用下的振动特性和响应情况。
Matlab提供了强大的信号处理和频谱分析工具,可以方便地进行动力学分析。
通过在结构中施加外力或外界激励,可以计算结构的振动模态、振型、频率等参数,快速识别结构的固有振动特性,并评估结构的抗震性能。
二、振动控制2.1 振动控制概述振动控制是指通过采取适当的措施,减少或消除结构振动带来的不利影响。
在工程实践中,振动控制常常用于解决结构的疲劳破坏、噪声污染、舒适性问题等。
Matlab提供了多种振动控制方法和工具箱,可用于设计和优化不同类型的振动控制系统。
2.2 主动振动控制主动振动控制是通过在结构中引入可控力或可控阻尼,以主动地减震和抑制结构的振动。
Matlab中的控制系统工具箱提供了丰富的控制算法和方法,可以实现主动振动控制系统的设计和仿真。

结构抗震计算时程分析法的计算要点收稿日期:2007-01-23作者简介:孟宪建(1965-),女,工程师,太原大学建工系,山西太原 030009孟宪建摘 要:介绍了时程分析法的应用范围、应用方法和计算步骤,并对时程分析计算结果的处理方法进行了阐述,论述了利用计算机进行结构动力时程分析的设计方法,以保证地震作用下的结构安全。
关键词:时程分析法,结构抗震,层间位移,动力反应中图分类号:T U 352.11文献标识码:A结构抗震计算的主要方法是对多遇地震采用振型分解反应谱方法进行分析,这种方法仅是一种静力分析方法,它是将地震剪力等效为水平力作用在结构上,然后按照静力学的方法进行分析计算,这种计算方法同实际地震反应尚有一定的差距,计算精度不够,不一定能够保证地震作用下结构的安全。
时程分析法是一种动力分析法,它是将结构物视为一个弹性振动体,将地震时地面运动产生的位移、速度、加速度作用在结构物上,然后用动力学的方法研究它的振动情况。
显然,时程分析法比振型分解反应谱法能更准确地反映地震是结构物的反应。
1 时程分析法应用范围GB 50011-2001建筑抗震设计规范规定:/特别不规则的建筑、甲类建筑和以下所列高度范围的高层建筑,应采用时程分析法进行多遇地震下的补充计算0。
采用时程分析法的房屋高度范围如下:1)8度,Ñ类,Ò类场地和7度:高度大于100m;2)8度,Ó类,Ô类场地:高度大于80m;3)9度:高度大于60m 。
特别不规则的建筑指的是:扭转不规则、凹凸不规则、楼板局部不连续、侧向刚度不规则、竖向抗侧力构件不连续、楼层承载力突变等。
如果采用新的结构形式或新的建筑材料,也应采用时程分析法进行多遇地震下的补充计算。
2 弹性动力时程分析法应用方法和计算步骤1)对结构进行常规的抗震验算(例如用振型分解反应谱方法),求得结构的内力和位移。
2)选用合适的数字化地震波(即地震地面运动加速度)。

基于MATLAB的地震数据的分析地震数据的分析是地震科学研究中的重要环节之一,可以帮助地震学家了解地震的特征、预测地震的趋势以及评估地震的影响程度。
MATLAB作为一种功能强大的数据处理和分析工具,在地震数据分析中也扮演着重要的角色。
本文将介绍基于MATLAB的地震数据分析方法和应用。
首先,地震数据通常是通过地震仪器采集到的地震波形数据,以地震波形数据为基础进行地震分析是地震学研究中的常见方法。
MATLAB提供了丰富的信号处理函数和工具箱,可以用于地震波形数据的预处理和分析。
通过MATLAB可以对地震波形数据进行滤波、降噪、去趋势、去仪器响应等操作,减少噪声对地震数据分析的影响。
其次,地震数据的谱分析也是地震学研究中的一项重要内容。
谱分析可以帮助地震学家了解地震数据在不同频率上的能量分布情况,揭示地震波的频谱特征。
MATLAB提供了多种谱分析函数和工具箱,如快速傅里叶变换(FFT)、功率谱密度估计、波谱比等,可以用于地震数据的频谱分析。
地震学家可以通过MATLAB计算地震波的功率谱密度,绘制地震波的频谱图,进一步了解地震数据的频率特征。
此外,地震数据的时频分析也是地震学研究中的重要内容之一、时频分析可以揭示地震波的时变特征,对地震波形的瞬态信号进行分析。
MATLAB提供了时频分析函数和工具箱,如小波变换、短时傅里叶变换等,可以用于地震数据的时频分析。
地震学家可以通过MATLAB计算地震波形的时频谱,提取地震波形的瞬态特征,进一步分析地震的发展过程。
最后,MATLAB还可以用于地震数据的可视化分析。
通过MATLAB的绘图函数,可以将地震数据以图形的形式展示出来,直观地反映地震数据的变化趋势和特征。
地震学家可以通过MATLAB绘制地震波形图、频谱图、时频图等,辅助地震数据的分析和研究。
在应用方面,基于MATLAB的地震数据分析方法已经广泛应用于地震学研究和地震监测预警等领域。
例如,在地震预测方面,研究人员可以通过分析历史地震数据,利用MATLAB对地震数据进行模式识别和预测建模,从而提高地震预测的准确性和可靠性。

基于matlab的地震活动性分析Matlab在地震活动性图像分析中的应用1),李红光2)1)河北省地震局2)中国地震应急搜救中心摘要:地震活动性分析是地震预测、地震工程的一个重要依据,地震活动性分析又多是通过图像来表现。
Matlab是一种简单易学、强大的计算功能和编程可视化的计算机语言。
本文用Matlab语言编程,实现了地震统计区内地震的快速选取,并根据这些选中的地震进行地震活动性分析。
关键词:Matlab语言;地震活动性引言地震活动性研究就是通过分析一定震级区间内的地震时间、空间的分布特征,探讨其物理含义,进而对地震发生的规律进行科学总结。
通过地震活动性研究,可对地壳介质非均匀性和运动形态有宏观的了解和总体把握,因此可服务于地震预测和地球动力过程等研究[1]。
在地震安全性评价中,通过地震活动性分析,为工程场地一定时间内的地震活动性趋势和地震环境做出评价,为合理划分潜源区和确定其地震活动性参数提供依据[2]。
地震活动图像的分析方法很多,有简单的图像描述法,如地震震中分布、蠕变曲线、M-T图等;也有采用统计参数表征地震活动时空图像特征的方法,如b值、地震活动度S、地震能流密度、地震强度因子MF分布等。
Matlab具有强大的计算能力、计算结果可视化和编程效率高的优势,它是地震活动性分析的一个有力工具。
Matlab是1984年由美国MathWorks公司推出的荣誉产品。
早在20世纪80年代中期,Matlab就在我国出现,大规模流行时再90年代中期以后。
现在Matlab已被广泛应用在科学研究、工程计算等方面。
M atlab采用全新的数据类型和面向对象编程技术,采用了新控制流和函数结构,特别是包含很多常用的子函数,非计算机专业人员非常容易用Matlab来实现很复杂的计算程序。
并且Maltab提供了图像处理功能,可以很方便的生成图形。
在地震活动性数字图像分析中,用Matlab可以很简单、方便的实现研究人员的思想。

基于Matlab数值方法的结构地震反应分析
胡涛
【期刊名称】《工程建设与设计》
【年(卷),期】2014(000)007
【摘要】通过Matlab语言编写了3个时程分析程序,分别采用Duhamel积分法、Newmark-beta法及Rong-kuta法.在求解多自由度结构体系时,采用振型分解法
将多自由度结构体系问题转化为多个广义单自由度结构体系问题,然后对所得计算
结果按一定准则进行叠加,求出结构地震反应.首先,对莱3层钢筋混凝土框架结构进行时程分析,计算结果与已有文献吻合较好,证明了所编程序的正确性;其次,通过对计算时间的分析对比,表明Rong-kuta法效率最高.论文可为相关工程及设计人员在
选择计算方法时提供参考.
【总页数】4页(P65-67,70)
【作者】胡涛
【作者单位】香港华艺设计顾问(深圳)有限公司,广东深圳518031
【正文语种】中文
【中图分类】TU352.11
【相关文献】
1.基于 CFD/CSD 耦合的结构几何非线性静气动弹性数值方法研究 [J], 聂雪媛;黄程德;杨国伟
2.基于MATLAB数值方法在机械工程领域的应用分析 [J], 胡享平;黄亚宇
3.基于Matlab的开关变换器混沌研究数值方法 [J], 王诗兵;周宇飞;陈军宁
4.线性方程组的几种数值方法的MATLAB程序 [J], 吴专保
5.基于Matlab的数值分析算法演示系统开发——非线性方程的数值方法 [J], 柯双
因版权原因,仅展示原文概要,查看原文内容请购买。

Matlab在地震模拟和结构动力学中的应用地震是自然界中一种具有巨大破坏力的现象,对于建筑结构的性能和安全性具有重要影响。
为了确保建筑物的安全,我们需要对地震作用下的结构响应进行准确可靠的研究和分析。
在这方面,Matlab作为一种强大的科学计算软件,广泛应用于地震模拟和结构动力学领域。
一、地震模拟地震模拟是一种利用计算模型来模拟地震过程的方法。
Matlab提供了强大的数值计算和图形化能力,使得地震模拟成为可能。
首先,Matlab提供了丰富的数值计算函数和工具箱,可以进行地震波的生成和处理。
通过使用这些函数,我们可以从已有地震记录中提取出合适的地震波形,或者生成符合特定要求的地震波。
得到地震波数据后,可以通过Matlab的图形化能力,将地震波形以图表的形式展示出来,更加直观地理解地震波的特征和动态。
其次,Matlab还提供了各种数值方法和算法,用于求解地震动力学方程。
通过建立适当的数学模型,结合地震波数据,可以利用Matlab进行地震模拟。
这些数值方法和算法包括有限元法、有限差分法、时程分析等,可以根据实际问题的需要,选择合适的方法进行模拟和分析。
最后,Matlab还能进行地震动力学结果的后处理和分析。
通过将模拟结果导入到Matlab中,我们可以对结构的位移响应、加速度响应和应力响应等进行详细统计和分析。
同时,我们还可以对不同模型进行对比研究,评估结构的破坏程度和性能安全性。
二、结构动力学分析结构动力学分析是研究建筑结构在地震作用下的响应和行为的一门学科。
Matlab在结构动力学分析中有着广泛的应用。
首先,Matlab提供了方便的结构建模和预处理工具。
我们可以通过Matlab编写脚本来描述结构的几何形状、材料特性和支承条件等。
结构的参数化描述和自动生成可以极大地简化建模过程,提高工作效率。
其次,Matlab提供了各种求解结构动力学方程的数值方法和算法。
结构动力学方程包括线性和非线性动力学方程,可以通过Matlab进行求解。


基于MATLAB工具箱的地震预测模型
魏红梅;黄世源;贺曼秋
【期刊名称】《防灾减灾学报》
【年(卷),期】2007(023)003
【摘要】地震分析和预测对未来地震趋势有一定预见性.本文建立了基于MATLAB 工具箱的地震预测模型,通过建模、局限性分析,认为多元线性和非线性回归方法不适合地震预测,基于BP神经网络的方法在地震预报中有一定应用价值.
【总页数】5页(P64-68)
【作者】魏红梅;黄世源;贺曼秋
【作者单位】重庆市地震局,重庆,401147;重庆市地震局,重庆,401147;重庆市地震局,重庆,401147
【正文语种】中文
【中图分类】P315.7
【相关文献】
1.基于Matlab神经网络工具箱的电力负荷组合预测模型 [J], 刘双;杨丽徙;王志刚;贾德峰;陈根永
2.基于MATLAB工具箱的PCA-RBF广西降雨量预测模型研究 [J], 李洁
3.基于MATLAB工具箱的神经网络在地震预报中的应用 [J], 温岩;乔兵;李忠伟;邵喜彬
4.基于MATLAB神经网络工具箱的岩爆预测模型 [J], 孟陆波;李天斌;王震宇
5.基于MATLAB工具箱的BP神经网络年径流量预测模型研究——以塔城地区乌拉斯台河为例 [J], 雷晓云;张丽霞;梁新平
因版权原因,仅展示原文概要,查看原文内容请购买。

MATLAB在地震工程与结构动力学中的应用研究一、引言地震工程与结构动力学是研究地震对建筑物和结构物的破坏作用以及结构响应的学科,是现代工程领域的重要分支之一。
为了更好地研究和理解结构的动态响应行为,工程师和研究人员采用了各种建模、分析和仿真方法。
而MATLAB作为一款强大的数学软件工具,在地震工程与结构动力学中扮演着重要的角色,本文将探讨MATLAB在该领域的应用研究。
二、地震响应分析地震响应分析是地震工程和结构动力学中的重要研究内容之一。
而MATLAB 提供了丰富的数值计算和分析函数库,可用于模拟和预测在地震发生时建筑物和结构物的响应。
1. 数值模拟地震响应分析中,数值模拟是研究地震力对结构的作用、结构响应和破坏机理的重要手段。
MATLAB中的有限元分析工具箱、有限差分工具箱以及大量的数值计算函数,为工程师和研究人员提供了强大的数值模拟能力。
通过使用MATLAB 编写数值模拟程序,可以模拟结构在不同地震力作用下的动态响应,进一步研究和分析结构的稳定性和安全性。
2. 响应谱分析响应谱分析是利用结构的动态特征值(频率、振型)与地震输入的地面运动响应之间的关系,来计算结构响应的一种方法。
MATLAB提供了各种处理时间序列和求解特征值问题的函数,如FFT、FFT2、eig等,可以有效地进行响应谱的计算和分析。
工程师和研究人员可以利用MATLAB进行响应谱分析,研究结构的稳定性和振动特性,为结构的设计和优化提供科学依据。
三、地震波分析地震波是地震中传播的弹性波,对结构的破坏起着至关重要的作用。
通过对地震波的分析与处理,可以更好地评估结构的地震响应和耐震性能。
1. 地震波模拟地震波模拟是通过模拟地震波传播和地震波在结构上的动力响应,为地震工程提供重要的数据支持。
在MATLAB中,可以使用时间域分析方法或频域分析方法来模拟地震波的传播和响应。
MATLAB提供了用于处理地震波的滤波器设计、频谱分析和时频分析等工具箱和函数,方便工程师和研究人员进行地震波的模拟和分析,为地震工程的设计和评估提供准确的输入参数。
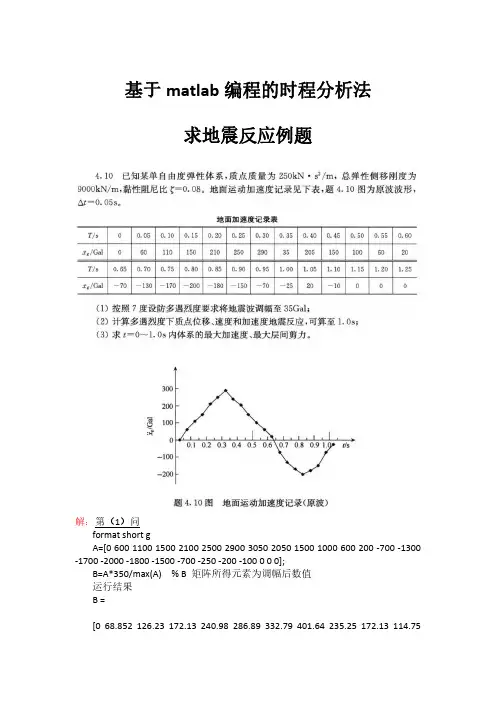
基于matlab编程的时程分析法求地震反应例题解:第(1)问format short gA=[0600110015002100250029003050205015001000600200-700-1300 -1700-2000-1800-1500-700-250-200-100000];B=A*350/max(A)%B矩阵所得元素为调幅后数值运行结果B=[068.852126.23172.13240.98286.89332.79401.64235.25172.13114.7568.85222.951-80.328-149.18-195.08-229.51-206.56-172.13-80.328 -28.689-22.951-11.475000]第(2)问第(3)问最大层间剪力为2817.69KN,最大加速度-556.95mm/s²解:第(1)问【同4.10(1)】format short gA=[0600110015002100250029003050205015001000600200-700-1300 -1700-2000-1800-1500-700-250200-100000];B=xg*2200/max(A)运行结果B=[0432.79793.4410821514.81803.32091.82524.61478.7 1082721.31432.79144.26-504.92-937.7-1226.2-1442.6-1298.4 -1082-504.92-180.33-144.26-72.131000]第(2)问第(3)问最大层间剪力为15059.904KN,最大加速度2019.447mm/s²附代码4.10弹性分析format short gag=[068.852126.23172.13240.98286.89332.79401.64235.25172.13114.75 68.85222.951-80.328-149.18-195.08-229.51-206.56-172.13-80.328-28.689];m=250;k=9000;zeta=0.08;t=0.05;deltaag=zeros(1,21);deltaP=zeros(1,21);deltax=zeros(1,21);deltaa=zeros(1,21);deltav =zeros(1,21);x=zeros(1,21);v=zeros(1,21);a=zeros(1,21);deltaag(21)=20-(-25);%Δag矩阵最后一个数是用1.05s的加速度减去1.00秒时候的加速度c=2*sqrt(k*m)*zeta;%求得阻尼系数c=2*0.08*√9000*250=240K=k+6*m/(t^2)+3*c/t;%求得刚度矩阵K(在弹性计算中刚度恒定,因此设为一个固定的数,以方便计算for n=1:20deltaag(n)=ag(n+1)-ag(n);end%计算变地面加速度矩阵for i=1:21deltaP(i)=-m*[deltaag(i)-6*v(i)/t-3*a(i)]+c*[3*v(i)+a(i)*t/2];deltax(i)=deltaP(i)/K;deltaa(i)=6*deltax(i)/(t^2)-6*v(i)/t-3*a(i);deltav(i)=a(i)*t+deltaa(i)*t/2;if i<21a(i+1)=a(i)+deltaa(i);v(i+1)=v(i)+deltav(i);x(i+1)=x(i)+deltax(i);endend%%绘图tmatrix=0:0.05:1;plot(tmatrix,a,'-bo','LineWidth',2,'color','k','MarkerSize',5,'MarkerEdgeColor','black',' MarkerFaceColor','red');title('加速度反应');xlabel('时间/s');ylabel('加速度/(mm/s^2)');text(0.2,200,'弹性结果');plot(tmatrix,x,'-bo','LineWidth',2,'color','k','MarkerSize',5,'MarkerEdgeColor','black',' MarkerFaceColor','red');title('位移反应');xlabel('时间/s');ylabel('位移/(mm)');text(0.2,5,'弹性结果');4.11弹塑性分析format short gag1=[0432.79793.4410821514.81803.32091.82524.61478.71082721.31432.79 144.26-504.92-937.7-1226.2-1442.6-1298.4-1082-504.92 -180.33];k1=zeros(1,21);m=250;k1(1)=9000;zeta=0.08;t=0.05;K1=zeros(1,21);deltaag1=zeros(1,21);deltaP1=zeros(1,21);deltax1=zeros(1,21);deltaa1=zeros(1,21);deltav1=zeros(1,21);x1=zeros(1,21);v1=zeros(1,21);a1=zeros(1,21);deltaag1(21)=-144.26-(-180.33);%Δag矩阵最后一个数是用1.05s的加速度减去1.00s时候的加速度c=2*sqrt(k1(1)*m)*zeta;%求得阻尼系数c=2*0.08*√9000*250=240for p=1:20deltaag1(p)=ag1(p+1)-ag1(p);end%计算变地面加速度矩阵for j=1:21deltaP1(j)=-m*(deltaag1(j)-6*v1(j)/t-3*a1(j))+c*(3*v1(j)+a1(j)*t/2);if abs(x1(j))<=2k1(j)=9000;elsek1(j)=0;endK1(j)=k1(j)+6*m/(t^2)+3*c/t;deltax1(j)=deltaP1(j)/K1(j);deltaa1(j)=6*deltax1(j)/(t^2)-6*v1(j)/t-3*a1(j);deltav1(j)=a1(j)*t+deltaa1(j)*t/2;if j<21a1(j+1)=a1(j)+deltaa1(j);v1(j+1)=v1(j)+deltav1(j);x1(j+1)=x1(j)+deltax1(j);endEnd%%绘图plot(tmatrix,a1,'-bo','LineWidth',2,'color','k','MarkerSize',5,'MarkerEdgeColor','black', 'MarkerFaceColor','red');title('加速度反应');xlabel('时间/s');ylabel('加速度/(mm/s^2)');text(0.2,200,'弹塑性分析结果');plot(tmatrix,x1,'-bo','LineWidth',2,'color','k','MarkerSize',5,'MarkerEdgeColor','black', 'MarkerFaceColor','red');title('位移反应');xlabel('时间/s');ylabel('位移/(mm)');text(0.7,-50,'弹塑性分析结果');。
地震数据的MATLAB分析地震带给人类的损失是巨大的,汶川大地震依旧在我们的记忆深处清晰存在。
大地震的每次不约而至,都对国家和人民造成了巨大的损失。
地震预测是世界性难题,全世界的地震科学家不断在探索,尽最大努力减少其破坏性。
地震台站提供的地震观测资料的可靠性和准确性,是地震学家进行地震预测的基础[1]。
但是地震波信号变化的不平稳性和复杂性给地震的分析和预测带来了很大困难,并且在地震波的原始记录中往往还掺杂着来自外界的各种干扰,如仪器、环境噪声、爆破、采矿、火车的震动等,这些都给地震波的分析带来了严重影响,甚至导致分析结果的错误。
为保证地震分析的准确性,可先对原始记录进行频谱分析,选择性能优良的滤波器对其进行优化处理,把干扰信号尽量滤除,然后再对处理后的地震波数据进行分析处理,则会得到良好的效果。
地震记录的数字化使得利用计算机对地震信号进行分析处理得以实现。
在数字信号的分析处理中,Fourier变换和数字滤波器的应用极为普遍,语音、雷达、地震、图像、机械振动、地质勘探等众多领域都广泛采用数字滤波器。
MATLAB是一种集数值分析、矩阵运算、信号处理和图像显示于一体、功能极其强大的高性能软件,其工具箱中包含了各种经典和现代数字信号处理技术,很容易实现Fourier变换和各种数字滤波器的设计,在地震数据的分析处理中起着重要作用。
在地震波的原始记录数据中往往夹杂不同频率范围的噪声干扰信号,为了显示出地震波数据中的优势频率和干扰频率,保证地震分析的准确性,应首先采用频谱分析,再针对干扰波的频率范围,设计合适的滤波器参数。
在对有限长信号序列进行频谱分析时,离散Fourier 变换(DFT )应用非常广泛,它可以很好地反映序列的频谱特性。
设()x n 是一个长度为N 的有限长序列,则()x n 的N 点离散傅里叶变换为()120()(), 0,1,...,1N j N kn n X k x n ek N π--===-∑在MATLAB 中可调用函数()f t X =fft x ,N 来进行快速傅里叶变换。
2008年第6期总第120期福 建 建 筑F u j i a nA r c h i t e c t u r e &C o n s t r u c t i o nN o 6·2008V o l ·120基于M a t l a b 求解建筑结构地震响应的时程分析法孟宪萍(开封市供水总公司 475004)摘 要:本文基于m a t l a b 阐述了我国《建筑抗震设计规范》(G B 50011-2001)规定的求解建筑结构地震响应的时程分析法,应用m a t l a b 语言编制了时程分析法求解建筑结构地震响应的计算程序,并以一三层钢筋混凝土结构为工程算例,应用基于m a t l a b 的时程分析法进行结构的地震响应计算。
结果表明,基于m a t l a b 的时程分析计算效率较高。
关键词:M A T L A B 地震响应 时程分析法中图分类号:T U 312+.1 文献标识码:A 文章编号:1004-6135(2008)06-0038-03T h e t i m e -h i s t o r y m e t h o db a s e d o nm a t l a b o f r e s o l v i n g t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e sM e n g X i a n p i n g(K a i f e n g Wa t e r S u p p l y C o m p a n y 475004)A b s t r a c t :I nt h i s p a p e r ,t h e t i m e -h i s t o r y m e t h o dw h i c h i s m e n t i o n e d i n t h e c o d e f o r s e i s m i c d e s i g n o f b u i l d i n g s (GB 50011-2001)t or e s o l v e t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e s i s d i s c u s s e d b a s e d o nm a t l a b .T h e c a l c u l a t i o np r o g r a m s o f t h et i m e -h i s t o r y m e t h o da r e w o r k e do u t u s i n g t h e l a n g u a g e m a t l a b .T a k i n g a t h r e es t o r y r e i n f o r c e d c o n c r e t e f r a m e s t r u c t u r e a s a ne x a m p l e ,t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e i s r e s o l v e d b y u s i n g t h e c a l c u l a t i o n p r o g r a m s o f t h e t i m e -h i s t o r y m e t h o d .T h e r e s u l t i n d i c a t e s t h a t T h e t i m e -h i s t o r y m e t h o d b a s e do n m a t l a bo f r e s o l v i n gt h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e s i s e f f i c i e n t .K e y w o r d s :M A T L A B e a r t h q u a k e r e s p o n s e t i m e -h i s t o r y a n a l y s i s m e t h od 作者简介:孟宪萍,女,1966年出生,主要从事建筑结构设计及建筑咨询。
使用MATLAB进行地震响应分析与结构优化地震响应分析与结构优化是地震工程中的重要研究内容,通过使用MATLAB这一强大的工具,可以对结构在地震作用下的响应行为进行深入分析,并进一步进行结构的优化设计。
本文将探讨如何使用MATLAB进行地震响应分析与结构优化的步骤和方法,并通过实例进行说明。
一、地震响应分析地震响应分析是指在地震波作用下,结构的应力、应变和位移等响应情况的分析。
地震波是地震时由震源产生的地震能量在地球内部传播所产生的波动。
在进行地震响应分析时,需要先选取合适的地震波记录作为输入,然后进行模拟计算,并获取结构的响应结果。
在MATLAB中进行地震响应分析,可以利用其中的工具箱和函数。
首先,需要将地震波记录进行读取和处理,可以使用MATLAB中的文件读取函数和信号处理函数。
读取地震波记录后,可以进行滤波和降尺度处理,以使其适用于结构响应分析。
接着,需要进行指定结构的建模和定义,可以使用MATLAB中的结构类对象进行建模,并设置结构的材料和截面属性。
之后,可以利用地震波输入对结构进行地震动力分析,得到结构的响应结果。
二、结构优化设计结构优化设计是指通过调整结构的材料和几何参数,使其满足特定的性能要求,以达到最佳的设计效果。
在地震工程中,结构的优化设计常常与地震响应特性有关,可以通过优化设计来提高结构的地震抗震性能。
在MATLAB中进行结构优化设计,可以利用其中的优化工具箱和函数。
首先,需要确定设计目标和约束条件,例如最小化结构的质量或最大化结构的刚度,并设置约束条件,如保持结构的安全性能。
接着,可以利用MATLAB中的优化算法进行设计优化,例如遗传算法、模拟退火算法等。
在迭代优化过程中,可以通过定义适应度函数来评估设计的优劣,使优化算法能够搜索到最优解。
三、综合实例为了更好地说明使用MATLAB进行地震响应分析与结构优化的方法和步骤,下面将以一座钢筋混凝土框架结构为例进行说明。
首先,需要在MATLAB中导入地震波记录,并进行预处理,包括去除基线漂移、滤波以及降尺度处理。
基于MATLAB的地震台站数据分析张鹏【摘要】运用MATLAB程序对地震台站记录数据进行处理,得到地震加速度时程曲线和地震加速度反应谱,进而可以得到地震持续时间、主周期、峰值加速度等,通过分析这些数据,对地震作用下的结构破坏进行了分析评价,并据此提出了相关的抗震设计建议.【期刊名称】《山西建筑》【年(卷),期】2013(039)025【总页数】3页(P31-33)【关键词】MATLAB;地震数据分析;地震破坏【作者】张鹏【作者单位】扬州大学建筑科学与工程学院,江苏扬州 225127【正文语种】中文【中图分类】TU352.1随着计算机技术的不断发展,越来越多的计算机技术应用于工程领域。
借助其强大的数据处理能力和良好的人机交互,可以方便进行多种工程应用。
MATLAB就是其中的一种,MATLAB语言在建筑抗震工程中的应用也很广泛。
在工程抗震领域,地震动的基本参数是地震波的分析、抗震措施的研究以及建筑物的抗震设计等的重要基础。
而MATLAB能够有效地进行台站数据的处理,从而得到地震动的基础参数,从而将其应用于科学研究和工程实践。
1 台站数据处理根据台站记录的加速度数据,通过MATLAB的处理,可以得到地震加速度时程曲线和地震加速度反应谱。
台站记录的数据是一定地点、一定场地类型的不同方向加速度每隔一段时间的数值。
通过MATLAB处理可以得到一定方向上加速度随时间变化的规律,X轴对应于时间的变化,Y轴对应于加速度的大小和方向,这样就可以得到该方向的地震加速度时程曲线。
图1~图3分别表示该点东西方向、南北方向和上下方向的加速度时程曲线。
图1 东西方向加速度时程曲线图2 南北方向加速度时程曲线若给定地震时地面运动的加速度记录和体系的阻尼比,则可计算出质点的最大加速度反应Sa与体系自振周期T的一条关系曲线,并且对于不同的阻尼比值就可以得到不同的 Sa—T曲线[1],即为地震加速度反应谱。
图4~图6分别表示东西方向、南北方向和上下方向在不同阻尼比时的加速度反应谱。
2008年第6期总第120期福 建 建 筑F u j i a nA r c h i t e c t u r e &C o n s t r u c t i o nN o 6·2008V o l ·120基于M a t l a b 求解建筑结构地震响应的时程分析法孟宪萍(开封市供水总公司 475004)摘 要:本文基于m a t l a b 阐述了我国《建筑抗震设计规范》(G B 50011-2001)规定的求解建筑结构地震响应的时程分析法,应用m a t l a b 语言编制了时程分析法求解建筑结构地震响应的计算程序,并以一三层钢筋混凝土结构为工程算例,应用基于m a t l a b 的时程分析法进行结构的地震响应计算。
结果表明,基于m a t l a b 的时程分析计算效率较高。
关键词:M A T L A B 地震响应 时程分析法中图分类号:T U 312+.1 文献标识码:A 文章编号:1004-6135(2008)06-0038-03T h e t i m e -h i s t o r y m e t h o db a s e d o nm a t l a b o f r e s o l v i n g t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e sM e n g X i a n p i n g(K a i f e n g Wa t e r S u p p l y C o m p a n y 475004)A b s t r a c t :I nt h i s p a p e r ,t h e t i m e -h i s t o r y m e t h o dw h i c h i s m e n t i o n e d i n t h e c o d e f o r s e i s m i c d e s i g n o f b u i l d i n g s (GB 50011-2001)t or e s o l v e t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e s i s d i s c u s s e d b a s e d o nm a t l a b .T h e c a l c u l a t i o np r o g r a m s o f t h et i m e -h i s t o r y m e t h o da r e w o r k e do u t u s i n g t h e l a n g u a g e m a t l a b .T a k i n g a t h r e es t o r y r e i n f o r c e d c o n c r e t e f r a m e s t r u c t u r e a s a ne x a m p l e ,t h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e i s r e s o l v e d b y u s i n g t h e c a l c u l a t i o n p r o g r a m s o f t h e t i m e -h i s t o r y m e t h o d .T h e r e s u l t i n d i c a t e s t h a t T h e t i m e -h i s t o r y m e t h o d b a s e do n m a t l a bo f r e s o l v i n gt h e e a r t h q u a k e r e s p o n s e o f t h e s t r u c t u r e s i s e f f i c i e n t .K e y w o r d s :M A T L A B e a r t h q u a k e r e s p o n s e t i m e -h i s t o r y a n a l y s i s m e t h od 作者简介:孟宪萍,女,1966年出生,主要从事建筑结构设计及建筑咨询。
收稿日期:2008-03-251 引言我国《建筑抗震设计规范》(G B 50011-2001)第5章对时程分析法的使用情况作出了规定。
时程分析法又称为直接动力法或逐步积分法。
采用时程分析法可以计算出结构在地震过程中每一瞬时的反应,可用来求解建筑结构的几何及物理线性与非线性动力响应。
与经典的反应谱方法相比,有很多的优点,但是它也存在许多不足,主要有计算模型的合理选择困难;地震波输入的不确定性;在计算过程中要进行刚度矩阵等的不断修正,每一时刻的结果都受到此刻之前的结果的影响等,导致计算分析工作量较大。
虽然目前在结构弹塑性时程分析时,结构动力增量微分方程已有较为成熟的算法以及相关的大型分析软件可以利用,但是其计算分析工作量仍然十分繁重,不但耗费机时,结果处理复杂,而且同计算者本身的经验和对结构在地震作用下的损伤形态和破坏顺序的假定相关,这些都带有一定的主观性。
但是随着计算机的普及,时程分析法正逐步被抗震规范接受。
本文在详细阐述了时程分析法基本原理基础上,结合m a t -l a b 语言编制了时程分析法求解建筑结构地震响应的计算程序,并以一三层钢筋混凝土结构为例进行验证。
2 时程分析法基本原理2.1 结构在地震作用下的动力微分方程多自由度体系建筑结构在地震作用下的运动运动微分方程为[M ]{x ··}+[C ]{x ·}+[K ]{x }=-[M ]{x ··g }(1)其中,[M ],[C ],[K ]分别为建筑结构质量、阻尼和刚度矩阵,{x ··g }为地面运动加速度。
2.2 建筑结构的计算模型建筑结构计算模型一般应根据结构形式及构造特点、分析精度以及计算机容量等情况确定。
用时程分析法求解时,由于计算工作量大,在尽量真实再现结构动力反应特点的前提下,尽可能对结构予以简化。
对于传统的多层房屋结构,最简单且应用最广的模型是层间剪切模型,如图1所示,在这种模型中,房屋的质量集中在各楼层,在振动过程中各楼层式中保持为水平,结构的变形表现为层间错动,各层的层间位移互不影响。
对于以剪切变形为主的结构,一般都可以采用这种模型,如多层砖房以及横梁线刚度远比柱线刚度大的强梁弱柱型框架结构.但是对于强柱弱梁型的框架结构,用这种模型计算时误差较大,但有时为了简化计算,对于各跨相等的底层框架和建筑物宽度远大于高度的多层框架结构亦可以近似地应用。
图1 层间剪切型模型计算简图 图2 杆系模型计算简图为了精确计算可以采用如图2所示的杆系模型。
该模型假定楼板在自身平面内为绝对刚性,以构件作为基本杆件单元而将梁柱简化为以中性轴表示的无质量杆,将质量集中于各结点,利用构件连接处的变形协调条件建立各构件变形关系,利用构件的恢复力特性集成整个结构的弹塑性刚度[1],然后采用数值积分方法对结构进行地震反应分析。
这种模型一般适用于强柱弱梁的框架结构,可以用它来求出地震过程中各杆逐渐开裂并进入塑性阶段的过程以及整个结构的影响,但是计算较繁。
我国《建筑抗震设计规范》(G B 50011-2001)规定,规则结构可以使用平面杆系模型计算罕遇烈度地震作用下的结构弹塑性变形,对于不规则结构应采用空间杆系结构模型。
2.3 输入地震波的选择2.3.1 选波意义,结构的地震反应是输入地震和结构自身的动力特性共同作用的结果。
在采用时程分析法求解结构地震反应时,需要首先确定输入结构的地震地面运动加速度。
而观测结果表明,地震波具有强烈的随机性,结构的弹塑性时程分析结果也表明,结构的地震反应随输入地震波的不同会有很大不同,误差有时会高达几倍至几十倍,所以要保证时程分析结果的可靠性,必须正确合理地选择地震波。
2.3.2 选择方法及选用数量,目前关于地震波的选择有三种方法:(1)拟建场地的实际地震记录。
(2)过去典型的强震记录。
(3)人工合成场地地震波。
过去典型强震记录常用的主要有E l c e n t r o 波、T a f t 波、天津波等。
在选择时应充分考虑地震动三要素。
即对于振幅,首先要考虑该被选择的地震与所考虑设防的地震有较好的相似性,有足够大的幅值及其峰值加速度应与设计烈度相当;其次,记录地点的地基土质条件与拟建场地土质条件宜相近。
对于频谱选择,应该使所选地震波的卓越周期尽可能与拟建场地的地震周期一致,并且所选地震波的震中距尽可能与拟建场地震中距一致。
对于强震持时,工程实践中确定持时的原则是应使地震记录最强烈部分包括在持时之内、若对结构仅进行弹性最大地震反应分析,持续时间可取短些;若对结构进行弹塑性最大地震反应分析,持时应取长些、一般可以取持时为结构基本周期的5~10倍。
人工合成场地地震波是根据随机振动理论产生的符合所需统计特征的地震波。
对于人工地震波的选择主要有三点要求,(1)人工地震波加速度峰值与设计烈度相当.(2)人工地震波的反应谱尽可能与规范规定的相应场地上的反应谱特征相近.(3)人工地震波的总持续时间和强震的平稳段持续时间应与按建筑场地的地震地质背景资料确定的相符。
研究表明,在充分考虑地震动三要素情况下,采用3~5条地震波可基本上保证时程分析结果的合理性。
我国《建筑抗震设计规范》(G B 50011-2001)规定至少选择两条实际地震波和一条人工波[2]。
2.4 恢复力模型国内外已提出许多结构及构件的恢复力模型,其中最常用的恢复力模型主要有双线性模型(兰伯格-奥斯古德模型)和克拉夫、武腾青等提出的三线型刚度退化模型。
根据构件的不同材料及不同力学特性,可以选用不同的更接近构件实际受力特性的计算模型。
如对钢结构时程分析时可以采用最简单的双线型恢复力模型(见图3);对以受弯为主的钢筋混凝土构件则可以采用三线型刚度退化恢复力模型(见图4)。
图3 双线型恢复力模型 图4 退化三线型恢复力模型2.5 地震反应的数值模拟在地震反应运动方程⑴中,地震地面运动加速度是一系列复杂的随机函数,同时在弹塑性反应中刚度图5 逐步积分法地震动输入矩阵与阻尼矩阵亦随时间变化,因此不可能求出解析解,而只能采取数值分析方法求解。
所以常将式⑴转变成下面的增量方程式。
[M ]{■x ··}+[C ]{■x ·}+[K ]{■x }=-[M ]{■x ··g }⑵图6 弹性时程分析法程序设计框图对于上式⑵需用逐步积分法求解。