基于matlab的非线性薛定谔方程的数值算法研究
- 格式:pdf
- 大小:534.79 KB
- 文档页数:7


MATLAB中的非线性优化算法详解在计算机科学和工程领域,非线性优化是一个非常重要的问题。
它涉及到在给定一些约束条件下,寻找使得目标函数取得最优值的变量取值。
MATLAB作为一种强大的数值计算工具,提供了多种非线性优化算法来解决这个问题。
本文将详细介绍一些常用的非线性优化算法,并探讨它们的特点和适用场景。
1. 数学背景在介绍非线性优化算法之前,我们先来了解一下非线性优化的基本数学背景。
一个非线性优化问题可以表示为以下形式:minimize f(x)subject to g(x) ≤ 0h(x) = 0其中,f(x)是目标函数,g(x)是不等式约束条件,h(x)是等式约束条件。
x是优化变量。
目标是找到x使得f(x)取得最小值,并且满足约束条件。
2. 黄金分割法黄金分割法是一种经典的非线性优化算法。
它基于一个简单的原则:将搜索区间按照黄金分割比例分为两段,并选择一个更优的区间进行下一次迭代。
该算法的思想简单明了,但是它的收敛速度比较慢,特别是对于高维问题。
因此,该算法在实际应用中较少使用。
3. 拟牛顿法拟牛顿法是一类比较常用的非线性优化算法。
它通过近似目标函数的梯度信息来进行迭代优化。
拟牛顿法的核心思想是构造一个Hessian矩阵的近似矩阵,来更新搜索方向和步长。
其中,DFP算法和BFGS算法是拟牛顿法的两种典型实现。
DFP算法是由Davidon、Fletcher和Powell于1959年提出的,它通过不断迭代来逼近最优解。
该算法的优点是收敛性比较好,但是它需要存储中间结果,占用了较多的内存。
BFGS算法是由Broyden、Fletcher、Goldfarb和Shanno于1970年提出的。
它是一种变种的拟牛顿法,通过逼近Hessian矩阵的逆矩阵来求解最优解。
BFGS算法在存储方面比DFP算法更加高效,但是它的计算复杂度相对较高。
4. 信赖域法信赖域法是一种迭代优化算法,用于解决非线性优化问题。
它将非线性优化问题转化为一个二次规划问题,并通过求解这个二次规划问题来逼近最优解。

matlab数值薛定谔方程薛定谔方程是描述量子力学中粒子的行为的基本方程。
在数值计算中,我们可以使用数值方法来求解薛定谔方程。
下面我将从多个角度来回答关于在MATLAB中数值求解薛定谔方程的问题。
1. 数值方法的选择:在MATLAB中,我们可以采用多种数值方法来求解薛定谔方程,其中常用的方法包括有限差分法、有限元法和谱方法等。
选择合适的数值方法取决于问题的特点和计算资源的可用性。
2. 离散化:在数值计算中,我们需要将薛定谔方程离散化为有限个点上的代数方程。
通常,我们会将空间离散化为网格,并在每个网格点上计算波函数的值。
时间离散化则是通过迭代的方式逐步求解时间演化。
3. 有限差分法:有限差分法是一种常见的数值方法,它将导数近似为有限差分。
在薛定谔方程中,我们可以将二阶导数近似为中心差分,然后使用差分方程来求解离散化的薛定谔方程。
4. 有限元法:有限元法是一种广泛应用于偏微分方程求解的数值方法。
在薛定谔方程中,我们可以使用有限元法将波函数表示为一组基函数的线性组合,并通过求解线性方程组来确定系数。
5. 谱方法:谱方法是一种基于函数展开的数值方法,它使用一组特定的基函数来表示波函数。
在薛定谔方程中,我们可以使用傅里叶级数或其他正交多项式作为基函数,并通过求解线性方程组来确定系数。
6. 边界条件:在数值求解薛定谔方程时,我们需要指定合适的边界条件。
常见的边界条件包括固定边界条件和周期性边界条件,具体取决于问题的物理背景。
7. 算法实现:在MATLAB中,我们可以使用内置的数值计算函数和工具箱来实现数值求解薛定谔方程。
例如,可以使用MATLAB的PDE Toolbox来求解偏微分方程,或者使用MATLAB的FFT函数来进行傅里叶变换。
总结起来,数值求解薛定谔方程是一个复杂而重要的问题,需要根据具体情况选择合适的数值方法并进行适当的离散化和边界条件处理。
MATLAB提供了丰富的数值计算工具和函数,可以帮助我们实现数值求解薛定谔方程的算法。

Matlab中的非线性优化和非线性方程求解技巧在科学和工程领域中,我们经常会遇到一些复杂的非线性问题,例如最优化问题和方程求解问题。
解决这些问题的方法主要分为线性和非线性等,其中非线性问题是相对复杂的。
作为一种强大的数值计算工具,Matlab提供了许多专门用于解决非线性优化和非线性方程求解的函数和方法。
本文将介绍一些常用的Matlab中的非线性优化和非线性方程求解技巧。
非线性优化是指在给定一些约束条件下,寻找目标函数的最优解的问题。
在实际应用中,往往需要根据实际情况给出一些约束条件,如等式约束和不等式约束。
Matlab中的fmincon函数可以用于求解具有约束条件的非线性优化问题。
其基本语法如下:[x,fval] = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)其中,fun是目标函数,x0是初始值,A、b是不等式约束矩阵和向量,Aeq、beq是等式约束矩阵和向量,lb、ub是变量的上下边界。
x表示最优解,而fval表示最优解对应的目标函数值。
另外,非线性方程求解是指寻找使得方程等式成立的变量值的问题。
Matlab中提供的fsolve函数可以用于求解非线性方程。
其基本语法如下:x = fsolve(fun,x0)其中,fun是方程函数,x0是初始值,x表示方程的解。
除了fmincon和fsolve函数之外,Matlab还提供了一些其他的非线性优化和非线性方程求解函数,例如lsqnonlin、fminunc等,这些函数分别适用于无约束非线性优化问题和带约束非线性方程求解问题。
除了直接调用这些函数外,Matlab还提供了一些可视化工具和辅助函数来帮助我们更好地理解和解决非线性问题。
例如,使用Matlab的优化工具箱可以实现对非线性优化问题的求解过程可视化,从而更直观地观察到优化算法的收敛过程。
此外,Matlab还提供了一些用于计算梯度、雅可比矩阵和海塞矩阵的函数,这些函数在求解非线性问题时非常有用。
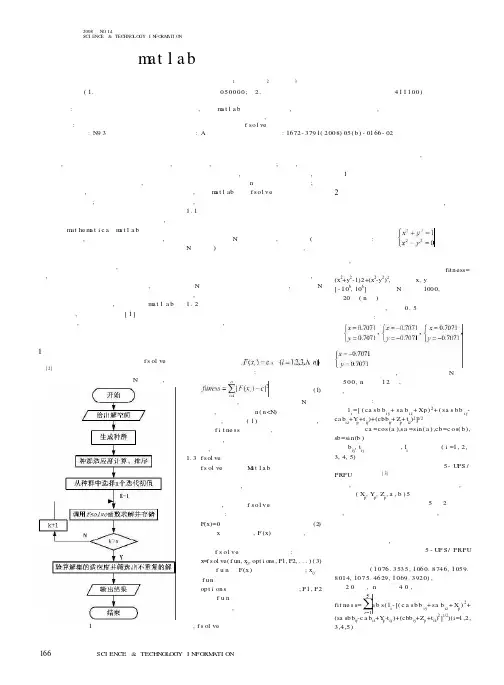


科学计算—理论、方法及其基于MATLAB 的实现与分析解非线性方程(组)(一)直接法二分法:设方程()0=x f 在区间[]b a ,上有唯一解,并且()()0<b f a f ,如方程()f x x x x x =-++=3223030.sin .(1)首先要确定适当的包含根的区间,这可以依据闭区间上连续函数的介值定理来确定,例如,()f 1110=-+<sin ,()f 222090=->sin .,所以方程 (1)至少有一个实根属于区间[]12,,图1表明区间[]12,中只含有一个根,显然方程 (1)的根不易直接求得。
在区间[-1,0]、[0,1]和[1,2]的情形,如下图1所示 例1 plotNL_fun01.mplotNL_fun01clearx=-1:0.05:2;f=x.^3-2.3*x.^2+x.*sin(x)+0.3; plot(x,f,'r',x,0*x,'k')title('The Image of f(x)=x^3-2.3*x^2+x*sin(x)+0.3') xlabel('\fontsize {12} \fontname {宋体} 图1') axis square二分法的求根过程:用*x 表示方程()0=x f 在区间[]b a ,上的根,对于给定的精度要求0>ε,取区间[]b a ,的中点21ba x +=,并按下式进行判断: ()()()()()⎪⎩⎪⎨⎧∈⇒<∈⇒<=⇒=],[0],[001*11*1*11b x x b f x f x a x a f x f x x x f (2) 以()()01<a f x f 为例,如果ε≤-2ab ,那么区间[]1,x a 内的任何一点都可以作为方程()0=x f 的近似根。
二分法适用于一个方程的场合,收敛速度是线性的,二分次数的估计:()b aN b a N-≤⇒≥--22εεln ln ln (3) 2、黄金分割法:在区间[]b a ,内取对称的两点:()()()⎩⎨⎧-+=--+=a b a x a b a x ββ211 (4) 使得()()()()()618.025125101102221≈+-=−−→−±-=⇒=-+⇒--=--=--=--->ββββββββa b a b ab a x a x a x a b a b按这种方法选取点1x 和2x ,每次去掉的区间长度至少是原区间长度的0.618倍,()()()()()()()()⎪⎪⎩⎪⎪⎨⎧∉∈⇒<⋃∉∈⇒<∉∈⇒<=⇒==⇒=],[],[0],[],[],[0],[],[0002*2*221*21*211*1*1*22*11x a x b x x b f x f b x x a x x x x x f x f b x x x a x a f x f x x x f x x x f (5) 适用于一个方程的场合,收敛速度是线性的,迭代次数的估计:()()215lnln ln 215--->⇔<⎪⎪⎭⎫ ⎝⎛--a b N a b Nεε (6) (二)迭代法首先将方程(组)写成等价的迭代形式:()()0f x x x ϕ=⇔= (7)由此确定了相应的迭代法:()[]10,n n x x x a b ϕ+=⎧⎪⎨∀∈⎪⎩ (8)迭代收敛的图像解释对于非线性方程(组)的迭代法来说,同样面临收敛性问题,为说明收敛性条件,先看下面的例子:例2:让我们来求如下方程的根()f x x x x x =-++=3223030.sin .下面,我们采用迭代法求方程 (1)位于区间]01[,-中的根,为此构造迭代算法如下:()()x x xx g x -+==3.2sin 3.0 (9)()()x g x x x x n n nn n +==+-10323.sin ., n =12,, (10)在区间]01[,-中任取一个迭代初值x 0,如取初值8.00-=x .执行下面的程序:EqutIteration.m:open EqutIteration.m EqutIterationN =29下面欲求1.5附近的根,为此分别取初值4.10=x ,9.10=x ,迭代的结果如下:open Ex_IteraConv01 Ex_IteraConv01N = 31收敛性定理:(收敛的充分性条件)设方程()f x =0在[]a b ,上存在唯一解,()x g x =是方程的等价形式,如果1、()g x 在[]a b ,上连续可微; 2、对任何x a b ∈[],,()g x a b ∈[],; 3、()'≤<g x L 1,则对任何x a b 0∈[],,由迭代算法()x g x n n +=1, (11)生成的序列{}x n 收敛于方程()f x =0在[]a b ,上的唯一解。

matlab数值薛定谔方程摘要:I.引言- 介绍薛定谔方程- 介绍matlab 数值求解方法II.薛定谔方程的数值求解方法- 有限差分法- 有限元法- 谱方法III.matlab 数值求解薛定谔方程的步骤- 准备薛定谔方程的数值模型- 选择数值求解方法- 编写matlab 代码- 运行代码,分析结果IV.结果与讨论- 结果展示- 结果分析- 结果验证V.结论- 总结matlab 数值求解薛定谔方程的方法- 展望未来的研究方向正文:I.引言薛定谔方程是量子力学中的一个基本方程,用于描述一个微观粒子在给定势能场中的运动状态。
然而,由于薛定谔方程本身是一个偏微分方程,它的求解在大多数情况下是非常困难的。
matlab 作为一种强大的科学计算软件,可以用于数值求解薛定谔方程。
本文将介绍薛定谔方程的数值求解方法,以及如何使用matlab 进行数值求解。
II.薛定谔方程的数值求解方法薛定谔方程的数值求解方法主要有以下几种:1.有限差分法:将薛定谔方程的解表示为离散的点,通过差分代替微分,将方程转化为一个线性代数方程组,从而求解薛定谔方程。
2.有限元法:将薛定谔方程的解表示为有限个基函数的线性组合,通过插值或逼近基函数,将方程转化为一个线性代数方程组,从而求解薛定谔方程。
3.谱方法:通过在一组基函数上将薛定谔方程进行投影,将方程转化为一个线性代数方程组,从而求解薛定谔方程。
III.matlab 数值求解薛定谔方程的步骤使用matlab 进行数值求解薛定谔方程的步骤如下:1.准备薛定谔方程的数值模型:首先需要根据实际问题建立薛定谔方程的数值模型,包括势能场、边界条件等。
2.选择数值求解方法:根据问题的特点和求解需求,选择合适的数值求解方法,如有限差分法、有限元法或谱方法。
3.编写matlab 代码:根据所选方法,编写matlab 代码,实现薛定谔方程的数值求解。
4.运行代码,分析结果:运行编写的matlab 代码,得到薛定谔方程的数值解。


MATLAB数值薛定谔方程介绍薛定谔方程是量子力学中描述微观粒子行为的基本方程之一。
它描述了粒子的波函数随时间的演化。
在实际研究中,常常需要通过数值方法来求解薛定谔方程,特别是对于复杂的体系或无法通过解析方法求解的情况。
MATLAB作为一种强大的数值计算工具,提供了丰富的函数和工具箱,可以帮助我们求解薛定谔方程。
本文将介绍如何使用MATLAB进行数值求解,并给出一些示例代码和注意事项。
数值方法求解薛定谔方程通常需要使用数值方法,其中最常用的方法之一是有限差分法。
有限差分法将波函数离散化为网格点上的数值,通过近似微分来代替薛定谔方程中的导数项,从而转化为一个矩阵方程。
具体来说,我们可以将一维薛定谔方程表示为:iℏ∂Ψ(x,t)∂t=−ℏ22m∂2Ψ(x,t)∂x2+V(x)Ψ(x,t)其中,Ψ(x,t)是波函数,m是粒子的质量,V(x)是势能函数。
为了使用有限差分法求解,我们将空间坐标x离散化为网格点x i,时间t离散化为时间步长Δt,波函数Ψ(x,t)在网格点上的值用Ψi n表示,其中i表示网格点的索引,n表示时间步的索引。
将导数项用中心差分近似表示,我们可以得到:iℏΨi n+1−Ψi nΔt=−ℏ22mΨi+1n−2Ψi n+Ψi−1nΔx2+V i nΨi n其中,Δx是空间步长,V i n表示势能函数在网格点x i上的值。
通过这个差分方程,我们可以逐步更新波函数的值,从而得到波函数随时间的演化。
MATLAB代码示例下面是一个简单的MATLAB代码示例,演示如何使用有限差分法求解一维薛定谔方程。
% 定义参数hbar = 1; % 约化普朗克常数m = 1; % 粒子质量L = 10; % 空间范围N = 1000; % 网格点数dx = L/N; % 空间步长dt = 0.01; % 时间步长% 初始化波函数x = linspace(-L/2, L/2, N); % 空间坐标psi = exp(-x.^2); % 初始波函数% 求解薛定谔方程for n = 1:1000% 计算势能函数V = 0.5*x.^2;% 更新波函数psi = psi - 1i*dt*(hbar/(2*m))*(circshift(psi,-1,2)-2*psi+circshift(psi,1, 2))/(dx^2) - 1i*dt*V.*psi;% 绘制波函数随时间的演化plot(x, abs(psi).^2);xlim([-L/2, L/2]);ylim([0, 1]);xlabel('x');ylabel('|\psi|^2');title(['Time step ', num2str(n)]);drawnow;end在这个示例中,我们假设粒子质量m=1,空间范围L=10,网格点数N=1000。

⾮线性薛定谔⽅程的数值代码>> %This code solves the NLS equation with the split-step method >> % idu/dz-sgn(beta2)/2d^2u/d(tau)^2+N^2*|u|^2*u=0>> %Specify input parameters>> clear all;%distance=input;%beta2=input;N=1;%soliton ordermshape=input;chirp0=0;%input pulse chirp(default value)%---set simulation parametersnt=1024;Tmax=32;%FFT points and window sizestep_num=round(20*distance*N^2);% No.of z steps todeltaz=distance/step_num;%step size in zdtau=(2*Tmax)/nt; %step size in tau%---tau and omega arraystau=(-nt/2:nt/2-1)*dtau; %temporal gridomega=(pi./Tmax).*[(0:nt/2-1) (-nt/2:-1)] ;%frequency gird%---Input Field profileif mshape==0uu=sech(tau).*exp(-0.5i*chirp0*tau.^2); %solitonelse %super-Gaussianuu=exp(-0.5*(1+1i*chirp0).*tau.^(2*mshape));end%---Plot input pulse shape and spectrumtemp=fftshift(ifft(uu)).*(nt*dtau)/sqrt(2*pi);%spectrumfigure;subplot(2,1,1);plot(tau,abs(uu).^2,'--k');hold on;axis([-20 20 0 inf]);xlabel('Normalized Time')ylabel('Normalized Power')title('Input and Output Pulse Shape and Spectrum');subplot(2,1,2);plot(fftshift(omega)./(2.*pi),(abs(temp)).^2,'k');hold on;axis([-5 5 0 inf]);xlabel('Normalized Frequency')ylabel('Normalized Power')%store dispersive phase shifts to speedup codedispersion=exp(i*0.5*beta2*omega.^2*deltaz); %phase factorhhz=1i*N^2*deltaz;%nonlinear phase factor%**********************[Beginning of MAIN Loop]************************* % scheme:1/2N->D->1/2N;first half step nonlineartemp=uu.*exp(abs(uu).^2*hhz/2); %note hhz/2for n=1:step_numf_temp=ifft(temp).*dispersion;uu=fft(f_temp);temp=uu.*exp(abs(uu).^2*hhz);enduu=temp.*exp(-abs(uu).^2*hhz/2); %Final fieldtemp;fftshift(ifft(uu)).*(nt*dtau)/sqrt(2*pi);% Final spectrum%**********************[End of MAIN Loop]*************************%---Plot output pulse shape and spectrumsubplot(2,1,1)plot(tau,abs(uu).^2,'--k')subplot(2,1,2)plot(fftshift(omega)./(2.*pi),abs(temp).^2,'k')。
如何用matlab解薛定谔方程?数值求解的无量纲化技术我前面讲了 matlab解二次微分方程的方法。
薛定谔方程当然是个二次微分方程. 所以,上一讲的matlab 的ode函数是可以解薛定谔方程的。
不过,在求解之前,我们还有个工作必须先做。
薛定谔方程中有个hbar,它的数值是如此之小,而且还要平方。
还有电子电荷e,光速c, 电子质量m 这样的数值也是如此。
这样的数值是不适合在计算程序中出现的。
凡是天文数值都不适合在计算程序中出现。
有个很优美的技术来消除它们,就是无量纲化。
这个技术是我们做计算的时候必须做的,所以,我在这里讲讲这个事情。
无量纲化,就是用一些特征的长度做长度单位,用一些特征的能量做能量单位。
假设我们研究的问题是原子,我们就可以用玻尔半径a = 0.529埃为长度单位,以氢原子基态能量的绝对值 13.6eV 为能量单位。
为了用它们做无量纲化,我们需要它们的公式形式:a = hbar^2 /me^2, |E0| = e^2/2a。
氢原子的径向波函数满足的薛定谔方程是[(-hbar^2/2m) (d^2/dr^2 + (2/r) d/dr) - e^2/r] R(r) = E R(r).把这方程两边除上述|E0|,得到 [a^2 (d^2/dr^2 + (2/r) d/dr) - 2a/r] R(r) = E R(r)。
这里的E 是以|E0| = 13.6eV 为单位的。
然后,把 a 除到导数下面的r上,方程就变成[(d^2/dr^2 + (2/r) d/dr) - 2/r] R(r) = E R(r),这里的r 是以a 为单位的。
这个方程里面的每个量都仅仅是一些无量纲的数了,方程大大简化了。
我们最后需要求解的方程是这个无量纲化的薛定谔方程:[(d^2/dr^2 + (2/r) d/dr) - 2/r] R(r) = E R(r)。
这方程怎么解,上一讲已经讲过了。
好不好懂,请给个意见。
第20卷第10期大 学 物 理Vol.20No.102001年10月COLL EGE PHYSICS Oct.2001基础物理教学现代化问题理论力学中非线性问题的MAT LAB 数值解 收稿日期:2001-05-08 作者简介:胡静(1942—),女,广东顺德人,北京师范大学物理系副教授,主要从事力学和理论力学的教学和研究工作.胡 静,彭芳麟,管 靖,卢圣治(北京师范大学物理系,北京 100875)摘要:在21世纪,理论力学必须讨论非线性问题,并培养学生解决非线性问题的能力;数学软件MA TLAB 的强大功能和简单易学,为实现这一目标提供了可能性.本文介绍“理论力学计算机模拟实验”课程中用数值计算处理非线性问题的实例.关键词:MA TLAB 软件;数值计算;非线性问题中图分类号:O 31;G 434 文献标识码:B 文章编号:100020712(2001)1020039203 计算机和信息技术促使自然科学迅猛发展,尤其是使非线性科学的研究如虎添翼,取得突破,成为当前和未来科学研究的前沿之一;计算机和信息技术的高度发展,也对人才的培养提出了新的要求,教育、教学现代化的改革面临严峻的挑战.在新的21世纪,理论力学课程中原来就广泛存在的非线性问题,不能再因数学困难而采取回避的态度了;非线性科学的基础知识———非线性振动的基础理论应作为新的理论基础引入教材,应把学生的目光引向非线性问题;同时一些新的科技成果在教材中也应有所反映.理论力学课程的任务不能再局限于以前教学大纲的要求,我们必须把计算机技术引入教学,进行教学方法的改革,把培养学生运用计算机进行学习、研究理论力学问题(特别是非线性问题)的能力作为课程的任务,这种能力的培养不是单纯计算机课程能够完成的.非线性微分方程求解析解的问题至今未能解决,目前这个问题有3个解决途径:1)进行变量变换使之变为线性方程.但如何寻找这种变量变换,还没有一般方法;2)用解析方法进行近似求解,这种方法适用于弱非线性情况;3)用计算机进行数值求解.前两种方法是重要的,解的解析表达有利于进行理论分析,应继续进行研究.当前两种方法无能为力时,只能依靠第三种方法,这种方法是快速和普遍有效的,还有利于新的规律的发现,有利于创新能力的培养.非线性科学研究中的许多突破,如孤立子、混沌等的研究就是依靠计算机进行数值研究取得的,有些竟是在无意中发现的.从当前数理方面学术刊物发表的论文看,许多成果都是研究某一非线性问题,利用计算机进行数值求解取得的.自然界的现象本来就是复杂的,本质上属于非线性现象,用线性方程描述往往只是某种程度上的近似.在理论力学课程中本来非线性问题就有很多.如在质点力学中,只要力与坐标和速度的关系是非线性的,动力学方程就是非线性的;单体问题、二体问题和三体问题中一般情况的微分方程组也是非线性的;更不用说刚体定点运动动力学中,欧拉动力学方程和欧拉运动学方程本身就是高度非线性的.以前这些问题因为在教学中缺少处理手段,和缺少对非线性问题所包含的丰富内容的认识,因此一直都把它们回避了.理论力学是研究宏观机械运动的普遍规律的,其内容不能再停留在牛顿时代和哈密顿时代的理论,不能再局限于只研究线性问题这个小范围内,信息技术的发展已使我们拥有处理非线性问题的手段和能力,简单易学且功能强大的MA TLAB 数学软件提供了处理非线性问题的非常好的工具.现选取我们在“理论力学计算机模拟实验”课程中解决非线性问题的几个实例作一简要介绍.1 有阻力的抛体问题通常空气阻力与速度的关系R =f (v )不是线性的,导致动力学方程的非线性,这是课程中首先遇到的一个非线性问题.通常采用自然坐标法,求得一个v 依赖于θ的一阶非线性微分方程[1],这个方程只有当阻力与速度成线性关系时才能求出解析解.对于一般情况,由于求解析解的困难,以往教学中就不再讨论了.许多教材不得已采用阻力与速度成正比这种不符合实际的规律,用直角坐标系建立起线性的运动微分方程组,进行求解并讨论有阻力的抛体问题的特征.现在利用MA TLAB软件解决一般情况下的抛体问题就轻而易举了,可直接用直角坐标建立运动微分方程,只要几行程序(由于篇幅有限,恕不列出),用数值解法就可画出其轨道,演示其运动情况.可计算出轨道最高点的高度,抛体的最大射程和终极速率等;也可求任意时刻抛体的位置和速度;还可以把阻力与速率的不同方次成比例时的轨道叠在一张图上进行比较.这种方法不仅具有形象、快速的特点,而且具有很大的实用价值.2 质点在万有引力场中运动的问题众所周知,这种情况用极坐标建立起来的运动微分方程是非线性的,通常我们用变量变换(u=1/r)方法,使轨道方程成为线性方程,解决了轨道的求解问题;但始终不能求出r=r(t)和θ=θ(t)的解析表达式,这是长期困扰我们的问题.为了确定行星的运动,必须引入平近点角和偏近点角概念,走一条曲折的路,最后还必须用近似方法求解非线性的开普勒方程,其费时费力的程度可想而知.今天,人类进入宇航时代,人们必须掌握飞行器的精确的运动规律,解决这个问题有非常重要的现实的意义.利用MA TLAB软件数值计算功能,只需给出两个极坐标的运动微分方程和初始条件,用简单的几行程序就可得出任一时刻质点的位置和速度,并可模拟出运行的图像.3 水星近日点的进动这一现象的观测是广义相对论正确性的著名验证.广义相对论的修正归结于在比尼公式中引入一个很小的修正项[2]:ε/r4,使之成为非线性方程.利用MA TLAB软件,适当放大ε的数值能演示椭圆轨道进动的情况.4 大幅度单摆的运动这是一个古老的非线性问题,它的求解归结于求第一类椭圆积分问题.如果用近似求解的方法,则将sinθ展开到θ3项,用小参数展开方法逐级近似求解,但这种方法不适用于幅角较大的情况.若用MA TLAB 软件进行数值求解,就可不作任何近似,很容易画出不同初始条件下的相图,看出运动如何从振动向转动演变;可求出周期随振幅变化的曲线;还可通过快速傅里叶变换求出幅角较大时的频谱,说明在非线性情况下谐频的产生.5 倒摆的非线性受迫振动这是能够产生混沌现象的著名实验,描述其运动的是达芬(duffing)方程[3]d2xd t2+γd xd t-x+x3=f cosωt有了数学方程就可以利用MA TLAB软件进行计算机模拟,只需少数几行程序[4]就能揭示混沌产生的机理.图1描绘出两条位移曲线,由于对初值敏感,初阶段两曲线重合,以后运动就分开了,随着时间的增大两者差别越来越大,表明运动的不可预测性.图2为显示倒摆有奇怪吸引子的混沌现象的相图.还可对倒摆运动作模拟演示.图1 初值有微小差别的两条位移曲线图2 倒摆运动的相图以前我们只能用口头阐述和在黑板上画图的方法来介绍这一实验,现在,我们的学生就能重复科学家所做的工作,这对学生是一种怎样的体验呢!04大 学 物 理 第20卷6 自激振动 范・德・波耳(V an d er pol)方程中的极限环自激振动是一种对科学技术非常有意义而在自然界又广泛存在的非线性振动.我们知道,对线性阻尼振动系统,严格的周期运动只能由受周期性驱动力作用的受迫振动产生;而对非线性系统,有一种自激振动系统,在非振动的能源供给下,它能产生严格的周期运动,这是人们十分感兴趣的现象.自激系统是一个非线性的有阻尼的振动系统,在振动过程中伴随有能量损耗,但系统存在一种机制,使能量能够由非振动能源通过系统本身的反馈调节,及时适量地得到补充,从而产生一个稳定的不衰减的周期运动,这样的振动称为自激振动.一个典型的自激系统是三极管振荡系统,描述其振动的方程是范・德・波耳方程d 2x d t2-μ(x 20-x 2)d xd t +ω20x =0它等价于两个一阶微分方程:d x d t=y d y d t=μ(x 20-x 2)y -ω20x 给出任一初始条件,通过MA TLAB 软件进行数值计算,可动态演示其相轨道都将趋向于一条闭合曲线,此闭合曲线称为极限环.极限环以外的相轨道向里盘旋,而极限环以内的相轨道则向外盘旋,都趋向极限环.极限环的存在说明存在严格的周期运动.数值计算时可取x 2=1,ω20=1,μ=0.3.还可对极限环进行快速傅里叶分析,得出它是由基频、谐频的振动合成的.与近似计算结果相符.图3 极限环的形成7 一个非线性稳定性问题利用MA TLAB 软件数值计算,动态演示一个系统相对于平衡态的扰动的非线性演化,说明有些稳定性问题不能由扰动方程的线性化方法完全解决,在临界情况需要由扰动方程的高次项决定.研究下列扰动运动微分方程的零解的稳定性:d xd t=-y +ax 3d yd t=x +ay 3其中a 为常数.这种情况可以证明属于临界情况.以xy 为相平面,用数值解可证明其稳定性要由高阶项决定:1)a >0时,相点离原点的距离随时间而增大,因而运动是不稳定的;2)a <0时,相点离原点的距离随时间而减小,最后趋于零,运动是渐近稳定的;3)a =0时,相轨道是圆,因而运动是稳定的.以前在处理圆运动的轨道稳定性问题和刚体绕主轴转动的稳定性问题时往往将扰动方程线性化后,求特征根,从特征根情况作出判断.但是这两种情况都属于临界情况,所以这种方法是不可靠的,需要寻找严格的方法,或通过数值解加以证明.以上的介绍是初步的,涉及的力学内容和MA T 2LAB 软件的功能也不够全面.我们在“理论力学计算机模拟实验”课程[4]中还利用MA TLAB 软件的其它功能,如符号计算功能等解决力学中不同类型的问题,课程中课题总数有20多个.在教学实践中,从学生掌握软件使用和力学内容的情况看,教学效果是很好的.百闻不如一见,一见不如亲自参加实践.如果你亲眼目睹MA TLAB 软件功能的演示,亲自运用并获得成功时,对这软件就会产生一种令人神往,如获至宝的感受.也会给你一种信心和能力,相信自己也能在科学事业中做出更多的贡献.我们希望有更多的教师和学生能更早的在这一教学现代化的改革中受益!参考文献:[1] 胡慧玲,林纯镇,吴惟敏.理论力学基础教程[M ].北京:高等教育出版社,1986.74.[2] [美]Marion J B.质点和系统的经典动力学[M ].北京:高等教育出版社,1985.256.[3] 漆安慎,杜婵英.力学[M ].北京:高等教育出版社,1997.399.[4] 管靖,彭芳麟,胡静等.理论力学教学现代化———“理论力学计算机模拟实验”课程的探索[J ].大学物理,2001,20(8):38.14第10期 胡 静等:理论力学中非线性问题的MA TLAB 数值解。
非线性方程的解法1引言数学物理中的许多问题归结为解函数方程的问题,即,0)(=x f (1.1)这里,)(x f 可以是代数多项式,也可以是超越函数。
若有数*x 为方程0)(=x f 的根,或称函数)(x f 的零点。
设函数)(x f 在],[b a 内连续,且0)()(<b f a f 。
根据连续函数的性质知道,方程0)(=x f 在区间],[b a 内至少有一个实根;我们又知道,方程0)(=x f 的根,除了极少简单方程的根可以用解析式表达外,一般方程的根很难用一个式子表达。
即使能表示成解析式的,往往也很复杂,不便计算。
所以,具体求根时,一般先寻求根的某一个初始近似值,然后再将初始近似值逐步加工成满足精度要求为止。
如何寻求根的初始值呢?简单述之,为了明确起见,不妨设)(x f 在区间],[b a 内有一个实的单根,且0)(,0)(><b f a f 。
我们从左端出点a x =0出发,按某一预定的步长h 一步一步地向右跨,每跨一步进行一次根的“搜索”,即检查每一步的起点k x 和1+k x (即,h x k +)的函数值是否同号。
若有:0)(*)(≤+h x f x f k k (1.2)那么所求的根必在),(h x x k k +内,这时可取k x 或h x k +作为根的初始近似值。
这种方法通常称为“定步长搜索法”。
另外,还是图解法、近似方程法和解析法。
2迭代法2.1迭代法的一般概念迭代法是数值计算中一类典型方法,不仅用于方程求根,而且用于方程组求解,矩阵求特征值等方面。
迭代法的基本思想是一种逐次逼近的方法。
首先取一个精糙的近似值,然后用同一个递推公式,反复校正这个初值,直到满足预先给定的精度要求为止。
对于迭代法,一般需要讨论的基本问题是:迭代法的构造、迭代序列的收敛性天收敛速度以及误差估计。
这里,主要看看解方程迭代式的构造。
对方程(1.1),在区间],[b a 内,可改写成为:)(x x ϕ=(2.1)取],[0b a x ∈,用递推公式:)(1k k x x ϕ=+, ,2,1,0=k (2.2)可得到序列:∞==0210}{,,,,k k k x x x x x (2.3)当∞→k 时,序列∞=0}{k k x 有极限x ~,且)(x ϕ在x ~附近连续,则在式(2.2)两边极限,得,)~(~x x ϕ=即,x ~为方程(2.1)的根。
MATLAB实例:⾮线性⽅程数值解法(迭代解)MATLAB实例:⾮线性⽅程数值解法(迭代解)很久之前写过⼀篇关于“”,本博⽂相当于之前这⼀篇的延续与拓展,介绍四种求解⼀元⾮线性⽅程的数值解法(迭代解),包括:⽜顿迭代法,Halley迭代法,Householder迭代法以及预测校正⽜顿-哈雷迭代法(Predictor-Corrector Newton-Halley,PCNH),具体参考⽂献[1],来源于这篇⽂章:THREE-STEP ITERATIVE METHOD WITH EIGHTEENTH ORDER CONVERGENCE FOR SOLVING NONLINEAR EQUATIONS。
1. 迭代更新公式2. MATLAB程序newton.mfunction [x1, k]=newton(t1,esp,m)syms x;fun=x^3+4*(x^2)-10;for k=1:mif abs(subs(diff(fun,'x'),x,t1))<espx1=t1;break;elseif subs(diff(fun,'x',2),x,t1)==0break;disp('解题失败!')elset0=t1;t1=t0-subs(fun,x,t0)/subs(diff(fun,'x'),x,t0);if abs(t1-t0)<espx1=t1;break;endendendend% x1=vpa(x1,15);halley.mfunction [x1, k]=halley(t1,esp,m)syms x;fun=x^3+4*(x^2)-10;for k=1:mif abs(subs(diff(fun,'x'),x,t1))<espx1=t1;break;elseif subs(diff(fun,'x',2),x,t1)==0break;disp('解题失败!')elset0=t1;t1=t0-(2*subs(fun,x,t0)*subs(diff(fun,'x'), x, t0))/(2*(subs(diff(fun,'x'), x, t0))^2-subs(fun, x, t0)*subs(diff(fun,'x',2),x,t0)); if abs(t1-t0)<espx1=t1;break;endendendend% x1=vpa(x1,15);householder.mfunction [x1, k]=householder(t1,esp,m)syms x;fun=x^3+4*(x^2)-10;for k=1:mif abs(subs(diff(fun,'x'),x,t1))<espx1=t1;break;elseif subs(diff(fun,'x',2),x,t1)==0break;disp('解题失败!')elset0=t1;t1=t0-(subs(fun, x, t0))/(subs(diff(fun,'x'),x,t0))-(((subs(fun, x, t0))^2)*subs(diff(fun,'x',2),x,t0))/(2*(subs(diff(fun,'x',2),x,t0))^3); if abs(t1-t0)<espx1=t1;break;endendendend% x1=vpa(x1,15);PCNH.mfunction [x1, k]=PCNH(t1,esp,m)syms x;fun=x^3+4*(x^2)-10;for k=1:mif abs(subs(diff(fun,'x'),x,t1))<espx1=t1;break;elseif subs(diff(fun,'x',2),x,t1)==0break;disp('解题失败!')elset0=t1;w=t0-subs(fun,x,t0)/subs(diff(fun,'x'),x,t0);y=w-(2*subs(fun,x,w)*subs(diff(fun,'x'), x, w))/(2*(subs(diff(fun,'x'), x, w))^2-subs(fun, x, w)*subs(diff(fun,'x',2),x,w)); t1=y-(subs(fun, x, y))/(subs(diff(fun,'x'),x,y))-(((subs(fun, x, y))^2)*subs(diff(fun,'x',2),x,y))/(2*(subs(diff(fun,'x',2),x,y))^3);if abs(t1-t0)<espx1=t1;break;endendendend% x1=vpa(x1,15);demo.mclearclc% Input: 初始值,迭代终⽌条件,最⼤迭代次数[x1, k1]=newton(1,1e-4,20); % ⽜顿迭代法[x2, k2]=halley(1,1e-4,20); % Halley迭代法[x3, k3]=householder(1,1e-4,20); % Householder迭代法[x4, k4]=PCNH(1,1e-4,20); % 预测校正⽜顿-哈雷迭代法(PCNH)fprintf('⽜顿迭代法求解得到的⽅程的根为:%.15f, 实际迭代次数为:%d次\n', x1, k1);fprintf('Halley迭代法求解得到的⽅程的根为:%.15f, 实际迭代次数为:%d次\n', x2, k2);fprintf('Householder迭代法求解得到的⽅程的根为:%.15f, 实际迭代次数为:%d次\n', x3, k3);fprintf('预测校正⽜顿-哈雷迭代法(PCNH)求解得到的⽅程的根为:%.15f, 实际迭代次数为:%d次\n', x4, k4); %% 函数图像x=-5:0.01:5;y=x.^3+4.*(x.^2)-10;y_0=zeros(length(x));plot(x, y, 'r-', x, y_0, 'b-');xlabel('x');ylabel('f(x)');title('f(x)=x^3+4{x^2}-10');saveas(gcf,sprintf('函数图像.jpg'),'bmp'); %保存图⽚3. 数值结果求解$f(x)=x^3+4{x^2}-10=0$⽅程在$x_0=1$附近的根。
数值分析中求解非线性方程的MATLAB求解程序(6种)数值分析中求解非线性方程的MATLAB求解程序(6种)1.求解不动点function [k,p,err,P]=fixpt(g,p0,tol,max1)%求解方程x=g(x) 的近似值,初始值为p0%迭代式为Pn+1=g(Pn)%迭代条件为:在迭代范围内满足|k|<1(根及附近且包含初值)k为斜率P(1)=p0;for k=2:max1P(k)=feval(g,P(k-1));err=abs(P(k)-P(k-1));relerr=err/(abs(P(k))+eps);p=P(k);if (err<tol)|(relerr<tol)< p="">break;endendif k==max1disp('超过了最长的迭代次数')endP=P';2.二分法function [c,err,yc]=bisect(f,a,b,delta)%二分法求解非线性方程ya=feval(f,a);yb=feval(f,b);if ya*yb>0break;max1=1+round((log(b-a)-log(delta))/log(2));for k=1:max1c=(a+b)/2;yc=feval(f,c);if yc==0a=c;b=c;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;endif b-a<delta< p="">break;endendc=(a+b)/2;err=abs(b-a);yc=feval(f,c);3.试值法function [c,err,yc]=regula(f,a,b,delta,epsilon,max1) %试值法求解非线性方程%f(a)和飞(b)异号ya=feval(f,a);yb=feval(f,b);if ya*yb>0disp('Note:f(a)*f(b)>0');for k=1:max1dx=yb*(b-a)/(yb-ya);c=b-dx;ac=c-a;yc=feval(f,c);if yc==0break;elseif yb*yc>0b=c;yb=yc;elsea=c;ya=yc;enddx=min(abs(dx),ac);if abs(dx)<delta|abs(yc)<epsilon< p="">break;endendc;err=abs(b-a)/2;yc=feval(f,c);4.求解非线性方程根的近似位置function R=approot(X,epsilon)%求解根近似位置%为了粗估算方程f(x)=0在区间[a,b]的根的位置,%使用等间隔采样点(xk,f(xk))和如下的评定准则:%f(xk-1)与f(xk)符号相反,%或者|f(xk)|足够小且曲线y=f(x)的斜率在%(xk,f(xk))附近改变符号。
matlab证明涡旋光束自聚焦matlab证明涡旋光束自聚焦引言光束的自聚焦现象一直是光学研究领域的一个重要课题。
特别是涡旋光束的自聚焦现象,因其独特的光学性质和广泛的应用前景而备受关注。
本文将使用MATLAB仿真工具来证明涡旋光束的自聚焦现象,并探讨其涡旋数和光束参数对自聚焦过程的影响。
1. 涡旋光束的特性涡旋光束是一种相位呈螺旋状分布的光束,具有自旋角动量和轨道角动量等特性。
它的相位分布可以表示为exp(ilφ),其中l是涡旋数,φ是光束的极角。
涡旋光束在传播过程中会产生自聚焦现象,即光束的横向尺寸会自动调整,使得整个光束逐渐变细,并最终形成一个强度极大的光束核心。
2. 自聚焦方程模型涡旋光束的自聚焦过程可以通过非线性薛定谔方程来描述。
在本文中,我们使用一个经典的非线性薛定谔方程模型来模拟涡旋光束的自聚焦现象:i ∂A/∂z + Δ⊥A + β|A|^2 A = 0 (1)其中A是复振幅,z是传播距离,Δ⊥是横向Laplacian算子,β是非线性系数,|A|^2 表示复振幅的模的平方。
3. MATLAB仿真模拟为了证明涡旋光束的自聚焦现象,我们使用MATLAB进行数值仿真。
我们需要设定涡旋数、光束起始尺寸和非线性系数等参数。
我们使用有限差分法或薛定谔方程传播算法对方程(1)进行数值求解。
在MATLAB中,我们可以定义一个自定义的函数来代表方程(1)。
通过使用该函数,我们可以通过迭代法计算出光束在传播过程中的强度和相位分布。
4. 涡旋光束的自聚焦过程在MATLAB中,我们可以观察到涡旋光束的自聚焦过程。
随着传播距离的增加,光束的横向尺寸逐渐减小,同时光束的强度也增强。
当传播距离足够大时,光束核心会形成一个明显的峰值,而光束边缘则变得非常模糊。
5. 涡旋数和光束参数的影响通过改变涡旋数和光束参数,我们可以观察到涡旋光束自聚焦过程的差异。
当涡旋数增加时,光束的自聚焦速度加快,并且光束核心的强度增加。