中国气象科学数据共享服务网的中国气象科学数据

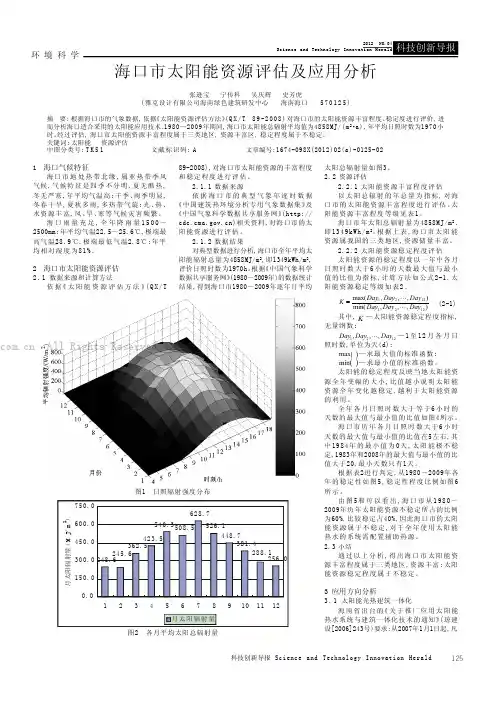
125科技创新导报 Science and Technology Innovation Herald 环 境 科 学1 海口气候特征海口市地处热带北缘,属亚热带季风气候,气候特征是四季不分明,夏无酷热,冬无严寒,年平均气温高;干季、雨季明显,冬春干旱,夏秋多雨,多热带气旋;光、热、水资源丰富,风、旱、寒等气候灾害频繁。

海口雨量充足,全年降雨量1500～2500mm;年平均气温22.5～25.6℃,极端最高气温28.9℃,极端最低气温2.8℃;年平均相对湿度为81%。

2 海口市太阳能资源评估2.1数据来源和计算方法依据《太阳能资源评估方法》(Q X /T 89-2008),对海口市太阳能资源的丰富程度和稳定程度进行评估。

2.1.1数据来源依据海口市的典型气象年逐时数据《中国建筑热环境分析专用气象数据集》及《中国气象科学数据共享服务网》(http://)相关资料,对海口市的太阳能资源进行评估。

2.1.2数据结果对典型数据进行分析,海口市全年平均太阳能辐射总量为4858MJ/m 2,即1349kWh/m 2,评价日照时数为1970h。

根据《中国气象科学数据共享服务网》(1980～2009年)的数据统计结果,得到海口市1980～2009年逐年月平均太阳总辐射量如图3。

2.2资源评估2.2.1太阳能资源丰富程度评估以太阳总辐射的年总量为指标,对海口市的太阳能资源丰富程度进行评估。

太阳能资源丰富程度等级见表1。

海口市年太阳总辐射量为4858MJ/m 2、即1349k Wh/m 2。

根据上表,海口市太阳能资源属我国的三类地区,资源储量丰富。

2.2.2太阳能资源稳定程度评估太阳能资源的稳定程度以一年中各月日照时数大于6小时的天数最大值与最小值的比值为指标,计算方法如公式2-1,太阳能资源稳定等级如表2。

),,,min(),,,max(12211221Day Day Day Day Day Day K(2-1)其中,K —太阳能资源稳定程度指标,无量纲数;1221,,,Day Day Day —1至12月各月日照时数,单位为天(d);max —求最大值的标准函数; min —求最小值的标准函数。

中国气象数据网气温气象学上把表示空气冷热程度的物理量称之为空气温度，简称气温（英文名称 air temperature ）。

公众天气 高的百叶箱中的温度表上测得的，由于温度表保持了良好的 通风性并避免了阳光直接照射，因而具有较好的代表性。

国 采用摄氏度（C ）为单位。

气温的单位除上面提到的用摄氏度（C ）表示，有的以华氏度（F ）表示。

摄氏与华氏的换 算关系是： C=5/9 （F-32）， F=9/5C+32 （式中 C-摄氏温度）。

气温是用来衡量地球表面大气温度分布状况和变化态势的 重要指标。

它根据需要分为定时气温 （基本站每日观测 4 次， 基准站每日观测 24 次），平均气温，最高气温、最低气温、 极端最高气温、极端最低气温。

1 ）定时气温气象部门每天 02 时、08 时、 14 时、20 时（北京时）每隔 6预报中所说的气温，是在植有草皮的观测场中离地面1.5 米际上标准气温度量单位是摄氏度（C ）中国气温记录一般 F-华氏温度，小时进行一次观测或者02 时、05 时、08 时、11 时、14 时、17 时、20 时、23 时每隔3 小时进行气温观测。

为了特殊需要（如航空），甚至进行间隔1 小时、半小时的气象观测。

2）平均气温指某一段时间内，各次观测的气温值的算术平均值。

通常通过气温的平均情况来表达气温一段时间内的状况。

根据计算时间长短不同，可分日平均气温、月平均气温、年平均气温、累年平均气温等。

1）日平均气温：由于不同气象站，每天观测次数不等，中国气象部门统一规定，日平均气温是把每天02 时、08 时、14 时、20 时四次测量的气温求平均，还可以计算为某一天的最高气温和最低气温的平均值，精确到0.1 度。

2）月平均气温：某一月的多日平均气温的平均值。

3）年平均气温：某年的多日平均气温（或多月平均气温）的平均值。

4）累年平均气温：累年某日平均值由历年该日平均值平均求得，但是资料必须具有连续20 年以上的数据，且闰年只取前365 天；累年某月平均值由历年该月平均值平均求得；累年年平均值由累年月平均值平均求得。

西藏地区近40年温度和降水量变化的时空格局分析杨文才;多吉顿珠;范春捆;周启龙【摘要】全球气候变化将对农田、林地、草原等生态系统产生不同程度的影响，而制定科学合理的气候变化应对策略，需要准确把握区域气候变化的时空特征与规律。

为了全面了解西藏地区温度和降水指标的时空格局，深入分析了1971—2010年间的年平均温度和降水量年值及季节值的变化趋势和时空格局。

结果表明，（1）年平均温度普遍升高，有39.72%的地区累计升高1.6~2.4℃，10.72%的地区累计升高2.4~3.2℃，局部地区累计升高4℃以上，在空间分布上，仅错那县、墨脱县和察隅县三县的南部地区年平均温度下降，其余地区年平均温度升高。

从降水量变化来看，有42.09%的区域变化在±1 mm∙a-1之间，与40年前相比，有12.41%的地区年降水减少40 mm以上，45.49%的地区呈增加趋势。

从空间分布来看，降水量减少区域主要分布在阿里东北到那曲西北一带、日喀则西部到阿里狮泉河一带、日喀则南部以及林芝东南部。

（2）从季节平均温度、降水量的变化来看，4个季节温度均以升高为主，增幅高低顺序为秋季>春季>冬季>夏季；四季降水量差异较大，春季和夏季以增多为主，秋季和冬季以减少为主，其中，冬季减少最多，面积占比达96.78%。

（3）近40年来，温度变化存在显著的突变点，突变时间存在空间分异性。

（4）温度的明显升高和降水量的时空差异将导致局部地区气候干湿变化。

藏西地区易发生全年干旱，藏南和藏东南地区易发生季节干旱，这将给农业生产、天然草地牧草生长和草原畜牧业带来不利影响。

研究认为相关部门和农牧民都应该重视并尽快制定科学合理的应对策略和方案，以应对不确定性的气候变化。

%In the context of global climate change, climate change will affect the ecological environment of agriculture, forestry and grassland to varying degrees. To formulate a scientific and reasonable climate changeresponse strategy, we need to accurately grasp the temporal and spatial characteristics and laws of regional climate change. In order to comprehensively analyze and understand the spatial and temporal pattern of temperature and precipitation in Tibet, the annual mean temperature and annual precipitation value and the seasonal variation trend and spatial-temporal pattern of 1971—2010 were analyzed. The results show that: (1) The annual average temperature increased in general, 39.72% of the total area increased 1.6~2.4℃, 10.72% of the total area increased2.4~3.2℃, some areas increased by 4℃ above.The spatial distribution:only the average annual temperature in the southern region of the three counties (Cuona, Medog and Zayu counties) decreased, while the average temperature in other areas increased. Precipitation change: 42.09% of the area changes in ±1 mm∙a-1, 12.41% of the area (compared with 40 years ago), the annual precipitation decreased by 40mm above, 45.49% area shows an increasing trend. The spatial distribution of precipitation: precipitation reduction area is mainly distributed in the northeast of Ali to the northwest of Naqu, Shigatse west to Ali Shiquanhe area, south of Shigatse and southeast of Nyingchi. (2) The seasonal mean temperature and precipitation of the four seasons showed that the temperature increased in all four seasons, the order of increase wasautumn>spring>winter>summer; The precipitation in the four seasons is greatly different, and the increase is mainly in the spring and summer, and the decrease is mainly in the autumn and winter, among the four seasons the precipitation of winter decreased the most reached an area of 96.78%.(3) During the recent 40 years, the temperature change has obvious mutation point, and the mutation time has spatial differentiation. (4) Due to the obvious increase of temperature and the difference of precipitation, it will lead to the change of dry and wet climate in some areas. The drought in the western part of Tibet is easy to occur throughout the year. Seasonal drought is easy to occur in southern Tibet and southeastern Tibet, which will adversely affect agricultural production, natural grassland forage growth and grassland animal husbandry. The study suggests that the relevant departments and farmers and herdsmen should pay attention to and formulate scientific and reasonable response strategies and programs as soon as possible to deal with the uncertainty of climate change.【期刊名称】《生态环境学报》【年(卷),期】2016(025)009【总页数】7页(P1476-1482)【关键词】气候变化;温度;降水量;时空格局;西藏【作者】杨文才;多吉顿珠;范春捆;周启龙【作者单位】西藏自治区农牧科学院草业科学研究所，西藏拉萨 850009;西藏自治区农牧科学院草业科学研究所，西藏拉萨 850009;西藏自治区农牧科学院农业研究所，西藏拉萨 850032;西藏自治区农牧科学院草业科学研究所，西藏拉萨850009【正文语种】中文【中图分类】X16第三次气候变化国家评估报告指出，近百年（1909—2011年）来中国陆地区域平均增温0.9～1.5 ℃，高于第二次气候变化国家评估报告平均增温0.5～0.8 ℃的结论。

科技部、财政部关于发布国家科技资源共享服务平台优化调整名单的通知文章属性•【制定机关】科学技术部,财政部•【公布日期】2019.06.05•【文号】国科发基〔2019〕194号•【施行日期】2019.06.05•【效力等级】部门规范性文件•【时效性】现行有效•【主题分类】基础研究与科研基地正文科技部财政部关于发布国家科技资源共享服务平台优化调整名单的通知国科发基〔2019〕194号教育部、自然资源部、农业农村部、卫生健康委、市场监管总局、林草局、中科院、地震局、气象局、药监局科技、财务主管部门，广东省科技厅、财政厅：为落实《科学数据管理办法》和《国家科技资源共享服务平台管理办法》的要求，规范管理国家科技资源共享服务平台（简称国家平台），完善科技资源共享服务体系，推动科技资源向社会开放共享，科技部、财政部对原有国家平台开展了优化调整工作，通过部门推荐和专家咨询，经研究共形成“国家高能物理科学数据中心”等20个国家科学数据中心、“国家重要野生植物种质资源库”等30个国家生物种质与实验材料资源库。

请你们组织依托单位进一步加强对各国家平台的管理，根据相关管理办法要求，制定国家平台五年建设运行实施方案，进一步明确国家平台功能定位和目标任务，梳理本领域科技资源体系架构，推进相关领域科技资源向国家平台汇聚与整合，强化科技资源开发应用与分析挖掘利用，提升科技资源使用效率和科技创新支撑能力，完善科技资源存储、管理和安全所需基础设施，健全网络安全保障体系，创新运行管理机制，加强评价考核组织管理，开展国际交流与合作，充分发挥法人单位主体责任，为科学研究、技术进步和社会发展提供高质量的科技资源共享服务。

特此通知。

附件：国家科技资源共享服务平台名单科技部财政部2019年6月5日附件国家科技资源共享服务平台名单序号国家平台名称依托单位主管部门1 国家高能物理科学数据中心中国科学院高能物理研究所中科院中国科学院北京基因组研究2 国家基因组科学数据中心中科院所3 国家微生物科学数据中心中国科学院微生物研究所中科院中国科学院国家空间科学中4 国家空间科学数据中心中科院心5 国家天文科学数据中心中国科学院国家天文台中科院中国科学院遥感与数字地球6 国家对地观测科学数据中心中科院研究所7 国家极地科学数据中心中国极地研究中心自然资源部8 国家青藏高原科学数据中心中国科学院青藏高原研究所中科院9 国家生态科学数据中心中国科学院地理科学与资源研究所中科院10国家材料腐蚀与防护科学数据中心北京科技大学教育部11国家冰川冻土沙漠科学数据中心中国科学院寒区旱区环境与工程研究所中科院12 国家计量科学数据中心中国计量科学研究院市场监管总局13 国家地球系统科学数据中心中国科学院地理科学与资源研究所中科院14 国家人口健康科学数据中心中国医学科学院卫生健康委15国家基础学科公共科学数据中心中国科学院计算机网络信息中心中科院16 国家农业科学数据中心中国农业科学院农业信息研究所农业农村部17国家林业和草原科学数据中心中国林业科学研究院资源信息研究所林草局18 国家气象科学数据中心国家气象信息中心气象局19 国家地震科学数据中心中国地震台网中心地震局20 国家海洋科学数据中心国家海洋信息中心自然资源部国家重要野生植物种质资源21中国科学院昆明植物研究所中科院库中国农业科学院作物科学研农业农村部22 国家作物种质资源库究所中国农业科学院郑州果树研农业农村部23 国家园艺种质资源库究所中国热带农业科学院热带作24 国家热带植物种质资源库农业农村部物品种资源研究所中国林业科学研究院林业研林草局25 国家林业和草原种质资源库究所中国农业科学院北京畜牧兽26 国家家养动物种质资源库农业农村部医研究所27 国家水生生物种质资源库中国科学院水生生物研究所中科院中国水产科学研究院黄海水农业农村部28 国家海洋水产种质资源库产研究所29 国家淡水水产种质资源库中国水产科学研究院农业农村部中国疾病预防控制中心寄生卫生健康委30 国家寄生虫资源库虫病预防控制所中国农业科学院农业资源与31 国家菌种资源库农业农村部农业区划研究所32 国家病原微生物资源库中国疾病预防控制中心卫生健康委33 国家病毒资源库中国科学院武汉病毒研究所中科院34 国家人类生殖和健康资源库国家卫生健康委科学技术研究所卫生健康委35国家发育和功能人脑组织资源库中国医学科学院基础医学研究所卫生健康委36国家健康和疾病人脑组织资源库浙江大学教育部37 国家干细胞资源库中国科学院动物研究所中科院38 国家干细胞转化资源库同济大学教育部39 国家植物标本资源库中国科学院植物研究所中科院40 国家动物标本资源库中国科学院动物研究所中科院41 国家岩矿化石标本资源库中国地质大学（北京）教育部42 国家标准物质资源库中国计量科学研究院市场监管总局43国家生物医学实验细胞资源库中国医学科学院基础医学研究所卫生健康委44国家模式与特色实验细胞资源库中国科学院上海生命科学研究院中科院45 国家啮齿类实验动物资源库中国食品药品检定研究院药监局46国家鼠和兔类实验动物资源库中国科学院上海生命科学研究院中科院47国家非人灵长类实验动物资源库中国科学院昆明动物研究所中科院48 国家禽类实验动物资源库中国农业科学院哈尔滨兽医研究所农业农村部49 国家犬类实验动物资源库广州医药研究总院有限公司广东省科技厅50 国家遗传工程小鼠资源库南京大学教育部。

china meteorological forcing dataset 中国气象强迫数据集（ChinaMeteorologicalForcingDataset）是一种基于气象观测数据的数据集，用于模拟气候模型和生态系统模型等应用。

该数据集包括了全国范围内的气温、降水、风速和相对湿度等参数，并提供了高质量的气象数据。

该数据集是由中国科学院地理科学与资源研究所气候环境变化
研究室（Climate Environment Change Research Center）开发的，经过多年的研究和实践，已成为国内外广泛使用的气象强迫数据集之一。

该数据集的特点在于其具有高时空分辨率、全国覆盖、长时间序列和高质量的数据质量等优点。

目前，该数据集已被广泛应用于气候模拟、生态系统模拟、水文模拟、农业生产预测等领域。

在气候模拟方面，该数据集为气候变化研究提供了重要的数据基础，可以帮助研究人员更好地了解气候变化的趋势和规律。

在生态系统模拟方面，该数据集可以用于模拟不同气候条件下生态系统的变化，为生态系统管理和保护提供重要的科学依据。

在水文模拟方面，该数据集可以用于模拟不同降水条件下的径流变化，为水资源管理和保护提供重要的科学依据。

总之，中国气象强迫数据集（China Meteorological Forcing Dataset）是一种重要的气象数据集，对于气候变化研究、生态系统管理和水资源管理等领域具有重要的应用价值。

该数据集的不断完善和更新将为相关领域的研究提供更为精准和可靠的数据支持。

我国科技资源共享的现状及其分析世界各发达国家均普遍重视提高科技资源的管理水平、努力实现科技资源的广泛共享，从而为科学研究和技术开发提供有效支持，这也是其能够快速发展科技、赢得竞争优势的基础所在。

各国政府往往通过立法和国家的政策积极引导和推动科技资源的保护与共享。

在我国，科技资源的共享问题近年来开始引起国家和各地方的重视。

本文将梳理我国科技资源共享的现状，并对此进行分析。

一、我国科技资源共享现状建国以来，特别是改革开放以来，我国的科技资源建设工作取得了一定的进展。

积累了一些重点领域的常规科学数据和文献，建立了部分区域性的观测与监测网络，收集整理了一定数量的种源和标本，拥有了一批科技基础设施等。

"九五"以来，在资源整合方面，进行了积极的探索，推动了科学数据、大型科学仪器、自然科技资源和科技图书文献资源的共建共享工作。

(一)科学数据领域科学数据是人类社会科技活动所产生的基本数据、资料，以及按照不同需求而系统加工的数据产品和相关信息，具有明显的潜在价值和可开发价值，并在应用过程中得以增值，是信息时代最基本、最活跃、影响面最宽的科技资源。

建国以来，我国在许多科学领域组织开展了不同程度、规模不等的观测、探测、调查和试验研究工作，通过科技攻关、高技术研究及产业化、重大基础研究与科研基地的建设等，积累了大批宝贵的科学数据和基于这些科学数据所得出的大量综合性信息，基本构成了我国海量科学数据的大致轮廓。

目前为止，我国已先后建成一批国家级科学数据中心；建成规模不等、质量各异的科学数据库5000个到6000个，内容基本覆盖了科学技术的各个领域。

各有关部委还相继成立了专门的信息中心，负责收集和整理本部门所采集的各类数据资料，通过建立数据库和产品加工，向用户提供信息服务以及相应的技术支撑。

目前这些信息中心已经成为所在政府部门向社会提供公益性、基础性服务的重要窗口。

科技部在促进科学数据的共享过程中发挥了较大的作用，一方面通过科技计划支持一批科学数据库的建设，另一方面还专门设立了国家科技基础性工作专项，先后启动和支持了一批急需的科技基础数据库建设项目。

时空CoKriging的变异函数建模胡丹桂;舒红;胡泓达【摘要】在对地观测中,所研究的地学变量不仅具有时间、空间特征,还受其他变量的影响,采用多元时空相关数据,可以提高时空估值的精度.时空CoKriging是多元时空插值中一种常用的方法,建立时空变异函数和协变异函数是时空CoKriging插值的关键一步.以东北三省为试验区,利用该地区气象站观测数据的月平均空气相对湿度为主变量,引入同时间同位置的月平均空气温度作为协变量,对空气相对湿度和空气温度进行时空变异函数和时空协变异函数建模.实验结果表明,采用和度量时空模型的时空变异函数的随机性空间结构建模的实际拟合效果较好.【期刊名称】《华中师范大学学报（自然科学版）》【年(卷),期】2015(049)004【总页数】8页(P596-602,622)【关键词】多元时空变量;和度量模型;变异函数;空气相对湿度【作者】胡丹桂;舒红;胡泓达【作者单位】武汉大学测绘遥感信息工程国家重点实验室,武汉430079;武汉职业技术学院计算机学院,武汉430074;武汉大学测绘遥感信息工程国家重点实验室,武汉430079;武汉大学测绘遥感信息工程国家重点实验室,武汉430079【正文语种】中文【中图分类】P208地统计学是以区域化变量理论为基础，以变异函数为工具，研究那些在空间分布上既有随机性又有结构性的自然现象的科学.在自然科学及社会科学领域，有些变量不仅具有空间特征，而且具有时间特征，这时要把所研究的变量看成是时空随机函数.时空插值方法已成为解决时空离散点到连续体上的一种必不可少的映射方法，时空克里金是时空插值法中常用的一种方法[1].Marc G.Genton[2]，Matthew W. Mitchell [3]等对可分离时空协方差函数进行了理论研究和测试，对其优缺点进行了深入的探讨；Cressie and Huang[4]，Chunsheng Ma [5]，E. Porcu [6]，Gneiting[7]等提出了不可分离的，平稳的协方差函数，允许时空交互；徐爱萍[8]，L.De Cesare[9]，D.E.Myers [10]，S. De Iaco [11]等将积和模型应用于时空变异函数模型的建立中.他们虽然考虑到了时间空间特征，但仅局限于单变量.相对照，传统的多元统计分析方法虽然考虑了多变量，却很少考虑到多元信息的空间特征.但是，在诸如水文、石油、土壤、农林、大气和环保等科学研究中，所研究的变量不仅具有时间、空间特征，而且还在时间空间域中受其他相关变量的影响.将克里金法应用于时空多元变量的插值研究中，一方面需要将克里金法进行时空扩展，另一方面将单变量插值的克里金扩展到多变量协同克里金.建立有效的多元时空协方差变异函数模型是研究时空协同克里金插值的关键一步.因此，本文将传统地统计学扩展到多元时空地统计学，构建多元时空变异函数及协变异函数.以东北三省72个气象站点1996年～2005年的月均空气相对湿度数据为例，以同时间同位置的月均空气温度为协变量，为时空协同克里金插值建立时空变异函数和时空协变异函数.采用了和度量变异函数模型来拟合变量的时空变异结构，将气象要素模拟从空间维扩展至时空维.同时，考虑了气温数据对相对湿度的影响，在拟合相对湿度变异函数的过程中，加入了气温作为协变量，将时空克里金插值扩展到了时空协同克里金插值.1.1 区域和数据介绍实验研究的是我国东北三省(黑龙江、吉林、辽宁)，站点地处38.90°～52.97°N，119.70°～132.97°E之间.地面观测台站所观测的资料来自1996年1月～2005年12月东北三省月空气相对湿度.本实验数据通过中国气象科学数据共享服务网获取，共有观测站点87个，由于部分站点数据严重缺失，实验只采用72个观测站数据，站点分布如图1.实验数据为1996年1月～2005年12月的月平均相对湿度和月平均气温值.由于空气相对湿度与空气温度相关性较好，我国东北地区，冬季干燥、夏季湿润，空气温度对空气湿度有着一定程度的相关影响，故选取空气温度为协变量.在实验中，对空气湿度和空气温度分别进行时空变异函数及两者的协变异函数拟合.1.2 数据预处理时空变异函数构造的重要前提是假设时空变量满足二阶平稳.时空空气相对湿度、空气温度数据可以看作为空间站点上的时间序列，时间序列一般包括：周期项、趋势项、随机项.因此空气相对湿度变量的时间序列分解为：式中为周期项为趋势项为随机项为时间序列.随机项 R(t)满足二阶平稳，以塔河站观测时间序列分解为例.图 2是将观测空气湿度时间序列分解为趋势项、周期项和随机项；图 3是将观测空气温度时间序列分解为趋势项、周期项和随机项.可以看出从1996年 1 月到 2005 年 12 月10年的月平均空气湿度及月平均空气温度均存在明显的周期性，不利于时空变异函数建模.但是时间序列没有存在明显的趋势，因此，只对数据进行去周期项处理.为保持数据连续性和整体趋势变化，时间序列分解后的趋势项和随机项保留，因为趋势项不明显，对数据平稳性影响不大.采用时序分解中的加法模型，将变量的周期项提取出来，余下的部分用于时空插值实验.用自相关图检法[12]判断去周期数据的平稳性，如图 4图 5所示，空气相对湿度和空气温度他们的时间序列的自相关系数(ACF)均随延迟时期数很快衰减到±0.1以内，图示表明去周期项后数据近似平稳.空气湿度和温度变量在空间上也要满足二阶平稳，将每一测站上的时间序列经过去周期项后计算移动平均值，根据移动平均值探索空间空气湿度和温度的变化趋势.用空间散点图展示空间分布趋势，图 6是对湿度空间站点数据趋势面的拟合.通过实验对比，发现不管是湿度还是温度均采用3次多项式(2)进行拟合，具有较好的拟合效果.式中，value为月均空气湿度，x，y为空间坐标信息，a，b，c，d，e，f，g为3次多项式通过拟合得到的系数.去除趋势后空间数据分布呈现平稳性，图 7是月平均空气湿度站点数据去空间趋势后拟合面.分别对空气湿度和空气温度各站的时间序列进行平稳性处理再对整个空间数据进行平稳处理，最终满足构造时空变异函数的前提条件，即随机变量近似时空上的二阶平稳.时空多元信息统计学是以协同区域化变量理论为基础，以互变异函数为基本工具，研究那些定义于同一时空域中，既有统计相关又有空间位置相关及时间序列相关的多元时空结构自然现象的科学.所谓协同区域化是指那些在统计意义上及时间序列和空间位置上均具有某种程度的相关性并且定义于同一时间序列及空间域的区域化变量.是一个多元的时空随机场[13]，且式中一般d≤3)表示空间坐标，而t∈T为时间坐标.多元时空随机场的一种简单情况是二元时空随机场.时空协同克里金最普遍的情况是增加一个相关的协变量，来提高对主变量的插值精度，例如，空气相对湿度和空气温度.时空协同克里金(CoKriging)法的插值公式：式中为(s，t)0处空气湿度估算值；Z1(s，t)1i为各点空气湿度；λ1i为赋予各个站点空气湿度的一组权重系数；Z2(s，t)2j为各点空气温度；λ2j为赋予各个站点温度的一组权重系数；N1、N2分别为空气湿度和空气温度用于湿度插值站点数，其中N1≤N2.2.1 时空直接变异函数建模假设Z={Z(s，t)，s、t∈Rd+1}(d+1表示欧式空间维加时间维)表示为时空随机场，设定时空随机场中两位置的时空距离h=(hs，ht)， hs为矢量，代表样本空间距离同时也包含方向信息，ht为样本时间距离.当Z(s，t)满足二阶平稳时可定义其协方差函数为[9]：显然，协方差函数只与距离有关，与空间和时间位置无关.在地统计学中，随机变量Z(s，t)的期望不变(时空二阶平稳性)，协方差矩阵具有对称正定性.理论上，满足下列要求的连续函数可以定义为有效变异函数[9]：1)可分离时空协方差模型地统计学中协方差函数模型(如球状模型、指数模型和高斯模型等)不能直接用于时空随机变量的统计分析，必需进行时空扩展.如果一个随机场Z的时空协方差函数可完全表示成纯空间和纯时间协方差函数相乘，则该时空协方差函数被认为是可分离的 [14].Mitchell Genton， Gumpertz(2005) [3]，MontserratFuentes(2004)[15]等文献中提出了可分离型模型.这类模型相对容易构建，且计算机实现插值效率较高，但往往要求一些比较理想的假设 [16-17]，损失了精细的时空结构信息或丢失了时空交互信息.可分离型时空协方差函数可表示为：式中,C(hs，ht)是变量的时空协方差函数， Cs(hs)、Ct(ht)分别是纯空间协方差和纯时间协方差函数.Cs(hs)、Ct(ht)的具体形式有多种选择，或者同为一种模型，比如高斯模型，或者为不同模型，比如Cs(hs)为球形模型，Ct(ht)为指数模型，或是其他满足正定条件的函数.2)时空积和模型另一类称为不可分离型时空协方差函数，它是将已知的纯空间协方差与纯时间协方差函数通过加乘、混合、积分等变换得到.积和式变异函数来拟合时空地理数据的时空变异结构，协方差函数和变异函数如下[9]：式中， C(hs，ht)为时空协方差，Cs(hs)为空间协方差， Ct(ht)为时间协方差，γ(hs，ht)、γs(hs)、γt(ht)分别是对应的时空、空间、时间变异函数，而C(0，0)、Cs(0)、Ct(0)分别是对应的基台值.这里，假定γ(0，0)=γs(0)=γt(0)=0，满足k1>0、k2≥0、k3≥0，并通过正定条件由下式决定，推导过程见文献[18]：3)时空和度量模型时空和度量模型也是不可分离时空变异函数模型.采用和度量模型变异函数来拟合时空地理数据的时空变异结构，协方差函数可以表示为[19]：式中，C(hs，ht)是空间间隔距离为hs，时间间隔距离为ht的协方差函数；Cs(hs)+Ct(ht)考虑了带状异向性(在不同方向上有不同变异函数基台值)；而考虑了几何异向性，它其实是度量模型[20]，度量模型是通过一个各向异性比率α，把时间距离单位转换成空间距离单位，因为空间距离和时间距离的量纲不同.比如，α为20 km/d，表示时间距离上的1 d相当于空间距离上的20 km.把这3个协方差函数参数化为普通结构后，如指数模型、球状模型、高斯模型等.完整的和度量协方差函数模型一共包含10个不同参数：纯时间协方差函数的块金、基台值和变程，纯空间协方差函数的块金、基台值和变程，时空协方差函数的块金、基台值和变程以及一个各向异性比率α.时空和度量变异函数为[19]：2.2 时空协变异函数建模在使用时空CoKriging来研究变量的时空变异性时，关键的一步就是决定变量之间的时空协变异函数.它用来描述两变量之间交叉的时空连续性.协变异函数定义为：式中为同一位置上的两个不同变量为月均空气湿度为月均空气温度.在实际计算中，不需要直接利用以上定义来计算协变异函数，可用以下比较简单的方法来间接求得[21].先定义一个新的变量：即在同一个位置上，将两个变量的样本数值相加，所得之和即是新变量在该点的样本值，然后计算新变量的变异函数：而这一新变量的变异函数与原变量的变异函数和协变异函数有如下关系：因此可得：式(18)表明，要求出γ12(hs，ht)，先分别拟合得到分别采用时空可分离模型、时空积和模型、时空和度量模型3种不同的时空结合方法，对两个时空变量空气湿度和空气温度，采用时间去周期空间去趋势后的残差，来拟合时空变异函数.如图 8是空气相对湿度的残差的时空经验变异函数和理论变异函数.图 9是空气温度的残差的时空经验变异函数和理论变异函数.并采用均方根差RMSD(root-mean-squared-difference)指标来判断一个经验变异函数拟合的好坏.表1分别是3种不同方法得到的模型的RMSD值，从表 1可以看出，针对这两个时空变量，和度量时空模型的拟合效果最好.本实验中，采用和度量时空模型来建立空气湿度的残差和空气温度的残差的时空变异函数.图10是将空气湿度的残差和温度的残差之和作为一个新变量，这个新变量的经验变异函数和经和度量时空模型拟合的理论变异函数.使用和度量模型中的时空变异函数模型拟合数据，其中球状模型被选为空间和时间变异函数，等式右边第3项度量时空变异模型为指数模型[19].这3个组件都具有块金(C0)，偏基(C1)和变程(r)的参数，度量时空变异模型还有各向异性比这个参数，一共10个参数.表 2是空气相对湿度的残差，使用和度量模型拟合时空变异函数的10个不同参数的值.表 3是空气温度的残差，使用和度量模型拟合时空变异函数的10个不同参数的值.表 4是空气湿度残差与温度残差之和，使用和度量模型拟合时空变异函数的10个不同参数的值.经过和度量时空模型拟合后，空气湿度残差的理论变异函数γ11为：γ11(hs，ht)=1.01+7.41×经过和度量时空模型拟合后，空气温度残差的理论变异函数γ22为：经过和度量时空模型拟合后，空气湿度残差和空气温度残差之和的理论变异函数为：所以，根据式(18)，空气湿度的残差和空气温度的残差时空协变异函数γ12为：等式(22)右边的已由式(19)、(20)、(21)求出.式(19)γ11、式(20)γ22分别是空气湿度和空气温度的直接变异函数，式(22)γ12是空气湿度和空气温度的协变异函数.求出了γ11、γ22、γ12，就可以得到时空协同克里金插值公式(4)中的λ值，从而可以完成时空协同克里金插值.有效的变异函数模型是克里金插值的基础，本文的重点对时空协同克里金的变异函数进行建模分析.在拟合变异函数之前，首先对变量进行时间上去周期，空间上去趋势处理，以保证时空变量的平稳性.得到插值结果后，必须先将其加上之前去除的周期项和趋势项，才是最终估计结果.结果表明，空气相对湿度和空气温度在纯空间和纯时间上均符合球状模型，并且分别用3种不同的方法对这两个变量进行时空变异函数建模，发现在可分离模型、积和模型、和度量模型这3种模型中，和度量模型的拟合效果最好.完成时空直接变异函数拟合后，最后根据D.E.Myers[21]提出的方法，进行时空协变异函数建模.本文研究了多元时空数据进行时空直接变异函数和时空协变异函数的建模，不仅考虑了时间空间信息，而且还考虑了其他协变量.时空变异函数是时空克里金插值模型的权重参数构建的基础，对后续的时空协同克里金插值精度影响非常大.后续研究中，将研究大样本下的时空协同克里金插值结果(估计量)的统计性质(无偏、最优、相合性、线性插值结果的渐近正态性)，发展适应性多元时空统计模型应用于多个地学领域时空数据分析并评价插值精度.【相关文献】[1] 李莎，舒红，徐正全. 利用时空Kriging进行气温插值研究[J].武汉大学学报:信息科学版，2012， 37(2)：237-241.[2] Genton M G. Separable approximations of space-time covariance matrices[J]. Environmetrics， 2007， 18: 681-695.[3] Mitchell M W， Genton M G， Gumpertz M L. Testing for Separability of space-time covariances[J]. Environmetrics， 2005， 16: 819-831.[4] Cressie N， Huang H C. Classes of nonseparable spatio-temporal stationary covariance functions[J]. Journal of the American Statistical Association， 1999， 94:1330-1340．[5] Ma C S. Spatio-temporal stationary covariance models[J]. Journal of Multivariate Analysis， 2003， 86: 97-107.[6] Porcu E， Gregori P， Mateu J. Nonseparable stationary anisotropic space-time covariance functions [J]. Environmental Research and Risk Assessment， 2006， 21: 113-122.[7] Gneiting T. Nonseparable， stationary covariance functions for space-time data[J]. Journal of the American Statistical Association， 2002， 97: 590-600．[8] 徐爱萍，圣文顺，舒红. 时空积和模型的数据插值与交叉验证[J]. 武汉大学学报：信息科学版，2012， 37(7)：766-770.[9] De Cesare L， Myers D E， Posa D. Product-Sum covariance for space-time modeling: an environmental application[J]. Environmetrics， 2001， 12: 11-23．[10] Myers. D E. Space-time correlation models and contaminant plumes[J]. Environmetrics， 2002， 13:535-553.[11] De Iaco S， Myers D E， Posa D. Space-time analysis using a general product-sum model[J]. Statistics & Probability Letters， 2001， 52 (1):21-28.[12] 王燕.应用时间序列分析 [M].第2版.北京：中国人民大学出版社， 2008: 111-130.[13] De Iaco S， Palma M， Posa D. Modeling and prediction of multivariate space-time random fields[J]. Computational Statistics & Data Analysis， 2005， 48: 525-547.[14] Mateu J， Porcu E， Gregori P. Recent advances to model anisotropic space-time data[J]. Statistical Methods and Applications， 2008， 17: 209-23.[15] Fuentes M. Testing for separability of spatial-temporal covariance functions[J]. Journal of Statistical Planning and Inference， 2006， 136: 447-466.[16] Stein M. Space-time covariance functions[J]. Journal of the American Statistical Association， 2005， 100:310-321．[17] Fuentes M， Chen L， Davis J M. A class of nonseparable and nonstationary spatial temporal covariance functions[J]. Environmetrics， 2008， 19: 487-507.[18] De Cesare L， Myers D E， Posa D. Estimating and modeling space-time correlation structures[J]. Statistics &Probability Letters， 2001， 51(1):9-14．[19] Daniel A. Griffith G B, Heuvelink M. Deriving space-time variograms from Space-TimeAutoregressive (STAR) model specifications[J]. The International Archives of the Photogrammetry， Remote Sensing and Spatial Information Sciences， 2009， 38(2):15-19.[20] Dimitrakopoulos R， Luo X. Spatiotemporal Modeling: Covariances and Ordinary Kriging Systems [C]// Dimitrakopoulos R. Geostatistics for the Next Century. Springer Netherlands: Kluwer Academic Publishers， 1994(6):88-93．[21] Myers D E. Matrix formulation of Cokriging[J]. Mathematical Geology，1982， 14 (3):249-257.。

第２６卷第５期２００７年９月地理科学进展ＰＲＯＧＲＥＳＳＩＮＧＥＯＧＲＡＰＨＹＶｏｌ．２６，Ｎｏ．５Ｓｅｐｔ．，２００７收稿日期：２００７－０６；修订日期：２００７－０７．基金项目：国家科技基础条件平台，地球系统科学数据共享网（２００６ＤＫＡ３２３００）。

作者简介：刘润达，男（１９８０－），河南许昌人，博士生。

研究方向：科学数据共享，网络信息资源整合技术等。

科学数据共享关键问题探索———以地球系统科学数据共享网为例刘润达１，２，诸云强１（１．中国科学院地理科学与资源研究所，北京１００１０１；２．中国科学院研究生院，北京１０００３９）摘要：作为科学基础设施，科学数据共享平台建设可促进科技原始性创新，提高国家科技竞争能力。

本文回顾我国近年推动科学数据共享方面的工作，指出科学数据共享实施过程中所遇到的主要问题；针对这些问题，在共享理念、数据资源整合和平台建设三个方面探索科学数据共享今后发展的重点和工作方法。

具体结合地球系统科学数据共享网建设实践，提出搭建科学数据交换平台，构建科学数据共享联盟；将科学数据共享与科研项目相结合，实行主动服务；建立强大的科学数据搜索引擎；重视文档、信息服务等。

关键词：数据共享；科学数据；数据联盟；数据中介１引言科学数据作为现代科学可持续发展的重要资源，与科技创新是密不可分的［１］。

为促进科学数据资源的共享和交换，许多发达国家和国际组织都开展了一系列的基于计算机网络的科学数据共享的研究和实践，目的是将长期积累的科学数据为本国以及全球的可持续发展等研究提供数据支撑服务。

例如世界数据中心（ＷＤＣ，ＷｏｒｌｄＤａｔａＣｅｎｔｅｒ）等国际组织的成立，在世界范围内进行科学数据共享的工作［２，３］；美国及欧洲的一些发达国家建立了国家级科学数据中心群和数据共享服务网络［４￣６］，如ＮＡＳＡ主持的ＤＡＡＣｓ，全球变化数据和信息系统，全球变化主目录（ＧＣＭＤ）等。

我国自上世纪８０年代起就开始在多个层面上推动科学数据的共享。

Vol.39 No.1Jan. 2021第 39 卷第 1 期2021 年 01 月干旱地区农业研究Agricultural Research in the Arid Areas 文章编号：1000-7601（2021）01-0148-10 doi ：10.7606/j.issn.1000-7601.2021.01.20基于核熵成分分析的综合干旱指数的构建与应用—以黑河流域中上游为例郭盛明S 粟晓玲1，2，吴海江打姜田亮打梁筝'，冯凯1（1.西北农林科技大学水利与建筑工程学院，陕西杨凌712100；2.西北农林科技大学旱区农业水土工程教育部重点实验室，陕西杨凌712100）摘要:针对传统单变量干旱指数难以全面表征干旱及部分综合干旱指数难以反映多变量之间的非线性关系等问题，采用标准化降水蒸散发指数（SPE7）、标准化径流指数（SR/）及标准化土壤湿度指数（SSM7） 3个单变量指数分别表征气象干旱、水文干旱和农业干旱，利用核熵成分分析法（KECA ）构造综合干旱指数（SMQ/），采用M-K 趋势 检验、小波分析及典型历史旱情验证等方法分析干旱的时空变化特征以及干旱指数的适用性。

以黑河流域中上游 为例，结果表明：研究区全年77.6%的区域表现为干旱不显著加重的趋势；在流域尺度上，干旱存在43 a 的长周期，15~23 a 的中周期，3~8 a 的短周期；20世纪90年代夏、秋两季及21世纪以来春、冬两季干旱发生频率较高，且整体 夏旱发生频率最高；1969年春、1997年秋和2009年冬的典型历史旱情验证表明SMD/优于其他3种单变量干旱指数。

说明基于KECA 构建的SMQ/是一种有效的干旱监测指数，在黑河流域中上游干旱监测中有好的适用性。

关键词：核熵成分分析（KECA ）；综合干旱指数；干旱指数构建；应用；黑河流域中图分类号:S161.3文献标志码:AConstruction and application of comprehensive drought index based on kernel entropy component analysis—A case study of the upper and middle Heihe River BasinGUO Shengming 1 , SU Xiaoling 1,2, WU Haijiang 1 , JIANG Tianliang 1 , LIANG Zheng 1 , FENG Kai 1（1. College of IFater Resources and Architecture Engineering, Northwest A&F University, Wangling, Shaanxi 712100, China ；2. Aey Laboratory of Arid Area Agricultural 即ater and Soil Engineering , Ministry of Education ,Northwest A&F University, Wangling, Shaanxi 712100）Abstract ： In view of the cavity that the traditional single variable drought indices are difficult to characterize the comprehensive drought situation , and some existed composite drought indices reflect poorly on the nonlinear re ­lationship among multiple variables. We adopted kernel entropy component analysis （ KECA ） to construct a com ­prehensive drought index （ SMD/） by considering three various single drought indices : the standardizedprecipitation evaporation index （ SPE/） to represent meteorological drought , standardized runoff index （ SR/） to characterize hydrological drought , and standardized soil moisture index （ SSM/） to show agricultural drought.Taking the upper and middle reaches of Heihe River Basin as an example to analyze the drought spatiotemporal var ­iation and the applicability of SMD/, the M-K trend test , wavelet analysis and typical historical drought events val ­idation were utilized. The results showed that 77.6% of the grids of the study area presented an insignificant worse ­ning trend of drought in the whole year. Drought had a long period of 43 a, a medium period of 15 〜 23 a and ashort period of 3 〜 8 a on the watershed scale. In the season of summer and autumn of 1990s as well as in spring and winter since the 21st century, the drought frequency was higher. Moreover, the overall frequency of summer drought收稿日期：2020-08-14修回日期：2020-09-15基金项目：国家自然科学基金项目（51879222）作者简介：郭盛明（1996-），男，河南驻马店人，硕士研究生，研究方向为水文干旱分析。