[K12学习]山西省太原市2016-2017学年高二物理下学期期中试题 理(扫描版)
- 格式:doc
- 大小:5.23 MB
- 文档页数:12

2016-2017学年山西省太原市高二下学期期中数学试卷(理科)一、选择题 (共12题;共24分)1.(2分)复数2﹣i的共轭复数是()A.2+i B.1+2i C.﹣2﹣i D.﹣2+i2.(2分)下列说法正确的是()A.类比推理、归纳推理、演绎推理都是合情推理B.合情推理得到的结论一定是正确的C.合情推理得到的结论不一定正确D.归纳推理得到的结论一定是正确的3.(2分)已知函数f(x)=2e x,则()A.f′(x)=f(x)+2B.f′(x)=f(x)C.f′(x)=3f(x)D.f′(x)=2f(x)4.(2分)已知复数z在复平面内对应的点为(3,4),复数z的共轭复数为z̅,那么z• z̅等于()A.5B.﹣7C.12D.255.(2分)已知函数f(x)=x2+bx+c在x=﹣1处取得极值﹣1,那么f(x)=()A.x2﹣2x﹣4B.x2+x﹣1C.x2+2x D.x2﹣26.(2分)利用反证法证明:“若x2+y2=0,则x=y=0”时,假设为()A.x,y都不为0B.x≠y且x,y都不为0C.x≠y且x,y不都为0D.x,y不都为07.(2分)曲线y=﹣ln(2x+1)+2在点(0,2)处的切线与直线y=0和y=2x围成的三角形的面积为()A.13B.12C.23D.18.(2分)给出如下“三段论”的推理过程:因为对数函数y=log a x(a>0且a≠1)是增函数,…大前提而y= log12x是对数函数,…小前提所以y= log12x是增函数,…结论则下列说法正确的是()A.推理形式错误B.大前提错误C.小前提错误D.大前提和小前提都错误9.(2分)∫1−1√1−x2dx等于()A.π4B.π2C.πD.2π10.(2分)已知复数2i﹣3是方程2x2+px+q=0的一个根,则实数p,q的值分别是()A.12,0B.24,26C.12,26D.6,811.(2分)已知函数f0(x)=sinx+cosx,f1(x)=f′0(x),f2(x)=f′1(x),…f n+1(x)=f′n(x),n∈N,那么f2017=()A.cosx﹣sinx B.sinx﹣cosx C.sinx+cosx D.﹣sinx﹣cosx 12.(2分)设函数f(x)=(e x﹣1)(x﹣1)k,k∈N*,若函数y=f(x)在x=1处取到极小值,则k 的最小值为()A.1B.2C.3D.4二、填空题 (共4题;共8分)13.(2分)复数z=(1+i)+(﹣2+2i)在复平面内对应的点位于第象限.14.(2分)已知f(x)=x+ln(x+1),那么f′(0)=.15.(2分)我们知道:在长方形ABCD中,如果设AB=a,BC=b,那么长方形ABCD的外接圆的半径R满足:4R2=a2+b2,类比上述结论回答:在长方体ABCD﹣A1B1C1D1中,如果设AB=a,AD=b,AA1=c,那么长方体ABCD﹣A1B1C1D1的外接球的半径R满足的关系式是.16.(2分)若函数f(x)=x3+(k﹣1)x2+(k+5)x﹣1在区间(0,2)上不单调,则实数k的取值范围为.三、解答题 (共7题;共70分)17.(10分)已知z1=1﹣i,z2=2+2i.(1)(5分)求z1•z2;(2)(5分)若1z = 1z1+ 1z2,求z.18.(10分)已知函数f(x)=x3﹣2x2﹣4x.(1)(5分)求函数y=f(x)的单调区间;(2)(5分)求函数f(x)在区间[﹣1,4]上的最大值和最小值.19.(10分)已知函数f(x)=x3+ 1x+1,x∈[0,1].(1)(5分)用分析法证明:f(x)≥1﹣x+x2;(2)(5分)证明:f(x)>34.20.(10分)已知数列{b n}满足b n=| a n+2a n−1|,其中a1=2,a n+1= 2a n+1.(1)(5分)求b1,b2,b3,并猜想b n的表达式(不必写出证明过程);(2)(5分)由(1)写出数列{b n}的前n项和S n,并用数学归纳法证明.21.(10分)已知数列{a n}的前n项和为S n,且满足a1= 12,2S n﹣S n S n﹣1=1(n≥2).(1)(5分)猜想S n的表达式,并用数学归纳法证明;(2)(5分)设b n=na n1+30a n,n∈N*,求b n的最大值.22.(10分)设函数f(x)=x2e ax,a>0.(1)(5分)证明:函数y=f(x)在(0,+∞)上为增函数;(2)(5分)若方程f(x)﹣1=0有且只有两个不同的实数根,求实数a的值.23.(10分)已知函数f(x)=(x2﹣x﹣1a)e ax(a>0).(1)(5分)求函数y=f(x)的最小值;(2)(5分)若存在唯一实数x0,使得f(x0)+ 3a=0成立,求实数a的值.答案解析部分1.【答案】A【解析】【解答】解:复数2﹣i 的共轭复数为2+i .故选:A .【分析】利用共轭复数的定义即可得出.2.【答案】C【解析】【解答】解:合情推理包含归纳推理和类推理,所谓归纳推理,就是从个别性知识推出一般性结论的推理.其得出的结论不一定正确, 故选:C【分析】根据演绎推理和合情推理的定义判断即可.3.【答案】B【解析】【解答】解:根据题意,f (x )=2e x ,则f′(x )=2(e x )′=2e x ,即有f′(x )=f (x ), 故选:B .【分析】根据题意,由函数f (x ),对其求导可得f′(x ),分析f (x )与f′(x )的关系,计算可得答案.4.【答案】D【解析】【解答】解:由题意,z=3+4i , 则z• z̅ = |z|2=(√32+42)2=25 . 故选:D .【分析】由已知可得z ,结合 z ⋅z̅=|z|2 求解.5.【答案】C【解析】【解答】解:∵函数f (x )=x 2+bx+c ,∴f′(x )=2x+b ,∵函数f (x )=x 2+bx+c 在x=﹣1处取得极值﹣1, ∴{f(−1)=1−b +c =−1f ′(−1)=−2+b =0 , 解得b=2,c=0, ∴f (x )=x 2+2x . 故选:C .【分析】求出f′(x)=2x+b,由函数f(x)=x2+bx+c在x=﹣1处取得极值﹣1,利用导数性质列出方程组,能求出f(x).6.【答案】D【解析】【解答】解:根据用反证法证明数学命题的方法,应先假设要证命题的否定成立,而要证命题的否定为“x,y不都为0”,故选D.【分析】根据用反证法证明数学命题的方法,应先假设要证命题的否定成立,求得要证命题的否定,可得答案.7.【答案】B【解析】【解答】解:∵y=﹣ln(2x+1)+2,∴y'=﹣2 2x+1∴y'|x=0=﹣2∴曲线y=﹣ln(2x+1)+2在点(0,2)处的切线方程为y﹣2=﹣2(x﹣0)即2x+y﹣2=0令y=0解得x=1,令y=2x解得x= 12,y=1∴切线与直线y=0和y=x围成的三角形的面积为12×1×1= 12,故选B.【分析】根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式,然后求出与y轴和直线y=2x的交点,根据三角形的面积公式求出所求即可.8.【答案】B【解析】【解答】解:因为大前提是:对数函数y=log a x(a>0且a≠1)是增函数,不正确,导致结论错误,所以错误的原因是大前提错误,故选:B.【分析】要分析一个演绎推理是否正确,主要观察所给的大前提,小前提和结论及推理形式是否都正确,根据这几个方面都正确,才能得到这个演绎推理正确9.【答案】B【解析】【解答】解:∫1−1√1−x2dx的几何意义是以(0,0)为圆心,1为半径的单位圆在x 轴上方部分(半圆)的面积∴∫1−1√1−x2dx= 12×π×12=π2故选B.【分析】利用积分的几何意义,再利用面积公式可得结论.10.【答案】C【解析】【解答】解:∵2i﹣3是关于x的方程2x2+px+q=0的一个根,由实系数一元二次方程虚根成对定理,可得方程另一根为﹣2i﹣3,则q2=(﹣3+2i)(﹣3﹣2i)=13,即q=26,﹣p2=﹣3+2i﹣3﹣2i=﹣6,即p=12故选:C【分析】由实系数一元二次方程虚根成对定理可得方程另一根为﹣2i﹣3,再由韦达定理得答案.11.【答案】A【解析】【解答】解:根据题意,∵f0(x)=sinx+cosx,∴f1(x)=f0′(x)=cosx﹣sinx,f2(x)=f1′(x)=﹣sinx﹣cosx,f3(x)=﹣cosx+sinx,f4(x)=sinx+cosx,以此类推,可得出f n(x)=f n+4(x)∴f2017(x)=f504×4+1(x)=f1(x)=cosx﹣sinx;故选:A【分析】根据题意,利用导数的运算法则依次计算f1(x)、f2(x)、f2(x)…的值,分析可得f n+4(x)=f n(x),即可得f2017(x)=f504×4+1(x)=f1(x),即可得答案.12.【答案】B【解析】【解答】解:f′(x)=e x(x﹣1)k+k(e x﹣1)(x﹣1)k﹣1=(x﹣1)k﹣1[e x(x﹣1)+k(e x﹣1)],若函数y=f(x)在x=1处取到极小值,则x>1时,f′(x)>0,x<1时,f′(x)<0,故k﹣1>0,k>1,而k∈N*,故k的最小值是2,故选:B.【分析】求出函数的导数,根据函数的极值点,得到k﹣1>0,结合k∈N*,求出k的最小值即可.13.【答案】二【解析】【解答】解:∵z=(1+i)+(﹣2+2i)=﹣1+3i,∴z在复平面内对应的点的坐标为(﹣1,3),位于第二象限.故答案为:二.【分析】利用复数代数形式的加减运算化简,求出z的坐标得答案.14.【答案】2【解析】【解答】解:根据题意,f(x)=x+ln(x+1),,则其导数f′(x)=1+ 1x+1则f′(0)=1+1=2;故答案为:2.【分析】根据题意,对函数f(x)求导可得f′(x)的解析式,将x=0代入即可得答案.15.【答案】4R2=a2+b2+c2【解析】【解答】解:从平面图形类比空间图形,模型不变.可得如下结论:在长方体ABCD﹣A1B1C1D1中,如果设AB=a,AD=b,AA1=c,那么长方体ABCD﹣A1B1C1D1的外接球的半径R满足的关系式是4R2=a2+b2+c2,故答案为:4R2=a2+b2+c2.【分析】从平面图形类比空间图形,从二维类比到三维模型不变.16.【答案】(﹣5,﹣2)【解析】【解答】解:f′(x)=3x2+2(k﹣1)x+k+5,若函数f(x)=x3+(k﹣1)x2+(k+5)x﹣1在区间(0,2)上单调,则4(k﹣1)2﹣12(k+5)≤0 ①或②或③或④.解①得﹣2≤k≤7;解②得k≥1;解③得k∈∅;解④得k≤﹣5.综上,满足函数f(x)=x3+(k﹣1)x2+(k+5)x﹣1在区间(0,2)上单调的k的范围为k≤﹣5或k≥﹣2.于是满足条件的实数k的范围为(﹣5,﹣2).故答案为:(﹣5,﹣2).【分析】求出原函数的导函数,由导函数在区间(0,2)上恒大于等于0或恒小于等于0求出k的取值范围,再取补集得答案.17.【答案】(1)解:∵z1=1﹣i,z2=2+2i.∴z1•z2=(1﹣i)(2+2i)=4(2)解:由1z = 1z1+ 1z2,得z=z1⋅z2z1+z2=4(1−i)+(2+2i)=43+i=65−25i【解析】【分析】(1)直接利用复数代数形式的乘法运算化简得答案;(2)把已知等式通分变形求得z,代入z1、z2,再由复数代数形式的乘除运算化简得答案.18.【答案】(1)解:∵函数f(x)=x3﹣2x2﹣4x,∴f′(x)=3x2﹣4x﹣4,由f′(x)>0,得x<﹣23或x>2,由f′(x)<0,得﹣23<x<2,∴函数y=f(x)的单调增区间是(﹣∞,﹣23),[2,+∞);单调减区间是[﹣23,2].(2)解:由f′(x)=3x2﹣4x﹣4=0,得x1=−23,x2=2,列表,得:∴f(x)在[﹣1,4]上的最大值为f(x)max=f(4)=16,最小值为f(x)min=f(2)=﹣8.【解析】【分析】(1)求出f′(x)=3x2﹣4x﹣4,利用导数性质能求出函数y=f(x)的单调增区间和单调减区间.(2)由f′(x)=3x2﹣4x﹣4=0,得x1=−23,x2=2,列表讨论能求出f(x)在[﹣1,4]上的最大值和最小值.19.【答案】(1)证明:∵x∈[0,1],∴x+1∈[1,2].要证明:f(x)≥1﹣x+x2,只要证明:x3(x+1)+1≥(x+1)(1﹣x+x2),只要证明:x4≥0,显然成立,∴f(x)≥1﹣x+x2(2)证明:∵1﹣x+x2=(x﹣12)2+ 34≥ 34,当且仅当x= 12时取等号,∵f(12)= 1924>34,f(x)≥1﹣x+x2,∴f(x)>34【解析】【分析】(1)利用分析法的证明步骤,即可得出结论.(2)利用配方法,结合(1),即可得出结论.20.【答案】(1)解:∵a1=2,a n+1= 2a n+1,∴a2=23,a3=65,又b n=| a n+2a n−1|,得b1=4,b2=8,b3=16,猜想:b n=2n+1(2)解:由(1)可得,数列{b n}是以4为首项,2为公比的等比数列,则有Sn =4×(1−2n)1−2=2n+1−4.证明:当n=1时,S1=21+2−4=4成立;假设当n=k时,有S k=2k+2−4,则当n=k+1时,S k+1=S k+b k+1=2k+2−4+2k+2=2k+3﹣4=2(k+1)+2﹣4.综上,S n=2n+2−4成立【解析】【分析】(1)由已知结合数列递推式求得b1,b2,b3,并猜想b n的表达式;(2)由等比数列的前n项和公式求得数列{b n}的前n项和S n,并用数学归纳法证明.21.【答案】(1)解:∵S1=a1= 12,2S n=S n S n﹣1+1(n≥2),∴2S2=S2S1+1= 12S2+1,∴S2= 23;∴2S3=S3S2+1= 23S3+1,∴S3= 34;由S1= 12,S2= 23,S3= 34,可猜想S n= nn+1;证明:①当n=1时,S1= 12,等式成立;②假设n=k时,S k= kk+1,则n=k+1时,∵2S k+1=S k+1•S k+1= kk+1•S k+1+1,∴(2﹣kk+1)S k+1=1,∴S k+1= k+1k+2= k+1(k+1)+1,即n=k+1时,等式也成立;综合①②知,对任意n∈N*,均有S n=n n+1(2)解:由(1)可知,n≥2时,a n=S n﹣S n﹣1=nn+1﹣n−1n= 1n(n+1),当n=1时,a1= 11×2= 12满足上式,∴a n=1n(n+1),∴b n=na n1+30a n=nn2+n+30=1n+30n+1,n∈N*,设f(n)=x+ 30x,则有f(x)在(0,√30)上为减函数,在(√30,+∞)为增函数,∵n∈N*,且f(5)=f(6)=11,∴当n=5或n=6时,b n有最大值112【解析】【分析】(1)由S1=a1= 12,2S n=S n S n﹣1+1(n≥2),通过计算可求得S1,S2,S3;可猜想S n=nn+1,再利用数学归纳法证明即可.(2)求出b n=1n+30n+1,n∈N*,构造函数f(n)=x+ 30x,则利用函数的单调性即可求出.22.【答案】(1)证明:f(x)的定义域R,求导,f′(x)=2xe ax+ax2e ax=xe ax(ax+2),当x∈(0,+∞)时,a>0,则e ax>0,则xe ax(ax+2)>0,则f′(x)>0,∴函数y=f(x)在(0,+∞)上为增函数(2)令f′(x)=0,记得x=﹣v或x=0,则当x=﹣2a 时,函数有极大值f(﹣2a)= 4a2e2,当x=0时,函数有极小值f(0)=0,当x<0时,f(x)>0,x→﹣∞时,f(x)→0,x→+∞时,f(x)→+∞,由f(x)﹣1=0,即f(x)=1有且只有两个不同的实数根,即4a2e2=1,解得:a= 2e,(负根舍去)实数a的值2e【解析】【分析】(1)求导,由x∈(0,+∞)则f′(x)>0,则函数y=f(x)在(0,+∞)上为增函数;(2)求导,f′(x)=0,根据函数的单调性即可求得f(x)极大值,由f(x)=1有且只有两个不同的实数根,即4a2e2=1,即可求得实数a的值.23.【答案】(1)解:函数y=f(x)的定义域为R,f′(x)=[ax2+(2﹣a)x﹣2]e ax.令f′(x)=0,得x=1,x=﹣2a<0,当x∈(﹣∞,﹣2a),(1,+∞)时,f′(x)>0,当x∈(﹣v,1)时,f′(x)<0.∴函数f(x)在(﹣∞,﹣2a ),(1,+∞)上递增,在∈(﹣2a,1)递减.注意到x<﹣2a ,x2﹣x﹣1a>0,f(1)=﹣eaa<0.∴函数y=f(x)的最小值为f(1)=﹣e aa(2)解:存在唯一实数x0,使得f(x0)+ 3a =0成立⇔函数y=f(x)图象与y=﹣3a<(﹣3a0)有唯一交点,结合(1)可得函数f(x)在(﹣∞,﹣2a ),(1,+∞)上递增,在∈(﹣2a,1)递减.注意到x<﹣2a ,x2﹣x﹣1a>0,f(1)=﹣eaa<0.∴当且仅当﹣1a e a=−3a时,存在唯一实数x0,使得f(x0)+ 3a=0成立,即a=ln3时,存在唯一实数x0,使得f(x0)+ 3a=0成立【解析】【分析】(1)函数y=f(x)的定义域为R,f′(x)=[ax2+(2﹣a)x﹣2]e ax.利用导数可得函数f(x)在(﹣∞,﹣2a ),(1,+∞)上递增,在∈(﹣2a,1)递减.注意到x<﹣2a ,x2﹣x﹣1a>0,f(1)=﹣eaa<0.即函数y=f(x)的最小值为f(1)(2)存在唯一实数x0,使得f(x0)+ 3a =0成立⇔函数y=f(x)图象与y=﹣3a<(﹣3a0)有唯一交点,结合图象且仅当﹣1a e a=−3a时,存在唯一实数x0,使得f(x0)+ 3a=0成立,即可求得实数a的值.11/ 11。
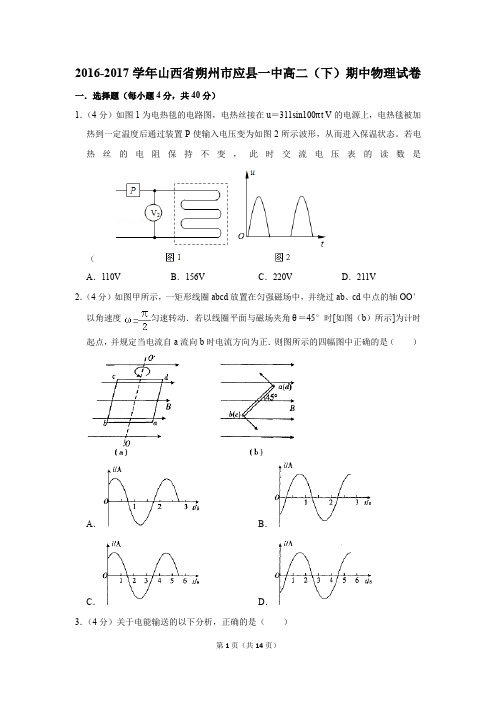
2016-2017学年山西省朔州市应县一中高二(下)期中物理试卷一.选择题(每小题4分,共40分)1.(4分)如图1为电热毯的电路图,电热丝接在u=311sin100πt V的电源上,电热毯被加热到一定温度后通过装置P使输入电压变为如图2所示波形,从而进入保温状态。
若电热丝的电阻保持不变,此时交流电压表的读数是(A.110V B.156V C.220V D.211V2.(4分)如图甲所示,一矩形线圈abcd放置在匀强磁场中,并绕过ab、cd中点的轴OO′以角速度匀速转动.若以线圈平面与磁场夹角θ=45°时[如图(b)所示]为计时起点,并规定当电流自a流向b时电流方向为正.则图所示的四幅图中正确的是()A.B.C.D.3.(4分)关于电能输送的以下分析,正确的是()A.由公式P=知,输电电压越高,输电线上功率损失越少B.由公式P=知,输电导线电阻越大,输电线上功率损失越少C.由公式P=I2R知,输电电流越大,输电导线上功率损失越大D.由公式P=UI知,输电导线上的功率损失与电流成正比4.(4分)一质点做简谐运动的位移x与时间t的关系如图所示,由图可知()A.频率是2HzB.t=0.5s时回复力的功率最大C.t=1.7s时的加速度为正,速度为负D.t=0.5s时,质点所受合外力为零5.(4分)一列波源在x=0处的简谐波,沿x轴正方向传播,周期为0.02s,t0时刻的波形如图所示。
此时x=12cm处的质点P恰好开始振动。
则()A.质点P开始振动时的方向沿y轴正方向B.波源开始振动时的方向沿y轴负方向C.此后一个周期内,质点P通过的路程为8cmD.这列波的波速为400m/s6.(4分)如图所示是两列相干水波的叠加情况,图中实线表示波峰,虚线表示波谷,设两列波的振幅均为5cm,且图示范围内振幅不变,波速和波长分别为1m/s和0.5m,C点是BE连线的中点.下列说法正确的是()A.C、E两点都保持静止不动B.图示时刻A、B两质点的竖直高度差为20cmC.图示时刻C点处于平衡位置且向水面上运动D.从图示时刻起经过了0.25s,B质点通过的路程为20cm7.(4分)如图所示,光线由空气射入半圆形玻璃砖,或由玻璃砖射入空气的光路图中,正确的是(玻璃的折射率为1.5)()A.图乙、丁B.图甲、丁C.图乙、丙D.图甲、丙8.(4分)关于自然光和偏振光,下列说法正确的是()A.自然光能产生光的干涉现象和衍射现象,而偏振光却不能B.只有自然光透过偏振片才能获得偏振光C.自然光只能是白光,而偏振光不能是白光D.自然光和偏振光都能使感光底片感光9.(4分)公园里洒光喷泉的水池中有处于同一深度的若干彩灯,在晚上观察不同颜色彩灯的深度和水面上被照亮的面积,下列说法正确的是()A.红灯看起来较浅且照亮的水面面积较小B.红灯看起来较深且照亮的水面面积较小C.红灯看起来较浅且照亮的水面面积较大D.红灯看起来较深且照亮的水面面积较大10.(4分)如图为红光或紫光通过双缝或单缝所呈现的图样,则()A.甲为紫光的干涉图样B.乙为紫光的干涉图样C.丙为红光的干涉图样D.丁为红光的干涉图样二、不定项选择题(每小题4分,共16分.每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对得4分,选不全的2分,选错或不答者的零分)11.(4分)如图所示,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线.则()A.分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距B.在真空中,a光的波长小于b光的波长C.玻璃砖对a光的折射率小于对b光的折射率D.若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失12.(4分)如图所示,ABCD是两面平行的透明玻璃,AB面和CD面平行,它们是玻璃和空气的界面,设为界面1和界面2.光线从界面1射入玻璃砖,再从界面2射出,回到空气中,如果改变光到达界面1时的入射角,则()A.只要入射角足够大,光线在界面1上可能发生全反射现象B.只要入射角足够大,光线在界面2上可能发生全反射现象C.不管入射角多大,光线在界面1上都不可能发生全反射现象D.光线穿过玻璃砖后传播方向不变,只发生侧移13.(4分)调压变压器是一种自耦变压器,它的构造如图所示.线圈AB绕在一个圆环形的铁芯上.AB间加上正弦交流电压U,移动滑动触头P的位置,就可以调节输出电压.在输出端连接了滑动变阻器R和理想交流电流表,变阻器的滑动触头为Q.则()A.保持P的位置不动,将Q向下移动时,电流表的读数变大B.保持P的位置不动,将Q向下移动时,电流表的读数变小C.保持Q的位置不动,将P沿逆时针方向移动时,电流表的读数变大D.保持Q的位置不动,将P沿逆时针方向移动时,电流表的读数变小14.(4分)如图所示为一单摆的振动图象,则()A.t1和t3时刻摆线的拉力等大B.t2和t3时刻摆球速度相等C.t3时刻摆球速度正在减小D.t4时刻摆线的拉力正在减小三、实验题(15题3+3=6分,16题共2+2+4=8分,共14分)15.(6分)某实验小组在利用单摆测定当地重力加速度的实验中:(1)用游标卡尺测定摆球的直径,测量结果如图所示,则该摆球的直径为cm。

山西省岢岚县中学2016-2017学年高二下学期期中考试物理试题一、选择题(每小题4分,共48分。
每小题给出的四个选项中,至少有一个选项是正确的。
请将正确选项前面的字母填在答卷的表格内)。
1. 有关磁感应强度的下列说法中,正确的是:A. 磁感应强度是用来表示磁场强弱的物理量B. 若有一小段通电导体在某点不受磁场力的作用,则该点的磁感应强度一定为零C. 若有一小段长为L,通以电流为I的导体,在磁场中某处受到的磁场力为F,则该处磁感应强度的大小一定是D. 由定义式可知,电流I越大,导线L越长,某点的磁感应强度就越小【答案】A【解析】试题分析:磁感应强度是用来表示磁场强弱的物理量,选项A正确;若有一小段通电导体在某点不受磁场力的作用,可能是电流方向与磁场方向平行,该点的磁感应强度不一定为零,选项B错误;若有一小段长为L,通以电流为I的导体,在磁场中某处受到的最大的磁场力为F,则该处磁感应强度的大小一定是,选项C错误;磁场中某点的磁感应强度与放入的电流大小和导线的长度无关,选项D错误;故选A.考点:磁感应强度【名师点睛】磁感应强度是描述磁场强弱和方向的物理量,B的定义式:是采用比值法定义的,B的大小与F、IL等无关,由磁场本身决定的,B是矢量,其方向与放在该处的通电导线中的电流方向垂直.2. 下列几种说法中正确的是:A. 线圈中磁通量变化越大,线圈中产生的感应电动势一定越大B. 线圈中磁通量越大,产生的感应电动势一定越大C. 线圈放在磁场越强的位置,产生的感应电动势一定越大D. 线圈中磁通量变化越快,线圈中产生的感应电动势越大【答案】D【解析】试题分析:感应电动势,与磁通量的变化率成正比,与磁通量的大小、磁通量的变化量没有关系,AB错;,线圈在磁感应强度变化率最大的位置,感应电动势最大,C错D对,故选D考点:考查法拉第电磁感应定律点评:难度较小,感应电动势只与磁通量的变化率成正比,与磁通量、磁通量的变化量、磁感强度都没有关系3. 在如图所示的电路中,E为电源电动势,r为电源内阻,R1和R3均为定值电阻,R2为滑动变阻器。

一、单项选择题(本题共7小题,每小题4分,共28分,每小题只有一个正确选项,多选、错选或不选均不得分) l 。
如图所示,单摆摆球的质量为 m ,摆长为L,摆球从最大位移A处由静止释放,摆球运动到最低点B 时的速度大小为v ,重力加速度为g ,不计空气阻力。
则摆球从A 运动到B 的过程中( )A .重力做的功为221υmB .重力的最大功率为mgvC .重力的功率先减小后增大D .摆球运动到最低点B 时绳的拉力为L m 2υ2。
如图所示.A 球振动后.通过水平细线迫使B 、C 、D 振动,下面说法中正确的是( )A .只有A 、B 振动周期相等B .C 摆长最小,所以C 的固有频率最大C .B 的振幅比C 的振幅大D .A 、B 、C 、D 的振动振幅相等3. 竖直向上抛出一个物体,经3s到达最高点,设第2s内该物体动量变化的大小为△P1,物体克服重力所做的功为W1,第3s内该物体动量变化的大小为△P2,物体克服重力所做的功为W 2,若不计空气阴力,则( )A。
△P1=△P2,W1〉W2 B。
△P1=△P2,W1=W2C.△P1>△P2,W1〉W2 D。
△P1〉△P2,W1<W24.如图所示为一列简谐横波的图象,波速为0.2m/s.则以下结论正确的是( )A.振源振动的频率为0。
4HzB.若质点a比质点b先回到平衡位置,则波沿x轴正方向传播C.图示时刻质点a、b、c所受的回复力大小之比为2∶1∶3D.经过0。
5 s,质点a、b、c通过的路程均为75 cm。
5. 一列简谐波在t=0时刻的波形如图中的实线所示,t=0。
02 s时刻的波形如图中虚线所示.若该波的周期T大于0。
02 s,则该波的传播速度可能是()A.2 m/s B.3 m/s C.4 m/s D.5 m/s6. 在光滑的水平面上用一个小于先后以相同的速率跟原来静止的A、B、C三球发生正碰。
与A球相碰后,小球仍然沿原方向运动;与B球相碰后,小球停止运动;与C球相碰后,小球被弹回方向运动.那么A、B、C三球所获得的动量大小比较,正确的是( )A、p A=p B=p C;B、p A>p B>p C;C、p A<p B<p C;D、因不知道被碰的三球质量,故无法比较7.消除噪音污染是当前环境保护的一个重要课题.内燃机、通风机等在排放各种高速气流的过程中都发出噪声,干涉型消声器可以用来削弱高速气流产生的噪声。

山西省朔州市应县2016-2017学年高二物理下学期期中试题时间:100分钟 满分:110分一.选择题(每小题4分,共40分)1、图甲为电热毯的电路示意图。
电热丝接在u=311sin 100πt (V)的电源上,电热毯被加热到一定温度后,通过装置P 使输入电压变为图乙所示波形,从而进入保温状态。
若电热丝电阻保持不变,此时交流电压表的读数是( ) A.110 VB.156 VC.220 VD.311 V2、如图甲所示,一矩形线圈abcd 放置在匀强磁场中,并绕过ab 、cd 中点的轴OO'以角速度ω逆时针匀速转动。
若以线圈平面与磁场夹角θ=45°时(如图乙)为计时起点,并规定当电流自a 流向b 时,电流方向为正。
则下列四幅图中正确的是( )3、关于电能输送的以下分析,正确的是( )A .由公式P =U 2R 知,输电电压越高,输电线上功率损失越少B .由公式P =U 2R知,输电导线电阻越大,输电线上功率损失越少C .由公式P =I 2R 知,输电电流越大,输电导线上功率损失越大 D .由公式P =UI 知,输电导线上的功率损失与电流成正比4、一质点做简谐运动的位移x 与时间t 的关系如图所示,由图可知( ) A .频率是2 HzB .t =0.5 s 时回复力的功率最大C .t =1.7 s 时的加速度为正,速度为负D .t =0.5 s 时,质点所受合外力为零5、一列波源在x =0处的简谐波,沿x 轴正方向传播,周期为0.02 s,t0时刻的波形如图所示.此时x=12 cm处的质点P恰好开始振动.则( ) A.质点P开始振动时的方向沿y轴正方向B.波源开始振动时的方向沿y轴负方向C.此后一个周期内,质点P通过的路程为8 cmD.这列波的波速为400 m/s6、如图所示表示两列相干水波的叠加情况,图中的实线表示波峰,虚线表示波谷.设两列波的振幅均为5cm,且在图示的范围内振幅不变,波速和波长分别为1m/s和0.5m.C点是BE 连线的中点,下列说法不正确的是( )A.C、E两点都保持静止不动B.图示时刻A、B两点的竖直高度差为20cmC.图示时刻C点正处在平衡位置且向水面运动D.从图示的时刻起经0.25s后,B点通过的路程为20cm7、如图所示,光线由空气射入半圆形玻璃砖,或由玻璃砖射入空气的光路图中,正确的是(玻璃的折射率为1.5)()A.图乙、丁B.图甲、丁C.图乙、丙D.图甲、丙8、关于自然光和偏振光,下列说法正确的是()A.自然光能产生光的干涉现象和衍射现象,而偏振光却不能B.只有自然光透过偏振片才能获得偏振光C.自然光只能是白光,而偏振光不能是白光D.自然光和偏振光都能使感光底片感光9、公园里灯光喷泉的水池中有处于同一深度的若干彩灯,在晚上观察不同颜色彩灯的深度和水面上被照亮的面积,下列说法正确的是( )A.红灯看起来较浅,红灯照亮的水面面积较小B.红灯看起来较深,红灯照亮的水面面积较小C.红灯看起来较浅,红灯照亮的水面面积较大D.红灯看起来较深,红灯照亮的水面面积较大10、下图为红光或紫光通过双缝或单缝所呈现的图样,则()A.甲为紫光的干涉图样B.乙为紫光的干涉图样C.丙为红光的干涉图样D.丁为红光的干涉图样二、不定项选择题(每小题4分,共16分.每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对得4分,选不全的2分,选错或不答者的零分)11、如图所示,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ,经折射后射出a、b两束光线.则( )A.分别用a、b光在同一个双缝干涉实验装置上做实验,a光的干涉条纹间距大于b光的干涉条纹间距B.在真空中,a光的波长小于b光的波长C.玻璃砖对a光的折射率小于对b光的折射率D.若改变光束的入射方向使θ角逐渐变大,则折射光线a首先消失12、如图所示,ABCD是两面平行的透明玻璃,AB面和CD面平行,它们是玻璃和空气的界面,设为界面1和界面2.光线从界面1射入玻璃砖,再从界面2射出,回到空气中,如果改变光到达界面1时的入射角,则( )A.只要入射角足够大,光线在界面1上可能发生全反射现象B.只要入射角足够大,光线在界面2上可能发生全反射现象C.不管入射角多大,光线在界面1上都不可能发生全反射现象D.光线穿过玻璃砖后传播方向不变,只发生侧移13、调压变压器是一种自耦变压器,它的构造如图所示。

2016-2017学年山西省太原市高二(下)期中数学试卷(理科) 一、选择题(本大题共12小题,每小题3分,共36分) 1.(3分)复数2﹣i的共轭复数是( ) A.2+i B.1+2i C.﹣2﹣i D.﹣2+i 2.(3分)下列说法正确的是( ) A.类比推理、归纳推理、演绎推理都是合情推理 B.合情推理得到的结论一定是正确的 C.合情推理得到的结论不一定正确 D.归纳推理得到的结论一定是正确的 3.(3分)已知函数f(x)=2ex,则( ) A.f′(x)=f(x)+2 B.f′(x)=f(x) C.f′(x)=3f(x) D.f′(x)=2f(x) 4.(3分)已知复数z在复平面内对应的点为(3,4),复数z的共轭复数为,那么z•等于( ) A.5 B.﹣7 C.12 D.25 5.(3分)已知函数f(x)=x2+bx+c在x=﹣1处取得极值﹣1,那么f(x)=( ) A.x2﹣2x﹣4 B.x2+x﹣1 C.x2+2x D.x2﹣2 6.(3分)利用反证法证明:“若x2+y2=0,则x=y=0”时,假设为( ) A.x,y都不为0 B.x≠y且x,y都不为0 C.x≠y且x,y不都为0 D.x,y不都为0 7.(3分)曲线y=﹣ln(2x+1)+2在点(0,2)处的切线与直线y=0和y=2x围成的三角形的面积为( ) A. B. C. D.1 8.(3分)给出如下“三段论”的推理过程: 因为对数函数y=logax(a>0且a≠1)是增函数,…大前提 而y=是对数函数,…小前提
所以y=是增函数,…结论 则下列说法正确的是( ) A.推理形式错误 B.大前提错误 C.小前提错误 D.大前提和小前提都错误 9.(3分)dx等于( )
A. B. C.π D.2π 10.(3分)已知复数2i﹣3是方程2x2+px+q=0的一个根,则实数p,q的值分别是( ) A.12,0 B.24,26 C.12,26 D.6,8 11.(3分)已知函数f0(x)=sinx+cosx,f1(x)=f′0(x),f2(x)=f′1(x),…fn+1