沪教课标版七年级下册数学:13.4 平行线的判定
- 格式:ppt
- 大小:303.00 KB
- 文档页数:10

上海市初中数学2019-2020学年度七年级数学同步教学案平行线的判定的深度剖析之二【知识点梳理】1.平行线的概念同一平面内不相交的两条直线叫做平行线.【注意】①“在同一平面内”是定义的首要前提条件,不可缺少,因为在空间里,还存在两条直线既不相交,也不平行的情况;②“不相交”是说两条直线向两个方向怎样延长都不会相交;③平常所说的两条射线或线段平行,实质上是指它们所在的直线平行;④在同一平面内,两条不重合的直线只有两种位置关系:平行与相交.2.平行线的表示方法平行线符号“∥”表示.如AB平行于CD表示为AB∥CD.3.平行线的基本性质(1)经过直线外一点,有且只有一条直线与已知直线平行.推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.平行公理及其推论是整个初中平面几何的基石,是其他公理、定理的基础,它们的作用十分重要.平行公理及其推论在说明直线平行时,经常用到.【注意】这条性质与垂线的性质很相似,但过任意一点都可以画垂线,而画平行线,只能是过直线外一点才可以.4.平行线的三种判定方法(1)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行,简单地说,同位角相等,两直线平行.(2)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单地说,内错角相等,两直线平行.(3)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,简单地说,同旁内角互补,两直线平行.基本图形如图所示:(1)如果12∠=∠,那么12//l l ;(2)如果32∠=∠,那么12//l l ;(3)如果24180∠+∠=︒,那么12//l l .【注意】①平行线的判定,实质上是同位角、内错角、同旁内角的识别,对于它们的识别,一要注意它们的位置特征,二要注意它们的图形特征.②判定两直线平行应根据所给条件,适当选用三种方法中的一种.③判定两直线平行还可以根据定义和平行的传递性(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).【典型例题讲解】【例l 】下列结论中正确的个数是 ( )①同一平面内不相交的两条直线必平行;②同一平面内不平行的两条直线必相交;③同一平面内不相交的两条线段必平行; ④同一平面内不平行的两条线段必相交.(A)l (B)2 (C)3 (D)4【分析】在同一平面内的两条直线的位置关系,只有相交与平行(重合的情形通常不考虑),所以①②是正确的;由于线段的特征,当两条线段不相交时,也有可能不平行,故③④是错误的.【解析】B .【方法总结】此类题首先要理解好概念进行判断,往往利用画出反例的图形进行判断.【例2】完成下列推理:(1)如图,已知AB ∥EF ,AB ∥CD .因为AB ∥EF , (已知),所以____∥____( )(2)如图所示,已知MN AB ⊥于M ,CD AB ⊥于D .因为MN AB ⊥于M ,CD AB ⊥于D (已知),∠=____=( ).所以NMB你能发现这两条直线MN与CD位置关系是.【分析】平行公理及其推论是解决这类问题的依据.这两个问题都可依据平行公理及其推论完成推理过程.【解析】(1) AB∥CD CD EF平行公理推论∠90︒垂直定义平行(2)CDB【方法总结】说明两直线平行的考法很多,利用平行公理说明两直线平行时,首先要明确想要说明的是哪两条直线平行,应通过哪些直线平行,来说明这两条直线平行.【借题发挥】平行线是( )A.没有公共点的两条直线B.在同一平面内,不相交的两条直线C.经过直线外一点,有且只有一条直线与这条直线平行D.永远不会相交的两条直线【解析】本题考查对平行线定义的理解,选B.【例3】如图所示,经过点M画MN∥OA,交OB于点N;画ME∥OB,交OA于点E.【分析】本题是利用平行线的基本画法来画.【解析】画法一落:把三角板的一边落在直线OA上;二靠:把直尺紧靠三角板的一边;三推:把三角板沿着直尺的边推到使刚才落在OA 上的边恰好经过已知点M 的位置;四画:沿着三角板经过点的边画直线MN ,交OB 于点N .用同样的方法画ME ∥OB .【方法总结】“一落二靠三推四画”是画平行线的基本方法.注意的是:画平行线的关键是过哪点画哪两条直线平行,因此一般画平行线时,应先说明过哪一点,再说明哪两条直线平行.【借题发挥】利用直尺和三角板画平行线.【解析】略,可参考例1的解析.【例4】如图所示,直线a 与b 被直线c 所截,如果12180∠+∠=︒,那么a ∥b .试简述理由.【解析】将∠1的邻补角记作∠3,则∠1+∠3180=︒(邻补角的定义).因为12180∠+∠=︒(已知),所以23∠=∠(同角的补角相等),所以a ∥b (同位角相等,两直线平行).【方法总结】(1)在几何图形中往往隐含着一些条件,而这些条件可在图形中挖掘.如本题中由图可知∠l 与∠3的邻补角关系.要学会观察图形,从中寻找条件.(2)几何解题过程中,每一步都要有一定的依据,请同学们务必充分注意.【例5】如图所示,∠1=70︒,∠2=110︒,问AB 与CD 平行吗?为什么?试用不同的方法来说明.【解析】我们用三种方法来判定AB 与CD 平行.方法一:因为2180CNM ∠+∠=︒(邻补角的定义),2110∠=︒(已知).所以180270CNM ∠=︒-∠=︒.又因为170∠=︒(已知).所以1CNM ∠=∠(等量代换),所以AB ∥CD (同位角相等,两直线平行).方法二:因为1BMN ∠=∠(对顶角相等),170∠=︒(已知).所以70BMN ∠=︒.由方法一知70CNM ∠=︒,所以CNM BMN ∠=∠ (等量代换),所以AB ∥CD (内错角相等,两直线平行).方法三:因为1BMN ∠=∠(对顶角相等),170∠=︒(已知),所以70BMN ∠=︒.因为2DNM ∠=∠(对顶角相等),2110∠=︒(已知),所以110DNM ∠=︒.所以180BMN DNM ∠+∠=︒(等式性质),所以AB ∥CD (同旁内角互补,两直线平行).【方法总结】本题是同一个题用三种方法来进行判断,由于判断途径不同,所以判断过程及方法也不一样,同一题常会有多种解题方法,读者必须充分重视,这有利于培养思维的灵活性,提高解题能力.【借题发挥】如图所示,145,2135∠=︒∠=︒,则直线1l 、2l 平行吗?为什么?【分析】由题目提供的条件可知,12180∠+∠=︒,而13180∠+∠=︒,由此可知23∠=∠.根据同位角相等,两直线平行,可得出1l ∥2l 的结论.【解析】直线1l 、2l 平行,理由如下:因为13180∠+∠=︒,145∠=︒所以3135∠=︒,又因为2135∠=︒,所以23∠=∠.所以1l ∥2l (同位角相等,两直线平行)【方法总结】要判定直线1l 、2l 平行,首先说明这两条直线被直线3l 所截,形成的同位角2∠、3∠相等,根据“同位角相等,两直线平行”,即可判定这两条直线平行.【例6】如图所示,已知1120,260∠=︒∠=︒.求证:AB ∥CD .【分析】要说明AB ∥CD ,只要得出同位角、内错角、同旁内角的关系即可.【证明】证法一:因为15180,1120∠+∠=︒∠=︒,所以560∠=︒,因为260∠=︒,所以25∠=∠,所以AB ∥CD (同位角相等,两直线平行).证法二:因为23∠=∠(对顶角相等).又因为260∠=︒(已知),所以360∠=︒(等量代换).因为15180∠+∠=︒(互补的定义),又因为1120∠=︒,所以560∠=︒(等式性质),所以35∠=∠(等量代换).所以AB ∥CD (内错角相等,两直线平行).证法三:因为23∠=∠,260∠=︒,所以360∠=︒,因为16∠=∠.1120∠=︒,所以6120∠=︒,所以36180∠+∠=︒,所以AB ∥CD (同旁内角互补.两直线平行).【方法总结】初步感知逻辑推理的过程及其表达,一定要做到有理有据.【借题发挥】如图所示:(1)因为3A ∠=∠,所以 ∥ ,理由是 ;(2)因为24∠=∠,所以 ∥ ,理由是 ;(3)因为46180∠+∠=︒,所以 ∥ ,理由是 ;(4)因为5∠= ,所以EF ∥ ,理由是 ;(5)因为5∠= ,所以BC ∥ ,理由是 .【分析】对于第(1)(2)(3)题,首先判断已知的两角是同位角、内错角、还是同旁内角,然后根据平行线的判定方法判定被截两直线平行;对于(4)(5)两题,条件和结论都不完整,故需前后综合考虑.【解析】(l) EF ∥AC .同位角相等,两直线平行;(2) EF ∥AC .内错角相等,两直线平行;(3) ED ∥BC ,同旁内角互补,两直线平行;(4) C ∠,AC ,同位角相等,两直线平行;(5) ∠4.ED ,内错角相等,两直线平行.【方法总结】本题考查的是平行线的判定方法,故要对平行线的三种判定理解透彻,要判定哪两条直线平行,一定要辨明是哪两条直线被第三条直线所截.【随堂练习】1.过一点画已知直线的平行线有 ( )A .有且只有一条B .有两条C .不存在D .不存在或仅一条【解析】过一点画已知直线的平行线分两种情况:当这个点在已知直线上时,平行线不存在;当这个点是已知直线外的一点时,有且仅有一条平行线平行已知直线,所以选D .2.在同一平面内,两条直线的位置关系可能是 ( )(A)相交或垂直 (B)垂直或平行(C)平行或相交 (D)相交或垂直或平行【解析】准确掌握同一平面内两直线的住置关系,在同一平面内,两直线的位置关系只有两种:相交或平行,两直线互相垂直是相交的一个特例.所以选C .3.如图所示,下列条件中,不能判定1l ∥2l 的是( )(A)13∠=∠ (B)23∠=∠(C)45∠=∠ (D)24180∠+∠=︒【解析】因为13∠=∠,所以1l ∥2l (内错角相等,两直线平行);因为45∠=∠,所以1l ∥2l (同位角相等,两直线平行);因为24180∠+∠=︒,所以1l ∥2l (同旁内角互补,两直线平行).因为2∠与3∠之间的关系和两直线之间是否平行没有任何关系,所以由23∠=∠不能判定两直线平行,故答案选B .判定两直线平行,必须严格按照平行线的判定方法.4.如图,要判定AD ∥BC ,只要说明内错角 = ,要判定AB ∥CD ,只要说明内错角 = .【解析】23∠=∠;14∠=∠5.如图,(1)因为∠1= (已知),所以DF ∥ ( )(2)因为∠2= (已知),所以BC ∥ ( )(3)因为∠2= (已知),所以EF ∥ ( )(4)因为∠3+ =180°(已知),所以EF ∥ ( )【解析】(1);B BC ∠;同位角相等,两直线平行(2)3;DE ∠;内错角相等,两直线平行(3);C AC ∠;同位角相等,两直线平行(4)5;AC ∠;同旁内角互补,两直线平行6.如图,(1)因为∠1=∠2(已知),所以 ∥ ( )(2)因为∠3=DCB ∠(已知)所以 ∥ ( )(3)因为∠4=∠EAF (已知),所以 ∥ ( )(4)因为180EAF ADC ∠+∠=︒所以 ∥ ( )【解析】(1)AD ;BC ; 内错角相等,两直线平行(2) AD ;BC ;内错角相等,两直线平行(3) BC ;AD ;同位角相等,两直线平行(4) ;DC AB ;同旁内角互补,两直线平行7.如图,直线a 、b 被直线c 所截,如果12∠=∠,那么a ∥b 吗?为什么?【解析】a ∥b .将∠l 的对顶角记作∠3,则有∠l =∠3(对顶角相等),又因为12∠=∠(已知),所以∠2=∠3(等量代换),所以a ∥b (同位角相等,两直线平行).8.如图,利用直尺和三角板,经过点P 画直线PE ∥OA 交OB 于点E ,画直线PF ∥OB交AO 的延长线于点F .【解析】如图所示:【课堂总结】【课后作业】1.看右图填空,并在括号内填人适当的理由.(1)如果内错角相等,即12∠=∠,能否判定//a b ?解 因为12∠=∠(已知)13∠=∠ ( ).所以32∠=∠,( )所以//a b ( ).(2)如果同旁内角互补,即24180∠+∠=︒,能否判定//a b ?解 因为24180∠+∠=︒ ( ).34180∠+∠=︒( ),所以 32∠=∠( ).所以//a b ( ).(3)由(1)、(2),可知两条直线平行的基本判定方法是: ,还有两种判定方法分别是: , .2.看图填空,并在括号内填写适当的理由.如右图,因为5∠= (已知),所以AD ∥BC ( ).因为2∠+ 180=︒(已知),所以AB ∥DC ( ).因为3∠= (已知),所以AB ∥DC ( ).3.选择题(1)如图1,DE 是过点A 的直线,如果要使//DE BC ,那么需要条件( )(A) ACB BAD ∠=∠; (B) ACB BAC ∠=∠;(C) ACB CAE ∠=∠; (D) ACB ABC ∠=∠.图1 图2 图3(2)如图2,直线a 、b 被直线c 所截,根据同旁内角互补,得到//a b 的结论,则已知互补的两个角是 ( ) (A)1∠和3∠; (B) 2∠和4∠;(C)2∠和5∠; (D) 2∠和3∠.(3)如图3,下列条件中,不能判断直线12//l l 的是 ( )(A) 13∠=∠; (B) 23∠=∠;(C) 45∠=∠; (D) 24180∠+∠=︒.(4)如图4,如果42,138B BDE ∠=︒∠=︒,那么 ( )(A)EF ∥BC ; (B) ED ∥AB ;(C) DF ∥AC ; (D)图中没有平行直线.图4 图5 图6(5)如图5,已知55,80,45B BAC CAD ∠=︒∠=︒∠=︒,可以判定AD ∥BC ,其根据是 ( )(A)内错角相等,两直线平行;(B)同位角相等,两直线平行;(C)同旁内角互补,两直线平行,(D)平行于同一直线的两直线平行.(6)如图6,下列说法中,错误的是 ( )(A)因为24∠=∠,所以AB ∥DC ;(B)因为13∠=∠,所以AD ∥BC ;(C)因为43180B ∠+∠+∠=︒,所以AD ∥BC ;(D)因为12180D ∠+∠+∠=︒,所以AB ∥DC .4.如图所示,已知直线EF 和AB 相交于点D ,180B ADE ∠+∠=︒,直线EF 与BC 平行吗?为什么?【答案】1.(1)对顶角相等;等量代换;同位角相等,两直线平行(2)已知;邻补角定义;等式性质;同位角相等,两直线平行(3)同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行2.6∠;内错角相等,两直线平行;6∠;同旁内角互补,两直线平行;5∠;同位角相等,两直线平行3.(1)C (2)D (3)B (4)B (5)C (6)C4.本题中,利用“同旁内角互补,两直线平行”,首先应判定这两直线被第三条直线所截,所形成的同旁内角互补.本题中还利用了“对顶角相等”这一重要命题.ADE ∠与BDF ∠是对顶角,根据“对顶角相等”即可得到180B ADE ∠+∠=︒.从而根据“同旁内角互补,两直线平行”,说明EF ∥BC .【解析】因为直线EF 和BC 相交于点D .所以ADE ∠= BDF ∠ (对顶角相等).因为180B ADE ∠+∠=︒,所以180B BDF ∠+∠=︒.所以EF ∥BC (同旁内角互补,两直线平行).。

数学七年级下第十三章相交线平行线13.4 平行线的判定(1)一、选择题1、下列说法正确的有〔〕①同一平面内不相交的两条直线是平行线;②同一平面内不相交的两条线段平行③过直线外一点有且只有一条直线与已知直线平行;④平行于同一条直线的两条直线平行A.1个B.2个C.3个D.4个2、在同一平面内,两条不重合直线的位置关系可能是〔〕A.平行或相交B. 垂直或平行C. 平行、垂直或相交D. 垂直或相交3.如图所示,下列条件中,能判断AD∥BC的是 ( )A. ∠ABD=∠BDCB. ∠BAD=∠BCDC. ∠BAC=∠ACDD. ∠ADB=∠CBD第3题第4题第5题第8题4.如图所示,下列推理正确的是 ( )A. 因为∠1=∠2,所以AB∥CDB. 因为∠1=∠3,所以AE∥CFC. 因为∠2=∠4,所以AB∥CDD. 因为∠2=∠4,所以AE∥CF5.如图所示,下列条件中,不能判断AB∥CE的是 ( )A. ∠ACE =∠AB.∠A=∠ECDC.∠B=∠ECDD.∠B+∠BCE=180°6. 已知直线a外有一点P,用三角尺过点P画直线b与a相交成90°,再过点P画直线c与b相交成90°,在这个图形中,相互平行的两条直线是 ( )A. a与bB. b与cC. a与cD. a与c或 b与c7.在同一个平面内,不相邻的两个直角,如果它们有一边在同一直线上,那么另一边相互 ( )A.平行B. 平行或垂直C. 平行或垂直或相交D. 垂直8、如图所示, 下列条件中,不能判断AB∥CD的是〔〕A. ∠ACD =∠BACB. ∠B=∠DCFC. ∠DAC=∠ACBD.∠B+∠BCD=180°二、填空题9. 叫做平行线。
10. 经过已知直线外一点,与这条已知直线平行。
11. 如果已知直线l1、l2被直线l所截得的一对同位角都是110°,那么直线l1、l2的位置关系是,理由是。

七年级下册数学平行线的判定七年级下册数学平行线的判定一、概述平行线是初中数学中的重要知识点,也是七年级下册的一项难点内容。
平行线的判定方法有多种,本文将对其中的三种方法进行详细介绍。
二、第一种判定方法:同旁内角等1.定义:同旁内角等定义为,两条直线上的同旁内角相等,则这两条直线是平行线。
2.具体步骤:(1)画两条直线l和m,并选择任意一点A点。
(2)在l上找到一点B,在m上找到一点C。
(3)以A点为圆心,在l上画一个圆,焦点在B点上;在m上画另一个圆,焦点在C点上。
(4)设两圆的交点分别为D、E、F。
(5)连接ADE、BCF,并证明∠ADE=∠BCF。
(6)如果∠ADE=∠BCF,则可得出l和m是平行线。
三、第二种判定方法:同位角相等1.定义:同位角相等定义为,两条直线被另外一条直线割成的同位角相等,则这两条直线是平行线。
2.具体步骤:(1)画两条直线l和m,并选择任意一条直线n,使得n与l和m相交。
(2)在l和m上各找到一组同位角,分别为A1、A2,B1、B2。
(3)连接A1B1、A2B2,并证明∠A1=∠A2。
(4)如果∠A1=∠A2,则可得出l和m是平行线。
四、第三种判定方法:反证法1.定义:反证法定义为,如果已知两条直线l和m不平行,则这两条直线必相交。
2.具体步骤:(1)画两条直线l和m,并选择任意一点A点。
(2)在l上找到一点B,在m上找到一点C,连接BC。
(3)如果BC与l平行,则BC与l的交点D无限远,不可能相交;同样,如果BC与m平行,则BC与m的交点E也无限远,不可能相交。
(4)如果BC既不与l平行也不与m平行,则l和m一定相交,与假设不符。
因此l和m是平行线。
五、总结以上是七年级下册数学平行线的三种判定方法。
在学习过程中,可以根据具体情况灵活运用不同的方法来判断平行线关系,掌握这些方法可以帮助学生提高数学水平,更好地应对课堂测试和考试。
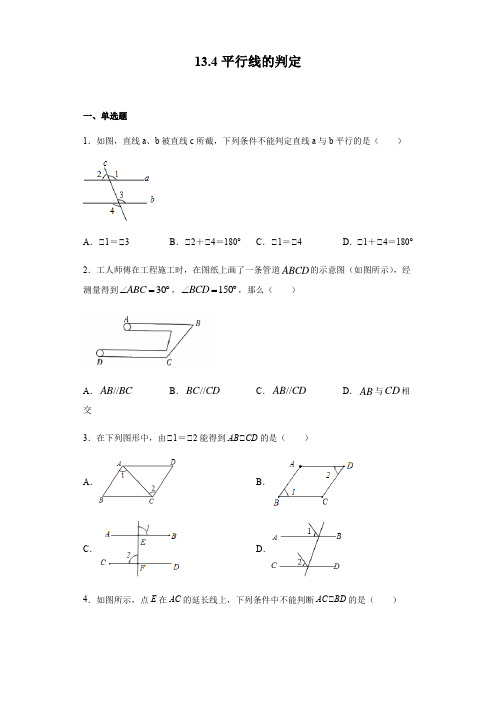
13.4平行线的判定一、单选题1.如图,直线a 、b 被直线c 所截,下列条件不能判定直线a 与b 平行的是( )A .∠1=∠3B .∠2+∠4=180°C .∠1=∠4D .∠1+∠4=180° 2.工人师傅在工程施工时,在图纸上画了一条管道ABCD 的示意图(如图所示),经测量得到30ABC ∠=︒,150BCD ∠=︒,那么( )A .//AB BCB .//BC CD C .//AB CD D .AB 与CD 相交 3.在下列图形中,由∠1=∠2能得到AB ∠CD 的是( )A .B .C .D .4.如图所示,点E 在AC 的延长线上,下列条件中不能判断AC ∠BD 的是( )A .∠3=∠4B .∠D +∠ACD =180°C .∠D =∠DCED .∠1=∠25.如图,能判定EB //AC 的条件是( )A .∠A =∠EBDB .∠A =∠ABEC .∠C+∠ABC=180°D .∠C =∠ABE 6.如图,能判断直线AB ∠CD 的条件是( )A .∠1=2∠2B .∠3=∠4C .∠1+∠3=180°D .∠3+∠4=180° 7.如图,直线AC 上有两点B ,C ,若∠DBG=90°,下列条件中不能判定DB∠CF 的是( )A .BG∠CFB .∠2=∠3C .∠2+∠3=90°D .∠1=∠3 8.在下列图形中,由12∠=∠一定能得到AB CD ∥的是( )A .B .C .D . 9.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的度数是( )A .第一次右拐50°,第二次左拐130°B .第一次左拐50°,第二次右拐50°C .第一次左拐50°,第二次左拐130°D .第一次右拐50°,第二次右拐50° 10.如图,下列条件中能判定//AB DC 的条件是( )A .12∠=∠B .1E ∠=∠C .3180A ︒∠+∠=D .3180C ︒∠+∠=二、填空题 11.如图,下列条件中:∠∠BAD +∠ABC =180°;∠∠1=∠2;∠∠3=∠4;∠∠BAD =∠BCD ,能判定AD ∠BC 的是_____.12.如图,不添加辅助线,请写出一个能判定DE ∠BC 的条件___________.13.下列说法中,∠对顶角相等;∠同位角相等;∠过一点有且只有一条直线与已知直线垂直;∠两点确定一条直线;∠同旁内角互补,两直线平行;正确的有_________(填序号)14.如图,现给出下列条件:∠1B ∠∠=,∠25∠∠=,∠34∠∠=,∠1D ∠∠=,∠B BCD 180∠∠+=︒.其中能够得到AB//CD 的条件是_______.(只填序号)15.如图,下列条件中:∠12∠=∠;∠34∠=∠;∠5D ∠=∠;∠1=6∠∠;∠180BAD D ∠+∠=︒;∠180BCD D ∠+∠=︒,能得//AD BC 的有_______________________ (只填序号).三、解答题16.如图,∠1=70°,∠2 =70°. 说明:AB∠CD .17.如图,AB∠CD ,∠B =70°,∠BCE =20°,∠CEF =130°,请判断AB 与EF 的位置关系,并说明理由.18.补充下列证明,并在括号内填上推理依据.已知:如图,在ABC 中,50,58,A C BD ∠=︒∠=︒平分ABC ∠交AC 于点D ,DE 交AB 于点E ,且36BDE ∠=︒,求证://DE BC .证明:180A C ABC ∠+∠+∠=︒,( ).50,58A C ∠=︒∠=︒,5058180ABC ∴︒+︒+∠=︒.( ),18050ABC ∴∠=︒-︒-_______=_________. BD 平分ABC ∠,12CBD ABC ∴∠=∠( ), 172362CBD ∴∠=⨯︒=︒, 36BDE ∠=︒,∴________=________,∴.( ).//BC DE19.如图∠,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC 于点G,交AC的延长线于点H,∠1+∠AFE=180°.(1)证明:BC∠EF;(2)如图∠,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.参考答案1.D2.C3.A4.D5.B6.D7.B8.A9.B10.D11.∠∠∠∠=∠12.DAB B 13.∠∠∠.14.∠∠∠15.∠∠∠16.如图:∠∠1=70°,∠∠3=∠1=70°,又∠∠2 =70°,∠∠3=∠2=70°,∠ AB ∠CD.17.AB∠EF ,理由如下:∠AB∠CD ,∠∠B=∠BCD ,∠∠B=70°,∠∠BCD=70°,∠∠BCE=20°,∠∠ECD=50°,∠CEF=130°,∠∠E+∠DCE=180°,∠EF∠CD ,∠AB∠EF .18.证明:180A C ABC ∠+∠+∠=︒,( 三角形内角和等于180︒ ).50,58A C ∠=︒∠=︒,5058180ABC ∴︒+︒+∠=︒.( 等量代换 ), 18050ABC ∴∠=︒-︒-58︒=72, BD 平分ABC ∠,12CBD ABC ∴∠=∠( 角平分线的定义 ),172362CBD ∴∠=⨯︒=︒,36BDE ∠=︒,∴CBD BDE =∠∠,//BC DE ∴.( 内错角相等,两直线平行 ).故答案为三角形内角和等于180︒;等量代换;58; 72︒;角平分线的定义;;CBD BDE ∠∠;内错角相等,两直线平行.19.证明:(1)∠∠1+∠AFE=180°,∠1+∠BCF=180°, ∠∠AFE=∠BCF ,∠BC∠EF ;(2)∠∠BEG=∠EDF ,∠DF∠EH ,∠∠DFE=∠FEH ,又∠BC∠EF ,∠∠FEH=∠2,又∠∠2=∠3,∠∠DFE=∠3,∠DF 平分∠AFE .。

§13.4 平行线的判定(2)班级:学科:数学课题:§13.4 平行线的判定(2)课时:1执教:一、教学目标确定的依据:教材分析平行线是空间与图形领域的基础知识,是《相交线与平行线》的重点,学习平行线的判定会为后面学习平行线性质、三角形、四边形等知识打下坚实的“基石”。
同时,本节学习将加深“角与平行线”的认识,也开始从有条理的口头表述逐渐过渡到书写自己的理由,为今后的几何证明打下基础。
学情分析学生对“同位角”,“内错角”,“同旁内角”和“平行线”四个概念已经了解,具备了探究直线平行的条件的基础,但在逻辑思维和合作交流的意识方面发展不够均衡。
从学生的认知特点上看比较局限于一问一答式的简单推理,不善于进行连续推理,因此在教学中要引导学生独立思考,培养学生良好的学习习惯。
二、教学的具体目标:1.知识与技能经历探索直线平行的条件的过程,掌握直线平行的条件,会应用判定方法在探究在同一平面内同垂直于同一直线的两条直线平行。
2.过程与方法会用判定方法1得出判定方法2和3,会用判定方法1,2得出方法3,会用判定方法1.2.3进行简单推理。
3.情感态度与价值观体会“由未知向已知”转化的数学思想是认识客观事物的基本方法经历观察、操作、想象、推理、交流等活动,并能积极、主动地进行自主探索或与同伴交流。
三、教学重点和难点:重点:掌握平行的判定方法。
难点:会进行文字语言,图形语言,符号语言之间的互译,理解“转化”的思想四、教具多媒体五、教学过程教学环节教师活动学生活动设计意图导入媒体演示1填空:复习三线八角图2:简单复习判定定理1以及它的符号语言3:通过同位角相等,找出对应的平行线。
回忆并回答问题从学生的已有知识经验出发,以学习过程中需要的符号推理为出发点,揭示本节课所需的知识准备。
为后续的证明过程的书写扫清障碍。
符合学生的认知规律。
新授活动体验、新知探究:提问:由同位角相等可以判定两直线平行,那么,能否利用内错角,或同旁内角来判定两直线平行呢?猜想:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行吗?如果同旁内角互补,那么这两条直线平行吗?能否利用所学的知识和方法证明上述结论猜想内错角需要满足什么条件,同旁内角需要满足什么条件才能使两条直线平行?让学生在教师的启发引导下积极地参与到观察学习对象的关键特征,寻求平行线的判定方法的探索活动中去,主动地学习,积极地思考。
