最新跨声速非定常空气动力计算与分析精品版
- 格式:doc
- 大小:171.00 KB
- 文档页数:15

单级跨音压气机三维非定常粘性流动计算西北工业大学刘前智周新海摘要本文以数值求解雷诺平均非定常N_s方程方法完成了单级跨音速压气机三维非定常粘性流动计算,给出了高分辨率HHD格式的时间推进有限差分解.对某跨音单级压气机进行了定常和非定常流的详细数值计算,设计转速下定常粘性流场计算所得到的性能参数与实验结果吻合鞍好.在此基础上,对最高效翠状态进行了动/静叶相互子扰的非定常流动计算.非定常流计算模式由于更接近于真实流动,在高性能压气机的设计与分析中具有广阔的应用前景.关键词:非定常流动Ns:Y程跨音速压气机动静叶相干一、引言在过去的十多年中所发展的三维定常流动的数值解法及其分析系统,已形成了目前的设计体系的基本框架,在工程实际中得到广泛应用.为了进一步地改进压气机和涡轮的气动设计方法,必须更准确地模述叶轮机中的实际流动.叶轮机中的流动是高度复杂的和非定常的,叶片不断承受着瞬时的、周期性的气动负荷及热负荷,这些非定常效应极大地影响叶轮机的气动性能和寿命.有效地预测叶轮机中动静叶排相干的非定常影响是改进目前的定常流设计方法和体系的一个重要课题,特别是对高性能多级跨音速风扇、压气机和涡轮来说,非定常干扰问题更加突出,追切需要发展相应的数值分析手段.国外从八十年代就开始了叶轮机动静叶排相干非定常流动方面的研究,从单级进展到研究多级叶排间的相干流动【1—4].不过,早期的工作多集中在对涡轮流动的分析上,近来对风扇压气机的研究也逐渐增多.国内在这一领域的研究也已开始,主要集中于三维非定常无粘流动的分析研究上[5~6】.本文着重研究了跨音速轴流叶轮机动静叶排相干的三维非定常粘性流:'JJli3汁算问题,以无波动、无自由参数的耗散(NND)格式【7】为基础,得到了高分辨率格式非定常N.S方程时间推进有限差分解,保证了非定常流场中激波的分辨率.采用Lu.SGS隐式解法[8J快速获得定常流场解,以最大限度地减少计算时间.利用本文方法对某单级跨音速压气机进行了数值分析,首先进行了设计转速下的不同状态定常粘性流场计算.在此基础上,选取了最高效率状态进行了非定常流动计算,并对计算结果进行了分析.本文计算所得到的周期性非定常解,有效地预估了动静叶排相干非定常效应及其对叶轮机内部流动的影响.二、基本方程、边界条件将圆柱坐标系(p,r,z)下的三维非定常粘性流动的平均N·S方程转换到一般曲线坐标系(f,玎,f)下,其形式为固/a+反E—Ev)/a;+反F一易)/却+文G—G,)/G=H(1)式中各项的意义详见文献(9].分子粘性系数u,由Suth口'land公式计算,而紊流粘性系数ut,由Baldwin-Lomax模型【lo】确定.进口边界(转子进口)上,给定总压、总温、气流的绝对切向和径向纾,*度沿径向的分布,出口边界(静子出口)上,给定内径处的静压,出口其他径向位置处的压力利用径向平衡方程确定.在物面边界,为减少网格数,采用壁面函数[11】求物面剪切应力,这时,在物面应用了速度滑移条件.周期边界的处理:当动静叶数目不相等(甚至相互不成整数倍)时,选择m个转子叶87片通道与n个静子叶片通道,m和n韵选取原则是尽量减少静子叶片几何调整的程度,又不致使计算工作量成倍增加.此时,转子叶排与静子叶排将用组合栅距(含数个叶片通道)来取代原单通道的栅距,在一个组合栅距上流动参数满足周期性条件.动静叶排问信息的传递将主要取决于叶排间交界面的处理方法.在定常流计算中,采用周向平均模型.在非定常流动计算时,则采用直接插值的方法传递叶排间的信息.三、数值方法.本文采用如下方法进行方程的时间离散:在作为非定常计算的初始场计算中,采用LU-SGS隐式解法,得到定常解.为了保证时间精度,非定常流动计算则采用了显式方法,其时间步长满足稳定性条件.方程的空间离散采用高分辨率NND格式。

高超声速空气动力设计与评估方法
高超声速空气动力设计与评估方法是指在高速飞行器研制过程中,采用一系列的设计方法和评估技术,对其空气动力性能进行精确分析和评估的过程。
高超声速空气动力设计的目的是优化飞行器的空气动力性能,提高其飞行速度和飞行高度,同时保证飞行安全和稳定性。
高超声速空气动力设计的主要内容包括:
1. 空气动力外形设计:通过对飞行器外形的优化设计,减少阻力,提高飞行速度和高度。
2. 空气动力仿真:采用计算流体力学模拟方法,对飞行器在高超声速速度下的空气动力表现进行预测和分析。
3. 空气动力试验:在风洞中进行实际的空气动力试验,检验仿真结果的准确性,并对飞行器的空气动力性能进行评估和优化。
4. 材料选择和加工工艺设计:根据飞行器的实际使用环境和要求,选择合适的材料,并设计适合的加工工艺,以保证飞行器的强度和稳定性。
5. 飞行试验:在实际的高超声速飞行试验中,对飞行器的空气动力性能进行评估和验证。
高超声速空气动力设计和评估方法的研究,对于我国高超声速飞行器的研制和飞行试验具有重要意义,也是我国航空航天科技领域的重要研究方向之一。
- 1 -。

低超声速来流中机翼跨声速非定常气动力数值解法
张建柏;张秀滨
【期刊名称】《空气动力学学报》
【年(卷),期】1993(011)003
【总页数】5页(P303-307)
【作者】张建柏;张秀滨
【作者单位】不详;不详
【正文语种】中文
【中图分类】V211.41
【相关文献】
1.跨声速机翼非定常气动力的全位势粘位迭代计算 [J], 陆志良;Voss.,R
2.超声速机翼—尾翼组合体的非定常气动力边界元法 [J], 周文伯;裘松刚
3.超声速来流中横向喷流角度对流动与混合特性的影响 [J], 杨银军;窦志国;段立伟
4.带操纵面机翼的非定常跨声速流数值解法 [J], 余涛; 张建柏
5.跨声速机翼操纵面非定常气动力Euler方程计算 [J], 董璐;郭同庆
因版权原因,仅展示原文概要,查看原文内容请购买。

第8卷㊀第6期2023年11月气体物理PHYSICSOFGASESVol.8㊀No.6Nov.2023㊀㊀DOI:10.19527/j.cnki.2096 ̄1642.1088基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析李泳德ꎬ㊀郭㊀力ꎬ㊀季㊀辰(中国航天空气动力技术研究院ꎬ北京100074)CharacterizationofTransonicAerodynamicDampingofRocketsBasedonCFD/CSDCouplingLIYong ̄deꎬ㊀GUOLiꎬ㊀JIChen(ChinaAcademyofAerospaceAerodynamicsꎬBeijing100074ꎬChina)摘㊀要:随着新型大推力火箭的发展ꎬ弯曲模态频率的不断降低ꎬ以及流动分离和跨声速飞行时产生的激波震荡等因素ꎬ其在跨声速飞行过程中更容易出现非定常振动发散ꎮ文章以某带助推的运载火箭模型为研究对象ꎬ通过数值计算获取火箭强迫振动时的气动阻尼ꎬ并对影响火箭气动阻尼的因素进行了分析ꎮ包括结构节点位置㊁振动振幅大小㊁脉动压力等ꎮ研究表明:助推主要起到增大气动阻尼的作用ꎻ前节点主要影响收缩段的气动阻尼ꎻ振动振幅大小和脉动压力对气动阻尼的影响可忽略不计ꎮ关键词:气动阻尼ꎻ数值计算ꎻ跨声速ꎻ气动弹性ꎻ运载火箭㊀㊀㊀收稿日期:2023 ̄09 ̄25ꎻ修回日期:2023 ̄10 ̄23第一作者简介:李泳德(1995 ̄)㊀男ꎬ工学硕士ꎬ助理工程师ꎬ主要研究方向为气动弹性分析ꎮE ̄mail:562064169@qq.com通信作者简介:季辰(1982 ̄)㊀男ꎬ工学博士ꎬ研究员ꎬ主要研究方向为气动弹性力学ꎮE ̄mail:jichen167@hotmail.com中图分类号:V475.1㊀㊀文献标志码:AAbstract:Withthedevelopmentofnewhigh ̄thrustrocketsꎬthedecreasingfrequencyofthebendingmodesoftherocketꎬaswellasthefactorssuchasflowseparationandshockoscillationsgeneratedduringtransonicflightmakeitmorepronetonon ̄constantvibration.Inthispaperꎬalaunchvehiclemodelwithboostwastakenastheresearchobjectꎬandtheaerody ̄namicdampingoftherocketduringforcedvibrationwasobtainedthroughnumericalcalculation.Thefactorsaffectingtheaerodynamicdampingoftherocketwereanalyzedꎬincludingthepositionofstructuralnodesꎬthemagnitudeofvibrationam ̄plitudeꎬpulsatingpressureandsoon.Thestudyshowsthattheboostmainlyplaystheroleofincreasingaerodynamicdamp ̄ingandthefrontnodemainlyaffectstheaerodynamicdampingofthecontractionsection.Thevibrationamplitudesizeandthepulsatingpressurehaveanegligibleeffectontheaerodynamicdamping.Keywords:aerodynamicdampingꎻnumericalcalculationꎻtransonicꎻaeroelasticityꎻlaunchvehicle引㊀言通常情况下人们认为气动力对火箭的振动起到阻尼作用ꎬ即气动阻尼为正值ꎮ然而随着大推力火箭发展ꎬ火箭的长细比逐渐加大ꎬ导致弯曲刚度越来越小ꎬ同时为了满足有效载荷的外形要求ꎬ火箭头部整流罩尺寸不断加大ꎬ后续箱体的直径却保持不变ꎬ形成了典型的锤头体外形ꎮ国内外大量的火箭研制经验表明[1 ̄9]ꎬ对于此类锤头体外形火箭的气动设计ꎬ必须要进行动态气动载荷与动态气弹稳定性分析ꎬ否则设计的疏忽可能会导致火箭结构出现毁灭性的破坏进而导致发射失败ꎮ目前常用的衡量气弹稳定性的方法是通过风洞试验来获取气动阻尼系数ꎮ早在1963年ꎬ美国国家航空航天局Ames研究中心(NASAAmesRe ̄searchCenter)采用半刚性模型开展试验研究[10]ꎬ获取火箭头部的气动阻尼来评估其稳定性ꎬ但这只能用来模拟火箭弯曲振型前节点之前部分的结构动力学特性ꎮ直到兰利研究中心(NASALangleyResearchCenter)开发了全弹性模型气动阻尼试验气体物理2023年㊀第8卷技术ꎬ其可以模拟整体的结构动力学特性以及气动外形ꎬ并应用于多款运载火箭研制[11 ̄15]ꎮ国内ꎬ中国航天空气动力技术研究院对气动阻尼问题开展过较多的研究[16 ̄20]ꎬ从模型设计方法㊁模型制作工艺㊁试验机构设计和数据处理等诸多方面ꎬ逐步改进实现了从半刚性模型到全弹性模型的过渡ꎬ并在多个型号上得到验证ꎮ然而通过风洞试验研究气动弹性问题ꎬ技术难度大ꎬ试验成本高ꎬ同时几乎不可能开展全尺寸试验ꎮ因此通过数值计算的方法开展相关研究是另一种重要的手段ꎮ刘子强等[21]实现了通过数值计算确定气动阻尼系数的技术和方法ꎬ并与试验结果进行对比ꎬ证实了该方法的可靠性ꎮ冉景洪等[22]通过模态数据结合准定常理论的方法分析了减阻杆加后体这一弹性结构的气动阻尼ꎬ结果表明减阻杆造成的分离流会对后体的气动阻尼系数产生影响ꎮ朱剑等[23]针对新一代捆绑式运载火箭发展了非结构网格下的气动阻尼计算方法ꎬ并分析了攻角㊁Mach数等参数对气动阻尼的影响ꎮ本文在之前的计算方法[23]的基础上采用IDDES模型ꎬ考虑脉动压力的影响ꎬ通过强迫振动的方式ꎬ针对捆绑式运载火箭的某一特定模态进行数值计算仿真ꎬ研究前节点位置ꎬ振动振幅ꎬ脉动压力等参数对气动阻尼的影响规律ꎮ1㊀计算方法图1为本文所用的捆绑式运载火箭的计算模型ꎬ是典型的锤头体结构ꎮ在跨声速阶段ꎬ其头部会产生激波造成激波边界层干扰ꎬ而在锤头体外形的过渡段会出现气流分离ꎮ为探究各部分气动阻尼的变化ꎬ将整个箭体分为头部㊁过渡段㊁弹身3个部分ꎮ图1㊀表面网格及区域划分Fig.1㊀Surfacegridandregiondivision1.1㊀流场仿真模型本文分别用Reynolds平均法(Reynolds ̄averagedNavier ̄StokesꎬRANS)和改进的延迟分离涡模拟(improveddelayeddetached ̄eddysimulationꎬID ̄DES)[24 ̄25]进行计算ꎬ在RANS方程中ꎬ将变量分为平均值和波动值两部分ꎬ对于速度分量有ui=ui+uᶄi其中ꎬi=1ꎬ2ꎬ3ꎬui和uᶄi分别代表平均量和波动量ꎬ对于压强和其他标量也采用类似的形式ꎬ将这种形式代入连续性方程和动量方程中ꎬ并写成张量形式∂ρ∂t+∂∂xi(ρui)=0(1)∂∂t(ρui)+∂∂xj(ρuiuj)=∂p∂xi+∂∂xjμ∂ui∂xj+∂uj∂xi-23δij∂uk∂xkæèçöø÷éëêêùûúú+∂∂xj(-ρuᶄiuᶄj)(2)其中ꎬiꎬjꎬk可分别取1ꎬ2ꎬ3ꎻρ是密度ꎻt是时间ꎻ当i=j时δij取0ꎬ否则取1ꎮ式(1)㊁(2)是RANS方程ꎬ由方程可知RANS方法将湍流脉动对平均流动的作用模化为Reynolds应力项即-ρuᶄiuᶄjꎬ之后采用湍流模型进行封闭ꎬ本文采用的湍流模型为SSTk ̄ω模型ꎬ其输运方程为∂∂t(ρk)+∂∂xi(ρkui)=∂∂xjΓk∂k∂xjæèçöø÷+Gk-Yk∂∂t(ρω)+∂∂xi(ρωui)=∂∂xjΓω∂ω∂xjæèçöø÷+Gω-Yω其中ꎬk和ω分别代表湍流动能和湍流耗散率ꎬΓk和Γω分别代表k和ω的有效扩散系数ꎬGk和Gω分别代表k和ω的生成率ꎬYk和Yω分别代表k和ω的耗散率ꎮ因此RANS方法只能计算大尺度的平均流动ꎬ本文采用IDDES方法计算脉动压力对气动阻尼的影响ꎮIDDES方法是由分离涡模拟(detached ̄eddysimulationꎬDES)方法改进而来ꎬ其本质思想与DES方法相同ꎬ是想以网格尺度和模型中的特征尺度隐式划分RANS和大涡模拟(large ̄eddysimulationꎬLES)区域ꎬ使其既能处理RANS方法无法得到的脉动场ꎬ也能降低LES方法在模拟高Reynolds数流动时所需的计算资源ꎮ区别在于当边界层较厚或者分离区域较窄时ꎬDES方法会出现如模型应力损耗(modeledstressdepletionꎬMSD)ꎬ网格诱导分离(grid ̄inducedseparationꎬGIS)以及对数层不匹配(logarithmic ̄layermismatchꎬLLM)问题[24]ꎬ而IDDES模型通过改良计算区域划分ꎬ结合延迟分离涡模拟(delayeddetached ̄eddysimulationꎬDDES)和03第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析壁面模型大涡模拟(wall ̄modeledlarge ̄eddysimula ̄tionꎬWMLES)ꎬ定义新的长度尺度解决了这些问题ꎬ具体公式详见文献[25]ꎮ流场网格如图2㊁图3所示ꎬ边界层采用棱柱层结构ꎬ并调整第1层网格高度使得y+小于1ꎬ远场部分采用六面体结构网格ꎬ与边界层的过渡层采用非结构网格ꎮ整体网格单元数量为4.2ˑ106ꎮ图2㊀y方向截面网格示意图Fig.2㊀Schematicdiagramofcross ̄sectionalgridinthey ̄direction图3㊀x方向截面网格示意图Fig.3㊀Schematicdiagramofcross ̄sectionalgridinthex ̄direction物面边界条件为无滑移壁面条件ꎬ远场采用压力远场边界条件ꎬ湍流模型采用SSTk ̄ω模型ꎬ采用密度基求解ꎬ气体黏性采用Sutherland定律ꎬ空间离散采用2阶迎风格式ꎬ对流通量采用Roe格式ꎮ1.2 结构分析模型结构与流场耦合分析过程中ꎬ结构部分可以采用模态方法描述ꎮ结构模态可以通过有限元方法与结构模态试验方法获得ꎮ本文采用有限元分析结果获得的模态ꎬ图4所示为结构的前3阶模态ꎬ本文只分析计算结果中气动阻尼最小的第2阶模态ꎮ(a)f=1.200Hz(b)f=2.460Hz(c)f=2.957Hz图4㊀结构的前3阶模态Fig.4㊀Firstthreemodesofthestructure由于火箭结构外形简单ꎬ一般不考虑其扭转影响ꎬ因此可以将其简化为简单的梁模型ꎬ这样就可以给出其模态振动方程q㊆i+2biωiq˙i+ω2iqi=fi(3)式中ꎬqi为第i阶模态的广义位移ꎬbi为第i阶模态的结构阻尼系数ꎬωi为第i阶模态的固有频率ꎬ13气体物理2023年㊀第8卷fi为第i阶模态下质量归一化的广义气动力ꎮ若将fi按照Taylor展开并略去高阶项ꎬ可以将其转化为气动阻尼项与气动刚度项的形式ꎬ则式(3)可写为q㊆i+2(bi+Bi)ωiq˙i+(Ki+1)ω2iqi=0(4)式中ꎬBi为气动阻尼系数ꎬKi为气动刚度系数ꎬ研究表明[26]ꎬ气动刚度相对于结构刚度为小量可以忽略不计ꎬ而在计算中结构阻尼往往设置为0ꎬ因此气动阻尼可以直接反映其气弹稳定性ꎮ1.3㊀气动阻尼分析原理气动阻尼的分析可以采用强迫振动或者自由振动的方式进行ꎬ这两种方法获得的时域数据不同ꎬ提取气动阻尼的方式也不同ꎮ强迫振动方法初始演化过程较短ꎬ因此计算量较小ꎬ同时能够分析某一种振动形式的气动阻尼ꎬ明确该振动形式是收敛还是发散ꎮ分析过程中能够获得不同部位与部件的气动阻尼ꎮ但是对于多模态相互作用引起的发散(例如颤振)较难预测ꎮ自由振动方法需要一定的自由演化时间才能够对时域数据进行分析ꎬ不过自由振动方法能够获得最能够吸收能量的模态及其振动频率ꎮ对于本研究所关注的问题ꎬ气动载荷对结构振动的过程中气动阻尼的影响较大ꎬ而对气动刚度与气动质量影响较小ꎬ即结构的固有振动频率受到来流的影响较小ꎬ其稳定性问题主要由气动阻尼的正㊁负引起ꎬ所以采用强迫振动方法分析ꎮ强迫振动下结构做简谐模态振动qi(t)=Asin(ωit)式中ꎬA表示振动的振幅ꎬ将其代入计算气动力的公式中[21]并做正交积分可得Bi=ʏl0Bx(x)dx=-1MiAω2iTʏl0ʏt0+Tt0G(xꎬt)cos(ωit)dtdx(5)式中ꎬMi为第i阶模态的模态质量ꎬT为整数倍周期ꎬG为广义气动力ꎮ根据式(5)便可以得到局部或分区域的气动阻尼ꎮ1.4㊀耦合计算流程首先进行模态分析ꎬ以确定结构的模态频率与振型ꎬ用以设计强迫振动的频率和振幅ꎮ非定常流场计算前先进行定常流场计算ꎬ来加快非定常计算的演化速度并增强收敛性ꎬ结构节点位移通过径向基函数(RBF)插值方法[27]映射到气动网格节点上ꎬ来进行网格的变形ꎬ这里径向基函数选用WendlandC2ꎬ如下所示φ(x)=(1-x)4(4x+1)最后将计算出来的广义力提取出来ꎬ截取演化完毕的整数倍周期ꎬ进行气动阻尼计算ꎮ耦合计算流程图如图5所示ꎮ图5㊀耦合计算流程图Fig.5㊀Flowchartofcoupledcalculation2㊀结果分析与讨论2.1㊀流场分析结果计算的来流Mach数范围为0.7~1.2ꎮ其中中截面的压力分布如图6所示ꎮ可以看出在头部出现了膨胀波以及跨声速激波ꎬ在过渡段存在流动分离ꎬ随着Mach数的增大ꎬ头部低压区域逐渐扩张ꎬ并且能明显看到ꎬ在流动再附的位置产生了再附激波ꎮ(a)Ma=0.7023第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析(b)Ma=0.75(c)Ma=0.80(d)Ma=0.85(e)Ma=0.88(f)Ma=0.90(g)Ma=0.92(h)Ma=0.96(i)Ma=0.9833气体物理2023年㊀第8卷(j)Ma=1.00(k)Ma=1.05(l)Ma=1.10图6㊀不同Mach数下的中截面压力分布Fig.6㊀PressuredistributioninthemiddlesectionatdifferentMachnumbers2.2 气动阻尼分布通过上述流场分析ꎬ可以看出火箭不同部位流动结构并不相同ꎬ在头部与箭身上ꎬ流动主要为附着流动ꎬ而在过渡段会出现较为复杂的波系结构以及流动分离ꎮ针对不同的流动结构随流向站位x的变化ꎬ设该位置上广义力与广义位移的相位差为φ(x)ꎬ并且简谐振动没有引入其他模态的广义力ꎬ则广义力的表达式为G(xꎬt)=Fgen sin[ωt+φ(x)]+F0(6)其中ꎬFgen为广义力的振动幅度ꎬF0为广义力的常数偏移量ꎮ将式(6)代入到式(5)中得到B(x)=-FgenMAω2Tʏt0+Tt0sin[ωt+φ(x)]cos(ωt)dt其中ꎬ广义力的常数偏移量F0的积分为0ꎬ因此省略ꎮ通过将等式中的正弦函数部分进行和差化积得到B(x)=-FgenMAω2Tʏt0+Tt0sin(ωt)cos[φ(x)]cos(ωt)dt+[ʏt0+Tt0sin[φ(x)]cos(ωt)cos(ωt)dt](7)式(7)中第1部分在整个周期中的积分为0ꎬ只有第2部分保留ꎬ因此得到B(x)=-Fgensin[φ(x)]MAω2Tʏt0+Tt0cos2(ωt)dt(8)式(8)中积分部分恒为正值ꎬ决定整个气动阻尼的部分只有相位角φ(x)的正弦值sin[φ(x)]ꎬ为了能够更加直观地获得相位角与气动阻尼B之间的关系ꎬ须将符号转化为对应的正弦函数转角ꎬ根据正弦关系ꎬ此转角为πꎬ因此得到B(x)=-Fgen(x)sin[φ(x)+π]MAω2Tʏt0+Tt0cos2(ωt)dt(9)图7为气动阻尼变化曲线ꎬ可以看出随着Mach数的增大ꎬ整体气动阻尼先增大后减少ꎬ在Mach数为0.98时达到最大值ꎬ过渡段与箭体的气动阻尼变化趋势与整体基本相同ꎬ而头部区域则不同ꎬ是随着Mach数的增大一直增大ꎬ只是增长速率变缓ꎮ图7㊀有助推时气动阻尼变化曲线Fig.7㊀Aerodynamicdampingchangecurvewithboost根据式(9)ꎬ得到相位角与气动阻尼B之间的关系为:当φ(x)ɪ(-πꎬ0)时ꎬ相位角滞后ꎬ气动阻尼B为负值ꎻ当φ(x)ɪ(0ꎬπ)ꎬ相位角提前ꎬ43第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析气动阻尼B为正值ꎻ为当φ(x)=0时ꎬ无相位角差别ꎬ气动阻尼B为0ꎮ在过渡段上ꎬ复杂的波系结构以及流动分离ꎬ使得气动力与结构位移之间会出现较为明显的迟滞现象ꎬ从而导致相位角φ(x)ɪ(-πꎬ0)ꎬ由此在过渡段上产生了负的气动阻尼ꎮ计算过程中的广义力与广义位移随时间变化曲线如图8所示ꎬ可以看出所有工况计算结果都表现良好ꎬ需要注意的是在非定常计算初期ꎬ演化的不完全导致广义力存在一些突变异常的结果ꎬ计算气动阻尼时须剔除ꎬ选择后面演化完全的周期ꎮ本文计算了9个周期ꎬ剔除了第1个周期出现的错误结果ꎬ采用后8个周期进行气动阻尼分析ꎮ强迫运动振幅为芯级直径的0.5%ꎮ(a)Ma=0.70㊀㊀㊀(b)Ma=0.75(c)Ma=0.80㊀㊀㊀(d)Ma=0.85(e)Ma=0.88㊀㊀㊀(f)Ma=0.9053气体物理2023年㊀第8卷(g)Ma=0.92㊀㊀㊀(h)Ma=0.96(i)Ma=0.98㊀㊀㊀(j)Ma=1.00(k)Ma=1.05㊀㊀㊀(l)Ma=1.10图8㊀不同工况下的广义力与广义位移随时间变化曲线Fig.8㊀Timedependentcurvesofgeneralizedforceandgeneralizeddisplacementunderdifferentoperatingconditions2.3㊀气动阻尼影响因素2.3.1㊀有无助推对气动阻尼的影响捆绑式运载火箭相比于传统的运载火箭ꎬ最大的区别就是在尾部四周捆绑了助推器ꎬ使得其流场特性变得复杂ꎬ因此须分析其对气动阻尼的影响ꎮ图7㊁图9分别为有无助推时气动阻尼变化曲线ꎬ可以看出随着Mach数的增大整体气动阻尼先增大后减少ꎬ在Mach数为0.98时达到最大值ꎬ过63第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析渡段与箭体的气动阻尼变化趋势与整体基本相同ꎬ而头部区域则不同ꎬ是随着Mach数的增大一直增大ꎬ只是增长速率变缓ꎮ对比两个图可知ꎬ助推主要起增大气动阻尼的作用ꎮ还可以看出有无助推情况下头部的气动阻尼变化很小ꎬ意味着在箭体尾部施加控制很难影响到头部的气动阻尼ꎬ特别是在超声速流场中ꎮ图9㊀无助推时气动阻尼变化曲线Fig.9㊀Aerodynamicdampingchangecurvewithoutboost2.3.2㊀前节点位置影响为了考察前节点位置变化对气动阻尼的影响ꎬ在保持振动频率不变㊁头部最大振型位置与振幅不变的条件下移动前节点ꎬ变化后的振型如图10所示ꎮ(a)Frontnodeafterthetransitionregion(b)Frontnodeinthetransitionregion(c)Frontnodebeforethetransitionregion图10㊀前节点变化后的振型Fig.10㊀Vibrationmodeafterthechangeofformernode根据对计算结果的分析分别获得了不同前节点位置的整体气动阻尼对比与过渡段气动阻尼对比ꎬ如图11㊁图12所示ꎬ可以看出前节点位置的改变并没有影响整体气动阻尼随Mach数增大而增大的趋势ꎬ且前节点在过渡段上与过渡段前的整体气动阻尼相差不大ꎬ而前节点在过渡段后的整体气动阻尼要高于另两种情况ꎬ因此过渡段与头部放在同一侧有助于提高气动阻尼ꎮ过渡段的气动阻尼会随着前节点的变化发生剧烈改变ꎬ前节点在过渡段前后随Mach数增大的变化规律相反ꎬ节点前后的振动相位变化导致不同节点位置过渡段的振动相位不同ꎬ进而导致气动阻尼发生变化ꎮ图11㊀不同节点位置的整体气动阻尼Fig.11㊀Overallaerodynamicdampingatdifferentnodepositions图12㊀不同节点位置的过渡段气动阻尼Fig.12㊀Aerodynamicdampingofthetransitionregionatdifferentnodepositions2.3.3㊀强迫振动振幅大小对气动阻尼的影响为了考察强迫振动振幅大小对气动阻尼的影响ꎬ在保证流场结构不发生改变的前提下ꎬ振动振幅分别为原来的一半和两倍ꎬ根据工程经验ꎬ如果振幅超过芯级直径的5%ꎬ则须考虑流场结构改变所造成的影响ꎮ图13㊁图14分别为不同振幅下的整体与头部气动阻尼ꎮ73气体物理2023年㊀第8卷图13㊀不同振幅下整体气动阻尼Fig.13㊀Overallaerodynamicdampingatdifferentamplitudes图14㊀不同振幅下头部气动阻尼Fig.14㊀Aerodynamicdampingoftheheadregionatdifferentamplitudes可以发现改变振幅无论是对整体气动阻尼还是头部气动阻尼来说变化都很小ꎬ这意味着气动阻尼的大小主要取决于气动力与结构振动的相位差ꎬ不依赖于振动幅度的大小ꎮ2.3.4㊀脉动压力对气动阻尼的影响为了模拟出脉动压力的影响ꎬ采用IDDES方法对火箭气动阻尼进行计算ꎬ计算来流Mach数为0.92ꎬ计算过程中的广义力与广义位移如图15所示ꎬ相较于图8可以看出广义力随时间变化曲线并不光滑ꎬ脉动压力的存在导致广义力由多个频率叠加而成ꎮ由于第2阶模态的频率为2.46Hzꎬ而由分离流㊁激波振荡等引起的脉动压力频率往往远大于此频率ꎬ因此这里选择3.5Hz为分界ꎬ将高于3.5Hz的部分视为由抖振脉动压力引起的广义力ꎬ低于3.5Hz的部分视为强迫振动引起的广义力ꎬ通过低通滤波把高于3.5Hz的广义力滤掉ꎬ可以获得由强迫振动引起的广义力与广义位移变化曲线ꎬ如图16所示ꎬ通过此广义力计算的气动阻尼为2.08ɢꎮ同样地ꎬ进行高通滤波将低于3.5Hz的广义力滤掉ꎬ可以获得由抖振脉动压力引起的气动阻尼为(2.94ˑ10-3)ɢꎬ由此得到脉动压力引起的气动阻尼变化为0.14%ꎬ可以忽略不计ꎮ同时使用RANS方法计算的气动阻尼为2.07ɢꎬ与IDDES的计算结果相比误差约为(2.94ˑ10-3+2.08-2.07)/2.07ʈ0.48%ꎬ这说明针对气动阻尼的模拟ꎬ抖振引起的脉动压力对气动阻尼的计算结果影响很小ꎬ起主要作用的还是广义力的变化ꎬ该变化由强迫振动引起的结构边界变化所导致ꎮ图15㊀基于IDDES的广义力与广义位移变化曲线Fig.15㊀VariationcuresofgeneralizedforceandgeneralizeddisplacementbasedonIDDES图16㊀滤波后的广义力与广义位移变化曲线Fig.16㊀Variationcuresofgeneralizedforceandgeneralizeddisplacementvariationcurveafterfiltering3㊀结论本文通过数值计算方法研究了火箭的气动阻尼特性ꎮ根据流动特征分析与理论推导ꎬ发现火箭过渡段几何外形的收缩导致该区域出现复杂的分离与激波结构ꎬ从而造成了气动力相对于结构振动83第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析相位的滞后ꎬ导致了该区域为气动负阻尼ꎬ即气动不稳定性的主要来源ꎮ在此机理的基础上ꎬ分析了前节点位置㊁振动振幅㊁脉动压力等因素对气动阻尼的影响规律ꎮ可以得出以下结论:1)助推增加了正阻尼区域的面积ꎬ从而相对于没有助推的构型起到了增加气动阻尼的作用ꎮ2)前节点位置的改变对过渡段气动阻尼影响很大ꎬ节点前后的振动方向相反ꎬ导致节点在过渡段前后的气动阻尼变化规律也截然相反ꎬ将过渡段与头部区域放在节点的同一侧有助于增加气动阻尼ꎮ3)在不改变流场结构的前提下ꎬ改变振动的振幅ꎬ气动力也会产生相应幅度的变化ꎬ因此结构振幅对气动阻尼的影响可忽略不计ꎮ4)高频部分的广义力对气动阻尼的贡献很小ꎬ即结构振动引起的广义力变化对气动阻尼起主要作用ꎬ而脉动压力对计算气动阻尼影响不大ꎬ可忽略不计ꎮ参考文献(References)[1]㊀CoeCF.Steadyandfluctuatingpressuresattransonicspeedsontwospace ̄vehiclepayloadshape[R].NASATMX ̄503ꎬ1961.[2]ColeSRJrꎬHenningTLꎬRaineyAG.NASAspaceve ̄hicledesigncriteria[R].NASASP ̄8001(REV)ꎬ1964. [3]EricssonLEꎬRedingJP.Analysisofflowseparationeffectsonthedynamicsofalargespacebooster[J].Jour ̄nalofSpacecraftandRocketsꎬ1965ꎬ2(4):481 ̄490. [4]RedingJPꎬEricssonLE.Effectofaeroelasticconsidera ̄tionsonseasat ̄Apayloadshrouddesign[J].JournalofSpacecraftandRocketsꎬ1981ꎬ18(3):241 ̄247. [5]程镇煌.宇航飞行器跨音速气动弹性问题探讨[J].上海航天ꎬ1997(6):16 ̄21.ChengZH.Discussionontransonicpneumaticelasticityofspacecraft[J].AerospaceShanghaiꎬ1997(6):16 ̄21(inChinese).[6]倪嘉敏.我国运载火箭气动设计回顾[C].近代空气动力学研讨会论文集ꎬ2005.NiJM.ReviewofaerodynamicdesignofChinaᶄslaunchvehicle[C].Proceedingsofthemodernaerodynamicssymposiumꎬ2005(inChinese).[7]臧涛成ꎬ胡焕性.大长细比弹箭弹性效应研究综述[J].弹道学报ꎬ1999ꎬ11(3):89 ̄93ꎬ96.ZangTCꎬHuHX.Areviewofgreatslendernessratioprojectileelasticeffectresearch[J].JournalofBallisticsꎬ1999ꎬ11(3):89 ̄93ꎬ96(inChinese). [8]吴志刚ꎬ杨超.细长体弹箭的气动弹性问题与研究方法[C].第九届(2005年)全国空气弹性学术交流会论文ꎬ2005.WuZGꎬYangC.Aeroelasticityproblemsandresearchmethodsofslenderbodymissiles[C].9thNationalSym ̄posiumonAeroelasticityꎬ2005(inChinese). [9]张贺ꎬ黄晓鹏.弹性细长旋转弹箭运动稳定性问题的研究进展[C].第九届(2005年)全国空气弹性学术交流会论文ꎬ2005.ZhangHꎬHuangXP.Researchprogressonthestabilityofelasticslenderrotatingprojectiles[C].9thNationalSymposiumonAeroelasticityꎬ2005(inChinese). [10]ColeHAJr.Dynamicresponseofhammerheadlaunchvehiclestotransonicbuffeting[R].NASATND ̄1982ꎬ1963.[11]BartelsREꎬWiesemanCDꎬMineckRE.ComputationalaeroelasticanalysisoftheAreslaunchvehicleduringas ̄cent[R].AIAA2010 ̄4374ꎬ2010.[12]AzevedoJLF.Aeroelasticanalysisoflaunchvehiclesintransonicflight[J].JournalofSpacecraftandRocketsꎬ1989ꎬ26(1):14 ̄23.[13]SinclairAꎬFlowersG.Low ̄orderaeroelasticmodeloflaunch ̄vehicledynamics[R].AIAA2010 ̄7725ꎬ2010. [14]DotsonKW.Transientcouplingoflaunchvehiclebendingresponseswithaerodynamicflowstatevariations[J].JournalofSpacecraftandRocketsꎬ2001ꎬ38(1):97 ̄104.[15]ColeSRꎬHenningTL.Buffetresponseofahammerheadlaunchvehiclewind ̄tunnelmodel[J].JournalofSpacecraftandRocketsꎬ1992ꎬ29(3):379 ̄385.[16]崔尔杰.流固耦合力学研究与应用进展[C].钱学森科学贡献暨学术思想研讨会论文集ꎬ2001.CuiEJ.Researchandapplicationprogressoffluid ̄struc ̄tureinteractionmechanics[C].ProceedingsofSeminarofQianXuesenScientificContributionsandAcademicThoughtsꎬ2001(inChinese).[17]冯明溪ꎬ王志安.火箭跨音速动导数和抖振实验[J].宇航学报ꎬ1987(1):55 ̄63.FengMXꎬWangZA.Experimentsoftransonicderiva ̄tivesandbuffetingofrocket[J].JournalofAstronauticsꎬ1987(1):55 ̄63(inChinese).[18]白葵ꎬ冯明溪.弹性模型实验技术[J].流体力学实验与测量ꎬ1999ꎬ13(1):38 ̄42.BaiKꎬFengMX.Aeroelasticmodelandthebuffetex ̄perimentaltechnique[J].ExperimentsandMeasurementsinFluidMechanicsꎬ1999ꎬ13(1):38 ̄42(inChinese). [19]JiCꎬRanJHꎬLiFꎬetal.Theaerodynamicdamping93气体物理2023年㊀第8卷testofelasticlaunchvehiclemodelintransonicflow[C].Proceedingsofthe64thInternationalAstronauticalCon ̄gressꎬ2013.[20]季辰ꎬ吴彦森ꎬ何岗ꎬ等.运载火箭气动阻尼风洞试验研究[C].第十二届全国空气弹性学术交流会论文集ꎬ2011.JiCꎬWuYSꎬHeGꎬetal.Experimentalstudyonaero ̄dynamicdampingwindtunneloflaunchvehicle[C].Pro ̄ceedingsofthe12thNationalAeroelasticityConferenceꎬ2011(inChinese).[21]刘子强ꎬ白葵ꎬ毛国良ꎬ等.锤头体弹性振动跨音速气动阻尼系数的确定[J].宇航学报ꎬ2002ꎬ23(6):1 ̄7.LiuZQꎬBaiKꎬMaoGLꎬetal.Thedeterminationofaerodynamicdampingonhammerheadlaunchvehiclesattransonicspeeds[J].JournalofAstronauticsꎬ2002ꎬ23(6):1 ̄7(inChinese).[22]冉景洪ꎬ刘子强ꎬ胡静ꎬ等.减阻杆气动阻尼研究[J].力学学报ꎬ2014ꎬ46(4):636 ̄641.RanJHꎬLiuZQꎬHuJꎬetal.Researchofaero ̄dampingforbluntwithspike[J].ChineseJournalofThe ̄oreticalandAppliedMechanicsꎬ2014ꎬ46(4):636 ̄641(inChinese).[23]朱剑ꎬ冉景洪ꎬ吴彦森ꎬ等.捆绑式运载火箭的气动阻尼数值计算方法[C].第十三届全国空气弹性学术交流会论文集.哈尔滨:中国力学学会ꎬ中国空气动力学会ꎬ2013.ZhuJꎬRanJHꎬWuYSꎬetal.Numericalcalculationmethodforaerodynamicdampingofbundlelaunchvehicles[C].Proceedingsofthe13thNationalAeroelasticityCon ̄ference.Harbin:ChineseSocietyofTheoreticalandAp ̄pliedMechanicsꎬChinaAeromechanicsSocietyꎬ2013(inChinese).[24]SpalartPR.Detached ̄eddysimulation[J].AnnualReviewofFluidMechanicsꎬ2009ꎬ41:181 ̄202. [25]GritskevichMSꎬGarbarukAVꎬSchützeJꎬetal.Devel ̄opmentofDDESandIDDESformulationsforthek ̄ωshearstresstransportmodel[J].FlowꎬTurbulenceandCombustionꎬ2012ꎬ88(3):431 ̄449.[26]季辰ꎬ吴彦森ꎬ侯英昱ꎬ等.捆绑式运载火箭跨声速气动阻尼特性试验研究[J].实验流体力学ꎬ2020ꎬ34(6):24 ̄31.JiCꎬWuYSꎬHouYYꎬetal.Experimentalstudyofaerodynamicdampingcharacteristicsofalaunchvehiclewithboostersintransonicflow[J].JournalofExperimentsinFluidMechanicsꎬ2020ꎬ34(6):24 ̄31(inChinese). [27]AllenCꎬRendallTCS.UnifiedapproachtoCFD ̄CSDinterpolationandmeshmotionusingradialbasisfunctions[R].AIAA2007 ̄3804ꎬ2007.04。

超声速翼型气动力对比计算研究超声速翼型是指在超过声速的空气流动条件下,流经翼型表面的速度大于声速。
超声速翼型的气动特性与亚声速翼型有很大的不同,因此对超声速翼型的气动力进行研究和计算,对于超声速飞行器的设计和性能优化具有重要意义。
超声速流动下的气动力分为横向力、升力和阻力三个方向。
首先,横向力是指垂直于飞行方向的力,用于控制超声速飞行器的横侧稳定性。
当超声速飞行器在飞行过程中发生偏离时,通过调整横向力的大小和方向可以使其重新回到预定的飞行轨迹。
横向力的计算可以通过数值模拟方法,如CFD(计算流体力学)进行。
通过CFD计算,可以得到超声速流动下的横向力系数。
其次,升力是指垂直于飞行方向且指向上方的力,用于支持超声速飞行器的重量。
超声速翼型的升力计算一般采用低阻力曲线翼型理论方法或CFD方法。
低阻力曲线翼型理论方法是根据翼型的几何形状和气动力学性质,通过一系列的计算公式推导得出升力系数。
CFD方法则是通过数值模拟方法对超声速流动的速度场和压力场进行计算,然后根据经验公式和实验数据计算升力系数。
最后,阻力是指沿飞行方向的阻碍运动的力,它是超声速飞行器在飞行中需要克服的主要力量。
超声速流动下的阻力包括压力阻力和摩擦阻力。
压力阻力是由于超声速流动中气体与翼型表面的冲击作用以及翼型附近湍流引起的。
摩擦阻力是由于超声速流动中气体与翼型表面的摩擦力引起的。
计算超声速流动下的阻力需要考虑这两种阻力的贡献,可以通过CFD方法进行计算,也可以采用经验公式进行估算。
综上所述,超声速翼型气动力的计算研究对于超声速飞行器的设计和优化至关重要。
通过数值模拟方法如CFD,可以计算得到超声速流动下的横向力系数、升力系数和阻力系数,为超声速飞行器的性能分析和改进提供重要依据。
同时,可以通过低阻力曲线翼型理论方法和经验公式估算得到升力系数和阻力系数,为初期设计提供快速的气动力估算手段。


速度场演化结构非定常气动力速度场演化结构非定常气动力是指空气流动的速度场在时间和空间上都发生了改变,造成气动力的变化。
在实际的气动力学问题中,流体的速度场通常是非定常的,因为空气在流动过程中,会受到外界环境的干扰和影响,以及流体本身的特性,例如流体粘性和湍流等。
因此,研究速度场演化结构非定常气动力对于设计和优化飞行器、建筑物以及其他需要考虑气动力的工程问题具有重要意义。
1. 运动方程:空气流动的速度场可以通过Navier-Stokes方程来描述。
Navier-Stokes方程是流体力学中最基本的方程之一,它描述了流体的连续性、动量守恒和能量守恒。
在非定常条件下,Navier-Stokes方程需要引入时间项来描述速度场的演化过程。
2. 湍流模型:湍流是非定常流动的一种常见形式,它在风力发电、飞行器设计等领域具有重要应用价值。
湍流的处理是气动力学研究中的一个重要问题,需要使用湍流模型来描述湍流的统计性质。
常用的湍流模型有雷诺平均Navier-Stokes方程(RANS)和大涡模拟(LES)等。
3.边界条件:边界条件对于非定常气动力的研究至关重要。
边界条件包括速度场、压力场以及物体表面的边界条件。
在非定常情况下,需要考虑流动的时间变化和空间变化对边界条件的影响。
对于速度场演化结构非定常气动力的研究,可以采用数值模拟的方法进行。
数值模拟是一种通过利用计算机对气动力学问题进行数值计算和分析的方法。
数值模拟方法中常用的有有限元法、有限体积法和有限差分法等。
在实际应用方面,速度场演化结构非定常气动力的研究对于飞行器的设计和安全性评价具有重要意义。
例如,对于飞机的气动外形设计和燃油效率的优化,需要考虑机翼和机身等部件对速度场的影响以及速度场演化对气动力的变化。
此外,速度场演化结构非定常气动力的研究还可以应用于建筑物的抗风设计、风洞实验以及地质工程等领域。
总而言之,速度场演化结构非定常气动力是一个复杂的问题,涉及到流体力学、湍流模型和数值模拟等多个领域的知识。



跨声速级不同转速下静叶的损失特性
跨声速级不同转速下静叶的损失特性是在关于跨声速飞行器研究和发展过程中必不可少的一个重要部分。
这些静叶损失特性可分为以下几个方面:
1、声速不同转速下静叶的空气动力特性:在跨声速飞行器中,由于转速不同
导致不同的声速,因此静叶的空气动力特性也随着转速的变化而发生变化,这必然会对飞行器的性能产生影响。
2、声速不同转速下静叶的热力特性:由于声速的不同,静叶将面临不同温度
和压力环境下的热力变化,其中热流和传热特性随着声速的变化而显著变化。
低声速下也会增大静叶的温度而影响叶片的强度和刚度。
3、声速不同转速下静叶的材料变形特性:飞行器的静叶部件将受到不同静力
环境的偏载,随着声速的不同,叶片的弹性变形也会发生变化,可能会影响叶片及其承载的工作条件。
4、声速不同转速下静叶的声学特性:随着转速对于声速的变化,静叶将同时
影响飞行器的噪声特性,这可能会影响飞行器的设计、性能和使用效果。
5、声速不同转速下静叶的流动特性:随着声速的变化,附着在叶片上的边界
层将倾向于更加紊流化,这将影响叶片的空气动力力学特性,因此,叶片的设计应充分考虑紊流的影响。
这些静叶损失特性的变化,对飞行器的设计、性能及使用效果都具有重要影响,其研究和应用对于跨声速飞行器的研究和发展都具有重要意义。
第41卷第11期2020年11月哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报Journal of Harbin Engineering UniversityVol.41ɴ.11Nov.2020NACA0012翼型跨声速强迫运动非定常气动力模型张庆1,2,叶正寅3(1.西安航空学院飞行器学院,陕西西安710077;2.南洋理工大学机械与航空工程学院,新加坡639798;3.西北工业大学航空学院,陕西西安710072)摘㊀要:传统的一阶线性叠加的气动力模型不再适用于现代高机动性飞行器的非定常气动力建模,为了考察更高阶的气动力模型对非定常迟滞效应模拟的适用程度,本文采用自主发展的求解器,分别计算了NACA0012翼型在跨声速来流条件下做单自由度强迫沉浮㊁俯仰以及沉浮/俯仰两自由度耦合运动的非定常气动力的变化规律㊂然后在Etkin 气动力模型的基础上,探讨了不同类型的高阶的气动导数在非定常气动力建模中的作用㊂研究结果表明:将Etkin 气动力模型中升力和俯仰力矩对迎角的导数项由一阶拓展至二阶就可以较为精确地重构出翼型在强迫运动各阶段的非定常升力和俯仰力矩㊂关键词:跨声速;气动导数;气动力建模;沉浮运动;俯仰运动;耦合运动;Etkin 模型;非定常气动力DOI :10.11990/jheu.201903018网络出版地址:http :// /kcms /detail /23.1390.u.20201028.1424.010.html 中图分类号:V211.41㊀文献标志码:A㊀文章编号:1006-7043(2020)11-1683-06Unsteady aerodynamic model of NACA 0012associated with forcedoscillations and translations in transonic flightZHANG Qing 1,2,YE Zhengyin 3(1.School of Aircraft,Xiᶄan Aeronautical University,Xiᶄan 710077,China;2.School of Mechanical &Aerospace Engineering,Nan-yang Technological University,Singapore 639798,Republic of Singapore;3.School of Aeronautics,Northwestern Polytechnical Uni-versity,Xiᶄan 710072,China)Abstract :It is unsuitable to model unsteady aerodynamics for high-agility modern aircraft by the traditional first-or-der linear superposition theory.For this study,in order to investigate the applicability of a higher order aerodynam-ic model to the simulation of hysteresis effects,the unsteady time histories of aerodynamics for NACA0012associat-ed with single-freedom forced motions,plunging and pitching,and coupled plunging and pitching motion under transonic conditions were investigated computationally based on in-house codes.The effects of various aerodynamic derivatives on aerodynamic models are discussed based on the Etkin aerodynamic model.Final results indicated that unsteady lift and pitching moment in forced single or coupled motions could be accurately regenerated if the Etkin model is expanded to the second order derivative of the angle of attack with respect to time.Keywords :transonic;aerodynamic derivative;aerodynamic model;plunging;pitching;coupled motion;Etkin model;unsteady aerodynamics收稿日期:2019-03-06.网络出版日期:2020-10-28.基金项目:国家自然科学基金重点项目(11732013);校级科研基金项目(2018KY1226).作者简介:张庆,男,讲师,博士;叶正寅,男,教授,博士生导师.通信作者:张庆,E-mail:zhangqing2220@.㊀㊀气动导数作为描述飞行器机动飞行和受扰动时气动特性的关键性气动参数,在飞行器气动性能㊁控制系统和总体设计中扮演着非常重要的作用[1-4]㊂在传统的飞行动力学相关问题的研究中,气动力的数据往往基于小扰动线性叠加原理计算出来,在这种准定常假设情况下,气动力仅仅表示为瞬时飞行状态参数的函数,并且可以以一种简单的解析函数关系式表示出来[2-5]㊂但是,现代飞行器的飞行包线普遍向大迎角区域扩展,在大迎角下飞机机动飞行产生的三维非定常分离流和涡流使得空气动力呈现高度非线性特性,气动力和力矩不仅依赖于瞬时迎角㊁侧滑角㊁姿态角等参数,而且与它们的时间历程有关,因此原来使用的低阶线性叠加模型将不再适用[5-6]㊂同时,由于机动飞行状态涵盖了较大的迎角㊁侧滑角㊁角速率的变化范围,如果采用风洞实验或是数值计算模拟,其时间成本和经济成本都难以接受[7-10]㊂哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报第41卷因此有必要建立起较大飞行包线内普适性较好的的非定常气动力模型[1,4]㊂Etkin模型是目前动导数求解时最常用的一种非定常气动力模型,Etkin模型物理意义明确,考虑了时间历史效应对气动导数的影响[3]㊂但是,在非定常气动力建模时,该模型中的各项气动导数对不同运动形式的非定常气动力的影响规律和适用程度尚不清楚㊂为此,本文结合Etkin气动力模型,研究了气动力关于迎角的一阶和二阶导数在气动力模型的作用,希望能精确地重构出翼型单自由度或是耦合强迫运动过程中的非定常气动力,为未来发展高效的㊁可靠的气动力模型提供参考数据㊂1㊀强迫运动非定常气动力模型本文的计算采用课题组自己开发的柔性体动力学问题求解软件GMFlow[11-13],其中流场求解部分采用基于SA模型的有限体积法[13],强迫运动时的网格变形方法为弹簧网格变形方法[14-16]㊂为了验证求解方法的正确性,首先计算了标准算例NACA0012翼型强迫俯仰运动的非定常气动力变化情况,将计算结果与文献中的计算结果和实验结果对比,对比结果见文献[13]㊂俯仰运动的运动规律可以描述为[15]:α(t)=α0+A sin(ωt)=α0+A sin(2πft)(1)式中:α0是初始位置处的迎角;A是简谐振动的振幅;ω是简谐振动的圆频率;f是简谐振动的频率㊂本文定义减缩频率为:k=ωC2Vɕ(2)式中C是翼型的弦长㊂在本文中,强迫运动时自由来流的马赫数为0.755,翼型弦长为1.0m,强迫运动的减缩频率为0.0814㊂俯仰运动的初始迎角为0.016ʎ,俯仰振幅为2.51ʎ㊂图1(a)是强迫俯仰运动时的升力系数和关于1/4弦点的俯仰力矩系数随时间的变化曲线,图中计算了3个周期的气动力,由图可知,在第1个计算周期的初始阶段,计算的结果收敛性较差,这主要是由于定常计算的步数不足㊂从第2个周期开始,力和力矩系数已经达到了较好的谐振性,可以认为计算结果已经收敛㊂因此,为了减小计算量,本文的所有强迫运动过程都只计算了3个运动周期㊂图1(b)是翼型强迫沉浮运动时的力和力矩系数变化情况,其运动规律为:z(t)=z0+z m sin(ωt)(3)式中:z0=0是初始位置处的纵向位移;z m=0.1m 是沉浮运动的振幅㊂考虑洗流影响,在沉浮运动的任一时刻,瞬时迎角为:α(t)=α0-ωz m cos(ωt)/Vɕ(4)㊀㊀图1(c)是翼型强迫俯仰/沉浮耦合运动时的力和力矩系数变化情况,其运动规律为式(1)和式(3)叠加㊂对比图1可知,虽然耦合运动形式是俯仰和沉浮运动的叠加,但是耦合运动的气动力和力矩并不等于俯仰运动和沉浮运动的简单叠加,这也说明了翼型强迫运动时气动力的非线性迟滞特性比较复杂,并不是简单的线性叠加关系㊂图1㊀不同运动过程升力和力矩系数随时间变化Fig.1㊀History of lift/moment coefficients in different mo-tions㊃4861㊃第11期张庆,等:NACA0012翼型跨声速强迫运动非定常气动力模型1.1㊀一阶气动模型根据Etkin 气动力模型[2-3],强迫运动过程中的非定常气动力可以表示为:ΔC j =C j -C j 0=C jαΔα+C j ̇αC 2V ɕ()Δ̇α+C jq C 2V ɕ()Δq (5)式中C j 0是平衡位置处的力系数或是力矩系数㊂由于式(5)中C j ̇α和C jq 的量纲相同,都是空气动力系数对角度随时间一阶变化率的导数,所以在本文中称式(5)为一阶气动力模型㊂根据强迫俯仰运动时运动规律可知:̇α(t )=q =Aωcos(ωt )(6)㊀㊀俯仰运动的非定常气动力可以表示为:ΔC j =A sin(ωt )㊃C jα+kA (cos(ωt )-1)(C j ̇α+C jq )(7)㊀㊀此处需要注意,由于ΔC j 是相对于初始位置的变化量,因此右侧是(cos(ωt )-1)而不是cos(ωt )㊂所以:C j ̇α+C jq =ʏT n +1T nΔC j cos(ωt )d t()kAπω()(8)㊀㊀根据强迫沉浮运动时运动规律可知:̇α(t )=ω2z m sin(ωt )/V ɕ(9)㊀㊀沉浮运动的非定常气动力可以表示为:ΔC j =C jα-ωz m cos(ωt )V ɕ+C j ̇αω2z m V ɕC2V ɕ()sin(ωt )(10)㊀㊀所以:C j ̇α=ʏT n +1T nΔC jsin(ωt )d t ()ω2z m πC2V 2ɕ()(11)㊀㊀将式(8)和式(11)相减就可以得到单独的C j ̇α和C jq ,根据图1(a)和图1(b)的结果,可以求得一阶气动力模型的各个导数值,升力系数对̇α和q 的导数值分别为-38.9457和6.6747,力矩系数对̇α和q 的导数值分别为-2.0595和-1.3344㊂1.2㊀二阶气动模型根据Etkin 气动力模型[2-3],非定常气动力可以表示为:ΔC j =C jαΔα+C j ̇αD 2V ɕ()Δ̇α+C jα㊃㊃D 2V ɕ()2Δα㊃㊃+C jqD 2V ɕ()Δq +C j ̇qD 2Vɕ()2Δ̇q (12)㊀㊀由于式中C jα㊃㊃和C j ̇q 的量纲相同,都是空气动力系数对角度随时间二阶变化率的导数,所以在本文中称式(12)为二阶气动力模型㊂与1.1节类似,由俯仰运动的气动力变化规律可以得到:C j ̇q=C jα/k 2-ʏT n +1T n ΔC j sin(ωt )d t ()k 2A πω()C j ̇α+C jq =ʏT n +1TnΔC j cos(ωt )d t ()kA πω()ìîíïïïïïï(13)㊀㊀由沉浮运动的气动力变化规律可以得到:C j ̇α=ʏT n +1T nΔC jsin(ωt )d t ()ω2z m πC 2V ɕ2()C jα㊃㊃=ʏT n +1T nΔC j cos(ωt )d t()(z m πV ɕ()+C jα)/k 2ìîíïïïïïï(14)㊀㊀式(13)减去式(14)就可以得到单独的C j ̇α和C jq ,根据图1(a)和图1(b)的结果,可以求得一阶和二阶气动力模型的各个气动导数值,一阶导数与上节完全相同,升力系数对α㊃㊃和̇q的导数值分别为578.5118和-38.2752,力矩系数对α㊃㊃和̇q的导数值分别为18.8996和12.9044㊂式(10)㊁(11)与式(12)~(14)相比,一阶气动导数完全一样,这也间接说明传统上忽略高阶导数的做法对低阶气动导数的求解结果并没有影响,这是传统上普遍采用Etkin 气动力模型进行小迎角㊁小扰动飞行包线范围内动态稳定性分析的重要原因㊂2㊀气动力建模结果比较为了定量考察这些气动力模型对强迫运动过程非定常迟滞效应模拟的适用程度,本节对比了这些气动力模型的计算结果与直接采用CFD 进行计算得到的结果㊂图2分别是采用一阶和二阶Etkin 气动力模型计算得到的强迫俯仰运动㊁强迫沉浮运动以及耦合运动的气动力与采用CFD 方法得到的气动力迟滞曲线的对比图㊂由图2(a)可知,对于强迫俯仰运动,采用二阶气动导数得到的升力系数与CFD 计算值完全重合,而采用一阶气动导数得到的升力系数误差随着迎角的增加而增大,在最大迎角位置比CFD 计算值大50%㊂对于俯仰力矩系数,一阶模型的误差较大,而二阶模型的结果与CFD 计算值虽然不像升力系数那样完全重合,但是吻合程度也较好㊂表1是俯仰运动不同位置处的不同变量对该时刻非定常气动力的贡献情况,需要注意的是,强迫俯仰运动时̇α与q 的数值相等,α㊃㊃与̇q的数值相等㊂由表1可知,在俯仰运动1/4周期时,到达抬头最大位置处,此时α㊃㊃对应的非定常升力和力矩分别占总的非定常升力和力矩的-37.98%和-45.72%,̇q对应的非定常升力和力矩分别占总的非定常升力和力矩㊃5861㊃哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报第41卷的2.51%和-31.21%㊂由于忽略了α㊃㊃与̇q的影响,所以一阶气动力模型对应的升力和力矩系数与CFD 计算值差别较大,见图2(a)㊂在俯仰运动3/4周期时,到达低头最大位置处㊂此时α㊃㊃与̇q这2项对非定常特性的贡献也比较大,所以与1/4周期时的情况类似,一阶模型的计算结果误差较大㊂而在1/2周期时,翼型低头经过初始位置,由于Δα㊁Δα㊃㊃以及̇q的数值刚好为0,此时非定常气动力主要由̇α和q 项产生,所以一阶气动力模型就能较为准确地重现出非定常气动力㊂在一个周期时,翼型抬头经过初始位置,此时的非定常气动力贡献情况与1/2周期时相反,此时由于Δ̇α和Δq 的数值刚好为0,此时非定常气动力主要由α㊁α㊃㊃以及̇q项产生㊂这些分析结果与图2(a)的结论一致,说明在俯仰运动过程中,二阶模型才能更准确地再现出非定常气动力和力矩㊂图2㊀不同运动过程升力和力矩系数迟滞曲线Fig.2㊀Comparison of lift /moment coefficients indifferent motions表1㊀俯仰运动不同位置非定常气动力分布情况Table 1㊀Percentage distributions at different time in thepitching motion %周期α̇αα㊃㊃q ̇q 0.25T 0.50T 0.75T 1.00TΔC L 109.4431.41-37.98-5.38 2.51ΔC m 76.0861.20-45.7239.65-31.21ΔC L0120.680-20.680ΔC m 060.68039.320ΔC L 228.27-65.52-79.2211.23 5.24ΔC m -74.8160.1844.9538.9930.69ΔC L 147.950-51.350 3.40ΔC m -8935.8505369.583666.27㊀㊀图2(b)是采用一阶和二阶Etkin 气动力模型计算得到的强迫沉浮运动的气动力与采用CFD 方法得到的气动力迟滞曲线的对比图㊂由图2(b)可知,对于强迫沉浮运动,采用二阶气动导数得到的升力系数与CFD 计算值几乎重合,而采用一阶气动导数得到的升力系数误差较大,在最大纵向位移位置比CFD 计算值大90%㊂对于俯仰力矩系数,一阶模型的误差较大,而二阶模型的结果与CFD 计算值虽然不像升力系数那样完全重合,但是吻合程度也较好㊂表2是沉浮运动不同位置处迎角的各阶导数对非定常气动力的贡献情况,由于强迫沉浮运动时没有俯仰角速度,所以在表2中没有出现q 和̇q 项对应的非定常气动力㊂由表2可知,在沉浮运动1/4周期时,到达纵向最大位置处,此时α㊃㊃对应的非定常升力和力矩分别占总的非定常升力和力矩的-94.84%和148.24%㊂由于忽略了α㊃㊃的影响,所以一阶气动力模型对应的升力和力矩系数与CFD 计算值差别较大,见图2(b)㊂在沉浮运动3/4周期时,到达纵向最小位置处㊂此时α㊃㊃对非定常特性的贡献也比较大,其数值分别为-36.92%和-49.93%,所以与1/4周期时的情况类似,一阶模型的计算结果误差较大㊂而在1/2周期时,翼型下沉经过初始位置,由于Δ̇α的数值刚好为0,此时非定常气动力主要由α和α㊃㊃产生㊂在一个周期时,翼型回到初始位置,此时的非定常气动力贡献情况与1/2周期时刚好相反,由于Δα和Δα㊃㊃的数值为0,所以此时非定常气动力主要由Δ̇α产生㊂这与图2(b)的结论一致,说明在沉浮运动过程中,二阶模型才能更准确地再现出非定常气动力和力矩㊂图2(c)是采用一阶和二阶Etkin 气动力模型计算得到的强迫俯仰/沉浮耦合运动的气动力与采用CFD 方法得到的气动力迟滞曲线的对比图㊂由图2(c)可知,对于强迫耦合运动,采用二阶气动导数得到的升力系数与CFD 计算值完全重合,而采用一阶气动导数得到的升力系数误差较大,在最大纵向位移位置比CFD 计算值大145%㊂对于俯仰力矩系数,一阶模型的误差较大,而二阶模型的结果与CFD 计算值虽然不像升力系数那样完全重合,但是㊃6861㊃第11期张庆,等:NACA0012翼型跨声速强迫运动非定常气动力模型吻合程度也较好㊂表2㊀沉浮运动不同位置非定常气动力分布情况Table 2㊀Percentage distributions at different time in theplunging motion %周期α̇αα㊃㊃0.25T 0.50T 0.75T 1.00TΔC L273.27-78.43-94.84ΔC m -246.70198.46148.24ΔC L153.150-53.15ΔC m 250.570-150.57ΔC L 106.3930.53-36.92ΔC m 83.0966.84-49.93ΔC L 0100.000ΔC m 0100.000㊀㊀表3是耦合运动不同位置处各导数对非定常气动力的贡献情况㊂由表3可知,在耦合运动1/4周期时,到达纵向最大位置处,此时也处于抬头的最大位置,此时α㊃㊃对应的非定常升力和力矩分别占总的非定常升力和力矩的-45.35%和-70.82%,̇q 对应的非定常升力和力矩分别占总的非定常升力和力矩的2.19%和-35.25%㊂由于忽略了α㊃㊃与̇q 这2项的影响,所以一阶气动力模型对应的升力和力矩系数与CFD 计算值差别较大,见图2(c)㊂在耦合运动3/4周期时,到达纵向最小位置处,此时也处于低头的最大位置㊂此时α㊃㊃对非定常特性的贡献也比较大,其数值分别为-245.66%和21.26%,̇q 对非定常特性的贡献分别为25.87%和23.00%,所以与1/4周期时的情况类似,一阶模型的计算结果误差较大㊂而在1/2周期时,翼型下沉经过初始位置,由于Δ̇q的数值刚好为0,对非定常气动力没有贡献㊂在一个周期时,翼型回到初始位置,此时Δq 的数值刚好为0,对非定常气动力没有贡献㊂虽然耦合运动气动力并不是单独运动的简单叠加,但是通过对经典Etkin 气动力模型的二阶延拓,能准确地再现出沉浮/俯仰耦合运动过程的非定常气动特性㊂表3㊀耦合运动不同位置非定常气动力分布情况Table 3㊀Percentage distributions at different time in thecoupled pitching /plunging motion %周期α̇αα㊃㊃q̇q0.25T 0.50T 0.75T 1.00TΔC L 130.6617.18-45.35-4.68 2.19ΔC m 117.8643.43-70.8244.78-35.25ΔC L77.3459.74-26.84-10.240ΔC m 25.2154.58-15.1535.360ΔC L 707.86-443.48-245.6655.4125.87ΔC m -35.2261.8521.1629.2123.00ΔC L 172.08-16.19-59.930 4.04ΔC m -349.6492.22210.81146.613㊀结论1)不论是强迫俯仰运动㊁沉浮运动,还是俯仰/沉浮耦合运动,将气动导数拓展至迎角和俯仰角的二阶导数,都可以十分精确地重现出强迫运动过程中的非定常升力变化情况㊂2)由于俯仰力矩的迟滞曲线并不是简单的椭圆形,二阶模型计算出的强迫运动过程的俯仰力矩与CFD 计算值的吻合程度不像升力那么好,说明俯仰力矩的模型要比升力更加复杂㊂3)俯仰/沉浮耦合运动的非定常气动力并不是俯仰运动和沉浮运动的简单叠加,说明精确的气动力建模还需要深入考虑其他变量的影响㊂本文的研究结果表明,Etkin 气动力模型对于非线性较强的气动力建模仍然具有较好的适用性,但是,对于三维流动以及接近失速迎角情况下的非定常气动力的建模,需要更加深入地讨论马赫数㊁减缩频率㊁更高阶导数以及交叉导数在非定常气动力模型中的作用㊂参考文献:[1]杨磊,叶正寅.倾转涵道倾转过渡阶段的非定常气动力[J].航空动力学报,2015,30(1):155-163.YANG Lei,YE Zhengyin.Unsteady aerodynamic force oftilt ducted fan during transition period[J].Journal of aero-space power,2015,30(1):155-163.[2]张庆,叶正寅.基于气动导数的类X -37B 飞行器纵向稳定性分析[J].北京航空航天大学学报,2020,46(1):77-85.ZHANG Qing,YE Zhengyin.Longitudinal stability analysis for X -37B like trans-atmospheric orbital test vehicle based on aerodynamic derivatives[J].Journal of Beijing Universi-ty of Aeronautics and Astronautics,2020,46(1):77-85.[3]ETKIN B.Dynamics of atmospheric flight[M].Mineola:Dover Publications,2012.[4]袁先旭,陈琦,谢昱飞,等.动导数数值预测中的相关问题[J].航空学报,2016,37(8):2385-2394.YUAN Xianxu,CHEN Qi,XIE Yufei,et al.Problems innumerical prediction of dynamic stability derivatives [J].Acta aeronautica et astronautica sinica,2016,37(8):2385-2394.[5]和争春,钱炜祺,朱国林,等.飞行器跨声速区俯仰力矩系数建模方法研究[J].空气动力学学报,2005,23(4):470-475.HE Zhengchun,QIAN Weiqi,ZHU Guolin,et al.Re-search on the modeling of pitching moment coefficient in transonic condition for flight vehicle[J].Acta aerodynami-ca sinica,2005,23(4):470-475.[6]GHOREYSHI M,CUMMINGS R M.Challenges in the aer-odynamics modeling of an oscillating and translating airfoil at large incidence angles[J].Aerospace science and tech-nology,2013,28(1):176-190.[7]NELSON R C,PELLETIER A.The unsteady aerodynamicsof slender wings and aircraft undergoing large amplitude㊃7861㊃哈㊀尔㊀滨㊀工㊀程㊀大㊀学㊀学㊀报第41卷maneuvers[J].Progress in aerospace sciences,2003,39 (2/3):185-248.[8]MARZOCCA P,LIBRESCU L,SILVA W A.Aeroelastic response of nonlinear wing sections using a functional series technique[J].AIAA journal,2002,40(5):813-824.[9]SILVA W A.Application of nonlinear systems theory to transonic unsteady aerodynamic responses[J].Journal of aircraft,1993,30(5):660-668.[10]SILVA W A.Simultaneous excitation of multiple-input/multiple-output CFD-based unsteady aerodynamic systems [J].Journal of aircraft,2008,45(4):1267-1274.[11]ZHANG Qing,HUA Ruhao,YE Zhengyin.Experimentaland computational investigation of novel vertical tail buffet suppression method for high sweep delta wing[J].Science China technological sciences,2015,58(1):147-157.[12]ZHANG Qing,YE Zhengyin.Novel method based on in-flatable bump for vertical tail buffeting suppression[J].Journal of aircraft,2015,52(1):367-371. [13]张庆.高速再入飞行器动力学问题研究[D].西安:西北工业大学,2018.ZHANG Qing.Research on flight dynamics of high-veloci-ty reentry vehicles[D].Xiᶄan:Northwestern Polytechni-cal University,2018.[14]RAUSCH R D,BATINA J T,YANG H T Y.Spatial ad-aptation of unstructured meshes for unsteady aerodynamic flow computations[J].AIAA journal,1992,30(5): 1243-1251.[15]BATINA J T.Unsteady Euler airfoil solutions usingunstructured dynamic meshes[J].AIAA journal,1990, 28(8):1381-1388.[16]KANDIL O A,CHUANG H A.Unsteady transonic airfoilcomputation using implicit Euler scheme on body-fixed grid[J].AIAA journal,1989,27(8):1031-1037.本文引用格式:张庆,叶正寅.NACA0012翼型跨声速强迫运动非定常气动力模型[J].哈尔滨工程大学学报,2020,41(11):1683-1688. ZHANG Qing,YE Zhengyin.Unsteady aerodynamic model of NACA0012associated with forced oscillations and translations in transonic flight[J].Jour-nal of Harbin Engineering University,2020,41(11):1683-1688.㊃8861㊃。
2020年跨声速非定常空气动力计算与分析精品版跨声速非定常空气动力计算Computation on Transonic Unsteady Aerodynamics北京大学力学与工程科学系理论与应用力学专业 00级陈雪梅摘要颤振问题一直是高速飞行器设计中的一大难题,特别在跨声速区段。
本文利用FLUENT6.1对一模型机翼的颤振行为进行了数值模拟,仿真机翼在高速气流中受激后扭曲变形最后发展成颤振的全过程,并对这一计算结果进行了初步分析,所得的算法具有普遍意义。
关键词:颤振,空气动力学,动网格[引言]早期的飞行器设计中的空气动力学分析都是将机翼﹑机身和其他气动部件当作刚体来处理。
但自第一架飞机诞生以来,空气动力学与飞机结构弹性的相互作用问题已经对航空技术的发展产生了重大影响,特别在‘彗星号’失事以后,人们对此倍加关心。
飞机在空气载荷作用下会出现可观的变形,这种变形将改变空气动载荷的分布,而它反过来又使变形发生变化。
在这种相互作用过程中,会引起振动,学术界称之为颤振。
这是一种自激振荡,它不断从气流中吸收能量。
当飞机发生颤振时,轻则出现不稳定和振动现象,重则因它引起材料‘疲劳’从而导致飞机在空中解体,以至机毁人亡。
在莱特兄弟首次试飞前,兰利的“空中旅行者”作了两次不成功的飞行试验。
第二次试飞时机翼和尾翼毁坏了,失败原因众说纷纭,气动弹性可能是第二次失败的罪魁祸首。
第一次世界大战中,英国的DH-9飞机尾翼颤振导致了飞行员死亡。
对此,英国空气动力学家贝尔斯托(L. Bairstow)首先对颤振进行了理论研究。
随着飞机速度的提高,空气动力增大,而重量小的结构形式使机翼抵抗变形的能力下降,所以气动弹性问题便得严重起来。
20世纪30年代初英国一家飞机连续发生有气动弹性引起的颤振事故,促使航空工程界对气动弹性问题普遍重视起来[摘自参考文献3,P118]。
其间的理论研究颇有成效。
美国力学家西奥多森(T. Theodorson)提交的研究报告对美国航空工业界建立颤振分析方法起了巨大作用。
50年代中后期,特别是60年代,一方面空气动力学理论的突破为非定常空气动力学研究提供了新方法;另一方面风洞技术高度发展,使振荡机翼非定常气动理论有了新的突破。
但由于理论方法的局限性以及风洞试验的高耗能及周期长等问题,计算空气动力学应运而生。
由于涉及到非定常空气动力学,颤振及气动弹性问题的研究十分困难。
目前国内关于颤振的研究主要还是基于试验,理论仅限于线性划分析。
近年来由于计算技术的飞速发展以及CFD的实际解题能力大大扩大,用数值方法解决这样复杂的问题已是可能。
采用计算流体力学方法可缩短周期、降低费用,特别在初选阶段,优化选型需要不断改变参数、重复计算。
对那些目前不能在特定的飞行状态下进行试验的未来飞行器来说,数值模拟方法可以减少其设计风险,并在风洞实验前预先筛选设计方案。
本文的研究是与北京航空航天大学合作进行的,机翼的振型和刚度由北航提供,我们负责气动力以及气动力与机翼振动的耦合计算。
气动力计算本身已是高度非线性问题,现在还需与机翼的弹性振动相耦合,其难度相当高。
这样的研究在国内尚属首次。
在计算种我们利用了Fluent6.1软件UDF 功能,这是我们的工作大大简化。
如今已完成计算的主过程,结果表明我们设计的颤振问题的直接算法是可行的,有通用价值的。
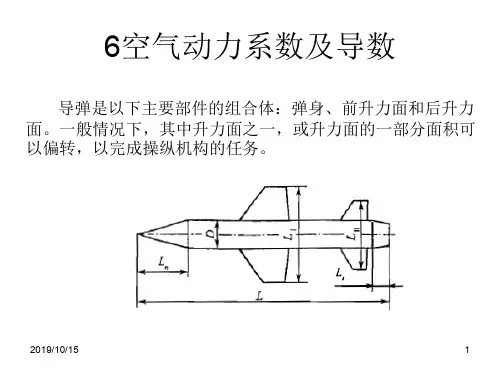
一.计算模型 1. 机翼几何外形如图(Fig1、Fig2)所示的后掠机翼,展长为1.5m ,根弦长为1.0m ,梢弦长为0.6m ,前缘后掠角为40︒,机翼平面位于xoy 平面内,根部固支。
翼剖面为对称薄翼型。
Fig1 Fig23.网格结构几何实体及网格用Fluent 自带前处理软件Gambit2.0生成。
OyxDCB40︒1.01.50.6计算区域采用前段、翼梢段、上下为6倍展长,尾部为10倍展长的长方体区域。
由于只计算一侧机翼的情形,因此取翼根部为对称面。
流场中包含机翼的一小部分采用非结构化网格(Fig3),以便于使用Fluent中提供的动网格手段进行计算。
其余部分采用结构化网格,以提高计算精度及加快收敛速度。
Fig3 (机翼网格图)4. 机翼振动的数学模型研究中假定机翼为弹性体,由于只研究小振幅下的振动,可假设振型为抛物线形式。
末梢位置呈周期性变化:«Skip Record If...»其中A为末梢的振幅,«Skip Record If...»为机翼周期性振动的圆频率,具体取为机翼振动的第一阶主频率«Skip Record If...»假定机翼最大偏角为«Skip Record If...»,则振幅振幅A具体取值为«SkipRecord If...»,«Skip Record If...»为机翼展长。
按照假定,整个机翼的振型为抛物线型,于是有«Skip Record If...»其中x,y,z为机翼坐标,t为运动时间。
5. 气流主控方程对机翼进行数值模拟的主控方程可以采用欧拉方程,也可以采用N-S方程。
对升力和力矩的计算采用欧拉方程即可提供足够的精度,欧拉方程计算收敛速度相对较快,结果与NS方程差别不大。
但欧拉方程无法准确计算阻力,而NS方程对升力阻力以及力矩均能计算得很好,但收敛速度相对较慢。
本文研究机翼在跨声速段的颤振问题,«Skip Record If...»。
因此,应该将此问题看成充分发展的湍流问题。
采用标准的«Skip Record If...»模型进行计算。
数值模拟采用的雷诺应力平均NS方程为«Skip Record If...»«Skip Record If...»«Skip Record If...»«Skip Record If...»为了使上述方程组封闭,采用Boussinesq 假设:«Skip Record If...»其中,k为湍流动能,«Skip Record If...»是湍流粘滞系数,可以通过湍流动能k,湍流耗散率«Skip Record If...»计算:«Skip Record If...»«Skip Record If...»湍流动能,«Skip Record If...»湍流耗散率满足的传输方程:«Skip Record If...»«Skip Record If...»这样就组成了封闭的方程组,即是标准«Skip Record If...»湍流模式,其中的经验常数为:«Skip Record If...»6. 网格重构算法计算中采用了Fluent提供的Dynamic-Mesh Modal,机翼部分为非结构化网格,因此使用动网格中的弹性系数算法和局部重构算法对网格进行重构。
在弹性系数算法中,将任意两个网格节点之间的边等效为一根弹簧。
先由用户给定的UDF(User-Defined-Function)函数,计算出边界上的结点位移。
此位移将在与此结点相连的任意一条边上产生一个弹性力,弹性力的大小与位移大小成正比。
由此,边界结点的位移就被传递到整个体网格。
在平衡状态下,每个结点所受的所有与它相连边上的弹性力之和为零。
该平衡条件产生了一个循环的计算结点位移的方程:«Skip Record If...»其中,«Skip Record If...»是结点i的位移,«Skip Record If...»是与结点i相连的节点数目,«Skip Record If...»结点i与相邻结点j之间的弹性常数,定义为: «Skip Record If...»当边界结点位移已知时,就可以用Jacobi扫描算法求解上述方程。
得到收敛解后,内部结点的位置被更新。
«Skip Record If...»其中,n+1和n分别代表下一个时间步和当前时间步。
当边界结点的位移相对局部网格的尺寸很大时,网格的质量将变得很差。
为避免这一问题,Fluent提供局部重构算法对坏质量网格进行合并或拆分。
此时坏质量网格定义为超过某一给定体,低于某一指定体积或者网格倾斜率大于某一数值的那些网格。
二.计算过程采用Segregated求解器,SIMPLE算法,利用有限体积法离散控制方程,采用一阶迎风差分格式,时间步长取为物理周期的«Skip Record If...»便可取得相当好的计算结果。
计算过程中监控机翼的升阻力以及力矩的变化趋势,阻力趋于稳定以及升力、力矩周期与物理振动周期吻合时结束计算。
实际计算中取来流马赫数«Skip Record If...»,边界均设为远场压力条件。
分别取攻角为«Skip Record If...»进行计算。
在数值模拟中的每一个计算步用UDF函数接口给定机翼上网格结点的位移,并利用弹性常数算法及局部重构算法对网格进行重构。
三.计算结果和分析1.«Skip Record If...»攻角时的计算结果:阻力系数图及升力系数图(Fig4和Fig5)Fig4 (阻力系数曲线) Fig5 (升力系数曲线)力矩系数图(Fig6)Fig6(零攻角力矩系数曲线)可以看到,阻力系数在计算稳定后保持不变,这是因为机翼只有沿垂直方向位移,对气流只产生竖直方向扰动,对水平方向的力并无太大影响。
升力与力矩的变化趋势与物理振动的变化趋势完全吻合( «Skip Record If...»),说明了计算的合理性。
计算结果表明初始时刻升力及力矩具有最大值。
此时机翼处于平衡位置,具有最大的运动速度,即对流场有最大的扰动,理论分析上此时的升力及力矩也应取得最大值,再一次证实数值模拟方法的正确性。
2. «Skip Record If...»攻角计算结果:«Skip Record If...»攻角阻力及升力系数图(Fig7,Fig8)Fig7 (2度攻角阻力系数曲线) Fig8 (2度攻角升力系数曲线)«Skip Record If...»攻角力矩系数图(Fig9)Fig9 (2度攻角力矩系数曲线)3.«Skip Record If...»攻角计算结果«Skip Record If...»攻角阻力及升力图(Fig10,Fig11)Fig10(«Skip Record If...»攻角阻力系数曲线) Fig11(«Skip Record If...»攻角升力系数曲线)«Skip Record If...»攻角力矩系数图(Fig12)Fig12(«Skip Record If...»攻角力矩系数曲线)可以明显看到,攻角变大时,阻力系数并没有太大的变化。