当前位置：文档之家 › 定常&非定常

定常&非定常

  • 格式：pdf
  • 大小：198.73 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

第5章_线性定常系统的综合

第5章_线性定常系统的综合
一般控制作用规律常取反馈的形式。

一、综合问题
给定系统状态空间描述：
Ax Bu, x y Cx
x(0) x0
t 0
(1)
A、B、C均为常阵且给定。 再给出所期望的性能指标：
1)对系统状态运动期望形式所规定的某些特征量。
2)对其运动过程所规定的某种期望形式或需取极小 （或极大）值的一个性能函数。 综合：寻找一个控制作用 u ，使得在其作用下，系统 运动的行为满足所给出的期望性能指标。
3. 状态反馈和输出反馈的基本结构形式均不太适用于工程实 际问题。状态反馈和输出反馈的通用结构形式较适用于工程 实际问题。带观测器的状态反馈系统，可解决系统状态不能 测量时的状态重构问题；带有补偿器的输出反馈系统，可解 决输出反馈基本结构形式不能任意配置极点的问题。 4. 状态反馈能保持原受控系统的能控性，但不一定能保持原 受控系统的能观测性。输出反馈能同时保持原受控系统的能 控性和能观测性。 5. 输出反馈是在物理上可构成的，状态反馈是在物理上不能 构成的。基此，输出反馈优于状态反馈。 6. 扩展状态反馈(即带状态观测器状态反馈系统)和扩展输出 反馈(即动态输出反馈系统)是等价的。
故(A BK)B的列向量可由 [B, AB]的列向量的线性 组合来表示。
结论1证明(续)
同理
2 (A BK) B (A BK)(A BK)B (A BK)(AB BKB)
A 2B ABKB BKAB BKBKB
2 故(A BK) B的列向量可由[B, AB, A 2B]的列向量的线性组 合表示。 n 1 以此类推(A BK) B的列向量可由[B, AB, A 2B A n 1B]的列向量
受控系统为： Ax Bu x y Cx 反馈控制规律 : u Hy v HCx v

定常与非定常流动

定常与非定常流动

定常流动流体（气体、液体）流动时，若流体中任何一点的压力，速度和密度等物理量都不随时间变化，则这种流动就称为定常流动；反之，只要压力，速度和密度中任意一个物理量随时间而变化，液体就是作非定常流动或者说液体作时变流动。

所以，定常流动时，管中流体每单位时间流过的体积(体积流量)qV为常量，流体每单位体积的质量(密度)ρ也是常量。

非定常流动流体的流动状态随时间改变的流动。

若流动状态不随时间而变化，则为定常流动。

流体通常的流动几乎都是非定常的。

分类按流动随时间变化的速率，非定常流动可分为三类：①流场变化速率极慢的流动：流场中任意一点的平均速度随时间逐渐增加或减小，在这种情况下可以忽略加速度效应，这种流动又称为准定常流动。

水库的排灌过程就属于准定常流动。

可认为准定常流动在每一瞬间都服从定常流动的方程，时间效应只是以参量形式表现出来。

②流场变化速率很快的流动：在这种情况下须考虑加速度效应。

活塞式水泵或真空泵所造成的流动，飞行器和船舶操纵问题中所考虑的流动都属这一类。

这类流动和定常流动有本质上的差别。

例如，用伯努利方程（见伯努利定理）描述这类流动，就须增加一个与加速度有关的项，成为：,式中为理想流体沿流线的速度分布；A和B表示同一流线上的两个点;P 为压强;为密度；g为重力加速度；z为重力方向上的坐标；ds为流线上的长度元。

③流场变化速率极快的流动：在这种情况下流体的弹性力显得十分重要，例如瞬间关闭水管的阀门。

阀门突然关闭时，整个流场中流体不可能立即完全静止下来，速度和压强的变化以压力波（或激波）的形式从阀门向上游传播，产生很大的振动和声响，即所谓水击现象。

这种现象不仅发生在水流中，也发生在其他任何流体中。

在空气中的核爆炸也会发生类似现象。

除上述三类流动外，某些状态反复出现的流动也被认为是一种非定常流动。

典型的例子是流场各点的平均速度和压强随时间作周期性波动的流动，即所谓脉动流，这种流动存在于汽轮机、活塞泵和压气机的进出口管道中。

线性定常系统的频率特性

线性定常系统的频率特性

一、实验目的
1、学习了解Matlab语言的实验环境。 学习了解Matlab语言的实验环境。 语言的实验环境 2、练习Matlab命令的基本操作。 练习Matlab命令的基本操作 命令的基本操作。 3、练习m文件的基本操作。 练习m文件的基本操作。 4、明确频率特性的概念及其物理意义。 明确频率特性的概念及其物理意义。 5、掌握频率特性的测试方法及原理; 掌握频率特性的测试方法及原理; 6、掌握频率特性的表示方法
Matlab工作界面窗口 Matlab工作界面窗口
在“command Window”命令窗口中命令提示 Window”命令窗口中命令提示 符位置键入如下命令： 符位置键入如下命令： help 显示Matlab的功能目录 显示Matlab的功能目录 help control 阅读控制系统工具箱命令清单。 阅读控制系统工具箱命令清单。 help step 阅读命令step的帮助文件内容 的帮助文件内容。 阅读命令step的帮助文件内容。
实验4 实验4 线性定常系统的频率特性
MATLAB软件是一套高性能的数值计算和可视化数 MATLAB软件是一套高性能的数值计算和可视化数 学软件， 学软件，具有强大的矩阵计算能力和良好的图形可视化 功能，为用户提供了非常直观和简洁的程序开发环境， 功能，为用户提供了非常直观和简洁的程序开发环境， 被誉为“巨人肩上的工具”以及“第四代计算机语言” 被誉为“巨人肩上的工具”以及“第四代计算机语言”， 在信号处理、图像处理、控制系统分析与设计、 在信号处理、图像处理、控制系统分析与设计、系统辨 识、工程优化、统计分析等许多学科领域都得到了广泛 工程优化、 的应用。 的应用。 MATLAB软件提供了专门的控制系统工具箱 MATLAB 软件提供了专门的控制系统工具箱 ， 控制 软件提供了专门的控制系统工具箱， 系统中的许多应用（ 如时域分析、 频域分析、 系统中的许多应用 （ 如时域分析 、 频域分析 、 根轨迹作 图等）都可以用一个简单的m函数命令来实现。 图等）都可以用一个简单的m函数命令来实现。尤其是所 提供的Simulink软件包 软件包， 提供的Simulink软件包，由于采用与传递函数动态框图非 常相似的结构图模型， 常相似的结构图模型 ， 并采用类似于电子示波器的模块 显示仿真曲线， 因此特别适用于“ 自动控制理论” 显示仿真曲线 ， 因此特别适用于 “ 自动控制理论 ” 课程 实验的系统仿真和分析。 实验的系统仿真和分析。

流体力学——定常流动

流体力学——定常流动

P0
A
h
B
图6 小孔流速
例2：流量计（汾丘里管）原理
H
v1 主管 细管
v2
图7流量计原理
如图7所示，它是一段中间细，两头粗的管子， 水平安装在待测管道中，求体积流量Q。
V1 、V2 分别表示粗部S1 、细部S2 处的流速，P1 、 P2分别表示粗部S1 、细部S2 处的压强 V2 > V1 ，P1> P2，P1 — P2 =ρgH 根据连续性原理，有V1 S1= V2S2
S2 S2’ S1 S1’
v2
v1
h2
h1
图5 推导伯努利方程
由于理想流体不可压缩有：Δm1=Δm2=Δm Δt时间内动能变化： ΔEk=1/2Δm V22 —1/2Δm V12 Δt时间内外力作功 S1处，压力f1=P1 S1 ，正功W1= f1V1Δt S2处，压力f2=P2 S2 ，负功W2= - f2V2Δt 重力作负功：W3= -Δm g(h2—h1) 总功W= P1S1V1Δt-P2S2V2Δt-Δmg(h2-h1) 根据连续性原理，V1S1=V2S2=Δm/ρΔt 综合上式有，W=(P1 -P2)Δm/ρ-Δmg(h2—h1)
（4）式就是伯努利方程。
伯努利方程的物理意义：
P：单位体积流体通过细流管截面时，压力所作的功。 又称流体单位体积的压力能。 1/2ρV2：流体单位体积所具有的动能。 ρgh：流体单位体积所具有的势能。
物理意义：对于细流管中定常流动的理想流体， 单位体积的压力能、动能、势能三者之和保持 不变。
伯努利方程的应用 例1：小孔流速的计算。 如图6.6所示，大桶侧壁 有一小孔，桶内盛满了 水，求水从小孔流出的 速度。 AB两点之间为一条流线 P0+ρv2/2 = P0+ρgh V = （2gh）1/2

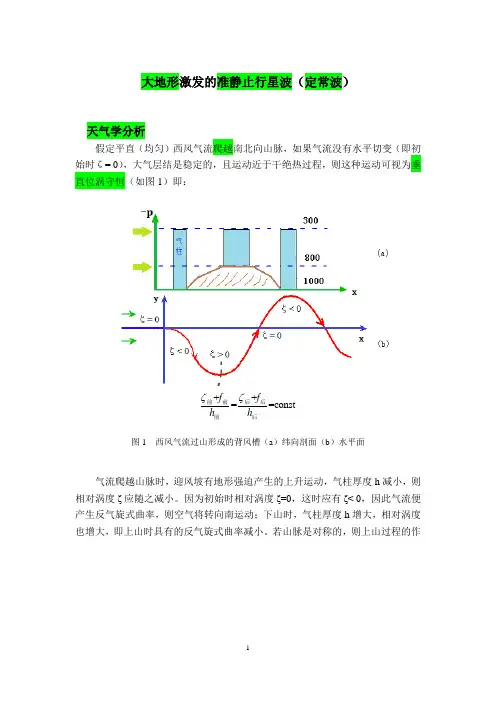
地形Rossby波与定常波

地形Rossby波与定常波

大地形激发的准静止行星波（定常波）天气学分析假定平直（均匀）西风气流爬越南北向山脉，如果气流没有水平切变（即初始时ζ= 0），大气层结是稳定的，且运动近于干绝热过程，则这种运动可视为垂直位涡守恒（如图1）即：++==constf f h h ζζ前前后后后前图1 西风气流过山形成的背风槽（a ）纬向剖面（b ）水平面气流爬越山脉时，迎风坡有地形强迫产生的上升运动，气柱厚度h 减小，则相对涡度ζ应随之减小。

因为初始时相对涡度ζ=0，这时应有ζ< 0，因此气流便产生反气旋式曲率，则空气将转向南运动；下山时，气柱厚度h 增大，相对涡度也增大，即上山时具有的反气旋式曲率减小。

若山脉是对称的，则上山过程的作图2 西风气流过山形成的背风槽示意图用被下山的相反作用所抵消，则在背风坡山脚，ζ恢复为零。

但是因为气流过山的全过程是反气旋路径，因此到达山脚时，气流已位于初始纬度0ϕ之南（即位于1ϕ维度），ƒ比初始时小，所以ζ必须比原来大（即下山时ζ增加的幅度大于上山时ζ减小的幅度），则在山脚变为正涡度，气流轨迹应为气旋式弯曲，即向北运动。

当气流返回到初始纬度0ϕ时，ζ应该回复到初始状态，即ζ=0.但是由于惯性作用（此时h=const ．，则位涡守恒→绝对涡度守恒），气流将继续向北运动→ƒ增大→ζ减小→反气旋式弯曲，到达一定纬度2ϕ时，气流又转向南运动……（重复上述过程）。

这样，山脉背风坡形成一系列的槽脊，但是由于摩擦作用，只有第一个槽在天气图上最清楚，称为背风槽或地形槽（见图2）。

由于是气流爬越山脉时为保持位涡守恒而形成的槽，故又称为地形Rossby （罗斯贝）波。

动力学理论数学推导据图3分析：假定平直西风爬越南北向山脉，气流无水平切变（即初始时ζ= 0），大气层结稳定，运动近似于无摩擦、干绝热过程。

过山前（0x <），有一均匀西风u ，气层厚度为H ，相对涡度00ζ=； 过迎风坡山脚（=0x ）后（0x >），由于存在山脉，设山脉高度为s h ，则气层厚度为s H h -，相对涡度00ζ≠。

线性定常系统的稳定性

线性定常系统的稳定性

四、例题详解
【例3】已知系统特征方程： s 5 2s 4 3s 3 6s 2 10s 15 0 试用劳斯稳定判据判断其稳定性。 解：1) 特征方程中各项系数>0 ——满足必要条件 2) 构造劳斯阵列：
s5 s
由“+”到 “-”符号变 化 1次 由“-”到 “+”符号 变化1次
四、例题详解
【证明】 欲使式(3)成立，则当
即当
成立是必要的，上式是渐近稳定的必要条件
四、例题详解
【证明】 当 即当
将式(10)+(11)可得 充分满足渐近稳定条件，即式(10)、(11)是系统渐近 稳定的充分条件。
四、例题详解
【例2】已知系统特征方程：
s 4 2s 3 3s 2 4s 5 0
四、例题详解
【解答】 根据劳斯判据
四、例题详解
【解答】 劳斯表中首列的 是无穷小正数，即 0 。由劳 斯表中首列各元素变号2次，故可知特征方程在右半 S平面有两个根，则方程发散不稳定。实际上，原方 程
四、例题详解
【例5】 某系统特征方程为 试确定特征方程的根在平面分布情况，并指出系统 的稳定性。
脉冲响应含有如下分量
[C0 sin(t 0 ) C1t sin(t 1 ) Cr 1t r 1 sin(t r 1 )]1(t )
(6)
s
因式时，其脉冲响应含有如下分量
D0 sin(t 0 ) D1t sin(t 1 )
2 2 (( s ) j )(( s ) j ) ( s ) 当含有 s

s n 1 s
n 2
b1
a1

结构振动理论-定常强迫振动的复数解法与频率响应函数

结构振动理论-定常强迫振动的复数解法与频率响应函数

bn
2 T
T /2
T / 2
f (t) sin ntdt
2 T
0
T / 2
Asin ntdt
2 T
T
0
/
2
A
sin
ntdt
2 ( A cosnt 0 ) 2 ( A cosnt T / 2 )
T n
T / 2 T n
0
2 2A (1 cos n ) 2A (1 cos n )
T n
n
bn
4A
如图所示基础激励振动系统： mx k(x y) c(x y)
整理后得到： mx cx kx ky cy
利用复数解法：
y Ye j t
x Xe je j t Xej(t)
m
o
x(t)
k
c
y Y cost
基础激励
单自由度系统的定常强迫振动
(m2 k jc)Xe j (k jc)Y
象的振动位移测试。 单自由度系统的定常强迫振动
加速度计： 令 y Ye j t 则 y 2Ye j t
Z
Y 2
(1 2 )2 (2 )2
|
Z
| |
y|
1 Ω2
1
(1 2 )2 (2 )2
4
0
如果测振仪设计得具有较高的固 3
有频率 ，使 / Ω 1
2
0.1
0.15 0.2
这时，记录下来的
同样，由于存在阻尼，我们只考虑(定常)稳态响应。
单自由度系统的定常强迫振动
设其稳态特解是 xc Xe jt
xc jX e jt xc 2 X e jt
代入原方程，消去
e jt 后，求出

定常与非定常流动

定常与非定常流动

定常流动流体（气体、液体）流动时，若流体中任何‎一点的压力，速度和密度等‎物理量都不随‎时间变化，则这种流动就‎称为定常流动‎；反之，只要压力，速度和密度中‎任意一个物理‎量随时间而变‎化，液体就是作非‎定常流动或者‎说液体作时变‎流动。

所以，定常流动时，管中流体每单‎位时间流过的‎体积(体积流量)qV为常量，流体每单位体‎积的质量(密度)ρ也是常量。

非定常流动流体的流动状‎态随时间改变‎的流动。

若流动状态不‎随时间而变化‎，则为定常流动‎。

流体通常的流‎动几乎都是非‎定常的。

分类按流动随时间‎变化的速率，非定常流动可‎分为三类：①流场变化速率‎极慢的流动：流场中任意一‎点的平均速度‎随时间逐渐增‎加或减小，在这种情况下‎可以忽略加速‎度效应，这种流动又称‎为准定常流动‎。

水库的排灌过‎程就属于准定‎常流动。

可认为准定常‎流动在每一瞬‎间都服从定常‎流动的方程，时间效应只是‎以参量形式表‎现出来。

②流场变化速率‎很快的流动：在这种情况下‎须考虑加速度‎效应。

活塞式水泵或‎真空泵所造成‎的流动，飞行器和船舶‎操纵问题中所‎考虑的流动都‎属这一类。

这类流动和定‎常流动有本质‎上的差别。

例如，用伯努利方程‎（见伯努利定理‎）描述这类流动‎，就须增加一个‎与加速度有关‎的项，成为：,式中为理想流‎体沿流线的速‎度分布；A和B表示同‎一流线上的两‎个点;P 为压强;为密度；g为重力加速‎度；z为重力方向‎上的坐标；ds为流线上‎的长度元。

③流场变化速率‎极快的流动：在这种情况下‎流体的弹性力‎显得十分重要‎，例如瞬间关闭‎水管的阀门。

阀门突然关闭‎时，整个流场中流‎体不可能立即‎完全静止下来‎，速度和压强的‎变化以压力波‎（或激波）的形式从阀门‎向上游传播，产生很大的振‎动和声响，即所谓水击现‎象。

这种现象不仅‎发生在水流中‎，也发生在其他‎任何流体中。

在空气中的核‎爆炸也会发生‎类似现象。

除上述三类流‎动外，某些状态反复‎出现的流动也‎被认为是一种‎非定常流动。

线性定常系统的可控性和可测性

线性定常系统的可控性和可测性

• 结论： 结论： 状态完全可控和可观的必要条件是： 状态完全可控和可观的必要条件是： 系统的传递函数或传递函数矩阵中不出现 相约现象。 相约现象。 或： 系统的传递函数或传递函数矩阵是不可约 的
六.线性系统可控性和可观性的对偶关系 1.对偶关系 对偶关系 • 设 • 设 • 称
S1 为系统∑（A,B,C,D 为系统∑ S2 为系统 S1 和 S2对偶 对偶.
• 对定义的说明 对定义的说明: 1). t0 时刻的状态应是任意的 也即x(t)的各 时刻的状态应是任意的,也即x(t)的各 也即x(t) 时的值无论如何给定,都存在容许 分量在 t0 时的值无论如何给定 都存在容许 控制,在 时刻将初始状态转移到零,系统方 控制,在 t1 时刻将初始状态转移到零,系统方 为可控,否则系统不可控 否则系统不可控. 为可控 否则系统不可控 2). t1 应为有限的时间 t1 的选取与 t0 有关 应为有限的时间, 有关, 趋于无穷则可控失去意义. 若 t1 趋于无穷则可控失去意义
y = [ β0
ˆ β1 ⋯ βn−1] x + du
• 其中
1 a 1 O n−1 p = An−1b ⋯ Ab b ⋮ ⋮ ⋱ a2 a3 ⋯ 1 a1 a2 ⋯ an−1 1
• 由于{A,b}对可控,故p一定是非奇异的 由于{A,b}对可控, {A,b}对可控 一定是非奇异的
0 0 ɺ = ⋮ ˆ x 0 −− −a0 1 0 ⋮ 0 0 1 ⋮ 0 ⋯ ⋯ ⋮ ⋯ 0 0 0 0 ⋮ ⋮ ˆ x + u 1 ⋮ ⋮ −− −an−1 1
−− −− −− −a1 −a2 ⋯
__ __ __ __ | __ ɺ = 1 0 ⋯ 0 | −a1 x + β1 u ˆ x ˆ 0 1 ⋯ 0 | −a2 β2 ⋮ ⋮ ⋱ ⋮ | ⋮ ⋮ 0 0 ⋯ 1 | −an−1 βn−1

线性定常系统的状态空间分析与综合2

线性定常系统的状态空间分析与综合2

从系统的机理出发
例 建立如右图所示机械系统的状
态空间表达式，并画出系统的状态图。
k F
根据牛顿第二定理有
m
或表示成
F ky f dy m d 2 y
dt
dt 2
d 2 y dy m dt2 f dt ky F
y f
机械位移系统
选择位移 y 和速度dy / dt为状态变量，令 x1 y, x2 dy / dt
同一个系统，状态变量的选取不是惟一的。 对于一般的物理系统，状态变量的个数应等于储能元 件的个数。
基本概念
用状态变量来表征系统时，还有如下基本概念：
状态向量 把描述系统的 n个状态变量 x1(t), x2 (t), , xn (t) 看作向
量x(t) 的分量，则x(t) 称为 n 维状态向量，记作
状态空间
x1(t)
x1
x(t
)
x2
(t
),
简记为
x
x2
xn
(t
)
xn
以状态变量 x1, x2, , xn为坐标轴所张成的n维空间，
称为状态空间。系统在任意时刻的状态，在状态空间中是一个
点，随时间推移，状态在变化，在状态空间中绘出一条轨迹，
称为状态轨线。
基本概念
状态方程 由系统的状态变量构成的一阶微分方程组，
则
x&1
x2
,
x&2
k m
x1
f m
x2
1 m
F,
y
x1
从系统的机理出发
用向量—矩阵表示的状态空间表达式为
x&1 x&2
0
k
m
1 f

12理想流体的定常流动

12理想流体的定常流动

2 机械能的变化量
势能的变化量：∆ Ep = mg∆h = ρg ∆V (h2 - h1) 动能的变化量：∆ Ek = ∆ m (v2/2) =ρ∆V(v22 - v21)/2 根据功能原理，则有： A = ∆Ep + ∆ Ek (p1-p2) ∆V= ρg ∆V (h2-h1) +ρ∆V(v22-v21)/2
【问题】
（ 1）
v ds v ds v ds 1 1 2 2 3 3
?
3
1 2
（ 2）
v毛细管 v动脉
?
四、 伯努利方程能量守恒定律在流体力学中的应用
理想液体伯努利方程的推导
理想液体伯努利方程
1 外力对液体所做的功 A = p1S1v1 ∆ t - p2S2v2 ∆ t = (p1-p2) ∆V
整理后得理想液体伯努利方程为： p1 +ρg h1 +ρv12 / 2 = p2+ρg h2 +ρv22/2
或 p+ρg h+ v2 ρ/2= C（C为常数）
理想流体在管道中稳定流动时，同一管道内任 一截面上的总能量应该相等。
理想液体伯努利方程的物理意义
在密闭管道内作定常流动的理想流 体具有三种形式的能量，即压力能、势 能和动能。在流动过程中，三种能量之 间可以互相转化，但各个过流断面上三 种能量之和恒为定值。
于极为次要的地位，就可以看成理想流体.
2.流线与流管 流线——曲线上的每一点的切线方向和位于该点 处流体质元的速度方向一致.流线不会相交。
v1
1
v2
2
3
v3
流管——通过流体内部某一截面的流线围成的管子.
一般流线分布随时间改变，流迹并不与流线重合. 由于流线不会相交，流管内、外的流体不会穿越管壁。

第4章 线性定常系统的线性变换

第4章 线性定常系统的线性变换

记： P1 x； A P1 AP； b P1b； c cP； y y x 变换后的状态空间表达式为：
x = Ax bu, y c x
这称为对系统进行了P变换。 对系统进行线性变换的目的在于使系统矩阵规 范化，以便于分析与计算。状态空间表达式的非奇 异变换不会改变系统原有性质，故称为等价变换。 利用线性变换后的规范化描述进行分析设计或计算， 得到所需结果后，再经过反变换 ，变换回原 x P 1 x 来的状态空间描述，得到最终结果。

0 0 ; 1 n 1
0 0 b Pb 0 1
其中：
n 1 cb cAb cb n2 n 1 0 cAn 1b n 1cAn 2b 2 cAb 1cb
第4章 线性定常系统的线性变换
2．无相同的特征值的可控标准形A阵
若A为友矩阵，且有n个互异实数特征值 1, 2 ,, n ，
则下列的范德蒙特矩阵P可使A对角化：
0 0 A 0 a0 1 0 0 0 1 0 0 0 1 an 1
13
第4章 线性定常系统的线性变换
三．化SISO可观测系统为可观测标准型（※）
结论：对于完全可观测的单输入—单输出系统
x Ax bu y cx
其中：A为n×n常阵，b，c分别为n维列向量和n维行 向量。设系统的特征多项式为
(s) det(sI A) sn n1sn1 1s 0
1 1 2 1 P 12 22 1n 1 2n 1 1 1 n 2 n nn 1

线性定常控制系统的数学模型

线性定常控制系统的数学模型

第三十八章线性定常控制系统的数学模型第一节控制系统模型的构成一、控制系统的模型描述控制系统动态特性的数学表达式称为系统的数学模型，它是分析和设计系统的依据。

数学模型应当既能足够准确地反映系统的动态特性，又具有较简单的形式。

实际系统都程度不同地存在非线性和分布参数特性，如果这些因素影响不大，则可忽略不计。

在正常工作点附近变化时，可以用线性化模型来处理；但当系统在大范围内变化时采用线性化的模型就会带来较大误差。

可以根据系统内部的变化机理写出有关的运动方程，或者通过实验测取系统的输入!输出数据，然后对这些数据进行处理，从而建立系统的数学模型。

前者是机理法，后者是测试法，又称系统辨识。

二、微分方和差分方程微分方程是连续系统最基本的数学模型，可按下列步骤建立："!将系统划分为单向环节，并确定各个环节的输入量、输出量。

单向环节是指后面的环节无负载效应，即后面的环节存在与否对该环节的动态特性没有影响。

#!根据系统内部机理，通过简化、线性化、增量化建立各个环节的微分方程。

$!消去中间变量，保留系统的输入量、输出量，得出系统的微分方程。

%!整理成标准形式，将含输出量的项写在方程左端，含输入量的项写在右端，并将各导数项按降阶排列。

设&!’，则单输入!单输出系统的微分方程的一般形式为(（"）（)）*+"(（&!"）（)）*…*+&!"(!（)）*+&(（)）,-./（’）（)）*-"/（’!"）（)）*…*-’!"/!（)）*-’/（)）（$0!"）离散系统在某一时刻12的输出(（1），可能既与同一时刻的输入与同一时刻的输入/（1）有关，又与过去时刻的输入(（1!"），…，/（1!’）有关；而且还与过去时刻的输出/（1!"），…，(（1!&）有关。

因此，&!’时，输入和输出之间的关系可表示为#（$）*%"#（$!"）*…*%"#（$!"）,&.’（$）*&"’（$!"）*…*&(’（$!(）（$0!#）不失一般性，可以假定/（1）,.，(（1）,.，13.。

1.2理想流体的定常流动

1.2理想流体的定常流动

v1
1 2
v2
3
v3
流管——通过流体内部某一截面的流线围成的管子.
一般流线分布随时间改变，流迹并不与流线重合. 由于流线不会相交，流管内、外的流体不会穿越管壁。
二、定常流动
空间各点流速不随时间变化称定常流动.
v v ( x, y, z )
在定常流动中流线分布不随时间改变，流线与 流迹相重合.
三、 连续性方程质量守恒定律在流体力学中的应用
连续性方程:
假设在流场内取一段细小的流管 理想流体做定常流动 则，在dt时间内，由于不考虑可压缩性
m1 = m2 u1S1dt = u2S2dt u1S1 = u2S2
或
Q= vS = 常数
结论：流体在管道中流动时，流过各个断面的流量 是相等的，因而流速和过流断面成反比。
（2）
v毛 细 管 v动 脉
?
四、 伯努利方程能量守恒定律在流体力学中的应用
理想液体伯努利方程的推导
理想液体伯努利方程
1 外力对液体所做的功 A = p1S1v1 ∆ t - p2S2v2 ∆ t = (p1-p2) ∆V 2 机械能的变化量
势能的变化量：∆ Ep = mg∆h = ρg ∆V (h2 - h1) 动能的变化量：∆ Ek = ∆ m (v2/2) =ρ∆V(v22 - v21)/2 根据功能原理，则有： A = ∆Ep + ∆ Ek (p1-p2) ∆V= ρg ∆V (h2-h1) +ρ∆V(v22-v21)/2
• 作业：5、6、9
【Example 1-5】
D ( P0 , h ', 0)
P19
B
1)
C ( P0 , 0, v )

第四章 定常条件下的大气边界层

第四章 定常条件下的大气边界层

应用π理论，可确定函数F的形式为： 应用π理论，可确定函数F的形式为：
L，首先由Obukhov提出（1946），中性层结条件下， 首先由Obukhov提出（1946），中性层结条件下， Obukhov提出 ），中性层结条件下 湍能浮力产生项和切变产生项相等的高度。 湍能浮力产生项和切变产生项相等的高度。
研究相似理论共分4 研究相似理论共分4步：
1）选择（推测）那些与研究对象相关的 选择（推测） 变量 根据π理论把变量组合成无量纲组 2）根据π理论把变量组合成无量纲组 3）进行试验，或者从早期的资料中积累 进行试验， 有关数据以决定无量纲组的值 对资料进行曲线拟合或者求回归方程， 4）对资料进行曲线拟合或者求回归方程， 以描述这些无量纲之间的关系
u L=− g κ w′θ ′
3 *
θ
< 0 不稳定 z = = 0 中性 L > 0 稳定
对上两式进行积分,并利用边界条件：时， 对上两式进行积分,并利用边界条件： ,u=0，得到非中性层结下近地层风、 z=Z0 ,u=0，得到非中性层结下近地层风、温廓线 的一般表达式如下: 的一般表达式如下:
零平面位移距离
气流越过林冠层时风速为高度的函数， 气流越过林冠层时风速为高度的函数，稠密林冠层的作用就像在 实际地面以上位移了某一距离的地面那样。 实际地面以上位移了某一距离的地面那样。
林冠顶部以上， 林冠顶部以上，风速廓线随高度是对数增大 对静力中性条件来说，我们能确定位移距离d 对静力中性条件来说，我们能确定位移距离d和粗糙度长度 所以： 所以0： z ，
相似尺度的分类
MoninMonin-Obukhov 相似性 混合层相似性 局地相似性 局地自由相似性 Rossby 相似性 适用范围 近地面层， 近地面层，U≠0，u*≠0 无风或轻风的自由对流 静力稳定层结 静力不稳定层结 大尺度模拟 特征尺度 L、z0、u*、θ*、q* Zi、w*、θ*、q* L、u*、θ*、q* 、u z、 u*、θ*、q* 、 表面尺度和边界层尺度

第三章定常一维流动1

第三章定常一维流动1

dT (k − 1) M 2 dA = T 1− M 2 A
p = ρRT
M =V a =V
dp dρ dT − − =0 p T ρ
1 dV dA ) = −( V 1− M 2 A
dM =− M 1+ k −1 2 M dA 2 2 A 1− M
kRT
dM dV dT − + =0 M V 2T
V 2 V 2 a *2 M 2 = 2 = *2 ⋅ 2 a a a
M2 λ = k −1 1+ ( M 2 − 1) k +1
2
沿流线的等熵关系式
V2 k k + RT = RT0 k −1 2 k −1
τ (λ ) ≡
T = T0 k −1 2 1 = 1− λ k −1 2 k +1 M 1+ 2
气体以低M数（M是小量）作定常等熵流动
1 k −1
ρ ⎛ k −1 2 ⎞ = ⎜1 + M ⎟ ρ0 ⎝ 2 ⎠
−
M2 = 1− + …… 2
k ⎡ ⎤ ⎞ p0 − p p ⎢⎛ k − 1 2 ⎞ k −1 ⎥ p ⎛ p0 ⎜ M ⎟ −1 = ⎜1 + ⎜ p − 1⎟ = 1 ⎟ 1 1 ⎥ 2 2 2 ⎝ 2 ⎢⎝ ⎠ ⎠ ρV ρV ρV ⎣ ⎦ 2 2 2 p 2k ⎞ ⎤ 1 ρ ⎡⎛ kM 2 k 4 ⎜1 + = + M + ……⎟ − 1⎥ = 1 + M 2 + …… ⎢ ⎟ 2 8 4 kV 2 ⎣⎜ ⎝ ⎠ ⎦
V2 cpT + = const 2
a2 V 2 + = const k −1 2
k p V2 + = const k −1 ρ 2

9.3 线性定常系统的响应

9.3 线性定常系统的响应
输出方程的解
18
1. 直接求解法
将状态方程 x’ Ax Bu 移项, 可得 x’ Ax Bu 将上式两边左乘以 eAt，则有 eAt[x’ Ax] eAtBu 即 d(eAtx)/dt eAtBu 在区间[t0, t]内对上式积分, 则有

t
t0
t d A e x ( ) d e A Bu( )d t d
1 a a2 a k 1 ( s a)1 2 3 ... k ... s s s s a 2t 2 ak t k e at 1 at ... ... 2! k!
L[e ] (s a) ，或 e L [(s a) ]
at at
10
x (t ) t t x (t0 )
0
的解, 也就是由初始时刻 t0 的初始状态 x(t0) 所引起的 无输入强迫项(无外力)时的自由运动 (free motion)
4
状态方程的求解方法
1. 级数展开法 series expansion
先观察标量常微分方程
x(t ) ax(t )
6
下面考虑向量状态方程的求解 为此, 设其解为t 的向量幂级数, 即 x(t) q0 q1t q2t2 … qktk … 式中, qk (k 1, 2, ...)为待定级数展开系数向量 将所设解代入该向量状态方程 x’ Ax, 可得 q1 2q2t 3q3t2 … kqktk-1 …
a q1 q0 , 1! a a2 q2 q1 q0 , 2 2! a ak , qk qk 1 q0 k k!
令x(t)的解表达式中 t 0, 可确定 q0 x(0) 因此, x(t)的解的表达式可写为
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
速度梯度
du dy
μ 粘度
符合牛顿粘性定律的流体称为牛顿型流体 μ单位 1 P＝100 cp＝0.1 Pa·S P 泊， cP厘泊 μ可由实验测定，粘度计 μ与P关系不大，但与T关系很大 注： 气体粘度一般远小于液体粘度 液体：μ随T↑而↓ 气体：μ随T↑而↑ 气体分子碰撞加剧

2.2.5 流动边界层 平板边界层 边界层的形成 边界层：由于流动受壁面影响而存在速度梯度区 域 边界层厚度：自壁面到流速达到流体主体流速99 ％处的厚度 Re数 ↑，边界层厚度越薄 边界层内速度梯度较大，即使流体粘度很小，也 会产生较大的内摩擦力
2

流体流动从管道入口开始形成边界层直到发展到 边界层在管道中心汇合为止的长度，称为稳定段 长度 层流下： 湍流：稳定段长度较短，一般为圆管直径的50～ 100倍 只有在稳定段后，流动型态和流速分布才能保持 稳定不变
2.2.6 动量传递 相当于牛顿粘性定律换一个角度考虑 层流流动的相邻两层流体中，流速较高的流体层 中的分子因分子扩散作用进入低速流体层中，促 使低速流体层加速 同时，低速层中的分子也因分子扩散作用进入告 诉流体层，使高速流体减速，相当于两相邻层流 体之间相互施加了一种反向的内摩擦力，即剪切 力
惯性力 爬流，可忽略 Re数大，惯性力起主要作用 粘性力 ③可用于判断两个流动系统是否相似 若系统几何相似，且Re数相同 → 两者流动型态相同 流体动力过程相似 Re =
②
Re数小，粘滞力起主要作用，
层流 ⎫ ⎬2种流动型态 湍流 ⎭ 过渡区域
注意：(1) 圆管d － 管直径， 非圆管 de － 当量直径 de ＝ 4 rH，4倍的水力直径，
τ =μ

ν=
μ ρ
du dy
τ =−
d ( ρu ) μ d ( ρu ) = −ν ρ dy dy

湍流：类似牛顿粘性定律
运动粘度m2⋅s-1

−1
τ ' = μ'

τ=
F 质量 ⋅ 速度 M ⋅ L ⋅T 动量 = M ⋅ L ⋅ T − 2 ⋅ L− 2 = = ＝ A 面积 ⋅ 时间 面积 ⋅ 时间 L2 ⋅ T ∴τ为单位时间通过单位面积传递的动量，可看作是动量传 递速率或动量通量 牛顿粘性定律也表明了动量传递速率与动量梯度成正比， 负号表示动量传递方向与速度梯擦力作用 → 速度分布 (中心最大，管壁处 为0) 对圆管内流体微元(半径为r，长l的水平流体柱) 作受力分析，匀速运动 注意：剪切力作用在圆柱侧面上
r＝R时，ur＝0 Δp 2 (R − r 2 ) ur = 积分 4 μl r＝0时，流速最大 Δp 2 r u max = R u r = u max [1 − ( ) 2 ] ∴ R 4 μl


套管：
π
rH = 4
(d12 − d 2 )
2
π ( d1 + d 2 )
=
1 ( d1 − d 2 ) 4
横截面积 rH = 润湿周边长 例：长方形管

但注意在计算横截面积时，应按实际计算，不能 认为 de 仅在计算Re时用
d e = 4rH = d1 − d 2
A=
π
rH＝
ab 2 （a + b）
∴流体流动时的摩擦阻力主要集中在边界层内，可简化流 体流动的求解(边界层外视为理想流体)

边界层内流体流动可能是层流，也可能为湍流。 对于给定的平板，无论对何种流体，边界层由层流转变 为湍流的地点，取决于临界雷诺数的数值
xu ρ 对光滑的平板壁面，边界层由层流转变为湍流的临界 Re = c 0 雷诺数范围为： xc μ
雷诺数： 因次(量纲)
L-长度 M-质量
Re =
[Re] =
ρud μ
M ⋅ L−3 ⋅ ( L / T ) ⋅ L = L0 M 0T 0 M ⋅ L−1 ⋅ T −1

T-时间
Re数意义： ①可用于判断流动型态： 3个区域 ⎧Re < 2000时 ⎪ ⎨Re > 4000时 ⎪2000 < Re < 4000 ⎩
层流时流体流过圆管某一截面的 平均流速为中心最大流速的1/2
3

湍流时
n在6和10之间 Re↑ n↑

r 1 u r = u max [1 − ( )] n R
4


圆管内层流流速为抛物线分布

平均流速
⇒
du ∑ F = 0 ⇒Δpπr = −μ ⋅ (2πrl) r dr Δp − du r = r ⋅ dr 2 μl
2
qv = A 代入 r u r = u max [1 − ( ) 2 ] R u=
⇒
∫ u ⋅ 2πrdr
R 0 r
πR 2
u=
1 u max 2
μ’ 涡流粘度 湍流总动量传递
μ ' d ( ρu ) du 或τ ' = dy ρ dy
μ ' 涡流动量扩散系数 ρ
μ + μ ' d ( ρu ) du τ = −( μ + μ ' ) = − dy ρ dy 由于层流内层、过渡层很薄，分子扩散传递动量 可忽略不计， 注意：μ为物性常数，μ’非物性常数，与流动状态 有关 ＝f (Re)，不易确定
2 × 10 5 < Re xc < 3 × 10 6
一般取Rexc＝5×105
即使流体流动处于高度湍流，在靠近固体壁面处 仍有一薄层流体呈层流状态，这层流体称为层流 内层 湍流流动物体内的摩擦阻力主要集中在层流内层 之中



圆管内流动边界层：在流体进入管口时，边界层很薄，随 后δ↑，最后边界层在管道中心会合，边界层厚度＝r 管内流体作层流时，边界层内也为层流 管内流体流动为湍流，管道入口处，仍形成层流边界层， 边界层增厚至一定厚度时，边界层内的流体流动开始由层 流过渡到湍流，并形成湍流边界层 与平板边界层类似 管壁处为层流内层 过渡层在中间 湍流层在外面
de = 4rH =
2ab a+b

4
de 2
1
(2) 系统内温度不一致时，注意规定定性温度，μ 和ρ均与T有关 (3) u 平均流速 2.2.4 牛顿粘性定律 实际流体流动时，会有阻碍流体流动的内摩擦 力，此特性为流体粘性 用粘度衡量粘性大小 牛顿粘性定律： τ 剪应力 N·m-2
τ =μ
2.2.2 定常态流动和非定常态流动 定常态：在流动系统内，任一空间位置上的流量、 流速、压力和密度等物理参数只随空间位置的改 变而改变，不随时间变化而变化 化工中连续生产中的流动属定常态流动 2.3 流动形态 1883年 Reynolds实验发现，流速u，管径d， 流体粘度μ，密度ρ均能引起流动状态 变化。
两种流型： 层流：质点流动方向永远与管轴平行，即与流体主流流动 方向平行，在与主流流动方向垂直的方向上无质点运动。 湍流：各质点不再按主流流动方向平行流动，而是彼此之 间激荡碰撞发生混扰，以至流体在某一点上的流动速度和 方向都呈现不规则的变化，有的质点垂直于主流的方向上 湍动而形成涡流。 雷诺准数：由大量实验研究，将影响流动型态的四个因素 归纳整理成一个复合数群。