2020年高考数学专题复习平面向量的数量积及应用举例

第三节平面向量的数量积及平面向量的应用举例1.（2020·南京模拟）已知向量a r =(1,2)，b r =(2,-3). 若向量c r 满足(c r +a r )∥b r ，c r ⊥(a r +b r)，则c r= ( )A. (79,73)B. (-73,79)C. (73,79)D. (-79,-73)2. （2020·湖南） 若非零向量a r ，b r 满足|a r |=|b r |，(2a r +b r )·b r =0,则a r 与b r的夹角为( )A. 30°B. 60°C. 120°D. 150° 3. 已知下列命题中：（1）若k ∈R ，且k b r =0，则k=0或b r =0r; （2）若a r ·b r =0，则a r =0r 或b r =0r;（3）若不平行的两个非零向量a r ,b r ，满足|a r |=|b r |，则(a r +b r )·(a r -b r)=0; （4）若a r 与b r 平行，则a r ·b r =|a r |·|b r|.其中真命题的个数是( )A. 0B. 1C. 2D. 34. 定义运算|a r ⊗b r |=|a r |·|b r |·sin θ,其中θ是向量a r , b r 的夹角，若|x r |=2,|y u r|=5，x r ·y u r =-6,则|x r ⊗y u r|=（ ）A. 8B. -8C. 8或-8D. 65. （2020·河北衡水中学仿真试卷）已知向量a r =(1,1), b r =(2,n)，若|a r +b r |=a r ·b r,则n为 ()A. -3B. -1C. 1D. 36. 已知a r =(2,1)与b r =(1,2)，要使|a r +t b r|最小，则实数t 的值为___________. 7. （2020·浙江）已知平面向量αu r ,βu r ,|αu r |=1,| βu r |=2, αu r ⊥(αu r -2βu r )，则|2αu r +βu r|的值是___________.8. 已知i r 、j r 为互相垂直的单位向量, a r =i r -2j r j ，b r =i r +λj r，且a r 与b r 的夹角为锐角，则实数λ的取值范围是___________.9. 已知向量a r ＝(sin θ ，1)，b r ＝(1，cos θ)，-2π＜θ＜2π.（1）若a r ⊥b r，则θ=___________; （2）｜a r ＋b r｜的最大值为. ___________10. (2020·大连模拟)已知a r ,b r ,c r 是单位向量，且a r ·b r =0,求(a r -c r )·(b r -c r)的最小值.11. （2020·江苏改编）在平面直角坐标系xOy 中，已知点A(－1,－2)、B(2,3)、 C(－2,－1).(1)求以线段AB 、AC 为邻边的平行四边形的两条对角线的长；(2)设实数t 满足(AB u u u r -t OC u u u r )·OC u u u r ＜t 2-5,求t 的取值范围.考点演练6.-45解析：|a r +t b r |=(a r +t b r )2=a r 2+2t a r b r +t2b r 2=5t 2+8t+5,当t=-45时|a r +t b r |最小.7. 10解析:由题意可知αu r ·(αu r -2βu r )=0,结合|αu r |2=1,| βu r |2=4,解得αu r ·βu r=12,所以|2αu r +βu r |2=4αu r 2+4αu r ·βu r +βu r 2=4+2+4=10,即|2αu r +βu r|=10.8. (-∞,-2)∪（-2, 12）解析：a r =(1,-2),b r =(1,λ),设a r 与b r夹角为θ,cos θ=a b a b r r g r r g =251λ+,∵θ为锐角， ∴2051λ>+,解得λ＜12且λ≠-2.9. -4π2+1解析:(1) a r ⊥br ⇒a r ·b r =0sin θ+cos θ=0⇒θ=-4π.(2)| a r +b r|=|(sin θ+1, cos θ+1)|22(sin 1)(cos 1)θθ+++===当θ=4π时|a r +b r |1=.10. 记A=(a r -c r )·(b r -c r),则A=a r ·b r -c r (a r +b r )+2c r .∵a r ,b r ,c r 为单位向量，∴|a r |=|b r |=|c r|=1, 又a r ·b r =0,∴a r ⊥b r . ∴|a r +b r∴A=1-c r ·(a r +b r )=1-|c r |·|a r +b r |cos 〈c r , a r +b r 〉〈c r , a r +b r〉. ∵〈c r , a r +b r〉∈ [0,π].∴当〈c r , a r +b r〉=0时，A min11. （1）由题设知AB u u u r=(3,5), AC u u u r =(-1,1),则|AB u u u r +AC u u ur |=(2,6),AB-AC=(4,4).所以|AB u u u r +AC u u u rAB u u u r -AC u u ur故所求的两条对角线的长分别为(2)由题设知：OC u u u r =(-2,-1), AB u u u r-t OC u u r =(3+2t,5+t).由(AB u u u r -t OC u u u r )·OC u u u r ＜t 2-5,得(3+2t,5+t)·(-2,-1)＜t 2-5,整理得t 2+5t+6＞0,∴t ＜-3或t ＞-2.。

课下层级训练(二十六) 平面向量的数量积及应用举例[A 级 基础强化训练]1．已知AB →＝(2,1)，点C (－1,0)，D (4,5)，则向量AB →在CD →方向上的投影为( ) A ．－322B ．－3 5C ．322D ．3 5C [因为点C (－1,0)，D (4,5)，所以CD →＝(5,5)，又AB →＝(2,1)，所以向量AB →在CD →方向上的投影为|AB →|cos 〈AB →，CD →〉＝AB →·CD →|CD →|＝1552＝322.]2．设向量a ，b 满足|a ＋b |＝10，|a －b |＝6，则a ·b ＝( ) A ．1 B ．2 C ．3D ．5A [由条件可得，(a ＋b )2＝10，(a －b )2＝6，两式相减得4a ·b ＝4，所以a ·b ＝1.] 3．已知向量a ＝(3，1)，b ＝(0,1)，c ＝(k ，3)，若a ＋2b 与c 垂直，则k ＝( ) A ．－3 B ．－2 C ．1D ．－1A [因为a ＋2b 与c 垂直，所以(a ＋2b )·c ＝0，即a ·c ＋2b ·c ＝0，所以3k ＋3＋23＝0，解得k ＝－3.]4．已知平面向量a ＝(1,2)，b ＝(4,2)，c ＝m a ＋b (m ∈R )，且c 与a 的夹角等于c 与b 的夹角，则m ＝( )A ．－2B ．－1C ．1D ．2D [∵a ＝(1,2)，b ＝(4,2)，∴c ＝m a ＋b ＝(m ＋4,2m ＋2)，|a |＝5，|b |＝25，∴a ·c ＝5m ＋8，b ·c ＝8m ＋20. ∵c 与a 的夹角等于c 与b 的夹角，∴c ·a |c |·|a |＝c ·b |c |·|b |，∴5m ＋85＝8m ＋2025，解得m ＝2.]5．已知F 1，F 2分别为椭圆C ：x 29＋y 28＝1的左、右焦点，点E 是椭圆C 上的动点，则EF 1→·EF 2→的最大值、最小值分别为( )A ．9,7B ．8,7C ．9,8D ．17,8B [由题意可知椭圆的左、右焦点坐标分别为F 1(－1,0)，F 2(1,0)，设E (x ，y )(－3≤x ≤3)，则EF 1→＝(－1－x ，－y )，EF 2→＝(1－x ，－y )，所以EF 1→·EF 2→＝x 2－1＋y 2＝x 2－1＋8－89x 2＝x 29＋7，所以当x ＝0时，EF 1→·EF 2→有最小值7，当x ＝±3时，EF 1→·EF 2→有最大值8.] 6．(2016·全国卷Ⅰ)设向量a ＝(m,1)，b ＝(1,2)，且|a ＋b |2＝|a |2＋|b |2，则m ＝__________.－2 [∵|a ＋b |2＝|a |2＋|b |2＋2a ·b ＝|a |2＋|b |2，∴a ·b ＝0. 又a ＝(m,1)，b ＝(1,2)，∴m ＋2＝0，∴m ＝－2.]7．(2018·安徽合肥检测)若非零向量a ，b 满足|a |＝1，|b |＝2，且(a ＋b )⊥(3a －b )，则a 与b 夹角的余弦值为__________.14[由(a ＋b )⊥(3a －b )可得(a ＋b )·(3a －b )＝0，又|a |＝1，|b |＝2，则可得a ·b ＝12，设a ，b 的夹角为θ，θ∈[0，π]，则cos θ＝a·b |a |·|b |＝14.] 8．已知在直角三角形ABC 中，∠ACB ＝90°，AC ＝BC ＝2，点P 是斜边AB 上的中点，则CP →·CB →＋CP →·CA →＝__________.4 [由题意可建立如图所示的坐标系．可得A (2,0)，B (0,2)，P (1,1)，C (0,0)，则CP →·CB →＋CP →·CA →＝(1,1)·(0,2)＋(1,1)·(2,0)＝2＋2＝4.]9．已知|a |＝4，|b |＝8，a 与b 的夹角是120°. (1)计算：①|a ＋b |，②|4a －2b |； (2)当k 为何值时，(a ＋2b )⊥(k a －b )．解 由已知得，a ·b ＝4×8×⎝ ⎛⎭⎪⎫－12＝－16. (1)①∵|a ＋b |2＝a 2＋2a ·b ＋b 2＝16＋2×(－16)＋64＝48， ∴|a ＋b |＝4 3.②∵|4a －2b |2＝16a 2－16a ·b ＋4b 2＝16×16－16×(－16)＋4×64＝768， ∴|4a －2b |＝16 3.(2)∵(a ＋2b )⊥(k a －b )，∴(a ＋2b )·(k a －b )＝0， ∴k a 2＋(2k －1)a ·b －2b 2＝0，即16k －16(2k －1)－2×64＝0，∴k ＝－7.即k ＝－7时，a ＋2b 与k a －b 垂直．10．已知向量a ＝(cos x ，sin x )，b ＝(3，－3)，x ∈[0，π]． (1)若a ∥b ，求x 的值；(2)记f (x )＝a ·b ，求f (x )的最大值和最小值以及对应的x 的值． 解 (1)因为a ＝(cos x ，sin x )，b ＝(3，－3)，a ∥b ， 所以－3cos x ＝3sin x .若cos x ＝0，则sin x ＝0，与sin 2x ＋cos 2x ＝1矛盾， 故cos x ≠0.于是tan x ＝－33. 又x ∈[0，π]，所以x ＝5π6.(2)f (x )＝a·b ＝(cos x ，sin x )·(3，－3)＝3cos x －3sin x ＝23cos ⎝⎛⎭⎪⎫x ＋π6.因为x ∈[0，π]，所以x ＋π6∈⎣⎢⎡⎦⎥⎤π6，7π6，从而－1≤cos ⎝⎛⎭⎪⎫x ＋π6≤32，于是，当x ＋π6＝π6，即x ＝0时，f (x )取得最大值3；当x ＋π6＝π，即x ＝5π6时，f (x )取得最小值－2 3.[B 级 能力提升训练]11．设a ，b 为单位向量，且a ⊥b ，若向量c 满足|c －(a ＋b )|＝|a －b |，则|c |的最大值是( )A ．2 2B ．2C ． 2D ．1A [由题意结合a ⊥b ，可设a ＝(1,0)，b ＝(0,1)，c ＝(x ，y )，则由|c －(a ＋b )|＝|a －b |，得|(x ，y )－(1,1)|＝|(1，－1)|，由此可得(x －1)2＋(y －1)2＝2，即c 对应的点的轨迹在以(1,1)为圆心的圆上，如图所示．∵圆过原点，∴|c |的最大值为圆的直径2 2.]12．(2017·全国卷Ⅲ)在矩形ABCD 中，AB ＝1，AD ＝2，动点P 在以点C 为圆心且与BD 相切的圆上．若AP →＝λAB →＋μAD →，则λ＋μ的最大值为( )A ．3B ．2 2C ． 5D ．2A [建立如图所示的直角坐标系，则C 点坐标为(2,1)．设BD 与圆C 切于点E ，连接CE ，则CE ⊥BD ． ∵CD ＝1，BC ＝2， ∴BD ＝12＋22＝5，EC ＝BC ·CD BD ＝25＝255，即圆C 的半径为255，∴P 点的轨迹方程为(x －2)2＋(y －1)2＝45.设P (x 0，y 0)，则⎩⎪⎨⎪⎧x 0＝2＋255cos θ，y 0＝1＋255sin θ(θ为参数)，而AP →＝(x 0，y 0)，AB →＝(0,1)，AD →＝(2,0)．∵AP →＝λAB →＋μAD →＝λ(0,1)＋μ(2,0)＝(2μ，λ)， ∴μ＝12x 0＝1＋55cos θ，λ＝y 0＝1＋255sin θ.两式相加，得λ＋μ＝1＋255sin θ＋1＋55cos θ＝2＋sin(θ＋φ)≤3⎝ ⎛⎭⎪⎫其中sin φ＝55，cos φ＝255， 当且仅当θ＝π2＋2k π－φ，k ∈Z 时，λ＋μ取得最大值3.]13．已知|a |＝2|b |，|b |≠0，且关于x 的方程x 2＋|a |x －a·b ＝0有两相等实根，则向量a 与b 的夹角是__________.2π3[由已知可得Δ＝|a |2＋4a·b ＝0， 即4|b |2＋4×2|b |2cos θ＝0，∴cos θ＝－12.又∵θ∈[0，π]，∴θ＝2π3.]14．已知向量a ＝⎝ ⎛⎭⎪⎫－12，32，OA →＝a －b ，OB →＝a ＋b ，若△OAB 是以O 为直角顶点的等腰直角三角形，则△OAB 的面积为__________.1 [由题意得，|a |＝1，又△OAB 是以O 为直角顶点的等腰直角三角形，所以OA →⊥OB →，|OA →|＝|OB →|.由OA →⊥OB →，得(a －b )·(a ＋b )＝|a |2－|b |2＝0，所以|a |＝|b |＝1，由|OA →|＝|OB →|，得|a －b |＝|a ＋b |， 所以a ·b ＝0. 所以|a ＋b |2＝|a |2＋| b |2＝2， 所以|OB →|＝|OA →|＝2，故S △OAB ＝12×2×2＝1.]15．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足(2a －c )BA →·BC →＝cCB →·CA →. (1)求角B 的大小；(2)若|BA →－BC →|＝6，求△ABC 面积的最大值． 解 (1)由题意得(2a －c )cos B ＝b cos C ．根据正弦定理得(2sin A －sin C )cos B ＝sin B cos C ， 所以2sin A cos B ＝sin(C ＋B )，即2sin A cos B ＝sin A ，因为A ∈(0，π)，所以sin A >0，所以cos B ＝22，又B ∈(0，π)，所以B ＝π4.(2)因为|BA →－BC →|＝6，所以|CA →|＝6，即b ＝6，根据余弦定理及基本不等式得6＝a 2＋c 2－2ac ≥2ac －2ac ＝(2－2)ac (当且仅当a ＝c 时取等号)，即ac ≤3(2＋2)， 故△ABC 的面积S ＝12ac sin B ≤32＋12，即△ABC 的面积的最大值为32＋32. 16．已知平面上一定点C (2,0)和直线l ∶x ＝8，P 为该平面上一动点，作PQ ⊥l ，垂足为Q ，且⎝⎛⎭⎪⎫PC →＋12PQ →·⎝ ⎛⎭⎪⎫PC →－12PQ →＝0.(1)求动点P 的轨迹方程；(2)若EF 为圆N ∶x 2＋(y －1)2＝1的任意一条直径，求PE →·PF →的最值． 解 (1)设P (x ，y )，则Q (8，y )．由⎝⎛⎭⎪⎫PC →＋12PQ →·⎝ ⎛⎭⎪⎫PC →－12PQ →＝0，得|PC →|2－14|PQ →|2＝0，即(2－x )2＋(－y )2－14(8－x )2＝0，化简得x 216＋y 212＝1.所以动点P 在椭圆上，其轨迹方程为x 216＋y 212＝1.(2)易知PE →＝PN →＋NE →， PF →＝PN →＋NF →， 且NE →＋NF →＝0，由题意知N (0,1)，所以PE →·PF →＝PN →2－NE →2＝(－x )2＋(1－y )2－1 ＝16⎝ ⎛⎭⎪⎫1－y 212＋(y －1)2－1＝－13y 2－2y ＋16＝－13(y ＋3)2＋19.因为－23≤y ≤23，所以当y ＝－3时，PE →·PF →取得最大值19， 当y ＝23时，PE →· PF →取得最小值12－4 3. 综上，PE →·PF →的最大值为19，最小值为12－4 3.。

5.2平面向量的数量积及其应用挖命题【考情探究】分析解读 1.向量的数量积是高考命题的热点,主要有以下几个方面:(1)平面向量的运算、化简、证明及其几何意义;(2)平面向量垂直的充要条件及其应用;(3)平面向量的综合应用,向量的坐标是代数与几何联系的桥梁,它融数、形于一体,具有代数形式和几何形式的双重身份,是中学数学知识的重要交汇点,常与平面几何、解析几何、三角函数等内容交叉渗透.2.预计2020年高考试题中,向量的数量积仍是高考的热点,应高度重视.破考点【考点集训】考点一平面向量的数量积1.(2018浙江温州二模(3月),9)已知向量a,b满足|a|=1,且对任意实数x,y,|a-xb|的最小值为,|b-ya|的最小值为,则|a+b|=()A. B.C.或D.或-答案C,其中A为△ABC的2.(2017浙江名校(杭州二中)交流卷三)已知向量a=(cos2A,-sin2A),b=-最小内角,且a·b=-,则角A等于 ()A. B.C. D. 或答案C考点二向量的综合应用1.(2018浙江名校协作体期初,12)在△ABC中,AB=3,BC=,AC=2,且O是△ABC的外心,则·=,·=.答案2;-2.(2018浙江绍兴高三3月适应性模拟,16)已知正三角形ABC的边长为4,O是平面ABC上的动点,且∠AOB=,则·的最大值为.答案炼技法【方法集训】方法1 利用数量积求长度和夹角的方法1.(2017浙江镇海中学模拟卷三,13)已知向量a,b满足|a-b|=1且|a|=2|b|,则a·b的最小值为,此时a与b的夹角是.答案-;π2.(2018浙江“七彩阳光”联盟期初联考,16)若向量a,b满足a2+a·b+b2=1,则|a+b|的最大值为.答案方法2 利用向量解决几何问题的方法1.(2018浙江新高考调研卷二(镇海中学),9)已知点P在边长为2的正方形ABCD的边上,点M在以P为圆心,1为半径的圆上运动,则·的最大值是()A.2B.1+C.1+2D.2+2答案C2.(2018浙江杭州二中期中,16)在半径为1的扇形AOB中,∠AOB=60°,C为弧AB上的动点,AB与OC交于点P,则·的最小值是.答案-过专题【五年高考】A组自主命题·浙江卷题组考点一平面向量的数量积1.(2017浙江,10,4分)如图,已知平面四边形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC与BD交于点O.记I1=·,I2=·,I3=·,则()A.I1<I2<I3B.I1<I3<I2C.I3<I1<I2D.I2<I1<I3答案C2.(2014浙江,8,5分)记max{x,y}=min{x,y}=设a,b为平面向量,则()A.min{|a+b|,|a-b|}≤min{|a|,|b|}B.min{|a+b|,|a-b|}≥min{|a|,|b|}C.max{|a+b|2,|a-b|2}≤|a|2+|b|2D.max{|a+b|2,|a-b|2}≥|a|2+|b|2答案D3.(2016浙江文,15,4分)已知平面向量a,b,|a|=1,|b|=2,a·b=1.若e为平面单位向量,则|a·e|+|b·e|的最大值是.答案4.(2015浙江文,13,4分)已知e1,e2是平面单位向量,且e1·e2=,若平面向量b满足b·e1=b·e2=1,则|b|=.答案考点二向量的综合应用1.(2018浙江,9,4分)已知a,b,e是平面向量,e是单位向量.若非零向量a与e的夹角为,向量b满足b2-4e·b+3=0,则|a-b|的最小值是()A.-1B.+1C.2D.2-答案A2.(2017浙江,15,6分)已知向量a,b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是,最大值是.答案4;23.(2016浙江,15,4分)已知向量a,b,|a|=1,|b|=2.若对任意单位向量e,均有|a·e|+|b·e|≤,则a·b 的最大值是.答案B组统一命题、省(区、市)卷题组考点一平面向量的数量积1.(2018课标全国Ⅱ理,4,5分)已知向量a,b满足|a|=1,a·b=-1,则a·(2a-b)=()A.4B.3C.2D.0答案B2.(2017课标全国Ⅱ,12,5分)已知△ABC是边长为2的等边三角形,P为平面ABC内一点,则·(+)的最小值是()A.-2B.-C.-D.-1答案B3.(2016课标全国Ⅱ,3,5分)已知向量a=(1,m),b=(3,-2),且(a+b)⊥b,则m=()A.-8B.-6C.6D.8答案D4.(2018北京文,9,5分)设向量a=(1,0),b=(-1,m).若a⊥(ma-b),则m=.答案-15.(2017课标全国Ⅰ理,13,5分)已知向量a,b的夹角为60°,|a|=2,|b|=1,则|a+2b|=.答案26.(2015广东,16,12分)在平面直角坐标系xOy中,已知向量m=-,n=(sin x,cos x),x∈.(1)若m⊥n,求tan x的值;(2)若m与n的夹角为,求x的值.解析(1)因为m⊥n,所以m·n=sin x-cos x=0. 即sin x=cos x,又x∈,所以tan x==1. (2)易求得|m|=1,|n|==1.因为m与n的夹角为,所以cos=··=-,则sin x-cos x=sin-=.又因为x∈,所以x-∈-.所以x-=,解得x=.考点二向量的综合应用1.(2018北京理,6,5分)设a,b均为单位向量,则“|a-3b|=|3a+b|”是“a⊥b”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案C2.(2018天津文,8,5分)在如图的平面图形中,已知OM=1,ON=2,∠MON=120°,=2,=2,则·的值为()A.-15B.-9C.-6D.0答案C3.(2018天津理,8,5分)如图,在平面四边形ABCD中,AB⊥BC,AD⊥CD,∠BAD=120°,AB=AD=1.若点E为边CD 上的动点,则·的最小值为()A. B. C. D.34.(2016四川,10,5分)在平面内,定点A,B,C,D满足||=||=||,·=·=·=-2,动点P,M满足||=1,=,则||2的最大值是()A. B.C. D.答案B5.(2017江苏,12,5分)如图,在同一个平面内,向量,,的模分别为1,1,,与的夹角为α,且tan α=7,与的夹角为45°.若=m+n(m,n∈R),则m+n=.答案 36.(2014江西,14,5分)已知单位向量e1与e2的夹角为α,且cos α=,向量a=3e1-2e2与b=3e1-e2的夹角为β,则cos β=.答案C组教师专用题组考点一平面向量的数量积1.(2016北京,4,5分)设a,b是向量,则“|a|=|b|”是“|a+b|=|a-b|”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案D2.(2016天津,7,5分)已知△ABC是边长为1的等边三角形,点D,E分别是边AB,BC的中点,连接DE并延长到点F,使得DE=2EF,则·的值为()A.-B.C.D.答案B3.(2016山东,8,5分)已知非零向量m,n满足4|m|=3|n|,cos<m,n>=.若n⊥(tm+n),则实数t的值为()A.4B.-4C.D.-答案B4.(2015福建,9,5分)已知⊥,||=,||=t.若点P是△ABC所在平面内的一点,且=+,则·的最大值等于()A.13B.15C.19D.215.(2015山东,4,5分)已知菱形ABCD的边长为a,∠ABC=60°,则·=()A.-a2B.-a2C.a2D.a2答案D6.(2015安徽,8,5分)△ABC是边长为2的等边三角形,已知向量a,b满足=2a,=2a+b,则下列结论正确的是()A.|b|=1B.a⊥bC.a·b=1D.(4a+b)⊥答案D7.(2015重庆,6,5分)若非零向量a,b满足|a|=|b|,且(a-b)⊥(3a+2b),则a与b的夹角为()A. B. C. D.π答案A8.(2014大纲全国,4,5分)若向量a、b满足:|a|=1,(a+b)⊥a,(2a+b)⊥b,则|b|=()A.2B.C.1D.答案B9.(2014四川,7,5分)平面向量a=(1,2),b=(4,2),c=ma+b(m∈R),且c与a的夹角等于c与b的夹角,则m=()A.-2B.-1C.1D.2答案D10.(2014天津,8,5分)已知菱形ABCD的边长为2,∠BAD=120°,点E,F分别在边BC,DC上,BE=λBC,DF=μDC.若·=1,·=-,则λ+μ=()A. B. C. D.答案C11.(2014课标Ⅱ,3,5分)设向量a,b满足|a+b|=,|a-b|=,则a·b=()A.1B.2C.3D.5答案A12.(2017课标全国Ⅲ文,13,5分)已知向量a=(-2,3),b=(3,m),且a⊥b,则m=.答案 213.(2017北京文,12,5分)已知点P在圆x2+y2=1上,点A的坐标为(-2,0),O为原点,则·的最大值为.答案 614.(2017山东理,12,5分)已知e1,e2是互相垂直的单位向量.若e1-e2与e1+λe2的夹角为60°,则实数λ的值是.答案15.(2016课标全国Ⅰ,13,5分)设向量a=(m,1),b=(1,2),且|a+b|2=|a|2+|b|2,则m=.答案-216.(2016江苏,13,5分)如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,·=4,·=-1,则·的值是.答案17.(2015湖北,11,5分)已知向量⊥,||=3,则·=.答案918.(2015天津,14,5分)在等腰梯形ABCD中,已知AB∥DC,AB=2,BC=1,∠ABC=60°.动点E和F分别在线段BC和DC上,且=λ,=,则·的最小值为.答案19.(2014江苏,12,5分)如图,在平行四边形ABCD中,已知AB=8,AD=5,=3,·=2,则·的值是.答案2220.(2014安徽,15,5分)已知两个不相等的非零向量a,b,两组向量x1,x2,x3,x4,x5和y1,y2,y3,y4,y5均由2个a和3个b排列而成.记S=x1·y1+x2·y2+x3·y3+x4·y4+x5·y5,S min表示S所有可能取值中的最小值.则下列命题正确的是(写出所有正确命题的编号).①S有5个不同的值;②若a⊥b,则S min与|a|无关;③若a∥b,则S min与|b|无关;④若|b|>4|a|,则S min>0;⑤若|b|=2|a|,S min=8|a|2,则a与b的夹角为.答案②④考点二向量的综合应用1.(2016课标全国Ⅲ,3,5分)已知向量=,=,则∠ABC=()A.30°B.45°C.60°D.120°答案A2.(2015湖南,8,5分)已知点A,B,C在圆x2+y2=1上运动,且AB⊥BC.若点P的坐标为(2,0),则|++|的最大值为()A.6B.7答案B3.(2017课标全国Ⅰ文,13,5分)已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=.答案74.(2015江苏,14,5分)设向量a k=cos,sin+cos(k=0,1,2,…,12),则(a k·a k+1)的值为.答案9【三年模拟】一、选择题(每小题4分,共24分)1.(2019届浙江温州普通高中适应性测试,9)已知向量a,b满足|a|=2,a2+2a·b+2b2=8,则a·b的取值范围是()A.[2-2,2+2]B.[-2-2,2-2]C.[-1,+1]D.[--1,-1]答案B2.(2019届衢州、湖州、丽水三地教学质量检测,8)如图,△OA1B1,△A1A2B2,△A2A3B3是边长相等的等边三角形,且O,A1,A2,A3四点共线.若点P1,P2,P3分别是边A1B1,A2B2,A3B3上的动点(不含端点),记I1=·,I2=·,I3=·,则()A.I1>I2>I3B.I2>I3>I1C.I2>I1>I3D.I3>I1>I2答案B3.(2018浙江嵊州第一学期期末质检,10)如图,已知矩形ABCD中,AB=3,BC=2,该矩形所在的平面内一点P满足||=1,记I1=·,I2=·,I3=·,则()A.存在点P,使得I1=I2B.存在点P,使得I1=I3C.对任意的点P,有I2>I1D.对任意的点P,有I3>I14.(2018浙江台州第一学期期末质检,9)已知m,n是两个非零向量,且|m|=1,|m+2n|=3,则|m+n|+|n|的最大值为()A. B. C.4 D.5答案B5.(2018浙江台州第一次调考(4月),9)已知单位向量e1,e2,且e1·e2=-,若向量a满足(a-e1)·(a-e2)=,则|a|的取值范围为()A.-B.-C. D.答案B6.(2018浙江杭州第二次教学质量检测(4月),9)记 M 的最大值和最小值分别为 M max 和 M min.若平面向量a,b,c 满足|a|=|b|=a·b=c·(a+2b-2c)=2,则()A.|a-c|max=B.|a+c|max=-C.|a-c|min=D.|a+c|min=-答案A二、填空题(单空题4分,多空题6分,共16分)7.(2019届浙江名校新高考研究联盟第一次联考,16)已知向量a,b满足|a|=2|b|,|a-b|=2,则a·b的取值范围为.答案-8.(2019届台州中学第一次模拟,14)已知向量a,b满足|a|=2,|b|=1,a,b的夹角为,则a与a-2b的夹角为.答案9.(2019届镇海中学期中,15)已知两个不共线的非零向量a,b满足|a|=2,|a-b|=1,则向量a,b的夹角的最大值是.答案30°10.(2018浙江金华十校第一学期期末调研,17)已知平面向量a,b,c满足|a|≤1,|b|≤1,|2c-(a+b)|≤|a-b|,则|c|的最大值为.答案。

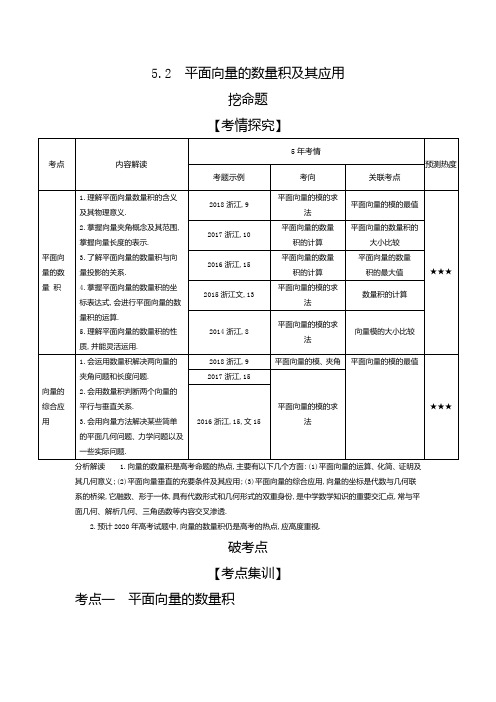
5.2　平面向量的数量积及其应用挖命题【考情探究】5年考情考点内容解读考题示例考向关联考点预测热度2018浙江,9平面向量的模的求法平面向量的模的最值2017浙江,10平面向量的数量积的计算平面向量的数量积的大小比较2016浙江,15平面向量的数量积的计算平面向量的数量积的最大值2015浙江文,13平面向量的模的求法数量积的计算平面向量的数量积1.理解平面向量数量积的含义及其物理意义.2.掌握向量夹角概念及其范围,掌握向量长度的表示.3.了解平面向量的数量积与向量投影的关系.4.掌握平面向量的数量积的坐标表达式,会进行平面向量的数量积的运算.5.理解平面向量的数量积的性质,并能灵活运用.2014浙江,8平面向量的模的求法向量模的大小比较★★★2018浙江,9平面向量的模、夹角平面向量的模的最值2017浙江,15向量的综合应用1.会运用数量积解决两向量的夹角问题和长度问题.2.会用数量积判断两个向量的平行与垂直关系.3.会用向量方法解决某些简单的平面几何问题、力学问题以及一些实际问题.2016浙江,15,文15平面向量的模的求法★★★分析解读 1.向量的数量积是高考命题的热点,主要有以下几个方面:(1)平面向量的运算、化简、证明及其几何意义;(2)平面向量垂直的充要条件及其应用;(3)平面向量的综合应用,向量的坐标是代数与几何联系的桥梁,它融数、形于一体,具有代数形式和几何形式的双重身份,是中学数学知识的重要交汇点,常与平面几何、解析几何、三角函数等内容交叉渗透.2.预计2020年高考试题中,向量的数量积仍是高考的热点,应高度重视.破考点【考点集训】考点一　平面向量的数量积1.(2018浙江温州二模(3月),9)已知向量a,b满足|a|=1,且对任意实数x,y,|a-x b|的最小值为,|b-y a|32的最小值为,则|a+b|=( ) 3A. B.75+23C.或D.或735+235-23答案　C2.(2017浙江名校(杭州二中)交流卷三)已知向量a =(cos 2A,-sin 2A),b =,其中A 为△ABC(12-sin 2A ,11+cos 2A)的最小内角,且a ·b =-,则角A 等于 ( )25A. B.π6π4C. D. 或π3π32π3答案　C 考点二　向量的综合应用1.(2018浙江名校协作体期初,12)在△ABC 中,AB=3,BC=,AC=2,且O 是△ABC 的外心,则·7AO AC = ,·= . AO BC 答案　2;-522.(2018浙江绍兴高三3月适应性模拟,16)已知正三角形ABC 的边长为4,O 是平面ABC 上的动点,且∠AOB=,则·的最大值为 . π3OC AB 答案　1633炼技法【方法集训】方法1　利用数量积求长度和夹角的方法1.(2017浙江镇海中学模拟卷三,13)已知向量a ,b 满足|a -b |=1且|a |=2|b |,则a ·b 的最小值为 ,此时a 与b 的夹角是 . 答案　-;π292.(2018浙江“七彩阳光”联盟期初联考,16)若向量a ,b 满足a 2+a ·b +b 2=1,则|a +b |的最大值12为 .答案　2105方法2　利用向量解决几何问题的方法1.(2018浙江新高考调研卷二(镇海中学),9)已知点P 在边长为2的正方形ABCD 的边上,点M 在以P 为圆心,1为半径的圆上运动,则·的最大值是( ) MA MCA.2B.1+2C.1+2D.2+2 22答案　C2.(2018浙江杭州二中期中,16)在半径为1的扇形AOB 中,∠AOB=60°,C 为弧AB 上的动点,AB 与OC 交于点P,则·的最小值是 . OP BP 答案　-116过专题【五年高考】A 组　自主命题·浙江卷题组考点一　平面向量的数量积1.(2017浙江,10,4分)如图,已知平面四边形ABCD,AB ⊥BC,AB=BC=AD=2,CD=3,AC 与BD 交于点O.记I 1=·OA ,I 2=·,I 3=·,则( )OB OB OC OC ODA.I 1<I 2<I 3B.I 1<I 3<I 2C.I 3<I 1<I 2D.I 2<I 1<I 3答案　C2.(2014浙江,8,5分)记max{x,y}=min{x,y}=设a,b 为平面向量,则( ){x ,x ≥y ,y ,x <y ,{y ,x ≥y ,x ,x <y ,A.min{|a +b |,|a -b |}≤min{|a |,|b |}B.min{|a +b |,|a -b |}≥min{|a |,|b |}C.max{|a +b |2,|a -b |2}≤|a |2+|b |2D.max{|a +b |2,|a -b |2}≥|a |2+|b |2答案　D 3.(2016浙江文,15,4分)已知平面向量a ,b ,|a |=1,|b |=2,a ·b =1.若e 为平面单位向量,则|a ·e |+|b ·e |的最大值是 . 答案　74.(2015浙江文,13,4分)已知e 1,e 2是平面单位向量,且e 1·e 2=,若平面向量b 满足b ·e 1=b ·e 2=1,则12|b |= . 答案　233考点二　向量的综合应用1.(2018浙江,9,4分)已知a ,b ,e 是平面向量,e 是单位向量.若非零向量a 与e 的夹角为,向量b 满足π3b 2-4e ·b +3=0,则|a -b |的最小值是( )A.-1B.+1C.2D.2-333答案　A 2.(2017浙江,15,6分)已知向量a,b 满足|a |=1,|b |=2,则|a+b |+|a-b |的最小值是 ,最大值是 . 答案　4;253.(2016浙江,15,4分)已知向量a ,b ,|a |=1,|b |=2.若对任意单位向量e ,均有|a ·e |+|b ·e |≤,则a ·b 6的最大值是 . 答案　12B 组　统一命题、省(区、市)卷题组考点一　平面向量的数量积1.(2018课标全国Ⅱ理,4,5分)已知向量a ,b 满足|a |=1,a ·b =-1,则a ·(2a -b )=( ) A.4B.3C.2D.0答案　B2.(2017课标全国Ⅱ,12,5分)已知△ABC 是边长为2的等边三角形,P 为平面ABC 内一点,则·(+)PA PB PC 的最小值是( )A.-2B.- C.- D.-13243答案　B 3.(2016课标全国Ⅱ,3,5分)已知向量a =(1,m),b =(3,-2),且(a +b )⊥b ,则m=( ) A.-8B.-6C.6 D.8答案　D 4.(2018北京文,9,5分)设向量a =(1,0),b =(-1,m).若a ⊥(m a-b ),则m= . 答案　-15.(2017课标全国Ⅰ理,13,5分)已知向量a ,b 的夹角为60°,|a |=2,|b |=1,则|a +2b |= . 答案　236.(2015广东,16,12分)在平面直角坐标系xOy 中,已知向量m =,n =(sin x,cos x),x ∈.(22,-22)(0,π2)(1)若m ⊥n ,求tan x 的值;(2)若m 与n 的夹角为,求x 的值.π3解析　(1)因为m ⊥n ,所以m ·n =sin x-cos x=0.2222即sin x=cos x,又x ∈,所以tan x==1.(0,π2)sin xcos x (2)易求得|m |=1,|n |==1.sin 2x +cos 2x 因为m 与n 的夹角为,π3所以cos ==,π3m ·n |m |·|n |2sin x -2cos x1×1则sin x-cos x=sin =.2222(x -π4)12又因为x ∈,所以x-∈.(0,π2)π4(-π4,π4)所以x-=,解得x=.π4π65π12考点二　向量的综合应用1.(2018北京理,6,5分)设a,b 均为单位向量,则“|a-3b |=|3a+b |”是“a ⊥b ”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件答案　C 2.(2018天津文,8,5分)在如图的平面图形中,已知OM=1,ON=2,∠MON=120°,=2,=2,则·BM MA CN NA BC OM 的值为( )A.-15B.-9C.-6D.0答案　C 3.(2018天津理,8,5分)如图,在平面四边形ABCD 中,AB ⊥BC,AD ⊥CD,∠BAD=120°,AB=AD=1.若点E 为边CD 上的动点,则·的最小值为( )AE BEA. B. C. D.32116322516答案　A 4.(2016四川,10,5分)在平面内,定点A,B,C,D 满足||=||=||,·=·=·=-2,动点DA DB DC DA DB DB DC DC DA P,M 满足||=1,=,则||2的最大值是( )AP PM MC BM A. B.434494C.D.37+63437+2334答案　B 5.(2017江苏,12,5分)如图,在同一个平面内,向量,,的模分别为1,1,,与的夹角为α,OA OB OC 2OA OC 且tan α=7,与的夹角为45°.若=m +n (m,n ∈R ),则m+n= .OB OC OC OA OB答案　36.(2014江西,14,5分)已知单位向量e 1与e 2的夹角为α,且cos α=,向量a =3e 1-2e 2与b =3e 1-e 2的夹13角为β,则cos β= . 答案　223C 组　教师专用题组考点一　平面向量的数量积1.(2016北京,4,5分)设a,b 是向量,则“|a |=|b |”是“|a+b |=|a-b |”的( ) A.充分而不必要条件B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件答案　D 2.(2016天津,7,5分)已知△ABC 是边长为1的等边三角形,点D,E 分别是边AB,BC 的中点,连接DE 并延长到点F,使得DE=2EF,则·的值为( ) AF BC A.- B. C. D.581814118答案　B 3.(2016山东,8,5分)已知非零向量m ,n 满足4|m |=3|n |,cos<m ,n >=.若n ⊥(t m +n ),则实数t 的值为13( ) A.4 B.-4C. D.-9494答案　B 4.(2015福建,9,5分)已知⊥,||=,||=t.若点P 是△ABC 所在平面内的一点,且=+,AB AC AB 1t AC AP AB |AB |4AC |AC |则·的最大值等于( )PB PC A.13B.15C.19D.21答案　A 5.(2015山东,4,5分)已知菱形ABCD 的边长为a,∠ABC=60°,则·=( )BD CD A.-a 2B.-a 2C.a 2D.a 232343432答案　D 6.(2015安徽,8,5分)△ABC 是边长为2的等边三角形,已知向量a ,b 满足=2a ,=2a +b ,则下列结论正AB AC 确的是( ) A.|b |=1B.a ⊥bC.a ·b =1D.(4a +b )⊥BC答案　D 7.(2015重庆,6,5分)若非零向量a ,b 满足|a |=|b |,且(a -b )⊥(3a +2b ),则a 与b 的夹角为( )223A. B. C. D.ππ4π23π4答案　A 8.(2014大纲全国,4,5分)若向量a 、b 满足:|a |=1,(a +b )⊥a ,(2a +b )⊥b ,则|b |=( )A.2 B. C.1 D.222答案　B 9.(2014四川,7,5分)平面向量a =(1,2),b =(4,2),c =m a +b (m ∈R ),且c 与a 的夹角等于c 与b 的夹角,则m=( )A.-2B.-1C.1D.2答案　D10.(2014天津,8,5分)已知菱形ABCD 的边长为2,∠BAD=120°,点E,F 分别在边BC,DC 上,BE=λBC,DF=μDC.若·=1,·=-,则λ+μ=( )AE AF CE CF 23A. B. C. D.122356712答案　C 11.(2014课标Ⅱ,3,5分)设向量a,b 满足|a+b |=,|a-b |=,则a ·b =( )106A.1 B.2 C.3 D.5答案　A 12.(2017课标全国Ⅲ文,13,5分)已知向量a =(-2,3),b =(3,m),且a ⊥b ,则m= . 答案　213.(2017北京文,12,5分)已知点P 在圆x 2+y 2=1上,点A 的坐标为(-2,0),O 为原点,则·的最大值AO AP 为 . 答案　614.(2017山东理,12,5分)已知e 1,e 2是互相垂直的单位向量.若e 1-e 2与e 1+λe 2的夹角为60°,则实数3λ的值是 . 答案　3315.(2016课标全国Ⅰ,13,5分)设向量a =(m,1),b =(1,2),且|a +b |2=|a |2+|b |2,则m= . 答案　-216.(2016江苏,13,5分)如图,在△ABC 中,D 是BC 的中点,E,F 是AD 上的两个三等分点,·=4,·BA CA BF CF =-1,则·的值是 .BE CE答案　7817.(2015湖北,11,5分)已知向量⊥,||=3,则·= . OA AB OA OA OB 答案　918.(2015天津,14,5分)在等腰梯形ABCD 中,已知AB ∥DC,AB=2,BC=1,∠ABC=60°.动点E 和F 分别在线段BC 和DC 上,且=λ,=,则·的最小值为 . BE BC DF 19λDC AE AF 答案　291819.(2014江苏,12,5分)如图,在平行四边形ABCD 中,已知AB=8,AD=5,=3,·=2,则·的值CP PD AP BP AB AD 是 .答案　2220.(2014安徽,15,5分)已知两个不相等的非零向量a,b ,两组向量x 1,x 2,x 3,x 4,x 5和y 1,y 2,y 3,y 4,y 5均由2个a 和3个b 排列而成.记S=x 1·y 1+x 2·y 2+x 3·y 3+x 4·y 4+x 5·y 5,S min 表示S 所有可能取值中的最小值.则下列命题正确的是 (写出所有正确命题的编号). ①S 有5个不同的值;②若a ⊥b ,则S min 与|a |无关;③若a ∥b ,则S min 与|b |无关;④若|b |>4|a |,则S min >0;⑤若|b |=2|a |,S min =8|a |2,则a 与b 的夹角为.π4答案　②④考点二　向量的综合应用1.(2016课标全国Ⅲ,3,5分)已知向量=,=,则∠ABC=( )BA (12,32)BC (32,12)A.30°B.45°C.60°D.120°答案　A 2.(2015湖南,8,5分)已知点A,B,C 在圆x 2+y 2=1上运动,且AB ⊥BC.若点P 的坐标为(2,0),则|++PA PB PC |的最大值为( )A.6 B.7答案　B 3.(2017课标全国Ⅰ文,13,5分)已知向量a =(-1,2),b =(m,1).若向量a +b 与a 垂直,则m= . 答案　74.(2015江苏,14,5分)设向量a k =cos ,sin +cos (k=0,1,2,…,12),则(a k ·a k+1)的值kπ6kπ6kπ611∑k =0为 . 答案　93【三年模拟】一、选择题(每小题4分,共24分)1.(2019届浙江温州普通高中适应性测试,9)已知向量a,b 满足|a |=2,a 2+2a ·b+2b 2=8,则a ·b 的取值范围是( ) -2,2+2] B.[-2-2,2-2]3333C.[-1,+1] D.[--1,-1]3333答案　B 2.(2019届衢州、湖州、丽水三地教学质量检测,8)如图,△OA 1B 1,△A 1A 2B 2,△A 2A 3B 3是边长相等的等边三角形,且O,A 1,A 2,A 3四点共线.若点P 1,P 2,P 3分别是边A 1B 1,A 2B 2,A 3B 3上的动点(不含端点),记I 1=·,I 2=OB 1OP 3·,I 3=·,则( )OB 2OP 2OB 3OP 1A.I 1>I 2>I 3B.I 2>I 3>I 1C.I 2>I 1>I 3D.I 3>I 1>I 2答案　B3.(2018浙江嵊州第一学期期末质检,10)如图,已知矩形ABCD 中,AB=3,BC=2,该矩形所在的平面内一点P 满足||=1,记I 1=·,I 2=·,I 3=·,则( )CP AB AP AC AP AD AP A.存在点P,使得I 1=I 2B.存在点P,使得I 1=I 3C.对任意的点P,有I 2>I 1D.对任意的点P,有I 3>I 14.(2018浙江台州第一学期期末质检,9)已知m,n 是两个非零向量,且|m |=1,|m+2n |=3,则|m+n |+|n |的最大值为( )A. B. C.4 D.5510答案　B 5.(2018浙江台州第一次调考(4月),9)已知单位向量e 1,e 2,且e 1·e 2=-,若向量a 满足(a-e 1)·(a-e 2)=,则1254|a|的取值范围为( )A.B.[2-32,2+32][2-12,2+12]C. D.(0,2+12](0,2+32]答案　B 6.(2018浙江杭州第二次教学质量检测(4月),9)记 M 的最大值和最小值分别为 M max 和 M min .若平面向量 a,b,c 满足|a|=|b|=a ·b=c ·(a+2b-2c)=2,则( )A.|a-c |max = B.|a+c |max =3+723-72C.|a-c |min = D.|a+c |min =3+723-72答案　A 二、填空题(单空题4分,多空题6分,共16分)7.(2019届浙江名校新高考研究联盟第一次联考,16)已知向量a ,b 满足|a |=2|b |,|a -b |=2,则a ·b 的取值范围为 . 答案　[-89,8]8.(2019届台州中学第一次模拟,14)已知向量a ,b 满足|a |=2,|b |=1,a ,b 的夹角为,则a 与a -2b 的夹角π3为 . 答案　π39.(2019届镇海中学期中,15)已知两个不共线的非零向量a ,b 满足|a |=2,|a -b |=1,则向量a ,b 的夹角的最大值是 . 答案　30°10.(2018浙江金华十校第一学期期末调研,17)已知平面向量a,b,c 满足|a |≤1,|b |≤1,|2c -(a+b )|≤|a-b |,则|c |的最大值为 . 答案　2。

第3节 平面向量的数量积及其应用考试要求 1.理解平面向量数量积的含义及其物理意义；2.了解平面向量的数量积与向量投影的关系；3.掌握数量积的坐标表达式，会进行平面向量数量积的运算；4.能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系；5.会用向量的方法解决某些简单的平面几何问题.知 识 梳 理1.平面向量数量积的有关概念(1)向量的夹角：已知两个非零向量a 和b ，记OA →＝a ，OB →＝b ，则∠AOB ＝θ(0°≤θ≤180°)叫做向量a 与b 的夹角.(2)数量积的定义：已知两个非零向量a 与b ，它们的夹角为θ，则a 与b 的数量积(或内积)a ·b ＝|a ||b |cos__θ.规定：零向量与任一向量的数量积为0，即0·a ＝0.(3)数量积的几何意义：数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos__θ的乘积.2.平面向量数量积的性质及其坐标表示设向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，θ为向量a ，b 的夹角. (1)数量积：a ·b ＝|a ||b |cos θ＝x 1x 2＋y 1y 2. (2)模：|a |＝a ·a ＝x 21＋y 21. (3)夹角：cos θ＝a ·b |a ||b |＝x 1x 2＋y 1y 2x 21＋y 21·x 22＋y 22. (4)两非零向量a ⊥b 的充要条件：a ·b ＝0⇔x 1x 2＋y 1y 2＝0.(5)|a ·b |≤|a ||b |(当且仅当a ∥b 时等号成立)⇔|x 1x 2＋y 1y 2|≤ x 21＋y 21·x 22＋y 22. 3.平面向量数量积的运算律 (1)a ·b ＝b ·a (交换律).(2)λa ·b ＝λ(a ·b )＝a ·(λb )(结合律). (3)(a ＋b )·c ＝a ·c ＋b ·c (分配律). [微点提醒]1.两个向量a ，b 的夹角为锐角⇔a ·b >0且a ，b 不共线；两个向量a ，b 的夹角为钝角⇔a ·b <0且a ，b 不共线.2.平面向量数量积运算的常用公式 (1)(a ＋b )·(a －b )＝a 2－b 2. (2)(a ＋b )2＝a 2＋2a ·b ＋b 2. (3)(a －b )2＝a 2－2a ·b ＋b 2.基 础 自 测1.判断下列结论正误(在括号内打“√”或“×”)(1)两个向量的夹角的范围是⎣⎢⎡⎦⎥⎤0，π2.( )(2)向量在另一个向量方向上的投影为数量，而不是向量.( )(3)两个向量的数量积是一个实数，向量的加、减、数乘运算的运算结果是向量.( ) (4)若a ·b ＝a ·c (a ≠0)，则b ＝c .( ) 解析 (1)两个向量夹角的范围是[0，π].(4)由a ·b ＝a ·c (a ≠0)得|a ||b |·cos〈a ，b 〉＝|a ||c |·cos〈a ，c 〉，所以向量b 和c 不一定相等.答案 (1)× (2)√ (3)√ (4)×2.(必修4P108A10改编)设a ，b 是非零向量.“a ·b ＝|a ||b |”是“a ∥b ”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充分必要条件D.既不充分也不必要条件解析 设a 与b 的夹角为θ.因为a ·b ＝|a |·|b |cos θ＝|a |·|b |，所以cos θ＝1，即a 与b 的夹角为0°，故a ∥b .当a ∥b 时，a 与b 的夹角为0°或180°， 所以a ·b ＝|a |·|b |cos θ＝±|a |·|b |，所以“a ·b ＝|a |·|b |”是“a ∥b ”的充分而不必要条件. 答案 A3.(必修4P108A2改编)在圆O 中，长度为2的弦AB 不经过圆心，则AO →·AB →的值为________. 解析 设向量AO →，AB →的夹角为θ，则AO →·AB →＝|AO →||AB →|·cos θ＝|AO →|cos θ·|AB →|＝12|AB→|·|AB →|＝12×(2)2＝1.答案 14.(2018·全国Ⅱ卷)已知向量a ，b 满足|a |＝1，a ·b ＝－1，则a ·(2a －b )＝( ) A.4B.3C.2D.0解析 a ·(2a －b )＝2|a |2－a ·b ＝2×12－(－1)＝3. 答案 B5.(2018·上海嘉定区调研)平面向量a 与b 的夹角为45°，a ＝(1，1)，|b |＝2，则|3a ＋b |等于( )A.13＋6 2B.2 5C.30D.34解析 依题意得a 2＝2，a ·b ＝2×2×cos 45°＝2，|3a ＋b |＝（3a ＋b ）2＝9a 2＋6a ·b ＋b 2＝18＋12＋4＝34. 答案 D6.(2017·全国Ⅰ卷)已知向量a ＝(－1，2)，b ＝(m ，1).若向量a ＋b 与a 垂直，则m ＝________.解析 由题意得a ＋b ＝(m －1，3)，因为a ＋b 与a 垂直，所以(a ＋b )·a ＝0，所以－(m －1)＋2×3＝0，解得m ＝7. 答案 7考点一 平面向量数量积的运算【例1】 (1)若向量m ＝(2k －1，k )与向量n ＝(4，1)共线，则m ·n ＝( ) A.0B.4C.－92D.－172(2)(2018·天津卷)在如图的平面图形中，已知OM ＝1，ON ＝2，∠MON ＝120°，BM →＝2MA →，CN →＝2NA →，则BC →·OM →的值为( )A.－15B.－9C.－6D.0解析 (1)由题意得2k －1－4k ＝0，解得k ＝－12，即m ＝⎝⎛⎭⎪⎫－2，－12， 所以m ·n ＝－2×4＋⎝ ⎛⎭⎪⎫－12×1＝－172.(2)连接OA .在△ABC 中，BC →＝AC →－AB →＝3AN →－3AM →＝3(ON →－OA →)－3(OM →－OA →)＝3(ON →－OM →)， ∴BC →·OM →＝3(ON →－OM →)·OM →＝3(ON →·OM →－OM →2)＝3×(2×1×cos 120°－12)＝3×(－2)＝－6.答案 (1)D (2)C规律方法 1.数量积公式a ·b ＝|a ||b |cos θ在解题中的运用，解题过程具有一定的技巧性，需要借助向量加、减法的运算及其几何意义进行适当变形；也可建立平面直角坐标系，借助数量积的坐标运算公式a ·b ＝x 1x 2＋y 1y 2求解，较为简捷、明了.2.在分析两向量的夹角时，必须使两个向量的起点重合，如果起点不重合，可通过“平移”实现.【训练1】 (1)在△ABC 中，AB ＝4，BC ＝6，∠ABC ＝π2，D 是AC 的中点，E 在BC 上，且AE ⊥BD ，则AE →·BC →等于( ) A.16B.12C.8D.－4(2)(2019·皖南八校三模)已知|a |＝|b |＝1，向量a 与b 的夹角为45°，则(a ＋2b )·a ＝________.解析 (1)以B 为原点，BA ，BC 所在直线分别为x ，y 轴建立平面直角坐标系(图略)，A (4，0)，B (0，0)，C (0，6)，D (2，3).设E (0，t )，BD →·AE →＝(2，3)·(－4，t )＝－8＋3t ＝0，∴t ＝83，即E ⎝ ⎛⎭⎪⎫0，83， AE →·BC →＝⎝⎛⎭⎪⎫－4，83·(0，6)＝16.(2)因为|a |＝|b |＝1，向量a 与b 的夹角为45°，所以(a ＋2b )·a ＝a 2＋2a ·b ＝|a |2＋2|a |·|b |cos 45°＝1＋ 2. 答案 (1)A (2)1＋ 2 考点二 平面向量数量积的应用多维探究角度1 平面向量的垂直【例2－1】 (1)(2018·北京卷)设向量a ＝(1，0)，b ＝(－1，m ).若a ⊥(m a －b )，则m ＝________.(2)(2019·宜昌二模)已知△ABC 中，∠A ＝120°，且AB ＝3，AC ＝4，若AP →＝λAB →＋AC →，且AP →⊥BC →，则实数λ的值为( ) A.2215B.103C.6D.127解析 (1)a ＝(1，0)，b ＝(－1，m )，∴a 2＝1，a ·b ＝－1， 由a ⊥(m a －b )得a ·(m a －b )＝0，即m a 2－a ·b ＝0. ∴m －(－1)＝0，∴m ＝－1. (2)因为AP →＝λAB →＋AC →，且AP →⊥BC →，所以有AP →·BC →＝(λAB →＋AC →)·(AC →－AB →)＝λAB →·AC →－λAB →2＋AC →2－AB →·AC →＝(λ－1)AB →·AC →－λAB →2＋AC →2＝0，整理可得(λ－1)×3×4×cos 120°－9λ＋16＝0， 解得λ＝2215.答案 (1)－1 (2)A规律方法 1.当向量a ，b 是非坐标形式时，要把a ，b 用已知的不共线向量作为基底来表示且不共线的向量要知道其模与夹角，从而进行运算.2.数量积的运算a ·b ＝0⇔a ⊥b 中，是对非零向量而言的，若a ＝0，虽然有a ·b ＝0，但不能说a ⊥b .角度2 平面向量的模【例2－2】 (1)已知平面向量α，β，|α|＝1，|β|＝2，α⊥(α－2β)，则|2α＋β|的值是________.(2)(2019·杭州调研)已知直角梯形ABCD 中，AD ∥BC ，∠ADC ＝90°，AD ＝2，BC ＝1，P 是腰DC 上的动点，则|PA →＋3PB →|的最小值为________.解析 (1)由α⊥(α－2β)得α·(α－2β)＝α2－2α·β＝0， 所以α·β＝12，所以(2α＋β)2＝4α2＋β2＋4α·β＝4×12＋22＋4×12＝10，所以|2α＋β|＝10.(2)建立平面直角坐标系如图所示，则A (2，0)，设P (0，y )，C (0，b )，则B (1，b ).所以PA →＋3PB →＝(2，－y )＋3(1，b －y )＝(5，3b －4y )， 所以|PA →＋3PB →|＝25＋（3b －4y ）2(0≤y ≤b )， 所以当y ＝34b 时，|PA →＋3PB →|取得最小值5.答案 (1)10 (2)5规律方法 1.求向量的模的方法：(1)公式法，利用|a |＝a ·a 及(a ±b )2＝|a |2±2a ·b ＋|b |2，把向量的模的运算转化为数量积运算；(2)几何法，利用向量的几何意义.2.求向量模的最值(范围)的方法：(1)代数法，把所求的模表示成某个变量的函数，再用求最值的方法求解；(2)几何法(数形结合法)，弄清所求的模表示的几何意义，结合动点表示的图形求解.角度3 平面向量的夹角【例2－3】 (1)(2019·衡水中学调研)已知非零向量a ，b 满足|a ＋b |＝|a －b |＝233|a |，则向量a ＋b 与a －b 的夹角为________.(2)若向量a ＝(k ，3)，b ＝(1，4)，c ＝(2，1)，已知2a －3b 与c 的夹角为钝角，则k 的取值范围是________.解析 (1)将|a ＋b |＝|a －b |两边平方，得a 2＋b 2＋2a ·b ＝a 2＋b 2－2a ·b ，∴a ·b ＝0. 将|a ＋b |＝233|a |两边平方，得a 2＋b 2＋2a ·b ＝43a 2，∴b 2＝13a 2.设a ＋b 与a －b 的夹角为θ，∴cos θ＝（a ＋b ）·（a －b ）|a ＋b |·|a －b |＝a 2－b 2233|a |·233|a |＝23a 243a 2＝12.又∵θ∈[0，π]，∴θ＝π3.(2)∵2a －3b 与c 的夹角为钝角， ∴(2a －3b )·c <0，即(2k －3，－6)·(2，1)<0，解得k ＜3. 又若(2a －3b )∥c ， 则2k －3＝－12，即k ＝－92.当k ＝－92时，2a －3b ＝(－12，－6)＝－6c ，此时2a －3b 与c 反向，不合题意.综上，k 的取值范围为⎝ ⎛⎭⎪⎫－∞，－92∪⎝ ⎛⎭⎪⎫－92，3. 答案 (1)π3 (2)⎝⎛⎭⎪⎫－∞，－92∪⎝ ⎛⎭⎪⎫－92，3 规律方法 1.研究向量的夹角应注意“共起点”；两个非零共线向量的夹角可能是0或π；注意向量夹角的取值范围是[0，π]；若题目给出向量的坐标表示，可直接套用公式cos θ＝x 1x 2＋y 1y 2x 21＋y 21·x 22＋y 22求解. 2.数量积大于0说明不共线的两向量的夹角为锐角，数量积等于0说明不共线的两向量的夹角为直角，数量积小于0且两向量不共线时两向量的夹角为钝角.【训练2】 (1)已知向量a ＝(－2，3)，b ＝(3，m )，且a ⊥b ，则m ＝________.(2)(一题多解)(2017·全国Ⅰ卷)已知向量a ，b 的夹角为60°，|a |＝2，|b |＝1，则|a ＋2b |＝________.(3)(2017·山东卷)已知e 1，e 2是互相垂直的单位向量，若3e 1－e 2与e 1＋λe 2的夹角为60°，则实数λ的值是________. 解析 (1)由a ⊥b ，得a ·b ＝0， 又a ＝(－2，3)，b ＝(3，m )， ∴－6＋3m ＝0，则m ＝2.(2)法一 |a ＋2b |＝（a ＋2b ）2＝a 2＋4a ·b ＋4b 2＝22＋4×2×1×cos 60°＋4×12＝12＝2 3.法二 (数形结合法)由|a |＝|2b |＝2知，以a 与2b 为邻边可作出边长为2的菱形OACB ，如图，则|a ＋2b |＝|OC →|.又∠AOB ＝60°，所以|a ＋2b |＝2 3. (3)由题意知|e 1|＝|e 2|＝1，e 1·e 2＝0，|3e 1－e 2|＝（3e 1－e 2）2＝3e 21－23e 1·e 2＋e 22＝3－0＋1＝2. 同理|e 1＋λe 2|＝1＋λ2.所以cos 60°＝（3e 1－e 2）·（e 1＋λe 2）|3e 1－e 2||e 1＋λe 2|＝3e 21＋（3λ－1）e 1·e 2－λe 2221＋λ2＝3－λ21＋λ2＝12， 解得λ＝33. 答案 (1)2 (2)2 3 (3)33考点三 平面向量与三角函数【例3】 (2019·潍坊摸底)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，向量m ＝(cos(A －B )，sin(A －B ))，n ＝(cos B ，－sin B )，且m ·n ＝－35.(1)求sin A 的值；(2)若a ＝42，b ＝5，求角B 的大小及向量BA →在BC →方向上的投影. 解 (1)由m ·n ＝－35，得cos(A －B )cos B －sin(A －B )sin B ＝－35，所以cos A ＝－35.因为0<A <π，所以sin A ＝1－cos 2A ＝1－⎝ ⎛⎭⎪⎫－352＝45.(2)由正弦定理，得a sin A ＝bsin B ，则sin B ＝b sin A a ＝5×4542＝22，因为a >b ，所以A >B ，且B 是△ABC 一内角，则B ＝π4.由余弦定理得(42)2＝52＋c 2－2×5c ×⎝ ⎛⎭⎪⎫－35，解得c ＝1，c ＝－7舍去，故向量BA →在BC →方向上的投影为|BA →|cos B ＝c cos B ＝1×22＝22.规律方法 平面向量与三角函数的综合问题的解题思路：(1)题目条件给出向量的坐标中含有三角函数的形式，运用向量共线或垂直或等式成立等，得到三角函数的关系式，然后求解.(2)给出用三角函数表示的向量坐标，要求的是向量的模或者其他向量的表达形式，解题思路是经过向量的运算，利用三角函数在定义域内的有界性，求得值域等.【训练3】 (2019·石家庄模拟)已知A ，B ，C 分别为△ABC 的三边a ，b ，c 所对的角，向量m ＝(sin A ，sin B )，n ＝(cos B ，cos A )，且m ·n ＝sin 2C .(1)求角C 的大小；(2)若sin A ，sin C ，sin B 成等差数列，且CA →·(AB →－AC →)＝18，求边c 的长. 解 (1)由已知得m ·n ＝sin A cos B ＋cos A sin B ＝sin(A ＋B )， 因为A ＋B ＋C ＝π，所以sin(A ＋B )＝sin(π－C )＝sin C ， 所以m ·n ＝sin C ，又m ·n ＝sin 2C ， 所以sin 2C ＝sin C ，所以cos C ＝12.又0<C <π，所以C ＝π3.(2)由已知及正弦定理得2c ＝a ＋b . 因为CA →·(AB →－AC →)＝CA →·CB →＝18， 所以ab cos C ＝18，所以ab ＝36.由余弦定理得c 2＝a 2＋b 2－2ab cos C ＝(a ＋b )2－3ab所以c 2＝4c 2－3×36， 所以c 2＝36，所以c ＝6.[思维升华]1.计算向量数量积的三种方法定义、坐标运算、数量积的几何意义，要灵活运用，与图形有关的不要忽略数量积几何意义的应用.2.求向量模的常用方法利用公式|a |2＝a 2，将模的运算转化为向量的数量积的运算.3.利用向量垂直或平行的条件构造方程或函数是求参数或最值问题常用的方法与技巧. [易错防范]数量积运算律要准确理解、应用，例如，a ·b ＝a ·c (a ≠0)不能得出b ＝c ，两边不能约去一个向量.数量积运算不满足结合律，(a ·b )·c 不一定等于a ·(b ·c ).数学运算、数学建模——平面向量与三角形的“四心”1.数学运算是指在明晰运算的基础上，依据运算法则解决数学问题的素养.通过学习平面向量与三角形的“四心”，学生能进一步发展数学运算能力，形成规范化思考问题的品质，养成一丝不苟、严谨求实的科学精神.2.数学建模要求在熟悉的情境中，发现问题并转化为数学问题，能够在关联的情境中，经历数学建模的过程，理解数学建模的意义.本系列通过学习平面向量与三角形的“四心”模型，能够培养学生用模型的思想解决相关问题.设O 为△ABC 所在平面上一点，内角A ，B ，C 所对的边分别为a ，b ，c ，则 (1)O 为△ABC 的外心⇔|OA →|＝|OB →|＝|OC →|＝a2sin A. (2)O 为△ABC 的重心⇔OA →＋OB →＋OC →＝0.(3)O 为△ABC 的垂心⇔OA →·OB →＝OB →·OC →＝OC →·OA →. (4)O 为△ABC 的内心⇔aOA →＋bOB →＋cOC →＝0. 类型1 平面向量与三角形的“重心”【例1】 已知A ，B ，C 是平面上不共线的三点，O 为坐标原点，动点P 满足OP →＝13[(1－λ)OA→＋(1－λ)OB →＋(1＋2λ)·OC →]，λ∈R ，则点P 的轨迹一定经过( ) A.△ABC 的内心 B.△ABC 的垂心 C.△ABC 的重心D.AB 边的中点解析 取AB 的中点D ，则2OD →＝OA →＋OB →， ∵OP →＝13[(1－λ)OA →＋(1－λ)OB →＋(1＋2λ)OC →]，∴OP →＝13[2(1－λ)OD →＋(1＋2λ)OC →]＝2（1－λ）3OD →＋1＋2λ3OC →，而2（1－λ）3＋1＋2λ3＝1，∴P ，C ，D 三点共线，∴点P 的轨迹一定经过△ABC 的重心. 答案 C类型2 平面向量与三角形的“内心”问题【例2】 在△ABC 中，AB ＝5，AC ＝6，cos A ＝15，O 是△ABC 的内心，若OP →＝xOB →＋yOC →，其中x ，y ∈[0，1]，则动点P 的轨迹所覆盖图形的面积为( ) A.1063B.1463C.4 3D.6 2解析 根据向量加法的平行四边形法则可知，动点P 的轨迹是以OB ，OC 为邻边的平行四边形及其内部，其面积为△BOC 的面积的2倍.在△ABC 中，设内角A ，B ，C 所对的边分别为a ，b ，c ，由余弦定理a 2＝b 2＋c 2－2bc cos A ，得a ＝7.设△ABC 的内切圆的半径为r ，则 12bc sin A ＝12(a ＋b ＋c )r ，解得r ＝263， 所以S △BOC ＝12×a ×r ＝12×7×263＝763.故动点P 的轨迹所覆盖图形的面积为2S △BOC ＝1463.答案 B类型3 平面向量与三角形的“垂心”问题【例3】 已知O 是平面上的一个定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP →＝OA →＋λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|cos B + AC →|AC →|cos C ，λ∈(0，＋∞)，则动点P 的轨迹一定通过△ABC 的( ) A.重心B.垂心C.外心D.内心解析 因为OP →＝OA →＋λ⎝ ⎛⎭⎪⎪⎫AB →|AB →|cos B + AC →|AC →|cos C ， 所以AP →＝OP →－OA →＝λ⎝⎛⎭⎪⎪⎫AB →|AB →|cos B +AC →|AC →|cos C ， 所以BC →·AP →＝BC →·λ⎝⎛⎭⎪⎪⎫AB →|AB →|cos B +AC →|AC →|cos C ＝λ(－|BC →|＋|BC →|)＝0，所以BC →⊥AP →，所以点P 在BC 的高线上， 即动点P 的轨迹一定通过△ABC 的垂心. 答案 B类型4 平面向量与三角形的“外心”问题【例4】 已知在△ABC 中，AB ＝1，BC ＝6，AC ＝2，点O 为△ABC 的外心，若AO →＝xAB →＋yAC →，则有序实数对(x ，y )为( )A.⎝ ⎛⎭⎪⎫45，35B.⎝ ⎛⎭⎪⎫35，45C.⎝ ⎛⎭⎪⎫－45，35D.⎝ ⎛⎭⎪⎫－35，45 解析 取AB 的中点M 和AC 的中点N ，连接OM ，ON ，则OM →⊥AB →，ON →⊥AC →， OM →＝AM →－AO →＝12AB →－(xAB →＋yAC →)＝⎝ ⎛⎭⎪⎫12－x AB →－yAC →，ON →＝AN →－AO →＝12AC →－(xAB →＋yAC →)＝⎝ ⎛⎭⎪⎫12－y AC →－xAB →.由OM →⊥AB →，得⎝ ⎛⎭⎪⎫12－x AB →2－yAC →·AB →＝0，①由ON →⊥AC →，得⎝ ⎛⎭⎪⎫12－y AC →2－xAC →·AB →＝0，②又因为BC →2＝(AC →－AB →)2＝AC →2－2AC →·AB →＋AB →2，所以AC →·AB →＝AC →2＋AB →2－BC→22＝－12，③把③代入①、②得⎩⎪⎨⎪⎧1－2x ＋y ＝0，4＋x －8y ＝0，解得x ＝45，y ＝35.故实数对(x ，y )为⎝ ⎛⎭⎪⎫45，35.答案 A基础巩固题组 (建议用时：40分钟)一、选择题1.已知向量a ＝(m －1，1)，b ＝(m ，－2)，则“m ＝2”是“a ⊥b ”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件解析 当m ＝2时，a ＝(1，1)，b ＝(2，－2)， 所以a ·b ＝(1，1)·(2，－2)＝2－2＝0， 所以a ⊥b ，充分性成立；当a ⊥b 时，a ·b ＝(m －1，1)·(m ，－2)＝m (m －1)－2＝0， 解得m ＝2或m ＝－1，必要性不成立. 所以“m ＝2”是“a ⊥b ”的充分不必要条件. 答案 A2.(2019·北京通州区二模)已知非零向量a ，b 的夹角为60°，且|b |＝1，|2a －b |＝1，则|a |＝( ) A.12B.1C. 2D.2解析 由题意得a ·b ＝|a |×1×12＝|a |2，又|2a －b |＝1，∴|2a －b |2＝4a 2－4a ·b ＋b 2＝4|a |2－2|a |＋1＝1，即4|a |2－2|a |＝0，又|a |≠0， 解得|a |＝12.答案 A3.(2019·石家庄二模)若两个非零向量a ，b 满足|a ＋b |＝|a －b |＝2|b |，则向量a ＋b 与a 的夹角为( ) A.π3B.2π3C.5π6D.π6解析 设|b |＝1，则|a ＋b |＝|a －b |＝2. 由|a ＋b |＝|a －b |，得a ·b ＝0，故以a 、b 为邻边的平行四边形是矩形，且|a |＝3， 设向量a ＋b 与a 的夹角为θ，则cos θ＝a ·（a ＋b ）|a |·|a ＋b |＝a 2＋a ·b |a |·|a ＋b |＝|a ||a ＋b |＝32，又0≤θ≤π，所以θ＝π6.答案 D4.如图，在等腰梯形ABCD 中，AB ＝4，BC ＝CD ＝2，若E ，F 分别是边BC ，AB 上的点，且满足BE BC ＝AF AB＝λ，则当AE →·DF →＝0时，λ的值所在的区间是( )A.⎝ ⎛⎭⎪⎫18，14B.⎝ ⎛⎭⎪⎫14，38C.⎝ ⎛⎭⎪⎫38，12D.⎝ ⎛⎭⎪⎫12，58 解析 在等腰梯形ABCD 中，AB ＝4，BC ＝CD ＝2， 可得〈AD →，BC →〉＝60°，所以〈AB →，AD →〉＝60°，〈AB →，BC →〉＝120°， 所以AB →·AD →＝4×2×12＝4，AB →·BC →＝4×2×⎝ ⎛⎭⎪⎫－12＝－4，AD →·BC →＝2×2×12＝2， 又BE BC ＝AF AB＝λ，所以BE →＝λBC →，AF →＝λAB →，则AE →＝AB →＋BE →＝AB →＋λBC →， DF →＝AF →－AD →＝λAB →－AD →，所以AE →·DF →＝(AB →＋λBC →)·(λAB →－AD →) ＝λAB →2－AB →·AD →＋λ2AB →·BC →－λAD →·BC →＝0，即2λ2－7λ＋2＝0，解得λ＝7＋334(舍去)或λ＝7－334∈⎝ ⎛⎭⎪⎫14，38.答案 B5.(2017·浙江卷)如图，已知平面四边形ABCD ，AB ⊥BC ，AB ＝BC ＝AD ＝2，CD ＝3，AC 与BD 交于点O .记I 1＝OA →·OB →，I 2＝OB →·OC →，I 3＝OC →·OD →，则( )A.I 1＜I 2＜I 3B.I 1＜I 3＜I 2C.I 3＜I 1＜I 2D.I 2＜I 1＜I 3解析 如图所示，四边形ABCE 是正方形，F 为正方形的对角线的交点，易得AO <AF ，而∠AFB ＝90°，∴∠AOB 与∠COD 为钝角，∠AOD 与∠BOC 为锐角，根据题意，I 1－I 2＝OA →·OB →－OB →·OC →＝OB →·(OA →－OC →)＝OB →·CA →＝|OB →||CA →|·cos∠AOB <0，∴I 1<I 2，同理I 2>I 3，作AG ⊥BD 于G ，又AB ＝AD ，∴OB <BG ＝GD <OD ，而OA <AF ＝FC <OC ，∴|OA →||OB →|<|OC →||OD →|， 而cos∠AOB ＝cos∠COD <0，∴OA →·OB →>OC →·OD →， 即I 1>I 3.∴I 3<I 1<I 2. 答案 C 二、填空题6.(2019·杭州二模)在△ABC 中，三个顶点的坐标分别为A (3，t )，B (t ，－1)，C (－3，－1)，若△ABC 是以B 为直角顶点的直角三角形，则t ＝________. 解析 由已知，得BA →·BC →＝0， 则(3－t ，t ＋1)·(－3－t ，0)＝0，∴(3－t )(－3－t )＝0，解得t ＝3或t ＝－3， 当t ＝－3时，点B 与点C 重合，舍去.故t ＝3. 答案 37.若非零向量a ，b 满足|a |＝3|b |＝|a ＋2b |，则a ，b 夹角θ的余弦值为________. 解析 |a |＝|a ＋2b |，两边平方得，|a |2＝|a |2＋4|b |2＋4a ·b ＝|a |2＋4|b |2＋4|a ||b |·cos θ. 又|a |＝3|b |，所以0＝4|b |2＋12|b |2cos θ，得cos θ＝－13.答案 －138.(2019·佛山二模)在Rt△ABC 中，∠B ＝90°，BC ＝2，AB ＝1，D 为BC 的中点，E 在斜边AC 上，若AE →＝2EC →，则DE →·AC →＝________.解析 如图，以B 为坐标原点，AB 所在直线为x 轴，BC 所在直线为y 轴，建立平面直角坐标系，则B (0，0)，A (1，0)，C (0，2)，所以AC →＝(－1，2).因为D 为BC 的中点，所以D (0，1)， 因为AE →＝2EC →，所以E ⎝ ⎛⎭⎪⎫13，43，所以DE →＝⎝ ⎛⎭⎪⎫13，13，所以DE →·AC →＝⎝ ⎛⎭⎪⎫13，13·(－1，2)＝－13＋23＝13.答案 13三、解答题9.在平面直角坐标系xOy 中，点A (－1，－2)，B (2，3)，C (－2，－1).(1)求以线段AB ，AC 为邻边的平行四边形两条对角线的长； (2)设实数t 满足(AB →－tOC →)·OC →＝0，求t 的值. 解 (1)由题设知AB →＝(3，5)，AC →＝(－1，1)， 则AB →＋AC →＝(2，6)，AB →－AC →＝(4，4). 所以|AB →＋AC →|＝210，|AB →－AC →|＝4 2. 故所求的两条对角线的长分别为42，210.(2)由题设知：OC →＝(－2，－1)，AB →－tOC →＝(3＋2t ，5＋t ). 由(AB →－tOC →)·OC →＝0，得 (3＋2t ，5＋t )·(－2，－1)＝0， 从而5t ＝－11，所以t ＝－115. 10.在平面直角坐标系中，O 为坐标原点，已知向量a ＝(－1，2)，又点A (8，0)，B (n ，t )，C (k sin θ，t )(0≤θ≤π2).(1)若AB →⊥a ，且|AB →|＝5|OA →|，求向量OB →；(2)若向量AC →与向量a 共线，当k >4，且t sin θ取最大值4时，求OA →·OC →. 解 (1)由题设知AB →＝(n －8，t )， ∵AB →⊥a ，∴8－n ＋2t ＝0. 又∵5|OA →|＝|AB →|，∴5×64＝(n －8)2＋t 2＝5t 2，得t ＝±8. 当t ＝8时，n ＝24；当t ＝－8时，n ＝－8， ∴OB →＝(24，8)或OB →＝(－8，－8). (2)由题设知AC →＝(k sin θ－8，t )， ∵AC →与a 共线，∴t ＝－2k sin θ＋16，t sin θ＝(－2k sin θ＋16)sin θ＝－2k (sin θ－4k )2＋32k.∵k >4，∴0<4k<1，∴当sin θ＝4k 时，t sin θ取得最大值32k.由32k＝4，得k ＝8，此时θ＝π6，OC →＝(4，8)，∴OA →·OC →＝(8，0)·(4，8)＝32.能力提升题组 (建议用时：20分钟)11.在△ABC 中，∠C ＝90°，AB ＝6，点P 满足CP ＝2，则PA →·PB →的最大值为( ) A.9B.16C.18D.25解析 ∵∠C ＝90°，AB ＝6，∴CA →·CB →＝0，∴|CA →＋CB →|＝|CA →－CB →|＝|BA →|＝6，∴PA →·PB →＝(PC →＋CA →)·(PC →＋CB →)＝PC →2＋PC →·(CA →＋CB →)＋CA →·CB → ＝PC →·(CA →＋CB →)＋4，∴当PC →与CA →＋CB →方向相同时，PC →·(CA →＋CB →)取得最大值2×6＝12， ∴PA →·PB →的最大值为16. 答案 B12.(2018·浙江卷)已知a ，b ，e 是平面向量，e 是单位向量.若非零向量a 与e 的夹角为π3，向量b 满足b 2－4e ·b ＋3＝0，则|a －b |的最小值是( ) A.3－1 B.3＋1 C.2D.2－ 3解析 设O 为坐标原点，a ＝OA →，b ＝OB →＝(x ，y )，e ＝(1，0)，由b 2－4e ·b ＋3＝0得x 2＋y 2－4x ＋3＝0，即(x －2)2＋y 2＝1，所以点B 的轨迹是以C (2，0)为圆心，1为半径的圆.因为a 与e 的夹角为π3，所以不妨令点A 在射线y ＝3x (x >0)上，如图，数形结合可知|a －b |min ＝|CA →|－|CB →|＝3－1.答案 A13.(2019·安徽师大附中二模)在△ABC 中，AB ＝2AC ＝6，BA →·BC →＝BA →2，点P 是△ABC 所在平面内一点，则当PA →2＋PB →2＋PC →2取得最小值时，AP →·BC →＝________. 解析 ∵BA →·BC →＝|BA →|·|BC →|·cos B ＝|BA →|2， ∴|BC →|·cos B ＝|BA →|＝6， ∴CA →⊥AB →，即A ＝π2，以A 为坐标原点建立如图所示的坐标系，则B (6，0)，C (0，3)，设P (x ，y )，则PA →2＋PB →2＋PC →2＝x 2＋y 2＋(x －6)2＋y 2＋x 2＋(y －3)2＝3x 2－12x ＋3y 2－6y ＋45＝3[(x －2)2＋(y －1)2＋10]∴当x ＝2，y ＝1时，PA →2＋PB →2＋PC →2取得最小值， 此时AP →·BC →＝(2，1)·(－6，3)＝－9. 答案 －914.在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且满足(2a －c )BA →·BC →＝cCB →·CA →. (1)求角B 的大小；(2)若|BA →－BC →|＝6，求△ABC 面积的最大值. 解 (1)由题意得(2a －c )cos B ＝b cos C .根据正弦定理得(2sin A －sin C )cos B ＝sin B cos C ，所以2sin A cos B ＝sin(C ＋B )，即2sin A cos B ＝sin A ，因为A ∈(0，π)，所以sin A >0， 所以cos B ＝22，又B ∈(0，π)，所以B ＝π4. (2)因为|BA →－BC →|＝6，所以|CA →|＝6，即b ＝6，根据余弦定理及基本不等式得6＝a 2＋c 2－2ac ≥2ac －2ac ＝(2－2)ac (当且仅当a ＝c 时取等号)，即ac ≤3(2＋2). 故△ABC 的面积S ＝12ac sin B ≤3（2＋1）2，因此△ABC 的面积的最大值为32＋32.新高考创新预测15.(新定义题型)对任意两个非零的平面向量α和β，定义α⊗β＝|α||β|cos θ，其中θ为α和β的夹角.若两个非零的平面向量a 和b 满足：①|a |≥|b |；②a 和b 的夹角θ∈⎝⎛⎭⎪⎫0，π4；③a ⊗b 和b ⊗a 的值都在集合{x |x ＝n 2，n ∈N }中，则a ⊗b 的值为________.解析 a ⊗b ＝|a ||b |cos θ＝n 2，b ⊗a ＝|b ||a |cos θ＝m 2，m ，n ∈N .由a 与b 的夹角θ∈⎝⎛⎭⎪⎫0，π4，知cos 2θ＝mn 4∈⎝ ⎛⎭⎪⎫12，1，故mn ＝3，m ，n ∈N .因为|a |≥|b |，所以0<b ⊗a ＝m 2<1，所以m ＝1，n ＝3，所以a ⊗b ＝32.答案 32。

••>必过教材美定义图示范围共线与垂直已知两个非零向量a和b, 作0)A = a, OB = b,则/ AOB就是a与b的夹角设a是a与b的夹角，则a的取值范围是o°< a 180°0= 0。

或0= 180 °a// b, 0= 90°a丄b定义设两个非零向量a, b的夹角为0,贝U数量|a||b|cos 0叫做a与b的数量积，记作a b投影|a|cos 0叫做向量a在b方向上的投影，I b lcos 0叫做向量b在a方向上的投影几何意义数量积a b等于a的长度|a|与b在a的方向上的投影|b|cos 0的乘积⑴a b= b a.(2) (扫)b= 4a b)= a ( %).(3) ( a + b) c = a c + b c.4. 平面向量数量积的有关结论i i22结论几何表示坐标表小模|a |=^/a^a|a |=Q x：+ y：夹角cos 0= a b |a||b|X1X2+ y i y2 cos 0=v x^y2 v x i r y：a丄b的充要条件 a b= 0yy：=0|a b |与|a||b|的关系|a b|w|a||b||X1X2+ y1y2|w第三节平面向量的数量积与平面向量应用举例［小题体验］1 .已知 |a |= 2, |b |= 6, a b =- 6.3,则 a 与 b 的夹角 B 为()D.J答案：D./3由题意可得 a b = |a ||b |cos 〈 a , b > = 2x 3^2^= 3.3.已知向量a , b 均为单位向量，若它们的夹角为 60°则|a + 3b|=()A. 7B. 10C. 13D . 41解析：选C 依题意得a b =孑 则|a + 3b |= a 2+ 9b 2 + 6a b = 13.4.已知两个单位向量 a , b 的夹角为60° c = t a + (1 -1)b .若 b c = 0，贝U t= _____________ .1解析：因为向量a , b 为单位向量，所以b 2= 1,又向量a , b 的夹角为60°所以a b =?, 由 b c = 0，得 b [ta + (1 -t)b] = 0,即 t a b + (1 — t)b 2= 0，所以｛+(1 -1)= 0,所以 t = 2.答案：25.已知正方形 ABCD 的边长为2, E 为CD 的中点，贝U AE -BD = ___________ .- > --- > ----- > --- > --- > --- > --- > 1 ----- > ------- > -- >解析：选向量的基底为 AB , AD ,贝U BD = AD - AB , AE = AD + - AB ,所以AE ・BD = AD —+ ^AB —>(T lD - >A B )= 2.答案：2*•)必过易错关1.数量积运算律要准确理解、应用，例如， a b = a c (a ^0)不能得出b = c ,两边不能约去一个向量.2 .两个向量的夹角为锐角，则有 a b > 0,反之不成立；两个向量夹角为钝角，则有2.已知向量 a 和向量 b 的夹角为 30° |a|= 2, |b| = V3,则向量a 和向量b 的数量积a b解析：选Cv 0，反之不成立.3. a b= 0不能推出a= 0或b= 0,因为a b= 0时，有可能a丄b.4. 在用|a|= 孑求向量的模时，一定要把求出的a2再进行开方.［小题纠偏］1 .若a, b是两个互相垂直的非零向量，给出以下式子：① a b= 0:②a+ b= a —b:③|a+ b|= |a —b|;④a2+ b2= （a+ b）2.其中正确的个数是（）A. 1 B . 2C . 3D . 4解析：选C 因为a, b是两个互相垂直的非零向量，所以a b= 0;所以（a+ b）2= a2+ b2 + 2a b= a2 + b2; （a —b）2= a2+ b2—2a b= a2+ b2;所以（a+ b）2= （a —b）2，即|a+ b| = |a—b|.故①③④是正确的，②是错误的.1 r,2.设向量a, b满足|a|= |b|= 1, a b= —^，则|a+ 2b|=解析：|a+ 2b|= a+ 2b 2= |a|2+ 4a b+ 4|b|2= . 1 + 4x — 2 + 4 = 3.答案：3考点一平面向量的数量积的运算基础送分型考点自主练透［题组练透］1 .设a= (1,—A. (—15,12)D . —11解析：选C ••• a + 2b = (1, —2) + 2( —3,4) = (—5,6),••• (a+ 2b) c= (—5,6) (3,2) =—3.2. （2018浙江考前冲刺）若两个非零向量a, b满足|a+ b|= |a—b|= 2|b|= 4，则向量a在a+ b 上的投影为（）A. 3C. 6解析：选B 由|a+ b|= |a—b|,得a2+ 2a b + b2= a2—2a b+ b2,即卩a b = 0, 由|a+ b|= 2|b|，得a2+ 2a b+ b2= 4b2,即卩a2= 3b2,所以|a|= , 3|b|= 2 3,2a在a+ b上的投影为a_ a + b= — = 3.所以向量|a+ b | |a + b|3 .如图, 在等腰直角三角形ABC中，/ C = 90° AC = 2,-- >AD =解析：法一：由题意知，AC = BC= 2, AB = 2 2,-- > > > > >••• AB -AD = AB (AC + CD )-- > > > >=AB -AC + AB CD-- > ---- > ---------------- >---- >=| AB | | AC |cos 45+ | AB | |CD |cos 45=2 2X 2X 2 + 2 2 X 1 X 22= 6.法二：建立如图所示的平面直角坐标系，由题意得A(0,2), B(-2,0),D( —1,0),•••卓=(—2,0) —(0,2) = (—2,—2),--- >AD = (—1,0) —(0,2) = (—1,—2),二>AB T AD = —2 X (—1) + (—2)X (—2) = 6.答案：6-- > ---- > -- > ----- >4. （2019台州模拟）以O为起点作三个不共线的非零向量OA , OB , OC ,使AB =—2 -C , |-A|= 4,竺 + 豊=竺，则-T-； = ________________________|OA| |O B| | O C |解析：法一：由卑 + 竺=竺，平方得豐聲 =—1，即cos/ AOB = —J因| OA| | OB| | OC | | OA| | O B |为O A , 0B不共线，所以0°<Z AOB V 180° 所以/ AOB = 120。

一、知识纲要1、向量的相关概念：《必修 4》 第二章平面向量（1） 向量： 既有大小又有方向的量叫做向量，记为 AB 或a 。

向量又称矢量。

①向量和标量的区别：向量既有大小又有方向；标量只有大小，没有方向。

普通的数量都是标量，力是一种常见的向量。

②向量常用有向线段来表示，但也不能说向量就是有向线段，因为向量是自由的，可以平移；有向线段有固定的起点和终点，不能随意移动。

（2） 向量的模：向量的大小又叫向量的模，它指的是：表示向量的有向线段的长度。

记作：| AB |或｜ a ｜。

向量本身不能比较大小，但向量的模可以比较大小。

（3） 零 向 量： 长度为 0 的向量叫零向量，记为0 ，零向量的方向是任意的。

①｜ a ｜＝0； ② 0 与 0 的区别：写法的区别，意义的区别。

（4） 单位向量：模长为 1 个单位长度的非零向量叫单位向量。

若向量a 是单位向量，则｜ a ｜= 1 。

2、 向量的表示：（1）几何表示法：用带箭头的有向线段表示，如 AB ，注意：方向是“起点指向终点”。

→（2） 符号表示法：用一个小写的英文字母来表示，如 a ， b 等；（3）坐标表示法：在平面内建立直角坐标系，以与 x 轴、 y 轴正方向相同的两个单位向量i 、 j 为基底向量，则平面内的任一向量 a 可表示为 a = xi + y j = ( x , y ) ，称( x , y ) 为向量 a 的坐标， a ＝( x , y ) 叫做向量 a 的坐标表示。

此时｜ a ｜。

若已知 A ( x 1 , y 1 )和B ( x 2 , y 2 ) ，则 AB = ( x 2 -x 1，y 2 -y 1 ) ， 即终点坐标减去起点坐标。

特别的，如果向量的起点在原点，那么向量的坐标数值与向量的终点坐标数值相同。

注意 注意 注意 注意a 3、 向量之间的关系：（1）平行（共线）：对于两个非零向量，若它们的方向相同或相反的，那么就称这种关系 为平行，记作a ∥ b 。

2020年高考文科数学一轮总复习：平面向量的数量积及应用举例第3讲 平面向量的数量积及应用举例1．平面向量的数量积2．向量的夹角＝设则0(1)a·b ＝b·a .(2)(λa )·b ＝λ(a·b )＝a ·(λb )． (3)(a ＋b )·c ＝a·c ＋b·c .4．平面向量数量积的坐标运算及有关结论已知非零向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，a 与b 的夹角为θ，a ·b ＝x 1x 2＋y 1y 2.判断正误(正确的打“√”，错误的打“×”)(1)向量在另一个向量方向上的投影为数量，而不是向量．( )(2)两个向量的数量积是一个实数，向量的加、减、数乘运算的运算结果是向量．( ) (3)由a ·b ＝0可得a ＝0或b ＝0.( ) (4)(a ·b )c ＝a (b ·c )．( )(5)两个向量的夹角的范围是⎣⎡⎦⎤0，π2.( )(6)若a ·b >0，则a 和b 的夹角为锐角；若a ·b <0，则a 和b 的夹角为钝角．( ) 答案：(1)√ (2)√ (3)× (4)× (5)× (6)×(2018·高考全国卷Ⅱ)已知向量a ，b 满足|a|＝1，a·b ＝－1，则a·(2a －b )＝( ) A ．4 B ．3 C ．2D ．0解析：选B.a ·(2a －b )＝2a 2－a ·b ＝2－(－1)＝3，故选B.已知a ·b ＝－122，|a |＝4，a 和b 的夹角为135°，则|b |为( ) A ．12 B ．6 C ．3 3D ．3解析：选B.a ·b ＝|a ||b |cos 135°＝－122，所以|b |＝－1224×⎝⎛⎭⎫－22＝6.(2018·高考北京卷)设向量a ＝(1，0)，b ＝(－1，m )．若a ⊥(m a －b )，则m ＝____________． 解析：由题意得，m a －b ＝(m ＋1，－m )，根据向量垂直的充要条件可得1×(m ＋1)＋0×(－m )＝0，所以m ＝－1.答案：－1已知向量a ，b 满足(a ＋2b )·(5a －4b )＝0，且|a |＝|b |＝1，则a 与b 的夹角θ为________． 解析：因为(a ＋2b )·(5a －4b )＝0，|a |＝|b |＝1，所以6a ·b －8＋5＝0，即a ·b ＝12.又a ·b ＝|a ||b |cos θ＝cos θ，所以cos θ＝12.因为θ∈[0，π]，所以θ＝π3.答案：π3平面向量数量积的运算(师生共研)(1)(2019·河南漯河高级中学模拟)已知向量a ＝(－2，m )，b ＝(1，2)，若向量a 在向量b 方向上的投影为2，则实数m ＝( )A ．－4B ．－6C ．4D.5＋1(2)(一题多解)(2018·高考天津卷)在如图的平面图形中，已知OM ＝1，ON ＝2，∠MON ＝120°，BM →＝2MA →，CN →＝2NA →，则BC →·OM →的值为( )A ．－15B ．－9C ．－6D ．0【解析】 (1)由题意可得a ·b ＝－2＋2m ，且|b |＝12＋22＝5，则向量a 在向量b 方向上的投影为a ·b |b |＝－2＋2m 5＝2，解得m ＝5＋1.故选D.(2)法一：连接OA .因为BC →＝AC →－AB →＝3AN →－3AM →＝3(ON →－OA →)－3(OM →－OA →)＝3(ON →－OM →)，所以BC →·OM →＝3(ON →－OM →)·OM →＝3(ON →·OM →－|OM →|2)＝3×(2×1×cos 120°－12)＝3×(－2)＝－6.故选C.法二：在△ABC 中，不妨设∠A ＝90°，取特殊情况ON ⊥AC ，以A 为坐标原点，AB ，AC 所在直线分别为x 轴，y 轴建立如图所示的平面直角坐标系，因为∠MON ＝120°，ON ＝2，OM ＝1， 所以O ⎝⎛⎭⎫2，32，C ⎝⎛⎭⎫0，332，M ⎝⎛⎭⎫52，0，B ⎝⎛⎭⎫152，0. 故BC →·OM →＝⎝⎛⎭⎫－152，332·⎝⎛⎭⎫12，－32＝－154－94＝－6.故选C.法三：如图，连接MN .因为BM →＝2MA →，CN →＝2NA →，所以AM AB ＝13＝AN AC ，所以MN ∥BC ，且MN BC ＝13，所以BC →＝3MN →＝3(ON →－OM →)， 所以BC →·OM →＝3(ON →·OM →－OM →2) ＝3(2×1×cos 120°－12)＝－6.故选C. 【答案】 (1)D (2)C计算向量数量积的三个方法(1)定义法：已知向量的模与夹角时，可直接使用数量积的定义求解，即a ·b ＝|a ||b |cos θ(θ是a 与b 的夹角)．(2)基向量法：计算由基底表示的向量的数量积时，应用相应运算律，最终转化为基向量的数量积，进而求解．(3)坐标法：若向量选择坐标形式，则向量的数量积可应用坐标的运算形式进行求解．1．设向量a ＝(－1，2)，b ＝(m ，1)，如果向量a ＋2b 与2a －b 平行，那么a 与b 的数量积等于( )A ．－72B ．－12C ．32D ．52解析：选D.a ＋2b ＝(－1＋2m ，4)，2a －b ＝(－2－m ，3)，由题意得3(－1＋2m )－4(－2－m )＝0，则m ＝－12，所以a ·b ＝－1×⎝⎛⎭⎫－12＋2×1＝52. 2．(一题多解)(2019·云南省第一次统一检测)在▱ABCD 中，|AB →|＝8，|AD →|＝6，N 为DC 的中点，BM →＝2MC →，则AM →·NM →＝( )A ．48B ．36C ．24D ．12解析：选C.法一：AM →·NM →＝(AB →＋BM →)·(NC →＋CM →)＝⎝⎛⎭⎫AB →＋23AD →·⎝⎛⎭⎫12AB →－13AD →＝12AB →2－29AD →2＝12×82－29×62＝24. 法二(特例图形)：若▱ABCD 为矩形，建立如图所示坐标系，则N (4，6)，M (8，4)．所以AM →＝(8，4)，NM →＝(4，－2)， 所以AM →·NM →＝(8，4)·(4，－2)＝32－8＝24.3．已知锐角三角形ABC ，|AB →|＝|AC →|＝2，BD →＝2CD →，则AD →·BC →的取值范围是________． 解析：因为BD →＝2CD →，所以AD →－AB →＝2(AD →－AC →)，则AD →＝2AC →－AB →， 于是AD →·BC →＝(2AC →－AB →)·(AC →－AB →)＝2AC →2＋AB →2－3AC →·AB →，即AD →·BC →＝2×4＋4－3×4cos θ＝12(1－cos θ)(θ为AB →，AC →的夹角)， 因为△ABC 是锐角三角形，所以θ∈⎝⎛⎭⎫0，π2，于是12(1－cos θ)∈(0，12)，即AD →·BC →的取值范围是(0，12)． 答案：(0，12)平面向量数量积的应用(多维探究) 角度一 求两平面向量的夹角(1)设向量a ＝(3，1)，b ＝(x ，－3)，且a ⊥b ，则向量a －b 与a 的夹角为( )A ．30°B ．60°C ．120°D ．150°(2)(2019·成都市第二次诊断性检测)已知平面向量a ，b 的夹角为π3，且|a |＝1，|b |＝12，则a ＋2b 与b 的夹角是( )A.π6 B.5π6 C.π4D.3π4【解析】 (1)因为向量a ＝(3，1)，b ＝(x ，－3)，且a ⊥b ， 所以3x －3＝0，解得x ＝3，所以a －b ＝(3，1)－(3，－3)＝(0，4)， 所以|a －b |＝4.又|a |＝2，所以(a －b )·a ＝|a |2＝4， 设向量a －b 与a 的夹角为θ， 则cos θ＝（a －b ）·a |a －b ||a |＝44×2＝12.因为0°≤θ≤180°，所以θ＝60°.故选B.(2)因为|a ＋2b |2＝|a |2＋4|b |2＋4a ·b ＝1＋1＋4×1×12×cos π3＝3，所以|a ＋2b |＝3，又(a＋2b )·b ＝a ·b ＋2|b |2＝1×12×cos π3＋2×14＝14＋12＝34，所以cos 〈a ＋2b ，b 〉＝（a ＋2b ）·b |a ＋2b ||b |＝343×12＝32， 又〈a ＋2b ，b 〉∈[0，π]， 所以a ＋2b 与b 的夹角为π6.【答案】 (1)B (2)A 角度二 求平面向量的模已知平面向量a ，b 的夹角为π6，且|a |＝3，|b |＝2，在△ABC 中，AB →＝2a ＋2b ，AC →＝2a －6b ，D 为BC 中点，则|AD →|等于( )A ．2B ．4C ．6D ．8【解析】 因为AD →＝12(AB →＋AC →)＝12(2a ＋2b ＋2a －6b )＝2a －2b ，所以|AD →|2＝4(a －b )2＝4(a 2－2b ·a ＋b 2)＝4×⎝⎛⎭⎫3－2×2×3×cos π6＋4＝4，则|AD →|＝2.【答案】 A角度三 两平面向量垂直问题已知向量AB →与AC →的夹角为120°，且|AB →|＝3，|AC →|＝2.若AP →＝λAB →＋AC →，且AP→⊥BC →，则实数λ的值为________．【解析】 因为AP →⊥BC →，所以AP →·BC →＝0. 又AP →＝λAB →＋AC →，BC →＝AC →－AB →， 所以(λAB →＋AC →)·(AC →－AB →)＝0， 即(λ－1)AC →·AB →－λAB →2＋AC →2＝0，所以(λ－1)|AC →||AB →|cos 120°－9λ＋4＝0. 所以(λ－1)×3×2×(－12)－9λ＋4＝0.解得λ＝712.【答案】712平面向量数量积求解问题的策略(1)求两向量的夹角：cos θ＝a ·b|a ||b |，要注意θ∈[0，π]．(2)两向量垂直的应用：两非零向量垂直的充要条件是：a ⊥b ⇔a ·b ＝0⇔|a －b |＝|a ＋b |. (3)求向量的模：利用数量积求解长度问题的处理方法有： ①a 2＝a ·a ＝|a |2或|a |＝a ·a ；②|a ±b |＝（a ±b ）2＝a 2±2a ·b ＋b 2； ③若a ＝(x ，y )，则|a |＝x 2＋y 2.1．已知向量a ，b 满足|a |＝1，|b |＝2，a －b ＝(3，2)，则|a ＋2b |＝( ) A ．2 2 B ．2 5 C.17D.15解析：选C.因为a －b ＝(3，2)，所以|a －b |＝5，所以|a －b |2＝|a |2－2a ·b ＋|b |2＝5－2a ·b ＝5，则a ·b ＝0，所以|a ＋2b |2＝|a |2＋4a ·b ＋4|b |2＝17，所以|a ＋2b |＝17.故选C.2．已知在四边形ABCD 中，AB →＋CD →＝0，(AB →－AD →)·AC →＝0，则四边形ABCD 是( ) A ．矩形 B ．正方形 C ．菱形D ．梯形解析：选C.因为AB →＋CD →＝0，所以AB →＝－CD →＝DC →，所以四边形ABCD 是平行四边形．又(AB →－AD →)·AC →＝DB →·AC →＝0，所以四边形的对角线互相垂直，所以四边形ABCD 是菱形．3．(一题多解)(2019·益阳、湘潭调研)已知向量a ，b 满足|a |＝1，|b |＝2，a ＋b ＝(1，3)，记向量a ，b 的夹角为θ，则tan θ＝________．解析：法一：因为|a |＝1，|b |＝2，a ＋b ＝(1，3)，所以(a ＋b )2＝|a |2＋|b |2＋2a ·b ＝5＋2a ·b ＝1＋3，所以a ·b ＝－12，所以cos θ＝a ·b |a |·|b |＝－14，又θ∈[0，π]，所以sin θ＝1－⎝⎛⎭⎫－142＝154，所以tan θ＝sin θcos θ＝－15. 法二：因为a ＋b ＝(1，3)，所以|a ＋b |＝1＋3＝2，记OA →＝a ，AB →＝b ，则OB →＝a ＋b ，由题意知|AB →|＝|OB →|＝2，|OA →|＝1，θ＝π－∠OAB ，所以在等腰三角形OBA 中，tan ∠OAB＝22－⎝⎛⎭⎫12212＝15，所以tan θ＝－tan ∠OAB ＝－15. 答案：－15向量数量积的综合应用(师生共研)(2017·高考江苏卷)已知向量a ＝(cos x ，sin x )，b ＝(3，－3)，x ∈[0，π]． (1)若a ∥b ，求x 的值；(2)记f (x )＝a·b ，求f (x )的最大值和最小值以及对应的x 的值． 【解】 (1)因为a ＝(cos x ，sin x )，b ＝(3，－3)，a ∥b ， 所以－3cos x ＝3sin x .若cos x ＝0，则sin x ＝0，与sin 2x ＋cos 2x ＝1矛盾，故cos x ≠0. 于是tan x ＝－33. 又x ∈[0，π]，所以x ＝5π6.(2)f (x )＝a ·b ＝(cos x ，sin x )·(3，－3)＝3cos x －3sin x ＝23cos ⎝⎛⎭⎫x ＋π6.因为x ∈[0，π]，所以x ＋π6∈⎣⎡⎦⎤π6，7π6，从而－1≤cos ⎝⎛⎭⎫x ＋π6≤32.于是，当x ＋π6＝π6，即x ＝0时，f (x )取到最大值3；当x ＋π6＝π，即x ＝5π6时，f (x )取到最小值－2 3.平面向量与三角函数的综合问题(1)题目条件给出的向量坐标中含有三角函数的形式，运用向量共线或垂直或等式成立等，得到三角函数的关系式，然后求解．(2)给出用三角函数表示的向量坐标，要求的是向量的模或者其他向量的表达形式，解题思路是经过向量的运算，利用三角函数在定义域内的有界性，求得值域等．1．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，已知向量m ＝⎝⎛⎭⎫sin A 2，cos A 2，n ＝⎝⎛⎭⎫cos A 2，－cos A 2，且2m ·n ＋|m |＝22，则∠A ＝________． 解析：因为2m ·n ＝2sin A 2cos A 2－2cos 2 A 2＝sin A －(cos A ＋1)＝2sin ⎝⎛⎭⎫A －π4－1，又|m |＝1，所以2m ·n ＋|m |＝2sin ⎝⎛⎭⎫A －π4＝22， 即sin ⎝⎛⎭⎫A －π4＝12. 因为0<A <π，所以－π4<A －π4<3π4，所以A －π4＝π6，即A ＝5π12.答案：5π122．(2019·山东模拟)在△ABC 中，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，已知向量m ＝(cos B ，2cos 2 C2－1)，n ＝(c ，b －2a )，且m·n ＝0.(1)求∠C 的大小；(2)若点D 为边AB 上一点，且满足AD →＝DB →，|CD →|＝7，c ＝23，求△ABC 的面积． 解：(1)因为m ＝(cos B ，cos C )，n ＝(c ，b －2a )，m ·n ＝0， 所以c cos B ＋(b －2a )cos C ＝0，在△ABC 中，由正弦定理得 sin C cos B ＋(sin B －2sin A )cos C ＝0， sin A ＝2sin A cos C ，又sin A ≠0，所以cos C ＝12，而C ∈(0，π)，所以∠C ＝π3.(2)由AD →＝DB →知，CD →－CA →＝CB →－CD →，所以2CD →＝CA →＋CB →， 两边平方得4|CD →|2＝b 2＋a 2＋2ba cos ∠ACB ＝b 2＋a 2＋ba ＝28.① 又c 2＝a 2＋b 2－2ab cos ∠ACB ，所以a 2＋b 2－ab ＝12.② 由①②得ab ＝8，所以S △ABC ＝12ab sin ∠ACB ＝2 3.函数思想与数形结合思想在数量积中的应用(2018·高考浙江卷)已知a ，b ，e 是平面向量，e 是单位向量．若非零向量a 与e的夹角为π3，向量b 满足b 2－4e·b ＋3＝0，则|a －b |的最小值是( )A ．3－1B ．3＋1C ．2D ．2－ 3【解析】 法一：设O 为坐标原点，a ＝OA →，b ＝OB →＝(x ，y )，e ＝(1，0)，由b 2－4e ·b ＋3＝0得x 2＋y 2－4x ＋3＝0，即(x －2)2＋y 2＝1，所以点B 的轨迹是以C (2，0)为圆心，1为半径的圆．因为a 与e 的夹角为π3，所以不妨令点A 在射线y ＝3x (x >0)上，如图，数形结合可知|a －b |min ＝|CA →|－|CB →|＝3－1.故选A.法二：由b 2－4e·b ＋3＝0得b 2－4e·b ＋3e 2＝(b －e )·(b －3e )＝0.设b ＝OB →，e ＝OE →，3e ＝OF →，所以b －e ＝EB →，b －3e ＝FB →，所以EB →·FB →＝0，取EF 的中点为C ，则B 在以C 为圆心，EF 为直径的圆上，如图．设a ＝OA →，作射线OA ，使得∠AOE ＝π3，所以|a －b |＝|(a －2e )＋(2e －b )|≥|a －2e |－|2e －b |＝|CA →|－|BC →|≥3－1.故选A.【答案】 A求向量的夹角与模的范围问题经常应用函数思想与数形结合思想．模的最值问题多采用将其表示为某一变量或某两个变量的函数，利用求函数值域的方法确定最值，体现了函数思想的运用，又多与二次函数、基本不等式相联系；求向量夹角的范围问题，根据条件，利用向量的线性运算的几何意义，依据图形通过数形结合确定夹角的范围．(2019·河南郑州模拟)已知平面向量a ，b ，c 满足|a |＝|b |＝|c |＝1，若a ·b ＝12，则(a ＋b )·(2b－c )的最小值为( )A ．－2B ．3－ 3C ．－1D ．0解析：选B.由|a |＝|b |＝1，a ·b ＝12，可得〈a ，b 〉＝π3，令OA →＝a ，OB →＝b ，以OA →的方向为x 轴的正方向建立如图所示的平面直角坐标系，则a ＝OA →＝(1，0)，b ＝OB →＝⎝⎛⎭⎫12，32，设c ＝OC →＝(cos θ，sin θ)(0≤θ＜2π)，则(a ＋b )·(2b －c )＝2a ·b －a ·c ＋2b 2－b ·c ＝3－(cosθ＋12cos θ＋32sin θ)＝3－3sin ⎝⎛⎭⎫θ＋π3，则(a ＋b )·(2b －c )的最小值为3－3，故选B.[基础题组练]1．已知向量a ＝(1，1)，b ＝(0，2)，则下列结论正确的是( ) A ．a ∥b B ．(2a －b )⊥b C ．|a |＝|b |D ．a ·b ＝3解析：选B.对于A ，1×2－0×1≠0，错误；对于B ，2a －b ＝(2，0)，b ＝(0，2)，则2×0＋0×2＝0，所以(2a －b )⊥b ，正确；对于C ，|a |＝2，|b |＝2，错误；对于D ，a ·b ＝1×0＋1×2＝2，错误．2．设a ＝(1，2)，b ＝(1，1)，c ＝a ＋k b .若b ⊥c ，则实数k 的值等于( ) A ．－32B ．－53C.53D.32解析：选A.c ＝a ＋k b ＝(1，2)＋k (1，1)＝(1＋k ，2＋k )，因为b ⊥c ，所以b ·c ＝0，b ·c ＝(1，1)·(1＋k ，2＋k )＝1＋k ＋2＋k ＝3＋2k ＝0，所以k ＝－32.3．已知向量a ＝(1，2)，b ＝(2，－3)．若向量c 满足(c ＋a )∥b ，c ⊥(a ＋b )，则c ＝( ) A.⎝⎛⎭⎫79，73 B.⎝⎛⎭⎫－73，－79 C.⎝⎛⎭⎫73，79D.⎝⎛⎭⎫－79，－73 解析：选D.设c ＝(m ，n )，则a ＋c ＝(1＋m ，2＋n )，a ＋b ＝(3，－1)，因为(c ＋a )∥b ，则有－3(1＋m )＝2(2＋n )；又c ⊥(a ＋b )，则有3m －n ＝0，解得m ＝－79，n ＝－73.所以c ＝⎝⎛⎭⎫－79，－73.4．已知向量a ，b 满足|a |＝1，(a ＋b )·(a －2b )＝0，则|b |的取值范围为( ) A ．[1，2] B ．[2，4] C.⎣⎡⎦⎤14，12D.⎣⎡⎦⎤12，1解析：选D.由题意知b ≠0，设向量a ，b 的夹角为θ，因为(a ＋b )·(a －2b )＝a 2－a ·b －2b 2＝0，又|a |＝1，所以1－|b |cos θ－2|b |2＝0，所以|b |cos θ＝1－2|b |2，因为－1≤cos θ≤1，所以－|b |≤1－2|b |2≤|b |，所以12≤|b |≤1，所以|b |的取值范围是⎣⎡⎦⎤12，1. 5．若单位向量e 1，e 2的夹角为π3，向量a ＝e 1＋λe 2(λ∈R )，且|a |＝32，则λ＝________．解析：由题意可得e 1·e 2＝12，|a |2＝(e 1＋λe 2)2＝1＋2λ×12＋λ2＝34，化简得λ2＋λ＋14＝0，解得λ＝－12.答案：－126．(2019·江西七校联考)已知向量a ＝(1，3)，b ＝(3，m )，且b 在a 上的投影为－3，则向量a 与b 的夹角为________．解析：因为b 在a 上的投影为－3，所以|b |cos 〈a ，b 〉＝－3，又|a |＝12＋（3）2＝2，所以a ·b ＝|a ||b |cos 〈a ，b 〉＝－6，又a ·b ＝1×3＋3m ，所以3＋3m ＝－6，解得m ＝－33，则b ＝(3，－33)，所以|b |＝32＋（－33）2＝6，所以cos 〈a ，b 〉＝a ·b |a ||b |＝－62×6＝－12，因为0≤〈a ，b 〉≤π，所以a 与b 的夹角为2π3.答案：2π37．已知向量a ＝(2，－1)，b ＝(1，x )． (1)若a ⊥(a ＋b )，求|b |的值；(2)若a ＋2b ＝(4，－7)，求向量a 与b 夹角的大小． 解：(1)由题意得a ＋b ＝(3，－1＋x )． 由a ⊥(a ＋b )，可得6＋1－x ＝0， 解得x ＝7，即b ＝(1，7)， 所以|b |＝50＝5 2.(2)由题意得，a ＋2b ＝(4，2x －1)＝(4，－7)， 故x ＝－3，所以b ＝(1，－3)，所以cos 〈a ，b 〉＝a ·b |a ||b |＝（2，－1）·（1，－3）5×10＝22，因为〈a ，b 〉∈[0，π]， 所以a 与b 夹角是π4.8．已知|a |＝4，|b |＝3，(2a －3b )·(2a ＋b )＝61. (1)求a 与b 的夹角θ； (2)求|a ＋b |；(3)若AB →＝a ，BC →＝b ，求△ABC 的面积． 解：(1)因为(2a －3b )·(2a ＋b )＝61， 所以4|a |2－4a ·b －3|b |2＝61. 又|a |＝4，|b |＝3， 所以64－4a ·b －27＝61， 所以a ·b ＝－6，所以cos θ＝a ·b |a ||b |＝－64×3＝－12.又0≤θ≤π，所以θ＝2π3.(2)|a ＋b |2＝(a ＋b )2 ＝|a |2＋2a ·b ＋|b |2＝42＋2×(－6)＋32＝13，所以|a ＋b |＝13. (3)因为AB →与BC →的夹角θ＝2π3，所以∠ABC ＝π－2π3＝π3.又|AB →|＝|a |＝4，|BC →|＝|b |＝3， 所以S △ABC ＝12×4×3×32＝3 3.[综合题组练]1．(2019·郑州质量预测)在矩形ABCD 中，AB ＝3，BC ＝3，BE →＝2EC →，点F 在边CD 上．若AB →·AF →＝3，则AE →·BF →的值为( )A ．0 B.833C ．－4D ．4解析：选C.BE →＝2EC →⇒|BE →|＝23|BC →|＝233.设AB →与AF →的夹角为α，AB →·AF →＝3⇒|AF →|cos α＝1⇒|DF →|＝1.以A 为坐标原点建立平面直角坐标系，AD 为x 轴，AB 为y 轴，则B (0，3)，F (3，1)，E ⎝⎛⎭⎫233，3.因此BF →＝(3，－2)，AE →·BF →＝233×3－2×3＝2－6＝－4，故选C.2．(2019·陕西质检(一))已知P 为△ABC 所在平面内一点，AB →＋PB →＋PC →＝0，|AB →|＝|PB →|＝|PC →|＝2，则△ABC 的面积等于( )A. 3 B ．2 3 C ．3 3D ．4 3解析：选B. 由|PB →|＝|PC →|得，△PBC 是等腰三角形，取BC 的中点D ，连接PD ，则PD ⊥BC ，又AB →＋PB →＋PC →＝0，所以AB →＝－(PB →＋PC →)＝－2PD →，所以PD ＝12AB ＝1，且PD ∥AB ，故AB ⊥BC ，即△ABC 是直角三角形，由|PB →|＝2，|PD →|＝1可得|BD →|＝3，则|BC →|＝23，所以△ABC 的面积为12×2×23＝2 3.3．(2019·武汉市武昌区调研考试)在矩形ABCD 中，AB ＝2，AD ＝1.边DC 上的动点P (包含点D ，C )与CB 延长线上的动点Q (包含点B )满足|DP →|＝|BQ →|，则P A →·PQ →的最小值为________．解析：以点A 为坐标原点，分别以AB ，AD 所在直线为x 轴，y 轴建立如图所示的平面直角坐标系，设P (x ，1)，Q (2，y )，由题意知0≤x ≤2，－2≤y ≤0. 因为|DP →|＝|BQ →|，所以|x |＝|y |，所以x ＝－y . 因为P A →＝(－x ，－1)，PQ →＝(2－x ，y －1)， 所以P A →·PQ →＝－x (2－x )－(y －1) ＝x 2－2x －y ＋1 ＝x 2－x ＋1 ＝⎝⎛⎭⎫x －122＋34， 所以当x ＝12时，P A →·PQ →取得最小值，为34.答案：344．已知向量a ，b 满足|a |＝1，|b |＝2，若对任意的单位向量e ，均有|a ·e |＋|b ·e |≤6，则a ·b 的最大值是________．解析：由题意得，|(a ＋b )·e |≤|a ·e |＋|b ·e |≤6，所以|a ＋b |≤6，所以|a |2＋|b |2＋2a ·b ≤6，所以a ·b ≤12，即a ·b 的最大值是12.答案：125．在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，向量m ＝(cos(A －B )，sin(A －B ))，n ＝(cos B ，－sin B )，且m·n ＝－35.(1)求sin A 的值；(2)若a ＝42，b ＝5，求角B 的大小及向量BA →在BC →方向上的投影． 解：(1)由m·n ＝－35，得cos(A －B )cos B －sin(A －B )sin B ＝－35，所以cos A ＝－35.因为0<A <π，所以sin A ＝1－cos 2A ＝1－⎝⎛⎭⎫－352＝45. (2)由正弦定理a sin A ＝b sin B ，得sin B ＝b sin A a ＝5×4542＝22，因为a >b ，所以A >B ，则B＝π4，由余弦定理得()422＝52＋c 2－2×5c ×⎝⎛⎭⎫－35，解得c ＝1. 故向量BA →在BC →方向上的投影为 |BA →|cos B ＝c cos B ＝1×22＝22.6.在如图所示的平面直角坐标系中，已知点A (1，0)和点B (－1，0)，|OC →|＝1，且∠AOC ＝θ，其中O 为坐标原点．(1)若θ＝34π，设点D 为线段OA 上的动点，求|OC →＋OD →|的最小值；(2)若θ∈⎣⎡⎦⎤0，π2，向量m ＝BC →，n ＝(1－cos θ，sin θ－2cos θ)，求m ·n 的最小值及对应的θ值．解：(1)设D (t ，0)(0≤t ≤1)， 由题意知C ⎝⎛⎭⎫－22，22， 所以OC →＋OD →＝⎝⎛⎭⎫－22＋t ，22，所以|OC →＋OD →|2＝12－2t ＋t 2＋12＝t 2－2t ＋1＝⎝⎛⎭⎫t －222＋12， 所以当t ＝22时，|OC →＋OD →|有最小值，为22. (2)由题意得C (cos θ，sin θ)，m ＝BC →＝(cos θ＋1，sin θ)，则m ·n ＝1－cos 2θ＋sin 2θ－2sin θcos θ＝1－cos 2θ－sin 2θ＝1－2sin ⎝⎛⎭⎫2θ＋π4， 因为θ∈⎣⎡⎦⎤0，π2，所以π4≤2θ＋π4≤5π4， 所以当2θ＋π4＝π2，即θ＝π8时，sin ⎝⎛⎭⎫2θ＋π4取得最大值1. 所以当θ＝π8时，m ·n 取得最小值为1－ 2.。