2014年高三一模填选难题解析(1)(普陀、长宁、嘉定、静安、闸北、宝山)

2014年上海市嘉定区高考数学一模试卷（理科）一、填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1．（4分）函数y＝log2（x﹣2）的定义域是．2．（4分）已知i是虚数单位，复数z满足，则|z|＝．3．（4分）已知函数y＝f（x）存在反函数y＝f﹣1（x），若函数y＝f（x﹣1）的图象经过点（3，1），则f﹣1（1）的值是．4．（4分）已知数列{a n}的前n项和S n＝n2（n∈N*），则a8的值是．5．（4分）已知圆锥的母线长为5cm，侧面积为20πcm2，则此圆锥的体积为cm3．6．（4分）已知θ为第二象限角，，则＝．7．（4分）已知双曲线（a＞0，b＞0）满足，且双曲线的右焦点与抛物线的焦点重合，则该双曲线的方程为．8．（4分）分别从集合A＝{1，2，3，4}和集合B＝{5，6，7，8}中各取一个数，则这两数之积为偶数的概率是．9．（4分）在平面直角坐标系中，△ABC的顶点坐标分别为A（1，2），B（﹣7，3），点C在直线y＝4上运动，O为坐标原点，G为△ABC的重心，则的最小值为．10．（4分）若存在，则实数r的取值范围是．11．（4分）在平面直角坐标系中，动点P到两条直线3x﹣y＝0与x+3y＝0的距离之和等于4，则P到原点距离的最小值为．12．（4分）设集合A＝{（x，y）|（x﹣4）2+y2＝1}，B＝{（x，y）|（x﹣t）2+（y﹣at+2）2＝1}，如果命题“∃t∈R，A∩B≠∅”是真命题，则实数a的取值范围是．13．（4分）已知函数是偶函数，直线y＝t与函数f （x）的图象自左至右依次交于四个不同点A、B、C、D，若|AB|＝|BC|，则实数t的值为．14．（4分）某种平面分形图如图所示，一级分形图是一个边长为1的等边三角形（图（1））；二级分形图是将一级分形图的每条线段三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边（图（2））；将二级分形图的每条线段三等边，重复上述的作图方法，得到三级分形图（图（3））；…；重复上述作图方法，依次得到四级、五级、…、n级分形图．则n级分形图的周长为．二、选择题（本大题共有4题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，每题选对得5分，否则一律得零分．15．（5分）设向量，，则“∥”是“x＝2”的（）A．充分非必要条件B．必要非充分条件C．充分必要条件D．既非充分又非必要条件16．（5分）若展开式中只有第六项的二项式系数最大，则展开式中的常数项是（）A．180B．120C．90D．4517．（5分）将函数y＝sin2x（x∈R）的图象分别向左平移m（m＞0）个单位，向右平移n（n＞0）个单位，所得到的两个图象都与函数的图象重合，则m+n的最小值为（）A．B．C．πD．18．（5分）设函数f（x）的定义域为D，若存在闭区间[a，b]⊆D，使得函数f （x）满足：①f（x）在[a，b]上是单调函数；②f（x）在[a，b]上的值域是[2a，2b]，则称区间[a，b]是函数f（x）的“和谐区间”．下列结论错误的是（）A．函数f（x）＝x2（x≥0）存在“和谐区间”B．函数f（x）＝e x（x∈R）不存在“和谐区间”C．函数（x≥0）存在“和谐区间”D．函数（a＞0，a≠1）不存在“和谐区间”三、解答题（本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.）19．（12分）如图，正三棱锥A﹣BCD的底面边长为2，侧棱长为3，E为棱BC 的中点．（1）求异面直线AE与CD所成角的大小（结果用反三角函数值表示）；（2）求该三棱锥的体积V．20．（14分）已知函数f（x）＝2sin x cos x+2，x∈R．（1）求函数f（x）的最小正周期和单调递增区间；（2）在锐角三角形ABC中，若f（A）＝1，，求△ABC的面积．21．（14分）已知椭圆C的中心在原点，焦点在x轴上，长轴长为4，且点在椭圆C上．（1）求椭圆C的方程；（2）设P是椭圆C长轴上的一个动点，过P作方向向量的直线l交椭圆C于A、B两点，求证：|P A|2+|PB|2为定值．22．（16分）已知函数（m为实常数）．（1）若函数y＝f（x）图象上动点P到定点Q（0，2）的距离的最小值为，求实数m的值；（2）若函数y＝f（x）在区间[2，+∞）上是增函数，试用函数单调性的定义求实数m的取值范围；（3）设m＜0，若不等式f（x）≤kx在有解，求k的取值范围．23．（18分）数列{a n}的首项为a（a≠0），前n项和为S n，且S n+1＝t•S n+a（t≠0）．设b n＝S n+1，c n＝k+b1+b2+…+b n（k∈R+）．（1）求数列{a n}的通项公式；（2）当t＝1时，若对任意n∈N*，|b n|≥|b3|恒成立，求a的取值范围；（3）当t≠1时，试求三个正数a，t，k的一组值，使得{c n}为等比数列，且a，t，k成等差数列．2014年上海市嘉定区高考数学一模试卷（理科）参考答案与试题解析一、填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1．（4分）函数y＝log2（x﹣2）的定义域是（2，+∞）．【解答】解：要使函数有意义，则x﹣2＞0，即x＞2，∴函数的定义域为（2，+∞），故答案为：（2，+∞）．2．（4分）已知i是虚数单位，复数z满足，则|z|＝．【解答】解：∵复数z满足，∴z＝，化为4z＝，即z＝，∴|z|＝＝．故答案为：．3．（4分）已知函数y＝f（x）存在反函数y＝f﹣1（x），若函数y＝f（x﹣1）的图象经过点（3，1），则f﹣1（1）的值是2．【解答】解析：若函数y＝f（x﹣1）的图象经过点（3，1），则有1＝f（3﹣1）⇒f（2）＝1⇒f﹣1（1）＝2．故答案为：2．4．（4分）已知数列{a n}的前n项和S n＝n2（n∈N*），则a8的值是15．【解答】解：∵数列{a n}的前n项和，∴a8＝S8﹣S7＝64﹣49＝15．故答案为：15．5．（4分）已知圆锥的母线长为5cm，侧面积为20πcm2，则此圆锥的体积为16πcm3．【解答】解：∵圆锥的母线长是5cm，侧面积是20πcm2，设圆锥的半径为r，∴有πr×5＝20π⇒r＝4，∴圆锥的高为＝3，∴圆锥的体积为×π×r2×3＝16πcm3．故答案：16πcm3．6．（4分）已知θ为第二象限角，，则＝﹣．【解答】解：∵θ为第二象限角，且sinθ＝，∴cosθ＝﹣＝﹣，∴tanθ＝﹣，则原式＝＝＝﹣．故答案为：﹣7．（4分）已知双曲线（a＞0，b＞0）满足，且双曲线的右焦点与抛物线的焦点重合，则该双曲线的方程为．【解答】解：由，可得，∴∵双曲线的右焦点与抛物线的焦点重合，∴c＝，∵c2＝a2+b2，∴a＝1，b＝，∴双曲线的方程为．故答案为：．8．（4分）分别从集合A＝{1，2，3，4}和集合B＝{5，6，7，8}中各取一个数，则这两数之积为偶数的概率是．【解答】解：从集合A＝{1，2，3，4}和集合B＝{5，6，7，8}中各取一个数，基本事件共有4×4＝16个，∵两数之积为偶数，∴两数中至少有一个是偶数，A中取偶数，B中有4种取法；A中取奇数，B中必须取偶数，故基本事件共有2×4+2×2＝12个，∴两数之积为偶数的概率是＝．故答案为：．9．（4分）在平面直角坐标系中，△ABC的顶点坐标分别为A（1，2），B（﹣7，3），点C在直线y＝4上运动，O为坐标原点，G为△ABC的重心，则的最小值为9．【解答】解：设C（x，4），由重心定理可得，∴．∴＝＝＝，当x＝3时，的最小值为9．故答案为：9．10．（4分）若存在，则实数r的取值范围是．【解答】解：∵存在，∴0＜，∴3r2+4r+1≥0且2r+1≠0，r≠0，∴r≤﹣1或r≥﹣．故答案为：．11．（4分）在平面直角坐标系中，动点P到两条直线3x﹣y＝0与x+3y＝0的距离之和等于4，则P到原点距离的最小值为2．【解答】解：∵3x﹣y＝0与x+3y＝0的互相垂直，且交点为原点，∴设P到直线的距离分别为a，b，则a≥0，b≥0，则a+b＝4，即b＝4﹣a≥0，得0≤a≤4，由勾股定理可知OP＝＝＝，∵0≤a≤4，∴当a＝2时，OP的距离最小为OP＝＝，故答案为：．12．（4分）设集合A＝{（x，y）|（x﹣4）2+y2＝1}，B＝{（x，y）|（x﹣t）2+（y﹣at+2）2＝1}，如果命题“∃t∈R，A∩B≠∅”是真命题，则实数a的取值范围是．【解答】解：∵A＝{（x，y）|（x﹣4）2+y2＝1}，表示平面坐标系中以M（4，0）为圆心，半径为1的圆，B＝{（x，y）|（x﹣t）2+（y﹣at+2）2＝1}，表示以N（t，at﹣2）为圆心，半径为1的圆，且其圆心N在直线ax﹣y﹣2＝0上，如图．如果命题“∃t∈R，A∩B≠∅”是真命题，即两圆有公共点，则圆心M到直线ax﹣y﹣2＝0的距离不大于2，即，解得0≤a≤．∴实数a的取值范围是；故答案为：．13．（4分）已知函数是偶函数，直线y＝t与函数f （x）的图象自左至右依次交于四个不同点A、B、C、D，若|AB|＝|BC|，则实数t的值为．【解答】解：∵函数f（x）是偶函数，∴f（﹣x）＝f（x），当x＜0时，﹣x＞0，即f（﹣x）＝ax2﹣2x+1＝﹣x2+bx+c，∴a＝﹣1，b＝﹣2，c＝1，即f（x）＝，作出函数f（x）的图象如图：直线y＝t与函数f（x）的图象自左至右依次交于四个不同点A、B、C、D，不妨是对应的横坐标分别为a，b，c，d，则A，B关于x＝﹣1对称，即，①∵函数是偶函数，∴c＝﹣b，d＝﹣a，若|AB|＝|BC|，则B是A，C的中点，∴，②，解得a＝3b，代入①解得b＝，a＝，当b＝，时f（b）＝f（）＝﹣（）2﹣2（）+1＝2＝，即t＝，故答案为：．14．（4分）某种平面分形图如图所示，一级分形图是一个边长为1的等边三角形（图（1））；二级分形图是将一级分形图的每条线段三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边（图（2））；将二级分形图的每条线段三等边，重复上述的作图方法，得到三级分形图（图（3））；…；重复上述作图方法，依次得到四级、五级、…、n级分形图．则n级分形图的周长为．【解答】解：第一个三角形的周长＝1+1+1＝3，观察发现：第二个图形在第一个图形的周长的基础上多了它的周长的，第三个在第二个的基础上，多了其周长的．第二个周长：3×（1+）＝3×＝4，第三个周长：3×（1+）×＝3××＝3•（）2第四个周长：3×××＝3•（）3，…故第n个图形的周长是第一个周长的•（）n﹣1倍，即周长是3•（）n﹣1．故答案为：．二、选择题（本大题共有4题，满分20分）每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，每题选对得5分，否则一律得零分．15．（5分）设向量，，则“∥”是“x＝2”的（）A．充分非必要条件B．必要非充分条件C．充分必要条件D．既非充分又非必要条件【解答】解：∵向量，，∴若∥，则（x﹣1）（x+1）﹣3＝x2﹣4＝0，即x＝±2，∴“∥”是“x＝2”的必要不充分条件．故选：B．16．（5分）若展开式中只有第六项的二项式系数最大，则展开式中的常数项是（）A．180B．120C．90D．45【解答】解：由题意可得只有第六项的二项式系数最大，∴n＝10．故展开式的通项公式为T r+1＝••2r•x﹣2r＝2r••，令＝0，求得r＝2，故展开式中的常数项是22＝180，故选：A．17．（5分）将函数y＝sin2x（x∈R）的图象分别向左平移m（m＞0）个单位，向右平移n（n＞0）个单位，所得到的两个图象都与函数的图象重合，则m+n的最小值为（）A．B．C．πD．【解答】解：将函数y＝sin2x（x∈R）的图象向左平移m（m＞0）个单位，得函数y＝sin2（x+m）＝sin（2x+2m），∵其图象与的图象重合，∴sin（2x+2m）＝sin（2x+），∴2m＝，故m＝（k∈Z），当k＝0时，m取得最小值为；将函数y＝sin2x（x∈R）的图象向右平移n（n＞0）个单位，得到函数y＝sin2（x ﹣n）＝sin（2x﹣2n），∵其图象与的图象重合，∴sin（2x﹣2n）＝sin（2x+），∴﹣2n＝，故n＝﹣，当k＝﹣1时，n取得最小值为，∴m+n的最小值为π，故选：C．18．（5分）设函数f（x）的定义域为D，若存在闭区间[a，b]⊆D，使得函数f （x）满足：①f（x）在[a，b]上是单调函数；②f（x）在[a，b]上的值域是[2a，2b]，则称区间[a，b]是函数f（x）的“和谐区间”．下列结论错误的是（）A．函数f（x）＝x2（x≥0）存在“和谐区间”B．函数f（x）＝e x（x∈R）不存在“和谐区间”C．函数（x≥0）存在“和谐区间”D．函数（a＞0，a≠1）不存在“和谐区间”【解答】解：函数中存在“倍值区间”，则：①f（x）在[a，b]内是单调函数；②或．A．若f（x）＝x2（x≥0），若存在“倍值区间”[a，b]，则此时函数单调递增，则由，得，∴，∴f（x）＝x2（x≥0）存在“倍值区间”[0，2]，∴A正确．B若f（x）＝e x（x∈R），若存在“倍值区间”[a，b]，则此时函数单调递增，则由，得，即a，b是方程e x＝2x的两个不等的实根，构建函数g（x）＝e x﹣2x，∴g′（x）＝e x﹣2，∴函数在（﹣∞，ln2）上单调减，在（ln2，+∞）上单调增，∴函数在x＝ln2处取得极小值，且为最小值．∵g（ln2）＝2﹣ln2＞0，∴g（x）＞0，∴e x﹣2x＝0无解，故函数不存在“倍值区间”，∴B正确．C．若函数（x≥0），f′（x）＝，若存在“倍值区间”[a，b]⊆[0，1]，则由，得，∴a＝0，b＝1，即存在“倍值区间”[0，1]，∴C正确．D．若函数（a＞0，a≠1）．不妨设a＞1，则函数在定义域内为单调增函数，若存在“倍值区间”[m，n]，则由，得，即m，n是方程log a（a x﹣）＝2x的两个根，即m，n是方程a2x﹣a x+＝0的两个根，由于该方程有两个不等的正根，故存在“倍值区间”[m，n]，∴D结论错误．故选：D．三、解答题（本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.）19．（12分）如图，正三棱锥A﹣BCD的底面边长为2，侧棱长为3，E为棱BC 的中点．（1）求异面直线AE与CD所成角的大小（结果用反三角函数值表示）；（2）求该三棱锥的体积V．【解答】解：（1）取BD中点F，连结AF、EF，因为EF∥CD，所以∠AEF就是异面直线AE与CD所成的角（或其补角）．…（2分）在△AEF中，，EF＝1，…（1分）所以．…（2分）所以，异面直线AE与CD所成的角的大小为．…（1分）（2）作AO⊥平面BCD，则O是正△BCD的中心，…（1分）连结OE，，…（1分）所以，…（1分）所以，．…（2分）20．（14分）已知函数f（x）＝2sin x cos x+2，x∈R．（1）求函数f（x）的最小正周期和单调递增区间；（2）在锐角三角形ABC中，若f（A）＝1，，求△ABC的面积．【解答】解：（1）f（x）＝2sin x cos x+＝sin2x+＝2sin（2x+），∴函数f（x）的最小正周期为π，由2kπ﹣≤2x+≤2kπ+，（k∈Z），得，∴函数f（x）的单调增区间是[k，k]（k∈Z），（2）由已知，f（A）＝2sin（2A+）＝1，∴sin（2A+）＝，∵0＜A＜，∴，∴2A+＝，从而A＝，又∵＝，∴，∴△ABC的面积S＝＝＝．21．（14分）已知椭圆C的中心在原点，焦点在x轴上，长轴长为4，且点在椭圆C上．（1）求椭圆C的方程；（2）设P是椭圆C长轴上的一个动点，过P作方向向量的直线l交椭圆C于A、B两点，求证：|P A|2+|PB|2为定值．【解答】（1）解：∵C的焦点在x轴上且长轴为4，故可设椭圆C的方程为（a＞b＞0），∵点在椭圆C上，∴，解得b2＝1，∴椭圆C的方程为．（2）证明：设P（m，0）（﹣2≤m≤2），∵直线l方向向量，∴直线l的方程是，联立⇒2x2﹣2mx+m2﹣4＝0（*）设A（x1，y1），B（x2，y2），则x1、x2是方程（*）的两个根，∴x1+x2＝m，，∴＝＝＝（定值）．22．（16分）已知函数（m为实常数）．（1）若函数y＝f（x）图象上动点P到定点Q（0，2）的距离的最小值为，求实数m的值；（2）若函数y＝f（x）在区间[2，+∞）上是增函数，试用函数单调性的定义求实数m的取值范围；（3）设m＜0，若不等式f（x）≤kx在有解，求k的取值范围．【解答】解：（1）设P（x，y），则，＝，当m＞0时，解得；当m＜0时，解得，∴或．（2）由题意，任取x1、x2∈[2，+∞），且x1＜x2，则＝＞0，∵x2﹣x1＞0，x1x2＞0，所以x1x2﹣m＞0，即m＜x1x2，由x2＞x1≥2，得x1x2＞4，所以m≤4．∴m的取值范围是（﹣∞，4]；（3）由f（x）≤kx，得，∵，∴，令，则t∈[1，2]，所以k≥mt2+2t+1，令g（t）＝mt2+2t+1，t∈[1，2]，于是，要使原不等式在有解，当且仅当k≥g（t）min（t∈[1，2]）．∵m＜0，∴图象开口向下，对称轴为直线，∵t∈[1，2]，∴当，即时，g（t）min＝g（2）＝4m+5；当，即时，g（t）min＝g（1）＝m+3，综上，当时，k∈[4m+5，+∞）；当时，k∈[m+3，+∞）．23．（18分）数列{a n}的首项为a（a≠0），前n项和为S n，且S n+1＝t•S n+a（t≠0）．设b n＝S n+1，c n＝k+b1+b2+…+b n（k∈R+）．（1）求数列{a n}的通项公式；（2）当t＝1时，若对任意n∈N*，|b n|≥|b3|恒成立，求a的取值范围；（3）当t≠1时，试求三个正数a，t，k的一组值，使得{c n}为等比数列，且a，t，k成等差数列．【解答】解：（1）∵S n+1＝t•S n+a①当n≥2时，S n＝t•S n+a②，﹣1①﹣②得，a n+1＝t•a n（n≥2），又由S2＝t•S1+a，得a2＝t•a1，∴{a n}是首项为a，公比为t的等比数列，∴（n∈N*）；（2）当t＝1时，a n＝a，S n＝na，b n＝na+1，由|b n|≥|b3|，得|na+1|≥|3a+1|，（n﹣3）a[（n+3）a+2]≥0（*）当a＞0时，n＜3时，（*）不成立；当a＜0时，（*）等价于（n﹣3）[（n+3）a+2]≤0（**）n＝3时，（**）成立．n≥4时，有（n+3）a+2≤0，即恒成立，∴．n＝1时，有4a+2≥0，．n＝2时，有5a+2≥0，．综上，a的取值范围是；（3）当t≠1时，，，＝，∴当时，数列{c n}是等比数列，∴，又∵a，t，k成等差数列，∴2t＝a+k，即，解得．从而，，．∴当，，时，数列{c n}为等比数列．。

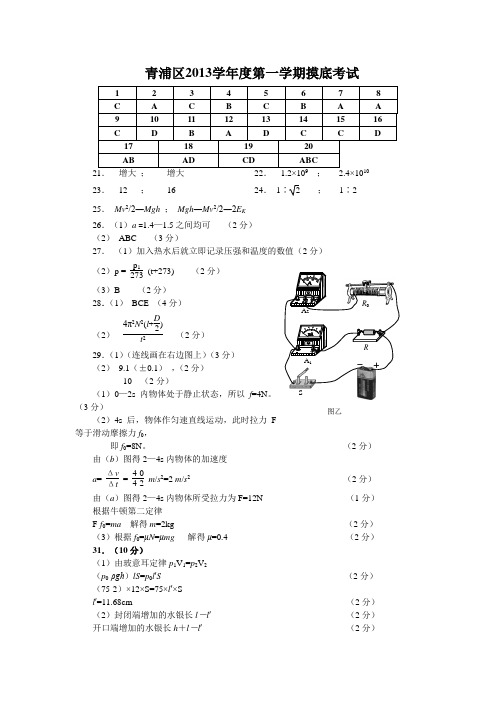
青浦区2013学年度第一学期摸底考试21． 增大 ； 增大 22． 1.2×10 ； 2.4×10 23． 12 ； 16 24． 1∶2 ； 1∶2 25． Mv 2/2―Mgh ； Mgh ―Mv 2/2―2E K26．（1）a =1.4—1.5之间均可 （2分） （2） ABC （3分）27． （1）加入热水后就立即记录压强和温度的数值（2分） （2）p =p 1273(t+273) （2分） （3）B （2分） 28．（1） BCE （4分） （2） 4π2N 2(l +D2)t2（2分） 29．（1）（连线画在右边图上）（3分）（2） 9.1（±0.1） ，（2分）10 （2分）（1）0—2s 内物体处于静止状态，所以f =4N 。

（3分） （2）4s 后，物体作匀速直线运动，此时拉力F 等于滑动摩擦力f 0，即f 0=8N 。

（2分） 由（b ）图得2—4s 内物体的加速度a =Δv Δt= 4-04-2 m /s 2=2 m /s 2 （2分）由（a ）图得2—4s 内物体所受拉力为F=12N （1分）根据牛顿第二定律F-f 0=ma 解得m =2kg （2分） （3）根据f 0=μN =μmg 解得μ=0.4 （2分） 31．（10分）（1）由玻意耳定律p 1V 1=p 2V 2（p 0-ρgh）lS =p 0l ʹS （2分） （75-2）×12×S=75×l ʹ×Sl ʹ=11.68cm （2分） （2）封闭端增加的水银长l －l ʹ （2分） 开口端增加的水银长h ＋l －l ʹ （2分）图乙S R 0所以，加入的水银总长为hʹ= h＋2（l－lʹ）=2+2（12－11.68）cm=2.64cm （2分）32．（12分）（1）以小球b为研究对象，设绳子拉力为T，由小球b受力平衡得T＝m b g/cos53°＝5N （2分）对小球a和小球b整体考虑，拉力F等于OB杆对b球的弹力（1分）所以F＝m b g tan53°＝4N （2分）（2）对小球a和b整体用机械能守恒定律，有m b g（L cos37°－L cos53°）＝12m b v b2＋12m a v a2 （3分）同时，小球a和b的速度满足v b cos37°＝v a sin37°（2分）两式联立，解得v b＝0.6m/s （2分）33．（16分）（1）导体棒即将离开Ⅰ时，金属框受到的安培力沿斜面向下，对金属框由平衡条件得f max = Mg sin300 + F A1max（1分）求得：F A1max =2N（1分）导体棒受安培力：F A1max = B2L2v1R=2N（1分）求得：v1 = 1m/s（1分）导体棒刚进入Ⅱ时，金属框受到的安培力沿斜面向上，对金属框由平衡条件得f max′ = F A2max－Mg sin300 （1分）求得：F A2max =12N（1分）导体棒受安培力：F A2max = B2L2v2R= 12N（1分）求得：v2 = 6m/s（1分）导体棒在两磁场边界之间运动时，mg sin300 = ma，求得：a = 5m/s2（1分）d= v22－v122a= 3.5m（1分）（2）导体棒离开Ⅰ之前，速度至少要达到v1 = 1m/s。

2014年高三一模填选难题解析（教师版）填空题1.（2014年普陀一模文理12）已知全集}8,7,6,5,4,3,2,1{=U ，在U 中任取四个元素组成的集合记为 },,,{4321a a a a A =，余下的四个元素组成的集合记为},,,{4321b b b b A C U =， 若43214321b b b b a a a a +++<+++，则集合A 的取法共有 种. 答案：31详解：可根据枚举法进行解题.正面枚举：利用1234123436a a a a b b b b +++++++=以及43214321b b b b a a a a +++<+++ 可知123418a a a a +++<，进行枚举（依据字典排序）451,2,3,678⎧⎪⎪⎪⎨⎪⎪⎪⎩；561,2,4,78⎧⎪⎪⎨⎪⎪⎩； 61,2,5,78⎧⎪⎨⎪⎩； 71,2,6,8⎧⎨⎩； 561,3,4,78⎧⎪⎪⎨⎪⎪⎩； 61,3,5,78⎧⎪⎨⎪⎩； 71,3,6,8⎧⎨⎩； 61,4,5,7⎧⎨⎩；562,34,78⎧⎪⎪⎨⎪⎪⎩，； 62,3,57⎧⎨⎩； 总共31种； 反面枚举：由于对称性可知43214321b b b b a a a a +++<+++与43214321b b b b a a a a +++<+++对应的情况应该是相同的，所以只需要算出总数：48C =70，以及12341234=a a a a b b b b ++++++的总数即可12341234==18a a a a b b b b ++++++，则1234,,,a a a a 可为1,2,7,8；1,3,6,8；671,4,58⎧⎨⎩； 672,358⎧⎨⎩；2,4,5,7；3,4,5,6；总共8种，故43214321b b b b a a a a +++<+++的情况为708312-=. 教法指导：本题主要考查了排列组合问题中枚举的应用，注意点是枚举过程中要寻到一条准线，按照这条准线来枚举做到不重不漏；另外就是需要注意问题化归（像反面进行枚举就是抓住大于以及小于的情况一样，所以可以从等于入手）2.（2014年普陀一模文理14） 已知函数⎩⎨⎧<+≥-=0),1(0,2)(x x f x a x f x ，若方程0)(=+x x f 有且仅有两个解，则实数a 的取值范围是 . 答案：a <2详解：本题考查了函数的有关性质.若方程f(x)+x=0有且仅有两个解，令h(x)=-x ，则(x)h 图像与()f x 图像有且仅有两个交点，即f(x)+a 与-x+a 图像有两个交点.如图所示：易知a <2.教法指导：本题是一个典型的数形结合的问题，将方程的根的问题转化为两个函数图像的交点问题， 注意如何构造两个函数尤为重要.3.（2014年长宁一模文14）设a 为非零实数，偶函数1||)(2+-+=m x a x x f (x ∈R )在区间(2,3)上存在 唯一零点，则实数a 的取值范围是 . 答案： )25,310(--详解：(方法一)1||)(2+-+=m x a x x f 与21y x =+为偶函数，故||y a x m =-为偶函数，0a ≠， 故0m =. 2()||1f x x a x =++在(2,3)上存在唯一零点可转化为1,()y a y x x==-+在(2,3)上 有唯一交点.通过图形易知10532a -<<-. (方法二)1||)(2+-+=m x a x x f 与21y x =+为偶函数，故||y a x m =-为偶函数，0a ≠， 故0m =. 2()||1f x x a x =++在(2,3)上存在唯一零点可转化为2()1f x x ax =++在(2,3)上 有唯一零点.（1） 考虑21=0x ax ++中=0∆的情况，此时方程的根为1x =不符合条件； （2） 考虑两个端点异号(2)(3)0f f <g【利用根的存在性定理】(5+2)(103)0a a +<得10532a -<<-； （3） 考虑两个端点其中一个函数值为0的情况，(2)=0f 得52a =-，25()12f x x x =-+零点为2x =与12x =，不符合条件；(3)=0f 得103a =-，210()13f x x x =-+零点为3x =与13x =，不符合条件；综上：10532a -<<-教法指导：本题考查了特殊函数（二次函数）的零点问题，该类问题一方面可以利用参变分离转化为两个函数的交点问题，特别是有解与一解问题利用此方法就很简洁明了，并且很直观.对于方法二中利用根的分布思考时容易遗漏情况（3），所以老师在讲这类方法时需要举出另一个容易漏解的例子. 变式：函数2()4f x x x a =-+在(0,3)上有一个零点，求a 的范围. 答案：(0,3]{4}U .4.（2014年长宁一模理14）定义：{}123min ,,,,n a a a a L 表示123,,,,n a a a a L 中的最小值．若定义()f x ={}2min ,5,21x x x x ---，对于任意的n *∈N ，均有(1)(2)(21)(2)()f f f n f n kf n +++-+≤L 成立，则常数k 的取值范围是 ． 答案：]0,21[-详解：本题考查了分段函数，不等式恒成立问题.由题意得，当0x >时，221,03()5,3x x x f x x x ⎧--<<=⎨-≥⎩，所以(1)2f =-，(2)1f =-，(3)2f =，(4)1f =，(5)0f =，(6)1f =-,… 则当1n =时，(1)(2)(1)f f kf +≤，即32k -≤-，解得32k ≤； 当2n =时，(1)(2)+(3)(4)(2)f f f f kf ++≤，即0k ≤-，解得0k ≤； 当3n =时，(1)(2)+(3)+(6)(3)f f f f kf ++≤L ，即k ≤-12，解得12k ≥-； 当4n =时，(1)(2)+(3)+(8)(4)f f f f kf ++≤L ，即6k ≤-,解得6k ≥-； 当5n =时，(1)(2)+(3)+(10)(5)f f f f kf ++≤L ，即150-≤，恒成立； 当6n =时，k ≤32；故n ≥6时，k 的取值应都是小于等于一个正数.综上所述， 要使(1)(2)++(21)(2)()f f f n f n kf n +-+≤L 恒成立，则k 的取值范围应取上述所求解的交集，即1,02⎡⎤-⎢⎥⎣⎦.教法指导：本题考查了数列的恒成立问题，若利用参变分离亦可解决，不过计算量上偏大， 而且需要分段清晰.5.（2014年嘉定一模理13文14）已知函数是偶函数，直线与函数 的图像自左至右依次交于四个不同点、、、，若，则实数的值为________．答案：详解：由函数()f x 是偶函数可知()()f x f x =-，⎪⎩⎪⎨⎧<++-≥++=0,,0,12)(22x c bx x x x ax x f t y =)(x f A B C D ||||BC AB =t 47即2()2+1f x ax x=+2()2()a x x=-+-22()ax x f x=-=-2x=-+bx c+，故1,2a b=-=-，1c=，则2221,0()21,0x x xf xx x x⎧-++=⎨--+<⎩…，由函数图像可知:①当0x…时，221y tx x y=⎧⎨-++=⎩，解得12x t=±-，故C点坐标为(12,)t t--②当0x<时，221y tx x y=⎧⎨--+=⎩，解得12x t=-±-.因为AB BC=可知，22222t t--=-，得74t=.第5题图教法指导：本题主要考查了函数奇偶性以及方程求解能力,如果刻意去用韦达定理求解会陷入死胡同. 6.（2014年嘉定一模理14）某种平面分形图如下图所示，一级分形图是一个边长为的等边三角形（图（1））；二级分形图是将一级分形图的每条线段三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边（图（2））；将二级分形图的每条线段三等边，重复上述的作图方法，得到三级分形图（图（3））；…；重复上述作图方法，依次得到四级、五级、…、级分形图．则级分形图的周长为_____．答案：详解：注意观察每个分形图的线段长度会在下一级分形图中变为43倍的折线；一级分形图的图形周长为4333⎛⎫=⋅ ⎪⎝⎭，二级分形图的图形周长为1214443333-⎛⎫⎛⎫=⋅=⋅⎪ ⎪⎝⎭⎝⎭，三级分形图的图形周长为231164433333-⎛⎫⎛⎫=⋅=⋅⎪ ⎪⎝⎭⎝⎭，L，故n级分形图的图形周长为1433n-⎛⎫⋅ ⎪⎝⎭.教法指导：本题主要针对于孩子的归纳推理能力进行考查，重点需要注意相邻两个图形之间的关系，采用特殊化归纳得到一般的结论.7.（2014年静安一模理12）1n n1343-⎪⎭⎫⎝⎛⋅n图（1）图（2）图（3）……详解：（方法一）设()()1122,,,A x y B x y ，PA的直线方程为y kx k =+，则PB的直线方程为y kx k =-+，分别与椭圆方程22124x y +=联立得：()))2222240k x kk x k+++-=由题知，1是方程的一个根，根据根与系数的关系得：1x =，同理2x =，则2122242k x x k -+=+，2122x x k -=+，则AB 的斜率为()212121212k x x ky y x x x x -++-=--22242k k k --⋅+==（方法二）利用特殊值将PA 斜率设为1则PB 斜率为-1,从而联立求解.(方法三) 利用图形中的极限位置思考，考虑PA 、PB 重合的情况；即过P 点做x 轴垂直的情况，交于椭圆与另外一点(1,P '，则AB 的斜率即过P '的切线斜率k ，利用2OP 22b k k a=-=-g可得k =教法指导：孩子需要熟练掌握直线与圆锥曲线联立韦达定理的应用，同时也得在填选的技巧中 记忆一些小结论. 8.（2014年静安一模理14）答案：4,4b a b =+= 详解：（方法一）由23344x x x -+=得 231 6160x x -+=所以()()3440x x --=，解得43x =或4x =.当2343443x x -+=时，解得43x =或83x =，因为223334(2)1144x x x -+=-+…，而413>，因此43a =，83b = 不合题意.当233444x x -+=时，解得0x =或4x =，而01<， 所以04a b ==，，则 04 4.a b +=+=（方法二）将不等式解集问题转化为方程根的问题，可看做23()344f x x x =-+夹在y a =与y b =部分的图像对应的x 的范围为[,]a b ，由图像易知：min ()()f a f a b f b b ≥⎧⎪=⎨⎪=⎩可解得04a b ==，教法指导：本题第二个方法相对简单直观，许多学生会把问题进行错误转换：23()344f x x x =-+ 在[,]a b 上的值域为[,]a b ，进而求出错误的答案，注意问题等价转换，并且注意不等式的 解集与对应方程的根的联系.9.（2014年闸北一模理9）设0,1a a >≠，已知函数()2sin 22,(0)xf x a x x π=+->至少有5个零点，则a 的取值范围为 答案：(0,1)(1,2)⋃详解：即函数2sin 2y x π=与2xy a =-在(0,)x ∈+∞上的交点个数，分两种情况01a <<和1a >；当01a <<时，在(0,)x ∈+∞两个函数图像有无数个交点，如下图所示当1a >时，如下图所示，在(0,)x ∈+∞要至少有5个零点，函数2xy a =-在1x =处要大于0即20,2a a -><，综上所述，(0,1)(1,2)a ∈⋃教法指导：这是一道典型的数形结合的题型，将零点问题转化成函数的交点个数问题，注意理解题意，审清题意，以及数与形之间的转化 变式练习（2014年闸北区一模文科9）设1,0≠>a a ，函数2|2sin |2)(-+=x a x f xπ（0>x ）有四个零点，则a 的值为 答案：2详解：如下图所示，函数2xy a =-在1x =处要等于010. （2014年闸北一模理10）设曲线22:23()C x y x y ++=+，则曲线C 所围封闭图形的面积为答案：323π+详解：因为图像关于x 轴、y 轴对称，所以可以先画第一象限的图像，第一象限0,0x y >>，绝对值 直接去掉，可得一段圆弧，然后关于x 轴、y 轴对称翻折，得到如下图像，根据题目数据， 可得150ABC ∠=︒，2AB =，可以先算第一象限的面积，由一个扇形与一个四边形构成，然后再乘以4，全面积为323π+教法指导：方程图像问题，含绝对值，所以根据象限分类讨论，根据相关 性质画出方程图像，割补法求面积 变式练习（2014年闸北区一模文科10）由曲线||||22y x y x +=+所围成的封闭图形的面积为 答案：2π+详解：根据题意，如下图，有四个半圆面积和一个正方形面积构成11. （2014年宝山一模理14） 关于函数()1x f x x =-，给出下列四个命题：①当0x >时，()y f x =单调递减且没有最值；②方程()(0)f x kx b k =+≠一定有解；③如果方程()f x k =有解，则解的个数一定是偶数； ④()y f x =是偶函数且有最小值； 则其中真命题是 答案：②④详解：含绝对值，分类讨论，先画1x >和01x <<的部分，然后根据偶函数画出左半部分， 函数图像如下图：①明显错误；③0k =时，解的个数为1；所以选②④教法指导：含绝对值数形结合题型，根据绝对值内的情况，进行分类讨论，结合函数性质，根据函数图象进行分析甄别12. （2014年闵行一模理12）设,i j r r依次表示平面直角坐标系x 轴、y 轴上的单位向量，且2a i a j -+-=r r r r2a i +r r 的取值范围是答案：[5详解：根据题意，2a i a j -+-=r r r r(1,0)的距离加上这个点到(0,2)的距离A 点的距离加上到B而AB，所以这个点的轨迹即线段AB ，而我们要求的取值范围的几何意义即转化成线段AB 上的点到点(2,0)-的距离的取值范围，最短距离即下图中的CD的长度，用点到直线的距离公式或者等面积法可求得5CD =，因为BC =3AC =，所以距离的最大值为3教法指导：用代数的方法计算，因为有根号，过程会很繁杂，结合向量的模的几何意义，转化成图形问题， 简洁明了，易于理解，教学过程中注意引导数形结合的使用13.（2014年闵行一模理13）22log (04)()2708(4)33x x f x x x x ⎧<≤⎪=⎨-+>⎪⎩，若,,,a b c d 互不相同， 且()()()()f a f b f c f d ===，则abcd 的取值范围是 答案：(32,35)详解：根据题意，如图所示，1ab =，2(12)12abcd cd c c c c ==-=-，45c <<，所以答案为(32,35)教法指导：这类题出现较多，典型的数形结合题型，要让学生熟悉各类函数图象，以及相应的性质， 尤其是对称性和周期性；在草稿纸上作图的时候，虽然是草图，但有必要做出一些特殊点 进行定位；写区间的时候，务必考虑区间的开闭情况 变式练习（2014年闵行区一模文科13）已知函数()11f x x =--，若关于x 的方程()f x t =()t R ∈恰有四个互不相等的实数根1234,,,x x x x （1234x x x x <<<），则1234x x x x ++⋅的取值范围是 答案：(3,4)详解：根据题意，如图所示120x x +=，21234343333(4)4x x x x x x x x x x ++⋅=⋅=⋅-=-，3(1,2)x ∈14.（2014年闵行一模理14）211,1k A x x kt t kt k ⎧⎫==+≤≤⎨⎬⎩⎭，其中2,3,......,2014k =， 则所有k A 的交集为 答案：5[2,]2详解：因为2,3,......,2014k =，所以2111k k <<，结合耐克函数的图像，如图所示，当211t k ≤≤时，1[2,]k A k k=+，因为2,3,......,2014k =时，1k k +递增，所以所有k A 的交集为5[2,]2教法指导：本题考查了耐克函数的图像与性质，结合图像以及函数的定义域，处理函数的值域问题； 难度不大，但学生可能会因为含有参数k 而产生畏难心理，可以让学生先求234,,A A A ， 发现一般规律，再总结归纳 变式练习（2014年闵行区一模文科14）已知42421()1x kx f x x x ++=++（k 是实常数），则()f x 的最大值与最小值的乘积为 答案：+23k15.（2014年徐汇一模理12）如图所示，已知点G 是△ABC 的重心，过G 作直线与AB 、AC 两边分别交于M 、N 两点，且,AM x AB AN y AC ==u u u u r u u u r u u u r u u u r ，则xy x y+的值为答案：13详解：解法一：∵,,M G N 三点共线，假设AG AM AN λμ=+u u u r u u u u r u u u r ，有=1λμ+，∵,AM x AB AN y AC ==u u u u r u u u r u u u r u u u r，∴AG AM AN λμ=+u u u r u u u u r u u u r ＝+x AB y AC λμu u u r u u u r ，因为G 是重心，所以1133AG AB AC =+u u u r u u u r u u u r即13=x y λμ=，∵=1λμ+，∴11133x y +=，化简xy x y +＝13解法二：特殊值法，取23x y ==教法指导：作为填空题，本题的第一做法应是解法二，但对于一些特别认真的学生，一定会问具体做法的， 要求我们能够写出具体过程；注意向量一些常用知识点，以及一些转化技巧16.（2014年徐汇一模理13） 一个五位数abcde 满足,,,a b b c d d e <>><且,a d b e >>(如37201,45412)，则称这个五位数符合“正弦规律”.那么，共有 个五位数符合“正弦规律” 答案：2892详解：根据题意，第二位最大，第四位最小，其他三个数介于二者之间；由此可以展开分类① 第二位数与第四位数相差2，情况为318⨯种；② 第二位数与第四位数相差3，情况为327⨯种； ③ 第二位数与第四位数相差4，情况为336⨯种；……以此类推，总共的情况为3333333318+27+36+45+54+63+72+81=2892⨯⨯⨯⨯⨯⨯⨯⨯种 教法指导：特殊元素优先原则，这里面最大的第二位数与最小的第四位数最特殊，由此可以展开分类；这类题型学生一般不知道从何下手，我们要教会学生发现规律，找出特殊元素或特殊位置，从而合理分类17.（2014年徐汇区一模理科14）定义区间(),c d 、[),c d 、(],c d 、[],c d 的长度均为()d c d c ->. 已知实数(),a b a b >.则满足111x a x b+≥--的x 构成的区间的长度之和为 答案：2详解：因为求的是区间的长度，原不等式111x a x b+≥--()a b >的解的区间长度和 不等式111x t x+≥-(0)t >的解的区间长度是一样的，因为只是图像发生了平移，移项通分 得220()x tx x tx x t --+≥-，因式分解后用数轴标根法解得22(0,(,22t t x t +-++∈⋃，区间长度之和为2222t t t +-++-2= 教法指导：因为含有两个字母，不等式不好解，所以我们要化归成一个字母的不等式问题，因为描述的是区间长度，根据题意，图像平移并不改变区间长度，就转化成一个字母，然后解出不等式即可求区间长度，注意转化化归的领会；当然，这道题也可以用特殊值法，不再赘述18.（2014年松江一模理11） 对于任意实数x ，x 表示不小于x 的最小整数，如 1.22,0.20=-=．定义在R 上的函数()2f x x x =+，若集合{}(),10A y y f x x ==-≤≤，则集合A 中所有元素的和为答案：4-详解：1x =-时，()3f x =-；10.5x -<≤-，()1f x =-；0.50x -<≤，()0f x =；{}3,1,0A =-- 教法指导：根据题目定义，引导学生发现规则，用枚举法列出所有元素即可，重在理解19.（2014年松江一模理13）已知函数()log 1(0,1)a f x x a a =->≠，若1234x x x x <<<， 且12()()f x f x =34()()f x f x ==，则12341111x x x x +++= 答案：2详解：解法一：设()log 1a f x x t =-=，∴log 1a x t -=±，1tx a ±-=，1tx a±-=±1t x a ±⇒=±四个根为1ta +，1ta -，11t a -，11t a +，它们的倒数为11t a +，11t a --，1t t a a -，1t t a a +倒数之和等于2解法二：特殊值，例如2a =，令()1f x =，解出四个根即可教法指导：本题直接求出四个解，并不难，就怕有些学生认为没这么简单，从而去从其他角度分析，反而复杂了，当然，本题可以借助数形结合的方法进行理解，作为填空题，特殊值不失为一种好方法20.（2014年松江一模理14） 设集合{1,2,3,,}A n =L ，若B ≠∅且B A ⊆，记()G B 为B 中元素的 最大值与最小值之和，则对所有的B ，()G B 的平均值＝ 答案：1n +详解：当最大值为n 时，最小值可以为1，2，3…n ，()G B 个数为n ，()G B 之和为12...n n n ++++⨯＝22(1)31222n n n n n ++=+；同理当最大值为1n -时，()G B 个数为1n -， 和为231(1)(1)22n n -+-；以此类推，所有()G B 的个数为(1)12 (2)n n n ++++=， 所有()G B 的和为1111(1)(21)(1)2222n n n n n ⋅+++⋅+ 22231(12...)(12...)22n n +++++++＝，除以()G B 的个数(1)2n n + 就是()G B 的平均值＝11(21)122n n ++=+ 教法指导：本题可以举一些{1,2,3,,}A n =L 的子集，让学生理解()G B 的意思，然后按最大值或者最小值进行分类，注意B 可能是个单元素集合，不要遗漏这种情况；这类题目注意培养学生的耐心21.（2014年青浦一模理13）已知直角坐标平面上任意两点11(,)P x y 、22(,)Q x y ，定义212121212121(,)x x x x y y d P Q y y x x y y ⎧--≥-⎪=⎨--<-⎪⎩为,P Q 两点的“非常距离”，当平面上动点(,)M x y到定点(,)A a b 的距离满足3MA =时，则(,)d M A 的取值范围是答案：[2详解：根据题意，通过比较两点的水平距离和垂直距离，较大的为“非常距离”，A 为定点，M 的轨迹 是A 为圆心，3为半径的圆，根据下图，例如1,A M 两点的垂直距离较大，那么此时,A M 的非常距离为图中的绿色线段部分，而2,A M 两点的水平距离相比垂直距离更大，那么非常距离为图中的紫色线段部分，可以得出M 与A 的水平距离或垂直距离最大为3， 即图中取4M 的时候教法指导：理解性的题型，注意引导学生如何理解题意，讲解时，一定要辅以图像帮助理解22.（2014年青浦一模理14）若不等式1(1)(1)31n na n +--<++对任意自然数n 恒成立，则实数a 的取值范围是答案：[3,2)-详解：当n 为奇数时，131a n -<++，1(3)1a n >-++，因为是恒成立，大于最大值，不等式右边的 最大值永远小于3-，所以3a ≥-；当n 为偶数时，131a n <-+，小于最小值，因为n N ∈，0n =时 取最小值2教法指导：恒成立问题均为最值问题，注意分类讨论，并且n 是自然数，讨论n 为偶数的时候，n 是可以取0的，学生可能会取2，这是个易错点，需要给学生强调23（2014年金山一模理13）如图，已知直线:4360l x y -+=，抛物线2:4C y x =图像上的一个动点P 到直线l 与y 轴的距离之和的最小值是 答案：1详解：如下图，11'11PH PA PH PB PH PF PH +=+-=+-≥-=，'PH 用点到直线距离公式求教法指导：这是2012长宁区二模题，注意圆锥曲线相关定义，进行巧妙的转化，结合图像引导学生分析24.（2014年金山一模理14）在三棱锥中，、、两两垂直，且.设是底面内一点，定义，其中、、分别是三棱锥、 三棱锥、三棱锥的体积.若1()(,2,)2f M x y =，且恒成立，则正实数的最小值为答案：6-详解：依题意得，122x y +=，122y x =-，将不等式中的a 分离得111(8)(2)6(16)22a x x x x≥--=-+，右边的最大值为6-6a ≥-教法指导：这是2012长宁区二模题，主要是理解题意，得出2x y +是个定值，要引导学生看透看似复杂的表象，抓住条件的本质，然后就是一道常见的恒成立题型25.（2014年奉贤一模理13）已知定义在R 上的函数()y f x =对任意的x 都满足(2)()f x f x +=-， 当11x -≤<时，3()f x x =，若函数()()log a g x f x x =-只有4个零点，则a 的取值范围是 答案：11(,)(3,5)53⋃详解：根据已知条件，()f x 周期为4，先画()f x 一个周期图像，当13x ≤<时，3(2)(2)()f x x f x -=-=-，3()(2)f x x =--，由此画出[1,3)-的图像，此为一个周期，图像如下，()()log a g x f x x =-只有4个零点，即()f x 与log a y x =只有4个交点，因为a 是未知的，需要分类讨论：①当01a <<时，有两个界值，如下图，此时5个交点，代入点(5,1)--，解出15a =此时3个交点，代入点(3,1)-，解得13a =②当1a >时，也有两个界值，如下图，此时3个交点，代入点(3,1)-，解得3a =P ABC -PA PB PC 3,2,1PA PB PC ===M ABC ()(,,)f M m n p =m n p M PAB -M PBC -M PCA -18ax y+≥a此时5个交点，代入点(5,1)，解得5a =教法指导：数形结合的题型，一定要结合图像分析，并且一些用于定位的特殊点要善于把握；另一方面，必须熟悉初等函数的所有性质以及函数图像的变换26.（2014年奉贤一模理14）已知函数()y f x =，任取t R ∈，定义集合：{(),(,()),(,()),t A y y f x P t f t Q x f x PQ ==≤点，设,t t M m 分别表示集合t A 中元素的最大值和最小值，记()t t h t M m =-，则（1）若函数()f x x =， 则(1)h = （2）若函数()sin 2f x x π=，则()h t 的最大值为答案：（1）2；（2）2详解：定义的意思是函数()y f x =在以定点P （点P 在函数图像上）这部分函数图像的值域即t A ，第一问，1t =，定点P (1,1)，如下图，蓝色实线段部分为符合定义的图像部分，这部分图像最大值为2，最小值为0，所以(1)h =2第二问，对于()sin2f x x π=，函数最大值与最小值之差为2，如下图，通过理解观察，可得出t A 能够同时包含最大值和最小值，所以()h t 的最大值为2，此时2,t k k Z =∈教法指导：这是一道理解性的定义题型，理解题目的定义很重要，然后结合函数图像进行分析就不难了27.（2014年黄浦一模理13）设向量()b a ,=α，()n m ,=β，其中R n m b a ∈,,,，由不等式≤恒成立，可以证明（柯西）不等式()()()22222n m b abn am ++≤+（当且仅当βα，即bm an =时等号成立）恒成立.己知+∈R y x ,，k <利用柯西不等式,可求得实数k 的取值范围是答案：)+∞详解：因为+,,0x y R ∈>k <k >+恒成立，令()=1,3=αβ⎛u ru r ，,||||w αβαβ=⋅≤⋅=u r u r u r u r 当且仅当39y x =即时等号成立，此时max w =max k w >=, 所以，实数k的取值范围是)+∞.教法指导：本题是新定义题型，运用类比思想，学会化归，不等式恒成立问题，参变分离转化成函数 求最值问题，注意等号成立的条件即可. 变式练习：（2014年黄浦区一模文科13）设向量()b a ,=α，()n m ,=β，其中R n m b a ∈,,,，由不等式≤恒成立，可以证明（柯西）不等式()()()22222n m b abn am ++≤+（当且仅当βα，即bm an=时等号成立）恒成立.己知+∈R y x ,，若k >+恒成立，利用柯西不等式,可求得实数k 的取值范围是答案：)+∞28.（2014年黄浦一模理14）用己知数列{}n a 满足()()*+∈=-+N n n a annn ,11，则数列{}na 的前2016项的和2016S 的值是___________． 答案：1017072详解：当*21()n k k N =-∈时，22121k k a a k --=- ① 当*2()n k k N =∈时，2+12+2k k a a k = ②当*21()n k k N =+∈时，222121k k a a k ++-=+ ③由①②得2121+1k k a a -+=，即任意两个连续奇数项之和为定值1， 所以()()()135720132015+++=504.a a a a a a +++L由②③得*222+41k k a a k k N +=+∈，即任意两个连续偶数项之和是等差数列，()()()()()()246820142016+++=41+1+43+1++41007+1=1016568.a a a a a a +++⨯⨯⨯L L所以，数列{}n a 的前2016项的和2016=1016568+504=1017072S .教法指导：本题的切入点是()1n-，所以分奇偶讨论，然后利用分组求和，最终转化为等差数列求和问题，使问题得以解决，注意分类思想的扑捉. 变式练习：（2014年黄浦区一模文科14）己知数列{}n a 满足421-=a，()()*+∈=-+N n n a a n nn ,11，则数列{}na 的前2013项的和2013s的值是___________．答案：101300029.（2014年杨浦一模理13）用设a ，b 随机取自集合{1,2,3}，则直线30ax by ++=与圆221x y +=有公共点的概率是 ．答案：59详解：这是道古典概型，事件A ：直线与圆有公共点，所以圆心到直线的距离，{}221,9,1,2,3d b a a b =≤≥-∈即，，下面分类讨论：当1a =时，291=83b b ≥-∴=，共1种情况符合题意； 当2a =时，294=53b b ≥-∴=，共1种情况符合题意； 当3a =时，299=01,2,3.b b ≥-∴=，共3种情况符合题意. 由加法原理，该事件A 共5种情况，总事件共33=9⨯种情况.所以，直线30ax by ++=与圆221x y +=有公共点的概率是5.9教法指导：本题考察直线与圆的位置关系，古典概率问题.注意审题，加法原理使问题得到解决. 变式练习：（2014年杨浦区一模文科13）在100件产品中有90件一等品，10件二等品，从中随机取出4件产品．则恰含1件二等品的概率是 .（结果精确到0.01） 答案：0.3030.（2014年杨浦一模理14）用已知函数()21(0)xf x a a =⋅+≠，定义函数(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩给出下列命题：①()()F x f x =； ②函数()F x 是奇函数；③当0a <时，若0mn <，0m n +>， 总有()()0F m F n +<成立，其中所有正确命题的序号是 . 答案：②、③详解：对于①：()()1=121F f a =+，但是，()1||1||2f a =+，而当210a +<时，()()1|1|=21F f a ≠-- ①错误；对于②：21,0,()21(0)=11,0.2x xxa x f x a a a x ⎧⋅+>⎪=⋅+≠⎨⎛⎫⋅+<⎪ ⎪⎝⎭⎩，()()f x f x -=-是偶函数，(),0,()(),0.f x x F x f x x >⎧=⎨-<⎩设0x >，则0x -<，()()()()F x f x f x F x -=--=-=-, 所以，函数()F x 是奇函数，②正确；对于③：当0a <时，()F x 在(),0-∞上和()0+∞，分别单调递减函数，若0mn <，0m n +>，则,m n >- 且m 与n -同号，所以()()()F m F n F n <-=-,()()0F m F n +<成立， ③正确.教法指导：本题考察分段函数的奇偶性，单调性，利用数形结合，本题解决更直观，快些，注意画图时， 注意对a 进行分类讨论. 变式练习：（2014年杨浦区一模文科14）函数()x f 是R 上的奇函数，()x g 是R 上的周期为4的周期函数，已知()()622=-=-g f ,且()()()()()()()()[]2122022222=-+-++f g g f g g f f ,则()0g 的值为 ． 答案：2.31.（2014年浦东一模理13）用表示集合S 中的元素的个数，设A B C 、、为集合，称(,,)A B C 为有序三元组．如果集合A B C 、、 满足1A B B C C A ===I I I ，且A B C =∅I I ，则称有序三元组(,,)A B C 为最小相交．由集合{}1,2,3,4的子集构成的所有有序三元组中，最小相交的有序三元组的个数为 ．答案：96.详解：设A,B,C 为{}1,2,3,4的三个子集，如图所示，因为A B C =∅I I 所以S =Φ不含任何元素，因为1A B B C C A ===I I I ，所以123,,M M M 中各有一个元素，将{}1,2,3,4中的元素排入，有333434C P P =种方法，由题意知，还剩下的一个元素，可以安排在 ,,P Q R ，也可以不排入，共有131+=4P 种方法，由分步原理得344=96P .教法指导：本题要注意分步原理与分类原理的综合运用，抽象出解题模型，从而使问题得到解决，当然也 可以用列举法，{}1,2,3,4有15个非空子集，显然A,B,C 中A 为含有1个或者4个元素的子集不符合题意， A 为含有2个或者3个元素的子集，列举即可求解.对于新定义题型，要善于讲陌生问题化归为熟悉模型， 注重基本原理的运用. 变式练习：（2014年杨浦区一模文科13）用表示集合S 中的元素的个数，设A B C 、、为集合，称(,,)A B C 为有序三元组．如果集合A B C 、、 满足1A B B C C A ===I I I ，且A B C =∅I I ，则称有序三元组(,,)A B C 为最小相交． 由集合{}1,2,3的子集构成的所有有序三元组中，最小相交的有序三元组的个数为 ． 答案：6.32.（2014年杨浦一模文理14）||S ||S已知函数**(),,y f x x y =∈∈N N ，对任意*n ∈N 都有[()]3f f n n =，且()f x 是增函数，则(3)f = ． 答案：6. 详解： ()()()()313ff n n f f =∴=Q ，()()**11f N f k N ∈∴=∈Q 设,由()f x 单调增函数知，()()()()3=11=,f f f k f k =≥ 所以()1f 只可能取1,2,3.i) 当()1=1f 时，()()()3=11=1,ff f =矛盾，舍去;ii) 当()1=2f 时，()()()()3=121=2,f f f f =≥符合单调递增条件，{}()*[()]3()()[()]3f f n n f n N n f n f f f n f n =∈=Q ，将换成得，;所以()()(3)=3,33(1)6f n f n f f ==于是，(1)(2)(3)f f f <<符合单调性，(3)=6f ∴； iii ）当()1=3f 时，()()()()3=13=1,f f f f =与单调性矛盾，舍去，综上所述，(3)=6f .教法指导：本题主要考察抽象函数的单调性，注意定义域和值域都是正整数，通过复合运算使问题得到 解决，给学生做适当的拓展，注意探究更一般的结论.33.（2014年虹口一模文理12）已知函数xx f 10)(=，对于实数m 、n 、p 有)()()(n f m f n m f +=+，)()()()(p f n f m f p n m f ++=++，则p 的最大值等于 ．答案：2lg2lg3-.详解： 由()()()f m n f m f n +=+得，101010m n m n +=+，从而1111010m n =+≥ 即104m n +≥，当且仅当m n =时等号成立.由()()()()f m n p f m f n f p ++=++， 得1101101p m n +=+-，由104m n +≥得411002lg2lg33p p <≤∴<≤-，，p 的最大值等于2lg2lg3-.教法指导：本题主要考察函数与不等式的综合应用，注意不等式中“一正二定三相等”的条件，通过等价变形，分离变量，转化成函数求最值问题，化归思想，将二元函数两个变元看做一个整体考虑解决问题.34.（2014年虹口一模文理13）已知函数2sin)(2πn n n f =，且)1()(++=n f n f a n ，则=++++2014321a a a a Λ ． 答案：4032-详解： 易知当*2,n k k N =∈为偶数时，2()4sin 0f n k k π==，所以()()()()()()()()20141232014222222221235720132015123579201320151223579201320154032S a a a a f f f f f f =++++=++++++⎡⎤⎣⎦=+-+-+-+-=++++++-⎡⎤⎣⎦=-L L L L教法指导：本题是一道数列与三角比结合的题目，利用三角函数周期性，化繁为简，转化成等差数列求和，使问题得到解决，注意项数计算个别学生需要给予指导，更进一步的，数列与三角比结合的题目给予拓展. 变式练习1：（2012年上海高考理科18）设1sin25n n a n π=，12...n n S a a a =+++（n N *∈），在12100,,...,S S S 中， 正数的个数是 ． 答案：100 变式练习2：（2012年上海高考文科18）若2sin sin (i)777n n S πππ=+++（n N *∈），则在12100,,...,S S S 中， 正数的个数是 ． 答案：8635.（2014年崇明一模文理14）已知,1->t 当[]2,+-∈t t x 时，函数||4||x x y x =的最小值为4-，则t 的取值范围是答案：2]详解：函数图像如下图所示，x 的区间是关于1x =对称的，当t 从-1渐渐变大时，x 的范围从x=1开始，慢慢向两边扩大，如下图，第三幅图向第四幅图变化的时候，函数的最小值为-4，第三幅图是t=0的时候，第四幅图是244x x -+=-的时候，解得2x t =-=-，所以t∈2]教法指导：本题图像是固定的，要注意区间是如何变化的，并且区间是关于x=1对称的，结合图像帮助理解，需要动态的思考选择题36.（2014年静安一模理18）答案：D详解：如图，在直线1l 与直线2l 处时，直线y x a =+与函数()y f x =在[]0,2内恰有两个交点，直线2l 与2y x =相切，联立解得114a =-，明显直线1l 过原点，即20a =，综上，a 的值是0或14-.教法指导：该题目比较简单，考查学生对于周期函数的理解以及数形结合的应用.37.（2014年长宁一模文理18）函数2xy =的定义域为[,]a b ，值域为[1,16]，a 变动时， 方程()b g a =表示的图形可以是 （ ）A ．B ．C ．D ．答案： B详解：本题考查了函数的图像.若0a >，则0b a >>，∴2xy =在定义域[,]a b 上的值域不可能为[1,16]， ∴0a ≤.又∵02=1，42=16，∴当=0a 时，4b =；当40a -<<时，4b =；当4a =-时，04b ≤≤.故选B.教法指导：主要针对于函数值域一定的情况下求定义域，注意定义域的不确定性，可以结合图像夹在1,16y y ==之间进行定义域的选取.38.（2014年嘉定一模理18）设函数的定义域为，若存在闭区间，使得函数满足：①在上是单调函数；②在上的值域是； 则称区间是函数的“和谐区间”．下列结论错误的是（ ） A ．函数（）存在“和谐区间” B ．函数（）不存在“和谐区间” C ．函数）存在“和谐区间” D ．函数（，）不存在“和谐区间” 答案：详解：利用(x)f 与2y x =的交点易知：A 中函数()2f x x =在区间[]0,2上单调递增，且其值域为[]0,4，故存在“和谐区间”；B 中函数()exf x =在x ∈R 上单调递增，且不存在“和谐区间”；C 中函数()241xf x x =+在区间[]0,1上单调递增，且其值域为[]0,2，故存在“和谐区间”；D 中函数，当2222log ,log 44a a x ⎡⎤-+∈⎢⎥⎣⎦上时，3223222222log ,log 2log ,2log 8844a a a ay ⎡⎤⎡⎤-+-+∈=⎢⎥⎢⎥⎣⎦⎣⎦，故满足 “和谐区间”的定义， )(x f D D b a ⊆],[)(x f )(x f ],[b a )(x f ],[b a ]2,2[b a ],[b a )(x f 2)(x x f =0≥x x e x f =)(R ∈x 14)(2+=x xx f (0≥x ⎪⎭⎫⎝⎛-=81log )(xa a x f 0>a 1≠a D ab O-4 4 ab O4-4a b O4 -4 ab O-4 4。

静安区2013学年第一学期教学质量检测高三年级地理试卷（考试时间：120分钟，满分：150分）2014.1全卷包括两大题；第一大题为选择题；第二大题为综合分析题。

考生注意：1.答卷前，务必用圆珠笔或钢笔在试卷和答题纸上将姓名、准考证号等填写清楚，并用2B 铅笔在答题纸上正确涂写准考证号码。

2.第一大题由机器阅卷，答案必须全部涂写在答题纸上，考生应将代表正确答案的小方格用2B铅笔涂黑。

注意试题题号与答题卡编号一一对应，不能错位。

答案需要更改时，必须将原选项用橡皮擦去，重新选择。

答案不能涂写在试卷上，涂写在试卷上一律不给分。

3.第二大题采用人工阅卷。

考生应用钢笔或圆珠笔将答案直接写在答题纸上，用铅笔答题或写在试卷上一律不给分。

一、选择题（共60分，每小题2分。

每小题只有一个正确答案）图1为到达地球太阳辐射量的分布图，图中曲线分别表示地表吸收大阳辐射量、地表反射太阳辐射量、大气上界太阳辐射量、云层反射太阳辐射量。

读图完成1～3题。

图11．图中曲线中A．①表示地表反射的太阳辐射量B．②表示大气上界的太阳辐射量C．③表示云层反射的太阳辐射量D．④表示地表吸收的太阳辐射量2．对近地面气温高低影响最直接的是A．①B．②C．③D．④3．④曲线表示的辐射量在南极地区比北极地区量大的原因主要是南极地区A．下垫面为冰川地面B．人口少C．环境污染严重D．地势较高某海洋考察船的航行日志记录：伦敦时间7时太阳从正东方海面升起；桅杆的影子在正北方时，太阳高度为63°；日落时伦敦时间为19时。

据此完成4～5题。

4．日志记录当天，该船航行在A ．北大西洋B ．南太平洋C ．北印度洋D ．南大西洋 5．日志记录当天考察船经过的海域，当天的天气状况可能为（ ）A ．阴雨绵绵B ．晴朗少云C ．风急浪高D ．台风肆虐图2为某日08时海平面气压分布图（单位：百帕）读图，回答第6～7题。

6．图中四地：A ．①云量最多B ．②风速最大C ．③风力最大D ．④气压最高 7．④地的风向可能为A ．偏东风B ．偏南风C ．偏西风D ．偏北风图2读近地面气压带、风带示意图（图3），回答8～9题。

2014年高三一模客观压轴题汇编（学生版）填空题1.（2014年普陀一模文理12）已知全集}8,7,6,5,4,3,2,1{=U ，在U 中任取四个元素组成的集合记为 },,,{4321a a a a A =，余下的四个元素组成的集合记为},,,{4321b b b b A C U =， 若43214321b b b b a a a a +++<+++，则集合A 的取法共有 种2.（2014年普陀一模文理14） 已知函数⎩⎨⎧<+≥-=0),1(0,2)(x x f x a x f x ，若方程0)(=+x x f 有且仅有两个解，则实数a 的取值范围是3.（2014年长宁一模文14）设a 为非零实数，偶函数1||)(2+-+=m x a x x f (x R )在区间(2,3)上存在唯一零点，则实数a 的取值范围是变式：函数2()4f x x x a =-+在(0,3)上有一个零点，则实数a 的取值范围是4.（2014年长宁一模理14）定义：{}123min ,,,,n a a a a 表示123,,,,n a a a a 中的最小值．若定义()f x ={}2min ,5,21x x x x ---，对于任意的n *∈N ，均有(1)(2)(21)(2)()f f f n f n kf n +++-+≤成立，则常数k 的取值范围是5.（2014年嘉定一模理13文14）已知函数⎪⎩⎪⎨⎧<++-≥++=0,,0,12)(22x c bx x x x ax x f 是偶函数，直线t y =与函数 )(x f 的图像自左至右依次交于四个不同点A 、B 、C 、D ，若||||BC AB =，则实数t 的值为6.（2014年嘉定一模理14）某种平面分形图如下图所示，一级分形图是一个边长为1的等边三角形（图（1））；二级分形图是将一级分形图的每条线段三等分，并以中间的那一条线段为一底边向形外作等边三角形， 然后去掉底边（图（2））；将二级分形图的每条线段三等边，重复上述的作图方法，得到三级分形图 （图（3））；…；重复上述作图方法，依次得到四级、五级、…、n 级分形图．则n 级分形图的 周长为7.（2014年静安一模理12）图（1） 图（2） 图（3）……8.（2014年静安一模理14）9.（2014年闸北一模理9）设0,1a a >≠，已知函数()2sin 22,(0)x f x a x x π=+->至少有5个零点，则a 的取值范围为变式练习（2014年闸北区一模文科9）设1,0≠>a a ，函数2|2sin |2)(-+=x a x f xπ（0>x ）有四个零点，则a 的值为10. （2014年闸北一模理10）设曲线22:23()C x y x y ++=+，则曲线C 所围封闭图形的面积为变式练习（2014年闸北区一模文科10）由曲线||||22y x y x +=+所围成的封闭图形的面积为11.（2014年宝山一模理14） 关于函数()1x f x x =-，给出下列四个命题：①当0x >时，()y f x =单调递减且没有最值；②方程()(0)f x kx b k =+≠一定有解；③如果方程()f x k =有解，则解的个数一定是偶数； ④()y f x =是偶函数且有最小值； 则其中真命题是12. （2014年闵行一模理12）设,i j 依次表示平面直角坐标系x 轴、y 轴上的单位向量， 且25a i a j -+-=，则2a i +的取值范围是13.（2014年闵行一模理13）22log (04)()2708(4)33x x f x x x x ⎧<≤⎪=⎨-+>⎪⎩，若,,,a b c d 互不相同， 且()()()()f a f b f c f d ===，则abcd 的取值范围是 变式练习（2014年闵行区一模文科13）已知函数()11f x x =--，若关于x 的方程()f x t =()t R ∈恰有四个 互不相等的实数根1234,,,x x x x （1234x x x x <<<），则1234x x x x ++⋅的取值范围是14.（2014年闵行一模理14）211,1k A x x kt t kt k ⎧⎫==+≤≤⎨⎬⎩⎭，其中2,3,......,2014k =， 则所有k A 的交集为变式练习（2014年闵行区一模文14）已知42421()1x kx f x x x ++=++（k 是实常数），则()f x 的最大值与最小值的乘积 为15.（2014年徐汇一模理12）如图所示，已知点G 是△ABC 的重心，过G 作直线与AB 、AC 两边分别交于M 、N 两点，且,AM x AB AN y AC ==，则xyx y+的值为16.（2014年徐汇一模理13） 一个五位数abcde 满足,,,a b b c d d e <>><且,a d b e >>(如37201,45412)，则称这个五位数符合“正弦规律”.那么，共有 个五位数符合“正弦规律”17.（2014年徐汇区一模理科14）定义区间(),c d 、[),c d 、(],c d 、[],c d 的长度均为()d c d c ->. 已知实数(),a b a b >.则满足111x a x b+≥--的x 构成的区间的长度之和为18.（2014年松江一模理11）对于任意实数x ，x 表示不小于x 的最小整数，如1.22,0.20=-=．定义在R 上的函数()2f x x x =+，若集合{}(),10A y y f x x ==-≤≤，则集合A 中所有元素的和为19.（2014年松江一模理13）已知函数()log 1(0,1)a f x x a a =->≠，若1234x x x x <<<， 且12()()f x f x =34()()f x f x ==，则12341111x x x x +++=20.（2014年松江一模理14） 设集合{1,2,3,,}A n =，若B ≠∅且B A ⊆，记()G B 为B 中元素的最大值与最小值之和，则对所有的B ，()G B 的平均值＝21.（2014年青浦一模理13）已知直角坐标平面上任意两点11(,)P x y 、22(,)Q x y ，定义212121212121(,)x x x x y y d P Q y y x x y y ⎧--≥-⎪=⎨--<-⎪⎩为,P Q 两点的“非常距离”，当平面上动点(,)M x y到定点(,)A a b 的距离满足3MA =时，则(,)d M A 的取值范围是22.（2014年青浦一模理14）若不等式1(1)(1)31n na n +--<++对任意自然数n 恒成立，则实数a 的取值范围是23（2014年金山一模理13）如图，已知直线:4360l x y -+=，抛物线2:4C y x =图像上的一个 动点P 到直线l 与y 轴的距离之和的最小值是24.（2014年金山一模理14）在三棱锥P ABC -中，PA 、PB 、PC 两两垂直，且3,2,1PA PB PC ===.设M 是底面ABC 内一点，定义()(,,)f M m n p =，其中m 、n 、p 分别是三棱锥M PAB -、三棱锥M PBC -、三棱锥M PCA -的体积。

2014年上海市宝山区高考数学一模试卷一、填空题（本大题满分56分）本大题共有14题每个空格填对得4分，否则一律得零分.1．（4分）已知复数3m+5+（1﹣m）i（i是虚数单位）对应的点在二、四象限的角平分线上，则实数m=．2．（4分）已知集合M={x|x2﹣2x≤0}，N={x|}，U=R，则图中阴影部分表示的集合是．3．（4分）函数y=3cosxcosx的最小正周期是．4．（4分）已知线性方程组的增广矩阵为，若该线性方程组无解，则a=．5．（4分）若函数y=f（x）的图象与y=ln﹣1的图象关于y=x对称，则f（x）=．6．（4分）函数y=f（x）的反函数f﹣1（x）=log（x﹣cos2），则方程f（x）=1的解是．7．（4分）阅读程序框图，运行相应的程序，当输入x的值为﹣25时，输出x的值为．8．（4分）已知复数z1满足（1+i）z1=﹣1+5i，z2=a﹣2﹣i，（a∈R），若，则a的取值范围是．9．（4分）若双曲线的渐近线方程为y=±3x，它的一个焦点与抛物线的焦点重合，则双曲线的标准方程为．10．（4分）（）6的展开式中，常数项为．（用数字作答）11．（4分）多瑙河三角洲的一地点A位于北纬45°东经30°，大兴安岭地区的一地点B位于北纬45°东经120°，设地球的半径为R，则A，B两地之间的球面距离是．12．（4分）从正方体的六个面中任意选取3个面，其中有2个面不相邻的概率为．13．（4分）函数y=sinx+cosx，x∈[﹣，]的值域是．14．（4分）关于函数f（x）=给出下列四个命题：①当x＞0时，y=f（x）单调递减且没有最值；②方程f（x）=kx+b（k≠0）一定有解；③如果方程f（x）=k有解，则解的个数一定是偶数；④y=f（x）是偶函数且有最小值．则其中真命题是．（只要写标题号）二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，选对得5分，否则一律得零分．15．（5分）设x为任意实数，则下列各式正确的是（）A．tan（arctanx）=x B．arcsin（sinx）=xC．sin（arcsinx）=x D．cos（arccosx）=x16．（5分）设a和b都是非零实数，则不等式a＞b和同时成立的充要条件是（）A．a＞b B．a＞b＞0C．a＞0＞b D．0＞a＞b 17．（5分）下列关于极限的计算，错误的是（）A．==B．（++…+）=++…+=0+0+…+0=0C．（﹣n）===D．已知a n=，则== 18．（5分）记X（x y 1），T=，X′=，则方程XTX′=0表示的曲线只可能是（）A．圆B．椭圆C．双曲线D．抛物线三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须写出必要步骤．19．（12分）如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，PA⊥平面ABCD，PC与平面ABCD所成角的大小为arctan2，M为PA的中点．（1）求四棱锥P﹣ABCD的体积；（2）求异面直线BM与PC所成角的大小（结果用反三角函数表示）．20．（14分）在△ABC中，A，B，C所对的边分别为a，b，c，，，（1）求C；（2）若，求a，b，c．21．（14分）给定曲线Γ：（5﹣m）x2+（m﹣2）y2=8，（m∈R）．（1）若曲线Γ是焦点为F1（﹣2，0），F2（2，0）的双曲线，求实数m的值；（2）当m=4时，记M是椭圆Γ上的动点，过椭圆长轴的端点A作AQ∥QM（O 为坐标原点），交椭圆于Q，交y轴于P，求的值．22．（16分）已知函数f（x）=ax2+ax和g（x）=x﹣a．其中a∈R且a≠0．（Ⅰ）若函数f（x）与g（x）的图象的一个公共点恰好在x轴上，求a的值；（Ⅱ）若函数f（x）与g（x）图象相交于不同的两点A、B，O为坐标原点，试问：△OAB的面积S有没有最值？如果有，求出最值及所对应的a的值；如果没有，请说明理由．（Ⅲ）若p和q是方程f（x）﹣g（x）=0的两根，且满足，证明：当x∈（0，p）时，g（x）＜f（x）＜p﹣a．23．（18分）若数列{a n}的每一项都不等于零，且对于任意的n∈N*，都有=q （q为常数），则称数列{a n}为“类等比数列”．已知数列{b n}满足：b1=b（b＞0），对于任意的n∈N*，都有b n•b n+1=﹣9×28﹣n．（1）求证：数列{b n}是“类等比数列”；（2）若{|b n|}是单调递减数列，求实数b的取值范围；（3）若b=2，求数列{b n}的前n项之积取最大值时n的值．2014年上海市宝山区高考数学一模试卷参考答案与试题解析一、填空题（本大题满分56分）本大题共有14题每个空格填对得4分，否则一律得零分.1．（4分）已知复数3m+5+（1﹣m）i（i是虚数单位）对应的点在二、四象限的角平分线上，则实数m=﹣3．【考点】A1：虚数单位i、复数．【专题】5N：数系的扩充和复数．【分析】根据复数的几何意义，求出对应的坐标，则对应的坐标满足方程y=﹣x 即可得到结论．【解答】解：复数3m+5+（1﹣m）i（i是虚数单位）对应的点的坐标为A（3m+5，1﹣m），∵A在二、四象限的角平分线y=﹣x上，∴1﹣m=﹣（3m+5），即2m=﹣6，解得m=﹣3，故答案为：﹣3【点评】本题主要考查复数的几何意义，根据复数和点的对应关系求出对应坐标是解决本题的关键，比较基础．2．（4分）已知集合M={x|x2﹣2x≤0}，N={x|}，U=R，则图中阴影部分表示的集合是（﹣∞，﹣3]∪（2，+∞）．【考点】1J：Venn图表达集合的关系及运算．【专题】11：计算题．【分析】根据阴影部分的元素属于集合N，而不属于集合M，从而得出阴影部分对应集合是（C U M）∩N，通过集合运算求得即可．【解答】解：由阴影部分的元素属于集合N，而不属于集合M，M=[0，2]，N=（﹣∞，﹣3]∪[1，+∞），∴C U M=（﹣∞，0）∪（2，+∞），阴影部分对应集合（C U M）∩N=（﹣∞，﹣3]∪（2，+∞）．故答案为：（﹣∞，﹣3]∪（2，+∞）．【点评】本题考查了Venn图表示集合关系及集合运算，进行集合运算要细心．3．（4分）函数y=3cosxcosx的最小正周期是π．【考点】H1：三角函数的周期性．【专题】56：三角函数的求值．【分析】函数解析式利用二倍角的正弦函数公式化为一个角的余弦函数，找出ω的值，代入周期公式即可求出最小正周期．【解答】解：y=3cosxcosx=3cos2x=（1+cos2x）=+cos2x，∵ω=2，∴最小正周期T==π．故答案为：π【点评】此题考查了三角函数的周期性及其求法，熟练掌握周期公式是解本题的关键．4．（4分）已知线性方程组的增广矩阵为，若该线性方程组无解，则a=2．【考点】OQ：系数矩阵的逆矩阵解方程组．【专题】11：计算题．【分析】将原方程组写成矩阵形式为Ax=b，其中A为3×3方阵，x为3个变量构成列向量，b为3个常数项构成列向量．而当它的系数矩阵D奇异时，或者说行列式D=0时，方程组有无数个解或无解．由此求得a值．【解答】解：系数矩阵D奇异时，或者说行列式D=0时，方程组有无数个解或无解．∴系数行列式D=0，即=0．解之得：a=2故答案为：2．【点评】本题主要考查系数矩阵的逆矩阵解方程组及克莱姆法则，克莱姆法则不仅仅适用于实数域，它在任何域上面都可以成立．5．（4分）若函数y=f（x）的图象与y=ln﹣1的图象关于y=x对称，则f（x）= e2x+2．【考点】4R：反函数．【专题】11：计算题；51：函数的性质及应用．【分析】利用反函数的定义通过解方程求出x的表达式，得到反函数y=f（x）的解析式．【解答】解：∵函数y=f（x）的图象与函数y=ln﹣1的图象关于直线y=x对称，由y=ln﹣1解得=e y+1，∴x=e2y+2，函数y=f（x）与函数y=lnx互为反函数，可得f（x）=e2x+2，故答案为：e2x+2．【点评】本题考查的知识点是函数的图象，函数解析式的求解及常用方法，其中根据同底的指数函数和对数函数互为反函数，得到函数y=f（x）的解析式，是解答本题的关键．6．（4分）函数y=f（x）的反函数f﹣1（x）=log（x﹣cos2），则方程f（x）=1的解是2．【考点】4R：反函数．【专题】51：函数的性质及应用．【分析】利用原函数与反函数的定义域与值域的对应关系，直接求解方程的解即可．【解答】解：∵原函数的定义域就是反函数的值域，原函数的值域就是反函数的定义域，∴f（x）=1的解就是求解反函数f﹣1（x）的值，∴f﹣1（x）=log（1﹣cos2）=log sin2=2，即f（x）=1的解为x=2．故答案为：2．【点评】本题考查原函数与反函数的对应关系，方程的解以及对数的运算性质，考查计算能力．7．（4分）阅读程序框图，运行相应的程序，当输入x的值为﹣25时，输出x的值为4．【考点】E7：循环结构．【专题】27：图表型．【分析】根据题意，按照程序框图的顺序进行执行，当|x|≤1时跳出循环，输出结果．【解答】解：当输入x=﹣25时，|x|＞1，执行循环，x==4；|x|=4＞1，执行循环，x==1，|x|=1，退出循环，输出的结果为x=3×1+1=4．故答案为：4．【点评】本题考查循环结构的程序框图，搞清程序框图的算法功能是解决本题的关键，按照程序框图的顺序进行执行求解，属于基础题．8．（4分）已知复数z1满足（1+i）z1=﹣1+5i，z2=a﹣2﹣i，（a∈R），若，则a的取值范围是（1，7）．【考点】A8：复数的模．【专题】11：计算题．【分析】首先整理复数，把两个复数整理成最简形式，写出复数的共轭复数，做差，写出要用的向量的模，解不等式，求出a的范围．【解答】解：∵复数z1满足（1+i）z1=﹣1+5i，∴=2+3iz2=a﹣2﹣i，∴，∵，∴＜，∴a2﹣8a﹣7＜0，∴1＜a＜7故答案为：（1，7）【点评】本题考查复数的求模，在运算过程中注意复数的除法运算和复数的模长的表示，注意一元二次不等式的整理和求解集．9．（4分）若双曲线的渐近线方程为y=±3x，它的一个焦点与抛物线的焦点重合，则双曲线的标准方程为．【考点】K8：抛物线的性质；KB：双曲线的标准方程．【专题】11：计算题．【分析】先由双曲线的渐近线方程为y=±x，易得知=3，再由抛物线的焦点为（，0）可得双曲线中c=，最后根据双曲线的性质c2=a2+b2列方程组，解得a2、b2即可．【解答】解：由双曲线渐近线方程可知=3 ①因为抛物线的焦点为（，0），所以c=②又c2=a2+b2③联立①②③，解得a2=1，b2=9，所以双曲线的方程为．故答案为为．【点评】本题考查双曲线的标准方程，以及双曲线的简单性质的应用，确定c和a2的值，是解题的关键．10．（4分）（）6的展开式中，常数项为15．（用数字作答）【考点】DA：二项式定理．【专题】11：计算题．【分析】本题是二项式展开式求项的问题，可由给出的式子求出通项表达式T r=+1（﹣1）r•，令x的次数为0即可．【解答】解：∵T r=（﹣1）r•，+1∴由6﹣3r=0得r=2，从而得常数项C6r=15，故答案为：15．【点评】本题考查二项式定理的基础知识与基本性质，二项式定理通常考查的内容有项、系数、和的运算等等，同时还会考查赋值法的数学思想，对这些知识要熟练地掌握，其在高考中的难度不大．11．（4分）多瑙河三角洲的一地点A位于北纬45°东经30°，大兴安岭地区的一地点B位于北纬45°东经120°，设地球的半径为R，则A，B两地之间的球面距离是．【考点】L*：球面距离及相关计算．【专题】5F：空间位置关系与距离．【分析】由已知中P和Q是地球上两点，A在北纬45°，东经30°，B在北纬45°，东经120°，A与B在同一纬度圈上，计算经度差，求出AB弦长，以及球心角，然后求出球面距离．【解答】解：地球表面上从A地（北纬45°，东经30°）到B地（北纬45°，西经120°）AB的纬圆半径是，经度差是90°，所以AB=R球心角是，A、B两地的球面距离是．故答案为：．【点评】本题考查球面距离及其它计算，考查空间想象能力，是基础题．其中计算出PQ弧对应的球心角是解答本题的关键．12．（4分）从正方体的六个面中任意选取3个面，其中有2个面不相邻的概率为．【考点】C6：等可能事件和等可能事件的概率．【专题】5I：概率与统计．【分析】所有的选法共有种，根据题意，使用间接法，首先分析从6个面中选取3个面的情况数目，再分析求出其中其中有2个面相邻，即8个角上3个相邻平面的情况数目，进而可得其中2个面不相邻的概率．【解答】解：所有的选法共有=20种，而其中有2个面相邻，即8个角上3个相邻平面，选法有8种，则满足条件的选法共有C63﹣8=12种，故其中2个面不相邻的概率是=，故答案为：．【点评】题考查组合的运用，等可能事件的概率，但涉及立体几何的知识，要求学生有较强的空间想象能力，属于中档题．13．（4分）函数y=sinx+cosx，x∈[﹣，]的值域是[﹣] ．【考点】HW：三角函数的最值．【专题】57：三角函数的图像与性质．【分析】利用三角函数的辅助角公式将函数进行化简，利用三角函数的图象和性质即可得到结论．【解答】解：y=sinx+cosx=2sin（x+），若x∈[﹣，]，则x+∈[﹣，]，则﹣≤sin（x+）≤1，即≤2sin（x+）≤2，∴函数的值域为[﹣]，故答案为：[﹣]．【点评】本题主要考查三角函数的图象和性质，利用辅助角公式将函数进行化简是解决本题的关键．14．（4分）关于函数f（x）=给出下列四个命题：①当x＞0时，y=f（x）单调递减且没有最值；②方程f（x）=kx+b（k≠0）一定有解；③如果方程f（x）=k有解，则解的个数一定是偶数；④y=f（x）是偶函数且有最小值．则其中真命题是②．（只要写标题号）【考点】3E：函数单调性的性质与判断；3K：函数奇偶性的性质与判断．【专题】51：函数的性质及应用．【分析】①x＞0时，由x≠1知y=f（x）不具有单调性，判定命题错误；②函数f（x）=是偶函数，在x＞0且k＞0时，判定函数y=f（x）与y=kx在第一象限内有交点；由对称性知，x＜0且k＞0时，函数y=f（x）与y=kx 在第二象限内有交点；得方程f（x）=kx+b（k≠0）有解；③函数f（x）=是偶函数，且f（x）=0，举例说明k=0时，方程f（x）=k有1个解；④函数f（x）=是偶函数，画出函数的图象，即可判断结论是否正确．【解答】解：①当x＞0时，y=f（x）==1+在区间（0，1）和（1，+∞）上分别是单调递减的函数，且无最值；∴命题①错误；②函数f（x）=是偶函数，当x＞0时，y=f（x）==1+在区间（0，1）和（1，+∞）上分别是单调递减的函数；当k＞0时，函数y=f（x）与y=kx在第一象限内一定有交点；由对称性知，当x＜0且k＞0时，函数y=f（x）与y=kx在第二象限内一定有交点；∴方程f（x）=kx+b（k≠0）一定有解；∴命题②正确；③∵函数f（x）=是偶函数，且f（x）=0当k=0时，函数y=f（x）与y=k的图象只有一个交点，∴方程f（x）=k的解的个数是奇数；∴命题③错误；④∵函数f（x）=是偶函数，x≠±1，x＞0时，y=f（x）==1+在区间（0，1）和（1，+∞）上分别是单调递减的函数；由对称性知，x＜0时，y=f（x）==1﹣在区间（﹣∞，﹣1）和（﹣1，0）上分别是单调递增的函数；如图所示，∴函数f（x）无最小值，命题④错误．故答案为：②．【点评】本题考查了含有绝对值的分式函数的图象与性质的问题，解题时应先去掉绝对值，化为分段函数，把分式函数分离常数，是易错题．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，选对得5分，否则一律得零分．15．（5分）设x为任意实数，则下列各式正确的是（）A．tan（arctanx）=x B．arcsin（sinx）=xC．sin（arcsinx）=x D．cos（arccosx）=x【考点】HV：反三角函数．【专题】56：三角函数的求值．【分析】根据反正切函数的定义，arctanx表示（﹣，）上正切值等于x的一个角，从而得出结论．【解答】解：根据反正切函数的定义，arctanx表示（﹣，）上正切值等于x的一个角，故有tan（arctanx）=x，故有A正确，故选：A．【点评】本题主要考查反三角函数的定义和性质，属于中档题．16．（5分）设a和b都是非零实数，则不等式a＞b和同时成立的充要条件是（）A．a＞b B．a＞b＞0C．a＞0＞b D．0＞a＞b【考点】R3：不等式的基本性质．【专题】35：转化思想；49：综合法；59：不等式的解法及应用．【分析】根据不等式a＞b和同时成立，可得把不等式a＞b的两边同时除以ab，不等式变号，故有a＞0＞b．【解答】解：设a和b都是非零实数，∵不等式a＞b和同时成立，∴把不等式a＞b的两边同时除以ab，不等式变号为，∴a、b异号，∴a＞0＞b，故选：C．【点评】本题主要考查不等式的基本性质，属于基础题．17．（5分）下列关于极限的计算，错误的是（）A．==B．（++…+）=++…+=0+0+…+0=0C．（﹣n）===D．已知a n=，则==【考点】6F：极限及其运算．【专题】21：阅读型；2A：探究型．【分析】题目中四个极限均为数列极限，A中分子分母最高次项次数相同，采用分子分母同时除以n2后求极限值；B和D需要先求和再取极限，C应先分子有理化，然后求极限．【解答】解：选项A求的是数列极限，采用分子分母同时除以n2后求极限值，正确；选项B应先求数列的前n项和，即，然后求得极限值为1，∴选项B错误；选项C是采用先分子有理化，然后分子分母同时除以n再取极限，正确；选项D是运用等比数列的求和公式先把奇数项和偶数项分别作和，然后求极限值，做法正确．故选：B．【点评】本题考查数列的极限及其求法，解答的关键是消去无穷大项，同时注意先化简再取极限，是基础题．18．（5分）记X（x y 1），T=，X′=，则方程XTX′=0表示的曲线只可能是（）A．圆B．椭圆C．双曲线D．抛物线【考点】OY：三阶矩阵．【专题】17：选作题；5R：矩阵和变换．【分析】利用矩阵的乘法，可得方程XTX′=0，即可得出结论．【解答】解：∵X（x y 1），T=，X′=，∴方程XTX′=0为Ax2﹣Ay2+Dx+Ey+D+E+F=0，∴方程XTX′=0表示的曲线只可能是双曲线．故选：C．【点评】本题考查矩阵的乘法，考查学生的计算能力，比较基础．三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须写出必要步骤．19．（12分）如图，在四棱锥P﹣ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，PA⊥平面ABCD，PC与平面ABCD所成角的大小为arctan2，M为PA的中点．（1）求四棱锥P﹣ABCD的体积；（2）求异面直线BM与PC所成角的大小（结果用反三角函数表示）．【考点】LF：棱柱、棱锥、棱台的体积；LM：异面直线及其所成的角．【专题】11：计算题．（1）先根据PA⊥平面ABCD以及PC与平面ABCD所成角的大小为arctan2，【分析】求出PA=4；再求出下底面面积即可求四棱锥P﹣ABCD的体积；（2）连接BD，交AC于点O，连接MO可得MO∥PC；所以∠BMO（或其补角）为异面直线BM与PC所成的角；然后在△BMO是直角三角形求得∠BMO即可．【解答】（本题满分（14分），第1小题（6分），第2小题8分）解：（1）连接AC，因为PA⊥平面ABCD，所以∠PCA为PC与平面ABCD所成的角…（2分）由已知，，而AC=2，所以PA=4．…（3分）底面积，…（4分）所以，四棱锥P﹣ABCD的体积．…（6分）（2）连接BD，交AC于点O，连接MO，因为M、O分别为PA、AC的中点，所以MO∥PC，所以∠BMO（或其补角）为异面直线BM与PC所成的角．…（8分）在△BMO中，，，，…（10分）（以下由余弦定理，或说明△BMO是直角三角形求得）或或．…（13分）所以，异面直线BM与PC所成角的大小为（或另外两个答案）．…（14分）【点评】本题主要考查棱锥的体积计算以及异面直线及其所成的角．在立体几何中找平行线是解决问题的一个重要技巧，这个技巧就是通过三角形的中位线找平行线，如果试题的已知中涉及到多个中点，则找中点是出现平行线的关键技巧．20．（14分）在△ABC中，A，B，C所对的边分别为a，b，c，，，（1）求C；（2）若，求a，b，c．【考点】9O：平面向量数量积的性质及其运算；HP：正弦定理．【专题】11：计算题．【分析】（1）先利用正弦定理把题设条件中的边转化成角的正弦，进而利用两角和的公式化简整理求的cotC的值，进而求得C．（2）根据求得ab的值，进而利用题设中和正弦定理联立方程组，求得a，b和c．【解答】解：（1）由得则有=得cotC=1即、（2）由推出；而，即得，则有解得．【点评】本题主要考查了正弦定理得应用．解题的关键是利用正弦定理解决三角形问题中的边，角问题．21．（14分）给定曲线Γ：（5﹣m）x2+（m﹣2）y2=8，（m∈R）．（1）若曲线Γ是焦点为F1（﹣2，0），F2（2，0）的双曲线，求实数m的值；（2）当m=4时，记M是椭圆Γ上的动点，过椭圆长轴的端点A作AQ∥QM（O 为坐标原点），交椭圆于Q，交y轴于P，求的值．【考点】KH：直线与圆锥曲线的综合．【专题】5E：圆锥曲线中的最值与范围问题．【分析】（1）曲线Γ化为标准方程得，由此利用双曲线的简单性质能求出m的值．（2）当m=4时，曲线Γ：x2+2y2=8，此时A（﹣2，0），由，得：，由此利用韦达定理结合题设条件能求出的值．【解答】解：（1）∵曲线Γ：（5﹣m）x2+（m﹣2）y2=8，（m∈R），化简得，…（2分）由题意得，，且m＜2，…（3分）又∵c=2，∴，解得m=﹣1，或m=4（舍）…（5分）∴m=﹣1．…（6分）（2）当m=4时，曲线Γ：x2+2y2=8，此时A（﹣2，0），…（7分）设直线OM方程为y=kx，由，得：，即，…（8分）∴OM2==x M2+（kx M）2=，…（10分）∵AQ∥OM，∴AQ方程为：y=k（x+2），于是P（o，2），AP==2•，…（11分）由，得：（1+2k2）x2+8k2x+16k2﹣8=0，从而AQ=•=．…（13分）∴==2．…（14分）【点评】本题考查双曲线中参数的求法，考查椭圆中线段比值的求法，综合性强，难度大，解题时要注意韦达定理的合理运用．22．（16分）已知函数f（x）=ax2+ax和g（x）=x﹣a．其中a∈R且a≠0．（Ⅰ）若函数f（x）与g（x）的图象的一个公共点恰好在x轴上，求a的值；（Ⅱ）若函数f（x）与g（x）图象相交于不同的两点A、B，O为坐标原点，试问：△OAB的面积S有没有最值？如果有，求出最值及所对应的a的值；如果没有，请说明理由．（Ⅲ）若p和q是方程f（x）﹣g（x）=0的两根，且满足，证明：当x∈（0，p）时，g（x）＜f（x）＜p﹣a．【考点】3A：函数的图象与图象的变换；IT：点到直线的距离公式；R6：不等式的证明．【专题】15：综合题；16：压轴题．【分析】（1）若函数f（x）与g（x）的图象的一个公共点恰好在x轴上，说明函数f（x）与g（x）有共同的零点，即g（x）的零点也在函数f（x）的图象上，代入易求出a值．（2）若函数f（x）与g（x）图象相交于不同的两点A、B，则将直线方程代入抛物线方程后，对应的二次方程有两不等的实数根，再将△OAB的面积函数表示出来，根据函数的性质，易得最值及对应的a值．（3）综合零点的性质和不等式的性质，不难证明当x∈（0，p）时，g（x）＜f （x）＜p﹣a【解答】解：（Ⅰ）设函数g（x）图象与x轴的交点坐标为（a，0），又∵点（a，0）也在函数f（x）的图象上，∴a3+a2=0．而a≠0，∴a=﹣1（Ⅱ）依题意，f（x）=g（x），即ax2+ax=x﹣a，整理，得ax2+（a﹣1）x+a=0，①∵a≠0，函数f（x）与g（x）图象相交于不同的两点A、B，∴△＞0，即△=（a﹣1）2﹣4a2=﹣3a2﹣2a+1=（3a﹣1）（﹣a﹣1）＞0．∴﹣1＜a＜且a≠0．设A（x1，y1），B（x2，y2），且x1＜x2，由①得，x1•x2=1＞0，．设点o到直线g（x）=x﹣a的距离为d，则，．=∴S△OAB=．∵﹣1＜a＜且a≠0，∴当时，S△OAB 有最大值，S△OAB无最小值．（Ⅲ）由题意可知f（x）﹣g（x）=a（x﹣p）（x﹣q）．∵，∴a（x﹣p）（x﹣q）＞0，∴当x∈（0，p）时，f（x）﹣g（x）＞0，即f（x）＞g（x）．又f（x）﹣（p﹣a）=a（x﹣p）（x﹣q）+x﹣a﹣（p﹣a）=（x﹣p）（ax﹣aq+1），x﹣p＜0，且ax﹣aq+1＞1﹣aq＞0，∴f（x）﹣（p﹣a）＜0，∴f（x）＜p﹣a，综上可知，g（x）＜f（x）＜p﹣a．【点评】本题考查的主要知识点是函数零点的性质，即两个函数的图象的交点在x轴上，则说明两个函数有共同的零点，即一个函数的零点也在另一个函数的图象上，应该满足另一个函数的方程；若函数在（a，b）上有零点，则f（a）•f（b）＜0．23．（18分）若数列{a n}的每一项都不等于零，且对于任意的n∈N*，都有=q（q为常数），则称数列{a n}为“类等比数列”．已知数列{b n}满足：b1=b（b＞0），对于任意的n∈N*，都有b n•b n+1=﹣9×28﹣n．（1）求证：数列{b n}是“类等比数列”；（2）若{|b n|}是单调递减数列，求实数b的取值范围；（3）若b=2，求数列{b n}的前n项之积取最大值时n的值．【考点】8B：数列的应用；8E：数列的求和．【专题】15：综合题；54：等差数列与等比数列．【分析】（1）利用b n•b n+1=﹣9×28﹣n，再写一式，可得，即可得出结论；（2）确定数列{|b n|}的通项，根据{|b n|}递减，所以|b2k﹣1|＞|b2k|＞|b2k+1|，即可求出实数b的取值范围；（3）若b=2，分类讨论，利用T n取最大值时，n=4k（k∈N*），当n为奇数时，令|b n•b n+1|＜1得，可得n≥13，即可求数列{b n}的前n项之积取最大值时n的值．【解答】（1）证明：因为b n•b n+1=﹣9×28﹣n，所以b n+1•b n+2=﹣9×27﹣n，所以，所以，数列{b n}是“类等比数列”．…（4分）（2）解：由b1=b，b1•b2=﹣9×27，得b2=﹣…（5分）所以b n=…（7分）因为{|b n|}递减，所以|b2k﹣1|＞|b2k|＞|b2k+1|，…（8分）解得：24＜b＜48．…（10分）（3）解：记数列{b n}的前n项之积为T n．当b=2时，b n=，由{b n}的通项公式可知．当n=4k﹣2或n=4k﹣1（k∈N*）时，T n＜0，…（12分）又因为0＜b4k＜1，所以T4k+1=b4k+1T4k＜T4k，+1因而T n取最大值时，n=4k（k∈N*）…（14分）当n为奇数时，令|b n•b n+1|＜1得，所以n≥13，…（16分）因而|b1•b2|＞1，…，|b11•b12|＞1，|b13•b14|＜1，|b15•b16|＜1，…所以|T2|＜|T4|＜…|T12|，|T12|＞|T14|＞，…．因而，当n=12时，T n取最大值．…（18分）【点评】本题考查新定义，考查数列的通项，考查数列{b n}的前n项之积，考查学生分析解决问题的能力，属于中档题．。

普陀区2014学年第一学期高三质量调研政治参考答案二、简答题（共32分）31、（1）答案示例：人民代表大会制度以突出人民的权力为核心，保障了人民当家作主权利的实现，为人民通过民主渠道管理国家事务提供了根本的制度保证。

（围绕“人民当家作主”展开，从人大制度的含义、内容和优越性角度回答，给2分。

）（2）答案示例：人大代表应代表人民的意志和利益，依照宪法和法律赋予的（审议权、提案权、表决权等）各项职权，参与行使国家权力。

人大代表在自己的工作和社会活动中，要协助宪法和法律的实施，与人民群众保持密切联系，听取和反映人民群众的意见和要求，努力为人民服务，并接受人民的监督。

32、（1）答案示例：党的领导角度：中国共产党是中国特色社会主义事业的领导核心，党始终坚持全心全意为人民服务的宗旨。

加强社会信用体系建设，是党贯彻落实依法治国和以德治国相结合方略的要求。

政府建设角度：我们的政府是党领导下的人民政府，坚持对人民负责，为人民服务是政府工作的根本出发点和归宿。

加快建设社会信用体系、构筑诚实守信的经济社会环境，是努力建设法治政府、责任政府和服务政府的体现。

（2）答案示例：国家：国家要加快建立信用监督和失信惩戒制度，综合运用各种调控手段，维护市场规则，规范市场秩序。

企业：企业要遵守法律和道德，积极承担社会责任，为社会提供优质的产品和服务，树立良好的信誉和企业形象。

个人：公民应树立诚信观念，遵守市场道德。

33、（1）答案示例：经济现象：改革开放以来，我国第一产业和第二产业在GDP中的比重不断下降；第三产业在GDP中的比重大幅度上升；2013年第三产业增加值占比首次超过第二产业，在三大产业中占首位。

意义：通过统计三大产业在GDP中所占比重的变化，能反映出我国社会经济结构的变动情况和发展趋势。

（2）答案示例：回答可以是“积极影响”，也可是“消极影响”。

积极影响：社会的产业结构调整和劳动就业结构密切联系（或：现代产业的发展和产业结构的优化升级，劳动力的就业结构必然发生相应的变化）。

答案：25. from 26. They 27.who 28. cleaner 29. that/which 30. had removed 31. Seeing 32. to clean分析：25. 本题考查的搭配问题remove.... from …, 做对本题的关键是要了解这个词语的搭配问题。

26. 本题考的是代词，要注意前后的语境及指代。

27. 本题考查的是非限制性定语从句的关系代词问题，比较容易。

28. 本题是属于给出限定词的题目，要看到前面的a lot, 这样就很容易填出clean的比较级。

29. 本题考查的是定语从句，也需要填关系代词，指代前面的先行词garbage, 用that和which都可以。

30．本题考查的时态问题，通过前面的by the end of…可知本题应填过去完成时，本题较容易。

31. enough 后往往要接to do 形式，所以本题答案为to clean ,难度不算太大。

答案：33. driving 34. an 35. when 36. were touched 37. what 38. Because of/ Owing to/ Dueto 39.checking 40. Could分析：33. 本题考查的是非谓语作定语，job跟drive是主动关系，所以填driving，本题很多学生会填to drive ,我们可以认为to do这种形式往往表示动作尚未发生，而这里表示的是从事的工作丢掉了，这不可能未发生，故填to drive是不合适的。

34. 本题填的是an, 要提醒学生看到单数可数名词时要考虑填冠词。

35. 本题考查的是状语从句的用法，根据句意可以看出应该是表示时间的，所以填when合适。

36. 本题填的是谓语动词，主语后面要填谓语，根据分析，本空要填被动语态。

37.38. 结合本句的句意，表达的应该是原因，又因为后面加的是名词，所以填以上几个表示原因的词组都可以。

2014年上海市静安区高考数学一模试卷（理科）一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1．（4分）已知集合A＝{（x，y）|x+y﹣1＝0}，B＝{（x，y）|y＝x2_1}，则A∩B＝．2．（4分）（理）已知cosα＝﹣，，则tan（+α）的值是．3．（4分）当x＞0时，函数y＝（a﹣8）x的值域恒大于1，则实数a的取值范围是．4．（4分）关于未知数x的实系数方程x2﹣bx+c＝0的一个根是1+3i（期中i是虚数单位），写出一个一元二次方程为．5．（4分）（理）某班有38人，现需要随机抽取5人参加一次问卷调查，抽到甲同学而未抽到乙同学的可能抽取情况有种．（结果用数值表示）6．（4分）（理）不等式|x﹣3|＜2x﹣1的解集是．7．（4分）若（其中a、b为有理数），则a+b＝．8．（4分）（理）已知方程sin2θ+cos2θ＝1，则当θ∈（﹣π，π）时，用列举法表示方程的解的集合是．9．（4分）（理）如图，平面内有三个向量、、，其中与的夹角为120°，与的夹角为30°，且||＝||＝2，||＝4，若＝λ+μ（λ、μ∈R），则λ+μ的值为．10．（4分）设抛物线y2＝mx的准线与直线x＝1的距离为3，则抛物线的方程为．11．（4分）（理）已知cos（﹣x）＝a，且0，则的值用a表示为．12．（4分）（理）已知椭圆C：＝1，过椭圆C上一点P（1，）作倾斜角互补的两条直线P A、PB，分别交椭圆C于A、B两点，则直线AB的斜率为．13．（4分）（理）若圆M：（x﹣a）2+（y﹣b）2＝6与圆N：（x+1）2+（y+1）2＝5的两个交点始终为圆N：（x+1）2+（y+1）2＝5的直径两个端点，则动点M（a，b）的轨迹方程为．14．（4分）（理）已知不等式a x2﹣3x+4≤b的解集为[a，b]，则b＝，且a+b的值为．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案．考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15．（5分）“m＝”是“直线（m+2）x+3my+1＝0与直线（m﹣2）x+（m+2）y ﹣3＝0相互垂直”的（）A．充分必要条件B．充分而不必要条件C．必要而不充分条件D．既不充分也不必要条件16．（5分）已知命题a：如果x＜3，那么x＜5；命题b：如果x≥3，那么x≥5；命题c：如果x≥5，那么x≥3．关于这三个命题之间的关系，下列三种说法正确的是（）①命题a是命题b的否命题，且命题c是命题b逆命题②命题a是命题b的逆命题，且命题c是命题b的否命题③命题b是命题a的否命题，且命题c是命题a的逆否命题．A．①③B．②C．②③D．①②③17．（5分）已知函数f（x）＝﹣x2+4x，x∈[m，5]的值域是[﹣5，4]，则实数m 的取值范围是（）A．（﹣∞，﹣1）B．（﹣1，2]C．[﹣1，2]D．[2，5）18．（5分）（理）已知函数f（x）是定义在实数集R上的以2为周期的偶函数，当0≤x≤1时，f（x）＝x2．若直线y＝x+a与函数y＝f（x）的图象在[0，2]内恰有两个不同的公共点，则实数a的值是（）A．﹣或﹣B．0C．0或﹣D．0或﹣三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19．（12分）《九章算术》是我国古代数学成就的杰出代表．其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积＝（弦×矢+矢2）．弧田（如图），由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差．按照上述经验公式计算所得弧田面积与其实际面积之间存在误差．现有圆心角为，弦长等于9米的弧田．（1）计算弧田的实际面积；（2）按照《九章算术》中弧田面积的经验公式计算所得结果与（1）中计算的弧田实际面积相差多少平方米？（结果保留两位小数）20．（14分）（理）（1）设x、y是不全为零的实数，试比较2x2+y2与x2+xy的大小；（2）设a，b，c为正数，且a2+b2+c2＝1，求证：++﹣≥3．21．（14分）（理）已知双曲线x2﹣y2＝a2（其中a＞0）．（1）若定点A（4，0）到双曲线上的点的最近距离为，求a的值；（2）若过双曲线的左焦点F1，作倾斜角为α的直线l交双曲线于M、N两点，其中α∈（，），F2是双曲线的右焦点．求△F2MN的面积S．22．（16分）设无穷数列{a n}的首项a1＝1，前n项和为S n（n∈N*），且点（S n﹣1，S n）（n∈N*，n≥2）在直线（2t+3）x﹣3ty+3t＝0上（t为与n无关的正实数）．（1）求证：数列{a n}（n∈N*）为等比数列；（2）记数列{a n}的公比为f（t），数列{b n}满足b1＝1，b n＝f（）（n∈N*，n ≥2），设c n＝b2nb2n﹣b2n b2n+1，求数列{c n}的前n项和T n；﹣1（3）（理）若（1）中无穷等比数列{a n}（n∈N*）的各项和存在，记S（t）＝a1+a2+…+a n+…，求函数S（t）的值域．23．（18分）（理）已知函数f（x）＝log a（其中a＞0且a≠1），g（x）是f （x）的反函数．（1）已知关于x的方程log a＝f（x）在区间[2，6]上有实数解，求实数m的取值范围；（2）当o＜a＜1时，讨论函数f（x）的奇偶性和增减性；（3）设a＝，其中p≥1．记b n＝g（n），数列{b n}的前n项的和为T n（n∈N*），求证：n＜T n＜n+4．2014年上海市静安区高考数学一模试卷（理科）参考答案与试题解析一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1．（4分）已知集合A＝{（x，y）|x+y﹣1＝0}，B＝{（x，y）|y＝x2_1}，则A∩B＝{（1，0），（﹣2，3）}．【解答】解：联立A与B中的方程得：，消去y得：x2+x﹣2＝0，即（x﹣1）（x+2）＝0，解得：x＝1或x＝﹣2，即y＝0或y＝3，则A∩B＝{（1，0），（﹣2，3）}．2．（4分）（理）已知cosα＝﹣，，则tan（+α）的值是．【解答】解：∵cosα＝﹣，α∈（，π），∴sinα＝＝＝，∴tanα＝＝﹣；∴tan（+α）＝＝＝．故答案为：．3．（4分）当x＞0时，函数y＝（a﹣8）x的值域恒大于1，则实数a的取值范围是a＞9．【解答】解：当0＜a﹣8＜1即8＜a＜9时，函数y＝（a﹣8）x在（0，+∞）上单调递减，则当x＞0时，（a﹣8）x＜（a﹣8）0＝1不符合题意，当a﹣8＞1即a＞9时，函数y＝（a﹣8）x在（0，+∞）上单调递增，则当x＞0时，（a﹣8）x＞（a﹣8）0＝1符合题意，∴实数a的取值范围是a＞9．故答案为：a＞9．4．（4分）关于未知数x的实系数方程x2﹣bx+c＝0的一个根是1+3i（期中i是虚数单位），写出一个一元二次方程为x2﹣2x+10＝0．【解答】解：由于关于未知数x的实系数方程x2﹣bx+c＝0的一个根是1+3i，根据实系数一元二次方程的虚根成对原理可知：1﹣3i也是此方程的一个虚根，∴，解得b＝2，c＝10．所求的方程为：x2﹣2x+10＝0．故答案为：x2﹣2x+10＝0．5．（4分）（理）某班有38人，现需要随机抽取5人参加一次问卷调查，抽到甲同学而未抽到乙同学的可能抽取情况有58905种．（结果用数值表示）【解答】解：除了甲、乙外还有36人，故从这36人中选出4个人，再把甲选上，即可满足条件，故所有的情况共有•＝58905种，故答案为：58905．6．（4分）（理）不等式|x﹣3|＜2x﹣1的解集是（，+∞）．【解答】解：由不等式|x﹣3|＜2x﹣1可得：，解得x＞，故答案为：（，+∞）．7．（4分）若（其中a、b为有理数），则a+b＝169．【解答】解：∵＝1+•+•+…+＝a+b，∴a＝1+2+4+8＝99，b＝+2+4＝70，∴a+b＝99+70＝169，故答案为：169．8．（4分）（理）已知方程sin2θ+cos2θ＝1，则当θ∈（﹣π，π）时，用列举法表示方程的解的集合是{}．【解答】解：（理）∵sin2θ+cos2θ＝1∴2sinθcosθ+cos2θ﹣sin2θ＝1∴2sinθcosθ＝2sin2θ∴sinθ＝0或cosθ＝sinθ又∵θ∈（﹣π，π）∴∴方程的解集为{}；故答案为{}9．（4分）（理）如图，平面内有三个向量、、，其中与的夹角为120°，与的夹角为30°，且||＝||＝2，||＝4，若＝λ+μ（λ、μ∈R），则λ+μ的值为6．【解答】解：∵＝λ+μ，且根据已知条件∴•＝﹣2λ+4μ＝0 ①∴*＝4*2*cos30°＝12即*＝4λ﹣2μ＝12 ②由①②得，∴μ＝2，λ＝4故答案为：610．（4分）设抛物线y2＝mx的准线与直线x＝1的距离为3，则抛物线的方程为y2＝8x或y2＝﹣16x．【解答】解：当m＞0时，准线方程为x＝﹣＝﹣2，∴m＝8，此时抛物线方程为y2＝8x；当m＜0时，准线方程为x＝﹣＝4，∴m＝﹣16，此时抛物线方程为y2＝﹣16x．∴所求抛物线方程为y2＝8x或y2＝﹣16x．故答案为；y2＝8x或y2＝﹣16x．11．（4分）（理）已知cos（﹣x）＝a，且0，则的值用a表示为2a．【解答】解：∵0＜x＜，∴0＜﹣x＜，∵cos（﹣x）＝a，∴sin（﹣x）＝，∴cos（+x）＝cos[﹣（﹣x）]＝sin（﹣x）＝，cos x＝cos[﹣（﹣x）]＝×a+×＝（a+），即cos2x＝2cos2x﹣1＝2×（a+）2﹣1＝a2+1﹣a2+2a﹣1＝2a，则原式＝＝2a．故答案为：2a12．（4分）（理）已知椭圆C：＝1，过椭圆C上一点P（1，）作倾斜角互补的两条直线P A、PB，分别交椭圆C于A、B两点，则直线AB的斜率为．【解答】解：由题意知，两直线P A，PB的斜率必存在，设PB的斜率为k，（k＞0），则PB的直线方程为，由，得，设B（x B，y B），则，＝，设A（x A，y A），同理可得，则x A﹣x B＝，y A﹣y B＝k（x A﹣1）﹣k（x B﹣1）＝4，∴AB的斜率k＝＝＝．故答案为：．13．（4分）（理）若圆M：（x﹣a）2+（y﹣b）2＝6与圆N：（x+1）2+（y+1）2＝5的两个交点始终为圆N：（x+1）2+（y+1）2＝5的直径两个端点，则动点M（a，b）的轨迹方程为（a+1）2+（b+1）2＝1．【解答】解：过圆M：（x﹣a）2+（y﹣b）2＝6的圆心坐标M（a，b），圆N：（x+1）2+（y+1）2＝5的圆心（﹣1，﹣1），∴圆心距为：，∴；即：（a+1）2+（b+1）2＝1．动点M（a，b）的轨迹方程为：（a+1）2+（b+1）2＝1．故答案为：：（a+1）2+（b+1）2＝114．（4分）（理）已知不等式a x2﹣3x+4≤b的解集为[a，b]，则b＝4，且a+b的值为4．【解答】解：画出函数f（x）＝＝的图象，可得f（x）min＝f（2）＝1，由图象可知：若a＞1，则不等式a x2﹣3x+4≤b的解集分两段区域，不符合已知条件．因此a≤1．此时恒成立．又∵不等式a x2﹣3x+4≤b的解集为[a，b]，∴a≤1＜b，f（a）＝f（b）＝b，可得，由，化为3b2﹣16b+16＝0，解得，或4．当b＝时，由，解得或，不符合题意，应舍去．∴b＝4，此时a＝0．∴a+b＝4．故答案分别为：4，4．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案．考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15．（5分）“m＝”是“直线（m+2）x+3my+1＝0与直线（m﹣2）x+（m+2）y ﹣3＝0相互垂直”的（）A．充分必要条件B．充分而不必要条件C．必要而不充分条件D．既不充分也不必要条件【解答】解：当m＝时，直线（m+2）x+3my+1＝0的斜率是，直线（m﹣2）x+（m+2）y﹣3＝0的斜率是，∴满足k1•k2＝﹣1，∴“m＝”是“直线（m+2）x+3my+1＝0与直线（m﹣2）x+（m+2）y﹣3＝0相互垂直”的充分条件，而当（m+2）（m﹣2）+3m•（m+2）＝0得：m＝或m＝﹣2．∴“m＝”是“直线（m+2）x+3my+1＝0与直线（m﹣2）x+（m+2）y﹣3＝0相互垂直”充分而不必要条件．故选：B．16．（5分）已知命题a：如果x＜3，那么x＜5；命题b：如果x≥3，那么x≥5；命题c：如果x≥5，那么x≥3．关于这三个命题之间的关系，下列三种说法正确的是（）①命题a是命题b的否命题，且命题c是命题b逆命题②命题a是命题b的逆命题，且命题c是命题b的否命题③命题b是命题a的否命题，且命题c是命题a的逆否命题．A．①③B．②C．②③D．①②③【解答】解：∵命题a：如果x＜3，那么x＜5；命题b：如果x≥3，那么x≥5；命题c：如果x≥5，那么x≥3．∴命题a与命题b互为否命题，命题a与命题c互为逆否命题，命题b与命题c互为逆命题，故①正确，②错误，③正确；即说法正确的命题有：①③故选：A．17．（5分）已知函数f（x）＝﹣x2+4x，x∈[m，5]的值域是[﹣5，4]，则实数m的取值范围是（）A．（﹣∞，﹣1）B．（﹣1，2]C．[﹣1，2]D．[2，5）【解答】解：∵f（x）＝﹣x2+4x＝﹣（x﹣2）2+4，∴当x＝2时，f（2）＝4，由f（x）＝﹣x2+4x＝﹣5，得x2﹣4x﹣5＝0，即x＝5或x＝﹣1，∴要使函数在[m，5]的值域是[﹣5，4]，则﹣1≤m≤2，故选：C．18．（5分）（理）已知函数f（x）是定义在实数集R上的以2为周期的偶函数，当0≤x≤1时，f（x）＝x2．若直线y＝x+a与函数y＝f（x）的图象在[0，2]内恰有两个不同的公共点，则实数a的值是（）A．﹣或﹣B．0C．0或﹣D．0或﹣【解答】解：∵f（x）是定义在实数集R上的以2为周期的偶函数，∴当﹣1≤x≤0时，f（x）＝f（﹣x）＝x2．即﹣1≤x≤1时，f（x）＝x2．作出函数f（x）在[0，2]上的图象如图：则当直线经过点A（1，1）时，满足条件此时1＝1+a，解得a＝0，当直线y＝x+a与y＝x2相切时，也满足条件，此时x2＝x+a，即x2﹣x﹣a＝0，则判别式△＝1+4a＝0，解得a＝，故a＝0或a═．故选：D．三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤.19．（12分）《九章算术》是我国古代数学成就的杰出代表．其中《方田》章给出计算弧田面积所用的经验公式为：弧田面积＝（弦×矢+矢2）．弧田（如图），由圆弧和其所对弦所围成，公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差．按照上述经验公式计算所得弧田面积与其实际面积之间存在误差．现有圆心角为，弦长等于9米的弧田．（1）计算弧田的实际面积；（2）按照《九章算术》中弧田面积的经验公式计算所得结果与（1）中计算的弧田实际面积相差多少平方米？（结果保留两位小数）【解答】解：（1）扇形半径r＝3，…（2分）扇形面积等于＝＝9π（m2）…（5分）弧田面积＝﹣r2sin＝9π﹣（m2）…（7分）（2）圆心到弦的距离等于，所以矢长为．按照上述弧田面积经验公式计算得（弦×矢+矢2）＝（9×+）＝（+）．…（10分）∴9π﹣﹣（+）＝1.51664798≈1.52（m2）…（12分）按照弧田面积经验公式计算结果比实际少1.52平米．20．（14分）（理）（1）设x、y是不全为零的实数，试比较2x2+y2与x2+xy的大小；（2）设a，b，c为正数，且a2+b2+c2＝1，求证：++﹣≥3．【解答】证明：（1）证法1：∵x、y是不全为零的实数，∴2x2+y2﹣（x2+xy）＝x2+y2﹣xy＝+y2＞0，∴2x2+y2＞x2+xy．证法2：当xy＜0时，x2+xy＜2x2+y2；当xy＞0时，作差：x2+y2﹣xy≥2xy﹣xy＝xy＞0；又因为x、y是不全为零的实数，∴当xy＝0时，2x2+y2＞x2+xy．综上，2x2+y2＞x2+xy．（2）证明：∵++﹣﹣3＝++﹣﹣3＝a2（+）+b2（+）+c2（+）﹣2（++）＝a2+b2+c2≥0（当且仅当a＝b＝c时，取得等号），∴++﹣≥3．21．（14分）（理）已知双曲线x2﹣y2＝a2（其中a＞0）．（1）若定点A（4，0）到双曲线上的点的最近距离为，求a的值；（2）若过双曲线的左焦点F1，作倾斜角为α的直线l交双曲线于M、N两点，其中α∈（，），F2是双曲线的右焦点．求△F2MN的面积S．【解答】解：（1）设点P在双曲线上，由题意得：|AP|2＝（x﹣4）2+y2＝2（x﹣2）2+8﹣a2，由双曲线的性质，得|x|≥a．（i）若0＜a≤2，则当x＝2时，AP有最小值．最小值|AP|2＝8﹣a2＝5，∴．（ii）若a＞2，则当x＝a时，AP有最小值，此时|AP|2＝a2﹣8a+16＝5，解得．（2），，直线l与x轴垂直时，|MN|＝2a，此时，△F2MN的面积＝．直线l与x轴不垂直时，直线l方程为，设M（x1，y1），N（x2，y2），将代入双曲线方程，整理得：，，，＝，点F2到直线MN距离，△F2MN的面积＝．22．（16分）设无穷数列{a n}的首项a1＝1，前n项和为S n（n∈N*），且点（S n﹣1，S n）（n∈N*，n≥2）在直线（2t+3）x﹣3ty+3t＝0上（t为与n无关的正实数）．（1）求证：数列{a n}（n∈N*）为等比数列；（2）记数列{a n}的公比为f（t），数列{b n}满足b1＝1，b n＝f（）（n∈N*，n ≥2），b2n﹣b2n b2n+1，求数列{c n}的前n项和T n；设c n＝b2n﹣1（3）（理）若（1）中无穷等比数列{a n}（n∈N*）的各项和存在，记S（t）＝a1+a2+…+a n+…，求函数S（t）的值域．【解答】（1）证明：因为点（S n，S n）（n∈N*，n≥2）在直线（2t+3）x﹣3ty+3t﹣1＝0（t为与n无关的正实数）上，所以（2t+3）S n﹣3tS n+3t＝0，﹣1＝3t（n∈N*，n≥2）．即有3tS n﹣（2t+3）S n﹣1当n＝2时，3t（a1+a2）﹣（2t+3）a1＝3t．由a1＝1，解得a2＝，所以＝，当n≥2时，有3tS n+1﹣（2t+3）S n＝3t①3tS n﹣（2t+3）S n﹣1＝3t②①﹣②，得3ta n+1﹣（2t+3）a n＝0，整理得＝．所以数列{a n}是公比为的等比数列；…（4分）（2）解：由（1）知，f（t）＝＝+，则b n＝f（）＝b n+，﹣1于是数列{b n}是公差d＝的等差数列，即b n＝，…（7分）﹣b2n+1）则T n＝b2（b1﹣b3）+b4（b3﹣b5）+…+b2n（b2n﹣1＝﹣2d（b2+b4+…+b2n）＝…（10分）（3）解：（理）由0＜＜1解得：t＞3．…（12分）所以S＝＝＝3+＞3所以函数S（t）的值域为（3，+∞）．…（16分）23．（18分）（理）已知函数f（x）＝log a（其中a＞0且a≠1），g（x）是f （x）的反函数．（1）已知关于x的方程log a＝f（x）在区间[2，6]上有实数解，求实数m的取值范围；（2）当o＜a＜1时，讨论函数f（x）的奇偶性和增减性；（3）设a＝，其中p≥1．记b n＝g（n），数列{b n}的前n项的和为T n（n∈N*），求证：n＜T n＜n+4．【解答】解：（1）由转化为求函数m＝（x﹣1）（7﹣x）在x∈[2，6]上的值域，该函数在[2，4]上递增，在[4，6]上递减，∴m的最小值5，最大值9．∴m的取值范围为[5，9]．（2）f（x）＝log a的定义域为（﹣∞，﹣1）∪（1，+∞），定义域关于原点对称，又f（﹣x）＝log a＝，即f（﹣x）＝﹣f（x），∴函数f（x）为奇函数．下面讨论在（1，+∞）上函数的增减性．任取1＜x1＜x2，令t（x）＝，则t（x1）﹣t（x2）＝﹣＝，因为1＜x1＜x2，∴t（x1）﹣t（x2）＝＜0，又当0＜a＜1时，y＝log a x是减函数，∴log a t（x1）＞log a t（x2）．由定义知在（1，+∞）上函数是减函数．又因为函数f（x）是奇函数，所以在（﹣∞，﹣1）上函数也是减函数．（3）∵g（x）＝；因为a＝，p≥1，∴0＜a≤，1＜g（1）＝＝1+≤3＜5．设k≥2，k∈N*时，则b k＞1，且b k＝＝1+由二项式定理（1+p）k＝1+p1+…+p k得：b k≤1+﹣1+＝1+﹣，从而n＜T n＜b1+（n﹣1）+2﹣＜b1+n+1≤n+4．。

2014年上海市闸北区高考数学一模试卷一、填空题(60分，本大题共10个小题，要求在答题纸相应位题序的空格内直接填写结果，每个空格填对得6分，否则一律零分）．1．（6分）设α=2014°﹣360°×k，β=2014°，若α是与β终边相同的最小正角，则k=．2．（6分）已知双曲线5x2﹣4y2=20的右焦点与抛物线y2=2px的焦点重合，则p=．3．（6分）设，则函数的最小正周期为．4．（6分）已知函数，则不等式f（x）＞1的解集为．5．（6分）已知直线l的一个法向量，其中ab＞0，则l的倾斜角为．6．（6分）相距480米有两个垂直于水平地面的高塔AB和CD，两塔底B，D的中点为P，已知AB=280米，CD=320米，则cos∠APC的值是．7．（6分）设a＞0，b＞0，a+b=2，则下列不等式恒成立的有．①ab≤1；②；③a2+b2≥2．8．（6分）若公差为d的等差数列{a n}的项数为奇数，a1=1，奇数项的和是175，偶数项的和是150，则d=．9．（6分）设a＞0，a≠1，函数f（x）=a x+2|sin2πx|﹣2（x＞0）至少有5个零点，则a的取值范围为．10．（6分）由曲线x2+y2=|x|+|y|所围成的图形面积为．二、选择题．11．（6分）如果S={x|x=2n+1，n∈Z}，T={x|x=4k±1，k∈Z}，那么（）A．S真包含于T B．T真包含于SC．S=T D．S与T没有交集12．（6分）在平面内，设A，B为两个不同的定点，动点P满足：（k 为实常数），则动点P的轨迹为（）A．圆B．椭圆C．双曲线D．不确定13．（6分）给出下列等式：13+23=32，13+23+33=62，13+23+33+43=102，…现设，n∈N*，n≥2，则=（）A．0B．1C．2D．4三、解答题（共4小题，满分42分）14．（10分）设△ABC的三个内角A，B，C的对边分别为a，b，c，且满足：．（1）求A的大小；（2）若，试判断△ABC的形状，并说明理由．15．（10分）定义域为的函数f（x）=2x﹣2﹣x，g（x）=2x+2﹣x（1）请分别指出函数y=f（x）与函数y=g（x）的奇偶性、单调区间、值域和零点；（将结论填入答题卡，不必证）（2）设，请判断函数y=h（x）的奇偶性、单调区间，并证明你的结论．（必要时，可以（1）中的结论作为推理与证明的依据）16．（10分）如图所示，一块椭圆形的铁板Γ的长轴长为4米，短轴长2米．（1）请你以短轴的端点A为直角顶点，另外两个锐角的顶点B，C都在椭圆铁板的边缘，截取等腰直角三角形，并求该三角形的面积（结果保留一位小数）；（2）请你按（1）中所述的方法，再切割出一个面积不同的等腰直角三角形，并求该三角形的面积（结果保留一位小数）．17．（12分）如图，在y轴的正半轴上依次有点A1，A2，…A n，…，其中点A1（0，1）、A2（0，10）且|A n﹣1A n|=3|A n A n+1|（n=2，3，4，…），在射线y=x（x≥0）上一次有点B1，B2，…B n，…，点B1（3，3），且（n=2，3，4，…）．（1）求点A n、B n的坐标（用含n的式子表示）．（2）设四边形A n B n B n+1A n+1的面积为S n，解答下列问题：①求数列{S n}的通项公式；②问{S n}中是否存在连续的三项S n，S n+1，S n+2（n∈N*）恰好成等差数列？若存在，求出所有这样的三项；若不存在，请说明理由．2014年上海市闸北区高考数学一模试卷参考答案与试题解析一、填空题(60分，本大题共10个小题，要求在答题纸相应位题序的空格内直接填写结果，每个空格填对得6分，否则一律零分）．1．（6分）设α=2014°﹣360°×k，β=2014°，若α是与β终边相同的最小正角，则k=5．【考点】G2：终边相同的角．【专题】56：三角函数的求值．【分析】利用终边相同的角的集合定理即可得出．【解答】解：∵β=2014°=360°×5+214°，α是与β终边相同的最小正角．∴α=2014°﹣360°×k=214°，解得k=5．故答案为：5．【点评】本题考查了终边相同的角的集合定理，属于基础题．2．（6分）已知双曲线5x2﹣4y2=20的右焦点与抛物线y2=2px的焦点重合，则p= 6．【考点】K8：抛物线的性质．【专题】5D：圆锥曲线的定义、性质与方程．【分析】由双曲线5x2﹣4y2=20化为，可得a2=4，b2=5，利用c2=a2+b2，解得c．可得双曲线的右焦点为F（c，0），即为抛物线y2=2px的焦点，可得，解得p．【解答】解：由双曲线5x2﹣4y2=20化为，可得a2=4，b2=5，∴c2=a2+b2=9，解得c=3．∴双曲线的右焦点为F（3，0），即为抛物线y2=2px的焦点，∴，解得p=6．故答案为：6．【点评】本题考查了双曲线与抛物线的标准方程及其性质，属于基础题．3．（6分）设，则函数的最小正周期为2π．【考点】GP：两角和与差的三角函数；H1：三角函数的周期性．【专题】11：计算题；57：三角函数的图像与性质．【分析】利用向量坐标运算求得函数的解析式，再对解析式化简，从而求得函数的最小正周期．【解答】解：f（x）=•=3cosx﹣sinx=cos（x+φ），∴函数的最小正周期为2π，故答案是2π．【点评】本题考查了向量的数量积公式，两角和的余弦公式及三角函数的最小正周期的求法，关键是利用三角公式对函数式进行化简．4．（6分）已知函数，则不等式f（x）＞1的解集为{x|x＜﹣1或x＞2} ．【考点】4O：对数函数的单调性与特殊点；5B：分段函数的应用．【专题】59：不等式的解法及应用．【分析】根据分段函数的表达式，讨论当x＞0和x≤0时，解不等式即可求不等式的解集．【解答】解：由分段函数可知，若x≤0，由f（x）＞1得，x2＞1，∴x＜﹣1．若x＞0，由f（x）＞1得log2x＞1，此时x＞2，综上不等式的解为x＜﹣1或x＞2，即不等式的解集为：{x|x＜﹣1或x＞2}，故答案为：{x|x＜﹣1或x＞2}．【点评】本题主要考查不等式的解法，要注意对x进行分类讨论．5．（6分）已知直线l的一个法向量，其中ab＞0，则l的倾斜角为．【考点】I2：直线的倾斜角．【专题】5B：直线与圆．【分析】利用直线的法向量与直线的斜率的关系即可得出．【解答】解：设直线的倾斜角为θ，则直线的斜率为tanθ．∵直线l的一个法向量是，∴，∴，∵ab＞0，∴．故答案为：．【点评】本题考查了直线的法向量与直线的斜率的关系，属于基础题．6．（6分）相距480米有两个垂直于水平地面的高塔AB和CD，两塔底B，D的中点为P，已知AB=280米，CD=320米，则cos∠APC的值是．【考点】HU：解三角形．【专题】58：解三角形．【分析】计算出△APC的三边，再利用余弦定理，可得结论．【解答】解：如图所示，AP==40，CP==400，AC==40．在△APC中，cos∠APC===．故答案为：．【点评】本题考查余弦定理的运用，考查学生利用数学知识解决实际问题，正确运用余弦定理是关键．7．（6分）设a＞0，b＞0，a+b=2，则下列不等式恒成立的有①③．①ab≤1；②；③a2+b2≥2．【考点】7F：基本不等式及其应用．【专题】59：不等式的解法及应用．【分析】利用基本不等式的性质逐一进行判定即可判断出答案．【解答】解：∵a＞0，b＞0，a+b=2，∴a+b=2≥2，即ab≤1，当且仅当a=b=1时取等号，故①正确；∵（+）2=a+b+2=2+2≤4，当且仅当a=b=1时取等号，∴+≤2，故②不正确；∵4=（a+b）2=a2+b2+2ab≤a2+b2+2，当且仅当a=b=1时取等号，∴a2+b2≥2，故③正确，∴不等式恒成立的有①③．故答案为：①③．【点评】本题考查不等式的基本性质，解题时要注意均值不等式的合理运用．属于基础题．8．（6分）若公差为d的等差数列{a n}的项数为奇数，a1=1，奇数项的和是175，偶数项的和是150，则d=4．【考点】83：等差数列的性质．【专题】54：等差数列与等比数列．【分析】设等差数列的项数为2n+1，利用a1=1，奇数项的和是175，偶数项的和是150，根据等差数列的求和公式建立方程组，即可得出结论．【解答】解：设等差数列的项数为2n+1，则∵a1=1，奇数项的和是175，偶数项的和是150，∴，∴n=13，d=4．故答案为：4【点评】本题考查等差数列的求和公式，考查学生的计算能力，正确运用等差数列的求和公式是关键．9．（6分）设a＞0，a≠1，函数f（x）=a x+2|sin2πx|﹣2（x＞0）至少有5个零点，则a的取值范围为（0，1）∪（1，2）．【考点】52：函数零点的判定定理；H6：正弦函数的奇偶性和对称性．【专题】51：函数的性质及应用；57：三角函数的图像与性质．【分析】由题意可得函数y=a x﹣2的图象（蓝线）和函数y=﹣2|sin2πx|的图象（红线）至少有5个交点，可得a1﹣2＜0．再结合a＞0，a≠1，求得a的值．【解答】解：根据函数f（x）=a x+2|sin2πx|﹣2（x＞0）至少有5个零点，可得函数y=a x﹣2的图象（蓝线）和函数y=﹣2|sin2πx|的图象（红线）至少有5个交点，如图所示：可得a1﹣2＜0，解得a＜2．再结合a＞0，a≠1，可得a的范围是（0，1）∪（1，2），故答案为：（0，1）∪（1，2）．【点评】本题主要考查函数的零点的个数判断，体现了转化以及数形结合的数学思想，属于中档题．10．（6分）由曲线x2+y2=|x|+|y|所围成的图形面积为2+π．【考点】J2：圆的一般方程．【专题】11：计算题；31：数形结合；32：分类讨论．【分析】通过对x，y的取值讨论，去掉绝对值符号，说明曲线的图形形状，画出图形，即可解答所求问题．【解答】解：当x，y≥0时，曲线x2+y2=|x|+|y|互为x2+y2=x+y，曲线表示以为圆心，以为半径的圆，在第一象限的部分；当x≥0，y≤0时，曲线x2+y2=|x|+|y|互为x2+y2=x﹣y，曲线表示以为圆心，以为半径的圆，在第四象限的部分；当x≤0，y≥0时，曲线x2+y2=|x|+|y|互为x2+y2=﹣x+y，曲线表示以为圆心，以为半径的圆，在第二象限的部分；当x≤0，y≤0时，曲线x2+y2=|x|+|y|互为x2+y2=﹣x﹣y，曲线表示以为圆心，以为半径的圆，在第三象限的部分；如图所求曲线x2+y2=|x|+|y|所围成的图形面积为：=2+π．故答案为：2+π．【点评】本题是中档题，考查曲线所围成的图形面积的求法，注意分类讨论思想的应用，数形结合的应用，考查计算能力．二、选择题．11．（6分）如果S={x|x=2n+1，n∈Z}，T={x|x=4k±1，k∈Z}，那么（）A．S真包含于T B．T真包含于SC．S=T D．S与T没有交集【考点】18：集合的包含关系判断及应用．【专题】29：规律型．【分析】根据集合S和T的元素关系进行判断即可．【解答】解：当n为偶数，设n=2k，k∈Z，则x=2n+1=4k+1，当n为奇数，设n=2k﹣1，k∈Z，则x=2n+1=4k﹣2+1=4k﹣1，∴集合S和T的元素相同，∴S=T．故选：C．【点评】本题主要考查集合关系的判断，利用集合元素之间的关系是解决本题的关键，注意要对n进行讨论．12．（6分）在平面内，设A，B为两个不同的定点，动点P满足：（k 为实常数），则动点P的轨迹为（）A．圆B．椭圆C．双曲线D．不确定【考点】KC：双曲线的性质；KK：圆锥曲线的轨迹问题．【专题】5A：平面向量及应用；5B：直线与圆．【分析】利用平面的数量积运算即可得出轨迹方程．【解答】解：设A（﹣c，0），B（c，0）（c＞0），P（x，y）．则=（﹣c﹣x，﹣y），=（c﹣x，﹣y）．∵满足：（k为实常数），∴（﹣c﹣x，﹣y）•（c﹣x，﹣y）=k2，化为x2﹣c2+y2=k2，即x2+y2=c2+k2故动点P的轨迹是原点为圆心，以为半径的圆．故选：A．【点评】本题考查了向量数量积运算、圆的标准方程，属于基础题．13．（6分）给出下列等式：13+23=32，13+23+33=62，13+23+33+43=102，…现设，n∈N*，n≥2，则=（）A．0B．1C．2D．4【考点】8J：数列的极限．【专题】54：等差数列与等比数列．【分析】先根据等式求出a n，再利用数列的求和公式、极限公式，即可得出结论．【解答】解：由题意，，∴===2．故选：C．【点评】本题考查数列的通项与求和，考查数列的极限，正确确定数列的通项是关键．三、解答题（共4小题，满分42分）14．（10分）设△ABC的三个内角A，B，C的对边分别为a，b，c，且满足：．（1）求A的大小；（2）若，试判断△ABC的形状，并说明理由．【考点】HU：解三角形．【专题】58：解三角形．【分析】（1）利用正弦定理，可得tanA=，从而可求A的大小；（2）利用二倍角公式，结合辅助角公式，可得三角形的形状．【解答】解：（1）∵，∴由正弦定理可得=1，∴tanA=，∵0°＜A＜180°，∴A=60°；（2）∵，∴1﹣cosB+1﹣cosC=1，∴cosB+cosC=1，∴cosB+cos（120°﹣B）=1，∴cosB﹣cosB+sinB=1，∴cosB+sinB=1，∴sin（B+30°）=1，∴B=60°，∴C=60°，∴△ABC是等边三角形．【点评】本题考查正弦定理的运用，考查二倍角公式，考查学生的计算能力，正确运用二倍角公式是关键．15．（10分）定义域为的函数f（x）=2x﹣2﹣x，g（x）=2x+2﹣x（1）请分别指出函数y=f（x）与函数y=g（x）的奇偶性、单调区间、值域和零点；（将结论填入答题卡，不必证）（2）设，请判断函数y=h（x）的奇偶性、单调区间，并证明你的结论．（必要时，可以（1）中的结论作为推理与证明的依据）【考点】3E：函数单调性的性质与判断；3K：函数奇偶性的性质与判断．【专题】51：函数的性质及应用．【分析】（1）利用函数的解析式，直接可以判断奇偶性、单调区间、值域和零点；（2）先化简函数，可得结论，再证明结论成立即可．【解答】解：（1）函数f（x）=2x﹣2﹣x为奇函数，在R上单调递增，值域为R，零点为0；函数g（x）=2x+2﹣x为偶函数，在（0，+∞）上单调递增，在（﹣∞，0）上单调递减，值域为[2，+∞），无零点；（2）==函数为奇函数，在R为增函数．证明如下：的定义域为R，则h（﹣x）===﹣h（x），∴函数为奇函数，∵h（x）==1﹣，∴h′（x）=＞0，∴函数在R为增函数．【点评】本题考查函数的性质，考查学生分析解决问题的能力，考查学生的计算能力，属于中档题．16．（10分）如图所示，一块椭圆形的铁板Γ的长轴长为4米，短轴长2米．（1）请你以短轴的端点A为直角顶点，另外两个锐角的顶点B，C都在椭圆铁板的边缘，截取等腰直角三角形，并求该三角形的面积（结果保留一位小数）；（2）请你按（1）中所述的方法，再切割出一个面积不同的等腰直角三角形，并求该三角形的面积（结果保留一位小数）．【考点】K4：椭圆的性质；KH：直线与圆锥曲线的综合．【专题】5D：圆锥曲线的定义、性质与方程．【分析】（1）以椭圆的中心为坐标原点建立平面直角坐标系，取AB所在直线斜率为1，则AC所在直线斜率为﹣1，写出AB，AC所在直线方程后和椭圆方程联立，分别求出B，C的横坐标，得到BC长度，BC边上的高等于BC的一半，由三角形的面积公式求得面积；（2）设AB所在直线斜率为k，则AC所在直线斜率为，写出AB，AC的方程，由弦长公式求得|AB|，|AC|的长度，由|AB|=AC|求出k的值，代入得三角形的面积．【解答】解：（1）建立如图所示的平面直角坐标系，则椭圆方程为：．∵∠BAC=90°，设k AB=1，k AC=﹣1．∴AB边所在直线方程为：y=x+1，AC边所在直线方程为y=﹣x+1．联立，得5x2+8x=0，解得x=0或x=﹣．∴点B横坐标为．联立，得5x2﹣8x=0，解得x=0或x=．∴点C横坐标为．∴|AB|=．则等腰直角三角形ABC的面积为：S=；（2）设AB所在的直线方程为：y=kx+1，则AC所在的直线方程为：．将AB所在的直线方程代入椭圆方程，得（1+4k2）x2+8kx=0．可求得，同理可求得，．不妨设k＞0，令|AB|=|AC|，得，即k3﹣4k2+4k﹣1=0，解得k=1或．当k=1时，所截取等腰直角三角形面积为2.6平方米，为（1）中所求；≈2.1．当时，代入得S△ABC所截取等腰直角三角形面积为2.1平方米．【点评】本题考查了椭圆的应用，考查了直线与椭圆的位置关系，训练了弦长公式的用法，考查了学生的计算能力，是中档题．17．（12分）如图，在y轴的正半轴上依次有点A1，A2，…A n，…，其中点A1（0，1）、A2（0，10）且|A n﹣1A n|=3|A n A n+1|（n=2，3，4，…），在射线y=x（x≥0）上一次有点B1，B2，…B n，…，点B1（3，3），且（n=2，3，4，…）．（1）求点A n、B n的坐标（用含n的式子表示）．（2）设四边形A n B n B n+1A n+1的面积为S n，解答下列问题：①求数列{S n}的通项公式；②问{S n}中是否存在连续的三项S n，S n+1，S n+2（n∈N*）恰好成等差数列？若存在，求出所有这样的三项；若不存在，请说明理由．【考点】8M：等差数列与等比数列的综合．【专题】54：等差数列与等比数列．【分析】（1）利用|A nA n|=3|A n A n+1|，及|A1A2|=9，结合等比数列的通项公式求﹣1得|A n A n+1|，结合等比数列的求和公式，可得|A1A2|+|A2A3|+…+|A n﹣1A n|，从而得出A n的坐标；确定{|OB n|}是以3为首项，2为公差的等差数列，可求B n的坐标；（2）①连接A n B n+1，设四边形A n B n B n+1A n+1的面积为S n，则S n=；②对于存在性问题，可先假设存在，即假设存在不同的三项S n，S n+1，S n+2（n∈N*）恰好成等差数列，代入求出结果，若出现矛盾，则说明假设不成立，即不存在；否则存在．【解答】解：（1）|A nA n|=3|A n A n+1|，且|A1A2|=10﹣1=9，﹣1∴|A n A n+1|=|A1A2|=9×=．∴|A1A2|+|A2A3|+…+|A n﹣1A n|=9+3+1+…+=，∴A n的坐标（0，），∵|OB n|﹣|OB n﹣1|=2（n=2，3，…）且|OB1|=3，∴{|OB n|}是以3为首项，2为公差的等差数列∴|OB n|=3+（n﹣1）×2=（2n+1），∴B n的坐标为（2n+1，2n+1）．（2）①连接A n B n+1，设四边形A n B n B n+1A n+1的面积为S n，则S n==•（）n﹣3×（2n+3）+•2[﹣]•=+．②由S n，S n+1，S n+2（n∈N*）恰好成等差数列，可得2（）=+++∴18（n+1）=27n+3（n+2），∴n=1，∴存在连续的三项S1，S2，S3恰好成等差数列．【点评】本题考查数列与函数的结合、等比数列的通项公式、等差关系的确定等基础知识，考查运算求解能力，考查化归与转化思想．属于难题．。