2018-2019学年高中数学北师大版选修2-1练习：第三章2.2 抛物线的简单性质(一) 1 含解析

[基础达标]1.过点(－1，0)且与抛物线y 2＝x 有且仅有一个公共点的直线有( ) A ．1条 B ．2条 C ．3条D ．4条解析：选C.点(－1，0)在抛物线y 2＝x 的外部，过此点与抛物线有一个公共点的直线有三条．其中两条切线，一条相交直线(平行x 轴)．2.过抛物线y ＝x 2上的点M (12，14)的切线的倾斜角是( )A ．30°B ．45°C ．60°D ．90°解析：选B.由题意可设切线方程为y －14＝k (x －12)，代入y ＝x 2，化简得4x 2－4kx ＋2k －1＝0，由Δ＝16k 2－16(2k －1)＝0，得k ＝1，∴切线的倾斜角为45°.3.抛物线y ＝ax 2＋1与直线y ＝x 相切，则a 等于( ) A.18 B ．14C.12D ．1解析：选B.由⎩⎪⎨⎪⎧y ＝ax 2＋1y ＝x消去y 整理得ax 2－x ＋1＝0，由题意a ≠0，Δ＝(－1)2－4a ＝0.∴a ＝14.4.抛物线y ＝x 2上一点到直线2x －y －4＝0的距离最小的点的坐标是( ) A ．(12，14)B ．(1，1)C ．(32，94)D ．(2，4)解析：选B.令y ＝x 2的切线方程为2x －y ＋c ＝0，代入y ＝x 2整理得x 2－2x －c ＝0.由Δ＝(－2)2＋4c ＝0，∴c ＝－1，∴x ＝1，y ＝1.切点(1，1)到直线2x －y －4＝0的距离最小．5.已知直线y ＝k (x ＋2)(k >0)与抛物线C ：y 2＝8x 相交于A ，B 两点，F 为C 的焦点．若|F A |＝2|FB |，则k ＝( )A.13 B ．23C.23D ．223解析：选D.设A (x 1，y 1)，B (x 2，y 2)，易知x 1>0，x 2>0，y 1>0，y 2>0，由⎩⎪⎨⎪⎧y ＝k （x ＋2），y 2＝8x ，得k 2x 2＋(4k 2－8)x ＋4k 2＝0， ∴x 1x 2＝4，①∵|F A |＝x 1＋p2＝x 1＋2，|FB |＝x 2＋p2＝x 2＋2，且|F A |＝2|FB |，∴x 1＝2x 2＋2.② 由①②得x 2＝1，∴B (1，22)，代入y ＝k (x ＋2)，得k ＝223.故选D.6.抛物线y ＝－x 2上的点到直线4x ＋3y －8＝0距离的最小值是________．解析：设切线为4x ＋3y ＋C ＝0，代入y ＝－x 2整理得3x 2－4x －C ＝0，由Δ＝(－4)2＋12C ＝0得， C ＝－43，故最小距离为8＋4342＋32＝2815. 答案：28157.设已知抛物线C 的顶点为坐标原点，焦点为F (1，0)，直线l 与抛物线C 相交于A ，B 两点．若AB 的中点为(2，2)，则直线l 的方程为________．解析：由题意知C 的方程为y 2＝4x ，设A (x 1，y 1)，B (x 2，y 2)，则y 21＝4x 1，y 22＝4x 2，两式作差，(y 1＋y 2)(y 1－y 2)＝4(x 1－x 2)，k AB ＝4y 1＋y 2＝44＝1，又直线l 过(2，2)，故l 的方程为y ＝x . 答案：y ＝x8.将两个顶点在抛物线y 2＝2px (p >0)上，另一个顶点是此抛物线焦点的正三角形的个数记为n ，则n ＝________．解析：根据抛物线对称性知正三角形的一边平行于y 轴，又过焦点与x 轴的夹角为30°的直线有两条，故符合题意的正三角形有两个．答案：29.已知顶点在原点，焦点在x 轴的负半轴的抛物线截直线y ＝x ＋32所得的弦长|P 1P 2|＝42，求此抛物线的方程．解：设抛物线方程为y 2＝－2px (p >0)，把直线方程与抛物线方程联立得⎩⎪⎨⎪⎧y ＝x ＋32，y 2＝－2px ，消元得x 2＋(3＋2p )x＋94＝0①，判别式Δ＝(3＋2p )2－9＝4p 2＋12p >0，解得p >0或p <－3(舍)， 设P 1(x 1，y 1)，P 2(x 2，y 2)，则①中由根与系数的关系得x 1＋x 2＝－(3＋2p )，x 1·x 2＝94，代入弦长公式得1＋1·（3＋2p ）2－9＝42，解得p ＝1或p ＝－4(舍)，把p ＝1代入抛物线方程y 2＝－2px (p >0)中，得y 2＝－2x . 综上，所求抛物线方程为y 2＝－2x .10.A 、B 为抛物线y 2＝2px (p >0)上两点，O 为原点，若OA ⊥OB ，求证：直线AB 过定点． 证明：设A (x 1，y 1)，B (x 2，y 2)， ∵OA ⊥OB ⇒x 1x 2＋y 1y 2＝0，A ，B 在抛物线上⇒y 21y 22＝4p 2x 1x 2， ∴⎩⎪⎨⎪⎧y 1·y 2＝－4p 2x 1·x 2＝4p 2，l AB ：y －y 1＝2p y 1＋y 2(x －x 1)，∴y －y 1＝2py 1＋y 2(x －y 212p )，∴y ＝2py 1＋y 2·x －y 21y 1＋y 2＋y 1＝2py 1＋y 2·x －4p 2y 1＋y 2 ＝2p y 1＋y 2(x －2p )， ∴直线AB 过定点(2p ，0)．[能力提升]1.已知抛物线y 2＝2px (p >0)与圆(x －a )2＋y 2＝r 2(a >0)有且只有一个公共点，则( ) A ．r ＝a ＝p B ．r ＝a ≤p C ．r <a ≤pD ．r <a ＝p解析：选B.当r <a 时，根据圆与抛物线的对称性可知，圆(x －a )2＋y 2＝r 2(a >0)与抛物线y 2＝2px (p >0)要么没有交点，要么交于两点或四点，与题意不符；当r >a 时，易知圆与抛物线有两个交点，与题意不符；当r ＝a 时，圆与抛物线交于原点，要使圆与抛物线有且只有一个公共点，必须使方程(x －a )2＋2px ＝r 2(x ≥0)有且仅有一个解x ＝0，可得a ≤p .故选B.2.已知直线y ＝a 交抛物线y ＝x 2于A ，B 两点，若该抛物线上存在点C ，使得∠ACB 为直角，则a 的取值范围为________．解析：设C (x ，x 2)，由题意可取A (－a ，a )，B (a ，a )， 则CA →＝(－a －x ，a －x 2)，CB →＝(a －x ，a －x 2)，由于∠ACB ＝π2，所以CA →·CB →＝(－a －x )(a －x )＋(a －x 2)2＝0，整理得x 4＋(1－2a )x 2＋a 2－a ＝0， 即y 2＋(1－2a )y ＋a 2－a ＝0，所以⎩⎪⎨⎪⎧－（1－2a ）≥0，a 2－a ≥0，（1－2a ）2－4（a 2－a ）>0，解得a ≥1. 答案：[1，＋∞)3.已知过点A (－4，0)的动直线l 与抛物线G ：x 2＝2py (p >0)相交于B ，C 两点，当直线l 的斜率是12时，AC →＝4AB →.(1)求抛物线G 的方程；(2)设线段BC 的中垂线在y 轴上的截距为b ，求b 的取值范围．解：(1)设B (x 1，y 1)，C (x 2，y 2)，当直线l 的斜率是12时，l 的方程为y ＝12(x ＋4)，即x ＝2y －4，由⎩⎪⎨⎪⎧x 2＝2py ，x ＝2y －4，得2y 2－(8＋p )y ＋8＝0， ∴⎩⎨⎧y 1y 2＝4，y 1＋y 2＝8＋p 2，又∵AC →＝4AB →，∴y 2＝4y 1， 由这三个表达式及p >0得y 1＝1，y 2＝4，p ＝2，则抛物线的方程为x 2＝4y .(2)由题意可设l ：y ＝k (x ＋4)，BC 的中点坐标为(x 0，y 0)．由⎩⎪⎨⎪⎧x 2＝4y ，y ＝k （x ＋4），得x 2－4kx －16k ＝0， ∴x 0＝2k ，y 0＝k (x 0＋4)＝2k 2＋4k ，∴线段BC 的中垂线方程为y －2k 2－4k ＝－1k(x －2k )，∴线段BC 的中垂线在y 轴上的截距为：b ＝2k 2＋4k ＋2＝2(k ＋1)2， 由Δ＝16k 2＋64k >0得k >0或k <－4. ∴b ∈(2，＋∞)．4．已知抛物线C 的顶点为O (0，0)，焦点为F (0，1)． (1)求抛物线C 的方程；(2)过点F 作直线交抛物线C 于A 、B 两点，若直线AO ，BO 分别交直线l ：y ＝x－2于M ，N 两点， 求|MN |的最小值.解：(1)由题意可设抛物线C 的方程为x 2＝2py (p >0)，则p2＝1，所以抛物线C 的方程为x 2＝4y .(2)设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为y ＝kx ＋1.由⎩⎪⎨⎪⎧y ＝kx ＋1，x 2＝4y ，消去y ，整理得x 2－4kx －4＝0，所以x 1＋x 2＝4k ，x 1x 2＝－4. 从而|x 1－x 2|＝4k 2＋1.由⎩⎪⎨⎪⎧y ＝y 1x 1x ，y ＝x －2，解得点M 的横坐标x M ＝2x 1x 1－y 1＝2x 1x 1－x 214＝84－x 1. 同理，点N 的横坐标x N ＝84－x 2.所以|MN |＝2|x M －x N |＝2|84－x 1－84－x 2| ＝82|x 1－x 2x 1x 2－4（x 1＋x 2）＋16|＝82k 2＋1|4k －3|.令4k －3＝t ，t ≠0，则k ＝t ＋34.当t >0时，|MN |＝2 2 25t 2＋6t＋1>2 2. 当t <0时，|MN |＝2 2（5t ＋35）2＋1625≥852. 综上所述，当t ＝－253，即k ＝－43时，|MN |的最小值是85 2.。

2018-2019学年高中数学第三章圆锥曲线与方程3.2.2 抛物线的简单性质（二）训练案北师大版选修2-1编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年高中数学第三章圆锥曲线与方程3.2.2 抛物线的简单性质（二）训练案北师大版选修2-1）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年高中数学第三章圆锥曲线与方程3.2.2 抛物线的简单性质（二）训练案北师大版选修2-1的全部内容。

3。

2。

2 抛物线的简单性质［A.基础达标]1．抛物线y＝ax2＋1与直线y＝x相切，则a等于（)A。

错误! B. 错误!C。

错误!D．1解析：选B.由错误!消去y整理得ax2－x＋1＝0，由题意a≠0，Δ＝(－1）2－4a＝0.所以a＝错误!.2．已知抛物线C:y2＝4x的焦点为F，直线y＝2x－4与C交于A,B两点，则cos∠AFB＝( ) A。

错误!B。

错误!C．－35D．－错误!解析：选D。

由错误!得错误!或错误!令B（1，－2），A（4，4)，又F（1，0)，所以由两点间距离公式，得|BF｜＝2，|AF|＝5，|AB｜＝3错误!，所以cos∠AFB＝错误!＝4＋25－452×2×5＝－错误!.3．A，B是抛物线x2＝y上任意两点（非原点)，当错误!·错误!最小时，错误!，错误!所在两条直线的斜率之积k OA·k OB＝（)A。

错误!B．－错误!C。

错误!D．－错误!解析：选B。

由题意可设A(x1,x错误!),B(x2,x错误!),错误!＝(x1，x错误!)，错误!＝(x2，x错误!),错误!·错误!＝x1x2＋（x1x2）2＝(x1x2＋错误!)2－错误!≥－错误!,当且仅当x1x2＝－错误!时错误!·错误!取得最小值．此时k OA·k OB＝错误!·错误!＝x1x2＝－错误!.4．设抛物线C:y2＝2px（p>0）的焦点为F，点M在C上,｜MF｜＝5。

,[学生用书单独成册])(时间：分钟，满分：分)一、选择题(本大题共小题，每小题分，共分．在每小题给出的四个选项中，只有一项是符合题目要求的)．双曲线－＝的渐近线方程为()．＝±．＝±．＝±．＝±解析：选.双曲线的标准方程为－＝，故其渐近线方程为＝±＝±.．抛物线＝的焦点坐标是()．(，)．(，)．(，)．(，)解析：选＝的焦点坐标为(，)，即(，)．．若双曲线－＝上一点到它的右焦点的距离是，那么点到它的左焦点的距离是()．．或．以上都错．＋解析：选.设，为其左、右焦点，由双曲线定义＝＝＝，所以＝或.．已知椭圆：＋＝(＞＞)的左、右两个焦点分别为，，是上的点，⊥，∠＝°，则椭圆的离心率是()解析：选.因为＝，所以＝°，所以＝，＝＝.由椭圆定义：＋＝＝，故＝＝.．已知抛物线＝(>)的准线与圆＋－－＝相切，则的值为()．．解析：选.抛物线方程可化为＝(>)，由于圆＋(－)＝与抛物线的准线＝－相切，所以－＝，所以＝.．设，是双曲线－＝的两个焦点，过右焦点作倾斜角为的弦，则△的面积为()．解析：选.直线的方程为＝－，将其代入－＝，整理得：－＋＝，因为＋＝，＝，所以＋＝－＋－＝.＝(－)(－)＝－.－＝＝.△＝－＝××＝.．若直线过点(，)与双曲线－＝只有一个公共点，则这样的直线有()．条．条．条．条解析：选.双曲线方程可化为－＝，知(，)为双曲线的右顶点，故符合要求的直线有条，其中一条是切线，另两条是交线(分别与两渐近线平行)．．已知定直线与平面α成°角，点是平面α内的一动点，且点到直线的距离为，则动点的轨迹是()．椭圆的一部分．圆．椭圆．抛物线的一部分解析：选.以为轴，底面半径为的圆柱被与成°的平面α所截，截面边界线为椭圆．．已知椭圆＋＝(＞＞)与双曲线－＝有公共的焦点，且它们的离心率互为倒数，则该椭圆的标准方程是()＋＝＋＝＋＝＋＝解析：选.因为双曲线的离心率为＝，所以椭圆的离心率为，即＝，又因为－＝＝，所以＝，＝.故椭圆的标准方程为＋＝.．已知抛物线＝上有一条长为的动弦，则中点到轴的最短距离为()．．解析：选.设(，)，(，)．抛物线准线方程为＝－.根据梯形中位线定理，得所求距离为：＝＝－，由抛物线定义得＝－≥－＝，当、、三点共线时取等号，故选.二、填空题(本大题共小题，每小题分，共分．把答案填在题中的横线上)．双曲线－＝的离心率等于．解析：因为＝，＝，所以＝＝，所以＝＝.答案：．与椭圆＋＝共焦点且过点(，)的双曲线方程是．解析：由此双曲线与＋＝共焦点，故该双曲线可设为－＝，将(，)代入双曲线得＝.故双曲线方程为－＝.答案：－＝．椭圆＋＝内一点(，)，过点的弦恰好以为中点，那么这条弦所在的直线方程为．解析：设该弦与椭圆交于(，)，(，)，＋＝，①＋＝，②①－②得，(＋)(－)＋(＋)(－)＝，又因为＋＝，＋＝.所以＝＝－，故该弦所在直线为－＝－(－)，即＋－＝.答案：＋－＝．抛物线＝上距点(，)(>)最近的点恰好是抛物线的顶点，则的取值范围是．解析：设(，)为抛物线上任一点，则＝(－)＋＝－(－)＋＝[－(－)]＋－.因为>，所以－>－.由于≥，且由题意知当＝时，最小．则对称轴＝－应满足－<－≤，所以<≤.答案：(，]．从一块短轴长为的椭圆形玻璃镜中划出一块面积最大的矩形，其面积的取值范围是[，]，则该椭圆离心率的取值范围是．解析：由对称性知矩形中心在原点，且两组对边平行于轴，轴，设矩形在第一象限的顶点坐标为(，)(＞，＞)，矩形＝＝(·)≤(＋)＝∈[，]，所以≤≤，即≤≤，＝＝－()∈[，]，故∈[，]．答案：[，]三、解答题(本大题共小题，共分．解答应写出必要的文字说明、证明过程或演算步骤)．(本小题满分分)已知椭圆的中心在原点，焦点在轴上，长轴长为，且两个焦点恰好将长轴三等分．求椭圆的标准方程及其离心率．解：设椭圆的方程为＋＝(>>)，由题意知：＝，＝，解得＝，＝，故＝－＝，所以椭圆的方程是＋＝，离心率＝＝＝.．(本小题满分分)代表实数，讨论方程＋－＝所表示的曲线．解：当<时，曲线－＝为焦点在轴上的双曲线；当＝时，曲线－＝为两条平行于轴的直线＝或＝－；当<<时，曲线＋＝为焦点在轴上的椭圆；当＝时，曲线＋＝为一个圆；当>时，曲线＋＝为焦点在轴上的椭圆．．(本小题满分分)已知直线：＝＋与椭圆：＋＝交于，两点．。

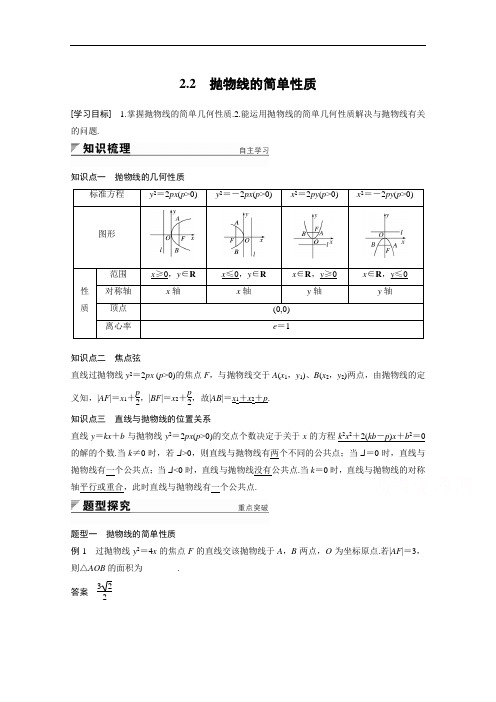
2.2抛物线的简单性质[学习目标] 1.掌握抛物线的简单几何性质.2.能运用抛物线的简单几何性质解决与抛物线有关的问题.知识点一抛物线的几何性质x≥0，y∈R x≤0，y∈R x∈R，y≥0x∈R，y≤0知识点二焦点弦直线过抛物线y2＝2px (p>0)的焦点F，与抛物线交于A(x1，y1)、B(x2，y2)两点，由抛物线的定义知，|AF|＝x1＋p2，|BF|＝x2＋p2，故|AB|＝x1＋x2＋p.知识点三直线与抛物线的位置关系直线y＝kx＋b与抛物线y2＝2px(p>0)的交点个数决定于关于x的方程k2x2＋2(kb－p)x＋b2＝0的解的个数.当k≠0时，若Δ>0，则直线与抛物线有两个不同的公共点；当Δ＝0时，直线与抛物线有一个公共点；当Δ<0时，直线与抛物线没有公共点.当k＝0时，直线与抛物线的对称轴平行或重合，此时直线与抛物线有一个公共点.题型一抛物线的简单性质例1过抛物线y2＝4x的焦点F的直线交该抛物线于A，B两点，O为坐标原点.若|AF|＝3，则△AOB的面积为________.答案322解析 由题意设A (x1，y 1)，B (x 2，y 2)(y 1>0，y 2<0)，如图所示，|AF |＝x 1＋1＝3， ∴x 1＝2，y 1＝2 2.设AB 的方程为x －1＝ty ，由⎩⎪⎨⎪⎧y 2＝4x ，x －1＝ty 消去x 得y 2－4ty －4＝0.∴y 1y 2＝－4.∴y 2＝－2，x 2＝12，∴S △AOB ＝12×1×|y 1－y 2|＝322.反思与感悟 (1)注意抛物线各元素间的关系：抛物线的焦点始终在对称轴上，抛物线的顶点就是抛物线与对称轴的交点，抛物线的准线始终与对称轴垂直，抛物线的准线与对称轴的交点和焦点关于抛物线的顶点对称.(2)解决抛物线问题要始终把定义的应用贯彻其中，通过定义的运用，实现两个距离之间的转化，简化解题过程.跟踪训练1 已知抛物线的对称轴在坐标轴上，以原点为顶点，且经过点M (1，－2).求抛物线的标准方程和准线方程.解 (1)当抛物线的焦点在x 轴上时， 设其标准方程为y 2＝mx (m ≠0). 将点M (1，－2)代入，得m ＝4. ∴抛物线的标准方程为y 2＝4x ；(2)当抛物线的焦点在y 轴上时，设其标准方程为x 2＝ny (n ≠0). 将点M (1，－2)代入，得n ＝－12.∴抛物线的标准方程为x 2＝－12y .故所求的抛物线的标准方程为y 2＝4x 或x 2＝－12y .准线方程为x ＝－1或y ＝18.题型二 抛物线的焦点弦问题例2 已知抛物线方程为y 2＝2px (p >0)，过此抛物线的焦点的直线与抛物线交于A ，B 两点，且|AB |＝52p ，求AB 所在的直线方程.解 由题意知焦点F ⎝⎛⎭⎫p 2，0，设A (x 1，y 1)，B (x 2，y 2)， 若AB ⊥x 轴，则|AB |＝2p <52p ，不满足题意.所以直线AB 的斜率存在，设为k ，则直线AB 的方程为y ＝k ⎝⎛⎭⎫x －p2，k ≠0. 由⎩⎪⎨⎪⎧y ＝k ⎝⎛⎭⎫x －p 2，y 2＝2px ，消去x ，整理得ky 2－2py －kp 2＝0. 由根与系数的关系得y 1＋y 2＝2pk，y 1y 2＝－p 2. 所以|AB |＝(x 1－x 2)2＋(y 1－y 2)2 ＝⎝⎛⎭⎫1＋1k 2·(y 1－y 2)2 ＝1＋1k2·(y 1＋y 2)2－4y 1y 2＝2p ⎝⎛⎭⎫1＋1k 2＝52p ， 解得k ＝±2.所以AB 所在的直线方程为y ＝2⎝⎛⎭⎫x －p 2 或y ＝－2⎝⎛⎭⎫x －p2. 反思与感悟 (1)解决抛物线的焦点弦问题时，要注意抛物线定义在其中的应用，通过定义将焦点弦长度转化为端点的坐标问题，从而可借助根与系数的关系进行求解. (2)设直线方程时要特别注意斜率不存在的直线应单独讨论.跟踪训练2 已知直线l 经过抛物线y 2＝6x 的焦点F ，且与抛物线相交于A 、B 两点. (1)若直线l 的倾斜角为60°，求|AB |的值； (2)若|AB |＝9，求线段AB 的中点M 到准线的距离. 解 (1)因为直线l 的倾斜角为60°， 所以其斜率k ＝tan60°＝3， 又F ⎝⎛⎭⎫32，0. 所以直线l 的方程为y ＝3⎝⎛⎭⎫x －32.联立⎩⎪⎨⎪⎧y 2＝6x ，y ＝3⎝⎛⎭⎫x －32， 消去y 得x 2－5x ＋94＝0.若设A (x 1，y 1)，B (x 2，y 2).则x 1＋x 2＝5， 而|AB |＝|AF |＋|BF |＝x 1＋p 2＋x 2＋p2＝x 1＋x 2＋p .∴|AB |＝5＋3＝8.(2)设A (x 1，y 1)，B (x 2，y 2)，由抛物线定义知 |AB |＝|AF |＋|BF |＝x 1＋p 2＋x 2＋p2＝x 1＋x 2＋p ＝x 1＋x 2＋3，所以x 1＋x 2＝6，于是线段AB 的中点M 的横坐标是3， 又准线方程是x ＝－32，所以M 到准线的距离等于3＋32＝92.题型三 直线与抛物线的位置关系例3 已知直线l ：y ＝kx ＋1，抛物线C ：y 2＝4x ，当k 为何值时，直线l 与抛物线C 有： (1)一个公共点？ (2)两个公共点？ (3)没有公共点？解 将直线l 和抛物线C 的方程联立得⎩⎪⎨⎪⎧y ＝kx ＋1，y 2＝4x ，消去y ，得k 2x 2＋(2k －4)x ＋1＝0.(*)当k ＝0时，方程(*)只有一个解，为x ＝14，此时y ＝1.∴直线l 与抛物线C 只有一个公共点⎝⎛⎭⎫14，1，此时直线l 平行于x 轴. 当k ≠0时，方程(*)为一元二次方程，Δ＝(2k －4)2－4k 2，①当Δ>0，即k <1且k ≠0时，直线l 与抛物线C 有两个公共点，此时直线l 与抛物线C 相交； ②当Δ＝0，即k ＝1时，直线l 与抛物线C 有一个公共点，此时直线l 与抛物线C 相切； ③当Δ<0，即k >1时，直线l 与抛物线C 没有公共点，此时直线l 与抛物线C 相离. 综上所述，(1)当k ＝1或k ＝0时，直线l 与抛物线C 有一个公共点； (2)当k <1且k ≠0时，直线l 与抛物线C 有两个公共点； (3)当k >1时，直线l 与抛物线C 没有公共点.反思与感悟 直线与抛物线交点的个数，等价于直线方程与抛物线方程联立得到的方程组解的个数.注意直线斜率不存在和得到的方程二次项系数为0的情况.跟踪训练3 如图，过抛物线y 2＝x 上一点A (4,2)作倾斜角互补的两条直线AB ，AC 交抛物线于B ，C 两点，求证：直线BC 的斜率是定值. 证明 设k AB ＝k (k ≠0)， ∵直线AB ，AC 的倾斜角互补， ∴k AC ＝－k (k ≠0)，∴直线AB 的方程是y ＝k (x －4)＋2.由方程组⎩⎪⎨⎪⎧y ＝k (x －4)＋2，y 2＝x ，消去y 后，整理得k 2x 2＋(－8k 2＋4k －1)x ＋16k 2－16k ＋4＝0. ∵A (4,2)，B (x B ，y B )是上述方程组的解. ∴4·x B ＝16k 2－16k ＋4k 2，即x B ＝4k 2－4k ＋1k 2.以－k 代换x B 中的k ，得x C ＝4k 2＋4k ＋1k 2，∴k BC ＝y B －y C x B －x C ＝k (x B －4)＋2－[－k (x C －4)＋2]x B －x C＝k (x B ＋x C －8)x B －x C ＝k (8k 2＋2k 2－8)－8kk 2＝－14.所以直线BC 的斜率为定值.1.以x 轴为对称轴的抛物线的通径(过焦点且与对称轴垂直的弦)长为8，若抛物线的顶点在坐标原点，则其方程为( ) A.y 2＝8xB.y 2＝－8xC.y 2＝8x 或y 2＝－8xD.x 2＝8y 或x 2＝－8y答案 C解析 设抛物线y 2＝2px 或y 2＝－2px (p >0)， 依题意得x ＝p2，代入y 2＝2px 或y 2＝－2px 得|y |＝p ，∴2|y |＝2p ＝8，p ＝4.2.若抛物线y 2＝x 上一点P 到准线的距离等于它到顶点的距离，则点P 的坐标为( ) A.(14，±24) B.(18，±24) C.(14，24) D.(18，24) 答案 B解析 由题意知，点P 到焦点F 的距离等于它到顶点O 的距离，因此点P 在线段OF 的垂直平分线上，而F (14，0)，所以点P 的横坐标为18，代入抛物线方程得y ＝±24，故点P 的坐标为(18，±24)，故选B. 3.抛物线y ＝4x 2上一点到直线y ＝4x －5的距离最短，则该点坐标为( ) A.(1,2) B.(0,0) C.(12，1) D.(1,4)答案 C解析 因为y ＝4x 2与y ＝4x －5不相交，设与y ＝4x －5平行的直线方程为y ＝4x ＋m .则⎩⎪⎨⎪⎧y ＝4x 2，y ＝4x ＋m ，⇒4x 2－4x －m ＝0.① 设此直线与抛物线相切，此时有Δ＝0， 即Δ＝16＋16m ＝0，∴m ＝－1. 将m ＝－1代入①式，x ＝12，y ＝1，故所求点的坐标为(12，1).4．设O 为坐标原点，P 是以F 为焦点的抛物线y 2＝2px (p >0)上任意一点，M 是线段PF 上的点，且|PM |＝2|MF |，则直线OM 的斜率的最大值为( ) A.33 B.23 C.22D ．1答案 C解析 如图，由题可知F ⎝⎛⎭⎫p 2，0，设P 点坐标为⎝⎛⎭⎫y 22p ，y 0，显然，当y 0<0时，k OM <0；y 0>0时，k OM >0，要求k OM 最大值，不妨设y 0>0.则＝＋＝＋13＝＋13(－)＝13＋23＝⎝⎛⎭⎫y 206p ＋p 3，y 03，k OM ＝y 03y 206p ＋p 3＝2y 0p ＋2p y 0≤222＝22，当且仅当y 20＝2p 2等号成立．故选C.5.已知直线x －y ＋1＝0与抛物线y ＝ax 2相切，则a ＝________.答案 －14解析 由⎩⎪⎨⎪⎧x －y ＋1＝0，y ＝ax 2，消去y 得ax 2－x －1＝0， ∵直线与抛物线相切，∴a ≠0且Δ＝1＋4a ＝0. ∴a ＝－14.1.讨论抛物线的几何性质，一定要利用抛物线的标准方程；利用简单性质，也可以根据待定系数法求抛物线的方程.2.直线与抛物线的相交弦问题共有两类，一类是过焦点的弦，一类是不过焦点的弦.解决弦的问题，大多涉及到抛物线的弦长、弦的中点、弦的斜率.常用的办法是将直线方程与抛物线方程联立，转化为关于x 或y 的一元二次方程，然后利用根与系数的关系，这样避免求交点.尤其是弦的中点问题，还应注意“点差法”的运用.3.判断直线与抛物线位置关系的两种方法(1)几何法：利用图像，数形结合，判断直线与抛物线的位置关系，但有误差影响判断的结果. (2)代数法：设直线l 的方程为y ＝kx ＋m ，抛物线的方程为y 2＝2px (p >0)，将直线方程与抛物线方程联立整理成关于x (或y )的一元二次方程形式：Ax 2＋Bx ＋C ＝0(或Ay 2＋By ＋C ＝0).相交：①有两个交点：⎩⎪⎨⎪⎧A ≠0，Δ>0；②有一个交点：A ＝0(直线与抛物线的对称轴平行或重合，即相交)；相切：有一个公共点，即⎩⎪⎨⎪⎧A ≠0，Δ＝0；相离：没有公共点，即⎩⎪⎨⎪⎧A ≠0，Δ<0.直线与抛物线有一个交点，是直线与抛物线相切的必要不充分条件.。

3.2双曲线的简单性质学习目标 1.了解双曲线的简单性质(范围、对称性、顶点、实轴长和虚轴长等).2.理解离心率的定义、取值范围和渐近线方程.3.掌握标准方程中a，b，c，e间的关系.4.能用双曲线的简单性质解决一些简单问题.知识点一双曲线的范围、对称性思考观察下面的图形：(1)从图形上可以看出双曲线是向两端无限延伸的，那么是否与椭圆一样有范围限制？(2)是不是轴对称图形？对称轴是哪条直线？是不是中心对称图形？对称中心是哪个点？梳理(1)双曲线x2a2－y2b2＝1(a>0，b>0)中要求x∈______________，y∈______.双曲线y2a2－x2b2＝1(a>0，b>0)中要求x∈____________，y∈________________.(2)双曲线的对称轴为__________，对称中心为______.知识点二双曲线的顶点思考(1)双曲线的顶点就是双曲线与坐标轴的交点，你认为对吗？为什么？(2)双曲线是否只有两个顶点？双曲线的顶点和焦点能在虚轴上吗？梳理双曲线x2a2－y2b2＝1(a>0，b>0)的顶点坐标为________，______；双曲线y2a2－x2b2＝1(a>0，b>0)的顶点坐标为______，______.知识点三渐近线与离心率思考1能否和椭圆一样，用a，b表示双曲线的离心率？思考2离心率对双曲线开口大小有影响吗？满足什么对应关系？梳理(1)渐近线：直线__________叫作双曲线x2a2－y2b2＝1(a>0，b>0)的渐近线.(2)离心率：双曲线的焦距与实轴长的比______，叫作双曲线的离心率，用e表示(e>1).(3)双曲线的性质见下表：类型一已知双曲线的标准方程研究其简单性质例1求双曲线nx2－my2＝mn(m>0，n>0)的实半轴长、虚半轴长、焦点坐标、离心率、顶点坐标和渐近线方程.引申探究将本例改为“求双曲线9y2－4x2＝－36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程”，请给出解答.反思与感悟 由双曲线的方程研究性质的解题步骤 (1)把双曲线方程化为标准形式是解决本题的关键. (2)由标准方程确定焦点位置，确定a ，b 的值. (3)由c 2＝a 2＋b 2求出c 的值，从而写出双曲线的性质.跟踪训练1 求双曲线9y 2－16x 2＝144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.类型二 由双曲线的性质确定标准方程 例2 求下列双曲线的标准方程.(1)与椭圆y 225＋x 216＝1有公共焦点，且过点(－2，10)；(2)过点(3,92)，离心率e ＝103.反思与感悟 (1)根据双曲线的某些性质求双曲线方程，一般用待定系数法转化为解方程(组)，但要注意焦点的位置，从而正确选择方程的形式. (2)巧设双曲线方程的六种方法与技巧①焦点在x 轴上的双曲线的标准方程可设为x 2a 2－y 2b 2＝1(a >0，b >0).②焦点在y 轴上的双曲线的标准方程可设为y 2a 2－x 2b2＝1(a >0，b >0).③与双曲线x 2a 2－y 2b 2＝1共焦点的双曲线方程可设为x 2a 2－λ－y 2b 2＋λ＝1(λ≠0，－b 2<λ<a 2).④与双曲线x 2a 2－y 2b 2＝1具有相同渐近线的双曲线方程可设为x 2a 2－y 2b 2＝λ(λ≠0).⑤渐近线为y ＝kx 的双曲线方程可设为k 2x 2－y 2＝λ(λ≠0). ⑥渐近线为ax ±by ＝0的双曲线方程可设为a 2x 2－b 2y 2＝λ(λ≠0).跟踪训练2 (1)求与双曲线y 24－x 23＝1有共同的渐近线，且经过点M (3，－2)的双曲线的标准方程；(2)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的离心率e ＝233，过点A (0，－b )和B (a,0)的直线与原点的距离为32，求此双曲线的标准方程.类型三 共轭双曲线与等轴双曲线 命题角度1 共轭双曲线例3 已知双曲线E 与双曲线x 216－y 29＝1共渐近线，且过点A (23，－3).若双曲线M 以双曲线E 的实轴为虚轴，虚轴为实轴，试求双曲线M 的标准方程.反思与感悟 双曲线x 2a 2－y 2b 2＝1(a >0，b >0)与双曲线y 2b 2－x 2a 2＝1(a >0，b >0)互为共轭双曲线，两者：(1)有共同的渐近线.(2)四个焦点共圆.(3)它们的离心率不同，设它们的离心率分别为e 1，e 2，则1e 21＋1e 22＝1.(4)焦点所在坐标轴不同，一个在x 轴上，另一个在y 轴上. 跟踪训练3 与双曲线x 29－y 216＝1有共同渐近线，且过点(－3,23)的双曲线的共轭双曲线的方程为________.命题角度2 等轴双曲线例4 已知等轴双曲线的焦点在x 轴上，且焦点到渐近线的距离是2，求此双曲线的方程.反思与感悟 (1)实轴和虚轴等长的双曲线叫作等轴双曲线.(2)等轴双曲线的性质：①渐近线方程为y ＝±x ；②渐近线互相垂直；③离心率e ＝ 2. (3)等轴双曲线的特征是a ＝b ，等轴双曲线的方程可以设为x 2－y 2＝λ(λ≠0).当λ>0时，双曲线的焦点在x 轴上；当λ<0时，双曲线的焦点在y 轴上.跟踪训练4 若双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的两条渐近线互相垂直，则双曲线的离心率e 为( )A. 2B.2C. 3D. 5类型四 直线与双曲线的位置关系命题角度1 直线与双曲线位置关系的判定与交点问题 例5 已知直线y ＝kx －1与双曲线x 2－y 2＝4. (1)若直线与双曲线没有公共点，求k 的取值范围； (2)若直线与双曲线有两个公共点，求k 的取值范围； (3)若直线与双曲线只有一个公共点，求k 的值.反思与感悟 研究直线与双曲线的位置关系，一般通过解直线方程与双曲线方程所组成的方程组⎩⎪⎨⎪⎧y ＝kx ＋m ， ①x 2a 2－y 2b 2＝1 ②的解的个数进行判断.①代入②得(b 2－a 2k 2)x 2－2a 2mkx －a 2m 2－a 2b 2＝0.当b 2－a 2k 2＝0，即k ＝±ba 时，直线与双曲线渐近线平行时，直线与双曲线交于一点.当b 2－a 2k 2≠0，即k ≠±ba时，Δ＝(－2a 2mk )2－4(b 2－a 2k 2)(－a 2m 2－a 2b 2).Δ>0⇔直线与双曲线有两个交点，称直线与双曲线相交； Δ＝0⇔直线与双曲线有一个交点，称直线与双曲线相切； Δ<0⇔直线与双曲线没有交点，称直线与双曲线相离.通过几何图形也可判定直线与双曲线的位置关系，一般通过直线与渐近线的位置关系进行判断(图中α为渐近线倾斜角，θ为直线l 倾斜角).如图①，θ＝α时，直线l 只与双曲线一支相交，交点只有一个； 如图②，θ>α时，直线l 只与双曲线一支相交，交点有两个； 如图③，θ<α时，直线l 与双曲线两支都相交，交点有两个.跟踪训练5 设双曲线C ：x 2a 2－y 2＝1(a >0)与直线l ：x ＋y ＝1相交于A ，B 两个不同的点.(1)求双曲线的离心率e 的取值范围；(2)设直线l 与y 轴的交点为P ，且P A →＝512PB →，求a 的值.命题角度2 直线与双曲线的相交弦及弦长问题例6 (1)求直线y ＝x ＋1被双曲线x 2－y 24＝1截得的弦长；(2)求过定点(0,1)的直线被双曲线x 2－y 24＝1截得的弦中点的轨迹方程.反思与感悟 (1)利用弦长公式|AB |＝1＋k 2|x A －x B |＝1＋k 2·(x A ＋x B )2－4x A x B ，求解的关键是正确应用根与系数的关系，整理时要始终保持两根之和、两根之积的形式.(2)涉及弦长的中点问题，常用“点差法”，将弦所在直线的斜率、弦的中点坐标联系起来，同时还应充分挖掘题目的隐含条件，寻找量与量间的关系. 其具体解题思路如下：设直线与双曲线相交所得弦AB 端点的坐标分别为A (x 1，y 1)，B (x 2，y 2)，直线AB 的斜率为k ，则|AB |＝1＋k 2|x 1－x 2|＝1＋k 2·(x 1＋x 2)2－4x 1x 2.涉及弦长的问题，常常设而不求.中点弦问题：设A (x 1，y 1)，B (x 2，y 2)是双曲线x 2a 2－y 2b2＝1(a >0，b >0)上不同的两点，且x 1≠x 2，x 1＋x 2≠0，M (x 0，y 0)为线段AB 的中点，则⎩⎨⎧x 21a 2－y 21b2＝1，x 22a 2－y22b 2＝1.两式相减可得y 1－y 2x 1－x 2·y 1＋y 2x 1＋x 2＝b 2a2，即k AB ·y 0x 0＝b 2a2.跟踪训练6 已知双曲线的方程为2x 2－y 2＝2.(1)过定点P (2,1)作直线交双曲线于P 1，P 2两点，当点P (2,1)是弦P 1P 2的中点时，求此直线方程；(2)过定点Q (1,1)能否作直线l ，使l 与此双曲线相交于Q 1，Q 2两点，且Q 是弦Q 1Q 2的中点？若存在，求出l 的方程；若不存在，请说明理由.1.设双曲线x 2a ＋y 29＝1的渐近线方程为3x ±2y ＝0，则a 的值为( )A.－4B.－3C.2D.12.已知双曲线x 2a 2－y 25＝1(a >0)的右焦点为(3,0)，则双曲线的离心率等于( )A.3414B.324C.32D.433.等轴双曲线的一个焦点是F 1(－6,0)，则其标准方程为( ) A.x 29－y 29＝1 B.y 29－x 29＝1 C.y 218－x 218＝1 D.x 218－y 218＝1 4.若双曲线x 24－y 2m ＝1的渐近线方程为y ＝±32x ，则双曲线的焦点坐标是________.5.设双曲线x 2a 2－y 2b2＝1(a >0，b >0)的虚轴长为2，焦距为23，则双曲线的渐近线方程为________.双曲线的综合问题常涉及其离心率、渐近线、范围等，与向量、三角函数、不等式等知识交汇考查综合运用数学知识的能力.(1)当与向量知识结合时，注意运用向量的坐标运算，将向量间的关系，转化为点的坐标问题，再根据根与系数的关系，将所求问题与条件建立关系求解.(2)当与直线有关时，常常联立直线与双曲线的方程，消元后利用一元二次方程的判别式、根与系数的关系构造相关关系求解. 提醒：完成作业 第三章 §3 3.2答案精析问题导学 知识点一思考 (1)有限制，因为x 2a2≥1，即x 2≥a 2，所以x ≥a 或x ≤－a .(2)关于x 轴、y 轴和原点都是对称的，x 轴、y 轴是双曲线的对称轴，原点是对称中心，又叫作双曲线的中心.梳理 (1)(－∞，－a ]∪[a ，＋∞) R R (－∞，－a ]∪[a ，＋∞) (2)x 轴、y 轴 原点 知识点二思考 (1)不对，双曲线的顶点是双曲线与其对称轴的交点，只有在标准形式下，坐标轴才是双曲线的对称轴，此时双曲线与坐标轴的交点是双曲线的顶点.(2)是，只有两个顶点.双曲线的顶点和焦点都不能在虚轴上，只能在实轴上. 梳理 (－a,0) (a,0) (0，－a ) (0，a ) 知识点三思考1 能，离心率e ＝ca ＝a 2＋b 2a ＝1＋b 2a2. 思考2 有影响，因为e ＝ca ＝a 2＋b 2a＝1＋b 2a 2，故当b a 的值越大，渐近线y ＝bax 的斜率越大，双曲线的开口越大，e 也越大，所以e 反映了双曲线开口的大小，即双曲线的离心率越大，它的开口就越大. 梳理 (1)y ＝±b a x (2)ca(3)y ＝±b a x y ＝±ab x题型探究例1 解 把方程nx 2－my 2＝mn (m >0，n >0)化为标准方程为x 2m －y 2n＝1(m >0，n >0)，由此可知，实半轴长a ＝m ， 虚半轴长b ＝n ，c ＝m ＋n ，焦点坐标为(m ＋n ，0)，(－m ＋n ，0)， 离心率e ＝ca ＝m ＋n m＝1＋nm， 顶点坐标为(－m ，0)，(m ，0)，所以渐近线方程为y ＝±n mx ， 即y ＝±mn mx . 引申探究解 将9y 2－4x 2＝－36变形为x 29－y 24＝1，即x 232－y 222＝1，所以a ＝3，b ＝2，c ＝13， 因此顶点坐标为(－3,0)，(3,0)， 焦点坐标为(－13，0)，(13，0)， 实轴长是2a ＝6，虚轴长是2b ＝4， 离心率e ＝c a ＝133，渐近线方程为y ＝±b a x ＝±23x .跟踪训练1 解 把方程9y 2－16x 2＝144化为标准方程y 242－x 232＝1.由此可知，实半轴长a ＝4，虚半轴长b ＝3；c ＝a 2＋b 2＝42＋32＝5，焦点坐标是(0，－5)，(0,5)； 离心率e ＝c a ＝54；渐近线方程为y ＝±43x .例2 解 (1)方法一 椭圆y 225＋x 216＝1的焦点为F 1(0，－3)，F 2(0,3)，设双曲线的标准方程为y 2a 2－x 2b 2＝1(a >0，b >0)，则有⎩⎪⎨⎪⎧10a 2－4b 2＝1，a 2＋b 2＝9，解得⎩⎪⎨⎪⎧a 2＝5，b 2＝4.故所求双曲线的标准方程为y 25－x 24＝1.方法二 由椭圆方程y 225＋x 216＝1知焦点在y 轴上，设所求双曲线的标准方程为y 225－λ－x 2λ－16＝1(16<λ<25).∵双曲线过点(－2，10)， ∴1025－λ－4λ－16＝1，解得λ＝20或λ＝7(舍去)，故所求双曲线的标准方程为y 25－x 24＝1.(2)由e 2＝109，得c 2a 2＝109，设a 2＝9k (k >0)，则c 2＝10k ，b 2＝c 2－a 2＝k . 于是，设所求双曲线方程为 x 29k －y 2k ＝1， ① 或y 29k －x 2k＝1，②把(3,92)代入①，得k ＝－161与k >0矛盾，无解； 把(3,92)代入②，得k ＝9，故所求双曲线的标准方程为y 281－x 29＝1.跟踪训练2 解 (1)设所求双曲线的方程为y 24－x 23＝λ(λ≠0).∵点M (3，－2)在双曲线上， ∴44－93＝λ，即λ＝－2. ∴双曲线的标准方程为x 26－y 28＝1.(2)∵e ＝233，∴c a ＝233，∴a 2＋b 2a 2＝43，∴a 2＝3b 2.①又∵直线AB 的方程为bx －ay －ab ＝0， ∴d ＝ab a 2＋b 2＝32， 即4a 2b 2＝3(a 2＋b 2).②解①②组成的方程组，得a 2＝3，b 2＝1. ∴双曲线的标准方程为x 23－y 2＝1.例3 解 由题意，设双曲线E 的方程为 x 216－y 29＝t (t ≠0). ∵点A (23，－3)在双曲线上，∴(23)216－(－3)29＝t ， ∴t ＝－14， ∴双曲线E 的标准方程为y 294－x 24＝1. 又双曲线M 与双曲线E 互为共轭双曲线，故双曲线M 的标准方程为x 24－y 294＝1. 跟踪训练3 y 24－x 294＝1 例4 解 设双曲线方程为x 2－y 2＝a 2(a >0)，则它的渐近线方程为y ＝±x ，焦点坐标为(2a,0)，(－2a,0)， ∴2a 2＝2，∴a ＝2，∴双曲线的方程为x 2－y 2＝2. 跟踪训练4 A例5 解 由⎩⎪⎨⎪⎧y ＝kx －1，x 2－y 2＝4， 得(1－k 2)x 2＋2kx －5＝0. ①(1)直线与双曲线没有公共点，则①式方程无解.∴⎩⎪⎨⎪⎧1－k 2≠0，Δ＝4k 2＋20(1－k 2)<0， 解得k >52或k <－52， 则k 的取值范围为k >52或k <－52. (2)直线与双曲线有两个公共点，则①式方程有两个不相等的根.∴⎩⎪⎨⎪⎧1－k 2≠0，Δ＝4k 2＋20(1－k 2)>0， 解得－52<k <52且k ≠±1. (3)直线与双曲线只有一个公共点，则①式方程只有一解.当1－k 2＝0，即k ＝±1时，①式方程只有一解；当1－k 2≠0时，应满足Δ＝4k 2＋20(1－k 2)＝0，解得k ＝±52，故k 的值为±1或±52. 跟踪训练5 解 (1)由⎩⎪⎨⎪⎧ x 2a 2－y 2＝1，x ＋y ＝1，得(1－a 2)x 2＋2a 2x －2a 2＝0，① 由题意得⎩⎪⎨⎪⎧ 1－a 2≠0，4a 4＋8a 2(1－a 2)>0，a >0，得0<a <2且a ≠1. 又双曲线的离心率e ＝1＋a 2a ＝1a 2＋1， ∴e >62且e ≠ 2. (2)设A (x 1，y 1)，B (x 2，y 2)，易知P (0,1)，∵＝512， ∴(x 1，y 1－1)＝512(x 2，y 2－1)， 故x 1＝512x 2. 又x 1，x 2是方程①的两个根，∴1712x 2＝－2a 21－a 2，512x 22＝－2a 21－a 2. 又a >0，∴a ＝1713. 例6 解 (1)由⎩⎪⎨⎪⎧ x 2－y 24＝1，y ＝x ＋1，得4x 2－(x ＋1)2－4＝0.化简得3x 2－2x －5＝0.设此方程的解为x 1，x 2，则有x 1＋x 2＝23，x 1x 2＝－53. 故所截得的弦长d ＝2·|x 1－x 2|＝2·(x 1＋x 2)2－4x 1x 2＝2·49＋203＝823.(2)方法一 ∵该直线的斜率不存在时，直线与双曲线无交点，故可设直线的方程为y ＝kx ＋1，它被双曲线截得的弦AB 对应的中点为P (x ，y ).由⎩⎪⎨⎪⎧ y ＝kx ＋1，x 2－y 24＝1，得(4－k 2)x 2－2kx －5＝0. 设此方程的解为x 1，x 2，则4－k 2≠0，Δ＝4k 2＋20(4－k 2)>0，∴16k 2<80，即|k |<5，k ≠±2，且x 1＋x 2＝2k 4－k 2，x 1x 2＝－54－k 2， ∴x ＝12(x 1＋x 2)＝k 4－k 2， y ＝12(y 1＋y 2)＝k 2(x 1＋x 2)＋1 ＝44－k 2. 由⎩⎨⎧ x ＝k 4－k 2，y ＝44－k 2消去k ，得4x 2－y 2＋y ＝0(y <－4或y ≥1).方法二 设弦的两个端点坐标分别为A (x 1，y 1)，B (x 2，y 2)，弦的中点为P (x ，y )，则⎩⎪⎨⎪⎧4x 21－y 21＝4， ①4x 22－y 22＝4. ② ①－②，得4(x 1＋x 2)(x 1－x 2)＝(y 1＋y 2)(y 1－y 2)，∴y 1＋y 2x 1＋x 2＝4(x 1－x 2)y 1－y 2， 即y x ＝4k ＝4x y －1(k 为直线AB 的斜率)， 整理得4x 2－y 2＋y ＝0(y <－4或y ≥1).跟踪训练6 解 (1)若直线斜率不存在，即P 1P 2垂直于x 轴，则由双曲线的对称性知弦P 1P 2的中点在x 轴上，不可能是点P (2,1)，所以直线l 斜率存在.故可设直线l 的方程为y －1＝k (x －2)，即y ＝kx －2k ＋1.由⎩⎪⎨⎪⎧2x 2－y 2＝2，y ＝kx －2k ＋1消去y 并化简， 得(2－k 2)x 2＋2k (2k －1)x －4k 2＋4k －3＝0.设直线l 与双曲线的交点P 1(x 1，y 1)，P 2(x 2，y 2).当2－k 2≠0，即k 2≠2时，有x 1＋x 2＝－2k (2k －1)2－k 2. 又点P (2,1)是弦P 1P 2的中点，∴－2k (2k －1)2－k 2＝4，解得k ＝4. 当k ＝4时，Δ＝4k 2(2k －1)2－4(2－k 2)(－4k 2＋4k －3)＝56×5>0. 当k 2＝2，即k ＝±2时，此时与渐近线的斜率相等，即k ＝±2的直线l 与双曲线不可能有两个交点.综上可知，所求直线的方程为4x －y －7＝0.(2)假设这样的直线l 存在，设Q 1(x 1，y 1)，Q 2(x 2，y 2)，则有x 1＋x 22＝1，y 1＋y 22＝1， ∴x 1＋x 2＝2，y 1＋y 2＝2，且⎩⎪⎨⎪⎧2x 21－y 21＝2，2x 22－y 22＝2， 两式相减，得(2x 21－2x 22)－(y 21－y 22)＝0， ∴2(x 1－x 2)(x 1＋x 2)－(y 1－y 2)(y 1＋y 2)＝0，∴2(x 1－x 2)－(y 1－y 2)＝0.若直线Q 1Q 2垂直于x 轴，则线段Q 1Q 2中点不可能是点Q (1,1)，∴直线Q 1Q 2斜率存在，于是k ＝y 1－y 2x 1－x 2＝2， ∴直线Q 1Q 2的方程为y －1＝2(x －1)，即y ＝2x －1.由⎩⎪⎨⎪⎧y ＝2x －1，2x 2－y 2＝2，得2x 2－(2x －1)2＝2， 即2x 2－4x ＋3＝0，∴Δ＝16－24<0.∴直线l 与双曲线没有公共点，因此这样的直线不存在. 当堂训练1.A2.C3.D4.(±7，0)5.y ＝±22x。

2.2.2 抛物线的简单性质（二）[A.基础达标]1．抛物线y ＝ax 2＋1与直线y ＝x 相切，则a 等于( ) A. 18 B. 14 C. 12D ．1 解析：选B.由⎩⎪⎨⎪⎧y ＝ax 2＋1，y ＝x 消去y 整理得ax 2－x ＋1＝0，由题意a ≠0，Δ＝(－1)2－4a＝0.所以a ＝14.2．已知抛物线C ：y 2＝4x 的焦点为F ，直线y ＝2x －4与C 交于A ，B 两点，则cos ∠AFB ＝( )A.45B.35 C ．－35 D ．－45解析：选D.由⎩⎪⎨⎪⎧y 2＝4x ，y ＝2x －4，得⎩⎪⎨⎪⎧x ＝1，y ＝－2或⎩⎪⎨⎪⎧x ＝4，y ＝4. 令B (1，－2)，A (4，4)，又F (1，0)， 所以由两点间距离公式，得|BF |＝2，|AF |＝5，|AB |＝35，所以cos ∠AFB ＝|BF |2＋|AF |2－|AB |22|BF |·|AF |＝4＋25－452×2×5＝－45. 3．A ，B 是抛物线x 2＝y 上任意两点(非原点)，当OA →·OB →最小时，OA →，OB →所在两条直线的斜率之积k OA ·k OB ＝( )A.12 B ．－12 C. 3 D ．－ 3解析：选B.由题意可设A (x 1，x 21)，B (x 2，x 22)， OA →＝(x 1，x 21)，OB →＝(x 2，x 22)， OA →·OB →＝x 1x 2＋(x 1x 2)2＝(x 1x 2＋12)2－14≥－14，当且仅当x 1x 2＝－12时OA →·OB →取得最小值．此时k OA ·k OB ＝x 21x 1·x 22x 2＝x 1x 2＝－12.4．设抛物线C ：y 2＝2px (p >0)的焦点为F ，点M 在C 上，|MF |＝5.若以MF 为直径的圆过点(0，2)，则C 的方程为( )A ．y 2＝4x 或y 2＝8xB ．y 2＝2x 或y 2＝8xC ．y 2＝4x 或y 2＝16xD ．y 2＝2x 或y 2＝16x解析：选C.设M (x 0，y 0)，A (0，2)，MF 的中点为N . 由y 2＝2px ，F (p2，0)，所以N 点的坐标为(x 0＋p 22，y 02)． 由抛物线的定义知，x 0＋p2＝5， 所以x 0＝5－p2.所以y 0＝2p （5－p2）.所以|AN |＝|MF |2＝52，所以|AN |2＝254.所以(x 0＋p22)2＋(y 02－2)2＝254. 即（5－p 2＋p2）24＋⎝⎛⎭⎪⎪⎫2p （5－p2）2－22＝254.所以 2p （5－p2）2－2＝0.整理得p 2－10p ＋16＝0. 解得p ＝2或p ＝8.所以抛物线方程为y 2＝4x 或y 2＝16x .5．已知抛物线C 的方程为x 2＝12y ，过点A (0，－1)和点B (t ，3)的直线与抛物线C 没有公共点，则实数t 的取值范围是( )A ．(－∞，－1)∪(1，＋∞)B ．(－∞，－22)∪(22，＋∞)C ．(－∞，－22)∪(22，＋∞)D ．(－∞，－2)∪(2，＋∞)解析：选D.当AB 的斜率不存在时，x ＝0，其与x 2＝12y 有公共点，不满足要求；当AB的斜率存在时，可设AB 所在直线的方程为y ＝kx －1，代入x 2＝12y ，整理得2x 2－kx ＋1＝0，Δ＝(－k )2－4×2<0，得k 2<8，B (t ，3)在y ＝kx －1上即3＝kt －1，(4t)2＝k 2<8，即t 2>2得t ∈(－∞，－2)∪(2，＋∞)．6．过抛物线y 2＝2px (p >0)的焦点F 的直线与抛物线交于A 、B 两点，若A 、B 在准线上的射影为A 1、B 1，则∠A 1FB 1等于________．解析：如图，由抛物线定义知|AA 1|＝|AF |，|BB 1|＝|BF |，所以∠AA 1F ＝∠AFA 1，又∠AA 1F ＝∠A 1FO ，所以∠AFA 1＝∠A 1FO ， 同理∠BFB 1＝∠B 1FO ，于是∠AFA 1＋∠BFB 1＝∠A 1FO ＋∠B 1FO ＝∠A 1FB 1. 故∠A 1FB 1＝90°. 答案：90°7．已知抛物线x 2＝4y 的焦点为F ，经过F 的直线与抛物线相交于A ，B 两点，则以AB 为直径的圆在x 轴上所截得的弦长的最小值是________．解析：由题意知满足题意的AB 所在直线的斜率存在，故AB 所在的直线方程可写为y ＝kx ＋1，代入x 2＝4y ，整理得x 2－4kx －4＝0，x 1＋x 2＝4k ，由y ＝kx ＋1可得y 1＋y 2＝kx 1＋1＋kx 2＋1＝4k 2＋2，|AB |＝y 1＋y 2＋p ＝4k 2＋4，故所截弦长＝2（2k 2＋2）2－（2k 2＋1）2＝24k 2＋3≥23，当k ＝0时弦长取最小值． 答案：2 38．已知定长为3的线段AB 的两个端点在抛物线y 2＝2x 上移动，M 为AB 的中点，则M 点到y 轴的最短距离为________．解析：如图所示，抛物线y 2＝2x 的准线为l ：x ＝－12，过点A 、B 、M分别作AA ′、BB ′、MM ′垂直于l ，垂足分别为A ′、B ′、M ′.由抛物线定义知|AA ′|＝|FA |，|BB ′|＝|FB |.又M 为AB 中点，由梯形中位线定理得|MM ′|＝12(|AA ′|＋|BB ′|)＝12(|FA |＋|FB |)≥12|AB |＝12×3＝32，则M到y 轴的距离d ≥32－12＝1(当且仅当AB 过抛物线的焦点时取“＝”)，所以d min ＝1，即M 点到y 轴的最短距离为1.答案：19．已知抛物线y 2＝12x 和点P (5，2)，直线l 经过点P 且与抛物线交于A 、B 两点，O 为坐标原点．(1)当点P 恰好为线段AB 的中点时，求l 的方程； (2)当直线l 的斜率为1时，求△OAB 的面积． 解：(1)设A (x 1，y 1)，B (x 2，y 2)， 因为A 、B 在抛物线上，所以y 21＝12x 1，y 22＝12x 2，两式相减，得(y 1＋y 2)(y 1－y 2)＝12(x 1－x 2)． 因为P 为线段AB 的中点， 所以x 1≠x 2，又y 1＋y 2＝4，所以k ＝y 1－y 2x 1－x 2＝12y 1＋y 2＝3，所以直线l 的方程为y －2＝3(x －5)，即3x －y －13＝0. 经验证适合题意．(2)由题意知l 的方程为y －2＝1·(x －5)即y ＝x －3. 由⎩⎪⎨⎪⎧y ＝x －3，y 2＝12x得x 2－18x ＋9＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝18，x 1x 2＝9.所以|AB |＝1＋k 2（x 1＋x 2）2－4x 1x 2 ＝2·324－36＝24.又点O 到直线x －y －3＝0的距离d ＝32，所以S △OAB ＝12|AB |·d ＝12×24×32＝18 2.10．如图，设抛物线C ：x 2＝4y 的焦点为F ，P (x 0，y 0)为抛物线上的任一点(其中x 0≠0)，过P 点的切线交y 轴于Q 点．(1)若P (2，1)，求证：|FP |＝|FQ |；(2)已知M (0，y 0)，过M 点且斜率为x 02的直线与抛物线C 交于A 、B 两点，若AM →＝λMB →(λ>1)，求λ的值．解：(1)证明：由抛物线定义知|PF |＝y 0＋1＝2， 设过P 点的切线方程为y －1＝k (x －2)， 由⎩⎪⎨⎪⎧y －1＝k （x －2），x 2＝4y 得x 2－4kx ＋8k －4＝0， 令Δ＝16k 2－4(8k －4)＝0得k ＝1， 可得PQ 所在直线方程为y ＝x －1， 所以得Q 点坐标为(0，－1)， 所以|QF |＝2，即|PF |＝|QF |.(2)设A (x 1，y 1)，B (x 2，y 2)，又M 点坐标为(0，y 0)，所以AB 方程为y ＝x 02x ＋y 0，由⎩⎪⎨⎪⎧x 2＝4y ，y ＝x 02x ＋y 0得x 2－2x 0x －4y 0＝0. 所以x 1＋x 2＝2x 0，x 1x 2＝－4y 0＝－x 20，① 由AM →＝λMB →得：(－x 1，y 0－y 1)＝λ·(x 2，y 2－y 0)， 所以x 1＝－λx 2，②由①②知⎩⎪⎨⎪⎧（1－λ）x 2＝2x 0，λx 22＝x 20，得(1－λ)2x 22＝4λx 22，由x 0≠0可得x 2≠0，所以(1－λ)2＝4λ，又λ>1，解得λ＝3＋2 2.[B.能力提升]1．已知抛物线y 2＝2px (p >0)与圆(x －a )2＋y 2＝r 2(a >0)有且只有一个公共点，则( ) A ．r ＝a ＝p B ．r ＝a ≤p C ．r <a ≤p D ．r <a ＝p解析：选B.当r <a 时，根据圆与抛物线的对称性可知，圆(x －a )2＋y 2＝r 2(a >0)与抛物线y 2＝2px (p >0)要么没有交点，要么交于两点或四点，与题意不符；当r >a 时，易知圆与抛物线有两个交点，与题意不符；当r ＝a 时，圆与抛物线交于原点，要使圆与抛物线有且只有一个公共点，必须使方程(x －a )2＋2px ＝r 2(x ≥0)有且仅有一个解x ＝0，可得a ≤p .故选B.2．如图，已知抛物线的方程为x 2＝2py (p >0)，过点A (0，－1)作直线l 与抛物线相交于P ，Q 两点，点B 的坐标为(0，1)，连接BP ，BQ ，设QB ，BP 的延长线与x 轴分别相交于M ，N 两点．如果QB 的斜率与PB 的斜率的乘积为－3，则∠MBN 的大小等于()A.π2 B.π4 C.2π3 D.π3 解析：选D.由题意设P (x 1，x 212p )，Q (x 2，x 222p)(x 1≠x 2)，设PQ 所在直线方程为y ＝kx －1代入x 2＝2py ，整理得：x 2－2kpx ＋2p ＝0，则⎩⎪⎨⎪⎧x 1＋x 2＝2kp ，x 1x 2＝2p .k QB ＝x 222p －1x 2，k PB ＝x 212p －1x 1，可得k QB ＋k PB ＝0，又因为k QB ·k PB ＝－3，所以k QB ＝－3，k PB ＝3，即∠BNM ＝π3，∠BMN ＝π3，所以∠MBN ＝π－∠BNM －∠BMN ＝π3.3．设抛物线y 2＝4x 的焦点为F ，过点M (2，0)的直线与抛物线相交于A ，B 两点，与抛物线的准线交于点C ，|BF |＝32，则S △BCFS △ACF＝________.解析：因为|BF |＝32，所以B 的横坐标为12，不妨设B 的坐标为(12，－2)，所以AB 的方程为y ＝223(x －2)，代入y 2＝4x ，得2x 2－17x ＋8＝0，解得x ＝12或8，故点A 的横坐标为8.故A 到准线的距离为8＋1＝9.S △BCF S △ACF ＝|BC ||AC |＝B 到准线的距离A 到准线的距离＝329＝16. 答案：164．抛物线y 2＝2px (p >0)的焦点为F ，已知点A ，B 为抛物线上的两个动点，且满足∠AFB＝120°，过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N ，则|MN ||AB |的最大值为________．解析：由余弦定理，得|AB |2＝|AF |2＋|BF |2－2|AF |·|BF |cos 120°＝|AF |2＋|BF |2＋|AF |·|BF |，过A ，B 作AA ′，BB ′垂直于准线，则|MN |＝12(|AA ′|＋|BB ′|)＝12(|FA |＋|FB |)，所以|MN ||AB |＝|FA |＋|FB |2|AB |＝|FA |＋|FB |2|AF |2＋|BF |2＋|FA |·|FB |＝12|AF |2＋|BF |2＋|FA |·|FB |（|AF |＋|BF |）2＝12（|AF |＋|BF |）2－|AF |·|BF |（|AF |＋|BF |）2＝121－|AF |·|BF |（|AF |＋|BF |）2≤121－（|AF |＋|BF |2）2（|AF |＋|BF |）2＝33，当且仅当|AF |＝|BF |时，等号成立．答案：335．已知抛物线C ：y 2＝2px(p >0)经过点P (2，4)，直线l ：y ＝3x －23交C 于A 、B 两点，与x 轴相交于点F .(1)求抛物线方程及其准线方程；(2)已知点M (－2，5)，直线MA 、MF 、MB 的斜率分别为k 1、k 2、k 3，求证：k 1、k 2、k 3成等差数列．解：(1)因为抛物线C ：y 2＝2px (p >0)经过点P (2，4)，所以42＝2p ×2，所以p ＝4，所以抛物线的方程是y 2＝8x ， 所以抛物线准线方程是x ＝－2.(2)因为直线l ：y ＝3x －23与x 轴相交于点F ， 所以F (2，0)．因为M (－2，5)，所以k 2＝5－0－2－2＝－54.设A (x 1，y 1)、B (x 2，y 2)，由方程组⎩⎨⎧y ＝3x －23，y 2＝8x得 3x 2－20x ＋12＝0.法一：x 1＋x 2＝203，x 1x 2＝4.所以k 1＝y 1－5x 1＋2＝3x 1－23－5x 1＋2， k 3＝y 2－5x 2＋2＝3x 2－23－5x 2＋2，所以k 1＋k 3＝（x 2＋2）（3x 1－23－5）＋（x 1＋2）（3x 2－23－5）（x 1＋2）（x 2＋2）＝23x 1x 2－5（x 1＋x 2）－83－20x 1x 2＋2（x 1＋x 2）＋4＝23×4－203×5－83－204＋2×203＋4＝－52，所以k 1＋k 3＝2k 2，所以k 1、k 2、k 3成等差数列．法二：⎩⎨⎧x 1＝6，y 1＝43，⎩⎪⎨⎪⎧x 2＝23，y 2＝－433，即A (6，43)、B (23，－433)，所以k 1＝y 1－5x 1＋2＝43－58，k 3＝y 2－5x 2＋2＝－433－523＋2＝－43＋158，所以k 1＋k 3＝－52，所以k 1＋k 3＝2k 2，所以k 1、k 2、k 3成等差数列．6．(选做题)已知抛物线E 的顶点在原点，焦点为F (2，0)， (1)求抛物线方程；(2)过点T (t ，0)作两条互相垂直的直线分别交抛物线E 于A ，B ，C ，D 四点，且M ，N 分别为线段AB ，CD 的中点，求△TMN 的面积最小值．解：(1)由题意知，p ＝4，故所求抛物线方程为 y 2＝8x .(2)根据题意得AB ，CD 的斜率存在，故设直线AB ：x ＝my ＋t ，直线CD ：x ＝－1my ＋t ，A (x 1，y 1)，B (x 2，y 2)，C (x 3，y 3)，D (x 4，y 4)， 由⎩⎪⎨⎪⎧x ＝my ＋t ，y 2＝8x 得y 2－8my －8t ＝0. 所以y 1＋y 22＝4m ⇒x 1＋x 22＝4m 2＋t ⇒M (4m 2＋t ，4m )，同理可得N (4m 2＋t ，－4m)，所以|TN |＝16m 4＋16m 2＝4|m |2m 2＋1， |TM |＝16m 4＋16m 2＝4|m |m 2＋1，所以S △TMN ＝12|TM ||TN |＝8(|m |＋1|m |)≥16.当且仅当|m |＝1时，面积取到最小值16.。