第3课时 二次函数3
- 格式:ppt
- 大小:3.09 MB
- 文档页数:20





人教版数学九年级上22.1.3二次函数y=a(x-h)2+k的图像和性质教学设计图象上下平移的口诀:k 值正上移,负下移. (3)归纳与总结:通过对二次函数 y = 2x 2 + 1, y = 2x 2 - 1 的探究,你能说出二次函数 y = ax 2 + k (a >0)的图象特征和性质吗? 一般地,当 a >0 时,抛物线 y = ax 2 + k 的对称轴是 y 轴,顶点是(0,k ),开口向上,顶点是抛物线的最低点,a 越大,抛物线的开口越小.当 x <0 时, y 随 x 的增大而减小,当 x >0 时, y 随 x 的增大而增大.当 a <0 时,抛物线 y = ax 2 + k 的对称轴是 y 轴,顶点是(0,k ),开口向下,顶点是抛物线的最高点,a 越小,抛物线的开口越小.当 x <0 时, y 随 x 的增大而增大,当 x >0 时, y 随 x 的增大而减小.完成相应练习2. 类比探究二次函数y=a(x-h)2的图象和性质画出二次函数y=-2,y=-2,y=-2的图象,并探究它们的图象特征和性质。
(1)自主学习:参照教材P33-34“探究”的填表、描点、画图。
(2)讨论:①观察y =-21(x +1)2,y =-21(x -1)2的图象,分别指出他们的开口方向、对称轴、顶点。
抛物线y =-21(x +1)2的开口向下,对称轴是经过点(-1,0)且与x 轴垂直的直线,把它记作x =-1,顶点是(-1,系,总结出二次函数y = ax 2+ k 的图象性质。
教师引导学生根据画函数图象的步骤画出函数的图象,交流合作,各组选派代表发表意见用从特殊到一般的学习方法,还培养了学生的交流沟通能力、总结归纳能力。
0);抛物线y =-21(x -1)2的开口向下,对称轴是x =1,顶点是(1,0).②y=-2,y=-2与抛物线y=-2有什么关系?归纳:抛物线y =a(x -h)2与抛物线y =ax 2有什么关系?抛物线y =a(x -h)2与y =ax 2形状相同,位置不同. 当h >0时,把抛物线y =ax 2向右平移h 个单位,可以得到抛物线y =a(x -h)2;当h <0时,把抛物线y =ax 2向左平移∣h ∣个单位,可以得到抛物线y =a(x -h)2.图象左右平移的口诀:h 值正右移,负左移.(3)归纳与总结: y=a(x-h)2的图像性质:a>0,开口向____,当x=___时,函数y 有最___值=____,在对称轴的左侧,y 随x 的增大而____,在对称轴的右侧,y 随x 的增大而____.a<0,开口向____,当x=____时,函数y 有最___值=____,在对称轴的左侧,y 随x 的增大而____,在对称轴的右侧,y 随x 的增大而_____.完成相应练习3. 类比探究二次函数y=a(x-h)2+k的图象和性质(1)自主学习:学生观察所画的函数图象,互相交流、探讨,再让学生发表各自的见解,教师补充完善。
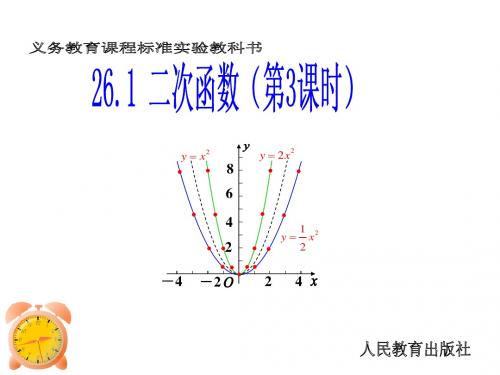
板块一、课前回顾要点一:二次函数2ax y =通过怎样的平移得到二次函数()22y h x a k ax y -=+=与?要点二:○1如何确定二次函数的开口方向?开口的大小跟什么有关? ○22ax y =、()22y h x a k ax y -=+=与的顶点坐标、对称轴、最值。
板块二、新课讲解知识点一、二次函数k h x a y +-=2)(的图象与性质 一、知识衔接由前面的知识,我们知道:○1函数22x y =的图象,向上平移2个单位,可以得到函数________________的图象; ○2函数22x y =的图象,向右平移3个单位,可以得到函数________________的图象;那么函数22x y =的图象,如何平移,才能得到函数2)3(22+-=x y 的图象呢?二、实践探索 (略)通过实践知道:2)3(22+-=x y 的图象是由22x y =先向右平移3个单位得到2)3(2-=x y ,再由2)3(2-=x y 的图象向上平移2个单位而得到的。
或:2)3(22+-=x y 的图象是由22x y =先向上平移2个单位得到22y 2+=x ,再由22y 2+=x 的图象向右平移3个单位而得到的。
(温馨提示:无论是先上下平移、还是先左右平移,只要严格按照平移规则进行,最后图象都是一样的。
)二次函数(三)归纳总结:由上可知:二次函数2)3(22+-=x y 的开口方向 、顶点坐标: 、 对称轴 、有 值(“最大”或“最小”)、在对称轴(左边)函数值的增减性:、在对称轴(右边)函数值的增减性: 。
三、二次函数k h x a y +-=2)(的图象与性质1. 二次函数的图象的上下平移,只影响二次函数2)(h x a y -=+k 中___________的值;左右平移,只影响__________________的值,抛物线的____________________不变,所以平移时,可根据 的改变,确定平移前、后的函数关系式及平移的路径. 2、理一理知识点y =ax 2y =ax 2+k y =a (x-h)2y =a (x -h)2+k 开口方向顶点 对称轴最值增减性 (对称轴右侧)3.抛物线y =a (x -h)2+k 与y =ax 2形状___________,位置________________. 4. 我们把k h x a y +-=2)(叫做二次函数的顶点式。