人教版数学九年级上册导学案：《圆》第2节 直线和圆和位置关系导学案2

24.2.2 直线和圆的位置关系(2)预习案一、预习目标及范围：1.判定一条直线是否是圆的切线并会过圆上一点作圆的切线.2.理解并掌握圆的切线的判定定理及性质定理.（重点）3.能运用圆的切线的判定定理和性质定理解决问题.（难点）预习范围：P97-98二、预习要点1、切线的判定定理：经过__________并且_______ 直线是圆的切线.定理必须满足两个条件：①____________②____ ________2、切线的性质定理：圆的切线_______经过切点的 .三、预习检测1、下列说法正确的是（）A、与圆有公共点的直线是圆的切线B、到圆心的距离等于圆的半径的直线是圆的切线C、垂直于圆的半径的直线是圆的切线D、过圆的半径的外端的直线是圆的切线2、直线AB经过⊙O上的点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.B探究案一、合作探究活动内容1：小组合作探究1: 切线的判定定理问题：已知圆O上一点A，怎样根据圆的切线定义过点A作圆O的切线？观察：（1）圆心O到直线AB的距离和圆的半径有什么数量关系?（2)二者位置有什么关系？为什么？归纳: 切线的判定定理——判一判：下列各直线是不是圆的切线？如果不是，请说明为什么？判断一条直线是一个圆的切线有三个方法：1.定义法：2.数量关系法：3.判定定理：探究2：切线的性质定理思考：如图，如果直线l是⊙O的切线，点A为切点，那么OA与l垂直吗？切线性质：探究3：性质定理的证明证法1：反证法A l证法2：构造法活动内容2：典例精析例1 已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.求证：直线AB是⊙O的切线.分析：由于AB过⊙O上的点C，所以连接OC，只要证明AB⊥OC即可.证明：例2 如图,△ABC 中，AB＝AC，O 是BC中点，⊙O与AB 相切于E.求证：AC 是⊙O 的切线．分析：根据切线的判定定理，要证明AC是⊙O的切线，只要证明由点O向AC所作的垂线段OF是⊙O的半径就可以了，而OE是⊙O的半径，因此只需要证明OF=OE.证明：归纳：证切线时辅助线的添加方法：(1)(2)有切线时常用辅助线添加方法(1)切线的其它重要结论(1)（2）二、随堂检测1.判断下列命题是否正确.⑴ 经过半径外端的直线是圆的切线.（）⑵ 垂直于半径的直线是圆的切线. （）⑶过直径的外端并且垂直于这条直径的直线是圆的切线. （）⑷ 和圆只有一个公共点的直线是圆的切线. （）⑸过直径一端点且垂直于直径的直线是圆的切线. （）2. 2.如图所示，A是⊙O上一点，且AO=5,PO=13,AP=12,则PA与⊙O的位置关系是 .3.如图，在⊙O 的内接四边形ABCD 中，AB 是直径，∠BCD =120°，过D 点的切线PD 与直线AB 交于点P ，则∠ADP 的度数为（ ）A ．40° B．35° C．30° D．45°4.如图,△ABC 中，AB =AC ，以AB 为直径的⊙O 交边BC 于P ， PE ⊥AC 于E . 求证:PE 是⊙O 的切线.5.已知：△ABC 内接于⊙O ，过点A 作直线EF .（1）如图1，AB 为直径，要使EF 为⊙O 的切线，还需添加的条件是（只需写出两种情况）：① _________ ；② _____________ .（2）如图2，AB 是非直径的弦，∠CAE =∠B ，求证：EF 是⊙O 的切线.参考答案预习检测：B图1图21.B2.证明：∵OA=OB,CA=CB，OC=OC∴△AOC≌△BOC∴∠ACO=∠BCO∵∠ACO+∠BCO=180o∴OC⊥AB又∵直线AB经过⊙O上的点C,∴直线AB是⊙O的切线.随堂检测1. ××√√√2.相切3.C4. 证明：连接OP.∵AB=AC,∴∠B=∠C.∵OB=OP，∴∠B=∠OPB，∴∠OBP=∠C.∴OP∥AC.∵PE⊥AC，∴PE⊥OP.∴PE为⊙O的切线.5. 证明：连接AO并延长交⊙O于D,连接CD,则AD为⊙O的直径. ∴ ∠D+ ∠DAC=90 °,∵ ∠D与∠B同对AC ,∴ ∠D= ∠B,又∵∠CAE= ∠B,∴ ∠D= ∠CAE,∴ ∠DAC+ ∠EAC=90°,∴EF是⊙O的切线.。

《直线与圆的位置关系》导学案一、学习目标1、理解直线与圆的三种位置关系：相交、相切、相离。

2、掌握直线与圆位置关系的判定方法，包括代数法和几何法。

3、能运用直线与圆的位置关系解决相关的实际问题。

二、学习重难点1、重点（1）直线与圆的三种位置关系的定义及判定。

（2）直线与圆位置关系的判定方法的应用。

2、难点（1）几何法判定直线与圆位置关系的原理。

（2）灵活运用直线与圆的位置关系解决综合问题。

三、知识链接1、圆的标准方程：＼（（x a)＾2 ＋（y b)＾2 ＝ r^2\），其中\（（a, b)＼）为圆心坐标，＼（r\）为圆的半径。

2、点\（P(x_0, y_0)＼）到直线\（Ax ＋ By ＋ C ＝ 0\）的距离公式：＼（d ＝＼frac{｜Ax_0 ＋ By_0 ＋ C|｝｛＼sqrt{A^2 ＋ B^2}｝＼）四、学习过程（一）引入通过展示一些生活中直线与圆的位置关系的实例，如太阳升起时地平线与太阳的位置关系、自行车车轮与地面的位置关系等，引出直线与圆的位置关系这一课题。

（二）直线与圆的位置关系的定义1、相交：直线与圆有两个公共点。

2、相切：直线与圆只有一个公共点。

3、相离：直线与圆没有公共点。

（三）直线与圆位置关系的判定方法1、代数法将直线方程与圆的方程联立，消去\（y\）（或\（x\））得到一个关于\（x\）（或\（y\））的一元二次方程，然后根据判别式\（＼Delta\）的值来判断直线与圆的位置关系。

（1）＼（＼Delta ＞ 0\），直线与圆相交。

（2）＼（＼Delta ＝ 0\），直线与圆相切。

（3）＼（＼Delta ＜ 0\），直线与圆相离。

2、几何法计算圆心到直线的距离\（d\），与圆的半径\（r\）进行比较。

（1）＼（d ＜ r\），直线与圆相交。

（2）＼（d ＝ r\），直线与圆相切。

（3）＼（d ＞ r\），直线与圆相离。

（四）例题讲解例 1：已知圆\（C\）：＼（x^2 ＋ y^2 2x 4y 4 ＝ 0\），直线\（l\）：＼（x 2y 2 ＝0\），判断直线\（l\）与圆\（C\）的位置关系。

课题：24.2.2 直线和圆的位置关系【学习目标】理解设⊙O的半径为r，直线L到圆心O的距离为d，则有：直线L和⊙O相交⇔d<r；直线L和⊙O相切⇔d=r；直线L和⊙O相离⇔d>r．理解切线的判定定理：理解切线的性质定理并熟练掌握以上内容解决一些实际问题．【学习重、难点】切线的判定定理；切线的性质定理及其运用它们解决一些具体的题目．一、自主探究同学们，我们前一节课已经学到点和圆的位置关系．设⊙O的半径为r，点P到圆心的距离OP=d，(b)二、自学指导自学课本Ｐ93---P98页思考下列问题：1、直线与圆的三种位置关系？2、切线定义：3、切线的性质：4、切线长定理：例:如图，已知Rt △ABC 的斜边AB=8cm ，AC=4cm ．（1）以点C 为圆心作圆，当半径为多长时，直线AB 与⊙C 相切？为什么？（2）以点C 为圆心，分别以2cm 和4cm 为半径作两个圆，这两个圆与直线AB 分别有怎样的位置关系？ 分析：（1）根据切线的判定定理可知，要使直线AB 与⊙C 相切，•那么这条半径应垂直于直线AB ，并且C 点到垂足的长就是半径，所以只要求出如图所示的CD 即可． （2）用d 和r 的关系进行判定，或借助图形进行判定． 解：（1）如图24-54：过C 作CD ⊥AB ，垂足为D ．在Rt △ABC 中∴CD=48因此，当半径为时，AB 与⊙C 相切．理由是：直线AB 为⊙C 的半径CD 的外端并且CD ⊥AB ，所以AB 是⊙C 的切线．（2）由（1）可知，圆心C 到直线AB 的距离cm ，所以当r=2时，d>r ，⊙C 与直线AB 相离； 当r=4时，d<r ，⊙C 与直线AB 相交．三、归纳小结（学生归纳，总结发言老师点评）1．直线和圆相交、割线、直线和圆相切，切线、切点、直线和圆相离等概念． 2．设⊙O 的半径为r ，直线L 到圆心O 的距离为d 则有： 直线L 和⊙O 相交⇔d<r 直线L 和⊙O 相切⇔d=r 直线L 和⊙O 相离⇔d>r3．切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线． 4．切线的性质定理，圆的切线垂直于过切点的半径． 5．应用上面的知识解决实际问题． 【课后反思】第1课时直线和圆的位置关系1．已知⊙O的直径为12 cm，圆心O到直线l的距离为5 cm，则直线l与⊙O的交点个数为( )A．0 B．1C．2 D．无法确定2．直线l与半径为r的⊙O相交，且点O到直线l的距离为6，则r的取值范围是( )A．r<6 B．r＝6C．r>6 D．r≥63．如图24­2­9所示，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为(－3,0)，将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为( )图24­2­9A．1 B．1或5C．3 D．54．已知⊙O的直径为6，圆心O到直线l的距离是4，则直线l与⊙O的位置关系是__ __．5．如图24­2­10，在△ABC中，AB＝AC＝10，BC＝16，若已知⊙A的半径为7，判断⊙A与直线BC的位置关系，并说明理由．图24­2­106．⊙O的半径为R，点O到直线l的距离为d，R，d是方程x2－4x＋m＝0的两根，当直线l与⊙O相切时，m的值为____．7．如图24­2­11，给定一个半径长为2的圆，圆心O到水平直线l的距离为d，即OM ＝d.我们把圆上到直线l的距离等于1的点的个数记为m.如d＝0时，l为经过圆心O的一条直线，此时圆上有4个到直线l的距离等于1的点，即m＝4.由此可知：图24­2­11(1)当d＝3时，m＝__ ______；(2)当m＝2时，d的取值范围是__ __．8．如图24­2­12，有两条公路OM，ON相交成30°角，沿公路OM方向离O点80 m处有一所学校A，当重型运输卡车P沿道路ON方向行驶时，在以P为圆心、50 m 长为半径的圆形区域内部会受到卡车噪声的影响，且卡车P与学校A的距离越近噪声影响越大，若已知重型运输卡车P沿道路ON方向行驶的速度为18 km/h.(1)对学校A的噪声影响最大时，求卡车P与学校A的距离；(2)求卡车P沿道路ON方向行驶一次给学校A带来噪声影响的时间．图24­2­12参考答案【分层作业】1．C 2.C 3.B 4.相离5.⊙A与直线BC相交. 理由略．6.4 7.(1)1 (2)1<d<3 8.(1)对学校A的噪声影响最大时，卡车P与学校A的距离为40 m．(2)卡车P沿道路ON 方向行驶一次给学校A带来噪声影响的时间为12s.。

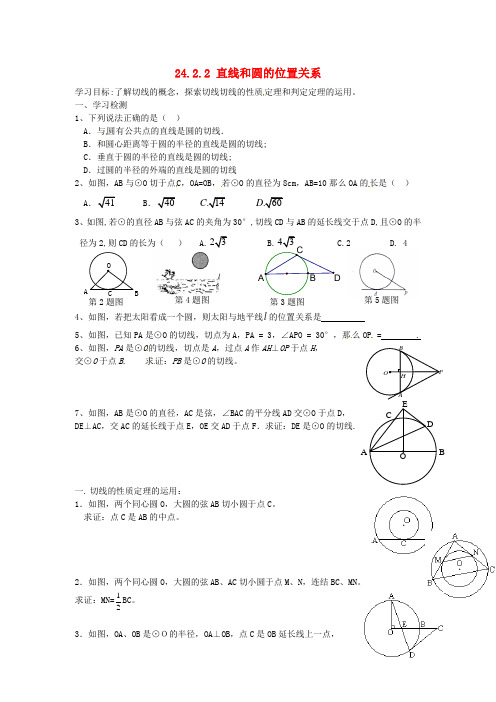
24.2.2 直线和圆的位置关系学习目标:了解切线的概念，探索切线切线的性质定理和判定定理的运用。

一、学习检测1、下列说法正确的是（ ）A ．与圆有公共点的直线是圆的切线．B ．和圆心距离等于圆的半径的直线是圆的切线;C ．垂直于圆的半径的直线是圆的切线;D ．过圆的半径的外端的直线是圆的切线2、如图，AB 与⊙O 切于点C ，OA=OB ，若⊙O 的直径为8cm ，AB=10那么OA 的长是（ ）ABC 3、如图,若⊙的直径AB 与弦AC 的夹角为30°,切线CD 与AB 的延长线交于点D,且⊙O 的半径为2,则CD 的长为（ ）A.B. C.2 D. 44、如图，若把太阳看成一个圆，则太阳与地平线l 的位置关系是5、如图，已知PA 是⊙O 的切线，切点为A ，PA = 3，∠APO = 30°，那么OP = .6、如图，PA 是⊙O 的切线，切点是A ，过点A 作AH ⊥OP 于点H ，交⊙O 于点B . 求证：PB 是⊙O 的切线。

7、如图，AB 是⊙O 的直径，AC 是弦，∠BAC 的平分线AD 交⊙O 于点D ， DE ⊥AC ，交AC 的延长线于点E ，OE 交AD 于点F ．求证：DE 是⊙O 的切线.一. 切线的性质定理的运用：1．如图，两个同心圆O ，大圆的弦AB 切小圆于点C 。

求证：点C 是AB 的中点。

2．如图，两个同心圆O ，大圆的弦AB 、AC 切小圆于点M 、N ，连结BC 、MN 。

求证：MN=12BC 。

3．如图，OA 、OB 是⊙Ｏ的半径，OA ⊥OB ，点C 是OB 延长线上一点，B第2题图第3题图 第4题图 第5题图过点C作⊙Ｏ的切线，点D是切点，连结AD交OB于点E。

求证：CD=CE4．如图所示，AB是⊙Ｏ的直径，CD切⊙Ｏ于点C，AD⊥CD。

求证：AC平分∠DAB。

二．切线的判定定理的运用：1．如图，AB是⊙Ｏ的直径，点C在⊙Ｏ上，AC平分∠DAB ，A D⊥CD。

新人教版九年级数学上册《直线和圆的位置关系2》导学案1. 理解掌握切线的判定定理和性质定理．2．判定一条直线是否为圆的切线；会过圆上一点画圆的切线．3．会运用圆的切线的性质与判定来解决相关问题．重点：切线的判定定理；切线的性质定理及其运用它们解决一些具体的题目．难点：切线的判定和性质及其运用．一、自学指导．(10分钟)自学：阅读教材P 97～98.归纳：1．经过__半径的外端__并且__垂直于这条半径__的直线是圆的切线．2．切线的性质有：①切线和圆只有__1个__公共点；②切线和圆心的距离等于__半径__；③圆的切线__垂直于__过切点的半径．3．当已知一条直线是某圆的切线时，切点的位置是确定的，辅助线常常是连接__圆心__和切点__，得到半径，那么半径__垂直于__切线．二、自学检测：学生自主完成，小组内展示，点评，教师巡视．(7分钟)1．如图，已知AB 是⊙O 的直径，PB 是⊙O 的切线，PA 交⊙O 于C ，AB ＝3 cm ，PB ＝4 cm ，则BC ＝__125__cm .2．如图，BC 是半圆O 的直径，点D 是半圆上一点，过点D 作⊙O 的切线AD ，BA ⊥DA 于点A ，BA 交半圆于点E ，已知BC ＝10，AD ＝4，那么直线CE 与以点O 为圆心，52为半径的圆的位置关系是__相离__．3．如图，AB 是⊙O 的直径，⊙O 交BC 的中点于点D ，DE ⊥AC 于E ，连接AD ，则下面结论正确的有__①②③④__．①AD ⊥BC ； ②∠EDA ＝∠B ；③OA ＝12AC; ④DE 是⊙O 的切线．4．如图，AB 为⊙O 的直径，PQ 切⊙O 于T ，AC ⊥PQ 于C ，交⊙O 于D ，若AD ＝2，TC ＝3，则⊙O 的半径是__10__．一、小组合作：小组讨论交流解题思路，小组活动后，小组代表展示活动成果．(7分钟)1．如图，AB 是⊙O 的直径，BC 切⊙O 于B ，AC 交⊙O 于P ，E 是BC 边上的中点，连接PE ，则PE 与⊙O 相切吗？若相切，请加以证明；若不相切，请说明理由．解：相切；证明：连接OP ，BP ，则OP ＝OB.∴∠OBP ＝∠OPB.∵AB 为直径，∴BP ⊥PC.在Rt △BCP 中，E 为斜边中点，∴PE ＝12BC ＝BE. ∴∠EBP ＝∠EPB.∴∠OBP ＋∠PBE ＝∠OPB ＋∠EPB.即∠OBE ＝∠OPE.∵BE 为切线，∴AB ⊥BC.∴OP ⊥PE ，∴PE 是⊙O 的切线．2．如图，AB 是⊙O 的直径，BC ⊥AB 于点B ，连接OC 交⊙O 于点E ，弦AD ∥OC ，连接CD.求证：(1)点E 是BD ︵的中点；(2)CD 是⊙O 的切线．证明：略．点拨精讲：(1)连接OD ，要证弧等可先证弧所对的圆心角等；(2)在(1)的基础上证△ODC 与△OBC 全等．二、跟踪练习：学生独立确定解题思路，小组内交流，上台展示并讲解思路．(9分钟)1．教材P98的练习．2．如图，∠ACB＝60°，半径为1 cm的⊙O切BC于点C，若将⊙O在CB上向右滚动，则当滚动到⊙O与CA也相切时，圆心O移动的水平距离是__3__c m.,第2题图),第3题图) 3．如图，直线AB，CD相交于点O，∠AOC＝30°，半径为1 cm的⊙P的圆心在射线OA上，且与点O的距离为6 cm，如果⊙P以1 cm/s的速度沿A向B的方向移动，则经过__4或8__秒后⊙P与直线CD相切．4．如图，以O为圆心的两个同心圆中，大圆的弦AB与小圆相切于点C，若大圆半径为10 cm，小圆半径为6 cm，则弦AB的长为__16__cm.,第4题图),第5题图) 5．如图，AB是⊙O的直径，点D在AB的延长线上，DC切⊙O于点C，若∠A＝25°，则∠D＝__40°__．学生总结本堂课的收获与困惑．(2分钟)圆的切线的判定与性质．学习至此，请使用本课时对应训练部分．(10分钟)。

第二十四章圆导学案（九）24．2．2 直线和圆的位置关系（2）一．学习目标：1、掌握切线的判定定理并会运用定理解决相关问题。

2、会过圆上一点画圆的切线 二．学习重点、难点：重点：切线的判定定理 难点：切线的判定 三．学习活动 （一）导学驱动切线的定义：____________________________________________。

几何语言：若⊙O 半径为r ，圆心O 到直线l 的距离为d ，则d_____r 直线l 与⊙O_______。

（二）探究交流问题：如图，在⊙O 中，过半径OA 的外端点A 作直线l ⊥OA ，则圆心O 到直线l 的距离为多少？直线l 和⊙O 有什么位置关系？（三）释疑内化1、如图，直线AB 经过⊙O 上的点C ，并且OA ＝OB ，CA ＝CB ， 求证：直线AB 是⊙O 的切线。

2、如图，点D 是∠AOB 的平分线OC 上任意一点，过D 作DE ⊥OB 于E ，以DE 为半径作⊙D ， 判断⊙D 与OA 的位置关系，并证明你的结论l总结切线的判定方法： （四）巩固迁移 课堂检测1、下列说法正确的是（ ）A.垂直于圆的半径的直线和圆相切；B.经过圆的半径外端的直线和圆相切C.经过半径的端点和这条半径垂直的直线是圆的切线D.经过直径的端点和这条直径垂直的直线是圆的切线2、如图，AB 是⊙O 的直径，∠ABT ＝45°，AT ＝AB ，求证：AT 是⊙O 的切线。

3、如图：在△ABC 中，AB=BC ，以AB 为直径的⊙O 与AC 交于点D ，过D 作DF ⊥BC ，交AB 的延长线于E ，垂足为F 。

求证：直线DE 是⊙O 的切线课后作业：1、如图，已知AB 是⊙O 的直径，AC 为弦，且平分BAD ∠，AD CD ⊥求证：CD 是⊙O 的切线；2、如图，△ABC 内接于⊙O ，AB 是⊙O 的直径，∠CAD ＝∠ABC ，判断直线AD 与⊙O 的位置关系，并说明理由。

新人教版九年级数学上册导学案：24.2.2直线和圆的位置关系（2）学习目标1．熟记切线的性质与判定。

2．会用切线的性质与判定解决一些问题。

一、预习导学一、知识链接1.过平面内的一点可以作个圆；过平面内的两点可以作个圆；不在同一直线上的可以确定一个圆，经过三角形的三个顶点的圆叫做三角形的。

三角形的圆心叫做这个三角形的，这个三角形叫做这个圆的。

2.三角形的外心就是三角形三条边的交点，它到三角形的距离相等。

3.已知点到圆心的距离和圆的半径，能否判断点与圆的位置关系？如果OC>r⇒点C在；如果OB=r⇒点B在；如果OA<r⇒点A在．二、探究新知：1，直线L和圆有两个公共点，这时我们就说这条直线和圆______，这条直线叫做圆的____．直线和圆有一个公共点，这时我们说这条直线和圆____，这条直线叫做圆的_____，这个点叫做______．直线和圆没有公共点，这时我们说这条直线和圆____.2.如何用圆心到直线的距离d和半径r之间的关系来确定三种位置关系呢？直线L和⊙O相交⇔ d r；直线L和⊙O相切⇔ d r；直线L和⊙O相离⇔ d r。

3.直线与圆的位置关系3种：_____、相切和______。

4、识别直线与圆的位置关系的方法：（1）一种是根据定义进行识别：直线L与⊙o没有公共点直线L与⊙o__________。

【温馨提示】理解几何图形是现实生活抽象出来的理解并掌握圆的切线直线L与⊙o只有一个公共点直线L与⊙o_________。

直线L与⊙o有两个公共点直线L与⊙o______。

（2）另一种是根据圆心到直线的距离d与圆半径r数量d>r 直线L与⊙o_______；d=r 直线L与⊙o__________； d<r 直线L与⊙o___________。

学以致用1、若∠OAB=30°，OA=10cm，则以O为圆心，6cm为半径的圆与射线AB的位置关系是（）A．相交 B．相切 C．相离 D．不能确定2、∠AOC=60°，点B 在OA上，且OB=32，若以B 为圆心，R为半径的圆与直线OC相离，则R的取值范围是。

九年数学上24.2.2直线和圆的位置关系2导学案
学习目标：
知识与技能：深刻理解切线的判定定理，并能初步运用它解决有关问题；
过程与方法：通过判定定理和切线判定方法的学习，培养观察、分析、归纳问题的能力；
情感与态度：通过自己实践发现定理，培养学习的主动性和积极性
重点：切线的判定定理和切线判定的方法；
难点：切线判定定理中所阐述的由位置来判定直线是圆的切线的两大要素：一是经过半径外端；二是直线垂直于这条半径；开始时掌握不
好并极容易忽视．
一、自主探究（前置性学习）
探究活动1、图中直线l是⊙O的切线，怎样判定？根据切线的定义可以判定一条直线是不是圆的切线，但有时使用定义判定很不方便．我们从另一个侧面去观察，那就是直线和圆的位置怎样时，直线也是圆的切线呢?
探究活动2、
如果直线l是⊙O的切线，切点为A，半径OA与直线l是不是一定垂直？
新知盘点：
预习质疑：
二、合作探究：
㈠交流展示
㈡学以致用
1、如图，已知⊙O的半径为R，直线AB经过⊙O上的点A，并且AB=R，∠OBA=45°。

求证：直线AB是⊙O的切线。

三、拓展探究：
如图7-106，⊙O的半径为8厘米，圆内弦AB＝83厘米，以O为圆心，4厘米为半径作小圆，求证：小圆与直线AB相切.。

《直线和圆的位置关系》导学案一、教学背景1、数学课程标准要求学生理解相交、相离、相切的概念，探索并了解直线和圆的位置关系；2、通过视频讲解的方式让学生不限场地不限时间自学本课知识点。

二、学习目标1、使学生理解并掌握直线和圆的三种位置关系，掌握其判定方法和性质；2、通过直线和圆的位置关系的探究，向学生渗透分类、分类、数形结合的思想，培养学生观察、分析和概括的能力；3、使学生从运动的观点来观察直线和圆相交、相切、相离的关系、培养学生的辩证唯物主义观点．三、教材的重点难点重点：直线和圆的三种位置关系。

难点：直线和圆的三种位置关系的性质与判定的应用。

四、教学方法PPT讲解式五、教学过程（一）画一画请同学们欣赏海上日出的动画,动画中的几何图形有请动手画一画：（二）想一想通过视频和动画你认为直线和圆的位置关系有种，你的分类依据是（三）直线和圆的位置关系（1）直线和圆没有公共点时,叫做这条直线和圆；(2)直线和圆有一个公共点时,叫做这条直线和圆；(3)直线和圆有两个公共点时,叫做这条直线和圆。

（四）位置关系和数量关系（五）例析六、知识小结1、判定直线与圆的位置关系的方法有____种：（1）根据定义，由________________ 的个数来判断；（2）根据性质，由_________________ 的关系来判断。

七、课后练习1．⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l与⊙O没有公共点，则d为（）A．d ＞3 B．d<3 C．d ≤3 D．d =32．圆心O到直线的距离等于⊙O的半径，则直线和⊙O的位置关系是（）A．相离 B.相交 C.相切 D.相切或相交3.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆与直线BC的位置关系是 ,以A为圆心, 为半径的圆与直线BC相切.4. 已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:1)若AB和⊙O相离, 则 ;2)若AB和⊙O相切, 则 ;3)若AB和⊙O相交,则 .5、如图,已知∠AOB= 30°,M为OB上一点,且OM=5cm，若以M为圆心,r为半径作圆,那么:1)当直线AB与⊙M相离时, r的取值范围是______________;2)当直线AB与⊙M相切时, r的取值范围是______________;3)当直线AB与⊙M有公共点时, r的取值范围是___________.。

《24.2.2直线和圆的位置关系（2）》导学案课题直线和圆的位置关系（2）数学年级九年级上册知识目标1．能判定一条直线是否为圆的切线，会过圆上一点画圆的切线．2．理解切线的判定定理和性质定理，会用这两个定理解决简单问题．3．经历观察、实验、猜想、证明等数学活动过程，发展合情推理能力和初步演绎推理能力．重点难点重点：理解圆的切线的判定定理和性质定理，并能运用它解决简单问题．难点：理解切线的判定定理，用反证法证明切线的性质定理．教学过程知识链接问题1：下雨天，转动的雨伞上的水滴是顺着伞的什么方向飞出去的?问题2：砂轮转动时，火花是沿着砂轮的什么方向飞出去的?都是沿着圆的切线的方向飞出的．如何判断一条直线是切线？今天我们来学习这个内容，切线的判定。

合作探究知识点1、切线的判定定理思考：1.如图，直线l 和⊙O有什么位置关系?相切2.如图，在⊙O中经过半径OA的外端点A作直线l⊥OA,则圆心O到直线l 的距离是多少？教师引导学生思考，分析，让学生知道，圆心O到直线l的距离就是⊙O的半径，直线l就是⊙O的切线．即由d=r可以得到直线l 是⊙O的切线．进一步思考：已知圆O上一点A，怎样根据圆的切线定义过点A作圆O的切线？观察：（1）圆心O到直线AB的距离和圆的半径有什么数量关系?（2）二者位置有什么关系？为什么？教师再次引导学生讨论点A与直线l的位置关系，从而得到●切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线．几何语言：∵OA是半径，OA⊥l于A∴l是⊙O的切线。

教师可举例相交、相离的情况，以深化对切线的理解．教师还可以举生活中的直线和圆相切的实例，培养学生的感性认识．例如，下雨天当你快速转动雨伞时飞出的水珠，在砂轮上打磨工件时飞出的火星，都是沿着圆的切线方向飞出的．总结前面我们学过的知识，我们有哪些判定直线是切线的方法，小组讨论，形成结论。

●判断一条直线是一个圆的切线有三个方法：1.定义法：直线和圆只有一个公共点时，我们说这条直线是圆的切线;2.数量关系法：圆心到这条直线的距离等于半径(即d=r)时，直线与圆相切；3.判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.例1、如左图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D．求证：AC是⊙O的切线．分析：根据切线的判定定理，要证明AC是⊙O的切线，只要证明由点O向AC所作的垂线段OE是⊙O的半径就可以了．而OD是⊙O的半径，因此需要证明OE＝OD．证明：如右图，过点O作OE⊥AC，垂足为E，连接OD，OA．∵⊙O与AB相切于点D，∴OD⊥AB．又△ABC为等腰三角形，O是底边BC的中点，∴AO是∠BAC的平分线．∴OE＝OD，即OE是⊙O的半径．这样，AC经过⊙O的半径OE的外端E，并且垂直于半径OE，所以AC与⊙O相切．教师引导学生分析自主尝试中的2题和3题的证法有何不同?然后交流讨论。