八年级数学第2讲.倍长中线与截长补短.尖子班.练习版

专题14倍长中线法与截长补短法构造全等三形模型一：倍长中线法构造全等三角形模型二：截长补短法构造全等三角形【典例分析】【模型一：倍长中线法构造全等三角形】△ABC 中,AD 是BC 边中线方式1到E ，使DE=AD ，连接BE方式2：间接倍长（1）作CF ⊥AD 于F，作BE⊥AD 的延长线于E（2）延长MD 到N，使DN=MD，连接CN【典例1】（2021春•吉安县期末）课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC 中，若AB ＝8，AC ＝6，求BC 边上的中线AD 的取值范围．小N延长边上（不一定是底边）的中线，使所延长部分与中线相等，然后往往需要连接相应的顶点，则对应角对应边都对应相等。

此法常用于构造全等三角形，利用中线的性质、辅助线、对顶角一般用“SAS ”证明对应边之间的关系。

（在一定范围中）明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE＝AD，请根据小明的方法思考：（1）由已知和作图能得到△ADC≌△EDB的理由是．A．SSS B．SAS C．AAS D．HL （2）求得AD的取值范围是．A．6＜AD＜8B．6≤AD≤8C．1＜AD＜7D．1≤AD≤7（3）如图2，AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．求证：AC＝BF．【变式1-1】（2021秋•肥西县期末）一个三角形的两边长分别为5和9，设第三边上的中线长为x，则x的取值范围是（）A．x＞5B．x＜7C．4＜x＜14D．2＜x＜7【变式1-2】如图，AE是△ABD的中线AB＝CD＝BD．求证：AB+AD＞2AE；【变式1-3】（2021秋•齐河县期末）（1）方法呈现：如图①：在△ABC中，若AB＝6，AC＝4，点D为BC边的中点，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE＝AD，再连接BE，可证△ACD≌△EBD，从而把AB、AC，2AD集中在△ABE中，利用三角形三边的关系即可判断中线AD的取值范围是（直接写出范围即可）．这种解决问题的方法我们称为倍长中线法；（2）探究应用：如图②，在△ABC中，点D是BC的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，判断BE+CF与EF的大小关系并证明；（3）问题拓展：如图③，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F、点E 是BC的中点，若AE是∠BAF的角平分线．试探究线段AB，AF，CF之间的数量关系，并加以证明．【模型二：截长补短法构造全等三角形】∙截长：1.过某一点作长边的垂线；2.在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。

32H A BF E 1GE F DCB AD C B A OG A BC D A B C D 初中几何之截长补短模型模型 截长补短如图①，若证明线段AB 、CD 、EF 之间存在 EF=AB+CD ，可以考虑截长补短法。

截长法：如图②，在EF 上截取EG=AB ，再证明 GF=CD 即可。

补短法：如图③，延长AB 至H 点，使BH=CD ， 再证明AH=EF 即可。

模型分析截长补短的方法适用于求证线段的和差倍分关系。

截长，指在长线段中截取一段等于已知线段；补短，指将短线段延长，延长部分等于已知线段。

该类题目中常出现等腰三角形、角平分线等关键词句，可以采用截长补短法构造全等三角形来完成证明过程。

模型实例例1．如图，已知在△ABC 中，∠C=2∠B ，AD 平分∠BAC 交BC 于点D 。

求证：AB=AC+CD 。

例2．如图，已知OD 平分∠AOB ，DC ⊥OA 于点C ，∠A=∠GBD 求证AO+BO=2CO 。

精练1．如图，在△ABC 中，∠BAC=60°，AD 是∠BAC 的平分线，且AC=AB+BD 。

求∠ABC 的度数。

2．如图，∠ABC+∠BCD=180°，BE 、CE 分别平分∠ABC 、∠BCD 。

求证：AB+CD=BC 。

EABC DEA BC D FE ABC DE A BCD OEA BC D3．如图，在△ABC 中，∠ABC=60°，AD 、CE 分别平分∠BAC 、∠ACB 。

求证AC=AE+CD 。

4．如图，在△ABC 中，∠ABC=90°，AD 平分∠BAC 交BC 于点D ，∠C=30°， BE ⊥AD 于点E 。

求证：AC-AB=2BE 。

5．如图，Rt △ABC 中，AC=BC ，AD 平分∠BAC 交BC 于点D ，CE ⊥AD 交AD 于F 点，交AB 于点E 。

求证：AD=2DF+CE 。

6．如图，五边形ABCDE 中，AB=AC ，BC+DE=CD ，∠B+∠E=180°。

全等三角形重要题型要点一：手拉手模型特点：由两个等顶角的等腰三角形或正方形组成，并且顶角的顶点为公共顶点的模型。

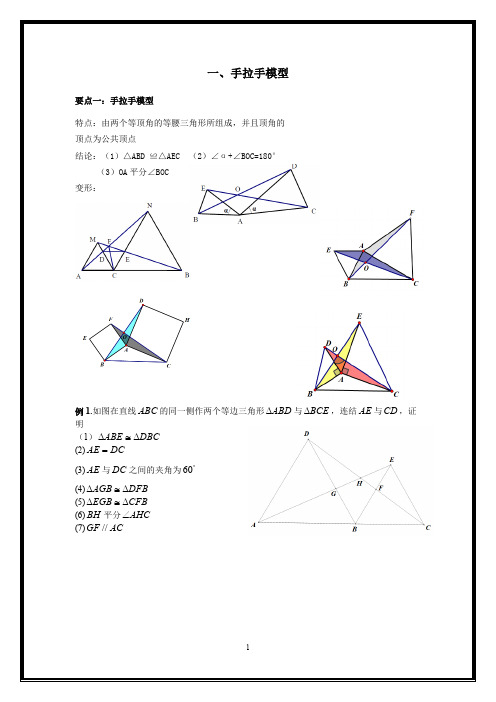
模型如下：例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明： （1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60 （4）DFB AGB ∆≅∆ （5）CFB EGB ∆≅∆ （6）BH 平分AHC ∠ （7）AC GF //变式精练1：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ， 证明（1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？ （2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？ （2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？ （2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？ （4）HB 是否平分AHC ∠？要点二：截长补短法若遇到证明线段的和差倍分关系时，通常考虑截长补短法，构造全等三角形。

倍长中线最全总结。

例题+练习(附答案)中线是三角形中的重要线段之一。

在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线。

倍长中线指的是延长三角形中线，使得延长后的线段是原中线的2倍。

其目的是为了构造一对8字型全等三角形（SAS），从而实现边角的转移。

以三角形ABC为例，延长中线AD至点E，使得DE=AD，连接BE。

根据三角形的SAS全等条件，可以得出结论：△ACD≌△BED，AC=BE，∠CAD=∠BED，AC∥BE。

同样地，延长中线CD至点F，使得DE=DF，连接CF。

根据三角形的SAS全等条件，可以得出结论：△BED≌△CFD，CF=BE，∠CFD=∠BED，CF∥BE。

在利用倍长中线法时，需要注意延长哪一条线段或者类中线。

倍长之后，需要考虑连接哪一条线段从而构造全等，实现所需的线段进行转移。

举例来说，如图所示，在三角形ABC中，需要证明AB+AC>2AD。

延长中线AD至点E，使得DE=AD，构造△ADC和△EDB，根据三角形的三边关系可得AB+AC>2AD。

另外，还有一道题目是需要求解AD的取值范围。

在三角形ABC中，D为BC的中点。

根据三角形的三边关系可得5-3<2AD<5+3，即AD的取值范围为1<AD<4.证明：延长AD到F，使DF=AD，连接BF（如图）。

因为AD是中线，所以BD=DC=AC，又因为DF=AD，所以BD=BF，所以AB>BF。

由三角形的三边关系，在三角形ABF中，有AB+BF>AF，即2AD<AB+AC，证毕。

2）因为AD是中线，所以BD=DC=AC，又因为DF=AD，所以BD=BF，所以AB>BF。

由相似三角形ADC和FDB，得到∠CAD=∠F，由边的大小关系可得到∠BAD>∠DAC，证毕。

3）同（2），由相似三角形ADC和FDB，得到AE/AD=BF/BD<1，即AE<AD，证毕。

i n ga re与，连结与，证BCE ∆AE CDosrofdoogeragnii rb ei n ga re go od fo r二、倍长与中点有关的线段考点说明：凡是出现中线或类似中线的线段，都可以考虑倍长中线，倍长中线的目的是可以旋转等长度的线段，从而达到将条件进行转化的目的。

．1()2AB AC <+Aean dAl l t h i ng si nt he i rb ei n ga re go 三、截长补短问题1：垂直平分线（性质）定理是_______________________________________________________问题2：角平分线（性质）定理是__________________________________________________________问题3：等腰三角形的两个底角________，简称______________；如果一个三角形有两个角相等，那么它们所对的边也______，简称____________．问题4：当见到线段的______________考虑截长补短，构造全等或等腰转移____、转移____，然后和_________重新组合解决问题．三角形全等之截长补短（一）一、单选题(共4道，每道25分)1.已知，如图，BM 平分∠ABC，P 为BM 上一点，PD⊥BC 于点D ，BD=AB+CD ．求证：∠BAP+∠BCP=180°．请你仔细观察下列序号所代表的内容：①；②∵∠1=∠2；③∠A=∠BEP；④AP=PE；⑤；⑥；⑦；⑧．以上空缺处依次所填最恰当的是( )A.①③⑥⑦B.①③⑤⑧C.②③⑥⑦D.②④⑤⑧2.已知，如图，BM 平分∠ABC，点P 为BM 上一点，PD⊥BC 于点D ，BD=AB+DC ．求证：∠BAP+∠BCP=180°．e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 请你仔细观察下列序号所代表的内容：①延长BA ，过点P 作PE⊥BA 于点E ；②延长BA 到E ，使AE=DC ，连接PE ；③延长BA 到E ，使DC=AE ；④；⑤；⑥；⑦．以上空缺处依次所填最恰当的是( )A.②④⑦B.①⑤⑥C.③④⑥D.①⑤⑦3.已知，如图，在五边形ABCDE 中，AB=AE ，AD 平分∠CDE，∠BAE=2∠CAD，求证：BC+DE=CD ．e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 请你仔细观察下列序号所代表的内容：①在CD 上截取CF=CB ，连接AF ；②在DC 上截取DF=DE ，连接AF ；③在DC 上截取DF=DE ；④AE=AF；⑤AF=AE，∠4=∠3；⑥∠4=∠3；⑦；⑧；⑨．以上空缺处依次所填最恰当的是( )A.①④⑨ B.③⑤⑧ C.①⑥⑦ D.②⑤⑨4.已知，如图，在五边形ABCDE 中，AB=AE ，∠BAE=2∠CAD，∠ABC+∠AED=180°，求证：BC+DE=CD ．请你仔细观察下列序号所代表的内容：①延长DE 到F ，使EF=BC ，连接AF ；②延长DE 到F ，使BC=EF ；e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o ③延长DE 到F ，连接AF ；④；⑤；⑥；⑦；⑧；⑨．以上空缺处依次所填最恰当的是( )A.③⑤⑥⑧B.①④⑥⑨C.①⑤⑥⑨D.②④⑦⑧r四、三角形全等旋转与截长补短专题问题一：题中出现什么的时候，我们应该想到旋转？(构造旋转的条件)问题二：旋转都有哪些模型？【例1】如图，P 是正△ABC 内的一点，若将△PBC 绕点B 旋转到△P ＇BA ，则∠PBP ＇的度数是( ) A ．45°B ．60° C ．90° D ．120°【例2】如图，正方形BAFE 与正方形ACGD 共点于A ，连接BD 、CF ，求证：BD ＝CF 并求出∠DOH 的度数。

学而思倍长中线与截长补短笔记说到“学而思倍长中线与截长补短”这几个词，听起来可能有点复杂吧？别急，咱们今天就来轻松聊聊这些数学概念，把它们讲得通俗易懂，保证你听完之后，能大呼一声：“原来是这么回事！”咱们从“倍长中线”这个词开始讲起。

说白了，它就是指一个三角形中，通过一个顶点，连接到对边中点的那条线段，叫做中线。

你看，三角形有三个顶点，对吧？其中任意一个顶点，如果你连线到对边的中点，这条线就叫做中线。

好了，这条中线有个非常有意思的性质——它的长度是可以通过三角形的边长来“计算”的，也就是说，中线的长度跟三角形的大小、形状有着密切的关系。

如果这条中线很长，那就意味着整个三角形的“体积”或者说“尺寸”也很大。

嗯，这种情况下，你就可以直观地感觉到，三角形不可能很“瘦”，一定得是那种相对“厚实”的存在。

听起来是不是有点抽象？其实挺简单的！想象一下，如果你拿着尺子量一量，中线越长，三角形就越“胖”对吧？这不就很容易理解了吗？接下来咱们再说“截长补短”这个词。

其实啊，这个就很形象了。

你看，生活中咱们常说“强中自有强中手”对吧？意思就是做任何事儿都有更厉害的人。

那数学里也一样，所谓“截长补短”就是通过调整和补充某些不足的部分来弥补短板，达到一个平衡的效果。

怎么说呢？如果你在一个三角形里看到有一条边特别长，而另一条边特别短，这时候你就可以通过“截长补短”的方式，把那些不平衡的地方调整过来，最终让三角形的各个边长都差不多，看上去更加和谐。

这个方法其实特别像咱们生活中的一些调整，比如当你发现自己某一方面的能力差了点，你是不是就会去加强那一部分，反过来让自己更加全面？“截长补短”不就这么回事吗？它就是利用“强”的去弥补“弱”的，让整体看起来更加完美。

这两者之间其实有很多相似之处。

比如“倍长中线”给人的感觉就是一种“加长”的状态，想象一下，那个中线如果特别长，三角形就会变得庞大。

而“截长补短”则是一种“调整”的方式，把过长的部分调整到适当的长度，然后补充短缺的地方。

12.2 三角形全等的判定（倍长中线）一、单选题1．在学完八上《三角形》一章后，某班组织了一次数学活动课，老师让同学们自己谈谈对三角形相关知识的理解．小峰说：“存在这样的三角形，他的三条高的比为1：2：3”．小慧说：“存在这样的三角形，其一边上的中线不小于其他两边和的一半”． 对以上两位同学的说法，你认为（ ）A ．两人都不正确B ．小慧正确，小峰不正确C ．小峰正确，小慧不正确D ．两人都正确2．已知△ABC 中，AB=5，AC=7，则BC 边上的中线a 的取值范围是（ ） A ．1＜a ＜6 B ．5＜a ＜7 C ．2＜a ＜12 D ．10＜a ＜14 3．AD 是∆ABC 中 BC 边上的中线，若 AB = 3 ， AD = 4 ，则 AC 的取值范围是（ ） A ．1 < AC < 7 B ．0.5 < AC < 3.5 C ．5 < AC < 11 D ．2.5 < AC < 5.5 4．三角形两边长为4和6，则第三边上的中线x 的取值范围是：（）A ．2＜x ＜10B ．1＜x ＜5C ．x ＞55．在△ABC 中，AB ＝5，AC ＝3，AD 为BC 边的中线，则AD 的长x 的取值范围( ) A ．58x ≤≤ B ．47x ≤≤ C ．14x << D ．7922x << 6．如图，在△ABC 中，AC=5，中线AD=7，则AB 边的取值范围是( )A ．1AB 29<<B ．4AB 24<<C ．5AB 19<<D ．9AB 19<<7．如图，在△ABC 中，AB ＝8，AC ＝6，AD 是BC 边上的中线，则AD 长的取值范围是( )A ．6<AD<8B ．2<AD<4C ．1<AD<7D ．无法确定 8．如图，AD 是ABC ∆的中线，E 是AD 上一点，连接BE 并延长交AC 于点F ，若EF=AF ， BE=7.5， CF=6，则EF=( ).A ．2.5B ．2C ．1.5D ．19．如图所示，△ABC 中，AB ＝3，AC ＝7，则BC 边上的中线AD 的取值范围是（ ）A ．4＜AD ＜10B ．0＜AD ＜10C ．3＜AD ＜7 D ．2＜AD ＜510．如图，在ABC 中，D 为BC 的中点，若3,4AC AD ==．则AB 的长不可能．．．是（）A ．5B ．7C ．8D ．911．已知AD 是△ABC 中BC 边的中线，若AB ＝4，AD ＝3，则AC 的长可以是（ ） A ．11 B ．11 C ．10 D ．912．如图，在△ABC 中，AB=8，AC=5，AD 是△ABC 的中线，则AD 的取值范围是（）A ．3<AD<13B ．1.5<AD<6.5C ．2.5<AD<7.5D ．10<AD<16二、填空题13．如图，在ABC 中，9AB =，3AC =，D 为BC 中点，则线段AD 的范围是______．14．在ABC 中，5AB =，3AC =，AD 是ABC 的中线，设AD 长为m ，则m 的取值范围是______．15．ABC 中，4AB =，6AC =， 则第三边BC 边上的中线m 的取值范围是______． 16．如图，ABC ∆中，D 为BC 的中点，E 是AD 上一点，连接BE 并延长交AC 于F ，BE AC =，且9BF =，6CF =，那么AF 的长度为__．17．如图，△ABC 中，BC 边上的中线AD 将△BAC 分成了两角△BAD 、∠DAC 分别为70°和40°，若中线AD 长为2.4cm ，则AC 长为________cm.三、解答题18．如图，ABC ∆中，3AB =，4AC =，AD 为中线，求中线AD 的取值范围．19．已知：如图，D 是△ABC 边BC 上一点，且CD ＝AB ，△BDA ＝△BAD ，AE 是△ABD 的中线．求证：AC ＝2AE ．20．如图，在ABC △和A B C '''中，AC A C ''=，'AB AB'=，D 、D 分别为BC 、B C ''的中点，且AD A D ''=，求证：ABC △△A B C '''．21．已知，在Rt ABC △中，90BAC ∠=︒，点D 为边AB 的中点，AE CD ⊥分别交CD ，BC 于点F ，E ．（1）如图1，△若AB AC =，请直接写出EAC BCD ∠-∠=______；△连接DE ，若2AE DE =，求证：DEB AEC ∠=∠；（2）如图2，连接FB ，若FB AC =，试探究线段CF 和DF 之间的数量关系，并说明理由．22．某数学兴趣小组在一次活动中进行了探究试验活动，请你来加入．（探究与发现）（1）如图1，AD 是ABC 的中线，延长AD 至点E ，使ED AD =，连接BE ，证明：ACD EBD △≌△． （理解与应用）（2）如图2，EP 是DEF 的中线，若5EF =，3DE =，设EP x =，则x 的取值范围是________． （3）如图3，AD 是ABC 的中线，E 、F 分别在AB 、AC 上，且DE DF ⊥，求证：BE CF EF +>．参考答案1．A解：假设存在这样的三角形，他的三条高的比为1：2：3，根据等积法，得到此三角形三边比为6：3：2，这与三角形三边关系相矛盾，故假设错误，所以这样的三角形不存在；假设存在这样的三角形，其一边上的中线不小于其他两边和的一半，延长中线成2倍，利用三角形全等，可得到三角形中线的2倍不小于（大于等于）其他两边之和，这与三角形三边关系矛盾，故假设错误，所以这样的三角形不存在；故选A．2．A解：延长AE到D，使AE=DE，连接BD．△AE是中线，△BE=CE，△AEC=△DEB，△△AEC△△DEB△（SAS），△BD=AC=7，又AE=a，△2＜2a＜12，△1＜a＜6．故选A．3．C解：如图，延长AD到E，使DE=AD=4，△AD是BC边上的中线，△BD=CD,在△ABD和△ECD中，△BD CDADB EDC DE AD=⎧⎪∠=∠⎨⎪=⎩，△△ABD△△ECD(SAS)，△CE=AB=3，△AB=3，AD=4，△AE−CE<AC<AE+EC，即8−3<AC<11，△5<AC<11，故选C.4．B解：如右图所示，AD是BC上的中线，AB=4，AC=6，延长AD到E，使DE=AD，连接BE，△D是BC中点，△BD=CD，又△△ADC=△BDE，AD=DE，△△ADC△△EDB，△BE=AC，在△ABE中，6-4＜2AD＜4+6，即1＜AD＜5，故选B．5．C解：延长中线AD到E，使DE=AD，连结CE，△AD为BC中线，△BD=CD，△△ADB=△EDC，△△ABD△△ECD（SAS），△CE=AB=5，△AE=2AD，在△AEC中，CE-AC<AE<CE+AC,即2<2AD<8，△1<AD<4．故选择：C．6．D解：延长AD到E，使DE=AD，连接BE在△ADC和△EDB中AD=DE,△ADC=△BDE,CD=BD△△ADC△△EDB（SAS）△AC=BE（全等三角形的对应边相等）△AC=5，AD=7△BE=5，AE=14在△ABE中，AE-BE＜AB＜AE+BE△AB边的取值范围是：9＜AB＜19故选D7．C解：延长AD到E，使AD=DE，连接BE，如图所示：△AD=DE，△ADC=△BDE，BD=DC，△△ADC△△EDB（SAS）△BE=AC=6，在△AEB中，AB-BE＜AE＜AB+BE，即8-6＜2AD＜8+6，△1＜AD＜7，故选：C．8．C解：如图，延长AD，使DG=AD，连接BG，△AD是△ABC的中线，△BD=CD，且DG=AD，△ADC=△BDG，△△ADC△△GDB（SAS），△AC=DG=CF+AF=6+AF，△DAC=△G，△EF=AF，△△DAC=△AEF，△△G=△AEF=△BEG，△BE=BG=7.5，△6+AF=BG=7.5，△AF=1.5=EF，故选择：C．9．D解：延长AD到E点，使AD=DE，连接EC △AD是中线△BD=CD又△ADB=△EDC，AD=DE△△ABD△△ECD△AB=CE=3在△ACE 中，AC=7，CE=3△7-3＜AE ＜7+3，即4＜AE ＜10△2AD=AE△2＜AD ＜5故选D10．A解：延长AD 到E ，使AD =DE =4，连接BE ，△D 是BC 的中点，△BD =CD又△BDE =△CDA△△ADC △△EDB ，△BE =AC =3由三角形三边关系得，AE BE AB AE BE -<<+即：511AB <<故选：A11．D解：延长AD至E，使DE=AD=3，连接CE．△BD=CD，△ADB=△EDC，AD=DE，△△ABD△△ECD，△CE=AB=4．在△ACE中，AE=2AD=6，CE=4AE-CE＜AC＜AE+CE，即6-4＜AC＜6+4，△2＜AC＜10．△AC的长可以是9故选：D．12．B解：延长AD到E，使AD=DE，连结BE．△AD是△ABC的中线，△BD=CD．在△ADC和△EDB中，CD BD ADC BDE AD DE =⎧⎪∠=∠⎨⎪=⎩，△△ADC△△EDB （SAS ），△AC=BE ．△AB -BE ＜AE ＜AB+BE ，△AB -AC ＜2AD ＜AB+AC ．△AB=8，AC=5，△1.5＜AD ＜6.5．故选：B13．36AD <<解：如图，延长AD 至E ，使DE AD =， AD 是ABC ∆中BC 边上的中线，BD CD ∴=，在ABD ∆和ECD ∆中，AD DE ADB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩，()ABD ECD SAS ∴∆≅∆，9CE AB ∴==，3AC =，9312∴+=，936-=，612AE ∴<<，36AD ∴<<．故答案为：36AD <<．14．14m <<解：如图，延长AD 至点E ，使AD ED =，连接CE ，则22AE AD m ==， AD 是ABC 的中线，BD CD ∴=，在ABD △和ECD 中，AD ED ADB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩，()ABD ECD SAS ∴≅，5CE AB ∴==，在ACE △中，由三角形的三边关系定理得：CE AC AE CE AC -<<+， 3AC =，53253m ∴-<<+，解得14m <<，故答案为：14m <<．15．15a <<解：延长AD 至点E ，使得DE=AD ，△点D 是BC 的中点，△BD=CD在△ABD 和△CDE 中，AD DE ADB CDE BD CD ⎧⎪∠∠⎨⎪⎩＝＝＝，△△ABD△△CDE （SAS ），△AB=CE ，△△ACE 中，AC -CE ＜AE ＜AC+CE ，即：AC -AB ＜AE ＜AC+AB ， △2＜AE ＜10，△1＜AD ＜5．故答案为：1＜AD ＜5．16．32；解：如图：延长AD 至G 使AD DG =，连接BG 在ACD ∆和GBD ∆中：CD BD ADC BDG AD DG =⎧⎪∠=∠⎨⎪=⎩△ACD GBD ∆≅∆△,CAD G AC BG ∠=∠=△BE AC =△BE BG =△G BEG ∠=∠△BEG AEF ∠=∠△AEF EAF ∠=∠△EF AF =△AF CF BF EF +=-即69AF EF +=- △32AF = 17．4.8解：延长AD 到E ，取DE=AE ，连接CE ，如图所示，在△ABD 和△ECD 中，BD=CD BDA=CDE AD=ED ⎧⎪∠∠⎨⎪⎩△()ABD ECD SAS ≅△△E=△BAD=70°在△AEC 中，7040=71801800︒︒︒︒︒∠=-∠-∠=--ACE E DAC △△E=△ACE ，△AC=AE=2AD=4.8cm故答案为4.818．1722AD << 解：延长AD 至点E ，使DE AD =，连接CE ，AD 是中线，BD CD ∴=，在ABD △和ECD 中，AD DE ADB CDE BD CD =⎧⎪∠=∠⎨⎪=⎩，()ABD CDE SAS ∴≅，4AB EC ∴==，在ACE 中，AC CE AE AC CE -<<+，43243AD ∴-<<+，127AD ∴<<， ∴1722AD <<． 19．见解析.解：延长AE 到F ，使EF=AE ，连接DF△AE 是△ABD 的中线．△BE=ED在△ABE 和△FDE 中，BE DE AEB DEF AE EF =⎧⎪∠=∠⎨⎪=⎩△△ABE△△FDE （SAS ）△AB=DF ，△BAE=△EFD△△ADB 是△ADC 的外角△△DAC+△ACD=△ADB=△BAD△△BAE+△EAD=△BAD△BAE=△EFD△△EFD+△EAD=△DAC+△ACD△△ADF=△ADC△AB=DC△DF=DC在△ADF 和△ADC 中，AD AD ADF ADC FD DC =⎧⎪∠=∠⎨⎪=⎩△△ADF△△ADC （SAS ）△AF=AC△AF=AE+EF ，AE=ED△AC=2AE20．详见解析解：如图，分别延长AD 、A D ''到E ，E '，使得AD DE =，A D D E ''''=， 连接BE 、B E ''，在△ACD 与△EDB 中AD DE ADC BDE CD BD =⎧⎪∠=∠⎨⎪=⎩△△ACD△△EDB （SAS ）同理可证A C D E B D ≅'''''',△AC=EB ，A C E B ='''';在△ABE 与A B E '''中，AB A B BE B E AE A E '''''=⎧'⎪=⎨⎪=⎩△△ABE A B E '≅''（SSS ）△BAD B A D '''∠=∠，'E E ∠=∠△'''DAC D A C ∠=∠,△△BAC=△BAD+△DAC ，B A C B A D D'A'C'∠∠∠'''''+'=, △BAC B A C ∠∠'''=；在△ABC 与A'B'C'中B AC AB A B BAC AC A C '''''''=⎧⎪∠=∠⎨⎪=⎩△△ABC A'B'C'≅（SAS ）21．（1）△45°；△见解析；（2）2CF DF =，理由见解析 解：（1）△△90EAC ACD ∠+∠=︒，90AEC BCD ∠+∠=︒ △EAC BCD AEC ACD ∠-∠=∠-∠△90EAC BAE ∠+∠=︒△ACD BAE ∠=∠又△AEC B BAE ∠=∠+∠△EAC BCD B BAE ACD ∠-∠=∠+∠-∠△45EAC BCD B ∠-∠=∠=︒故答案为45︒．△如图，延长ED 至点G ，使得DG DE =，连接AG ，△点D 为AB 的中点，△BD AD =，又△ADG BDE ∠=∠，△ADG △BDE ，△DGA DEB ∠=∠，△//AG BC ，△GAE AEC ∠=∠，又△2AE DE =，△AE EG =，△DGA GAE ∠=∠，△DEB AEC ∠=∠．（2）2CF DF =．如图，延长CD 至点H ，使得DH DF =，连接BH ，△AD BD =，ADF BDH ∠=∠， △HDB △FDA △，△BH AF =，90H AFD AFC ∠=∠=∠=︒， △BF AC =．△Rt HBF △△Rt FAC △，△2CF HF DF ==．22．（1）见解析；（2）14x <<；（3）见解析 解：（1）CD BD =，ADC EDB ∠=∠，AD ED =， ACD EBD ∴≌，（2）14x <<；如图，延长EP 至点Q ，使PQ PE =，连接FQ ，在PDE ∆与PQF ∆中，。

一、手拉手模型要点一：手拉手模型特点：由两个等顶角的等腰三角形所组成，并且顶角的 顶点为公共顶点结论：（1）△ABD ≌△AEC （2）∠α+∠BOC=180° （3）OA 平分∠BOC 变形：例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ （2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2：如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，证明（1）DBC ABE ∆≅∆ (2）DC AE =(3）AE 与DC 之间的夹角为︒60(4）AE 与DC 的交点设为H ,BH 平分AHC ∠例2：如图，两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问：（1）CDE ADG ∆≅∆是否成立？ （2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？例3：如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 问：（1）CDE ADG ∆≅∆是否成立？ （2）AG 是否与CE 相等？（3）AG 与CE 之间的夹角为多少度？ （4）HD 是否平分AHE ∠？例4：两个等腰三角形ABD ∆与BCE ∆，其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ，问：（1）DBC ABE ∆≅∆是否成立？ （2）AE 是否与CD 相等？（3）AE 与CD 之间的夹角为多少度？ （4）HB 是否平分AHC ∠？三、截长补短问题1：垂直平分线（性质）定理是_______________________________________________________问题2：角平分线（性质）定理是__________________________________________________________问题3：等腰三角形的两个底角________，简称______________；如果一个三角形有两个角相等，那么它们所对的边也______，简称____________．问题4：当见到线段的______________考虑截长补短，构造全等或等腰转移____、转移____，然后和_________重新组合解决问题．三角形全等之截长补短（一）一、单选题(共4道，每道25分)1.已知，如图，BM平分∠ABC，P为BM上一点，PD⊥BC于点D，BD=AB+CD．求证：∠BAP+∠BCP=180°．请你仔细观察下列序号所代表的内容：①；②∵∠1=∠2；③∠A=∠BEP；④AP=PE；⑤；⑥；⑦；⑧．以上空缺处依次所填最恰当的是( )A.①③⑥⑦B.①③⑤⑧C.②③⑥⑦D.②④⑤⑧2.已知，如图，BM平分∠ABC，点P为BM上一点，PD⊥BC于点D，BD=AB+DC．求证：∠BAP+∠BCP=180°．请你仔细观察下列序号所代表的内容：①延长BA，过点P作PE⊥BA于点E；②延长BA到E，使AE=DC，连接PE；③延长BA到E，使DC=AE；④；⑤；⑥；⑦．以上空缺处依次所填最恰当的是( )A.②④⑦B.①⑤⑥C.③④⑥D.①⑤⑦3.已知，如图，在五边形ABCDE中，AB=AE，AD平分∠CDE，∠BAE=2∠CAD，求证：BC+DE=CD．请你仔细观察下列序号所代表的内容：①在CD上截取CF=CB，连接AF；②在DC上截取DF=DE，连接AF；③在DC上截取DF=DE；④AE=AF；⑤AF=AE，∠4=∠3；⑥∠4=∠3；⑦；⑧；⑨．以上空缺处依次所填最恰当的是( )A.①④⑨B.③⑤⑧C.①⑥⑦D.②⑤⑨4.已知，如图，在五边形ABCDE中，AB=AE，∠BAE=2∠CAD，∠ABC+∠AED=180°，求证：BC+DE=CD．请你仔细观察下列序号所代表的内容：①延长DE到F，使EF=BC，连接AF；②延长DE到F，使BC=EF；③延长DE到F，连接AF；④；⑤；⑥；⑦；⑧；⑨．以上空缺处依次所填最恰当的是( )A.③⑤⑥⑧B.①④⑥⑨C.①⑤⑥⑨D.②④⑦⑧四、三角形全等旋转与截长补短专题问题一：题中出现什么的时候，我们应该想到旋转？(构造旋转的条件)问题二：旋转都有哪些模型？【例1】如图，P是正△ABC内的一点，若将△PBC绕点B旋转到△P＇BA ，则∠PBP＇的度数是( )A．45°B．60°C．90°D．120°【例2】如图，正方形BAFE与正方形ACGD共点于A，连接BD、CF，求证：BD＝CF并求出∠DOH 的度数。

初中数学试卷一、截长补短法证明三角形全等例1已知：AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求证：AE=AD+BE练习1如图，四边形ABCD中，AB∥DC，BE、CE分别平分∠ABC、∠BCD，且点E在AD上。

求证：BC=AB+DC。

2.已知∠ABC=3∠C，∠1=∠2，BE⊥AE，求证：AC-AB=2BE3如图，已知AD ∥BC ，∠PAB 的平分线与∠CBA 的平分线相交于E ，CE 的连线交AP 于D ．求证：AD +BC =AB ．4在△ABC 中，︒=∠90ACB ，BC AC =，直线MN 经过点C ，且MN AD ⊥于D ，MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时，求证： ①ADC ∆≌CEB ∆；②BE AD DE +=；(2)当直线MN 绕点C 旋转到图2的位置时，（1）中的结论还成立吗？若成立，请给出证明；若不成立，说明理由.6.如图,已知AC ∥BD ，EA 、EB 分别平分∠CAB 和∠DBA ，CD 过点E ，则AB 与AC+BD 相等PEDCBA吗？请说明理由例2已知，如图1-1，在四边形ABCD 中，BC ＞AB ，AD =DC ，BD 平分∠ABC . 求证：∠BAD +∠BCD =180°.例1. 练习已知，如图3-1，∠1=∠2，P 为BN 上一点，且PD ⊥BC 于点D ，AB +BC =2BD .求证：∠BAP +∠BCP =180°.2、倍长中线法证三角形全等例1 、求证：三角形一边上的中线小于其他两边和的一半。

ABCD图1-1ABCDP12N图3-1练习 1：△ABC 中，AB=5，AC=3，求中线AD 的取值范围例2.已知在△ABC 中，AB=AC ，D 在AB 上，E 在AC 的延长线上，DE 交BC 于F ，且DF=EF ，求证：BD=CE练习2已知在△ABC 中，AD 是BC 边上的中线，E 是AD 上一点，且BE=AC ，延长BE 交AC 于F ，求证：AF=EF例3已知：如图，在ABC ∆中，AC AB ≠，D 、E 在BC 上，且DE=EC ，过D 作BA DF //交AE 于点F ，DF=AC. 求证：AE 平分BAC ∠B第 1 题图ABFDECCEDB A练习3已知CD=AB ，∠BDA=∠BAD ，AE 是△ABD 的中线，求证：∠C=∠BAE 作业1、已知：如图，ABCD 是正方形，∠FAD =∠FAE . 求证：BE +DF =AE .2、五边形ABCDE 中，AB =AE ，BC +DE =CD ，∠ABC +∠AED =180°，求证：AD 平分∠CDE3、在四边形ABCD 中，AB ∥DC ，E 为BC 边的中点，∠BAE=∠EAF ，AF 与DC 的延长线相交于点F 。

全等三角形模型+例题【考纲要求】1. 了解全等三角形的概念和性质，能够准确地辨认全等三角形中的对应元素；2．探索三角形全等的判定方法，能利用三角形全等进行证明，掌握综合法证明的格式；3．会作角的平分线，了解角的平分线的性质，能利用三角形全等证明角的平分线的性质，会利用角的平分线的性质进行证明.【考点梳理】【全等三角形】知识点一、全等三角形的概念及表示1.两个能够完全重合的三角形叫做全等三角形全等三角形是特殊的全等图形，同样的，判断两个三角形是否为全等三角形，主要看这两个三角形的形状和大小是否完全相同，与它们所处的位置无关.2.全等三角形的对应关系：两个全等三角形重合在一起，重合的顶点叫对应顶点，重合的边叫对应边，重合的角叫对应角.3.全等三角形的表示：全等用符号“≌”表示，读作“全等于”.在记两个三角形全等时，要把对应顶点的字母写在对应的位置上，如△ABC和△DEF全等，记作△ABC≌△DEF，读作△ABC全等于△DEF.4.确定全等三角形对应关系的方法：（1）全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边；（2）全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角；（3）有公共边的，公共边是对应边；（4）有公共角的，公共角是对应角；（5）有对顶角的，对顶角一定是对应角；（6）两个全等三角形中一对最长的边（或最大的角）是对应边（或角）一对最短的边（或最小的角）是对应边（或角）.知识点二、全等三角形的性质1.最主要的性质：全等三角形的对应边相等，对应角相等.2.其它性质：（1）全等三角形对应边上的高线相等，对应边上的中线相等，对应角的角平分线相等；（2）全等三角形的周长相等，面积相等，但是，周长或面积相等的三角形不一定是全等三角形.知识点三、全等变换在不改变图形的形状和大小的前提下，只改变图形的位置叫做全等变换.常见的全等变换有平移变换、翻折变换、旋转变换，如下图所示：【探索三角形全等的条件】边角边两边及其夹角分别相等的两个三角形全等，简写为“边角边”或“SAS ”.在△ABC与△A’B’C’中，已知角边角两角及其夹边分别相等的两个三角形全等，简写“角边角”或“ASA ”.在△ABC与△A’B’C’中，已知角角边两角分别相等且其中一组等角的对边相等的两个三角形全等，简称为“角角边”或“AAS ”. 在△ABC 与△A’B’C’中，已知边边边三边分别相等的两个三角形全等，简称为“边边边”或“SSS ”.在△ABC 与△A’B’C’中，已知.斜边、直角边斜边和一条直角边分别相等的两个直角三角形全等，简称为“斜边、直角边”或“HL ”在Rt △ABC 与Rt △A’B’C’中，，已知.1. 只有两边及其夹角分别对应相等，才能判定两个三角形全等，“边边角”不能判定三角形全等；2. 在书写过程中，要按照边角边对应顺序书写，即对应顶点的字母写在对应的位置上.探究SSA全等篇异侧半角模型1.如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45º，则BE ＋DF＝EF .简证：如图，将△ADF 绕点A 顺时针旋转90º得到△ABG ，使得AD 与AB 重合， 通过证明△AEF ≌△AEG 即可得到BE ＋DF ＝EF .2.如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45º，则AE 平分∠BEF ，AF 平分∠DFE .简证：如图，将△ADF 绕点A 顺时针旋转90º得到△ABG ，使得AD 与AB 重合；将△ABE 绕点A 逆时针旋转90º得到△ADH ，使得AB 与AD 重合.3. 如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45º，则.简证：通过上述的全等直接可以得到，不再证明.4.如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45º，过点A 作AH ⊥EF 交EF 于点H ，则AH ＝AB .简证：由上述结论可知AE 平分∠BEF ，又∵AB ⊥BC ，∴AH ＝AB . 5.如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45º，则.简证：由结论1可得EF ＝BE ＋DF ，则＝CE ＋CF ＋EF ＝CE ＋CF ＋BE ＋DF ＝2AB .6. 如图，在正方形ABCD 中，E 、F 分别是BC 、CD 上的点，且∠EAF ＝45º，AE 、AF 分别与BD 相交于点M 、N ，则.简证：如图，将△AND 绕点A 顺时针旋90º得到△AGB ，连接GM .通过证明△AMG ≌△AMN 得MN ＝MG ，DN ＝BG ，∠GBE ＝90º，即可证.补充：等腰直角三角形与“半角模型”DCPBACDPB ADPCAB如图所示，在等腰直角三角形ABC中，若∠DCE＝45º，则.证明：如图，将△ACD绕着点C顺时针旋转90º得到△，连接.1.1二次全等证明1.已知：如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DF⊥AB于F，DE⊥AC于E．2.求证：△BDF≌△CDE．3.4.5.已知：如图，点A，E，F，C在同一直线上，AE=CF，过点E，F分别作DE⊥AC，BF⊥AC，连接AB，CD，BD，BD交AC于点G，AB=CD．6.求证：△DEG≌△BFG．7.3.已知：如图，在Rt△ACD中，∠ADC=90°，BE⊥AC于E，交CD于点F，AE=AD．求证：△CEF≌△BDF．4.已知：如图，在四边形ABCD中，AB=BC=CD=AD，BD平分∠ABC，E为BD上任意一点，连接AE，CE．求证：△ADE≌△CDE．5.已知：如图，在△ABC中，∠ACB=∠ABC=60°，∠EDF=60°，BD=CD，∠DBC=∠DCB=30°，∠BDC=120°，延长AC到点G，使CG=BE．6.求证：△EFD≌△GFD．7.6、已知：如图，点A，C在直线EF上，BC=AD，AB=CD，AE=CF．求证：∠E=∠F．7、已知，如图，AE=BF，AD=BC，CE=DF．求证：AO=BO．8、已知：如图，∠D=∠E，AM=ME=CN=DN．试猜想AB和BC的数量关系，并证明你的猜想．9、10、9.如图，在正方形ABCD中，∠ABC=∠BCD=90°，AB=BC=CD=AD．E为BC边上一点，且AE=DE，AE与对角线BD交于点F，∠ABF=∠CBF，连接CF交DE于点G．求证：DE⊥CF．10.已知：如图，在等边△ABC中，△C=△ABD=60°，AB=BC=AC，点D，E分别为BC，AC边上一点且AE=CD，连接AD，BE 相交于点F．11.求证：△1=△2．12.1.2截长补短 倍长中线例题1、如图，已知在ABC ∆中，AD 是BC 边上的中线，E 是AD 上一点，延长BE 交AC 于F ，AF EF =，求证：AC BE =．例题2、在Rt ABC ∆中，90BAC ∠=︒，点D 为BC 的中点，点E 、F 分别为AB 、AC 上的点，且ED FD ⊥．以线段BE 、EF 、FC 为边能否构成一个三角形？若能，该三角形是锐角三角形、直角三角形或钝角三角形？例题3、八年级一班数学兴趣小组在一次活动中进行了探究试验活动，请你和他们一起活动吧．【探究与发现】（1）如图1，AD 是△ABC 的中线，延长AD 至点E ，使ED=AD ，连接BE ，写出图中全等的两个三角形______【理解与应用】（2）填空：如图2，EP 是△DEF 的中线，若EF=5，DE=3，设EP=x ，则x 的取值范围是______．（3）已知：如图3，AD 是△ABC 的中线，∠BAC=∠ACB ，点Q 在BC 的延长线上，QC=BC ，求证：AQ=2AD ．F E D CB AF EDC B A例题4、如图，在△ABC中，已知∠ABC=45°，过点C作CD⊥AB于点D，过点B作BM⊥AC于点M，CD与BM相交于点E，且点E是CD的中点，连接MD，过点D作DN⊥MD，交BM于点N．（1）求证：△DBN≌△DCM；（2）请探究线段NE、ME、CM之间的数量关系，并证明你的结论．例题5、阅读下面的题目及分析过程，并按要求进行证明．已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE．求证：AB=CD．分析：证明两条线段相等，常用的一般方法是应用全等三角形或等腰三角形的判定和性质，观察本题中要证明的两条线段，它们不在同一个三角形中，且它们分别所在的两个三角形也不全等．因此，要证AB=CD，必须添加适当的辅助线，构造全等三角形或等腰三角形．现给出如下三种添加辅助线的方法，请任意选择其中一种，对原题进行证明．例题8、（1）如图，四边形ABPC中，AB AC∠=︒，求证：PB PC PABPC+=．=，60BAC∠=︒，120（2）如图，四边形ABCD中，AB BCAPC∠=︒，求证：ABC∠=︒，P为四边形ABCD内一点，且120=，60++≥．PA PC PD BDC 1A B C ED D E(C )B A C 1C 1A B C E D 1A B C E D1.3一线三等角例1：已知AB ⊥BD ，ED ⊥BD ，AB =CD ，BC =DE ，⑴求证：AC ⊥CE ；⑵若将△CDE 沿CB 方向平移得到①②③④等不同情形，1AB C D ，其余条件不变，试判断AC ⊥C 1E 这一结论是否成立？若成立，给予证明；若不成立，请说明理由.① ② ③ ④例2：等腰直角△ABC ，其中AB=AC ，∠BAC=90°，过B 、C 作经过A 点直线L 的垂线，垂足分别为M 、N ．（1）你能找到一对三角形的全等吗？并说明．（2）BM ，CN ，MN 之间有何关系？若将直线l 旋转到如图2的位置，其他条件不变，那么上题的结论是否依旧成立？例3.（1）如图，已知：在△ABC 中，∠BAC ＝90°，AB ＝AC ，直线m 经过点A ，BD ⊥直线m ，CE ⊥直线m ，垂足分别为点D 、E ．证明：DE ＝BD ＋CE ．（2）如图，将(1)中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC ＝a，其中a为任意锐角或钝角．请问结论DE＝BD＋CE是否成立？如成立，请你给出证明；若不成立，请说明理由．(3) 拓展与应用：如图，D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC 平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状．1.4半角模型1.在等腰Rt△ABC中，CA＝CB，∠ACB＝90º，O为AB的中点，∠EOF＝45º，交CA于F，交BC的延长线于E.（1）求证：EF＝CE＋AF；（2）如图2，当E在BC上，F在CA的反向延长线上时，探究线段AF、CE、EF之间的数量关系，并证明.2.如图，在四边形ABCD中，AB＝AD，∠B＋∠D＝180º，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，求证：EF＝BE＋FD.3. 如图，△ABC是边长为3的等边三角形，△BDC是等腰三角形，∠BDC＝120º，以D为顶点作一个60º的角，使其两边分别交AB于M，交AC于N，连接MN，则△AMN的周长是多少？4.如图，在等边△ABC中，∠ABC与∠ACB的角平分线相交于点O，点E、F分别在线段AB、BC上，连接EO、FO，满足∠EOF＝60º，连接EF.（1）①求证：OB＝OC；②求∠BOC的度数；（2）求证：CF＝BE＋EF.5. 在四边形ABDC中，AC＝AB，DC＝DB，∠CAB＝60º，∠CDB＝120º，E是AC上一点，F是AB延长线上一点，且CE＝BF.（1）试说明：DE＝DF；（2）在图1中，若G在AB上且∠EDG＝60º，试猜想CE、EG、BG之间的数量关系并证明；（3）若题中条件“∠CAB＝60º，∠CDB＝120º”改为“∠CAB＝，∠CDB＝，G在AB上，那么∠EDG 满足什么条件时，（2）中的结论仍然成立？”（直接写结果，不需证明）.。