工程制图3(制图基本原理与三视图,点投影)
- 格式:ppt
- 大小:3.72 MB
- 文档页数:47
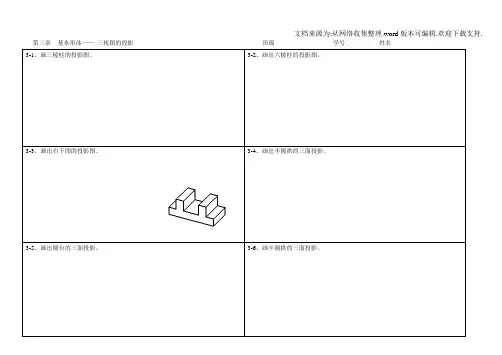
第三章基本形体——三视图的投影班级学号姓名3-1、画三棱柱的投影图。
3-2、画出六棱柱的投影图。
3-3、画出右下图的投影图。
3-4、画出半圆拱的三面投影。
3-5、画出圆台的三面投影。
3-6、画半圆拱的三面投影。
44 第三章基本形体——补绘基本形体的第三投影班级学号姓名
45
第三章基本形体——补绘基本形体的第三投影班级学号姓名
46
第三章平面立体表面上的点班级学号姓名
47 第三章平面立体表面上的点班级学号姓名
48 第三章平面体的截交线班级学号姓名
49
第三章平面体的截交线班级学号姓名
50
第三章平面体的截交线班级学号姓名
51 第三章平面体的截交线班级学号姓名
第三章平面体与平面体相交班级学号姓名
54 第三章平面体与平面体相交班级学号姓名
55 第三章平面体与平面体相交班级学号姓名
56 第三章曲面体上的点和直线班级学号姓名
57 第三章曲面体上的点和直线班级学号姓名
58
第三章曲面体截交线班级学号姓名
59 第三章曲面体截交线班级学号姓名
60 第三章曲面体截交线班级学号姓名
61 第三章曲面体截交线班级学号姓名
62 第三章曲面体与平面体、曲面体相交班级学号姓名
63 第三章曲面体与平面体、曲面体相交班级学号姓名
64 第三章曲面体与平面体、曲面体相交班级学号姓名
65 第三章曲面体与平面体、曲面体相交班级学号姓名
66
第三章曲面体与平面体、曲面体相交(应分两页)班级学号姓名
67 第三章曲面体与平面体、曲面体相交(应分两页)班级学号姓名
68 第三章曲面体与平面体、曲面体相交班级学号姓名
69。





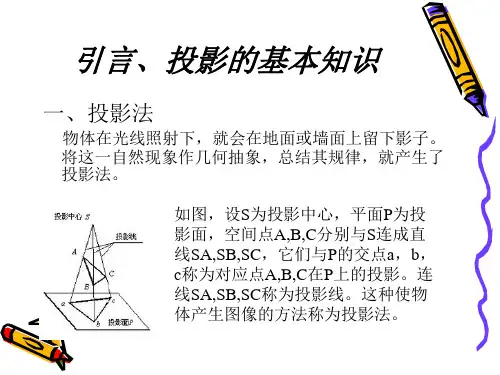




§3-2 点、直线、平面的投影任何物体的表面都是由点、线、面等几何元素组成。
如图3-11所示三棱锥,是由四个平面、六条棱线和四个点组成。
由于工程图样是用线框图形来表达,所以绘制三棱锥的三视图,实际上就是绘制构成三棱锥表面的这些点、棱线和平面的三面投影1。
因此,要正确绘制和阅读物体的三视图,须掌握这些基本几何元素的投影规律。
图3-11三棱锥一、点的投影1.点的三面投影形成如图3-12a所示,过空间点A分别向三个投影面作垂线,其垂足a、a′、a″2即为点A 在三个投影面上的投影。
按前述三投影面体系的展开方法将三个投影面展开(图3-12b),去掉表示投影面范围的边框,即得点A的三面投影图(图3-12c)。
图中a x、a y、a z分别为点的投影连线与投影轴OX、OY、OZ的交点。
图3-12点的三面投影形成2.点的三面投影规律从图3-12中点A的三面投影形成可得出点的三面投影规律:(1)点的正面投影与水平投影的连线垂直于OX轴,即a′a⊥OX。
(2)点的正面投影与侧面投影的连线垂直于OZ轴,即a′a″⊥OZ。
(3)点的水平投影到OX轴的距离等于点的侧面投影到OZ轴的距离,即aa x=a″a z.此外,从图3-12a还可看出点的投影到投影轴的距离,分别等于空间点到相应投影面的距1本书中,体的多面投影称为视图。
点、线、面等几何元素的投影一般称为投影图。
2空间点用大写字母表示,H面投影用相应的小写字母表示,V面投影用相应的小写字母加“′”表示,W 面投影用相应的小写字母加“″”表示。
离。
如:a′a z=aa YH反映点A到W面的距离;a′a x=a″a Yw反映点A到H面的距离; aa x=a″a z反映点A到V面的距离.根据上述点的三面投影规律,在点的三面投影中,只要知道其中任意两个面的投影,就可求作出该点的第三面投影。
〔例3-2〕已知点B的V面投影b′与H面投影b,求作W面投影b″(图3-13a)。