卫星测控中心

Mitec 功放 特点和优势 �支持标准和扩展频段 �易于安装 �高散热效率提高了平均无故障时间 �优越的相位噪声指标 �内置的1：1备份逻辑开关，替代了昂贵的外部控制器 �内置的过压、过流、过温保护和失锁关闭机制；内置遥测可以进行射频功率检 测、静音控制、跟踪报警信息 �支持http访问 �Snmp协议允许通过电脑、ipad、Iphone对设备进行监控 �支持rS485, rS232, ethernet and dry-contacts 监控接口
矿用本安型 无线网关 工业以太网交换机
R S 232
IP IP
专家远程诊断 空地闭一体化通信 平台服务器B
IP IP
多参数测定器和移动式 读卡器 矿用本安型手机、 摄像头1 矿用本安型手机、 低频无线应急通信 终端和网关 摄像头2 矿用应急通信系统 国家应急救援中 心或救援基地 省市应 急 救 援 中 心
职工总数： 职工总数 2000余人 其中专业技术人员 1200余人，中高级职称人员 800余人 ，享受政府特殊津贴 30余人。
微波暗室： 微波暗室 4个 环境试验中心： 环境试验中心 1个 电磁兼容实验室仪器设备 4000多台（套）
2001.88
其中高、精、尖仪器设备 150多套
便携式手动卫星通信天线
Mitec 功放主要产品系列
Ku频段 �10-16W Ku Band ABOX �8-20W Ku Band BUC �8-25WKu-Trekker �25-200W-Ku-Band_BUC C频段 �5-40W C-Band BUC �60-800W C-Band HP BUC
主要特性：
�高性能 采用环焦1.2米碳纤维天线面，具有高增益、 低旁瓣电平、高级化隔离度的特点； �采用5轴跟踪结构，圆锥扫描跟踪技术可实现跟踪 过程中的高指向精度，高响应速度 �自主独立运行 不依赖任何外部数据进行控制跟 踪，系统采用高精度GPS/INS融合船姿测量技术， 并将船姿以及导航数据实时输出。

酒泉卫星发射中心六大优势记者从有关部门获悉，选择酒泉卫星发射中心发射“神五”，有六大优势。

首先，酒泉卫星发射中习建场30余年，有相当雄厚的物质基础，生活设施基本齐全，技术保障、测控通信、铁路运输发配电等配套完善。

其次，航安全有保证，发射场区为戈壁滩，航区200公里以内基本为无人区，600公里以内没有人口密集的城镇和交通干线，火箭残骸坠落不会有太大的危害。

第三，发射场区占地数万平方公里，地势开阔，完全满足待发段和上升段航天员救生要求，也是先进的天地往返运输系统最理想的发射和回收着陆场所。

第四，场区干燥少雨，雪电日少，容易满足发射条件。

第五，场区里有一个大型机场，可以为航天器和参试人员提供快速交通通道。

最后一点是可以充分利用，由西至东，距离数千公里，基本形成陆上航天测控网。

中国共有几个卫星发射基地？各有什么特点？(2009-07-19 14:20:18转载标签：杂谈中国共有几个卫星发射基地？各有什么特点？ 1、酒泉卫星发射中心(内蒙-额济纳旗塞汉桃来 2、西昌卫星发射中心(四川凉山州冕宁县 3、太原卫星发射中心(山西岢岚县 4、文昌卫星发射中心(海南文昌市，在建酒泉卫星发射中心酒泉卫星发射中心是科学卫星、技术试验卫星和运载火箭的发射试验基地之一，是中国创建最早、规模最大的综合型导弹、卫星发射中心，也是中国唯一的载人航天发射场。

酒泉卫星发射中心位于中国西北部甘肃省酒泉市东北地区，海拔1000米，始建于1958年10月，占地面积约2800平方公里。

该地区地势平坦，人烟稀少，属内陆及沙漠性气候，年平均气温8．7摄氏度，相对湿度为35％－55％，常年干燥少雨，春秋两季较短，冬夏两季较长，一年四季多晴天，云量小，日照时间长，生活环境艰苦，但可为航天发射提供良好的自然环境条件。

每年约有300天可进行发射试验。

在载人航天飞行任务中，酒泉卫星发射中心主要承担发射场区的组织指挥，实施火箭的测试、加注、发射，逃逸塔测试，整流罩测试，人船箭地联合检查，船箭塔对接和整体转运，提供发射场区的气象、计量和技术勤务保障，并在紧急情况下组织实施待发段航天员撤离及逃逸救生。

航天发射中心的选址要求
文综知识点航天发射中心的选址要求1.海拔较高、纬度低物理知识告诉我们，卫星轨道倾角与发射场的纬度关系密切。

纬度越低，离赤道越近，既可以充分利用地球自转的离心力，又可缩短从地面到卫星轨道的距离，从而节省火箭燃料，增加火箭的有效负荷。

例如我国即将建成的文昌卫星发射中心火箭发射场，它距离赤道较近、纬度低，发射卫星时可以充分利用地球自转的离心力，因此文昌卫星发射中心能耗较低，使用同样燃料可以达到的速度也更快。

据称，它比西昌发射火箭的运载能力可提高10%至15%，卫星寿命可延长2年以上。

除此之外，还可避免一系列火箭研制上复杂的技术问题，简化制造过程，同时还能够满足将来发射大、小倾角卫星的要求，利于卫星和火箭部件的回收。

2.地形隐蔽，地质结构坚实发射基地需要有利的地理位置。

地形上要求地势平坦开阔，地质结构稳定坚实，避开地层断裂带和地震区。

在南北纵向山谷中形成的一些山间小盆地，不但利于发射场的整体布局，对地面发射设施、技术设备与跟踪测量、通信的建网布署也十分有益，而且还能满足扩建的要求和今后的发展。

3.气候适宜，水源充足稳定要有良好的气象及水文条件。

气象条件是影响发射的最直接、最关键因素。

发射场通常选择在雷雨少、湿度小、风速弱、温差变化小的地方。

还需要有充足的水源。

水主要用于发射台及相关设备的降温，满足发射场清洗废物和冷却用水的需要。

西昌地区属于亚热带高原季风气候区，年平均温度为摄氏十六度，是中国年气温变化最小的地区之一，西昌地区雨旱两季分明，日照多达三百二十天，几乎没有雾日，全年风速都很低。

每年只有六月至九月为雨季，多半是夜雨和午后阵雨，其余月份皆为旱季，多是晴天，。

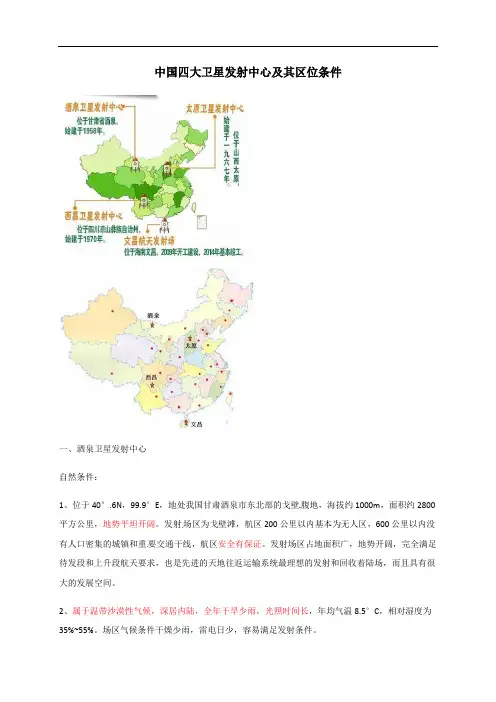
中国四大卫星发射中心及其区位条件一、酒泉卫星发射中心自然条件：1、位于40°.6N，99.9°E，地处我国甘肃酒泉市东北部的戈壁腹地，海拔约1000m，面积约2800平方公里，地势平坦开阔。

发射场区为戈壁滩，航区200公里以内基本为无人区，600公里以内没有人口密集的城镇和重要交通干线，航区安全有保证。

发射场区占地面积广，地势开阔，完全满足待发段和上升段航天要求，也是先进的天地往返运输系统最理想的发射和回收着陆场，而且具有很大的发展空间。

2、属于温带沙漠性气候，深居内陆，全年干旱少雨，光照时间长，年均气温8.5°C，相对湿度为35%~55%。

场区气候条件干燥少雨，雷电日少，容易满足发射条件。

社会经济条件：1、酒泉，矿产种类繁多。

工业门类齐全—我国古代飞天艺术的故乡，新中国石油工业的摇篮，现代航天工业的诞生地和发源地，贯穿欧亚大陆桥的交通要冲。

2、已建场30年，拥有雄厚的物质基础，生活设施基本齐全，技术保障。

测控通信，铁路运输，发配电等配套设施完善。

3、交通便利，通讯发达。

场区内已建有大型机场，既可以满足航天器使用飞机快速运输的要求，又可作为参试人员往返乘降飞机的场所。

4、可以充分利用西起喀什、东至福建闽西，距离数千公里，并已基本形成的陆上航天测控网。

二、太原卫星发射中心1.交通便利2.一年之中天气状况良好天数较多3.靠近北京，便于与北京航空航天控制中心联系三、西昌卫星发射中心1、首先是海拔高、纬度低。

发射场地处东经１０２度，北纬２８．２度，平均海拔１５００米。

而我们知道，卫星轨道倾角与发射场的纬度关系十分重大，纬度越低，离赤道越近，就既可以充分利用地球自转的离心力，又可缩短从地面到卫星轨道的距离，从而节省火箭燃料，增加火箭的有效负载。

此外，还可避免一系列火箭研制上复杂的技术问题，简化制造过程。

同时还能够满足将来发射大、小倾角卫星的要求，也有利于卫星和火箭部件的回收。

西昌卫星发射中心选址的主要原因：1、纬度低(北纬28．2度)，海拔高(1500米)，发射倾角好，地空距离短，纬度越低，离赤道越近，这既可充分利用地球自转的离心力，又可缩短地面到卫星轨道的距离，从而增加火箭的有效负荷。

2、峡谷地形好，地质结构坚实，有利于发射场的总体布局，对地面发射设施、技术设备及跟踪测量，通讯的布网有利，能满足多个发射场的建设。

3、晴好天气，“发射窗口”好。

西昌年平均气温18℃，是全国气候变化最小的地区之一，日照多达320天，几乎没有雾天，试验周期和允许发射的时间较多。

4、战备的目的，地处大山深处，便于隐藏。

原因第一，也是最重要的原因就是这些地方一般有适合发射的条件，比如晴天多，降水少，这对于卫星发射都是极有利的条件。

如果建在潮湿且多云的地方，则可能少有适合发射的天气。

第二，这些发射场一般都建设于特殊年代，保密和隐蔽是关键，因此都位于大后方。

如果建设于在现在所谓的发达地区，则很有可能被敌人破坏。

比如，赫赫有名的中国酒泉卫星发射中心就曾以“东风”为代号，已达到保密的目的，这也是“东风航天城”之名的来历。

第三，这些地区一般都是沙漠，属于无人区，对人类社会的印象较小。

比如，万一发射失败，可能会造成重大事故。

航天器残荷可能对当地造成影响。

而这些地方影响就很小。

第四，就是出于经济的原因。

这些发射场除了没有发射地球同步卫星的优势，在发生其他卫星，由于其纬度高，可以达到节省燃料和降低技术要求的目的，这也是一个很显著的优势。

甘肃酒泉该地区属内陆及沙漠性气候，地势平坦，人烟稀少，全年少雨，白天时间长，年平均气温8.5摄氏度，相对湿度为35%-55%，每年约有300天可进行发射试验，又可充分利用西起喀什、东至闽西，距离数千公里的陆上航天测控网，加上基地已建成多年，生活设施基本齐全，技术保障、测控通信、铁路运输、发配电等配套设施完善，条件很适合卫星及载人航天飞行器发射。

选址西昌也是同样的道理。

(华师版)初一数学最全最经典习题册- 豆丁网初一数学练习题... 3、某工厂从2000∽2003 年的年产值统计图，如图，则年产值在2500 万元以上的... pdf(华师版)初一数学最全最经典习题册热度: pdf(华师.../p-124501817.html 2012-8-9。

建 ，是 我 国唯 一 的载 人 航 天 发 射 场 。本世 纪 初 ，中 ， 在 载 人 航 天 发 射 场 东 部 新 建 又 了 卫星 发 射 工位 ，用 于长 征 二 号 Ｃ、长 征
火 箭点 火起 飞
《 太空探索 》２ ０ ０ ８年第 ３期 ， １ ２
维普资讯
酒泉 卫 星发射 中 心载人 航 天发 射场
人飞船成功升入太空 ，并于第二天安全返 二号 Ｄ、 目前 ，中心具备完成大倾角 、中低轨 长征四号 Ｂ 运载火箭发射卫星 。 中 回 ， 中国成为第三个独立掌握载人航天 ， 有 先 进 的跟 踪 、遥 测 和 控 制 系 统 ，配 道 的载人飞船 、返回式卫星及 中、高轨 道 使 具 技术的国家 。中国唯一的载人航天发射场 备 光 学 、雷 达 跟 踪 测 量 设 备 、无 线 电遥 测 太 阳 同 步轨 道 卫 星 的 发 射 能 力 。
境和保 障条件 ， 各大 系统 的射前技 术准备 体转运设施和脐带勤务塔等大型设施 。
主要 包括垂直 总装测试厂房 、 水平转载测 最大 限度地安排在技术区完成 ， 在发 射区
垂 直整 体 转运 设施 包括 活 动发射 平 试间 、测发控制楼 、飞船及有效载荷总装 只进行 简 单 的功能 检查 和准 备就加 注 发 台 、 转轨车 、 垂直转运轨道及基础 三部分 。
一
艘神舟试验飞船 、第一艘神舟载人飞船
的发射 。至 ２ ０ 年 １ ０７ ２月为止 ，中， 已完 成 了 ３ 多颗卫星和 ６ ０ 艘飞船 的成功 发射。 中心地处甘肃 、 内蒙古交界之处 的巴 丹吉林沙 漠西 部 ， 海拔 １ ０ 米 左右 ， ００ 区域
内多 戈壁 和沙 漠 ， 势 平 坦 、 烟 稀 少 ， 地 人 利 于 发 射 场 设 施 建 设 、测 量 控 制 设 备 布 设及

卫星航天发射基地的区位因素和返回地的选择条件小专题选址条件1,纬度条件：纬度低，线速度大，航天器的初始速度大，节省燃料，降低发射成本2.气候条件：气候干燥，降水少，多晴朗天气，空气能见度高3.地形条件：开阔平坦，相对周围地区地势较高,地质结构稳定4.交通条件：交通便利，便于仪器和设备的运输5.安全条件：人口稀少，以保证安全6、国防条件：建于山区、沙漠地区；其中影响卫星和飞船发射的最关键和最直接的因素是——气象因素（2）返回地点①人烟稀少的地区②地势开阔平坦的草原地区,水面少,便于发现目标和营救的地区或者在海洋上③距离发射场、控制中心位置适中,有利于监控、抢救等工作展开共同得出结论一、建立发射场，首先，要有可靠的安全保障。

需要建在人烟稀少的地域，有建立禁区的可能，以便运载火箭各级分离后坠落不致危及生命财产的安全。

如拜科努尔发射场位于哈萨克斯坦的半沙漠地带，东西长80千米，南北宽30千米，发射场区幅员辽阔，人烟稀少，是内陆发射的最佳场所。

二、其次，要有有利的地理位置。

在地形上要求地势平坦开阔，地质结构稳定坚实，避开地层断裂带和地震区。

在纬度位置上要求尽量选择在低纬度地区，最好选择在赤道附近。

三、再次，要有良好的气象及水文条件。

发射场通常选择在雷雨少、湿度小、风速弱、温差变化低的地方。

影响卫星发射和飞船发射的最直接、最关键因素是气象条件。

还需要有良好的水质，主要用于发射台及相关设备的降温。

四、便利的交通。

发射场常建在工业中心和铁路干线，便于大型火箭卫星的运输及回收。

如果通过海洋运输可解决大直径火箭内陆铁路运输的难题，以利于我国未来发展火箭及大型航天器的要求。

五、最后，还要有最佳的监测系统。

既要考虑监测系统的布局，又要照顾绵延几千千米的空中和地上监测站的设点。

如美国的卡纳维拉尔角发射场，运载火箭航区沿东南方伸向大西洋，航程可达8000千米，还可延伸到印度洋，航程延长到12000千米。

各跟踪和观测台站设在大西洋上的大马哈岛、达特克岛、安提瓜岛的阿森松岛上，与测量站相比，可减少海浪对测量精度的影响，具有较好的发射观测环境。

广东汕头科技西路 6 号 卫星应用系统、卫星通信系统
将迁往深圳
山西省太谷县新建路
133 号
空间飞行器地面设备和卫星应用产品
将迁往天津
北京市海淀区友谊路 航天器总装
104 号
小卫星研制
通信卫星领域的业务发展规划，各类通信卫星的 研发、总体设计及系统集成
科技六院 （ 067 基 航天推进技术研究院 地）
固体火箭发动机设计 固体火箭装药配方 固体发动机试验技术 情报档案所 固体发动机总装 固体发动机装药
四川省成都经济技术开发区航 战略导弹生产、火箭弹研制、火工品研
.\
院（062、 064 基 地）
天北路
制
下属单位
七部 研发中心
四川省成都经济技术开发区航 飞行器总体设计
天北路
7102 厂 长征机械厂
飞航导弹、海防导弹
飞航导弹总体设计 飞航导弹用冲压发动机、固体发动机、涡喷、涡扇发动机 飞航导弹控制系统 导弹雷达导引头 计量测试技术研究和测试设备 通信、计算机 结构复合材料、功能复合材料、热防护技术、分析测试技术、特种金属 材料应用、金属材料精密成形技术
.\
8357 津航计算机通讯研究 天津市河北区黄纬路
7304 厂
成都市龙泉驿区航天北路
制造厂）
涡喷发动机制造
7146 所 重庆航天机电设计院
重庆市石桥铺渝州路 60 号
地面火控系统、机载火控系统、发动机 控制系统
7140 站 四川航天计量测试研究所
四川省成都经济技术开发区航天北路
.\
4431 厂 成都燎原星光电子有限责任公司
成都市龙泉驿区星光东路 68 号 半导体器件、声表器件研制
科工七 中国航天建筑设计研究院

北斗显神威,航天封片记历史雨水2010年1月17日零点12分，在西昌卫星发射中心，我国用长征三号丙运载火箭将第三颗北斗导航卫星送入预定轨道，2010年宇航发射取得了开门红。

按照总体规划，2012年前后，预计将有10颗以上的组网卫星完成为亚太地区提供导航、授时和短报文通信服务；到2020年左右将建成覆盖全球的北斗卫星导航系统。

西昌卫星发射中心及有关航天单位为这次航天任务制发了纪念邮品，用它记录下北斗导航卫星的组网和推进的步伐，让航天纪念品来记录这段历史0巴。

第三颗北斗导航卫星发射纪念公函封西昌卫星发射中心制作。

纪念封规格：220mm×110mm；编号：.JF61；封、戳设计：宋经同、唐令权；印量：600枚；纪念封销四川冕宁沙坝2010.01.17.018B政邮戳北斗导航卫星__-G1发射海上测控纪念封在此次第三颗北斗导航卫星发射任务中，中国卫星海上测控部派远望三号、远望六号测控船分别赴太平洋预定海域执行海上测控任务，为此特发纪念封一枚。

纪念封规格：220mm×110mm：编号：YWJF-67：策划：孙建新、潘永猛；封、戳设计：刘学会；印量：2000枚；纪念封销北斗导航卫星__-G1发射海上测控纪念邮戳和江苏江阴2010.1.17.1远望2邮戳北斗导航卫星组网发射纪念封航天集邮网制作。

纪念封规格：220mm×110mm：编号：HTJY-F18：策划、设计：张海宁、蒋庆平、徐明、韩见弘；印量：100枚；纪念封盖四川冕宁沙坝2010.01.17.01邮政邮戳第三颗北斗导航卫星发射纪念封西昌卫星发射中心制作。

纪念封规格：175mm×110mm；编号：.JF61；策划、设计：雒庚伟；纪念封销四川冕宁沙坝201 0.01.17.01邮政日戳长征三号丙遥二运载火箭发射__-G1卫星纪念封四川省凉山州邮政局集邮公司制作。

纪念封规格：175mm×110mm；编号：XF54；封、戳设计：马家禄、彭乐宾、严虹；印量：500枚；纪念封销四川西昌卫星发射中心2010.01.17.08邮政日戳2009-122长征三号丙运载火箭发射北斗导航卫星第三颗组网卫星纪念封中国航天集邮协会制作。

太原卫星发射中心
太原卫星发射中心发射中心始建于1967年。目前，已建成具有多 功能、多发射方式，集指挥控制、测控通信、综合保障系统于一 体的现代化发射场。 1997年12月8日，该中心第一次执行国际商业发射，成功地将美 国摩托罗拉公司制造的两颗铱星送入预定轨道。 1999年5月10日，将风云一号气象卫星和实践五号科学实验卫星 送入轨道高度为870公里的太阳同步轨道。 1997年至2002年的5年多时间里，太原卫星发射中心一共发送22 颗卫星，成功率100%。 2003年10月21日，中心发射“资源一号”02星和“创新一号”搭 载星取得成功； 2004年7月25日，“探测二号”卫星从这里冲向太空，准确入轨； 2004年9月9日，两颗“实践六号”卫星从这里成功进入太空，相 映生辉； 2004年11月6日，中心发射“中国资源二号”卫星再传捷航天发射中心位于中国海南省文昌市， 是中国以前的一个发射亚轨道火箭（如弹道 导弹）的测试基地。现在正在扩张，将成为 中华人民共和国的第四个卫星发射中心。 主要承担地球同步轨道卫星、大质量极轨卫 星、大吨位空间站和深空探测卫星等航天器 的发射任务。
西昌卫星发射中心
西昌卫星发射中心（XSLC）又称“西昌卫星城”，始建于 1970年，隶属于中国人民解放军总装备部，它是以主要承 担地球同步轨道卫星的发射任务的航天发射基地，担负通 信、广播、气象卫星等试验发射和应用发射任务。 1984年6月8号成功发射我国第一颗地球同步轨道卫星 ； 1986年的2月1号，成功发射我国第一颗通信广播卫星-东 方红二号 ； 1990年成功发射我国承揽的商务卫星，亚洲一号 ； 截至2003年底，已先后成功组织了34次国内外卫星发射。 2004年4月，“试验卫星一号”和“纳星一号”在西昌卫 星发射中心顺利升空 ； 2007年10月24日18时05分04秒(UTC＋8时)，我国的首颗绕 月人造卫星——嫦娥一号在西昌卫星发射中心升空 。

（3）用户设备 用户设备是带有全向收发天线的接收和转发器，用于接收卫 星发射的S波段信号，从中提取由主控站发送给用户的数 字信息。用户设备简单，仅有接收和转发设备，成本低。 用户设备的特点： 1）快速开机定位功能：用户开机几秒钟可定位，其他系统 需要几分钟。 2）位置报告功能：用户与用户、用户管理部门，以及地面 中心之间均可实行双向报文通信，传递位置及其他信息， 目前其他系统不具备该功能。 3）双向授时功能：其他系统不具备该功能。 北斗系统采用有源定位体制，使得系统在用户容量、定位精 度、隐蔽性和定位频度等方面受到一定限制，无测速功能， 不能满足远程精确打击武器的制导要求。 优点是投资少，具有其他系统不具备的位置报告功能，性价 比较高，具有中国特色。
用户坐标改正数向量为
2(Y1 Y0 ) (Y1 Y0 )
01

01
(Y2 Y0 )
02
cos B0 sin L0
北斗双星导航定位系统服务区域
双星定位系统解算方法
双星导航定位系统的定位原理为三球交会测量原理：地面中 心通过两颗卫星向用户广播询问信号（出站信号），根据 用户响应的应答信号（入站信号）测量并计算出用户到两 颗卫星的距离；根据中心存储的数字地图或用户字带测高 仪测出的高程，计算出用户到地心的距离。根据三个距离 确定用户的位置，并通过出站信号将定位结果告知用户； 授时与报文通信功能也在出入站信号的传输过程中实现。 1、系统基本工作过程：由地面中心向卫星1和卫星2同时发 送出站询问信号（C波段）；两颗工作卫星接收后，经卫 星上的转发器变频放大后，向服务区内的用户广播（S波 段）；用户响应其中一颗卫星的询问信号，并同时向两颗 卫星发送入站信号（L波段，包括用户的申请服务内容）， 经过卫星转发给地面中心（C波段）；地面中心接收解调 用户发送的信号，分别测量出用户所在点至两颗卫星的距 离，再根据用户申请服务内容进行相关数据处理。

中国航天科技知识常识
中国航天科技知识常识包括以下几部分：
1.发射场：中国拥有四个主要的卫星发射中心，包括甘肃酒泉卫星发射中心、
四川西昌卫星发射中心、山西太原卫星发射中心以及海南文昌卫星发射中心。

2.卫星系列：中国成功发射了多种卫星系列，包括东方红一号卫星、实践十号
卫星、高分系列卫星、风云系列卫星、海洋系列卫星等。

其中，东方红一号
卫星是中国发射的第一颗人造地球卫星，标志着中国开始进入航天时代。

3.载人航天：中国已经成功实施了多次载人航天任务，包括神舟系列飞船和天
宫空间站等。

中国是继苏联和美国之后，第三个掌握载人航天技术的国家。

4.火箭技术：中国独立自主地研制了多种型号的“长征”系列运载火箭，用于发
射各种卫星和载人飞船。

5.测控技术：中国建立了完善的航天测控网，用于跟踪、监测和控制卫星、飞
船等航天器的运行。

6.空间站：中国正在建设自己的空间站，已经成功发射了天宫空间站的核心舱
和实验舱，未来还将进行多次载人飞行任务，以完成空间站的组装和运营。

以上是中国航天科技知识的一些常识，了解这些知识有助于更好地理解中国航天科技的发展历程和现状。

2013年6月11日17时38分， 长征二号F运载火箭在酒泉 卫星发射中心成功发射神舟 十号载人飞船，中国航天员 聂海胜、张晓光、王亚平搭 乘飞船出征太空。
2016年9月15日22时04分09秒天宫二号空间实验室在酒泉 卫星发射中心发射成功
2016年10月17日7时30分神舟十一号飞船在中国酒泉 卫星发射中心成功发射，并于2016年10月19日凌晨， 神舟十一号飞船与天宫二号自动交会对接成功。
1987年8月，在酒泉卫星发射中心发射的第九颗返回式卫 星，为法国马特拉公司搭载了两个微重力试验装置。卫 星成功回收后，该公司的相关试验取得圆满成功，这是 中国航天界打入世界航天市场的第一次尝试。
1990年4月7日，中国自行研制的“长征”三号运载火箭 在西昌卫星发射中心，把美国制造的亚洲1号通信卫星送 入预定的轨道，首次为国外用户发射卫星取得圆满成功。
1973年9月10日，中国在酒 泉卫星发射场用风暴1号运 载火箭发射长空1号卫星失 败。这是中国第一次卫星发 射失败。
1975年11月26日，中国首 颗FSW-0返回式地球卫星发 射成功，3天后顺利返回， 使中国成为世界上第三个掌 握卫星返回技术的国家。
1982年10月12日，潜艇水下发射 运载火箭获得成功，回收舱准确 地溅落在预定海域。
2011年11月3日，航天飞船神舟 八号开始向天宫一号最后靠拢， 从捕获到锁紧，对接完成约需 10分钟，并且组合体控制权在 天宫一号，最终顺利完成首次 交会对接。
2011年11月14日，神舟八号和 天宫一号开始第二次交会对接， 并顺利完成任务。
2012年6月16日成功发射神 舟九号飞船，搭载三名航天 员，与天宫一号实施首次载 人交会对接。
1999年11月20日，中国第一 艘无人试验飞船“神舟一号” 试验飞船在酒泉发射成功， 21小时后在内蒙古中部回收 场成功着陆。

2021年山东省枣庄市高考数学二模试卷一、单项选择题（每小题5分）．1．已知集合A＝{x|y＝lnx}，B＝{y∈Z|y＝2sin x}，则A∩B＝（）A．（0，2]B．[0，2]C．{1，2}D．{0，1，2}2．命题“∀n∈N，n2﹣1∈Q”的否定为（）A．∀n∈N，n2﹣1∉Q B．∀n∉N，n2﹣1∈QC．∃n∈N，n2﹣1∉Q D．∃n∈N，n2﹣1∈Q3．已知函数f（x）＝，则f（2021）＝（）A．B．2e C．D．2e24．已知点（1，1）在抛物线C：y2＝2px（p＞0）上，则C的焦点到其准线的距离为（）A．B．C．1D．25．大数学家欧拉发现了一个公式，e ix＝cos x+i sin x，i是虚数单位，e为自然对数的底数．此公式被誉为“数学中的天桥”．根据此公式，（cos+i sin）2022＝（）（注：底数是正实数的实数指数幂的运算律适用于复数指数幂的运算）A．1B．﹣1C．i D．﹣i6．若x6＝a0+a1（x+1）+a2（x+1）2+a3（x+1）3+……+a6（x+1）6，则a3＝（）A．20B．﹣20C．15D．﹣157．医用口罩由口罩面体和拉紧带组成，其中口罩面体分为内、中、外三层，内层为亲肤材质（普通卫生纱布或无纺布），中层为隔离过滤层（超细聚丙烯纤维熔喷材料层），外层为特殊材料抑菌层（无纺布或超薄聚丙烯熔喷材料层）．根据国家质量监督检验标准，医用口罩的过滤率是重要的指标，根据长期生产经验，某企业在生产线状态正常情况下生产的医用口罩的过滤率x～N（0.9372，0.01392），若x～N（μ，σ2）（σ＞0），则P（μ﹣2σ＜x≤μ+2σ）＝0.954.5，P（μ﹣3σ＜x≤μ+3σ）＝0.9973，0.9772550≈0.3164．有如下命题：甲：P（x≤0.9）＜0.5；乙：P（x＜0.4）＞P（x＞1.5）；丙：P（x＞0.9789）＝0.00135；丁：假设生产状态正常，记X表示一天内抽取的50只口罩中过滤率大于μ+2σ的数量，则P（X≥1）≈0.6．其中假命题是（）A．甲B．乙C．丙D．丁8．已知椭圆C与双曲线x2﹣y2＝1有相同的左焦点F1、右焦点F2，点P是两曲线的一个交点，且．过F2作倾斜角为45°的直线交C于A，B两点（点A在x轴的上方），且，则λ的值为（）A．3+B．3+C．2+D．2+二、多项选择题（每小题5分）．9．已知a＞0，b＞0，a+b2＝1，则（）A．a+b＜B．a﹣b＞﹣1C．D．10．已知函数f（x）＝|sin x|+|sin（x﹣）|，则（）A．f（x）在[，π]上的最小值是1B．f（x）的最小正周期是C．直线x＝（k∈Z）是f（x）图象的对称轴D．直线y＝x与f（x）的图象恰有2个公共点11．列昂纳多•斐波那契（LeonardoFibonacci，1170﹣1250年）是意大利数学家，1202年斐波那契在其代表作《算盘书》中提出了著名的“兔子问题”，于是得斐波那契数列，斐波那契数列可以如下递推的方式定义：用F（n）（n∈N*）表示斐波那契数列的第n项，则数列{F（n）}满足：F（1）＝F（2）＝1，F（n+2）＝F（n+1）+F（n）．斐波那契数列在生活中有着广泛的应用，美国13岁男孩AidanDwyer观察到树枝分叉的分布模式类似斐波那契数列，因此猜想可按其排列太阳能电池，找到了能够大幅改良太阳能科技的方法．苹果公司的Logo设计，电影《达芬奇密码》等，均有斐波那契数列的影子，下列选项正确的是（）A．[F（8）]2＝F（7）F（9）+1B．F（1）+F（2）+……+F（6）+1＝F（8）C．F（2）+F（4）+……+F（2n）＝F（2n+1）﹣2D．[F（1）]2+[F（2）]2+……+[F（n）]2＝F（n）•F（n+1）12．如图，正方体ABCD﹣A1B1C1D1的棱长为1，点P是△B1CD1内部（不包括边界）的动点．若BD⊥AP，则线段AP长度的可能取值为（）A．B．C．D．三、填空题：本题北4小题，每小题5分，共20分.13．已知某地区中小学生的人数和近视率情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则抽取的高中生中近视的人数为．14．如图，由四个全等的三角形与中间的一个小正方形EFGH拼成的一个大正方形ABCD 中，．设，则x+y的值为．15．写出一个图象关于直线x＝2对称且在[0，2]上单调递增的偶函数f（x）＝．16．2020年11月23日国务院扶贫办确定的全国832个贫困县全部脱贫摘帽，脱贫攻坚取得重大突破．为了使扶贫工作继续推向深入，2021年某原贫困县对家庭状况较困难的农民实行购买农资优惠政策．（1）若购买农资不超过2000元，则不给予优惠；（2）若购买农资超过2000元但不超过5000元，则按原价给予9折优惠；（3）若购买农资超过5000元，不超过5000元的部分按原价给予9折优惠，超过5000元的部分按原价给予7折优惠．该县家境较困难的一户农民预购买一批农资，有如下两种方案：方案一：分两次付款购买，实际付款分别为3150元和4850元；方案二：一次性付款购买．若采取方案二购买这批农资，则比方案一节省元．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤. 17．已知数列{a n}中，a1＝a2＝1，且a n+2＝a n+1+2a n，记b n＝a n+1+a n，求证：（1）{b n}是等比数列；（2）{b n}的前n项和T n．满足+…+．18．若f（x）＝sin（ωx+φ）（ω＞0，0＜φ＜）的部分图象如图所示，f（0）＝，f（）＝0．（1）求f（x）的解析式；（2）在锐角△ABC中，若A＞B，f（）＝，求cos，并证明sin A＞．19．如图，正方体ABCD﹣A1B1C1D1的棱长为1，点F在棱CC1上，过B，D1，F三点的正方体的截面α与直线AA1交于点E．（1）找到点E的位置，作出截面α（保留作图痕迹），并说明理由；（2）已知CF＝a，求α将正方体分割所成的上半部分的体积V1与下半部分的体积V2之比．20．天问一号火星探测器于2021年2月10日成功被火星捕获，实现了中国在深空探测领域的技术跨越．为提升探测器健康运转的管理水平，西安卫星测控中心组织青年科技人员进行探测器遥控技能知识竞赛，已知某青年科技人员甲是否做对每个题目相互独立，做对A，B，C三道题目的概率以及做对时获得相应的奖金如表所示．题目A B C 做对的概率0.80.60.4获得的奖金/元100020003000规则如下：按照A，B，C的顺序做题，只有做对当前题目才有资格做下一题．（1）求甲获得的奖金X的分布列及均值；（2）如果改变做题的顺序，获得奖金的均值是否相同？如果不同，你认为哪个顺序获得奖金的均值最大？（不需要具体计算过程，只需给出判断）21．已知动点M与两个定点O（0，0），A（3，0）的距离的比为，动点M的轨迹为曲线C．（1）求C的轨迹方程，并说明其形状；（2）过直线x＝3上的动点P（3，p）（p≠0）分别作C的两条切线PQ、PR（Q、R为切点），N为弦QR的中点，直线l：3x+4y＝6分别与x轴、y轴交于点E、F，求△NEF 的面积S的取值范围．22．已知函数f（x）＝a cos x+1﹣，且f'（）＝0．（1）求实数a的值，并判断f（x）在（0，）上的单调性；（2）对确定的k∈N*，求f（x）在[2kπ+，2kπ+π]上的零点个数．参考答案一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A＝{x|y＝lnx}，B＝{y∈Z|y＝2sin x}，则A∩B＝（）A．（0，2]B．[0，2]C．{1，2}D．{0，1，2}解：∵A＝{x|x＞0}，B＝{y∈Z|﹣2≤y≤2}＝{﹣2，﹣1，0，1，2}，∴A∩B＝{1，2}．故选：C．2．命题“∀n∈N，n2﹣1∈Q”的否定为（）A．∀n∈N，n2﹣1∉Q B．∀n∉N，n2﹣1∈QC．∃n∈N，n2﹣1∉Q D．∃n∈N，n2﹣1∈Q解：命题为全称命题，则命题的否定为∃n∈N，n2﹣1∉Q，故选：C．3．已知函数f（x）＝，则f（2021）＝（）A．B．2e C．D．2e2解：∵函数f（x）＝，∴f（2021）＝f（673×3+2）＝f（2）＝f（﹣1）＝e﹣1+ln2＝e﹣1×2＝．故选：A．4．已知点（1，1）在抛物线C：y2＝2px（p＞0）上，则C的焦点到其准线的距离为（）A．B．C．1D．2解：点（1，1）在抛物线C：y2＝2px（p＞0）上，可得1＝2p，所以p＝，所以抛物线的焦点到其准线的距离为p：．故选：B．5．大数学家欧拉发现了一个公式，e ix＝cos x+i sin x，i是虚数单位，e为自然对数的底数．此公式被誉为“数学中的天桥”．根据此公式，（cos+i sin）2022＝（）（注：底数是正实数的实数指数幂的运算律适用于复数指数幂的运算）A．1B．﹣1C．i D．﹣i解：（cos+i sin）2022＝cos+i sin＝cos（505π+）+i sin（505π+）＝﹣cos﹣i sin＝﹣i，故选：D．6．若x6＝a0+a1（x+1）+a2（x+1）2+a3（x+1）3+……+a6（x+1）6，则a3＝（）A．20B．﹣20C．15D．﹣15解：x6＝[﹣1+（1+x）]6＝a0+a1（x+1）+a2（x+1）2+a3（x+1）3+……+a6（x+1）6，则a3＝•（﹣1）3＝﹣20，故选：B．7．医用口罩由口罩面体和拉紧带组成，其中口罩面体分为内、中、外三层，内层为亲肤材质（普通卫生纱布或无纺布），中层为隔离过滤层（超细聚丙烯纤维熔喷材料层），外层为特殊材料抑菌层（无纺布或超薄聚丙烯熔喷材料层）．根据国家质量监督检验标准，医用口罩的过滤率是重要的指标，根据长期生产经验，某企业在生产线状态正常情况下生产的医用口罩的过滤率x～N（0.9372，0.01392），若x～N（μ，σ2）（σ＞0），则P（μ﹣2σ＜x≤μ+2σ）＝0.954.5，P（μ﹣3σ＜x≤μ+3σ）＝0.9973，0.9772550≈0.3164．有如下命题：甲：P（x≤0.9）＜0.5；乙：P（x＜0.4）＞P（x＞1.5）；丙：P（x＞0.9789）＝0.00135；丁：假设生产状态正常，记X表示一天内抽取的50只口罩中过滤率大于μ+2σ的数量，则P（X≥1）≈0.6．其中假命题是（）A．甲B．乙C．丙D．丁解：根据题意知u＝0.9372，σ＝0.0139．∴由正态分布曲线得：P（x≤0.9）＜P（x≤0.9372）＝0.5，∴甲正确；由正态分布曲线知：P（x＜0.4）＝P（x＞2×0.9372﹣0.4）＝P（x＞1.4744）＞P （x＞1.5），∴乙正确；∵P（μ﹣3σ＜x≤μ+3σ）＝P（0.8955＜x≤0.9787）＝0.9973，∴由正态分布曲线知：P （x＞0.9787）＝＝0.00135，∴丙正确；∵P（x≥μ+2σ）＝（1﹣0.9545）＝0.2275，∴P（x＜μ+2σ）＝1﹣0.2275＝0.9775，∴P（x≥1）＝1﹣P（x＝0）＝1﹣0.9772550≈1﹣0.3164＝0.6836，∴丁错误；故选：D．8．已知椭圆C与双曲线x2﹣y2＝1有相同的左焦点F1、右焦点F2，点P是两曲线的一个交点，且．过F2作倾斜角为45°的直线交C于A，B两点（点A在x轴的上方），且，则λ的值为（）A．3+B．3+C．2+D．2+解：设椭圆的方程为+＝1（a＞b＞0），双曲线的方程为x2﹣y2＝1的焦点为F1（﹣，0），F2（，0），可得a2﹣b2＝2，由，可得PF1⊥PF2，设|PF1|＝m，|PF2|＝n，则m+n＝2a，|m﹣n|＝2，且m2+n2＝|F1F2|2＝（2）2＝8，所以mn＝2，则4a2＝m2+n2+2mn＝8+4＝12，即a＝，b＝1，则椭圆的方程为+y2＝1，过F2作倾斜角为45°的直线的方程为y＝x﹣，联立，可得x2﹣2x+1＝0，解得x1＝，x2＝，交点为A（，），B（，），|AB|＝，|AF2|＝，所以λ＝＝3+．故选：A．二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得3分，有选错的得0分.9．已知a＞0，b＞0，a+b2＝1，则（）A．a+b＜B．a﹣b＞﹣1C．D．解：因为a＞0，b＞0，a+b2＝1，所以a＝1﹣b2＞0，解得0＜b＜1，对于A，a+b＝﹣b2+b+1，当b＝时，a+b取得最大值为，故a+b≤，故A错误，对于B，由0＜b＜1，可得﹣1＜﹣b＜0，由0＜a＜1，可得﹣1＜a﹣b＜1，故B正确，对于C，•b≤＝，当且仅当＝b＝时等号成立，故C正确，对于D，可设a＝cos2α，b＝sinα，α∈（0，），则＝，若≥﹣，则sinαcosα≤1，∴sin（α+）≤1恒成立，∴D正确．故选：BCD．10．已知函数f（x）＝|sin x|+|sin（x﹣）|，则（）A．f（x）在[，π]上的最小值是1B．f（x）的最小正周期是C．直线x＝（k∈Z）是f（x）图象的对称轴D．直线y＝x与f（x）的图象恰有2个公共点解：f（x）＝|sin x|+|﹣cos x|＝|sin x|+|cos x|．A：在[，π]，f（x）的最小值在x＝时取得，f（）＝1，故A正确．B：f（x+）＝|sin（x+）|+|cos（x+）＝|cos x|+|sin x|，f（x+）≠f（x）．故B错．C：x＝（k∈Z）是f（x）图像的对称轴，故C正确．D：当x＝时，y＝×＝1，当x＝π时，y＝×π＝2，故y＝x图像如图，共有2个交点．故选：ACD．11．列昂纳多•斐波那契（LeonardoFibonacci，1170﹣1250年）是意大利数学家，1202年斐波那契在其代表作《算盘书》中提出了著名的“兔子问题”，于是得斐波那契数列，斐波那契数列可以如下递推的方式定义：用F（n）（n∈N*）表示斐波那契数列的第n项，则数列{F（n）}满足：F（1）＝F（2）＝1，F（n+2）＝F（n+1）+F（n）．斐波那契数列在生活中有着广泛的应用，美国13岁男孩AidanDwyer观察到树枝分叉的分布模式类似斐波那契数列，因此猜想可按其排列太阳能电池，找到了能够大幅改良太阳能科技的方法．苹果公司的Logo设计，电影《达芬奇密码》等，均有斐波那契数列的影子，下列选项正确的是（）A．[F（8）]2＝F（7）F（9）+1B．F（1）+F（2）+……+F（6）+1＝F（8）C．F（2）+F（4）+……+F（2n）＝F（2n+1）﹣2D．[F（1）]2+[F（2）]2+……+[F（n）]2＝F（n）•F（n+1）解：由由题意知：F（1）＝1，F（2）＝1，F（3）＝2，F（4）＝3，F（5）＝5，F（6）＝8，F（7）＝13，F（8）＝21，F（9）＝34；[F（8）]2≠F（7）F（9）+1，A错；F（1）+F（2）+……+F（6）+1＝21＝F（8），B对；令n＝1，F（2）+F（4）＝4≠F（3）﹣2＝0，C错；因为本题为多选题，故选：BD．12．如图，正方体ABCD﹣A1B1C1D1的棱长为1，点P是△B1CD1内部（不包括边界）的动点．若BD⊥AP，则线段AP长度的可能取值为（）A．B．C．D．解：如图，连接AC，A1C1，在正方体ABCD﹣A1B1C1D1中，有AC⊥BD，由正方体的结构特征，可得AA1⊥平面ABCD，而BD⊂平面ABCD，则AA1⊥BD，∵AA1∩AC＝A，∴BD⊥平面AA1C1C，又点P是△B1CD1内部（不包括边界）的动点，平面AA1C1C∩平面B1CD1＝O1C，且BD ⊥AP，∴P的轨迹为线段O1C（不包括端点）．由正方体的棱长为1，可得，则，AC＝，由等面积法可得A到O1C的距离为．∴AP∈[，）．结合选项可得，线段AP长度的可能取值为ABC．故选：ABC．三、填空题：本题北4小题，每小题5分，共20分.13．已知某地区中小学生的人数和近视率情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则抽取的高中生中近视的人数为20．解：用分层抽样的方法抽取2%的学生进行调查，抽取的高中生人数为10000×2%×＝40人，则抽取的高中生中近视的人数为40×50%＝20人．故答案为：20．14．如图，由四个全等的三角形与中间的一个小正方形EFGH拼成的一个大正方形ABCD 中，．设，则x+y的值为．解：设AE＝1，则AF＝3，EF＝2，所以AB＝，在直角三角形ABF中，sin∠BAF＝，cos，如图所示，建立直角坐标系，设F（x，y），则y＝AF，x＝AF，即点F的坐标为（），又AD＝AB＝，所以点D（0，），B（，0），所以，，因为，即（）＝x（）+y（0，），所以，解得x＝，所以x+y＝，故答案为：．15．写出一个图象关于直线x＝2对称且在[0，2]上单调递增的偶函数f（x）＝﹣cos，（答案不唯一）．．解：结合余弦函数的性质可知，符合条件的函数f（x）＝﹣cos．故答案为：﹣cos．（答案不唯一）．16．2020年11月23日国务院扶贫办确定的全国832个贫困县全部脱贫摘帽，脱贫攻坚取得重大突破．为了使扶贫工作继续推向深入，2021年某原贫困县对家庭状况较困难的农民实行购买农资优惠政策．（1）若购买农资不超过2000元，则不给予优惠；（2）若购买农资超过2000元但不超过5000元，则按原价给予9折优惠；（3）若购买农资超过5000元，不超过5000元的部分按原价给予9折优惠，超过5000元的部分按原价给予7折优惠．该县家境较困难的一户农民预购买一批农资，有如下两种方案：方案一：分两次付款购买，实际付款分别为3150元和4850元；方案二：一次性付款购买．若采取方案二购买这批农资，则比方案一节省700元．解：由方案一可得出总价，第一次花3150元，可以判断出2000～5000区间，原价＝3150÷90%＝3500（元），第二次花4850元，可以判断出原价大于5000元，5000元以内的部分：5000×90%＝4500元，多出4850﹣4500＝350元，是打七折的部分，350÷0.7＝500元，总原价为：3500+5000+500＝9000元，由方案二：5000×90%+（9000﹣5000）×0.7＝7300元，∴所以比方案一节省：3150+4850﹣7300＝700元．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤. 17．已知数列{a n}中，a1＝a2＝1，且a n+2＝a n+1+2a n，记b n＝a n+1+a n，求证：（1）{b n}是等比数列；（2）{b n}的前n项和T n．满足+…+．【解答】证明：（1）a n+2＝a n+1+2a n，可得a n+2+a n+1＝2（a n+1+a n），记b n＝a n+1+a n，可得b n+1＝2b n，又b1＝a1+a2＝2，可得{b n}是首项和公比均为2的等比数列；（2）b n＝2n，T n＝＝2n+1﹣2，＝＝＝（﹣），所以++…+＝（1﹣+﹣+…+﹣）＝（1﹣）＜．18．若f（x）＝sin（ωx+φ）（ω＞0，0＜φ＜）的部分图象如图所示，f（0）＝，f（）＝0．（1）求f（x）的解析式；（2）在锐角△ABC中，若A＞B，f（）＝，求cos，并证明sin A＞．解：（1）由f（0）＝，可得sinφ＝，又因为0＜φ＜，所以φ＝，因为f（）＝0，由五点作图法可得ω+＝π，所以ω＝2，所以f（x）＝sin（2x+）．（2）由f（）＝，得sin（A﹣B）＝，又0＜A﹣B＜，故cos（A﹣B）＝，所以cos＝＝，所以sin＝，又A+B＞，所以A＝+＞+，又y＝sin x在（0，）上单调递增，A∈（0，），+∈（0，），所以sin A＞sin（+）＝×（+）＝．19．如图，正方体ABCD﹣A1B1C1D1的棱长为1，点F在棱CC1上，过B，D1，F三点的正方体的截面α与直线AA1交于点E．（1）找到点E的位置，作出截面α（保留作图痕迹），并说明理由；（2）已知CF＝a，求α将正方体分割所成的上半部分的体积V1与下半部分的体积V2之比．解：（1）∵D1∉BF，∴BF与D1可确定平面α，在平面α内过D1作D1E∥BF，且交AA1于E，连接EB，ED1，则四边形D1EBF就是要作的截面α．理由：由题意，平面α∩平面AD1＝D1E，平面α∩平面BC1＝BF，而平面AD1∥平面BC1，∴D1E∥BF，根据作图过程，D1E∥BF，则四边形D1EBF就是要作的截面．（2）由题意，CF＝a（0＜a＜1），由（1）的过程可知A1E＝a，连接D1B1，则平面α将正方体分割成的商半部分为四棱锥D1﹣A1EBB1与四棱锥D1﹣B1BFC1的组合体．＝＝．而正方体的体积为1，则，故α将正方体分割所成的上半部分的体积V1与下半部分的体积V2之比为1．20．天问一号火星探测器于2021年2月10日成功被火星捕获，实现了中国在深空探测领域的技术跨越．为提升探测器健康运转的管理水平，西安卫星测控中心组织青年科技人员进行探测器遥控技能知识竞赛，已知某青年科技人员甲是否做对每个题目相互独立，做对A，B，C三道题目的概率以及做对时获得相应的奖金如表所示．题目A B C 做对的概率0.80.60.4获得的奖金/元100020003000规则如下：按照A，B，C的顺序做题，只有做对当前题目才有资格做下一题．（1）求甲获得的奖金X的分布列及均值；（2）如果改变做题的顺序，获得奖金的均值是否相同？如果不同，你认为哪个顺序获得奖金的均值最大？（不需要具体计算过程，只需给出判断）解：（1）分别用A，B，C表示做对题目A，B，C的事件，则A，B，C相互独立，由题意可知，X的可能取值为0，1000，3000，6000，所以P（X＝0）＝，P（X＝1000）＝＝0.8×0.4＝0.32，P（X＝3000）＝＝0.8×0.6×0.6＝0.288，P（X＝6000）＝P（ABC）＝0.8×0.6×0.4＝0.192，所以甲获得的奖金X的分布列为：X0100030006000P0.20.320.2880.192故E（X）＝0×0.2+1000×0.32+3000×0.288+6000×0.192＝2336；（2）改变做题的顺序，获得奖金的均值不相同．决策的原则是选择期望值E（X）大的做题顺序，这称为期望值原则，做对的概率大表示题目比较容易，做对的概率小表示题目比较难．猜想：按照由易到难的顺序做题，即按照题目A，B，C的顺序做题，得到奖金的期望值最大．21．已知动点M与两个定点O（0，0），A（3，0）的距离的比为，动点M的轨迹为曲线C．（1）求C的轨迹方程，并说明其形状；（2）过直线x＝3上的动点P（3，p）（p≠0）分别作C的两条切线PQ、PR（Q、R为切点），N为弦QR的中点，直线l：3x+4y＝6分别与x轴、y轴交于点E、F，求△NEF 的面积S的取值范围．解：（1）设M（x，y），由，得，化简的x2+y2+2x﹣3＝0，即（x+1）2+y2＝4，故C是以（﹣1，0）为圆心，半径为2的圆；（2）以线段DP为直径的圆的方程为（x+1）（x﹣3）+（y﹣0）（y﹣p）＝0，整理可得x2+y2﹣2x﹣py﹣3＝0…①又Q，R在以DP为直径的圆上，且Q，R在C：x2+y2+2x﹣3＝0…②②﹣①得：4x+py＝0，所以，切点弦QR所在直线的方程为4x+py＝0，可见QR恒过原点O（0，0），联立方程，消去x整理可得：（16+p2）y2﹣8py﹣48＝0，设Q（x1，y1），R（x2，y2），则y，点N的纵坐标y，因为p≠0，显然y N≠0，所以点N与点D（﹣1，0），O（0，0）均不重合，因为N为弦QR的中点，且D（﹣1，0）为C的圆心，由圆的性质可得DN⊥QR，即DN⊥ON，所以点N在以OD为直径的圆上，圆心为G（﹣，0），半径为r＝，因为直线3x+4y＝6分别与x轴，y轴交于点E，F，所以E（2，0），F（0，），因此|EF|＝，圆心G（﹣，0）到直线3x+4y＝6的距离d＝，设△NEF的边EF上的高为h，则点N到直线3x+4y＝6的距离h的最小值为d﹣r＝，点N到直线3x+4y＝6的距离h的最大值为d+r＝＝2，所以S的最小值为S min＝＝，S，所以三角形NEF的面积S的取值范围为[]．22．已知函数f（x）＝a cos x+1﹣，且f'（）＝0．（1）求实数a的值，并判断f（x）在（0，）上的单调性；（2）对确定的k∈N*，求f（x）在[2kπ+，2kπ+π]上的零点个数．解：（1）f（x）的定义域为R，f′（x）＝﹣a sin x+，所以f'（）＝﹣a sin+＝1﹣a＝0，所以a＝1，则f′（x）＝﹣sin x+，因为函数y＝﹣sin x在（0，）上单调递减，y＝在（0，）上单调递减，所以f′（x）＝﹣sin x+在（0，）上单调递减，又f'（）＝0，所以当x∈（0，）时，f′（x）＞f'（）＝0，所以f（x）在（0，）上单调递增．（2）f′（x）＝﹣sin x+，f″（x）＝﹣cos x﹣，因为y＝﹣cos x在[2kπ+，2kπ+π]上单调递增，y＝﹣在[2kπ+，2kπ+π]上单调递增，所以f″（x）＝﹣cos x﹣在[2kπ+，2kπ+π]上单调递增，又f″（2kπ+）＝﹣cos（2kπ+）﹣＝﹣e﹣2kπ＜0，f″（2kπ+π）＝﹣cos（2kπ+π）﹣＝1﹣＞0，由零点存在定理及f″（x）的单调性，知存在唯一的x0∈（2kπ+，2kπ+π），使得f″（x0）＝0，从而当x∈（2kπ+，x0）时，f″（x）＜f″（x0）＝0，f′（x）单调递减，当x∈（x0，2kπ+π）时，f″（x）＞f″（x0）＝0，f′（x）单调递增，f′（2kπ+）＝﹣sin（2kπ+）+＝e﹣2kπ﹣1＜e0﹣1＝0，f′（x）在[2kπ+，2kπ+π]上的最小值f′（x）min＝f′（x0）＜f′（2kπ+）＜0，f′（2kπ+π）＝﹣sin（2kπ+π）+＝＞0，由零点存在定理及f′（x）的单调性，知存在唯一的x1∈（x0，2kπ+π），使得f′（x1）＝0，从而当x∈（2kπ+，x1）时，f′（x）＜f′（x1）＝0，f（x）单调递减，当x∈（x1，2kπ+π）时，f′（x）＞f′（x1）＝0，f（x）单调递增，f（2kπ+）＝cos（2kπ+）+1﹣＝1﹣e﹣2kπ＞1﹣e0＝0，f（2kπ+π）＝cos（2kπ+π）+1﹣＝﹣＜0，f（x）在[2kπ+，2kπ+π]上的最小值f（x）min＝f（x1）＜f（2kπ+π）＜0，由零点存在定理及f（x）的单调性，知f（x）在[2kπ+，2kπ+π]（k∈N*）上有且仅有一个零点．。

东方红三号卫星（DFH-3）中国新一代通信卫星，主要用于电视传输、广播、通信及数据传输等业务。

卫星上有24路C频段转发器，服务范围有中国大陆、海南、台湾及近海岛屿。

星上有24路C频段转发器，其中6路为中功率转发器；其它18路为低功率转发器。

服务区域包括：中国大陆、海南、台湾及近海岛屿。

中功率通道的EIRP≥37dbW，低功率通道的EIRP≥33.5dbW。

在地影期间，全部转发器工作。

卫星寿命末期输出功率≥1700W：卫星允许的有效载荷质量达170kg。

卫星工作于地球静止轨道，位置保持精度，东西和南北均为±0.1°；天线指向误差为：俯仰和滚动均为±0.15°，偏航为±O.5°。

卫星工作寿命8年，寿命末期单星可靠度为0.66。

卫星可与多种运载火箭相接口（ZC-3A、ARIANE－4等），卫星平台采用地球静止轨道卫星的公用平台（基本型），可作为中型的多种应用目的。

东方红三号卫星具有国际同类卫星（中型容量）的先进水平，其主要技术特点为：先进的卫星公用平台设计概念和模块化、舱段化总体构型设计技术，卫星分为推进舱、服务舱、通信舱，使平台能适应不同有效载荷的需要；中心承力筒加壁板的结构形式，以及碳纤维复合材料轻型结构；大质量液体晃动和柔性部件影响的全三轴姿态轨道控制方案；先进的双组元统一推进系统；一次展开式太阳电池阵与镉镍蓄电池联合供电及双独立调节母线方案；有效载荷的频率复用、波束成形技术；高热耗散和热流密度的热控设计；国际C频段统一载波测控体制；总控加专检设备的先进自动化测试系统；整星级EMC试验和不带工质的环境试验技术。

东方红三号卫星于1997年5月12日由中国运载火箭技术研究院研制的长征三号甲运载火箭发射升空，并准确进入倾角28.4°，周期10小时39分，近地点为207km，远地点为36194km的大椭圆转移轨道。

按预定飞行程序，在地面测控系统的测控管理下，卫星先后完成进入OBC太阳搜索模式；南北太阳电池阵展开；通信天线的展开；远地点变轨发动机经过第三次点火变轨，卫星进入准静止轨道，并完成定点捕获；5月20日16时卫星成功的定点于东经125°赤道上空。

条 少，安全性高。
件 5.交通条件:要有便利的交通，利于大型设备的运输。
6.国防安全:建在人烟稀少的地区。
7.其他因素:如科技因素、历史因素等。
航
天 器 返
1.地形平坦开阔，地质条件稳定； 2.人烟稀少 ；无大片森林， 无大河、湖泊；
回 3.降水较少，大气能见度高等。
基
地
的
选 例如：我国的航天发射器返回基地在内蒙古自治区中部地区。那里地势平坦，视野
酒泉卫星发射中心属内陆及沙漠性气候，地势平坦，人烟稀少， 全年少雨，白天时间长，年平均气温8.5℃，相对湿度为35%-55%， 每年约有300天可进行发射试验，加上基地已建成多年，生活设施基 本齐全，技术保障、测控通信、铁路运输、发配电等配套设施完善， 条件很适合卫星及载人航天飞行器（我国唯一）发射。
航天卫星发射基地的选择条件
四 大目
录
发 射 基 地
酒泉卫星发射基地 山西太原卫星发射基地 四川西昌卫星发射中心 海南文昌卫星发射中心
甘肃，内蒙古
酒泉卫星发射中心
中国四大卫星发射中心山西太原 Nhomakorabea星发射中心
四川
西昌卫星发射中心
海南
文昌卫星发射中心
航天器的发射时间
航天器的发射方向
一般选择在晴朗无云的夜晚，主要原 因是便于定位和跟踪观测。
我国航天器的发射时间：主要选择在 冬季，便于航天测控网对航天器的监控、 管理和回收。我国有多艘“远望号”监测 船分布在南半球纬度较高的海域，选择北 半球冬季发射是为了避开南半球冬季恶劣 的海况。
一般与地球的运动方向一致，向东发 射可充分利用地球自转线速度，节约能源。
酒泉卫星发射基地
位置：酒泉卫星发射中心分布于酒泉市及阿拉善盟两市盟方圆2800平方公里范围。 （40°57'45.19"N,100°17'39.01"E）