三角形的认识培优习题一(自己整理)

周测培优卷1三角形的认识及三边关系、内角和的应用一、我会填。

(每空2分，共16分)1．任意一个三角形都有( )条边，( )个角。

2．三角形任意两边长度的和( )第三边。

3．一个三角形最少有( )个锐角，最多有( )个直角。

4．一个三角形中最大的角是88°，这个三角形是( )三角形。

5．三条边都相等的三角形是( )，它的每个角都是( )度。

二、我会判断。

(对的打“√”，错的打“×”)(每题2分，共8分)1.( )2.( )3.( )4.( )三、我会选。

(把正确答案的字母填在括号里)(每题3分，共12分) 1．下面( )中的3条线段不能围成三角形。

A．6厘米、6厘米、6厘米B．8厘米、5厘米、4厘米C．3厘米、1厘米、2厘米2．等腰三角形的底角是( )。

A．锐角B．直角C．钝角3．一个等腰三角形，底是5厘米，腰是6厘米，它的周长是( )。

A．16厘米B．17厘米C．15厘米4．不能组成一个三角形的三个内角的是( )。

A．80度20度80度B．90度10度80度C．90度43度57度四、对号入座。

(10分)锐角三角形：( )直角三角形：( )钝角三角形：( )等腰三角形：( )等边三角形：( )五、我会画。

(共11分)1．请分别画出下面三角形底边上的高。

(8分)2．画一个三角形，使它既是直角三角形，又是等腰三角形。

(3分)六、算一算。

( 9分)求出下面三角形中∠1、∠2、∠3的度数。

七、解决问题。

(16＋18＝34分)1．如下图，小兔和小猴分别围成了一个篱笆，形状如下图。

谁围的比较牢固？为什么？2．用木条做一个三角形木框，选了一根长14厘米和一根长6厘米的木条，那么第三根木条的长可以是多少厘米？(取整厘米数)答案一、1. 3 3 2.大于 3.2 1 4.锐角5．等边三角形60二、1.√ 2.× 3.× 4.×三、1.C 2.A 3.B 4.C四、①④⑥⑧②⑦③⑤①④⑥⑧④⑧五、1.2.[点拨]画法不唯一。

八年级数学第十一章三角形1．已知，如图，在△ ABC 中，AD ，AE 分别是 △ ABC 的高和角平分线， 若∠B=30°，∠C=50°.求∠DAE 的度数。

2.如图，已知D 为△ABC 边BC 延长线上一点,DF ⊥AB 于F 交 AC 于E ，∠A=35°,∠D=42°，求∠ACD 的度数。

3.如图，在△ABC 中，AD 平分∠BAC ，∠B=∠C ，∠BAD=40°,且∠ADE=∠AED, 求∠CDE 的度数。

4。

在△ABC 中，∠A=40°，D 是BC 延长线上一点，∠ABC 的平分线与∠ACD 的平分线交于E ，求∠E 的度数．5在△ABC 中，D 为BC 上一点,∠BAD=∠ABC,∠ADC=∠ACD ，若∠BAC=63°，试求∠DAC 、∠ADC 的度数AE CDB 第1题图FDCBEA 第2题图D EA第3题图 ABC DE第4题ABCD 5参考答案1.∠DAE=10°2。

解：因为∠AFE=90°,所以∠AEF=90°—∠A=90°—35°=55°。

所以∠CED=•∠AEF=55°, 所以∠ACD=180°—∠CED-∠D=180°-55°-42=83°.3.解：设∠DAE=x,则∠BAC=40°+x. 因为∠B=∠C,所以2∠2=180°—∠BAC ，∠C=90°—12∠BAC=90°—12（40°+x ）. 同理∠AED=90°-12∠DAE=90°—12x. ∠CDE=∠AED-∠C=（90°-12x ）-［90°—12（40°+x)］=20°.4. 解：∠E=180°－（ACD ACB ABC 2121+∠+∠）=180°－（)(2121ABC A ACB ABC ∠+∠+∠+∠）=180°－（A ACB ABC ∠+∠+∠21) =A ∠21=4021⨯° =20°5。

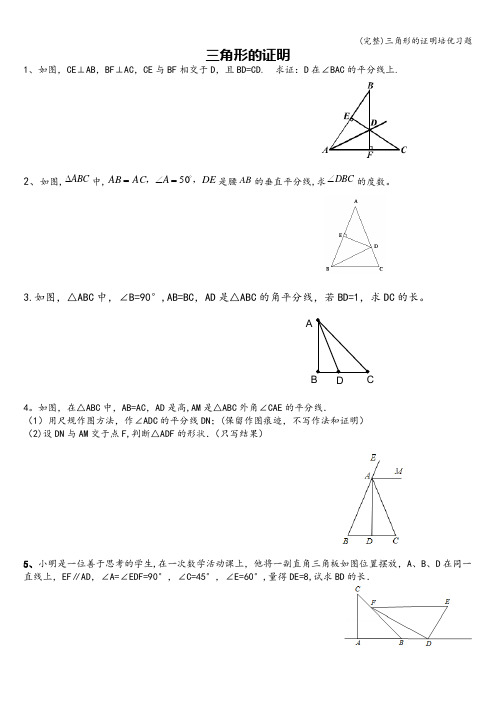
(完整)三角形的证明培优习题 DABC

三角形的证明 1、如图，CE⊥AB，BF⊥AC，CE与BF相交于D，且BD=CD. 求证：D在∠BAC的平分线上.

2、如图,ABC中,DEAACAB，，50是腰AB的垂直平分线,求DBC的度数。

3.如图，△ABC中，∠B=90°,AB=BC，AD是△ABC的角平分线，若BD=1，求DC的长。 4。如图，在△ABC中，AB=AC，AD是高,AM是△ABC外角∠CAE的平分线． （1）用尺规作图方法，作∠ADC的平分线DN；(保留作图痕迹，不写作法和证明） （2)设DN与AM交于点F,判断△ADF的形状．（只写结果）

5、小明是一位善于思考的学生,在一次数学活动课上，他将一副直角三角板如图位置摆放，A、B、D在同一直线上，EF∥AD，∠A=∠EDF=90°，∠C=45°，∠E=60°,量得DE=8,试求BD的长． (完整)三角形的证明培优习题 6、如图，在△ABC中,∠ACB＝90°，BC＝15，AC＝20，CD是高．(1）求AB的长；(2)求△ABC的面积；（3)求CD的长．

7、已知：如图，△ABC和△CDE都是等边三角形，点D在BC边上．求证:AD＝BE． 8、求证：等腰三角形两腰上的中线的交点到底边两个端点的距离相等． 9、已知:如图，等腰三角形ABC中，AC＝BC，∠ACB＝90°，直线l经过点C(点A、B都在直线l的同侧)，AD⊥l,BE⊥l，垂足分别为D、E．你知道线段AD、DE、BE的关系吗?证明你的结论。

10、已知：如图,在Rt△ABC中，∠C＝90°，沿过B点的一条直线BE折叠这个三角形， 使C点与AB边上的一点D重合． （1）当∠A满足什么条件时，点D恰为AB的中点？写出一个你认为适当的条件，并利用此条件证明D为AB的中点； （2）在（1）的条件下，若DE＝1，求△ABC的面积．

11、如图,在△ABD和△ACD中，已知AB＝AC，∠B＝∠C，求证：AD是∠BAC的平分线．

认识三角形（一） 一．边的大小关系，范围讨论例1 下列每组数分别是三根小木棒的长度，用它们能摆成三角形吗？为什么？（单位：cm ）（1） 1， 3， 3 （ ）（2） 3， 4， 7 （ ）（3） 5， 9， 13 （4） 14， 15， 30 （ ）例2已知一个三角形的两边长分别是3cm 和4cm ，则第三边长X 的取值范围是 ；若X是奇数，则X 的值是 ，这样的三角形有 个；若X 是偶数，则X 的值是 ；这样的三角形又有 个。

例3一个等腰三角形的一边是5cm ，另一边是7cm ,则这个三角形的周长是多少例4如图，在△ABC 中，AD 是BC 边上的中线，△ADC 的周长比△ABD 的周长多5cm ，AB 与AC 的和为11cm ，求AC 的长．过手变式练习：1 有一个三角形的两边分别为5和12，且周长为奇数，则满足条件的三角形的个数为__________2 已知一个三角形有两边相等，周长为56cm ，两边之比为3：2，则这个三角形各边的长为_______4 若a ，b ，c 是△ABC 的三边，试化简=+-+-++--c b a c b a c b a __________________5 已知在△ABC 中，010616222=++--bc ab c b a ，若a ，b ，c 是三角形的三边，求证b c a 2=+ 二．角的关系例1 AD 是△ABC 的一条高，也是△ABC 的角平分线，若∠B =40°,求∠BAC 的度数.例2如图，△ABC 中，∠ B ＝34°，∠ACB＝104°，AD 是BC 边上的高，AE 是∠ BAC 的平分线，求∠ DAE的度数．B CD E例3（1）如图所示，∠A +∠B +∠C +∠D +∠E = （ ）A.180°B.260°C.270°D.360°例4.一副三角板按图中的方式叠放，则∠α等于 （ ）A ．75°B ．60°C ．45°D ．30°过手变式练习：1、如图，已知 ∠E ＋∠F ＝∠H ，求：∠A ＋∠B ＋∠ACD ＋∠CDG 的度数．2、如图，∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ，并且与CD 、AB 分别相交于M 、N ．解答下列问题：(1)若∠D ＝40，∠B ＝36，求∠P 的度数；(2)如果图中的∠D 和∠B 为任意角时，其它条件不变，试问∠P 与∠D 、∠B 之间存在着怎样的数量关系？（直接写出结论即可）3、如图，BD 是△ABC 中∠ABC 的角平分线，CD 是△ABC 的外角∠ACE 的平分线，它与BD 的延长线交于点D ，我们将会得到∠A ＝2∠D 这一结论，试想一想为什么？并加以说明．5（1）在△ＡＢＣ中，∠A-∠B=20°，∠B-∠C=20°，求∠A 和∠C 的度数。

《三角形的初步认识》一、选择题1．下列各组线段中，能组成三角形的是（）A．4，6，10 B．3，6，7 C．5，6，12 D．2，3，62．在△ABC中，∠A﹣∠C=∠B，那么△ABC是（）A．等边三角形B．锐角三角形C．钝角三角形D．直角三角形3．如图所示，是用直尺和圆规作一个角等于已知角的示意图，则说明∠A′O′B′=∠AOB的依据是（）A．SAS B．SSS C．AAS D．ASA4．如图AB⊥AD，AB⊥BC，则以AB为一条高线的三角形共有（）个．A．1 B．2 C．3 D．45．如图所示，△BDC′是将长方形纸片ABCD沿BD折叠得到的，图中（包括实线、虚线在内）共有全等三角形（）对．A．2 B．3 C．4 D．56．下列是命题的是（）A．作两条相交直线B．∠α和∠β相等吗？C．全等三角形对应边相等 D．若a2=4，求a的值7．下列命题中，真命题是（）A．垂直于同一直线的两条直线平行B．有两边和其中一边上的高对应相等的两个三角形全等C．三角形三个内角中，至少有2个锐角D．有两条边和一个角对应相等的两个三角形全等8．如图，对任意的五角星，结论正确的是（）A．∠A+∠B+∠C+∠D+∠E=90° B．∠A+∠B+∠C+∠D+∠E=180°C．∠A+∠B+∠C+∠D+∠E=270°D．∠A+∠B+∠C+∠D+∠E=360°9．如图，在△ABC中，∠C=90°，AC=BC，AD是△ABC的角平分线，DE⊥AB于E．若AB=6cm，则△DEB的周长为（）A．5cm B．6cm C．7cm D．8cm10．如图，BF是∠ABD的平分线，CE是∠ACD的平分线，BF与CE交于G，若∠BDC=130°，∠BGC=100°，则∠A的度数为（）A．60° B．70° C．80° D．90°二、填空题11．工人师傅在做完门框后，为防止变形常常像图中所示的那样上两条斜拉的木条（即图中的AB，CD两根木条），这样做的依据是______．12．把命题“对顶角相等”改写成“如果…那么…”的形式：______．13．如图，在△ABC中，AD⊥BC于D，AE为∠BAC的平分线，且∠DAE=15°，∠B=35°，则∠C=______°．14．如图，AB=AC，要使△ABE≌△ACD，应添加的条件是______（添加一个条件即可）．15．命题“若x（1﹣x）=0，则x=0”是______命题（填“真”、假），证明时可举出的反例是______．16．已知三角形的三边长分别是3、x、9，则化简|x﹣5|+|x﹣13|=______．17．如图，在△ABC中，AB=AC，AB的中垂线DE交AC于点D，交AB于点E，如果BC=10，△DBC的周长为22，那么AB=______．18．如图所示，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论是______．（将你认为正确的结论的序号都填上）19．已知，∠α=50°，且∠α的两边与∠β的两边互相垂直，则∠β=______．20．若三角形的周长为13，且三边均为整数，则满足条件的三角形有______种．三、解答题21．如图，已知△ABC，请按下列要求作图：（1）用直尺和圆规作△ABC的角平分线CG．（2）作BC边上的高线（本小题作图工具不限）．（3）用直尺和圆规作△DEF，使△DEF≌△ABC．22．阅读填空：如图，已知∠AOB．要画出∠AOB的平分线，可分别在OA，OB上截取OC=OD，OE=OF，连结CF，DE，交于P 点，那么射线OP就是∠AOB的平分线．要证明这个作法是正确的，可先证明△EOD≌△______，判定依据是______，由此得到∠OED=∠______；再证明△PEC≌△______，判定依据是______，由此又得到PE=______；最后证明△EOP≌△______，判定依据是______，从而便可证明出∠AOP=∠BOP，即OP平分∠AOB．23．证明命题“全等三角形对应边上的高相等”．24．已知：如图，在△ABC中，∠BAC=90°，AB=AC，MN是经过点A的直线，BD⊥MN，CE⊥MN，垂足分别为D、E．（1）求证：①∠BAD=∠ACE；②BD=AE；（2）请写出BD，DE，CE三者间的数量关系式，并证明．《三角形的初步认识》参考答案与试题解析一、选择题1．下列各组线段中，能组成三角形的是（）A．4，6，10 B．3，6，7 C．5，6，12 D．2，3，6【解答】解：A、∵4+6=10，不符合三角形三边关系定理，∴以4、6、10为三角形的三边，不能组成三角形，故本选项错误；B、∵3+6＞7，6+7＜3，3+7＞6，符合三角形三边关系定理，∴以3、6、7为三角形的三边，能组成三角形，故本选项正确；C、∵5+6＜12，不符合三角形三边关系定理，∴以5、6、12为三角形的三边，不能组成三角形，故本选项错误；D、∵2+3＜6，不符合三角形三边关系定理，∴以2、3、6为三角形的三边，不能组成三角形，故本选项错误；故选B．2．在△ABC中，∠A﹣∠C=∠B，那么△ABC是（）A．等边三角形B．锐角三角形C．钝角三角形D．直角三角形【解答】解：∵∠A+∠B+∠C=180°，∴∠C+∠B=180°﹣∠A，而∠A﹣∠C=∠B，∴∠C+∠B=∠A，∴180°﹣∠A=∠A，解得∠A=90°，∴△ABC为直角三角形．故选D．3．如图所示，是用直尺和圆规作一个角等于已知角的示意图，则说明∠A′O′B′=∠AOB的依据是（）A．SAS B．SSS C．AAS D．ASA【解答】解：由作法易得OD=O′D′，OC=O′C′，CD=C′D′，依据SSS可判定△COD≌△C'O'D'，故选：B．4．如图AB⊥AD，AB⊥BC，则以AB为一条高线的三角形共有（）个．A．1 B．2 C．3 D．4【解答】解：∵AB⊥AD，AB⊥BC，∴以AB为一条高线的三角形有△ABD，△ABE，△ABC，△ACE，一共4个．故选D．5．如图所示，△BDC′是将长方形纸片ABCD沿BD折叠得到的，图中（包括实线、虚线在内）共有全等三角形（）对．A．2 B．3 C．4 D．5【解答】解：∵△BDC′是将长方形纸片ABCD沿BD折叠得到的，∴C′D=CD，BC′=BC，∵BD=BD，∴△CDB≌△C′DB（SSS），同理可证明：△ABE≌△C′DE，△ABD≌△C′DB，△ABD≌△CDB三对全等．所以，共有4对全等三角形．故选C．6．下列是命题的是（）A．作两条相交直线B．∠α和∠β相等吗？C．全等三角形对应边相等 D．若a2=4，求a的值【解答】解：A、“作两条相交直线”为描叙性语言，它不是命题，所以A选项错误；B、“∠α和∠β相等吗？”为疑问句，它不是命题，所以A选项错误；C、全等三角形对应边相等，它是命题，所以C选项正确；D、“若a2=4，求a的值”为描叙性语言，它不是命题，所以D选项错误．故选C．7．下列命题中，真命题是（）A．垂直于同一直线的两条直线平行B．有两边和其中一边上的高对应相等的两个三角形全等C．三角形三个内角中，至少有2个锐角D．有两条边和一个角对应相等的两个三角形全等【解答】解：A、同一平面内垂直于同一直线的两条直线平行，故错误，为假命题；B、有两边和其中一边上的高对应相等的两个三角形全等，故错误，为假命题；C、三角形的三个角中，至少有两个锐角，故正确，为真命题；D、有两边和其中一个角对应相等的两个三角形全等，错误，为假命题，故选C．8．如图，对任意的五角星，结论正确的是（）A．∠A+∠B+∠C+∠D+∠E=90° B．∠A+∠B+∠C+∠D+∠E=180°C．∠A+∠B+∠C+∠D+∠E=270°D．∠A+∠B+∠C+∠D+∠E=360°【解答】解：∵∠1=∠2+∠D，∠2=∠A+∠C，∴∠1=∠A+∠C+∠D，∵∠1+∠B+∠E=180°，∴∠A+∠B+∠C+∠D+∠E=180°，故选：B．9．如图，在△ABC中，∠C=90°，AC=BC，AD是△ABC的角平分线，DE⊥AB于E．若AB=6cm，则△DEB的周长为（）A．5cm B．6cm C．7cm D．8cm【解答】解：∵AD是△ABC的角平分线，DE⊥AB，∴CD=DE，∴△DEB的周长=BD+DE+BE，=BD+CD+BE，=BC+BE，=AC+BE，=AE+BE，=AB，∵AB=6cm，∴△DEB的周长=6cm．故选B．10．如图，BF是∠ABD的平分线，CE是∠ACD的平分线，BF与CE交于G，若∠BDC=130°，∠BG C=100°，则∠A的度数为（）A．60° B．70° C．80° D．90°【解答】解：连接BC．∵∠BDC=130°，∴∠DBC+∠DCB=180°﹣130°=50°，∵∠BGC=100°，∴∠GBC+∠GCB=180°﹣100°=80°，∵BF是∠ABD的平分线，CE是∠ACD的平分线，∴∠GBD+∠GCD=∠ABD+∠ACD=30°，∴∠ABC+∠ACB=110°，∴∠A=180°﹣110°=70°．故选B．二、填空题11．工人师傅在做完门框后，为防止变形常常像图中所示的那样上两条斜拉的木条（即图中的AB，CD两根木条），这样做的依据是三角形的稳定性．【解答】解：这样做的依据是三角形的稳定性，故答案为：三角形的稳定性．12．把命题“对顶角相等”改写成“如果…那么…”的形式：如果两个角是对顶角，那么它们相等．【解答】解：题设为：对顶角，结论为：相等，故写成“如果…那么…”的形式是：如果两个角是对顶角，那么它们相等，故答案为：如果两个角是对顶角，那么它们相等．13．如图，在△ABC中，AD⊥BC于D，AE为∠BAC的平分线，且∠DAE=15°，∠B=35°，则∠C= 65 °．【解答】解：如图，∵AD⊥BC，∴∠ADE=90°．又∵∠DAE=15°，∴∠AED=75°．∵∠B=35°，∴∠BAE=∠AED﹣∠B=40°．又∵AE为∠BAC的平分线，∴∠BAC=2∠BAE=80°，∴∠C=180°﹣∠B﹣∠BAC=65°．故答案是：65．14．如图，AB=AC，要使△ABE≌△ACD，应添加的条件是∠B=∠C或AE=AD （添加一个条件即可）．【解答】解：添加∠B=∠C或AE=AD后可分别根据ASA、SAS判定△ABE≌△ACD．故答案为：∠B=∠C或AE=AD．15．命题“若x（1﹣x）=0，则x=0”是假命题（填“真”、假），证明时可举出的反例是x=1 ．【解答】解：当x=1时，x（1﹣x）=0也成立，所以证明命题“若x（1﹣x）=0，则x=0”是假命题的反例是：x=1，故答案为：假，x=1．16．已知三角形的三边长分别是3、x、9，则化简|x﹣5|+|x﹣13|= 8 ．【解答】解：∵三角形的三边长分别是3、x、9，∴6＜x＜12，∴x﹣5＞0，x﹣13＜0，∴|x﹣5|+|x﹣13|=x﹣5+13﹣x=8，故答案为：8．17．如图，在△ABC中，AB=AC，AB的中垂线DE交AC于点D，交AB于点E，如果BC=10，△DBC的周长为22，那么AB= 12 ．【解答】解：∵AB的中垂线DE交AC于点D，交AB于点E，∴AD=BD，∵△DBC的周长为22，∴BC+CD+BD=BC+CD+AD=BC+AC=22，∵BC=10，∴AC=12．∵AB=AC，∴AB=12．故答案为：12．18．如图所示，∠E=∠F=90°，∠B=∠C，AE=AF．给出下列结论：①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN．其中正确的结论是①②③．（将你认为正确的结论的序号都填上）【解答】解：∵∠E=∠F=90°，∠B=∠C，AE=AF，∴△ABE≌△ACF，∴AC=AB，BE=CF，即结论②正确；∵AC=AB，∠B=∠C，∠CAN=∠BAM，∴ACN≌△ABM，即结论③正确；∵∠BAE=∠CAF，∵∠1=∠BAE﹣∠BAC，∠2=∠CAF﹣∠BAC，∴∠1=∠2，即结论①正确；∴△AEM≌△AFN，∴AM=AN，∴CM=BN，∴△CDM≌△BDN，∴CD=BD，∴题中正确的结论应该是①②③．故答案为：①②③．19．已知，∠α=50°，且∠α的两边与∠β的两边互相垂直，则∠β=130°或50°．【解答】解：①如图1，∵∠a+∠β=180°﹣90°﹣90°=180°，∠α=50°，∴∠β=130°，②如图2，若∠a的两边分别与∠β的两边在同一条直线上，∴∠a=∠β=50°，综上所述，∠β=130°或50°．故答案是：130°或50°．20．若三角形的周长为13，且三边均为整数，则满足条件的三角形有 4 种．【解答】解：设三边长分别为a≤b≤c，则a+b=13﹣c＞c≥，∴≤c＜，故c=5，或6；分类讨论如下：①当c=5时，b=4，a=4或b=3，a=5；②当c=6时，b=5，a=2或b=4，a=3；∴满足条件的三角形的个数为4，故答案为：4．三、解答题21．如图，已知△ABC，请按下列要求作图：（1）用直尺和圆规作△ABC的角平分线CG．（2）作BC边上的高线（本小题作图工具不限）．（3）用直尺和圆规作△DEF，使△DEF≌△ABC．【解答】解：（1）如图1，CG为所作；（2）如图1，AH为所作；（3）如图2，△DEF为所作．22．阅读填空：如图，已知∠AOB．要画出∠AOB的平分线，可分别在OA，OB上截取OC=OD，OE=OF，连结CF，DE，交于P 点，那么射线OP就是∠AOB的平分线．要证明这个作法是正确的，可先证明△EOD≌△FOC ，判定依据是SAS ，由此得到∠OED=∠OFC ；再证明△PEC≌△PFD ，判定依据是AAS ，由此又得到PE= PF ；最后证明△EOP≌△FOP ，判定依据是SSS ，从而便可证明出∠AOP=∠BOP，即OP平分∠AOB．【解答】解：作法：（1）分别在OA，OB上截取OC=OD，OE=OF，连接CF，DE，交于P点，（2）连接OP即可，在△EOD与△FOC中，，∴△EOD≌△FOC（SAS），∴∠OED=∠OFC，在△PEC与△PFD中，，∴△PEC≌△PFD（AAS），∴PE=PF．在△EOP与△FOP中，，∴△EOP≌△FOP（SSS），∴∠AOP=∠BOP，即OP平分∠AOB．故答案为：FOC，SAS，OFC；PFD，AAS，PF；△FOP，SSS，23．证明命题“全等三角形对应边上的高相等”．【解答】解：已知：如图，△ABC≌△EFC，AD、EH分别是△ABC和△EFC的对应边BC、FG上的高．求证：AD=EH．证明：∵△ABC≌△EFC，∴AB=EF，∠B=∠F，∵AD、EH分别是△ABC和△EFC的对应边BC、FG上的高，∴∠ADB=∠EHF=90°，在△ABD和△EFH中，∴△ABD≌△EFH（AAS），∴AD=EH．24．已知：如图，在△ABC中，∠BAC=90°，AB=AC，MN是经过点A的直线，BD⊥MN，CE⊥MN，垂足分别为D、E．（1）求证：①∠BAD=∠ACE；②BD=AE；（2）请写出BD，DE，CE三者间的数量关系式，并证明．【解答】解：（1）①∵∠BAC=90°，∴∠BAD+∠CAE=90°，∵CE⊥MN，∴∠ACE+∠CAE=90°，∴∠BAD=∠ACE；②∵BD⊥MN，∴∠BDA=∠AEC=90°，在△ABD和△CAE中，，∴△ABD≌△CAE，∴BD=AE；（2）∵△ABD≌△CAE，∴BD=AE，AD=CE，∵AE=AD+DE，∴BD=CE+DE．八年级数学培优三角形全等的判定试卷一、选择题（每小题3分，共30分）1、尺规作图是指（ ）A 、用直尺规范作图B 、用刻度尺和圆规作图C 、用没有刻度的直尺和圆规作图D 、直尺和圆规是作图工具2、在生产和生活中，①用人字架来建筑房屋；②用窗钩来固定窗扇；③在栅栏门上斜钉着一根木条；④商店的推拉活动防盗门等．其中用到三角形的稳定性的有（ ）A 、1种B 、2种C 、3种D 、4种3、[2014·黔西南]如图，已知AB ＝AD ，那么添加下面的一个条件后，仍无法判定△ABC ≌△ADC 的是（ ）A 、CB ＝CD B 、∠BAC ＝∠DAC C 、∠BCA ＝∠DCAD 、∠B ＝∠D ＝90°4、如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）A 、SSSB 、SASC 、AASD 、ASA5、如图，AB ＝CD ，AD ＝BC ，则图中的全等三角形共有（ ）A 、4对B 、3对C 、2对D 、1对（第3题） （第4题） （第5题） （第6题）6、如图，AD ＝AE ，BE ＝CD ，∠1＝∠2＝110°，∠BAE ＝60°，则∠C 的度数是（ ）A 、20°B 、30°C 、40°D 、50°7、如图，△ABC 中，∠ACB ＝90°，BE 平分∠ABC ，ED ⊥AB 于点D ，若AC ＝3cm ，则AE ＋DE 等于（ ）A 、2cmB 、3cmC 、4cmD 、5cm8、如图，在△ABC 中，∠A ：∠B ：∠C ＝3：5：10，又△C B A ’‘≌△ABC ，则∠‘BCA ：∠’BCB 等于（ ） A 、1：2 B 、1：3 C 、2：3 D 、1：49、如图所示，点E 是长方形ABCD 的边AD 延长线上的一点，且AD ＝DE ，连结BE 交CD 于点O ，连结AO ，下列结论不正确的是（ ）A 、△AOB ≌△BOC B 、△BOC ≌△EODC 、△AOD ≌△EOD D 、△AOD ≌△BOC（第8题） （第9题） （第10题）10、如图所示，△ABC 是不等边三角形，DE ＝BC ，以D 、E 为两个顶点作位置不同的三角形，使所作三角形与△ABC 全等，这样的三角形最多可以画出（ ）A、2个B、4个C、6个D、8个二、填空题（每小题4分，共24分）11、如图，△ABC中，AB＋AC＝6cm，BC的垂直平分线l与AC相交于点D，则△ABD的周长为cm．12、[2014·齐齐哈尔]如图，已知△ABC中AB＝AC，点D、E在BC上，要使△ABD≌△ACE，则只需添加一个适当的条件是（只填一个即可）．13、如图，根据尺规作图所留痕迹，可以求出∠ADC＝度．（第11题）（第12题）（第13题）14、在△ADB和△ADC中，下列条件：①BD＝DC，AB＝AC；②∠B＝∠C，∠BAD＝∠CAD；③∠B ＝∠C ，BD＝DC；④∠ADB＝∠ADC，BD＝DC．其中能得出△ADB≌△ADC的序号是．15、如图，小明为了测量河的宽度，他站在河边的点C，头顶为点D，面对河对岸，压低帽檐使目光正好落在河对岸的岸边点A，然后他姿势不变，在原地转了180°，正好看见他所在的岸上的一块石头点B，他测出BC＝30m，据此小明能得出河宽为，其理由是．（第15题）（第16题）16、如图，DA⊥AB，EA⊥AC，AB＝AD，AC＝AE，BE和CD相交于O，则∠DOE的度数为．三、解答题（共66分）17、（6分）两块含30°角的相同直角三角板，按如图位置摆放，使得两条相等的直角边AC，DE共线，那么，图中共有多少对全等三角形？请将它们写出来．18、（6分）[2014·邵阳]如图，已知点A、F、E、C在同一条直线上，AB∥CD，∠ABE＝∠CDF，AF＝CE．（1）从图中任找两组全等三角形；（2）从（1）中任选一组进行证明．19、（6分）请你在方格纸上画出以AB为边且与△ABC全等的三角形，一共可以画几个？20、（8分）（1）已知线段a、b，画△ABC，使AB＝AC＝a，BC＝b（保留作图痕迹）．（2）在△ABC中，作出∠A的平分线AD（保留作图痕迹）．21、（8分）如图，AB＝AD，BC＝CD，AC，BD相交于点E，由这些条件你能推出哪些结论（不再添加辅助线，不在标注其他字母，不写推理过程，只要求写出四个你认为正确的结论）？22、（10分）如图，在△AFD和△BEC中，点A、E、F、C在同一条直线上，有下面四个判断：①AD＝CB；②AE＝CF；③∠B＝∠D；④∠A＝∠C．请以其中三个为条件，剩下一个作为结论，编一道数学题，并写出解答过程．23、（10分）如图，△ABC中，AD为BC边上的高，AD＝BD，F为AD上一点且FD＝DC，延长BF交AD于点E，判断BE与AC是否垂直，并说明理由．24、（12分）已知：如图，AB＝CD，AD＝BC，经过AC的中点O的直线交AD的延长线于点E，交CB 的延长线于点F．求证：OE＝OF．参考答案：1~5：CCCDA 6~10：ABDAB11、6 12、BD＝CE 13、70°14、①②④15、30m 全等三角形的对应边相等16、90°17、3对，△ADM≌△ECN，△FOM≌△BON，△ABC≌△EFD18、（1）△ABE≌△CDF，△ABC≌△CDA；（2）∵AB∥CD，∴∠BAE＝∠DCF，∵AF＝CE∴AF＋FE＝CE＋FE，即AE＝CF在△△ABE 和△CDF 中⎪⎩⎪⎨⎧=∠=∠∠=∠CF AE DCF BAE CDF ABE ∴△ABE ≌△CDF （AAS ）19、3个，图形略 20、略21、①△ABC ≌△ADC ；②DE ＝BE ；③∠ACD ＝∠ACB ；④AC ⊥BD ．22、①②④→③证明：∵AE ＝CF ，∴AE ＋EF ＝CF ＋EF ，即AF ＝CE ，在△ADF 和△CBE ⎪⎩⎪⎨⎧=∠=∠=CE AF C A CB AD∴△ADF ≌△CBE （SAS ），∴∠B ＝∠D23、BE 与AC 垂直证明：AD 为BC 边上的高，∴∠BDF ＝∠ADC ＝90°，在△BDF 和△ADC 中⎪⎩⎪⎨⎧=∠=∠=DC DF ADC BDF AD BD ∴△BDF ≌△ADC （SAS ）∴∠DBF ＝∠DAC ，∵∠DBF ＋∠BFD ＝90°，∠BFD ＝∠AFE ，∴∠DAC ＋∠AFE ＝90°∴BE ⊥AC24、证明：在△ADC 和△CBA 中 ⎪⎩⎪⎨⎧===CA AC BA DC CB AD ∴△ADC ≌△CBA （SSS ）∴∠DAC ＝∠BCA∵O 为AC 中点，即OA ＝OC ，在△AOE 和△COF 中⎪⎩⎪⎨⎧=∠=∠∠=∠OC OA COF AOE BCA DAC∴△AOE ≌△COF （AAS ），∴OE ＝OF。

认识三角形练习题(好)认识三角形练习题一、选择题1. 在三角形ABC中，已知∠C=90°，AC=7，BC=12，则AB的长是多少？A. 5B. 9C. 14D. 17答案：C2. 已知三角形XYZ的三边分别为XY=5，YZ=6，ZX=8，判断该三角形是什么三角形？A. 等边三角形B. 直角三角形C. 钝角三角形D. 锐角三角形答案：B3. 三角形ABC中，已知∠A=60°，BC=8，AC=10，则AB的长是多少？A. 4B. 6C. 8D. 12答案：A4. 若三角形ABC的三边长分别为AB=5，BC=9，AC=7，则该三角形是什么三角形？A. 等边三角形B. 直角三角形C. 钝角三角形D. 锐角三角形答案：D二、填空题1. 已知三角形XYZ中，∠X=40°，∠Y=60°，则∠Z的度数为__________。

答案：80°2. 若三角形ABC为等腰三角形，且AB=AC，已知∠B=80°，则∠C的度数为__________。

答案：20°3. 在三角形PQR中，已知∠P=30°，∠Q=60°，则∠R的度数为__________。

答案：90°4. 若三角形ABC为等边三角形，且AB=7，则BC的长为__________。

答案：7三、解答题1. 已知三角形ABC中，AB=AC，已知∠B=30°，求∠C的度数。

解答：由题可知，∠B=∠C，且∠B=30°。

根据三角形内角和定理可知，∠A + ∠B + ∠C = 180°。

代入已知条件得到：∠A + 30° + 30° = 180°。

解方程可得：∠A = 120°。

由此可知，∠C = ∠A = 120°。

2. 已知三角形DEF中，DE=5，EF=12，DF=13，判断该三角形是什么三角形。

八上数学《三角形、全等三角形》培优训练题一、填空题1. a 、b 、c 是 白勺边长，IE 简 |a-b-c| + |a + b-c|-|-a-b-c| = ________________________ :2. 一条线段的长为“，若要使3a-1、牝+ 1、12-a 这三条线段组成一个三角形，则a 的取 值范围 ________________ :3. 如果三角形的一个角等于其它两个角的差，则这个三角形是 ____________ 三角形；4. -5. 三角形的三个外角都大于和它相邻的内角，则这个三角形为 ____________ 三角形：6. 四边形中最多有 ___________ 个内角是锐角， ____________ 个内角是钝角：7. 一个多边形除一个内角外，其余内角之和是2570。

，这个角的度数为 ______________ ;8. 多边形的内角和与某一个内角的度数总和为2190%则此多边形的边数为 ______________ :9. 多边形每一个内角都等于250。

，则从此多边形一个顶点发出的对角线有 ___________ 条;10. |H.正“边形的每一个外角都不大于40。

，则满足条件的多边形边数最少为 ________________ : 12.如图 1 所示，已知ZBOF=120° ,则ZA+ZB+ZC+ZD+ZE+ZF= ________________ ；11. 如图 2 所TK , Z1A| + ZA, + ZA3 + ZA4 + ZA ； + Z/驚的 i'Z 拦 ___________ o12. 如图3所示，BE 平分 ABD 交CD 于F, CE 平分 ACD 交AB 于G, AB 、CD 交于点O,且 A=48 , D=46 ,则 BEC= ___________ 。

2•如图4, AABC 的角平分线AD,中线BE 交于点O,则结论： 分练 ②BO 是ZkABD 的中线.其中（） A.①、②都正确B.①、②都不正确C.①正确②不正确D.①不正确，②正确 2. 已知AABC 中，ZABC 和的平分线交于点O,则ZBOC —龙（A.小于直角B.等于直角C.大于直角3. AABC 的三条外角平分线所在直线相交构成的三角形是（A.直角三角形B.钝角三角形C.锐角三角形 4）D.不能确定 ①AO 是SABE 的角平 1. ff A )D ・不能确龙 CD三、解答题1.如图所示，AABC 中，AD. BE 、CF 是角平分线，且它们交于点G, GH 丄BC .求证：ZBGD = ZCGH °2.如图所示.把AABC 纸片沿DE 折叠.(1)如图24所示，间的数疑关系，图2-1(2)如图2・2所示，当点A 落在四边形BCDE 外部A'位置时，试找岀上4与Zl 、Z2之间的数量关系,并证明•3•如图,ZAEB 、ZAFD 的平分线相交于0点，求证:ZE0F=l/2(ZDAB+ZBCD).图2-24 •如图所示，在AABC中，延长BC到点D, ZABC与ZACD的平分线交于人点，（1）试确定ZA与的关系，并说明理由。

第三周培优专题《三角形》1出题人：陈乐宇 审题人：刘凯迪班级： 姓名： 学号：一、热身题1、三角形的三个内角中，锐角的个数不少于（ ）A. 1 个B. 2 个C. 3个D. 不确定2. △ABC 中，∠A ：∠B ：∠C=1：2：3，CD ⊥AB 于点D ，若BC=a ，则AD 等于（ ）A a B a C a D a (1232323)3. 下列命题的逆命题是真命题的是（ ）A. 对顶角相等B. 若a=b ，则|a|=|b|C. 末位是零的整数能被5整除D. 直角三角形的两个锐角互余4. 如图，△ABC 中，AB=AC ，点D 在AC 边上，且BD=BC=AD ，则∠A 的度数为（ ）A. 30°B. 36°C. 45°D. 70°二、渐入佳境1. 等腰三角形的腰长为2cm ，面积等于1平方cm ，则它的顶角的度数为________。

2. 已知，如图，O 是△ABC 的∠ABC 、∠ACB 的角平分线的交点，OD ∥AB 交BC 于D ，OE ∥AC 交BC 于E ，若BC=10cm ，则△ODE 的周长________。

3. 如图，在Rt △ABC 中，∠B=90°，∠A=40°，AC 的垂直平分线MN 与AB 相交于D 点，则∠BCD 的度数是________。

第2题 第3题 第4题4. 如图，∠AOP=∠BOP=15°，PC ∥OA ，PD ⊥OA ，若PC=4，则PD 的长为________。

三、思维大考验1、如图，AD⊥CD，AB=10，BC=20，∠A=∠C=30°，求AD、CD的长。

2.如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高。

求证：AD垂直平分EF。

3、如图1，点C为线段AB上一点，△ACM，△CBN是等边三角形，直线AN、MC交于点E，BM、CN相交于点F.图1 图2（1）求证：AN=BM；（2）求证：△CEF为等边三角形；（3）将△ACM绕点C按逆时针方向旋转90°，其他条件不变，在图2中补出符合要求的图形，并判断第（1）、（2）两小题的结论是否仍然成立。

认识三角形知识点辅导及强化练习一、认识三角形1．三角形的定义：由不在同一直线上的三条线段首尾顺次连接所成的图形。

2．三角形的记法及三要素A 三角形的表示方法：△ABC三角形的三要素：顶点：A，B，C内角：∠A，∠B ,∠C边：AB，BC，ACBc a b3．找一找图中有几个三角形？怎么表示？A DEB C4．议一议从A点到B点处，走AC近，还是走ABC近？说明理由。

思考：在一个三角形中，任意两边之和与第三边长度有怎样的关系？为什么？A C 总结：三角形三边关系：三角形任意两边之和大于第三边。

5．做一做请任意画一个三角形，量出三边长度并填空。

(1)a=________ ，b=_________ ，c=________；(2)a－b____c，b－c____a ，a－c_____b(填“﹤”“﹥”)(3)通过以上比较，你认为三角形三边还存在怎样的关系？总结：三角形三边关系：三角形任意两边之差小于第三边。

例1．长度为6㎝，4㎝，3㎝的三条线段能否组成三角形？反馈练习：1．下列各组三条线段，能否构成三角形？(1)a=1㎝，b=2㎝，c=3㎝( )(2)a=1㎝，b=4㎝，c=2㎝( )(3)a=2㎝，b=3㎝，c=4㎝( )(4)a=6㎝，b=2㎝，c=3㎝( )例2．有两根长度分别为5㎝和8㎝的木棒，用长度为2㎝的木棒与它们能摆成三角形吗？为什么？长度为13㎝的木棒呢？问：能取一根木棒，与原来的两根木棒摆成三角形吗？反馈练习：1．已知三角形的三边a=8，b=6，则c 的取值范围是___________________。

2．已知三角形的三边长分别是3，8，x ，若x 的值为偶数，则x 的值为___________________。

例3．等腰三角形一边长为9㎝，另一边长为4㎝，则第三边长为___________________。

分情况讨论：① 9㎝为腰时，则三边长分别为9㎝，9㎝，4㎝ ② 4㎝为腰时，则三边长分别为4㎝，4㎝，9㎝变式训练：若将上题中的9㎝改成7㎝呢？则第三边的长为___________________。