第4章检测卷数学

第4章《一次函数》（单元基础卷）一、单选题（本大题共10小题，每小题3分，共30分）1．若点在函数的图象上，则的值是（ ）A ．1B ．－1C．D ．2．某一次函数的图象经过点（1，2），且y 随x 的增大而减小，则这个函数的表达式可能是（ ）A ．B ．C ．D ．3．已知点（-1，y 1），（4，y 2）在一次函数y=3x-2的图象上，则，，0的大小关系是（ ）A ．B ．C ．D ．4．已知一次函数不经过第三象限，则的取值范围是（ ）A ．B ．C ．D ．5．将一次函数y=kx+2的图象向下平移3个单位长度后经过点（-4，3），则k 的值为（ ）A ．-1B ．2C ．1D ．-26．一次函数与的图象如图，则下列结论：①；②；③当时，，其中正确的结论有（ ）A ．0个B ．1个C ．2个D ．3个7．对于一次函数，下列结论错误的是（ ）A ．函数值随自变量的增大而减小()2,A m -12y x =-m 1414-24y x =+31y x =-31y x =-+24y x =-+1y 2y 120y y <<120y y <<120y y <<210y y <<()2y k x k =-+k 2k ≠2k >02k <<02k ≤<1y kx b =+2y x a =+0k <0a >3x <12y y <24y x =-+B ．函数的图象不经过第三象限C ．函数的图象与x 轴的交点坐标为（0，4）D ．函数的图象向下平移4个单位长度得到的图象8．数形结合是解决数学问题常用的思想方法．如图，直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知，方程x+5=ax+b 的解是（ ）A ．x=20B ．x=5C ．x=25D ．x=159．如图，直线y 1＝x+3分别与x 轴、y 轴交于点A 和点C ，直线y 2＝﹣x+3分别与x 轴、y 轴交于点B 和点C ，点P （m ，2）是△ABC 内部（包括边上）的一点，则m 的最大值与最小值之差为（ ）A ．1B ．2C ．4D ．610．如图，函数的图象分别与x 轴、y 轴交于A ，B 两点，线段绕点A 顺时针旋转得到线段，则点C 的坐标为（ ）A ．B ．C ．D ．二、填空题（本大题共8小题，每小题4分，共32分）2y x =-22y x =-+AB 90︒AC (2,1)(1,2)(3,1)(1,3)11．函数x 的取值范围是________．12．已知点，都在直线上，则______．13．若点在直线上，则代数式的值为______．14．一次函数y=x+m+2的图象不经过第二象限，则m 的取值范围是 _______．15．若一次函数________．16．若一次函数y ＝kx+2的图象，y 随x 的增大而增大，并与x 轴、y 轴所围成的三角形的面积为2，则k ＝_____．17．如图，把放在平面直角坐标系内，其中，，点，的坐标分别为，，将沿轴向右平移，当点落在直线上时，线段扫过的面积为______．18．如图，已知点，，直线经过点．试探究：直线与线段有交点时的变化情况，猜想的取值范围是______．三、解答题（本大题共6小题，共58分）19．（8分）已知关于的函数，当，为何值时，它是正比例函数？20．（8分）一次函数（为常数，且）．y =()1,A m y ()21,B m y +23y x =-21y y -=(),P a b 21y x =-842a b -+y ax b =+=Rt ABC △90CAB а＝5cm =BC A B ()1,0()4,0ABC V x C 26y x =-BC 2cm ()2,3A -()2,1B y kx k =+()1,0P -AB k k x ||1(2)5m y m x n -=++-m n 1=-+y ax a a 0a <（1）若点在一次函数的图象上，求的值；（2）当时，函数有最大值2，求的值．21．（10分）如图，已知正比例函数的表达式为y＝﹣x ，过正比例函数在第四象限图象上的一点A 作x 轴的垂线，交x 轴于点H ，AH ＝2，求线段OA 的长．22．（10分）如图，已知点A(6，4)，直线l 1经过点B(0，2)、点C(3，−3)，且与x 轴交于点D ，连接AD 、AC ，AC 与x 轴交于点P ．()2,3-1=-+y ax a a 12x -≤≤a 12(1) 求直线l1的表达式，并求出点D的坐标；(2) 在线段AD上存在一点Q．使S△PDQ=S△PDC，请求出点Q的坐标；(3) 一次函数y=kx+k+5的图象为l2，若点A，D到l2的图象的距离相等，直接写出k的值．23．（10分）某快递公司为提高快递分拣的速度，决定购买甲、乙两种型号的机器人共20台来代替人工分拣，两种型号机器人的工作效率和价格如下表：型号甲乙每台每小时分拣快递件数/件800600每台价格/万元3 2.5设购买甲种型号的机器人x 台，购买这20台机器人所花的费用为y 万元．(1)求y 与x 之间的函数关系式；(2)若要求这20台机器人每小时分拣快递件数总和不少于12700件，则该公司至少需要购买几台甲种型号的机器人？此时所花费的费用为多少万元？24．（12分）如图，一次函数的图象与轴，轴分别交于，两点，在轴上有一点，动点从点以每秒2个单位长度的速度向左移动，y kx b =+x y (30)A ，(01)B ，y (03)C ，P A（1）求直线的表达式；（2）求的面积与移动时间之间的函数关系式；（3）当为何值时，≌，求出此时点的坐标．参考答案一、单选题1．AAB COP ∆S t t COP ∆AOB ∆P【分析】将x=-2代入一次函数解析式中求出m 值，此题得解．解：当x=-2时，y=-×（-2）=1，∴m=1．故选A ．2．D【分析】设一次函数关系式为y=kx+b ，y 随x 增大而减小，则k<0；图象经过点（1，2），可得k 、b 之间的关系式．综合二者取值即可．解：设一次函数关系式为y=kx+b ，∵图象经过点(1,2)，∴k+b=2；∵y 随x 增大而减小，∴k<0.即k 取负数，满足k+b=2的k 、b 的取值都可以故选：D.3．B【分析】根据点的横坐标利用一次函数图象上点的坐标特征，即可求出、的值，将其与0比较大小后即可得出结论．解：∵点（-1，），（4，）在一次函数y=3x-2的图象上，∴=-5，=10，∵10＞0＞-5，∴＜0＜．故选：B ．4．D【分析】根据一次函数的图象与k 、b 的关系列不等式组求解即可．解：∵一次函数的图象不经过第三象限，∴，，∴，故选：D ．5．A121y 2y 1y 2y 1y 2y 1y 2y ()2y k x k =-+20k -<0k ≥02k ≤<【分析】根据平移的规律得到y=kx+2-3，然后根据待定系数法即可求得k 的值，从而求得正比例函数的表达式．解：将一次函数y=kx+2的图象向下平移3个单位长度后得到y=kx+2-3=kx-1，∵平移后的函数图象经过点（-4，3），∴3=-4k-1，解得k=-1，故选：A ．6．B【分析】根据一次函数的增减性可得，再根据一次函数与轴的交点位于轴负半轴可得，然后根据当时，一次函数的图象位于一次函数的图象的上方可得，由此即可得出答案．解：对于一次函数而言，随的增大而减小，，结论①正确；一次函数与轴的交点位于轴负半轴，，结论②错误；由函数图象可知，当时，一次函数的图象位于一次函数的图象的上方，则，结论③错误；综上，正确的结论有1个，故选：B ．7．C【分析】根据一次函数的图象和性质，平移的规律以及函数图象与坐标轴的交点的求法即可判断．解：A 、∵k=-2<0，∴函数值随自变量的增大而减小，故选项不符合题意；B 、∵k=-2<0，b=4>0，函数经过第一、二、四象限，不经过第三象限，故选项不符合题意；C 、当y=0时，x=2，则函数图象与x 轴交点坐标是（2，0），故选项符合题意；D 、函数的图象向下平移4个单位长度得y=-2x+4-4=-2x ，故选项不符合题1y kx b =+0k <2y x a =+y y 0a <3x <1y kx b =+2y x a =+12y y > 1y kx b =+1y x 0k ∴< 2y x a =+y y 0a ∴<3x <1y kx b =+2y x a =+12y y >意；故选：C．8．A【分析】两直线的交点坐标为两直线解析式所组成的方程组的解．解：由图可知：直线y=x+5和直线y=ax+b交于点P（20，25），∴方程x+5=ax+b的解为x=20．故选：A．9．B【分析】由于P的纵坐标为2，故点P在直线y= 2上，要求符合题意的m 值，则P点为直线y= 2与题目中两直线的交点，此时m存在最大值与最小值，故可求得．解：∵点P (m， 2)是△ABC内部(包括边上)的点．∴点P在直线y= 2上，如图所示，，当P为直线y= 2与直线y2的交点时，m取最大值，当P为直线y= 2与直线y1的交点时，m取最小值，∵y2 =-x+ 3中令y=2，则x= 1，∵y1 =x+ 3中令y=2，则x= -1，∴m的最大值为1， m的最小值为- 1．则m的最大值与最小值之差为：1- (-1)= 2．故选：B．10．C【分析】过C点作CD⊥x轴于D，如图，先利用一次函数图象上点的坐标特征确定B（0，2），A（1，0），再证明△ABO≌△CAD，得到AD＝OB＝2，CD＝OA＝1，则C点坐标可求．解：过C 点作CD ⊥x 轴于D ，如图．∵y ＝−2x ＋2的图象分别与x 轴、y 轴交于A ，B 两点，∴当x ＝0时，y ＝2，则B （0，2），当y ＝0时，−2x ＋2＝0，解得x ＝1，则A （1，0）．∵线段AB 绕A 点顺时针旋转90°，∴AB ＝AC ，∠BAC ＝90°，∴∠BAO ＋∠CAD ＝90°，而∠BAO ＋∠ABO ＝90°，∴∠ABO ＝∠CAD ．在△ABO 和△CAD 中，∴△ABO ≌△CAD ，∴AD ＝OB ＝2，CD ＝OA ＝1，∴OD ＝OA ＋AD ＝1＋2＝3，∴C 点坐标为（3，1）．故选：C ．二、填空题11．且【分析】根据二次根式中被开方数大于等于0及分母不为0即可求解．解：由题意可知：，解得：且，故答案为：且．AOB CDA ABO CAD AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩0x ≥2x ≠020x x ≥⎧⎨-≠⎩0x ≥2x ≠0x ≥2x ≠【分析】分别把A 、B 的坐标代入，求得、再计算即可．解：把代入得＝2m －3，把代入得＝2（m ＋1）－3＝2m －1，∴＝（2m －1）－（2m －3）＝2m －1－2m ＋3＝2故答案为：213．6【分析】把点P 代入一次函数解析式，可得，化简带值可求出结论．解：∵点在直线上，∴，变形得：，代数式；故答案为：6．14．m ≤-2【分析】由一次函数y=x+m+2的图象不经过第二象限，可得k ＞0，b ≤0，列不等式求解即可．解：∵一次函数y=x+m+2的图象不经过第二象限，∴m+2≤0，解得m ≤-2，故答案为：m ≤-2．15．【分析】首先根据一次函数的位置确定a 和b 的值，然后化简二次根式求23y x =-1y 2y 21y y -()1,A m y 23y x =-1y ()21,B m y +23y x =-2y 21y y -21b a =-(),P a b 21y x =-21b a =-21a b -=()8428228216a b a b -+=--=-⨯=b-解：∵若一次函数y=ax+b 的图象经过第一、二、四象限，∴a ＜0，b ＞0，∴b-a ＞0，，故答案为-b ．16．1【分析】如图，根据题意可求出OA ．根据一次函数y ＝kx+2的图象，y 随x 增大而增大，即可利用k 表示出OB 的长，再根据三角形面积公式，即可求出k 的值．解：如图，令x=0，则y=2，∴A(0，2),∴OA=2．令y=0，则，∴B(，0)．∵一次函数y ＝kx+2的图象，y 随x 增大而增大，∴k ＞0，∴OB=，∵一次函数y ＝kx+2的图象与两坐标轴围成的三角形面积为2，∴，即，a a b a b -=--+=-2x k=-2k -2k 122OA OB ⋅=12222k ⨯⨯=解得：．故答案为：1．17．16【分析】先根据勾股定理求出C 点的坐标，得到C 点平移后的对应点C 1的纵坐标为4，与直线 相交，可得C 1坐标，由此推出CC 1距离，再求出四边形BCC 1B 1的面积即可．解：∵A （1，0），B （4，0）∴AB=3∵，∠CAB=90°，∴∴C （1，4），∴C 点平移后对应点C 1的纵坐标为4，∴把代入解得，∴CC 1=4，∴，故答案为：16．18．或【分析】根据题意，画出图象，可得当x=2时，y ≥1，当x=-2时，y ≥3，即可求解．解：如图，1k =26y x =-5BC =4AC ==4y =26y x =-5x =11116BCC B S CC AC =⨯=13k ≥3k ≤-观察图象得：当x=2时，y ≥1，即，解得：，当x=-2时，y ≥3，即，解得：，∴的取值范围是或．故答案为：或三、解答题19．解：是正比例函数，且且，解得，．即当，时，函数是正比例函数．20．解：（1）把（2，-3）代入得，解得；（2）∵a ＜0时，y 随x 的增大而减小，则当x=-1时，y 有最大值2，把x=-1代入函数关系式得 2=-a-a+1，解得，所以．21．解：∵AH ⊥x 轴，AH ＝2，点A 在第四象限，∴A 点的纵坐标为﹣2，21k k +≥13k ≥23k k -+≥3k ≤-k 13k ≥3k ≤-13k ≥3k ≤-||1(2)5m y m x n -=++- 20m ∴+≠||11m -=50n -=2m =5n =2m =5n =||1(2)5m y m x n -=++-1=-+y ax a 213a a -+=-4a =-12a =-12a =-代入得，解得x ＝4，∴A （4，﹣2），∴OH ＝4，∴OA．22．(1)解：设l 1的表达式为y=kx+b(k≠0)，∵l 1经过点B(0，2)、点C(3，−3)，∴，解得，∴l 1的函数表达式：y=x+2．∵点D 为l 1与x 轴的交点，故令y=0，x+2=0，解得x=，∴点D 坐标为，0)；(2)解：由（1）同理可得AD 所在直线的一次函数表达式为：，∵点Q 在线段上，∴设点Q 坐标为，其中．∵，∴，即，解得，满足题意．∴点Q 坐标为；(3)解：∵y=kx+k+5=(k+1)x+5，∴直线l 2过定点(-1，5)，12y x =-122x -=-==233b k b =⎧⎨-=+⎩532k b ⎧=-⎪⎨⎪=⎩53-53-6565516y x =-AD 516m m ⎛⎫- ⎪⎝⎭，665m ≤≤PDQ PDC S S =V V Q C y y =-5136m -=245=m 2435⎛⎫⎪⎝⎭∵点A ，D 到l 2的图像的距离相等，∴当l 2与线段AD 平行或过线段AD 中点，当l 2与线段AD 平行时，k=；当l 2过线段AD 中点(，2)时，∴2=k+k+5，解得：k=；综上，k 的值为或．23．(1)解：y 与x 之间的函数关系式为：y=3x+2.5（20-x ），=3x+50-2.5x=0.5x+50（0≤x ≤20）；(2)解：由题可得：800x+600（20-x ）≥12700，解得x ≥3.5，∴当x=4时，y 取得最小值，∴y 最小=0.5×4+50=52．∴该公司至少需要购买4台甲种型号的机器人；此时所花费的费用为52万元．24．解：解（1）设直线AB 的表达式为将，两点代入得解得 ∴AB 的表达式为（2） 561851851523-561523-(0)y kx b k =+≠(30)A ，(01)B ，301k b b +=⎧⎨=⎩131k b ⎧=-⎪⎨⎪=⎩113y x =-+3322÷=当时当时（3）若≌时当 时， ，此时P 的坐标为；当 时， ，此时P 的坐标为；302t <≤13(32)22S OP OC t =⋅=-32t >13(23)22S OP OC t =⋅=-COP ∆AOB ∆OP OB=(0,1)B 1OB =∴1OP ∴=321t -=1t =(1,0)231t -=2t =(1,0)-。

第4章：指数函数与对数函数基础检测卷（试卷满分150分，考试用时120分钟）一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求.1．函数()32x f x a -=+（0a >且1a ≠）的图象恒过定点（）A ．()0,1B ．()0,3C ．()3,3D ．()4,1【答案】C【解析】对于函数()f x ，则30x -=，可得3x =，则()0323f a =+=，所以，函数()32x f x a -=+（0a >且1a ≠）的图象恒过定点坐标为()3,3.故选：C.2．设3484log 4log 8log log 16m ⋅⋅=，那么m 等于（）A ．92B ．9C ．18D ．27【答案】B【解析】348lg 4lg8lg lg log 4log 8log 2lg3lg 4lg8lg3m mm ⋅⋅=⨯⨯== ,lg 2lg3lg9m ∴==，9m ∴=，故选：B.3．函数()()23log 1f x x =+的值域为（）A ．()0,∞+B ．[)0,∞+C ．()1,+∞D ．[)1,+∞【答案】B【解析】令21u x =+，则1u ≥，又3log y u =在[)1,+∞上单调递增，所以()233log 1log 10x +≥=，故函数()f x 的值域为[)0,∞+．故选：B ．4．碘—131经常被用于对甲状腺的研究，它的半衰期大约是8天（即经过8天的时间，有一半的碘—131会衰变为其他元素）.今年3月1日凌晨，在一容器中放入一定量的碘—131，到3月25日凌晨，测得该容器内还剩有2毫克的碘—131，则3月1日凌晨，放入该容器的碘—131的含量是（）A ．8毫克B ．16毫克C ．32毫克D ．64毫克【答案】B【解析】设3月1日凌晨放入该容器的碘—131的含量是x 毫克，由题意，3月1日凌晨到月25日凌晨共经历了3个半衰期，所以31()22x ⋅=，解得16x =，即放入该容器的碘—131的含量是16毫克.故选：B5．若函数(31)4,1()log ,1aa x a x f x x x -+<⎧=⎨≥⎩对任意12,x x ≠都有2121()()0f x f x x x -<-，则实数a 的取值范围是（）A ．()01，B ．103⎛⎫⎪⎝⎭，C ．]1(,17D ．1173⎡⎫⎪⎢⎣⎭，【答案】D 【解析】由2121()()0f x f x x x -<-得，()f x 在R 上是减函数，则有01310314log 1a a a a a <<⎧⎪-<⎨⎪-+≥⎩，解得1173a ≤<.故选：D.6．已知函数(log )a y x c =+（,a c 为常数，其中0,1a a >≠）的图象如图所示，则下列结论成立的是（）A ．1,1a c >>B ．1,01a c ><<C ．01,1a c <<>D ．01,01a c <<<<【答案】D【解析】由函数图象可知函数为单调递减函数，结合(log )a y x c =+可知01a <<，当1x =时，log 1)0,1,0(1a c c c +<∴+>∴>，当0x =时，log 0,01a c c >∴<<，故01c <<，故选：D7．函数32()236f x x x x =-+-在区间[2,4]-上的零点必属于区间（）A ．[2,1]-B ．[2.5,4]C ．[1,1.75]D ．[1.75,2.5]【答案】D【解析】解法一：二分法由已知可求得，(2)280f -=-<，(1)40f =-<，37(2.5)08f =>，(4)380f =>，97(1.75)064f =-<.对于A 项，因为()(2)10f f ->，所以A 项错误；对于B 项，因为()()2.540f f >，所以B 项错误；对于C 项，因为()()1 1.750f f >，所以C 项错误；对于D 项，因为()()1.75 2.50f f <，所以D 项正确.解法二：因为()()322()23623f x x x x x x =-+-=-+，所以()20f =，即函数32()236f x x x x =-+-在区间[2,4]-上的零点为2，故D 正确.故选：D.8．已知1312a ⎛⎫= ⎪⎝⎭，21log 3b =，121log 3c =，则（）A ．a b c >>B ．a c b>>C ．c a b>>D ．c b a>>【答案】C【解析】因为12x y ⎛⎫= ⎪⎝⎭在R 上单调递减，故1103111222⎛⎫⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，即1,12a ⎛⎫∈ ⎪⎝⎭，因为2log y x =在()0,∞+上单调递增，故221log log 103b =<=，因为12log y x =在()0,∞+上单调递减，故112211log log 132=>=c ，故c a b >>.故选：C ．二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9．下列运算中正确的是（）A ．383log 8log 5log 5=B136a =C ．若114a a -+=，则11223a a -+=D ．()2log 71ln ln e 72-⎛⎫+= ⎪⎝⎭【答案】BD【解析】对于选项A ，由换底公式可得353log 8log 8log 5=，故A 不正确；对于选项B22313333262a a a a +=⋅==，故B 正确；对于选项C ，设1122a a t -+=()0t >，两边分别平方可得122a a t -++=，因为114a a -+=，所以216t =，故11224a a -+=，故C 不正确；对于选项D ，()22log 7log 71ln ln e 2ln17072-⎛⎫+=+=+= ⎪⎝⎭，故D 正确．故选：BD ．10．关于函数()()01xf x a a a =>≠，且与函数()()log 01a g x x a a =>≠，且说法正确的有（）A ．()()f x g x 与互为反函数B ．()()f x g x 与的图像关于原点对称C ．()()f x g x 与必有一交点D ．()()f x g x 与的图像关于y x =对称【答案】AD【解析】()()0,1xf x a a a =>≠与函数()()log 0,1a g x x a a =>≠是互为反函数，图像关于y x =对称，故AD 选项正确;()()f x g x 与的图像不关于原点对称，故B 选项错误;当1a >时,()()f x g x 与没有交点，故C 选项错误;故选:AD.11．（多选）定义在[]1,1-上的函数()2943x xf x =-⋅+⋅，则下列结论中正确的是（）A ．()f x 的单调递减区间是[]0,1B ．()f x 的单调递增区间是[]1,1-C ．()f x 的最大值是()02f =D ．()f x 的最小值是()16f =-【答案】ACD【解析】设3x t =，[]1,1x ∈-，则3x t =是增函数，且1,33t ⎡⎤∈⎢⎥⎣⎦，又函数()2224212y t t t =-+=--+在1,13⎡⎤⎢⎥⎣⎦上单调递增，在[]1,3上单调递减，因此()f x 在[]1,0-上单调递增，在[]0,1上单调递减，故A 正确，B 错误；()()max 02f x f ==，故C 正确；()1019f -=，()16f =-，因此()f x 的最小值是6-，故D 正确．故选:ACD ．12．关于函数()|ln |2||f x x =-，下列描述正确的有（）A ．()f x 在区间(1,2)上单调递增B ．()y f x =的图象关于直线2x =对称C ．若1212,()(),x x f x f x ≠=则124x x +=D ．()f x 有且仅有两个零点【答案】ABD【解析】根据图象变换作出函数()f x 的图象（()ln 2f x x =-，作出ln y x =的图象，再作出其关于y 轴对称的图象，然后向右平移2个单位，最后把x 轴下方的部分关于x 轴翻折上去即可得），如图，由图象知()f x 在(1,2)是单调递增，A 正确，函数图象关于直线2x =对称，B 正确；12()()f x f x k ==，直线y k =与函数()f x 图象相交可能是4个交点，如图，如果最左边两个交点横坐标分别是12,x x ，则124x x +=不成立，C 错误，()f x 与x 轴仅有两个公共点，即函数仅有两个零点，D 正确．故选：ABD ．三、填空题：本题共4小题，每小题5分，共20分13．求函数y =的定义域______．【答案】(,3][1,)-∞-⋃+∞【解析】要使原函数有意义，则2ln(22)0x x +-≥，即2221x x +-≥，解得3x ≤-或1x ≥．所以，函数()f x =(,3][1,)-∞-⋃+∞．故答案为：(,3][1,)-∞-⋃+∞14．设a ∈R ，22()()21x xa a f x x ⋅+-=∈+R ，()f x 为奇函数，则a 的值为__________．【答案】1【解析】要使()f x 为奇函数，∵x ∈R ,∴需()()0f x f x +-=，∴()()1222,212121x x x xf x a f x a a +-=--=-=-+++，由12202121x x x a a +-+-=++,得()2212021x x a +-=+,1a ∴=．故答案为：1.15．已知函数()34x f x x =--在区间[1,2]上存在一个零点，用二分法求该零点的近似值，其参考数据如下：(1.6000)0.200f ≈，(1.5875)0.133f ≈，(1.5750)0.067f ≈，(1.5625)0.003f ≈，(1.5562)0.029f ≈-，(1.5500)0.060f ≈-，据此可得该零点的近似值为________．（精确到0.01）【答案】1.56【解析】因为(1.5625)0.003f ≈，(1.5562)0.029f ≈-，即(1.5625)(1.5562)0f f ⋅<，所以由零点存在定理可知()f x 的零点在()1.55621.5625，之间，近似值为1.56.故答案为：1.56.16．若方程2310x ax +-=的两根分别在区间(1,0)-和(0,1)内，则实数a 的取值范围是__________．【答案】(2,2)-【解析】令()231f x x ax =+-，因为方程2310x ax +-=的两根分别在区间(1,0)-和(0,1)内，所以()()()131********f a f f a ⎧-=-->⎪=-<⎨⎪-=+->⎩，解得22a -<<，故答案为：(2,2)-四．解答题：本小题共6小题，共70分。

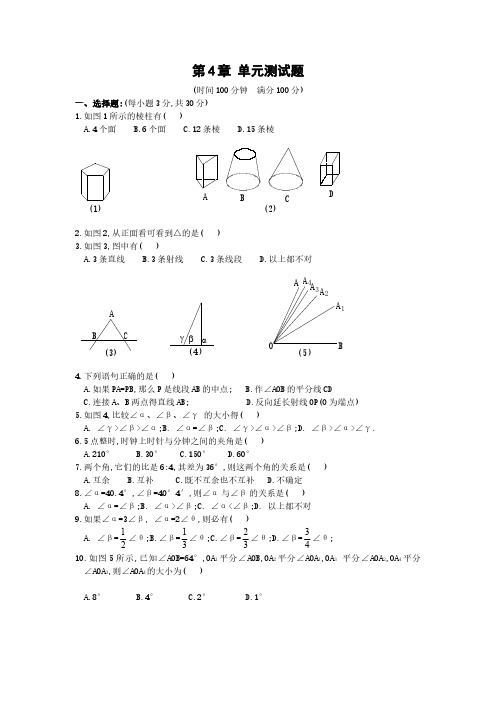
第4章 单元测试题(时间100分钟 满分100分)一、选择题:(每小题3分,共30分)1.如图1所示的棱柱有( )A.4个面B.6个面C.12条棱D.15条棱C(2)A DB2.如图2,从正面看可看到△的是( )3.如图3,图中有( )A.3条直线B.3条射线C.3条线段 D.以上都不对4.下列语句正确的是( )A.如果PA=PB,那么P是线段AB的中点;B.作∠AOB的平分线CDC.连接A、B两点得直线AB;D.反向延长射线OP(O为端点)5.如图4,比较∠α、∠β、∠γ 的大小得( )A. ∠γ>∠β>∠α;B. ∠α=∠β;C. ∠γ>∠α>∠β;D. ∠β>∠α>∠γ.6.5点整时,时钟上时针与分钟之间的夹角是( )A.210°B.30°C.150°D.60°7.两个角,它们的比是6:4,其差为36°,则这两个角的关系是( )A.互余B.互补C.既不互余也不互补D.不确定8.∠α=40.4°,∠β=40°4′,则∠α与∠β的关系是( )A. ∠α=∠β;B. ∠α>∠β;C. ∠α<∠β;D. 以上都不对9.如果∠α=3∠β, ∠α=2∠θ,则必有( )2310.如图5所示,已知∠AOB=64°,OA1平分∠AOB,OA2平分∠AOA1,OA3平分∠AOA2,OA4平分∠AOA3,则∠AOA4的大小为( )A.8°B.4°C.2°D.1°二、填空题:(每小题3分,共30分)11.已知线段AB=8cm,延长AB 至C,使AC=2AB,D 是AB 中点,则线段CD=______.12.如图,从城市A 到城市B 有三种不同的交通工作:汽车、火车、飞机,除去速度因素,坐飞机的时间最短是因为___________.13.57.32°=_______°_______′_______″;27°14′24″=_____°.14.已知∠a=36°42′15″,那么∠a 的余角等于________.15.∠1+∠2=180°,∠2+∠3=180°,根据________,得∠1=∠3.16.表示O 点南偏东15°方向和北偏东25°方向的两条射线组成的角等于____17.如图,∠AOC=90°,∠AOB=∠COD,则∠BOD=______°.航线铁路公路(6)A B18.102°43′32″+77°16′28″=________;98°12′25″÷5=_____.19.已知线段AB=acm,点A 1平分AB,A 2平分AA 1,A 3平分AA 2,……,____________cm.20.在平面上有任意四点,过其中任意两点画直线,能画_______条直线.三、解答题:(21、24、25、26每题6分,22、23题每题8分)21.根据下列语句画图:(1)画∠AOB=120°;(2)画∠AOB 的角平分线OC;(3)反向延长OC 得射线OD;(4)分别在射线OA、OB、OD 上画线段OE=OF=OG=2cm;(5)连接EF、EG、FG;(6)你能发现EF、EG、FG 有什么关系?∠EFG、∠EGF、∠GEF 有什么关系?22.已知线段AB=10cm,直线AB 上有一点C ,且BC=4cm,M 是线段AC 的中点,求AM 的长.23.如图,直线AB、CD 交于O 点,且∠BOC=80°,OE 平分∠BOC,OF 为OE 的反向延长线.(1)求∠2和∠3的度数.(2)OF平分∠AOD吗?为什么?24.一个角的补角与它的余角的度数之比是3:1,求这个角的度数.25.测量员沿着一块地的周围测绘.从A向东走600米到B,再从B向东南(∠ABC= 135°)走500米到C,再从C向西南(∠BCD=90°)走800米到D.用1厘米代表100米画图, 求DA的长(精确到10米)和DA的方向(精确到1°).北D CA B26.利用线段、角、三角形、圆等图形为你的学校设计一个校标,并简述你的设计思路.参考答案一、选择题1.D2.C3.C4.D5.C6.C7.B8.B9.C 10.B二、填空题11.12cm 12.两点之间,线段最短 13.57、19、12;27.2414. 53°17′45″ 15.同角的补角相等16.140° 17.90 18.180°;19°38′29″.　19. 20.1或4或6三、解答题21.(6)EF=EG=FG,∠EFG=∠EGF=∠FEG=60°22.AM=7cm或3cm23.(1)∠2=100°,∠3=40°;(2)∠AOF=40°,OF平分∠AOD24.设这个角为x0,( 180-x):(90-x)=3:1,x=45.第4章 单元测试题2检测时间：45分钟，满分：100分班级 学号 姓名 得分一、填空题：（每空2分，共46分）1．正方体有______条棱，_____个顶点， 个面.2．圆柱的侧面展开图是一个 ，圆锥的侧面展开图是一个 ，棱柱的侧面展开图是一个 。

七年级数学上册第4章图形的初步认识检测题新版华东师大版(时间：100分钟满分：120分)一、选择题(每小题3分，共30分)1．数轴是一条( B )A．射线B．直线C．线段D．以上都是2．下列四个几何体中，是三棱柱的为( C )3．下列说法中正确的是( A )A．两点之间的所有连线中，线段最短B．射线就是直线C．两条射线组成的图形叫做角D．小于平角的角可分为锐角和钝角两类4．(2022·宁波)如图所示几何体是由一个球体和一个圆柱组成的，它的俯视图是( C)5．在数轴上，点A，B在原点O的两侧，分别表示数a，2，将点A向右平移1个单位长度，得到点C，若CO＝BO，则a的值为( A )A．－3 B．－2 C．－1 D．16．(2021·随州)如图是由4个相同的小正方体构成的一个组合体，该组合体的三视图中完全相同的是( A )A．主视图和左视图B．主视图和俯视图C．左视图和俯视图D．三个视图均相同第6题图第8题图第9题图第10题图7．下列说法错误的是( B )A ．两个互余的角都是锐角B ．一个角的补角大于这个角本身C ．互为补角的两个角不可能都是锐角D ．互为补角的两个角不可能都是钝角8．(2021·河北)一个骰子相对两面的点数之和为7，它的展开图如图，下列判断正确的是( A )A ．A 代表B ．B 代表C ．C 代表D ．B 代表9．如图，已知∠AOB 是直角，∠AOC 是锐角，ON 平分∠AOC，OM 平分∠BOC，则∠MON 等于( A )A ．45°B ．45°＋12 ∠AOC C ．60°－12∠AOC D ．不能计算10．如图是一个几何体的三视图，其中主视图与左视图完全一样，则这个几何体的表面积是( B )A ．80－2πB ．80＋4πC ．80D ．80＋6π 二、填空题(每小题3分，共15分)11．(北京中考)在如图所示的几何体中，其三视图中有长方形的是__①②__．(写出所有正确答案的序号)第11题图第12题图第13题图12．如图，已知点A ，O ，C 在同一直线上，OE 平分∠AOB，OF 平分∠BOC，则∠EOF 的度数为__90__°.13．如图，已知AB ＝8 cm ，BD ＝3 cm ，C 为AB 的中点，则线段CD 的长为__1__cm . 14．经过一点A 画直线，可以画__无数__条；过不在同一直线上三点中的任意两点画直线，一共可能画__3__条．15．(青岛中考)如图，一个正方体由27个大小相同的小立方块搭成，现从中取走若干个小立方块，得到一个新的几何体．若新几何体与原正方体的表面积相等，则最多可以取走__16__个小立方块．三、解答题(共75分)16．(8分)已知平面上四点A ，B ，C ，D ，如图： (1)画直线AB ； (2)画射线AD ；(3)直线AB ，CD 相交于点E ；(4)连结AC ，BD 相交于点F.解：作图略17．(9分)如图，(1)∠AOC 是哪两个角的和； (2)∠AOB 是哪两个角的差；(3)如果∠AOB＝∠COD，那么∠AOC 与∠DOB 相等吗？ 解：(1)∠AOC 是∠AOB 与∠BOC 的和 (2)∠AOC 与∠BOC 的差或∠AOD 与∠BOD 的差 (3)相等．理由如下：∵∠AOB＝∠COD，∴∠AOB ＋∠BOC＝∠COD＋∠BOC，即∠AOC＝∠BOD18．(9分)如图，B ，C 两点把线段AD 分成2∶4∶3三部分，CD ＝6 cm . (1)求AD 的长；(2)若M 是AD 的中点，求线段MC 的长．解：(1)∵AB∶BC∶CD＝2∶4∶3，∴CD ＝39 AD ＝13 AD ，∵CD ＝6，∴AD ＝3CD ＝18 cm (2)由(1)知AD ＝18，∵M 是AD 的中点，∴MD ＝12 AD ＝12 ×18＝9(cm )，∴MC ＝MD －CD ＝9－6＝3(cm )19．(9分)一个正方体六个面分别标有字母A，B，C，D，E，F，其展开图如图所示，已知：A＝x2－2xy，B＝A－C，C＝3xy＋y2，若该正方体相对两个面上的多项式的和相等，试用x，y的代数式表示多项式D，并求当x＝－1，y＝－2时，多项式D的值．解：由展开图可知A与C相对，B与D相对，∴B＋D＝A＋C，又∵A＝x2－2xy，B＝A－C，C＝3xy＋y2，则D＝A＋C－B＝A＋C－(A－C)＝2C＝2(3xy＋y2)＝6xy＋2y2，当x＝－1，y＝－2时，6xy＋2y2＝12＋8＝20，故当x＝－1，y＝－2时，多项式D的值是2020．(9分)如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°，(1)求∠BOC的度数；(2)通过计算判断OE是否平分∠BOC.解：(1)∠BOC＝180°－∠AOC＝180°－50°＝130°(2)∵OD平分∠AOC，∴∠COD＝1 2∠AOC＝12×50°＝25°.∵∠DOE＝90°，∴∠COE＝90°－∠COD＝90°－25°＝65°，∴∠BOE＝∠BOC－∠COE＝130°－65°＝65°，∴∠COE＝∠BOE，∴OE平分∠BOC21．(10分)如图，直线SN与直线WE相交于点O，射线ON表示正北方向，射线OE表示正东方向．已知射线OB的方向是南偏东m°，射线OC的方向是北偏东n°，且m°的角与n°的角互余．(1)①若m＝50，则射线OC的方向是__北偏东40°__；②图中与∠BOE 互余的角有__∠BOS，∠EOC__，与∠BOE 互补的角有__∠BOW，∠COS__； (2)若射线OA 是∠BON 的平分线，则∠BOS 与∠AOC 是否存在确定的数量关系？如果存在，请写出你的结论以及计算过程；如果不存在，请说明理由．解：(2)∠AOC＝12 ∠BOS.因为射线OA 是∠BON 的平分线，所以∠NOA＝12 ∠BON.因为∠BOS＋∠BON＝180°，所以∠BON＝180°－∠BOS.所以∠NOA＝12 ∠BON ＝90°－12 ∠BOS.因为∠NOC＋∠BOS＝90°，所以∠NOC＝90°－∠BOS.所以∠AOC＝∠NOA－∠NOC＝90°－12∠BOS－(90°－∠BOS)＝12∠BOS22．(10分)如图①，已知线段AB ＝16 cm ，点C 为线段AB 上的一个动点(点C 不与A ，B 重合)，点D ，E 分别是AC 和BC 的中点．(1)求DE 的长；(2)知识迁移：如图②，已知∠AOB＝130°，过角的内部任一点C 画射线OC ，若OD ，OE 分别平分∠AOC 和∠BOC，试说明∠DOE 的大小与射线OC 的位置无关．解：(1)∵点D ，E 分别是AC 和BC 的中点，∴DC ＝12 AC ，CE ＝12 BC ，∴DE ＝DC ＋CE ＝12AC ＋12 BC ＝12 (AC ＋BC)＝12 AB ＝12 ×16＝8(cm ) (2)∵OD，OE 分别平分∠AOC 和∠BOC，∴∠DOC ＝12 ∠AOC，∠EOC ＝12 ∠BOC，∴∠DOE ＝∠DOC＋∠EOC＝12 (∠AOC＋∠BOC)＝12 ∠AOB＝65°，∴∠DOE 为一定值，与射线OC 的位置无关23．(11分)如图①所示，将一副三角尺的直角顶点重合在点O 处． (1)①∠AOD 和∠BOC 相等吗？说明理由；②∠AOC 和∠BOD 在数量上有何关系？说明理由；(2)若将这副三角尺按图②所示摆放，三角尺的直角顶点重合在点O 处． ①∠AOD 和∠BOC 相等吗？说明理由；②∠AOC 和∠BOD 在(1)中的数量关系还成立吗？说明理由．解：(1)①相等．理由：因为∠AOD＝90°＋∠BOD，∠BOC＝90°＋∠BOD，所以∠AOD 和∠BOC相等②∠AOC＋∠BOD＝180°.理由：因为∠AOC＋90°＋∠BOD＋90°＝360°，所以∠AOC＋∠BOD＝180°(2)①相等．理由：因为∠AOD＝90°－∠BOD，∠BOC＝90°－∠BOD，所以∠AOD和∠BOC相等②成立．理由：因为∠AOC＝90°＋90°－∠BOD，所以∠AOC ＋∠BOD＝180°。

第4章• 素养综合检测卷(考查范围:第4章　时间:60分钟　满分:100分)一、选择题(每小题4分,共32分)1. (2023浙江宁波外国语学校期中)根据下列表述,能确定位置的是( )A. 北偏东30°B. 民光影院2排C. 中山西路D. 东经120°,北纬35°2. (2022浙江湖州长兴期末)在平面直角坐标系中,若点A(a,b)在第二象限,则点B(ab,-b)所在的象限是( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. (2023浙江杭州观成教育集团期中)点P(m+3,m+1)在y轴上,则P点的坐标为( )A. (0,-2)B. (0,-4)C. (4,0)D. (2,0)4. (2023浙江宁波鄞州蓝青学校期中)在平面直角坐标系中,若点M(a+2,a-1)在第四象限,且点M到x轴的距离为2,则点M的坐标为( )A. (1,-2)B. (5,2)C. (2,-1)D. (-2,-3)5. (2022浙江杭州采荷中学期中)下列命题是真命题的是( )A. 若ab=0,则P(a,b)为坐标原点B. 若A(-1,-2),且AB平行于x轴,AB=5,则B点的坐标为(4,-2)C. 点P(1,2)关于原点对称的点的坐标是(-1,-2)D. 若关于x的一元一次不等式组x -a>0,1―2x>x-2无解,则a的取值范围是a>16. (2022青海中考改编)如图,A(2,0),AB=3,以点A为圆心,AB长为半径画弧交x轴负半轴于点C,则点C的坐标为( )A. (3,0)B. (1,0)C. (-1,0)D. (-3,0)7. (2023浙江宁波慈溪文锦书院期中)如图,每个小正方形的边长均为1,在所给网格中按下列要求操作:(1)在网格中建立平面直角坐标系,使A点的坐标为(4,2),B点的坐标为(1,-1);(2)在第一象限内找一格点C,使点C与线段AB构成一个以AB为底的等腰三角形,且腰长是无理数.此时C点的坐标是( )A. (2,1)B. (1,2)C. (2,2)D. (1,3)8. (2021河南郑州期末)在平面直角坐标系中,对△ABC进行如图所示的循环往复的轴对称变换,若原来点A的坐标是(1,2),则经过2 021次变换后点A的对应点的坐标为( )A.(1,-2)B.(-1,-2)C.(-1,2)D.(1,2)二、填空题(每小题4分,共24分)9. (2022山东烟台中考)观察如图所示的象棋棋盘,若“兵”所在的位置用(1,3)表示,“炮”所在的位置用(6,4)表示,那么“帅”所在的位置可表示为 .10. (2023浙江绍兴蕺山外国语学校期末)在平面直角坐标系中,点M(a,b)与点N(3,-1)关于x轴对称,则a+b的值为 .11. (2023浙江杭州临安石门中心学校期末模拟)在平面直角坐标系中,将点A(a,1)先向右平移3个单位,再向下平移2个单位,得到点B(5,b),则ab的值为 .12. 已知点A(2,0),B(-2,0),点P(0,t)是y轴上一动点,当△ABP为直角三角形时,点P的坐标为 .13. (2023浙江宁波江北实验中学期中)如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-2,-1),则点B的坐标为 .14. 【代数推理】如图,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3,已知A(1,3),A1(3,3),A2(5,3),A3(7,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换前后的三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成△OA4B4,则A4的坐标是 ,B4的坐标是 ;(2)若按(1)找到的规律将△OAB进行n次变换,得到△OA n B n,比较每次变换时三角形顶点有何变化,找出规律,推测A n的坐标是 ,B n的坐标是 .三、解答题44分)15. (2023浙江宁波余姚实验学校期中)(8分)已知点P(2m+4,m-1),试分别根据下列条件,求出点P的坐标.(1)点P在过点A(-2,-3),且与y轴平行的直线上;(2)点P在第四象限内,且到x轴的距离是到y轴距离的一半.16. (10分)在平面直角坐标系中,△ABC的位置如图所示.(1)点A关于x轴对称的点的坐标为 ,点B关于原点对称的点的坐标为 ;(2)将△ABC向右平移4个单位长度,再向上平移3个单位长度得到△A1B1C1,其中A、B、C分别和A1、B1、C1对应,画出△A1B1C1,并求点A1的坐标;(3)在x轴上找一点P,使得点P到B、C两点的距离相等,则点P的坐标为 ;(4)在y轴上找一点Q,使得△BCQ与△ABC的面积相等,求点Q的坐标.17. (2023浙江宁波镇海尚志中学期中)(12分)如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(1,1),三角板绕点P在坐标平面内旋转,一条直角边与x轴的正半轴交于点A,另一条直角边与y轴交于点B.(1)连结AB,请判断△PAB是什么三角形,并说明理由;(2)在三角板绕点P旋转的过程中,OA+OB是定值吗?若是,请求出定值;若不是,请说明理由;(3)当△POA为等腰三角形时,请直接写出所有满足条件的点B的坐标.18. (2023浙江兰溪外国语中学期中)(14分)在平面直角坐标系xOy中,对于给定的两点P,Q,若存在点M,使得△MPQ的面积等于k(S△MPQ=k),则称点M为线段PQ的“k值面积点”,例如:对于给定的两点P,Q,若存在点M,使得△MPQ的面积等于2(S△MPQ=2),则称点M为线段PQ的“2值面积点”.解答下列问题:如图,在平面直角坐标系xOy中,点P的坐标为(2,0).(1)在点A(-1,1),B(-1,2),C(2,-4) 中,线段OP的“1值面积点”是 ;(2)已知点D(0,t),E(0,t+3),当线段DE上存在线段OP的“5值面积点”时,求t的取值范围;(3)已知点G(2,a),H(2,b),且a,b满足2a+3b+m=0,3a+2b+m=―5,点M,N是线段GH的两个“4值面积点”,点M的纵坐标是5,若S△OMN=3S△GHN,且MN∥GH,直接写出点N的坐标.答案全解全析1. D　选项A中缺少距离,不能确定位置,故不符合题意;选项B中缺少列数,不能确定位置,故不符合题意;选项C不能确定位置,不符合题意;选项D中经、纬度可以确定位置,符合题意.故选D.2. C　∵点A(a,b)在第二象限,∴a<0,b>0,∴ab<0,-b<0,∴点B(ab,-b)在第三象限.故选C.3. A　∵点P(m+3,m+1)在y轴上,∴m+3=0,∴m=-3,∴m+1=-2,∴P点的坐标为(0,-2).故选A.4. A　∵点M(a+2,a-1)在第四象限,且点M到x轴的距离为2,∴a-1=-2,∴a=-1,∴a+2=1,∴点M的坐标为(1,-2).故选A.5. C　若ab=0,则a=0或b=0,∴点P(a,b)在x轴或y轴上,故A错误;若A(-1,-2),且AB平行于x轴,AB=5,则B点的坐标为(4,-2)或(-6,-2),故B 错误;点P(1,2)关于原点对称的点的坐标是(-1,-2),故C正确;化简不等式组可得x>a,x<1,∵不等式组无解,∴a≥1,故D错误.故选C.6. C　∵A(2,0),AC=AB=3,∴OC=AC-OA=3-2=1,∵点C在x轴的负半轴上,∴点C的坐标为(-1,0).故选C.7. A　建立如图所示的平面直角坐标系,点C的坐标为(2,1)时,△ABC 为等腰三角形,且腰长为无理数.故选A.8. C　△ABC第1次作轴对称变换后,点A的对应点在第二象限,坐标为(-1,2);△ABC第2次作轴对称变换后,点A的对应点在第三象限,坐标为(-1,-2);△ABC第3次作轴对称变换后,点A的对应点在第四象限,坐标为(1,-2);△ABC第4次作轴对称变换后,点A的对应点在第一象限,即回到原始位置,坐标为(1,2);……所以每4次轴对称变换为一个循环组,∵2 021÷4=505……1,∴经过2 021次轴对称变换后点A的对应点与第1次作轴对称变换后点A的对应点的位置相同,在第二象限,坐标为(-1,2).故选C.9. 答案　(4,1)解析　如图所示,“帅”所在的位置可表示为(4,1).10. 答案　4解析　∵点M(a,b)与点N(3,-1)关于x轴对称,∴a=3,b=1,∴a+b=4.11. 答案　-2解析　∵点A(a,1)先向右平移3个单位,再向下平移2个单位,得到的点的坐标为(a+3,-1),平移后得到点B(5,b),∴a+3=5,b=-1,∴a=2,b=-1,∴ab=2×(-1)=-2.12. 答案　(0,2)或(0,-2)解析　易知点A(2,0)与点B(-2,0)关于y轴对称,OA=OB=2,∴PA=PB,∴当△ABP为直角三角形时,∠APB为直角,∵O为AB的中点,∴OP=OA=OB=2,∴点P的坐标为(0,2)或(0,-2).13. 答案　(-3,1)解析　过点C作CE⊥x轴于E,过点B作BF⊥CE交CE的延长线于F,∵C(-2,-1),∴OE=2,CE=1,∵四边形OABC是正方形,∴OC=BC,易得∠COE=∠BCF,∵∠OEC=∠F=90°,∴△COE≌△BCF,∴BF=CE=1,CF=OE=2,∴EF=2-1=1,点B到y轴的距离为1+2=3,∴点B的坐标为(-3,1).14. 答案　(1)(9,3);(32,0)　(2)(1+2n,3);(2n+1,0)解析(1)∵A(1,3),A1(3,3),A2(5,3),A3(7,3),B(2,0),B1(4,0),B2(8,0),B3(16,0),∴A4(9,3),B4(32,0).(2)由A(1,3),A1(3,3),A2(5,3),A3(7,3)可得,横坐标依次加2,纵坐标不变,为3,∴A n(1+2n,3);由B(2,0),B1(4,0),B2(8,0),B3(16,0)可得,横坐标依次乘2,纵坐标不变,为0,∴B n(2n+1,0).15. 解析　(1)∵点P在过点A(-2,-3),且与y轴平行的直线上,∴2m+4=-2,解得m=-3,∴m-1=-4,∴P(-2,-4).(2)∵点P(2m+4,m-1)在第四象限内,∴点P 到x 轴的距离是-(m-1),到y 轴的距离是2m+4,∴-(m-1)=12(2m+4),解得m=-12,∴2m+4=3,m-1=-32,∴P 3,―16. 解析　(1)(-2,-1);(3,2).(2)如图,△A 1B 1C 1即为所求.点A 1的坐标为(2,4).(3)如图,点P 即为所求,点P 的坐标为(-1,0).(4)如图,点Q,点Q'即为所求,点Q 的坐标为(0,1)或(0,-5).17. 解析　(1)△PAB 是等腰直角三角形.理由:过点P 分别作x 轴,y 轴的垂线交于点F 、E,易知∠EPF=90°,∵∠BPA=90°,∴∠BPE+∠EPA=∠EPA+∠APF,∴∠BPE=∠APF,∵P(1,1),∴PF=PE,又∵∠BEP=∠AFP,∴△PBE ≌△PAF(ASA),∴PA=PB,∴△PAB 为等腰直角三角形.(2)OA+OB 是定值.由(1)得,△PBE ≌△PAF,∴BE=AF,∴OA+OB=OA+(OE+BE)=(OA+AF)+OE=OF+OE=2.(3)(0,1)、(0,0)、(0,2-2).18. 解析　(1)点A.如图,∵A(-1,1),B(-1,2),C(2,-4),P(2,0),∴S △AOP =12×2×1=1,S △OPB =12×2×2=2,S △OPC =12×2×4=4,∴点A 是线段OP 的“1值面积点”.(2)当三角形在x 轴上方时,t ≤5,t +3≥5,∴2≤t≤5;当三角形在x 轴下方时,t +3≥―5,t ≤―5,∴-8≤t≤-5.综上所述,t 的取值范围为2≤t≤5或-8≤t≤-5.(3)点N ,-55,65,,-详解:2a +3b +m =0①,3a +2b +m =―5②,①-②得b-a=5,∴GH=5,设d 表示点M 到GH 的距离,则点N 到GH 的距离也为d,∵M,N 是线段GH 的两个“4值面积点”,∴S △MGH =S △NGH =12×5d=4,∴d=85.①当MN 在直线GH 的左边时,∵MN ∥GH,d=85,G(2,a),H(2,b),∴点M,N 的横坐标为25,设,x ,∵点M 的纵坐标是5,S △OMN =3S △GHN =12,∴S OMN =12×25×|5-x|=12,解得x=-55或x=65,∴,-55,65;②当MN 在直线GH 的右边时,∵MN ∥GH,d=85,G(2,a),H(2,b),∴点M,N 的横坐标为185,设,y ,∵点M 的纵坐标是5,S △OMN =3S △GHN =12,∴S △OMN =12×185×|5-y|=12,解得y=353或y=-53,∴,,-综上所述,点N ,-55,65,,-。

人教版六年级上册《第4章圆》单元测试卷一、填一填．（第5题4分，每空1分，共20分．）1. 写出下面各题的最简整数比。

①圆的半径和直径的比是________，圆的周长和直径的比是________．②小圆的半径是4厘米，大圆的半径是6厘米。

小圆直径和大圆直径的比是________，小圆周长和大圆周长的比是________，小圆面积和大圆面积的比是________．2. 把一个圆分成如干等份，然后把它剪开，可以拼成一个近似的长方形，这个长方形的长相当于圆的________，宽相当于圆的________．3. 圆的周长是37.68分米，它的面积是________平方分米。

4. 一个圆的半径扩大3倍，周长就扩大________倍，面积就扩大________倍。

5. 一个圆的周长、直径、半径相加的和是9.28厘米，这个圆的直径是________厘米，面积是________平方厘米。

6. 在一个边长为12厘米的正方形纸板里剪出一个最大的圆，剩下的面积是________．7. 要在底面半径是10厘米的圆柱形水桶外面打上一个铁丝箍，接头部分是6厘米，需用铁丝________厘米。

8. 用圆规画一个圆，如果圆规两脚之间的距离是6厘米，画出的这个圆的周长是________厘米。

这个圆的面积是________平方厘米。

9. 用一根长12.56厘米的铁丝围成一个正方形，正方形的面积是________平方厘米；如果用这根铁丝围成一个圆，这个圆的面积是________平方厘米。

二、想一想、画一画．正确的画“√”，错的打“×”（每题2分，共10分）在一个圆里，两端都在圆上的线段叫做圆的直径。

________．（判断对错）半圆的周长是这个圆的周长的一半。

________．（判断对错）求圆的周长，用字母表示就是C=πd或C=2πr．________．圆的大小是由半径，直径或周长决定的。

________．（判断对错）一个圆的半径2厘米，它的周长和面积相等。

第四章数列章末检测（原卷版）(时间：120分钟，满分150分)一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2021年郑州模拟)已知数列1，3，5，7，…，2n－1，若35是这个数列的第n项，则n＝()A．20B．21C．22D．232．已知3，a＋2，b＋4成等比数列，1，a＋1，b＋1成等差数列，则等差数列的公差为()A．4或－2B．－4或2C．4D．－43．用数学归纳法证明1＋12＋14＋…＋12n－1>12764(n∈N*)成立，某初始值至少应取()A．7B．8C．9D．104．公差不为0的等差数列{a n}，其前23项和等于其前10项和，a8＋a k＝0，则正整数k ＝()A．24B．25C．26D．275．(2021年长春模拟)已知等比数列{a n}的各项均为正数，其前n项和为S n，若a2＝2，S6－S4＝6a4，则a5＝()A．10B．16C．24D．326．设等差数列{a n}的前n项和为S n，若2a8＝6＋a11，则S9＝()A．54B．45C．36D．277．已知各项都为正数的等比数列{a n}中，a2a4＝4，a1＋a2＋a3＝14，则满足a n·a n＋1·a n＋2＞19的最大正整数n的值为()A．3B．4C ．5D ．68．已知各项均为正数的数列{a n }的前n 项和为S n ，且S n 满足n (n ＋1)S 2n ＋(n 2＋n －1)S n －1＝0(n ∈N *)，则S 1＋S 2＋…＋S 2021＝()A ．12021B ．12022C ．20202021D ．20212022二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知n ∈N *，则下列表达式能作为数列0，1，0，1，0，1，0，1，…的通项公式的是()A ．a n ，n 为奇数，，n 为偶数B ．a n ＝1＋(－1)n2C ．a n ＝1＋cos n π2D ．a n ＝|sinn π2|10．(2022年宿迁期末)设等差数列{a n }前n 项和为S n ，公差d >0，若S 9＝S 20，则下列结论中正确的有()A ．S 30＝0B ．当n ＝15时，S n 取得最小值C ．a 10＋a 22>0D ．当S n >0时，n 的最小值为2911．已知等比数列{a n }的公比为q ，满足a 1＝1，q ＝2，则()A ．数列{a 2n }是等比数列B C ．数列{log 2a n }是等差数列D ．数列{a n }中，S 10，S 20，S 30仍成等比数列12．设等比数列{a n }的公比为q ，其前n 项和为S n ，前n 项积为T n ，并满足条件a 1>1，a 2019a 2020>1，a 2019－1a 2020－1<0，下列结论正确的是()A ．S 2019<S 2020B．a2019a2021－1<0C．T2020是数列{T n}中的最大值D．数列{T n}无最大值三、填空题：本题共4小题，每小题5分，共20分．13．若数列{a n}满足a1＝1，a n＋1＝2a n(n∈N*)，S n为{a n}的前n项和，则S8＝________．14．(2022年北京一模)中国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之余二，五五数之余三，问物几何？”，将上述问题的所有正整数答案从小到大组成一个数列{a n}，则a1＝________，a n＝________(注：三三数之余二是指此数被3除余2，例如“5”，五五数之余三是指此数被5除余3，例如“8”)．15．(2021年淮北期末)已知数列{a n}的通项公式为a n＝[lg n]([x]表示不超过x的最大整数)，T n为数列{a n}的前n项和，若存在k∈N*满足T k＝k，则k的值为__________．16．(2022年武汉模拟)对任一实数序列A＝(a1，a2，a3，…)，定义新序列△A＝(a2－a1，a3－a2，a4－a3，…)，它的第n项为a n＋1－a n.假定序列△(△A)的所有项都是1，且a12＝a22＝0，则a2＝________．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．(10分)(2022年北京二模)已知数列{a n}的前n项和为S n，a1＝1，________．是否存在正整数k(k＞1)，使得a1，a k，S k＋2成等比数列？若存在，求出k的值；若不存在，说明理由．－2a n＝0；②S n＝S n－1＋n(n≥2)；③S n＝n2这三个条件中任选一个，补充在上面从①a n＋1问题中并作答．18．(12分)(2022年平顶山期末)在等差数列{a n}中，设前n项和为S n，已知a1＝2，S4＝26.(1)求{a n}的通项公式；}的前n项和T n.(2)令b n＝1a n a n＋1，求数列{b n19．(12分)设a>0，函数f(x)＝ax＝1，a n＋1＝f(a n)，n∈N*.a＋x，令a1(1)写出a2，a3，a4的值，并猜想数列{a n}的通项公式；(2)用数学归纳法证明你的结论．20．(12分)(2022年潍坊模拟)若数列{a n}的前n项和S n满足S n＝2a n－λ(λ>0，n∈N*)．(1)求证：数列{a n}为等比数列，并求a n；(2)若λ＝4，b n n ，n 为奇数，2a n ，n 为偶数(n ∈N *)，求数列{b n }的前2n 项和T 2n .21．(12分)已知等比数列{a n }满足a n ＋1＋a n ＝9·2n －1，n ∈N *.(1)求数列{a n }的通项公式；(2)设b n ＝na n ，求数列{b n }的前n 项和S n .22．(12分)数列{a n }是公比为12的等比数列且1－a 2是a 1与1＋a 3的等比中项，前n 项和为S n ；数列{b n }是等差数列，b 1＝8，其前n 项和T n 满足T n ＝nλ·b n ＋1(λ为常数且λ≠1)．(1)求数列{a n }的通项公式及λ的值；(2)比较1T 1＋1T 2＋1T 3＋…＋1T n 与12S n 的大小．第四章数列章末检测（解析版）(时间：120分钟，满分150分)一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2021年郑州模拟)已知数列1，3，5，7，…，2n －1，若35是这个数列的第n 项，则n ＝()A ．20B ．21C ．22D ．23【答案】D【解析】由2n －1＝35＝45，得2n －1＝45，即2n ＝46，解得n ＝23.2．已知3，a ＋2，b ＋4成等比数列，1，a ＋1，b ＋1成等差数列，则等差数列的公差为()A ．4或－2B ．－4或2C ．4D ．－4【答案】C【解析】∵3，a ＋2，b ＋4成等比数列，1，a ＋1，b ＋1成等差数列，∴(a＋2)2＝3(b ＋4)，2(a ＋1)＝1＋b ＋1＝－2，4＝4，＝8.＝－2，＝－4时，a ＋2＝0与3，a ＋2，b ＋4＝4，＝8时，等差数列的公差为(a ＋1)－1＝a＝4.3．用数学归纳法证明1＋12＋14＋…＋12n －1>12764(n ∈N *)成立，某初始值至少应取()A ．7B ．8C ．9D ．10【答案】B 【解析】1＋12＋14＋…＋12n －1＝1－12n1－12>12764，整理得2n >128，解得n >7，所以初始值至少应取8.4．公差不为0的等差数列{a n }，其前23项和等于其前10项和，a 8＋a k ＝0，则正整数k ＝()A ．24B ．25C ．26D ．27【答案】C【解析】由题意设等差数列{a n }的公差为d ，d ≠0，∵其前23项和等于其前10项和，∴23a 1＋23×222d ＝10a 1＋10×92d ，变形可得13(a 1＋16d )＝0，∴a 17＝a 1＋16d ＝0.由等差数列的性质可得a 8＋a 26＝2a 17＝0，∴k ＝26.5．(2021年长春模拟)已知等比数列{a n }的各项均为正数，其前n 项和为S n ，若a 2＝2，S 6－S 4＝6a 4，则a 5＝()A ．10B ．16C ．24D ．32【答案】B【解析】设公比为q (q >0)，S 6－S 4＝a 5＋a 6＝6a 4.因为a 2＝2，所以2q 3＋2q 4＝12q 2，即q 2＋q －6＝0，解得q ＝2，则a 5＝2×23＝16.6．设等差数列{a n }的前n 项和为S n ，若2a 8＝6＋a 11，则S 9＝()A ．54B ．45C ．36D ．27【答案】A【解析】∵2a 8＝a 5＋a 11，2a 8＝6＋a 11，∴a 5＝6，∴S 9＝9a 5＝54.7．已知各项都为正数的等比数列{a n }中，a 2a 4＝4，a 1＋a 2＋a 3＝14，则满足a n ·a n ＋1·a n ＋2＞19的最大正整数n 的值为()A ．3B ．4C ．5D ．6【答案】B【解析】∵a 2a 4＝4，a n ＞0，∴a 3＝2，∴a 1＋a 2＝12，1＋a 1q ＝12，1q 2＝2，消去a 1，得1＋q q2＝6.∵q ＞0，∴q ＝12，∴a 1＝8，∴a n ＝8－1＝24－n ，∴不等式a n a n ＋1a n ＋2＞19化为29－3n ＞19，当n ＝4时，29－3×4＝18＞19，当n ＝5时，29－3×5＝164＜19，∴最大正整数n ＝4.8．已知各项均为正数的数列{a n }的前n 项和为S n ，且S n 满足n (n ＋1)S 2n ＋(n 2＋n －1)S n －1＝0(n ∈N *)，则S 1＋S 2＋…＋S 2021＝()A ．12021B ．12022C ．20202021D ．20212022【答案】D【解析】∵n (n ＋1)S 2n ＋(n 2＋n －1)S n －1＝0(n ∈N *)，∴(S n ＋1)[n (n ＋1)S n －1]＝0.又∵S n >0，∴n (n ＋1)S n －1＝0，∴S n ＝1n (n ＋1)＝1n －1n ＋1，∴S 1＋S 2＋…＋S 2021…20212022.二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．已知n ∈N *，则下列表达式能作为数列0，1，0，1，0，1，0，1，…的通项公式的是()A ．a n ，n 为奇数，，n 为偶数B ．a n ＝1＋(－1)n2C ．a n ＝1＋cos n π2D ．a n ＝|sinn π2|【答案】ABC 【解析】检验知A ，B ，C 都是所给数列的通项公式．10．(2022年宿迁期末)设等差数列{a n }前n 项和为S n ，公差d >0，若S 9＝S 20，则下列结论中正确的有()A ．S 30＝0B ．当n ＝15时，S n 取得最小值C ．a 10＋a 22>0D ．当S n >0时，n 的最小值为29【答案】BC 【解析】由S 9＝S 20⇒9a 1＋12×9×8d ＝20a 1＋12×20×19d ⇒a 1＋14d ＝0⇒a 15＝0.因为d >0，所以有S 30＝30a 1＋12×30×29d ＝30·(－14d )＋435d ＝15d ＞0，故A 不正确；因为d >0，所以该等差数列是单调递增数列，因为a 15＝0，所以当n ＝15或n ＝14时，S n 取得最小值，故B 正确；因为d >0，所以该等差数列是单调递增数列，因为a 15＝0，所以a 10＋a 22＝2a 16＝2(a 15＋d )＝2d >0，故C 正确；因为d >0，n ∈N *，所以由S n ＝na 1＋12n (n －1)d ＝n (－14d )＋12n (n －1)d ＝12dn (n －29)>0，可得n >29，n ∈N *，因此n 的最小值为30，故D 不正确．故选BC ．11．已知等比数列{a n }的公比为q ，满足a 1＝1，q ＝2，则()A ．数列{a 2n }是等比数列BC ．数列{log 2a n }是等差数列D ．数列{a n }中，S 10，S 20，S 30仍成等比数列【答案】AC【解析】等比数列{a n }中，由a 1＝1，q ＝2，得a n ＝2n －1，∴a 2n ＝22n －1，∴数列{a 2n }是等比数列，故A B 不正确；∵log 2a n ＝n －1，故数列{log 2a n }是等差数列，故C 正确；数列{a n }中，S 10＝1－2101－2＝210－1，同理可得S 20＝220－1，S 30＝230－1，不成等比数列，故D 错误．12．设等比数列{a n }的公比为q ，其前n 项和为S n ，前n 项积为T n ，并满足条件a 1>1，a 2019a 2020>1，a 2019－1a 2020－1<0，下列结论正确的是()A ．S 2019<S 2020B ．a 2019a 2021－1<0C ．T 2020是数列{T n }中的最大值D ．数列{T n }无最大值【答案】AB 【解析】若a 2019a 2020>1，则a 1q 2018×a 1q 2019＝a 21q 4037>1.又由a 1>1，必有q >0，则数列{a n }各项均为正值．又由a 2019－1a 2020－1<0，即(a 2019－1)(a 2020－1)<0，则有2019<1，2020>1或2019>1，2020<1，又由a 1>1，必有0<q <1，2019>1，2020<1.有S 2020－S 2019＝a 2020>0，即S 2019<S 2020，则A正确；有a 2020<1，则a 2019a 2021＝a 22020<1，则B 2019>1，2020<1，则T 2019是数列{T n }中的最大值，C ，D 错误．三、填空题：本题共4小题，每小题5分，共20分．13．若数列{a n }满足a 1＝1，a n ＋1＝2a n (n ∈N *)，S n 为{a n }的前n 项和，则S 8＝________．【答案】255【解析】由a 1＝1，a n ＋1＝2a n 知{a n }是以1为首项、2为公比的等比数列，所以S 8＝a 1(1－q 8)1－q ＝1·(1－28)1－2＝255.14．(2022年北京一模)中国古代数学著作《孙子算经》中有这样一道算术题：“今有物不知其数，三三数之余二，五五数之余三，问物几何？”，将上述问题的所有正整数答案从小到大组成一个数列{a n }，则a 1＝________，a n ＝________(注：三三数之余二是指此数被3除余2，例如“5”，五五数之余三是指此数被5除余3，例如“8”)．【答案】815n －7【解析】被3除余2的正整数可表示为3x ＋2，被5除余3的正整数可表示为5y ＋3，其中x ，y ∈N *，∴数列{a n }为等差数列，公差为15，首项为8，∴a 1＝8，a n ＝8＋15(n －1)＝15n －7.15．(2021年淮北期末)已知数列{a n }的通项公式为a n ＝[lg n ]([x ]表示不超过x 的最大整数)，T n 为数列{a n }的前n 项和，若存在k ∈N *满足T k ＝k ，则k 的值为__________．【答案】108【解析】a n，1≤n ＜10，，10≤n ＜100，，10k ≤n ＜10k ＋1.当1≤k ＜10时，T k ＝0，显然不存在；当10≤k ＜100时，T k ＝k －9＝k ，显然不存在；当100≤k ＜1000时，T k ＝99－9＋(k －99)×2＝k ，解得k ＝108.16．(2022年武汉模拟)对任一实数序列A ＝(a 1，a 2，a 3，…)，定义新序列△A ＝(a 2－a 1，a 3－a 2，a 4－a 3，…)，它的第n 项为a n ＋1－a n .假定序列△(△A )的所有项都是1，且a 12＝a 22＝0，则a 2＝________．【答案】100【解析】令b n ＝a n ＋1－a n ，依题意知数列{b n }为等差数列，且公差为1，所以b n ＝b 1＋(n －1)×1，a 1＝a 1，a 2－a 1＝b 1，a 3－a 2＝b 2，…，a n －a n －1＝b n －1，累加得a n ＝a 1＋b 1＋…＋b n －1＝a 1＋(n －1)b 1＋(n －1)(n －2)2.分别令n ＝12，n ＝22，得a 2－10a 1＋55＝0①，a 2－20a 1＋210＝0②，①×2－②，得a 2＝100.四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．(10分)(2022年北京二模)已知数列{a n }的前n 项和为S n ，a 1＝1，________．是否存在正整数k (k ＞1)，使得a 1，a k ，S k ＋2成等比数列？若存在，求出k 的值；若不存在，说明理由．从①a n ＋1－2a n ＝0；②S n ＝S n －1＋n (n ≥2)；③S n ＝n 2这三个条件中任选一个，补充在上面问题中并作答．解：若选①a n ＋1－2a n ＝0，则a 2－2a 1＝0，说明数列{a n }是首项为1，公比为2的等比数列，∴a 1＝1，a k ＝2k －1，S k ＋2＝1－2k ＋21－2＝2k ＋2－1.若a 1，a k ，S k ＋2成等比数列，则(2k －1)2＝1×(2k ＋2－1)＝2k ＋2－1.左边为偶数，右边为奇数，即不存在正整数k (k ＞1)，使得a 1，a k ，S k ＋2成等比数列．若选②S n ＝S n －1＋n (n ≥2)，即S n －S n －1＝n ⇒a n ＝n (n ≥2)且a 1＝1也适合此式，∴{a n }是首项为1，公差为1的等差数列，∴a k ＝k ，S k ＋2＝(k ＋2)(k ＋3)2.若a 1，a k ，S k ＋2成等比数列，则k 2＝1×(k ＋2)(k ＋3)2⇒k 2－5k －6＝0⇒k ＝6(k ＝－1舍去)，即存在正整数k ＝6，使得a 1，a k ，S k ＋2成等比数列．若选③S n ＝n 2，∴a n ＝S n －S n －1＝n 2－(n －1)2＝2n －1(n ≥2)，且a 1＝1适合上式．若a 1，a k ，S k ＋2成等比数列，则(2k －1)2＝1×(k ＋2)2⇒3k 2－8k －3＝0⇒k ＝＝－13舍去即存在正整数k ＝3，使得a 1，a k ，S k ＋2成等比数列．18．(12分)(2022年平顶山期末)在等差数列{a n }中，设前n 项和为S n ，已知a 1＝2，S 4＝26.(1)求{a n }的通项公式；(2)令b n ＝1a n a n ＋1，求数列{b n }的前n 项和T n .解：(1)设{a n }的公差为d ，由已知得4×2＋4×32d ＝26，解得d ＝3，所以a n ＝a 1＋(n －1)d ＝2＋3(n －1)＝3n －1.(2)b n ＝1a n a n ＋1＝1(3n －1)(3n ＋2)＝所以T n…＝16－13(3n ＋2)＝n 6n ＋4.19．(12分)设a >0，函数f (x )＝axa ＋x，令a 1＝1，a n ＋1＝f (a n )，n ∈N *.(1)写出a 2，a 3，a 4的值，并猜想数列{a n }的通项公式；(2)用数学归纳法证明你的结论．(1)解：∵a 1＝1，∴a 2＝f (a 1)＝f (1)＝a 1＋a，a 3＝f (a 2)＝a 2＋a ，a 4＝f (a 3)＝a3＋a ，猜想a n ＝a(n －1)＋a.(2)证明：①易知n ＝1时，猜想正确；②假设n ＝k 时，a k ＝a (k －1)＋a成立，则a k ＋1＝f (a k )＝a ·a k a ＋a k ＝a ·a (k －1)＋a a ＋a (k －1)＋a＝a (k －1)＋a ＋1＝a [(k ＋1)－1]＋a ，∴n ＝k ＋1时成立．由①②知，对任何n ∈N *，都有a n ＝a (n －1)＋a.20．(12分)(2022年潍坊模拟)若数列{a n }的前n 项和S n 满足S n ＝2a n －λ(λ>0，n ∈N *)．(1)求证：数列{a n }为等比数列，并求a n ；(2)若λ＝4，b nn ，n 为奇数，2a n ，n 为偶数(n ∈N *)，求数列{b n }的前2n 项和T 2n .(1)证明：∵S n ＝2a n －λ，当n ＝1时，得a 1＝λ.当n ≥2时，S n －1＝2a n －1－λ，∴S n －S n －1＝2a n －2a n －1，即a n ＝2a n －2a n －1，∴a n ＝2a n －1，∴数列{a n }是以λ为首项，2为公比的等比数列，∴a n ＝λ·2n －1.(2)解：∵λ＝4，∴a n ＝4·2n －1＝2n ＋1，∴b nn ＋1，n 为奇数，＋1，n 为偶数，∴T 2n ＝22＋3＋24＋5＋26＋7＋…＋22n ＋2n ＋1＝(22＋24＋…＋22n )＋(3＋5＋…＋2n ＋1)＝4－4n ·41－4＋n (3＋2n ＋1)2＝4n ＋1－43＋n (n ＋2)，∴T 2n ＝4n ＋13＋n 2＋2n －43.21．(12分)已知等比数列{a n }满足a n ＋1＋a n ＝9·2n －1，n ∈N *.(1)求数列{a n }的通项公式；(2)设b n ＝na n ，求数列{b n }的前n 项和S n .解：(1)设等比数列{a n }的公比为q .∵a n ＋1＋a n ＝9·2n －1，∴a 2＋a 1＝9，a 3＋a 2＝18，∴q ＝a 3＋a 2a 2＋a 1＝189＝2.又∵2a 1＋a 1＝9，∴a 1＝3，∴a n ＝3·2n －1，n ∈N *.(2)∵b n ＝na n ＝3n ·2n －1，∴13S n ＝1×20＋2×21＋…＋(n －1)×2n －2＋n ×2n －1①，∴23S n ＝1×21＋2×22＋…＋(n －1)×2n －1＋n ×2n ②，①－②，得－13S n ＝1＋21＋22＋…＋2n －1－n ×2n ＝1－2n 1－2－n ×2n ＝(1－n )2n －1，∴S n ＝3(n －1)2n ＋3.22．(12分)数列{a n }是公比为12的等比数列且1－a 2是a 1与1＋a 3的等比中项，前n 项和为S n ；数列{b n }是等差数列，b 1＝8，其前n 项和T n 满足T n ＝nλ·b n ＋1(λ为常数且λ≠1)．(1)求数列{a n }的通项公式及λ的值；(2)比较1T 1＋1T 2＋1T 3＋…＋1T n 与12S n 的大小．解：(1)由题意，得(1－a 2)2＝a 1(1＋a 3)，∴(1－a 1q )2＝a 1(1＋a 1q 2)．∵q ＝12，∴a 1＝12，∴a n.1＝λb 2，2＝2λb 3，＝λ(8＋d )，＋d ＝2λ(8＋2d )，∴λ＝12，d ＝8.(2)由(1)得b n ＝8n ，∴T n ＝4n (n ＋1)，∴1T n ＝令C n ＝1T 1＋1T 2＋…＋1T n ＝…∴18≤C n ＜14.∵S n ＝21－12＝1，∴12S n ＝121∴14≤12S n ＜12，∴C n ＜12S n 即1T 1＋1T 2＋1T 3＋…＋1T n ＜12S n .。

新人教版四年级上册《第4章平行四边形和梯形》单元测试卷一、填空题（33分）1. 如图中四边形有________，平行四边形有________，梯形有________．2. 线段有________个端点，射线有________个端点，直线________端点。

3. 同一平面内两条直线之间的位置关系有________和________，如果这两条直线相交成直角，就说这两条直线________，这个交点叫做________．4. 两条平行线间可以画________条垂直的线段，这些线段的长度都________．5. 从直线外一点到这条直线所画的________线段最短，它的长度叫做点到直线的________．6. 平行四边形有________组对边平行，梯形有________组对边平行。

7. 平行四边形对边________且________；________和________都是特殊的平行四边形。

8. 平行四边形具有________性，把平行四边形框架拉成长方形，它的周长________．9. 以平行四边形的一条边为底，能作出________条高，这些高的长度都________．10. 下列每组直线是互相平行的画√，互相垂直的画○11. 在如图中填编号。

①四边形②正方形③长方形④平行四边形⑤梯形。

二、判断，正确的画√，错误的画×（10分）两条互相垂直的直线一定相交，相交的两条直线也一定垂直。

________．（判断对错）同一平面内，两条直线都和同一条直线垂直，那么这两条直线也互相垂直。

________．（判断对错）三角形具有稳定性的特点，而平行四边形却有容易变形的特点。

________．（判断对错）3时整，时针和分针互相垂直。

________．（判断对错）三、选择（8分）长方形的对边互相________，相邻一组边互相________．A．重合B．平行C．垂直。

下列图形中，一定是轴对称图形的是（）A.平行四边形B.三角形C.梯形D.等腰梯形下面四句话中，错误的是（）A.平行四边形的四条边一定相等B.任意一个四边形的内角和都是360度C.一个梯形上底与下底间的距离处处相等D.两条直线相交可以成4个直角四、解答题（共4小题，满分25分）过点A画出已知直线的垂线和平行线。

2023-2024浙教版七年级上第4章《代数式》单元检测卷班级__________姓名__________学号__________成绩__________一、选择题（本大题共10小题，每小题3分，共30分，每小题只有一个正确答案） 1.下列式子写法规范的是( )A ．ax ÷4B ．a 2C ．－3xyD ．112a2.单项式y x 22-的系数和次数分别是（ ） A ．-2，2B ．-2，3C ．2，3D ．2，23.下列式子中，与3x 4y 3是同类项的是( )A ．－3y 3x 4B ．－x 3y 4C ．2x 2y 3D ．4x 4y 4.某校原来有学生x 人，在新学期开学时，转入学生n 人，转出学生(n －3)人，则该校 现有学生的人数是( )A ．x ＋3B ．x －3C ．x ＋2n －3D ．2n －3 5.下列去括号正确的是（ ）A ．a-(b ﹣c )＝a ﹣b ﹣c B. a-(b+c )＝a ﹣b ﹣c C. a+(b ﹣c )＝a ﹣b ﹣c D . a+(b ﹣c )＝a ﹣b+c6.用代数式表示：a 的2倍与3的和．下列表示正确的是（ ） A ．2a ﹣3B ．2a +3C ．2(a ﹣3)D ．2(a +3)7.下列运算中，正确的是（ ）． A ．325a b ab +=B ．325235a a a +=C ．22330a b ba -=D ．22541a a -=8.如图所示是一组有规律的图案，第1个图案由4个菱形组成，第2个图案由7个菱形组成，···，第n （n 是正整数）个图案中的菱形个数为（ ）A ． n 4B ．34-nC ．23+nD ．13+n 9.点O ，A ，B ，C 在数轴上的位置如图所示，其中O 为原点，BC ＝2，OA ＝OB ，若C 点所 表示的数为x ，则A 点所表示的数为（ ）A ．﹣2B ．﹣x ﹣2C ．x+2D ．﹣x+210.如图，A ，B 两地之间有一条东西走向的道路．在A 地的东边5 km 处设置第一个广告 牌，之后每往东12 km 就设置一个广告牌．一辆汽车从A 地的东边3 km 处出发，沿此道路向东行驶．当经过第n 个广告牌时，该辆汽车所行驶的路程为( )A ．(12n ＋5) kmB ．(12n ＋2) kmC ．(12n －10) kmD ．(12n －7) km二、填空题：（本大题共8小题，每小题4分，共32分.请把答案填在题中的横行上） 11.多项式3x ＋x 2＋2是________次________项式． 12.当2-=x 时，代数式25+-x 的值是13.已知苹果的价格为m 元/千克，购物袋的价格为0．3元/个，则购买2千克苹果和1个购物袋共需____________元．14.若x ＋2y ＝－1，则5－3x －6y ＝________．15.如图，阴影部分的面积用x 的代数式表示为____________．16.计算：()()y x y x +22－－= （第15题） 17.若3xy 2m 与x 2n ﹣3y 6是同类项，则2m+n 的值是18.某动物园利用杠杆原理称象：如图，在点P 处挂一根 质地均匀且足够长的钢梁（呈水平状态），将装有大象的铁 笼和弹簧秤（秤的重力忽略不计）分别悬挂在钢梁的点A ， B 处，当钢梁保持水平时，弹簧秤读数为k （N ）．若铁笼 固定不动，移动弹簧秤使BP 扩大到原来的n （n ＞1）倍，且钢梁保持水平，则弹簧秤读数为 （N ）（用含n ，k 的代数式表示）． （第18题） 三、解答题（本题共4小题，共38分．解答写出必要的文字说明、演算步骤） 19.(每小题5分，共10分)计算：(1)3x 2－2x 2＋x 2 (2)(4a 2b －5ab 2)－(3a 2b －4ab 2)20.(本题8分)先化简，再求值：5x－2(2x－3)＋(3x＋1)，其中x＝-2．21.(本题10分) 某公园有一块长方形草坪，长为a米，宽为b米．现在在草坪上修建了如图所示的十字路，已知十字路宽为2米．(1)用含a，b的代数式表示修建的十字路的面积；(2)若a＝30，b＝20，求草坪的面积．22.(本题10分) 设5a是一个两位数，其中a是十位上的数字（1≤a≤9）．例如，当a＝4时，5a表示的两位数是45．（1）尝试：①当a＝1时，152＝225＝1×2×100＋25；②当a＝2时，252＝625＝2×3×100＋25；③当a＝3时，352＝1225＝；……（2）归纳：25a与100a(a＋1)＋25有怎样的大小关系？试说明理由．（3）运用：若25a与100a的差为2525，求a的值．四、挑战自我（本大题共3小题，共20分）1.（本题5分）如图，两个六边形的面积分别为16和9，两个阴影部分的面积分别为a、b(a ＜b)，则b-a的值为()A.4B.5C.6D.72.（本题5分）某种杯子的高度是15cm，两个以及三个这样的杯子叠放时高度如图，n个这样的杯子叠放在一起高度是（用含n的式子表示）．3.（本题10分）某市为了鼓励居民节约用水，采用分阶段计费的方法按月计算每户家庭的水费：月用水量不超过20m3时，按2元/m3计算；月用水量超过20m3时，其中的20m3仍按2元/m3计算，超过部分按2.6元/m3计算．设某户家庭月用水量xm3．月份4月5月6月用水量15 17 21（1）用含x的式子表示：当0≤x≤20时，水费为元；当x＞20时，水费为元．（2）小林家第二季度用水情况如上表，小林家这个季度共缴纳水费多少元？参考答案 一、选择题 二、填空题：11.2，3； 12. 12；13.2m +0.3；14.8；15.4x +12.5；16.-3y ；17. 8 ；18.n； 三、解答题：19.(1)3x 2－2x 2＋x 2= 22x(2)(4a 2b －5ab 2)－(3a 2b －4ab 2)=22ab b a20.解：5x －2(2x －3)＋(3x ＋1)=5x -4x +6+3x +1=4x +7,当x =-2时，原式=4×（-2）+7=-1 21.解：(1)ab -（a -2）（b -2）=2a +2b -4（2）a ＝30，b ＝20，草坪的面积=（a -2）（b -2）=（30-2）（20-2）=504 22.解：（1）当a ＝3时，352＝1225＝ 3×4×100+25 ； （2） 25a =（10a+5）（10a+5）=100a (a ＋1)＋25（3）∵25a -100a=2525，∴100a (a ＋1)＋25-100a =2525，a 2=25，a =5或-5（舍去）∴a =5四、1.D ； 2. 3n +123.（1）用含x 的式子表示：当0≤x ≤20时，水费为 2x 元；当x ＞20时，水费为2.6x -12 元．（2）解：15×2+17×2+2.6×21-12=106.6；∴小林家这个季度共缴纳水费106.6元。

第4章一元一次方程检测卷一、选择题1．下列各等式中变形正确的是（）A．如果3x−5=2−2y，那么3x−2y=7B．如果14x=12y，那么2x=yC．如果x−24=1+3y5，那么5x−10=4+3yD．如果4a+2=2b−3，那么4a=2b−52．已知方程2x|a|+5=0是关于x的一元一次方程，则a的值是（）A．1 B．−1C．±1D．23．受季节影响，某商品每件售价按原价降低a%再降价6元后的售价是100元，那么该商品每件原售价可表示为（）A．941−a%B．1061−a%C．94(1−a%)D．106(1−a%)4．下面是一个被墨水污染过的方程：3x+12=2x+，答案显示方程的解是x=1，被墨水遮盖的是一个常数，则这个常数是（）A．12B．−12C．32D．−325．在排成每行七天的日历表中取下一个3×3的方块（如图），若方块中所有日期之和为207，则n的值为（）A．23 B．21 C．15 D．126．某商场在一次买卖中，同时卖出两件上衣，每件都以150元出售，若按成本计算，其中一件赢利50%，另一件亏本25%，在这次买卖中，该商场（）A．不盈不亏B．盈利20元C．亏损10元D．盈利50元7．“3·5”学雷锋日“献上一杯姜茶”活动中，小明为环卫工刘爷爷献上热茶并帮助刘爷爷打扫卫生，小明了解到，再过5年，刘爷爷的年纪正好是自己的4倍，小明今年13岁，设刘爷爷今年x岁，则可列方程为：（）A．4×(13+5)=x+5B．4x=13+5C．4×13=x+5D．(13+5)=4(x+5)8．某商场购进一批服装，每件服装销售的标价为400元，由于换季滞销，商场决定将这种服装按标价的六折销售，若打折后每件服装仍能获利20%，则该服装的进价是（ ）A ．160元B ．180元C ．200元D ．220元 二、填空题9．x ＝ 时，式子x−12与x−23互为相反数．10．关于x 的方程6x +7=19与3x =18−3m 的解相同，则m 的值为 ．11．一个两位数，十位上的数比个位上的数大3，个位上的数与十位上的数的和为7，这个两位数是 ．12．某次篮球比赛计分规则为：胜一场积2分，负一场积1分，没有平场，八一队在篮球联赛共14场比赛中积23分，那么八一队胜了 场．13．某班有学生45名，要选择两人作为班干部，结果有40人赞成甲做班干部，有37人赞成乙做班干部，对甲、乙两人都不赞成的人数是都赞成人数 19，那么对甲、乙两人都赞成的 人.三、计算题14．解方程（1）4x −2=10（2）7x =5x +4（3）x +5=3(1−x )（4）2(x+4)3−5x−16=1四、解答题15．机械加工车间有85名工人，平均每人每天可以加工大齿轮 16 个或小齿轮 10 个.已知2个大齿轮与3个小齿轮配成一套，则安排多少名工人加工大齿轮，多少名工人加工小齿轮，才能使每天加工的大、小齿轮刚好配套?16． A 、B 两地相距31千米，甲从 A 地骑自行车去B 地，1小时后乙骑摩托车也从 A 去 B 地.已知甲每小时行驶12千米，乙每小时行驶28 千米.（1）问乙出发后多少小时追上甲?（2）若乙到达 B 地后立即返回，则在返回路上与甲相遇时距乙出发多长时间?17．解一元一次方程时，发现这样一种特殊情况：2x +53=3的解为x =23，恰巧2+53−3=23，我们将这种类型的方程做如下定义：如果一个方程ax +b =c 的解满足x =a +b −c ，则称它为“巧合方程”，请解决以下问题．（1）请判断方程3x +34=3是否是巧合方程：______（直接写“是”或“不是”）；（2）已知方程12x+b=1是巧合方程，请求出b的值；（3）若4x+m=n和3x+n2=154都是巧合方程，请求出2mn−m+n的值．18．2023年双“十一”期间，坪山友谊书城制定了促销方案：若一次性购书金额不超过500元，则不优惠；若一次性购书金额超过500元，那么500元部分按九折优惠，超过500元的部分按八折优惠．（1）设一次性购买的书籍原价是800元，实际付款为元；（2）若小芳一次性购买的书籍的原价是a元（a>500），那么她实际付款元（用含a的代数式表示）（3）小冬在促销期间先后两次下单购买书籍，两次所购书籍的原价之和为1000元（第一次所购书籍的原价高于第二次），两次实际共付款930元，则小冬两次购物所购书籍的原价分别是多少元?19．某游泳馆每年夏季推出两种游泳付费方式，方式一：不购买会员证，每次游泳付费9元；方式二：先购买会员证，每张会员证100元，只限本人当年使用，凭证游泳每次再付费5元．设小明计划今年夏季游泳次数为x（x为正整数）．（1）根据题意，填写下表的空：游泳次数10 15 (x)方式一的总费用（元）90 135 ……①______方式二的总费用（元）150 ②_______ ……③_______（2）通过计算说明当x=27时，应选择哪种付费方式更合算；（3）若小明计划今年夏季游泳的总费用为270元，选择哪种付费方式，他的游泳次数比较多？。