理论力学典型例题5
- 格式:pptx
- 大小:91.15 KB
- 文档页数:1

1-3 试画出图示各构造中构件AB的受力争1-4 试画出两构造中构件ABCD的受力争1-5 试画出图 a 和 b 所示刚系统整体各个构件的受力争1-5a1-5b1- 8 在四连杆机构的ABCD的铰链 B 和 C上分别作用有力F1和 F2,机构在图示位置均衡。
试求二力F1和 F2之间的关系。
解:杆 AB,BC, CD为二力杆,受力方向分别沿着各杆端点连线的方向。
解法 1( 分析法 )假定各杆受压,分别选用销钉 B 和 C 为研究对象,受力以下图:yyFBCC xB Fo45BCx30o o F60F2CDF AB F1由共点力系均衡方程,对 B 点有:F x0F2F BC cos4500对 C点有:F x0FBC F1 cos3000解以上二个方程可得:F12 6F2 1.63F23解法 2( 几何法 )分别选用销钉 B 和 C 为研究对象,依据汇交力系均衡条件,作用在 B 和C 点上的力构成关闭的力多边形,以下图。
F F2BCF AB o30o45CD60oFF BC F1对 B 点由几何关系可知:F2F BC cos450对 C 点由几何关系可知:F BC F1 cos300解以上两式可得:F1 1.63F22-3 在图示构造中,二曲杆重不计,曲杆AB 上作用有主动力偶 M。
试求 A 和 C 点处的拘束力。
解: BC为二力杆 ( 受力以下图 ) ,故曲杆 AB 在 B 点处遇到拘束力的方向沿BC 两点连线的方向。
曲杆AB遇到主动力偶M的作用, A 点和 B 点处的拘束力一定构成一个力偶才能使曲杆AB保持均衡。
AB受力以下图,由力偶系作用下刚体的均衡方程有(设力偶逆时针为正):M0 F A10a sin(450 )M 0F A0.354Ma此中:tan 1。
对 BC杆有:F C FB F A0.354M 3aA,C两点拘束力的方向以下图。
2-4解:机构中 AB杆为二力杆,点A,B 出的拘束力方向即可确立。

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
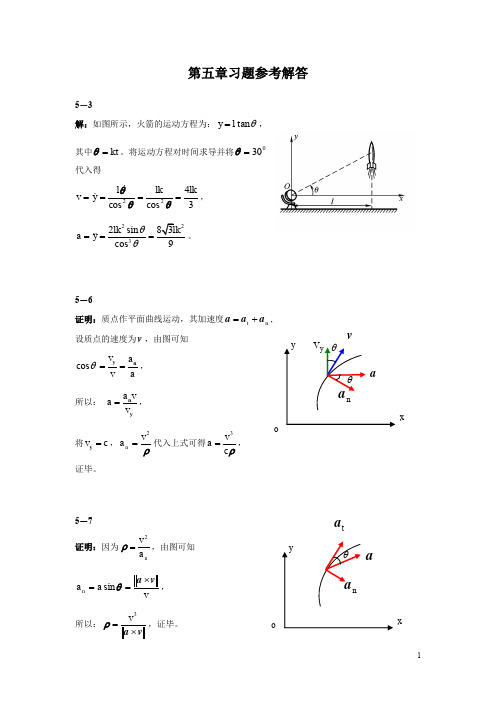


1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4FF解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
理论力学习题及答案理论力学习题及答案理论力学是物理学的基础学科之一,它研究物体运动的规律以及力的作用原理。
在学习理论力学的过程中,掌握一定的习题是非常重要的。
本文将提供一些理论力学的学习题及其答案,希望能够帮助读者更好地理解和掌握这门学科。
1. 一个质点在水平方向上受到一个恒力F的作用,已知质点的质量为m,求质点在水平方向上的加速度。
解答:根据牛顿第二定律,力等于质量乘以加速度,即F = ma。
所以质点在水平方向上的加速度为a = F / m。
2. 一个质点在竖直方向上受到一个重力作用,已知质点的质量为m,求质点在竖直方向上的加速度。
解答:根据牛顿第二定律,力等于质量乘以加速度,即mg = ma。
所以质点在竖直方向上的加速度为a = g,其中g为重力加速度。
3. 一个质点在竖直方向上受到一个重力作用和一个向上的恒力F的作用,已知质点的质量为m,求质点在竖直方向上的加速度。
解答:根据牛顿第二定律,力等于质量乘以加速度,即mg - F = ma。
所以质点在竖直方向上的加速度为a = (mg - F) / m。
4. 一个质点在斜面上受到一个斜面法向力N和一个斜面平行力F的作用,已知斜面的倾角为θ,求质点在斜面上的加速度。
解答:将斜面的坐标系选择为斜面的法线方向和水平方向,根据牛顿第二定律在斜面的法线方向和水平方向分别列出方程。
在斜面的法线方向上,N -mgcosθ = ma_n,其中a_n为质点在斜面法线方向上的加速度;在斜面的水平方向上,F - mgsinθ = ma_t,其中a_t为质点在斜面平行方向上的加速度。
通过这两个方程可以解得质点在斜面上的加速度。
5. 一个质点在圆周运动中,已知质点的质量为m,圆周的半径为r,求质点的向心加速度。
解答:向心加速度是质点在圆周运动中指向圆心的加速度。
根据牛顿第二定律,向心力等于质量乘以向心加速度,即F = ma_c。
而向心力可以表示为F =mω^2r,其中ω是质点的角速度。
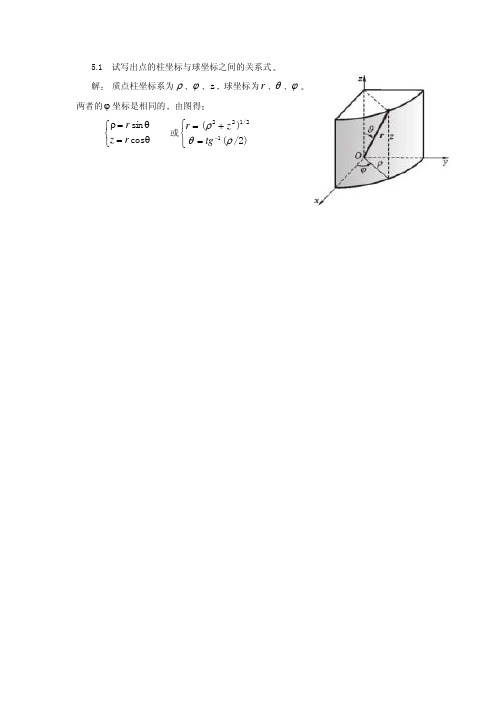
《理论力学》试题库第一部分填空题:第一类:1,已知某质点运动方程为x=2bcoskt,y=2bsinkt,其中b、k均为常量,则其运动轨迹方程为-—————-———--,速度的大小为——-—————-———,加速度的大小为—————————-—-。
2、已知某质点运动方程为x=2cos3t,y=2sin3t,z=4t则其运动速度的大小为,加速度的大小为 .3、已知某质点运动方程为r=e ct,θ=bt,其中b、c是常数,则其运动轨道方程为——-———-—-——-———-————--,其运动速度的大小为--———————-,加速度的大小为———-————————。
4、已知某质点的运动方程为x=2bcos2kt,y=bsin2kt,则其运动轨道方程为;速度大小为 ;加速度大小为。
5、已知质点运动的参数方程为y=bt,θ=at,其中a、b为常数,则此质点在极坐标系中的轨道方程式为,在直角坐标系中的轨道方程式为。
6、已知某质点的运动方程为r=at,θ=bt,其中a、b是常数,则其运动轨道方程为—-———-——-——-——————————,其运动速度的大小为——-———————,加速度的大小为—-—-———-————。
7、已知某质点运动方程为r=at,θ=b/t,其中a、b是常数,则其运动轨道方程为---—-———--————-,其运动速度的大小为—-—-—--———,加速度的大小为———-—————.8、已知某质点的运动方程为x=at,y=a(e t-e-t)/2,其中a为常数,则其运动轨道方程为—-—-——-—---—————---———,曲率半径为——-———————。
第二类:9、质点在有心力作用下,其————————————-—-—-———均守恒,其运动轨道的微分方程为—--——-——-——————--—————,通常称此轨道微分方程为比耐公式。
10、柯尼希定理的表达式为—-——-——————--————-—-,其中等式右边第一项和第二项分别为——————————————————————---—-—————-——————-——-——-———。
理论力学题库第一部分:概念题 理论力学的研究对象和研究方法内力的特点柯尼希(König)定理质心运动定理的物理意义地球自转对物体运动的影响实例如何处理可变质量物体的运动刚体的平动平面平行运动瞬心,瞬心的特点空间极迹, 本体极迹惯量椭球,惯量主轴刚体一般运动的动能回转效应表观重力平面平行运动的定义, 特点及自由度非惯性系中质点运动微分方程及各项的意义。
正则变换泊松定理拉格朗日力自由度,广义坐标约束,约束的类型,完整约束,理想约束循环坐标,循环动量,循环积分哈密顿函数的物理意义位形空间广义能量积分虚位移,虚功拉格朗日变量正则变量泊松括号的作用正则变换的目的,正则变换的条件,正则变换的关键广义势带电粒子在电磁场中的拉格朗日方程平面刚体, 定轴转动刚体, 定点运动刚体, 一般运动刚体, 平动刚体的自由度 面积常数的物理意义第二部分:证明题1 试导出可变质量物体的运动微分方程2 试导出有心运动的轨道微分方程3 证明在重力作用下火箭运动的速度为V=V 0 - gt+Vr ln(m 0/m), 其中V 0和m 0为火箭的初速度和初质量, Vr 为喷气速度(令为常数), g 是重力加速度, t 为时间.4 原始总质量为M 0的火箭, 发射时单位时间内消耗的燃料与M 0成正比, 即αM 0(α为比例常数), 并以相对速度Vr 喷射. 已知火箭本身质量为M, 求证只有当αVr > g 时火箭才能上升, 并证其最大速度为: Vr ln(M 0/M) – g(1– M/M 0)/α5 质点组对某点O 的总角动量等于其质心(质量为M)对点O 的角动量与整个质点组相对质心的角动量之和, 试证之.6 试导出Euler 动力学方程7 试导出质点组关于质心的动能定理8 试证面积常数.2θr h =9 导出两体问题的结论.10. 若x i =x I (q 1,q 2,…,q S , t), 试证: ααq x q x i &&∂∂=∂∂//; ααq x q x dtd i ∂∂=∂∂/)/(& 11 证明 ααpH p &=],[, ααq H q &=],[12 证明X y Z P P G −=],[, Z X y P P G −=],[13 若f=f (q,p,t), 一般tf dt df ∂∂≠, 有无特例? 若有, 试证之. 14 已知质点组点的动量P 和角动量G 的笛卡儿分量所组成的泊松括号Y X Z P P G =],[, 0],[=y Y P G , Y Z X P P G −=],[, 请直接写出以下结果=],[X Y P G ? =],[y X P G ? =],[X X P G ? =],[Z Y P G ?15 αββαδ=],[p q第三部分:运算题1. 如向互相垂直的均匀电磁场E , H 中发射一电量为e 的电子, 设电子的初速度V 0与E 及H 垂直, 试求电子的运动规律 (已知电子受力F =e E + e/c V × H , 其中V 为任一瞬时电子的速度, c 为光速)2. 一质量为m 的质点受引力的作用在一直线上运动, 引力值为m µ a 2 / x 2, 其中x 是相对于线上某一固定点(取为原点)的距离. 如质点在离原点2a 处静止出发, 求到达 a 处所需的时间.3. 已知一点作平面运动时, 其速度的大小为常数C, 矢径的角速度大小为常数ω. 求点的运动方程及其轨迹. 设t=0时, r=0, θ=0.4. 海防炮的炮弹质量为m, 自离海平面高h 处以初速V 0水平射出. 空气阻力可视为与速 度的一次方成正比, 即R = - km V , 其中k 为常数, 试求炮弹的运动方程.5. 任意二维光滑曲线y = y(x), 为保证质点在运动中不会脱离曲线的约束, 要求曲线段是向上凹的. 质点从y=y 0 ( y 0任意)高度静止下滑.(1) 试证曲线对质点的约束力2/32''02)'1/(])(2'1[y y y y y mg N +−++=(2) 由此推出椭圆 (x 2/a 2+y 2/b 2 = 1) 在≤y 0曲线段的约束力2/322242224])(/[])(3[y b a b y b a b mgay N −+−+−=6. 如果单摆在有阻力的媒质中振动, 并假定振幅很小, 故阻力与.θ 成正比, 且可写为 .2θmkl R =, 式中m 为摆锤质量, l 为摆长, k 为比例系数, .θ为角速度. 试写出下列 几种情况下单摆的运动微分方程.7.一质点沿着抛物线y2=2px运动, 其切向加速度为法向加速度的2k倍. 如质点从正焦弦(p/2, p)的一端以速度u出发, 试求其到达正焦弦另一端时的速率.8.一均匀圆盘, 质量为M, 半径为R, 静止地放在一光滑平面上, 圆盘中心固定. 质量为m的甲虫, 原先静止于圆盘边缘上, 尔后甲虫沿圆盘边缘爬动.(1)用三大守恒定律分析系统的守恒情况.(2)求盘心和甲虫的轨迹.9.在光滑的水平面上, 一个质量为m的小球以速度V0与一根长度为2a, 质量为M的静止均质杆碰撞(如图示). 试求碰后杆的质心C的速度(要求理论分析, 列出有关方程, 不必求解).10.一均匀圆盘, 质量为M, 半径为R, 静止地放在一光滑的平面上, 圆盘中心不固定. 质量为m的甲虫, 原先静止于圆盘边缘上, 尔后甲虫以匀相对速率u沿圆盘边缘爬动,(1)求质心C与盘心和甲虫间的距离(2)用三大守恒定律分析系统的守恒情况.(3)求盘心的平动速率和相对盘心的转动角速度.11.质量为m1和m2的两自由质点互相以力吸引, 引力与其质量成正比, 与距离平方成反比, 比例系数为k. 开始时, 两质点皆处于静止状态, 其间距离为a. 试求两质点的距离为a/2时它们的速度.12.一等腰直角三角形OAB在其自身平面内以匀角速度ω绕顶点O转动, 某一点P以匀相对速度沿AB边运动. 当三角形转了一周时, P点走过了AB. 如已知AB=b, 试求P 点在A时的绝对速度和绝对加速度.13.质量为m的质点位于一光滑水平面上, 此平面以等角速度ω通过平面上某一点O的铅直轴转动. 若质点受O吸引, 引力为F= -mω2r (r为质点相对于O的矢径). 试证在任何起始条件下, 质点以角速度2ω走一圆周轨迹.ω(方向铅直向上)转动, 管内有一弹性系数为14.一光滑管子在光滑水平面上以等角速度Ol的弹簧, 其一端联于转轴的O点, 另一端联一质点m. 开始时, 质点k, 自然长度为ol处, 且x&=0. 求质点的运动及它对管壁的压力(在整个运动过程中, 不超过弹位于x=o簧弹性限度)15.椭球状的杯子内放一重mg的小球, 杯子以等角速度ω绕其自身铅直轴转动, 小球与椭球杯处于相对静止状态, 求距离h16. 一直线以等角速度ω在一固定平面内绕其O端转动。