一道中考平面几何试题的证明、溯源与拓展

一道中考题的变式与拓展------株洲市枫叶中学张福来（412000）内容摘要：通过一道中考题的变式与拓展，介绍求可展曲面的几何体表面上两点间的最短路线长的思路和方法。

关键词：变式、侧面展开成平面图、最短路线长、创新、转化。

一些课本数学习题、中考数学试题在平常数学教学中若能变式拓展得当，既能提高学生数学学习兴趣，又能拓展学生的思维，使学生对所学知识和方法能举一反三、融会贯通，进而达到培养学生的创新意识和创新能力的目的。

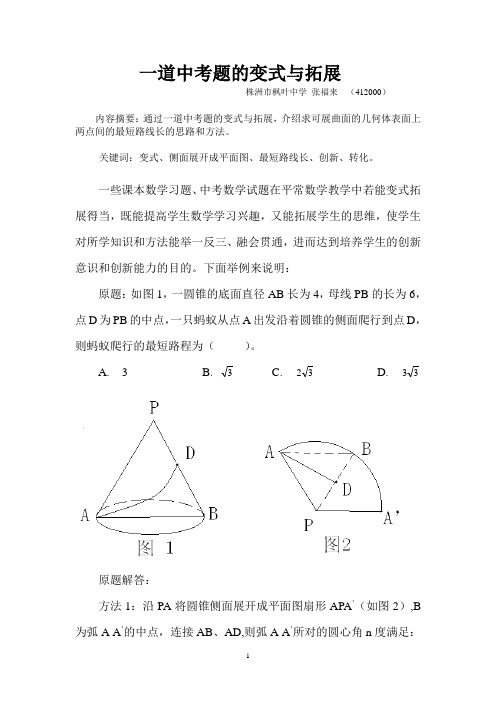
下面举例来说明：原题：如图1，一圆锥的底面直径AB长为4，母线PB的长为6，点D为PB的中点，一只蚂蚁从点A出发沿着圆锥的侧面爬行到点D，则蚂蚁爬行的最短路程为（）。

A. 3B.3C. 332 D. 3原题解答：方法1：沿PA将圆锥侧面展开成平面图扇形APA’（如图2）,B 为弧A A’的中点，连接AB、AD,则弧A A’所对的圆心角n度满足：6236022∙∙=∙ππn 解得n=120 即 120'=∠APA 从而60=∠APB 所以APB ∆为等边三角形，∴AD=6sin60。

=33即求 （∴选D ）方法2：如图3作轴截面图APB ∆，连接AD ，作AE ⊥PB,垂足为E,设BE=x 则 42－x 2=62－(6－x)2 解得 x=34 即BE=34 DE=35∴AD 2=DE 2+AE 2＞BE 2+AE 2=42∴AD ＞4又A 、D 间的曲线长更大于4, 而3 、3 、23都小于4， 故选项A 、B 、C 都不符合，只有选D 。

将原题结论变化，进一步理解和掌握解法1思路变式1：如图1，一圆锥的底面直径AB 长为4，母线PB 的长为6，一只蚂蚁从点A 出发沿着圆锥的侧面爬行到点B ，则蚂蚁爬行的最短路程为（ ）。

解：由原题解法1易知蚂蚁爬行的最短路程为图2中的弦AB 的长6变式2：如图1，一圆锥的底面直径AB 长为4，母线PB 的长为6，点D 为PB 的中点，一只蚂蚁从点A 出发沿着圆锥的侧面爬行一周回到起点A ，则蚂蚁爬行的最短路程为（ ）解：如图4连接A ’B ，PA ’BA 由原题解法1思路知四边形PA ’BA 为菱形，从而AA ’=2AD=63，故蚂蚁爬行的最短路程为63。

专题八：几何证明题问题解析几何证明题重在训练学生应用数学语言合情推理能力;几何证明题和计算题在中考中占有重要地位．根据新的课程标准;对几何证明题证明的方法技巧上要降低;繁琐性、难度方面要降低．但是注重考查学生的基础把握推理能力;所以几何证明题是目前常考的题型．热点探究类型一：关于三角形的综合证明题例题12016·四川南充已知△ABN和△ACM位置如图所示;AB=AC;AD=AE;∠1=∠2．1求证：BD=CE；2求证：∠M=∠N．分析1由SAS证明△ABD≌△ACE;得出对应边相等即可2证出∠BAN=∠CAM;由全等三角形的性质得出∠B=∠C;由AAS证明△ACM≌△ABN;得出对应角相等即可．解答1证明：在△ABD和△ACE中;;∴△ABD≌△ACESAS;∴BD=CE；2证明：∵∠1=∠2;∴∠1+∠DAE=∠2+∠DAE;即∠BAN=∠CAM;由1得：△ABD≌△ACE;∴∠B=∠C;在△ACM和△ABN中;;∴△ACM≌△ABNASA;∴∠M=∠N．点评本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．类型二：关于四边形的综合证明题例题22016·山东省滨州市·10分如图;BD是△ABC的角平分线;它的垂直平分线分别交AB;BD;BC 于点E;F;G;连接ED;DG．1请判断四边形EBGD的形状;并说明理由；2若∠ABC=30°;∠C=45°;ED=2;点H是BD上的一个动点;求HG+HC的最小值．考点平行四边形的判定与性质；角平分线的性质．分析1结论四边形EBGD是菱形．只要证明BE=ED=DG=GB即可．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EMC中;求出EM、MC即可解决问题．解答解：1四边形EBGD是菱形．理由：∵EG垂直平分BD;∴EB=ED;GB=GD;∴∠EBD=∠EDB;∵∠EBD=∠DBC;∴∠EDF=∠GBF;在△EFD和△GFB中;;∴△EFD≌△GFB;∴ED=BG;∴BE=ED=DG=GB;∴四边形EBGD是菱形．2作EM⊥BC于M;DN⊥BC于N;连接EC交BD于点H;此时HG+HC最小;在RT△EBM中;∵∠EMB=90°;∠EBM=30°;EB=ED=2;∴EM=BE=;∵DE∥BC;EM⊥BC;DN⊥BC;∴EM∥DN;EM=DN=;MN=DE=2;在RT△DNC中;∵∠DNC=90°;∠DCN=45°;∴∠NDC=∠NCD=45°;∴DN=NC=;∴MC=3;在RT△EMC中;∵∠EMC=90°;EM=．MC=3;∴EC===10．∵HG+HC=EH+HC=EC;∴HG+HC的最小值为10．点评本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识;解题的关键是利用对称找到点H的位置;属于中考常考题型．同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．类型三：关于圆的综合证明题例题32016·山东潍坊正方形ABCD内接于⊙O;如图所示;在劣弧上取一点E;连接DE、BE;过点D作DF∥BE交⊙O于点F;连接BF、AF;且AF与DE相交于点G;求证：1四边形EBFD是矩形；2DG=BE．考点正方形的性质；矩形的判定；圆周角定理．分析1直接利用正方形的性质、圆周角定理结合平行线的性质得出∠BED=∠BAD=90°;∠BFD=∠BCD=90°;∠EDF=90°;进而得出答案；2直接利用正方形的性质的度数是90°;进而得出BE=DF;则BE=DG．解答证明：1∵正方形ABCD内接于⊙O;∴∠BED=∠BAD=90°;∠BFD=∠BCD=90°;又∵DF∥BE;∴∠EDF+∠BED=180°;∴∠EDF=90°;∴四边形EBFD是矩形；2∵正方形ABCD内接于⊙O;∴的度数是90°;∴∠AFD=45°;又∵∠GDF=90°;∴∠DGF=∠DFC=45°;∴DG=DF;又∵在矩形EBFD中;BE=D同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．类型四：关于相似三角形的证明问题例题42016·黑龙江齐齐哈尔·8分如图;在△ABC中;AD⊥BC;BE⊥AC;垂足分别为D;E;AD与BE 相交于点F．1求证：△ACD∽△BFD；2当tan∠ABD=1;AC=3时;求BF的长．考点相似三角形的判定与性质．分析1由∠C+∠DBF=90°;∠C+∠DAC=90°;推出∠DBF=∠DAC;由此即可证明．2先证明AD=BD;由△ACD∽△BFD;得==1;即可解决问题．解答1证明：∵AD⊥BC;BE⊥AC;∴∠BDF=∠ADC=∠BEC=90°;∴∠C+∠DBF=90°;∠C+∠DAC=90°;∴∠DBF=∠DAC;∴△ACD∽△BFD．2∵tan∠ABD=1;∠ADB=90°∴=1;∴AD=BD;∵△ACD∽△BFD;∴==1;∴BF=AC=3．同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．3. 烟台市 2015 中考 -23如图;以△ABC 的一边AB 为直径的半圆与其它两边AC;BC 的交点分别为D 、E;且=．1试判断△ABC 的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD 的值．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD 中;E 、F 分别为边AB 、CD 的中点;BD 是对角线．1求证：△ADE ≌△CBF ；2若∠ADB 是直角;则四边形BEDF 是什么四边形 证明你的结论．5. 烟台市 2014 中考 -24如图;AB 是⊙O 的直径;延长AB 至P;使BP=OB;BD 垂直于弦BC;垂足为点B;点D 在PC 上．设∠PCB=α;∠POC=β．求证：tanα tan=．DCEF B A 图66. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．7. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE 交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．参考答案类型一：关于三角形的综合证明题同步练2016·山东省菏泽市·3分如图;△ACB和△DCE均为等腰三角形;点A;D;E在同一直线上;连接BE．1如图1;若∠CAB=∠CBA=∠CDE=∠CED=50°①求证：AD=BE；②求∠AEB的度数．2如图2;若∠ACB=∠DCE=120°;CM为△DCE中DE边上的高;BN为△ABE中AE边上的高;试证明：AE=2CM+BN．考点等腰三角形的性质．分析1①通过角的计算找出∠ACD=∠BCE;再结合△ACB和△DCE均为等腰三角形可得出“AC=BC;DC=EC”;利用全等三角形的判定SAS即可证出△ACD≌△BCE;由此即可得出结论AD=BE；②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC;再通过角的计算即可算出∠AEB的度数；2根据等腰三角形的性质结合顶角的度数;即可得出底角的度数;利用1的结论;通过解直角三角形即可求出线段AD、DE的长度;二者相加即可证出结论．解答1①证明：∵∠CAB=∠CBA=∠CDE=∠CED=50°;∴∠ACB=∠DCE=180°﹣2×50°=80°．∵∠ACB=∠ACD+∠DCB;∠DCE=∠DCB+∠BCE;∴∠ACD=∠BCE．∵△AC B和△DCE均为等腰三角形;∴AC=BC;DC=EC．在△ACD和△BCE中;有;∴△ACD≌△BCESAS;∴AD=BE．②解：∵△ACD≌△BCE;∴∠ADC=∠BEC．∵点A;D;E在同一直线上;且∠CDE=50°;∴∠ADC=180°﹣∠CDE=130°;∴∠BEC=130°．∵∠BEC=∠CED+∠AEB;且∠CED=50°;∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°．2证明：∵△ACB和△DCE均为等腰三角形;且∠ACB=∠DCE=120°;∴∠CDM=∠CEM=×180°﹣120°=30°．∵CM⊥DE;∴∠CMD=90°;DM=EM．在Rt△CMD中;∠CMD=90°;∠CDM=30°;∴DE=2DM=2×=2CM．∵∠BEC=∠ADC=180°﹣30°=150°;∠BEC=∠CEM+∠AEB;∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°;∴∠BEN=180°﹣120°=60°．在Rt△BNE中;∠BNE=90°;∠BEN=60°;∴BE==BN．∵AD=BE;AE=AD+DE;∴AE=BE+DE=BN+2CM．点评本题考查了等腰三角形的性质、全等三角形的判定及性质、解直角三角形以及角的计算;解题的关键是：1通过角的计算结合等腰三角形的性质证出△ACD≌△BCE；2找出线段AD、DE的长．本题属于中档题;难度不大;但稍显繁琐;解决该题型题目时;利用角的计算找出相等的角;再利用等腰三角形的性质找出相等的边或角;最后根据全等三角形的判定定理证出三角形全是关键．类型二：关于四边形的综合证明题同步练2016·山东省济宁市·3分如图;正方形ABCD的对角线AC;BD相交于点O;延长CB至点F;使CF=CA;连接AF;∠ACF的平分线分别交AF;AB;BD于点E;N;M;连接EO．1已知BD=;求正方形ABCD的边长；2猜想线段EM与CN的数量关系并加以证明．考点正方形的性质．分析1根据正方形的性质以及勾股定理即可求得；2根据等腰三角形三线合一的性质证得CE⊥AF;进一步得出∠BAF=∠BCN;然后通过证得△ABF≌△CBN得出AF=CN;进而证得△ABF∽△COM;根据相似三角形的性质和正方形的性质即可证得CN= CM．解答解：1∵四边形ABCD是正方形;∴△ABD是等腰直角三角形;∴2AB2=BD2;∵BD=;∴AB=1;∴正方形ABCD的边长为1；2CN=CM．证明：∵CF=CA;AF是∠ACF的平分线;∴CE⊥AF;∴∠AEN=∠CBN=90°;∵∠ANE=∠CNB;∴∠BAF=∠BCN;在△ABF和△CBN中;;∴△ABF≌△CBNAAS;∴AF=CN;∵∠BAF=∠BCN;∠ACN=∠BCN;∴∠BAF=∠OCM;∵四边形ABCD是正方形;∴AC⊥BD;∴∠ABF=∠COM=90°;∴△ABF∽△COM;∴=;∴==;即CN=CM．类型三：关于圆的综合证明题同步练枣庄市 2015 中考 -24如图;在△ABC中;∠ABC=90°;以AB的中点O为圆心、OA为半径的圆交AC于点D;E是BC的中点;连接DE;OE．1判断DE与⊙O的位置关系;并说明理由；2求证：BC2=CD 2OE；3若cos∠BAD=35;BE=6;求OE的长．思路分析：本题考查了切线的判定;垂径定理以及相似三角形的判定与性质等知识点．故对于题1可以连接OD;BD;由AB为圆O的直径;得到∠ADB为直角;从而得出三角形BCD为直角三角形;E为斜边BC 的中点;利用斜边上的中线等于斜边的一半;得到CE=DE;利用等边对等角得到一对角相等;再由OA=OD;利用等边对等角得到一对角相等;由直角三角形ABC中两锐角互余;利用等角的余角相等得到∠ADO与∠CDE互余;可得出∠ODE为直角;即DE垂直于半径OD;可得出DE为圆O的切线；对于题2首先可证明OE是△ABC的中位线;则AC=2OE;然后证明△ABC∽△BDC;根据相似三角形的对应边的比相等;即可证得；对于题3在直角△ABC中;利用勾股定理求得AC的长;之后根据三角形中位线定理OE的长即可求得．解题过程：1证明：连接OD;BD;∵AB为圆O的直径;∴∠ADB=90°;在Rt△BDC中;E为斜边BC的中点;∴CE=DE=BE=12 BC;∴∠C=∠CDE;∵OA=OD;∴∠A=∠ADO;∵∠ABC=90°;即∠C+∠A=90°;∴∠ADO+∠CDE=90°;即∠ODE=90°;∴DE⊥OD;又OD为圆的半径;∴DE为⊙O的切线；2证明：∵E是BC的中点;O点是AB的中点; ∴OE是△ABC的中位线;∴AC=2OE;∵∠C=∠C;∠ABC=∠BDC;∴△ABC∽△BDC;∴BC ACCD BC=;即BC2=AC CD．∴BC2=2CD OE；3解：∵cos∠BAD=35;∴sin∠BAC=45 BCAC=;又∵BE=6;E是BC的中点;即BC=12;∴AC=15．又∵AC=2OE;∴OE=12AC=152．规律总结：熟练把握切线的判定;垂径定理以及相似三角形的判定与性质等知识点是解决本题的关键．要证某线是圆的切线;已知此线过圆上某点;连接圆心与这点即为半径;再证垂直即可．类型四：关于相似三角形的证明问题同步练2016·湖北武汉·10分在△ABC中;P为边AB上一点．1 如图1;若∠ACP＝∠B;求证：AC2＝AP·AB；2 若M为CP的中点;AC＝2;① 如图2;若∠PBM＝∠ACP;AB＝3;求BP的长；② 如图3;若∠ABC＝45°;∠A＝∠BMP＝60°;直接写出BP的长．考点相似形综合;考查相似三角形的判定和性质;平行线的性质;三角形中位线性质;勾股定理..答案 1证△ACP∽△ABC即可；2①BP＝5；②71解析1证明：∵∠ACP＝∠B;∠BAC＝∠CAP;∴△ACP∽△ABC;∴AC：AB＝AP：AC;∴AC2＝AP·AB；2①如图;作CQ∥BM交AB延长线于Q;设BP＝x;则P Q＝2x∵∠PBM＝∠ACP;∠PAC＝∠CAQ;∴△APC∽△ACQ;由AC2＝AP·AQ得：22＝3－x35即BP②如图：作CQ⊥AB 于点Q;作CP 0＝CP 交AB 于点P 0;∵AC ＝2;∴AQ＝1;CQ ＝BQ; 设P0Q ＝PQ ＝1－x;BP －1＋x;∵∠BPM＝∠CP 0A ;∠BMP＝∠CAP 0;∴△AP 0C∽△MPB;∴00AP P C MP BP =;∴MP P0C ＝2012P C ==AP 0 BP ＝1＋x;解得x ∴BP ＝－11-．达标检测1. 2016·黑龙江哈尔滨·8分已知：如图;在正方形ABCD 中;点E 在边CD 上;AQ⊥BE 于点Q;DP⊥AQ 于点P ．1求证：AP=BQ ；2在不添加任何辅助线的情况下;请直接写出图中四对线段;使每对中较长线段与较短线段长度的差等于PQ 的长．考点正方形的性质；全等三角形的判定与性质．分析1根据正方形的性质得出AD=BA;∠BAQ=∠ADP;再根据已知条件得到∠AQB=∠DPA;判定△AQB≌△DPA 并得出结论；2根据AQ ﹣AP=PQ 和全等三角形的对应边相等进行判断分析．解答解：1∵正方形ABCD∴AD=BA;∠BAD=90°;即∠BAQ+∠DAP=90°∵DP⊥AQ∴∠ADP+∠DAP=90°∴∠BAQ=∠ADP∵AQ⊥BE 于点Q;DP⊥AQ 于点P∴∠AQB=∠DPA=90°∴△AQB≌△DPAAAS∴AP=BQ2①AQ﹣AP=PQ②AQ﹣BQ=PQ③DP﹣AP=PQ④DP﹣BQ=PQ2. 2016·四川内江9分如图6所示;△ABC 中;D 是BC 边上一点;E 是AD 的中点;过点A 作BC 的平行线交CE 的延长线于F;且AF ＝BD;连接BF ．1求证：D 是BC 的中点；2若AB ＝AC;试判断四边形AFBD 的形状;并证明你的结论．考点三角形例行;特殊四边形的性质与判定..1证明：∵点E 是AD 的中点;∴AE ＝DE ．∵AF ∥BC;∴∠AFE ＝∠DCE;∠FAE ＝∠CDE ．∴△EAF ≌△EDC ．∴AF ＝DC ．∵AF ＝BD;∴BD ＝DC;即D 是BC 的中点．2四边形AFBD 是矩形．证明如下：∵AF ∥BD;AF ＝BD;∴四边形AFBD 是平行四边形．∵AB ＝AC;又由1可知D 是BC 的中点;∴AD ⊥BC ．DC EF B A图6∴□AFBD是矩形．3. 烟台市 2015 中考 -23如图;以△ABC的一边AB为直径的半圆与其它两边AC;BC的交点分别为D、E;且=．1试判断△ABC的形状;并说明理由．2已知半圆的半径为5;BC=12;求sin∠ABD的值．思路分析：1连结AE;如图;根据圆周角定理;由=得∠DAE=∠BAE;由AB为直径得∠AEB=90°;根据等腰三角形的判定方法即可得△ABC为等腰三角形；2由等腰三角形的性质得BE=CE=BC=6;再在Rt△ABE中利用勾股定理计算出AE=8;接着由AB为直径得到∠ADB=90°;则可利用面积法计算出BD=;然后在Rt△ABD中利用勾股定理计算出AD=;再根据正弦的定义求解．解题过程：解：1△ABC为等腰三角形．理由如下：连结AE;如图;∵=;∴∠DAE=∠BAE;即AE平分∠BAC;∵AB为直径;∴∠AEB=90°;∴AE⊥BC;∴△ABC为等腰三角形；2∵△ABC为等腰三角形;AE⊥BC;∴BE=CE=BC=×12=6;在Rt△ABE中;∵AB=10;BE=6;∴AE==8;∵AB为直径;∴∠ADB=90°;∴AE BC=BD AC;∴BD==;在Rt△ABD中;∵AB=10;BD=;∴AD==;∴sin∠ABD===．规律总结：本题考查了圆周角定理：在同圆或等圆中;同弧或等弧所对的圆周角相等;都等于这条弧所对的圆心角的一半．推论：半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径．也考查了等腰三角形的判定与性质和勾股定理．4. 2015 内蒙古呼伦贝尔兴安盟;第22题7分如图;在平行四边形ABCD中;E、F分别为边AB、CD的中点;BD是对角线．1求证：△ADE≌△CBF；2若∠ADB是直角;则四边形BEDF是什么四边形证明你的结论．考点：平行四边形的性质；全等三角形的判定与性质；菱形的判定．分析：1由四边形ABCD是平行四边形;即可得AD=BC;AB=CD;∠A=∠C;又由E、F分别为边AB、CD的中点;可证得AE=CF;然后由SAS;即可判定△ADE≌△CBF；2先证明BE与DF平行且相等;然后根据一组对边平行且相等的四边形是平行四边形;再连接EF;可以证明四边形AEFD是平行四边形;所以AD∥EF;又AD⊥BD;所以BD⊥EF;根据菱形的判定可以得到四边形是菱形．解答：1证明：∵四边形ABCD是平行四边形;∴AD=BC;AB=CD;∠A=∠C;∵E、F分别为边AB、CD的中点;∴AE=AB;CF=CD;∴AE=CF;在△ADE和△CBF中;∵;∴△ADE≌△CBFSAS；2若∠ADB是直角;则四边形BEDF是菱形;理由如下：解：由1可得BE=DF;又∵AB∥C D;∴BE∥DF;BE=DF;∴四边形BEDF是平行四边形;连接EF;在 ABCD中;E、F分别为边AB、CD的中点;∴DF∥AE;DF=AE;∴四边形AEFD是平行四边形;∴EF∥AD;∵∠ADB是直角;∴AD⊥BD;∴EF⊥BD;又∵四边形BFDE是平行四边形;∴四边形BFDE是菱形．点评：本题主要考查了平行四边形的性质;全等三角形的判定以及菱形的判定;利用好E、F 是中点是解题的关键．5. 烟台市 2014 中考 -24如图;AB是⊙O的直径;延长AB至P;使BP=OB;BD垂直于弦BC;垂足为点B;点D在PC上．设∠PCB=α;∠POC=β．求证：tanα tan=．解析：连接AC先求出△PBD∽△PAC;再求出=;最后得到tanα tan=．解答：证明：连接AC;则∠A=∠POC=;∵AB是⊙O的直径;∴∠ACB=90°;∴tanα=;BD∥AC;∴∠PBD=∠A;∵∠P=∠P;∴△PBD∽△PAC;∴=;∵PB=0B=OA;∴=;∴tana tan===．点评：本题主要考查了相似三角形的判定与性质及圆周角的知识;本题解题的关键是求出△PBD∽△PAC;再求出tanα tan=．6. 2015 梧州;第25题12分如图;在正方形ABCD中;点P在AD上;且不与A、D重合;BP的垂直平分线分别交CD、AB于E、F两点;垂足为Q;过E作EH⊥AB于H．1求证：HF=AP；2若正方形ABCD的边长为12;AP=4;求线段EQ的长．考点：正方形的性质；全等三角形的判定与性质；勾股定理．所有分析： 1先根据EQ⊥BO;EH⊥AB得出∠EQN=∠BHM=90°．根据∠EMQ=∠BMH得出△EMQ∽△BMH;故∠QEM=∠HBM．由ASA定理得出△APB≌△HFE;故可得出结论；2由勾股定理求出BP的长;根据EF是BP的垂直平分线可知BQ=BP;再根据锐角三角函数的定义得出QF=BQ的长;由1知;△APB≌△HFE;故EF=BP=4;再根据EQ=EF﹣QF即可得出结论．解答： 1证明：∵EQ⊥BO;EH⊥AB;∴∠EQN=∠BHM=90°．∵∠EMQ=∠BMH;∴△EMQ∽△BMH;∴∠QEM=∠HBM．在Rt△APB与Rt△HFE中;;∴△APB≌△HFE;∴HF=AP；2解：由勾股定理得;BP===4．∵EF是BP的垂直平分线;∴BQ=BP=2;∴QF=BQ tan∠FBQ=BQ tan∠ABP=2×=．由1知;△APB≌△HFE;∴EF=BP=4;∴EQ=EF﹣QF=4﹣=．点评：本题考查的是正方形的性质;熟知正方形的性质及全等三角形的判定与性质是解答此题的关键．7.8. 2015 北海;第25题12分如图;AB、CD为⊙O的直径;弦AE∥CD;连接BE交CD于点F;过点E作直线EP与CD的延长线交于点P;使∠PED=∠C．1求证：PE是⊙O的切线；2求证：ED平分∠BEP；3若⊙O的半径为5;CF=2EF;求PD的长．考点：切线的判定．分析： 1如图;连接OE．欲证明PE是⊙O的切线;只需推知OE⊥PE即可；2由圆周角定理得到∠AEB=∠CED=90°;根据“同角的余角相等”推知∠3=∠4;结合已知条件证得结论；3设EF=x;则CF=2x;在RT△OEF中;根据勾股定理得出52=x2+2x﹣52;求得EF=4;进而求得BE=8;CF=8;在RT△AEB中;根据勾股定理求得AE=6;然后根据△AEB∽△EFP;得出=;求得PF=;即可求得PD的长．解答： 1证明：如图;连接OE．∵CD是圆O的直径;∴∠CED=90°．∵OC=OE;∴∠1=∠2．又∵∠PED=∠C;即∠PED=∠1;∴∠PED=∠2;∴∠PED+∠OED=∠2+∠OED=90°;即∠OEP=90°; ∴OE⊥EP;又∵点E在圆上;∴PE是⊙O的切线；2证明：∵AB、CD为⊙O的直径;∴∠AEB=∠CED=90°;∴∠3=∠4同角的余角相等．又∵∠PED=∠1;∴∠PED=∠4;即ED平分∠BEP；3解：设EF=x;则CF=2x;∵⊙O的半径为5;∴OF=2x﹣5;在RT△OEF中;OE2=OF2+EF2;即52=x2+2x﹣52;解得x=4;∴EF=4;∴BE=2EF=8;CF=2EF=8;∴DF=CD﹣CF=10﹣8=2;∵AB为⊙O的直径;∴∠AEB=90°;∵AB=10;BE=8;∴AE=6;∵∠BEP=∠A;∠EFP=∠AEB=90°;∴△AEB∽△EFP;∴=;即=;∴PF=;∴PD=PF﹣DF=﹣2=．点评：本题考查了切线的判定和性质;圆周角定理的应用;勾股定理的应用;三角形相似的判定和性质;熟练掌握性质定理是解题的关键．。

笔者曾利用2019年中考湖北武汉卷第23题参加湖北省宜昌市初中数学学科工作室“我讲中考压轴题”的活动展示.现呈现此题的相关解答、两道关联题的反思及教学启示.立足解题的通性、通法，借助几何直观，以更有效的方式打开学生的思路，引导学生掌握解题教学之道.一、试题呈现题目（2019年湖北·武汉卷）在Rt△ABC中，∠ABC=90°，AB BC=n，M是边BC上一点，连接AM.（1）如图1，若n=1，N是AB延长线上一点，CN 与AM垂直，求证：BM=BN.（2）过点B作BP⊥AM，点P为垂足，连接CP并延长交AB于点Q.①如图2，若n=1，求证：CP PQ=BM BQ.②如图3，若M是BC的中点，直接写出tan∠BPQ 的值.（用含n的式子表示.）MCA B N图1CMPA BQ图2CMPA BQ图3二、解法探究1.识别模式中探析因果觅路第（1）小题，如图4，延长AM交CN于点D，由核心元素CB⊥AB，AM⊥CN，AB=BC构成“三垂直”模型，且图形中元素的位置关系和数量关系是确定的，确定即可求.当n=1时，可确定△ABC是以∠ABC为直角的等腰直角三角形.要证BM=BN，只需要证明△ABM≌△CBN.由“CN与AM垂直”识别出“等角的余角相等”，可以证得∠MAB=∠NCB.结合已知条件AB=BC，∠ABM=∠CBN，可以证得△ABM≌△CBN.由全等三角形的性质，可得BM=BN.洞察结构明来路回归本源知去路——以一道中考试题的思路探究为例叶先玖摘要：通过对2019年中考湖北武汉卷第23题及关联试题的解法进行探究，探索借助几何直观识别图形，明晰图形结构，并利用确定性、本源性、全局性、动静互换等思维，整体把握空间形式和数量关系，积累有效的解答经验；探究回到基本概念和基本图形的措施，着眼于通性、通法，并着力于几何直观、最近发展区和思维过程等.以知晓方法的来路，形成自然简洁的解答策略.探寻引导学生及时反思解答的路径，点亮思维的去路，培养并优化学生分析与解决问题的能力．关键词：研题要点；几何直观；通性、通法收稿日期：2020-12-18作者简介：叶先玖（1971—），男，高级教师，主要从事初中数学教学课例及实践研究.ABNMC图4D2.几何直观里回归本源启思第（2）小题第①问，给出条件“过点B 作BP ⊥AM 和n =1”后，借助几何直观，审视图形结构并抓住变与不变的元素，则由AB =BC 易联想到三角形全等.由“三垂直”模型识别出△APB ∽△BPM ∽△ABM 等“子母型”相似.要证CP PQ =BM BQ ，可以回归到求线段长、三角形相似、平行线分线段成比例、利用面积比证明线段比等知识源及通法.因此，得到以下五种证明方法.证法1：确定△ABM .抓住AB =BC 这个条件，通过移拼△ABM 可得图5，即过点C 作AM 的垂线，垂足为点D ，且交AB 的延长线于点N .易证△CBN ≌△ABM ，所以BM =BN .由PB ⊥AM ，CN ⊥AM ，可得PB ∥CN .所以CP PQ =NB BQ .所以CP PQ =BM BQ.CA B QMPDN CA BQ MPD图5图6证法2：确定△ABM .抓住AB =BC 这个条件，通过移拼△ABM 可得图6，即过点C 作CD ∥AB ，交BP 的延长线于点D ，易证△CPD ∽△QPB .得CP PQ =CD QB .易证△ABM ≌△BCD .所以CD =BM .所以CP PQ =BM BQ.证法3：确定△ABP .抓住AB =BC 这个条件，通过移拼△ABP 可得图7，即过点C 作CD ⊥BP ，交BP 的延长线于点D ，过点Q 作QE ⊥BP 于点E ，易证△CPD ∽△QPE .得CP PQ =CD QE.易证△CDB ≌△BPA ，所以CD =BP .易证△BPM ∽△QEB .所以BP QE =BM QB.所以CP PQ =CD QE =BP QE =BM QB.CABQMPD E图7C A BQ MPD图8证法4：确定△ABM .如图8，过点Q 作QD ∥BC ，交BP 的延长线于点D ，易证△CPB ∽△QPD .得CP PQ =CB QD.易证△DQB ∽△ABM .所以AB DQ =MB BQ .因为AB =BC ，所以CB QD =BM BQ .所以CP PQ =BM BQ.证法5：如图9，由△BPC 和△BPQ 是等高三角形的图形结构，得CP PQ =S△BPC S △BPQ .过点P 作BC ，AB 的垂线，垂足分别为点D ，E ，则有S△BPC S △BPQ =12⋅BC ⋅PD12⋅BQ ⋅PE.只要分别求出确定的线段PD ，PE ，BM ，BQ 的长（具体计算可参考后文思路10的解答），通过计算即可以证得CP PQ =BM BQ.C ABQ MP图9DE 【思路说明】上述证法中，抓住AB =BC ，回归到旋转定义，动静互换，可洞察到图形中隐藏的“共点等边旋转”结构，即从全局性看，线段AB 绕点B 顺时针旋转90°得到线段BC ，则△ABM 绕点B 顺时针旋转90°得到△CBN .由第（1）小题及解答经验，借助平行线分线段成比例，结合线段之间的等量代换得到证法1.基于图形变换，抓住AB =BC 进行图形移拼，得到证法2和证法3.结合所证结论CP PQ =BM BQ ，直观觉察到“X 型”相似，借助中间比得到证法4.识别出△BPC 和△BPQ 等高，想到求线段的长，将线段的比转化为面积的比得到证法5.3.洞察结构中追根联想得法第（2）小题第②问通过回到正切定义，借助几何直观，捕捉到以下九种思路.思路1：如图10，过点C 作CE ∥AB ，交BP 的延长线于点E ，过点C 作CF ⊥BE 于点F .设BC =2，PM =t ，则BM =1，AB =2n .易证△APB ∽△BPM .所以BM AB=PM PB.则BP =2nt .由中位线定理，得CF =2PM =2t ，PF =BP =2nt .可得tan ∠BPQ =tan ∠CPF =CF PF =2t 2nt =1n.CAB Q MP EF图10CAB Q MP D图11思路2：如图11，过点C 作CD ∥AM ，交BP 的延长线于点D .设BC =2a ，PM =t .由∠PBM =∠MAB ，得PM PB =MB AB =a 2na.则PB =2nt .又由DC =2PM =2t ，DP =PB =2nt ，可得tan ∠BPQ =tan ∠CPD =DC DP =2t 2nt =1n .思路3：如图12，延长PM 到点H ，使MH =PM .连接CH ，易证△CMH ≌△BMP .所以CH =BP ，∠CHM =∠BPM =90°.因为AB BC =n ，BC =2BM ，所以AB BM =2n.设PM =MH =1.由已知易证△ABM ∽△BPM ，所以AB BP =BM PM.则PB =CH =2n .可得tan ∠BPQ =tan ∠HCP =PH CH =2MH CH =22n =1n.CMP HAB Q图12CMP HAB Q图13思路4：如图13，过点C 作CH ⊥AM ，交AM 的延长线于点H ，则CH ∥BP .易证△CMH ≌△BMP .所以CH =BP ，MH =MP .可得tan ∠BPQ =tan ∠PCH =PH CH =2PM BP =2tan ∠PBM =2tan ∠MAB =2×BM AB =BC AB =1n.思路5：如图14，过点B 作BD ∥QC ，交AM 的延长线于点D .设BC =2a ，PM =t .易证△BMD ≌△CMP .所以PM =DM .由∠PBM =∠MAB ，得PM PB =MB AB =a 2na.则PB =2nt .可得tan ∠BPQ =tan ∠PBD =PD PB =2t 2nt =1n.CAB QMP D图14CAB Q MP D图15思路6：如图15，过点M 作MD ∥PB ，交CQ 于点D .设BC =2a ，PM =t .由∠PBM =∠MAB ，得PM PB =MB AB=a 2na.则PB =2nt .由DM =12PB =nt ，且∠BPQ =∠PDM =90°，可得tan ∠BPQ =tan ∠PDM =PM DM =t nt =1n.思路7：如图16，过点B 作BD ∥AM ，交CQ 的延长线于点D ，得∠PBQ =∠MPB =90°.设BC =2a ，PM =t ，易求得BD =2PM =2t .由∠PBM =∠MAB ，得PM PB =MB AB=a 2na.所以PB =2nt .可得tan ∠BPQ =BD PB =2t 2nt =1n .CA BQM PD图16CAB Q MP 图17D 思路8：如图17，过点M 作MD ∥QC ，交BP 于点D .设BC =2a ，PM =t .由∠PBM =∠MAB ，得PM PB =MB AB=a 2na .所以PB =2nt .所以PD =DB =12PB =nt .可得tan ∠BPQ =tan ∠PDM =PM PD =t nt =1n.思路9：如图18，过点C 作AM 的垂线，垂足为点H ，且交AB 的延长线于点N .设BC =2a ，PM =t ，则AB =2na .易证∠NBC =∠MHN =90°，则点B ，M ，H ，N 在以MN 为直径的圆上.易证△ABM ∽△CBN .所以AB CB =AM CN.易求得CN =由切割线定理推论，可得CM ⋅CB =CH ⋅CN .进而可得CH =在Rt△CMH 中，根据勾股定理，易求得MH =a 4n 2+1.所以tan ∠BPQ =tan ∠PCH =PH CH =2MH CH =1n.【思路说明】从已知条件看，∠ABC =90°，AB BC=n ，BP ⊥AM ，M 是BC 的中点等核心要素是确定的；从图形看，增加了中点，会联想三角形中位线结构，或过中点作延长线构造三角形全等；从“直接写出tan ∠BPQ 的值”结论想到补直角三角形，或利用“锐角相等正切值相等”来解决问题.于是，借助前面识别图形结构的经验和补图经验，得到图10，通过关联性思考使得思路自然贯通.及时反思，发现BM AB =12n，察觉到图10中∠BPQ 与∠CPE 的关系，优化思路1得到思路2.洞察到中点M ，识别过中点作延长线构造全等三角形，得到思路3和思路4.识别出中位线结构，得到思路5~思路8.借助第（1）小题的解答，洞察到图中的对角互补，识别出隐圆，得到思路9.上述思路借助几何直观求正切值，自然且有效.三、解后反思1.思路自然，为什么受挫笔者坚持“练后精讲，不练不讲”.事实上，学生独立解答上述题目第（2）小题第②问时，有些学生先想到的是根据正切的定义去补形.现摘录学生的解题思路如下.思路10：如图19，过点Q 作QE ⊥PB 于点E .在Rt△PEQ 中，若能分别求出QE ，PE 的长，则tan ∠BPQ的值可求.CAB Q MP 图20FC ABQ M P 图19E思路11：如图20，过点B 作BF ⊥PQ 于点F .在Rt△PFB 中，若能分别求出BF ，PF 的长，则tan ∠BPQ的值可求.思路12：如图21，过点Q 作QD ⊥AM 于点D .若能分别求出PD ，DQ 的长，在Rt△PDQ 中，可求出tan ∠PQD 的值.进一步可得tan ∠BPQ =tan ∠PQD .CABQ MP图21D 图22思路13：如图22，以点B 为坐标原点，AB 方向为x 轴正半轴，BC 方向为y 轴正半轴建立平面直角坐标系.设BC =2，则点C ()0，2，点M ()0，1，点A ()-2n ，0.再作QE ⊥PB 于点E ，将问题转化为一次函数求解.只要求得点Q æèçöø÷-2n 1+2n 2，0，则可求得QE ，PE 的长，即tan ∠BPQ 的值可求.对于思路13，若能求出BQ 的长，则可以分别求出直线CQ ，AM 的解析式，联立可解得点P 的坐标.再求出直线PB 的解析式，从而可求出直线QE 的解析式，联立可解得点E 的坐标，便可以分别求出PE ，QE 的长.在Rt△PEQ 中，根据tan ∠BPQ =QEPE ，可以求得tan ∠BPQ的值.然而，这四种思路因学生求比值的通法不够熟练、耐心不足，解题过程计算量大等原因，最终没能求出BQ 长这一关键性的元素，导致这四种解答思路受挫.事实上，借助求比值的常规方法，不仅能求得BQ的长，而且图中相关线段的比值都是确定的、可求的，只不过计算量大，需要学生有足够的耐心.现以思路10为例进行解答.解：如图23，过点Q 作QE ⊥PB 于点E ，过点P 作PG ⊥BC 于点G.设BM =a ，PM =t .因为∠ABC =90°，BP ⊥AM .所以∠MAB =∠PBM.因为tan ∠MAB =12n，tan ∠PBM =t PB ，所以a 2na =t PB .解得PB =2nt .因为tan ∠MAB =PB AP =12n ，所以AP =4n 2t .因为PG ∥AB ，所以MG GB =PM AP =14n 2.因为MG +GB =a ，所以MG =a 1+4n 2，GB =4n 2a 1+4n 2.因为PG ∥AB ，所以PG AB =PM AM =t t +4n 2t =11+4n 2.所以PG =2na 1+4n2.因为PG ∥QB ，所以PG QB =CG CB.解得QB =2na 1+2n2.因为QE ∥AP ，所以QE AP =BE BP =QB AB =11+2n2.解得QE =4n 2t 1+2n 2，BE =2nt 1+2n 2.所以PE =PB -BE =2nt -2nt 1+2n 2=4n 3t 1+2n 2.所以tan∠BPQ =QE PE =4n 2t 1+2n 2⋅1+2n 24n 3t=1n .其实在设BC =2a 后，图中的元素均可求，设PM =t 是为了计算表达简洁.例如，思路3中，利用△APB ∽△BPM ∽△ABM “子母型相似”结构，可计算BP 的长；也可以延长CH 交AB 的延长线于点N （如图18），发现△ABM ∽△CHM ∽△CBN ，可计算出MH ，CH 的长，利用三角形全等可得PH 的长；或者发现B ，M ，H ，N 四点共圆，结合切割线定理和勾股定理求出相应线段的长，使问题得到解决.2.通性、通法的运用，如何更为熟练自然在思路10~思路13中，回归基本概念和基本图形应当是学生最自然的想法.然而，却受挫于求BQ 的长.为什么学生无法求出这个值？或许当学生对下面两道例题进行深入研究并能熟练应用后，会对上述思路的解答有所启发.例1如图24，过△ABC 的顶点C 任意作一条直线，与边AB 及中线AD 分别交于点F ，E ，求证：AE DE =2AF BF.ABCD F E图24借助平行线分线段成比例，此题有较多的解法.由D 为BC 的中点，直线BC 、直线AD 、直线AB 两两相交于点D ，B ，A ，且与这三条直线相关的是直线CF ，回到作平行线求比值的常规方法.可以进行如下解答.如图25，分别过点A ，B ，D 分别作直线CF 的垂线，垂线段分别记为h 1，h 2，h 3，则有h 1h 2=AF FB ，h 2h 3=BC CD ，h 3h 1=DE EA .将三式相乘，即可证得AE DE =2AF BF.ABCD FE h1h 2h 3图25借助这种优化后的求比值的通法，可对例2给出较为简洁的解法.例2如图26，线段OA ⊥OB ，点C 为OB 的中点，D 为线段OA 上一点，连接AC ，BD 交于点P.当OA =OB ，且D 为OA 中点时，求AP PC 的值.CA B Q MP 图23EGBA CODP图26BACO DP 图27h 1h 2h 3如图27，分别过点A ，O ，C 分别作直线BD 的垂线，垂线段分别记为h 1，h 2，h 3，则有h 1h 2=AD DO ，h2h 3=BO BC，h 3h 1=CP PA .将三式相乘，得AP CP =2.这种分别过点A ，O ，C 作直线BD 的垂线求比值的方法相对简洁，彰显了几何直观的魅力.这为笔者对前述题目进行多视角改编提供了支撑，就题挖掘与改编，可以更好地提升学生解题素养．题目的改编：锐角△ABC 中，∠ABC =60°，AB BC=n ，点M 是BC 上一动点，连接AM ，P 是AM 上一动点，连接CP 并延长交AB 于点Q .（1）如图28，若n =1，∠APQ =60°，求CQAM的值.（2）如图29，若n ≠1，CM BM =14，CP PQ =35，求AQQB 的值.（3）如图30，若n >1，CM BM =14，BP ⊥AM ，CQ ⊥AB ，求n 的值AB C MP Q A B C MP Q A BC MPQ 图28图29图30四、教学启示教育上的“慢”是客观规律，必须遵守，不能绕过去.在几何解题教学中，“绕”不过去的是“思”，“慢”的落脚点在“悟”.教学上的“慢”，应从确定性、本源性、全局性、动静互换等出发，回溯知识本源，着眼通性、通法，熟悉基本图形变换，浸润基本数学思想等处着力，展开理性分析和精准计算，知晓方法的来路，点亮学生思维的去路.1.教活思考习惯，理清思路来源由条件推算结论、由问题寻找条件、由问题前后的关联性逐步推理与计算，定性分析、定量计算是常用的解答手段.题目给出的图形中，线段之间、角之间必然有确定的逻辑联系和因果关系.因果明，则思之有路；图形定，则对应的数量关系及位置关系就随之确定.看条件、找结论、追其何处去是常用的分析、解决问题的思考方法.识图时，从全局入手，掌握“译式”方法，学会与条件“对话”，借助符号或未知数把条件转换到图形上，巧用图形建立联系.画图补形时，学生要懂得静能定位、动能生联系，主动发现点、边、角等元素之间的关系，关注变化中的不变，从图形结构中发现并拆分、重组常见的基本图形.这种动静互换思维，有助于寻找到相关元素之间的联系，从而联想到相关图形的性质、唤醒解答经验和方法，更好地展开定位分析和定量计算.解题时，要仔细审读条件，借助确定性、本源性、全局性、动静互换等思维，回归到知识源、特殊点和关键点展开联想，实现文字、图形、符号等数学语言的相互转化.例如，题目第（1）小题借助图形变换，还可以有以下思路.延长MB ，取BH =BM ，连接AH ，构造等腰三角形；或过点M ，A 分别作AB ，BC 的平行线，得矩形ABMH ，从特殊四边形的性质及CN ⊥AM 可推导出与∠NCB 相等的角，再通过三角形全等进行转化，证得BM =BN .就此小题而言，这些思路虽然复杂，但却与波利亚的解题理念相吻合，即拿一个有意义但又不复杂的题目去帮助学生挖掘问题的各个方面，使得通过这道题就好像通过一道“门户”，把学生引入一个完整的领域.把简单的题深入做，可以帮助学生更好地领悟解题的本质，引导学生发现知识之间的联系，形成深层次的思考，并借助图形变换及确定性、本源性、全局性、动静互换等解答后面两道小题，启发学生的思维.2.盘活思考方式，落细教学着力点，知晓方法来路笔者以2019年中考湖北武汉卷第23题为例，借助探究与类比，溯源强基，提炼求线段比值的方法.任何一种解法都依赖坚实的基础知识和扎实的数学基本功.易想难算、易算难想，解题思路没有捷径可走.熟练运用通性、通法后得到的巧妙解答是看透知识及方法本质后的火热思考，是真思考.在通性、通法的优化中，寻找着力固牢“四基”的讲题切入点，提升解题素养才是悟之必要.题目中内含“X型”“A型”“子母型”“隐圆”等基本图形，暗示着解题教学要着力于强化几何直观，洞察图形结构，丰富答题经验.在解答题目第（2）小题第①问时，有的学生从所求结论CPPQ =BMBQ出发，联想求线段成比例的通法，过点P作BC的平行线，或过点P作AB的平行线，或过点Q作AM的平行线，或过点Q作BC的平行线等，得到“A型”或“X型”等相似图形，暗示教学要着力于学生思维的最近发展区去应对和启发；洞察到“三垂直”结构，充分利用已知条件AB=AC，打开“另一扇窗”，凸显真实思维考量.3.激活思考方法，点亮思维去路解题研究无禁区，课堂教学有范围.对于教师来说，繁简解法、对错解法、优劣解法等都应该兼收并蓄.至于将哪一种解法用于课堂教学，则取决于教学要求和学生的实际情况.当前的数学教学，首先要在“如何让学生想得到”上下工夫，激活思考方式，启发学生在洞察结构上思本源，想通性、通法.题目第（2）小题第②问的解决，是先借助几何直观补形转化，再设元计算，从数的角度去剖析相关元素间的关系；从形的角度看，图10中，由“三垂直”模型，可得△ECB∽△MBA，利用相似三角形对应高的比等于相似比，得CFBP =BEAM=BCAB=1n.借助中位线定理，得BP=PF.于是可求得tan∠BPQ=tan∠CPF=CFPF=1n.笔者从形、数或形数结合等角度展开研题，并呈现各种繁与简的解法，为答疑学生的奇思妙想、放飞学生的思维做了充分准备.借助几何直观，把握图形结构，可以启发学生明了题意、展开联想，明白如何去想，“知其然”而得法.适度拓展，适时一题多解或多解归一，明了为什么要这样去想，知晓解法本质，“知其所以然”，达到举一反三.教师要引导学生回归知识本源，及时反思，充分经历试错、析错、纠错的过程，抓联系、知因果，突破思路，展开作图、计算、推理，厚植由确定展开理性分析与推算等必备的解题能力，让学生在尝试和慢悟中学会选择、转化、比较和优化，把握规律，灵活贯通，在还可以怎样去想上下足工夫，撬动思维的杠杆，推动学生进行深度思考，以点亮思维的去路．参考文献：［1］钱德春.解题教学应关注思维方式与思维心理［J］.中学数学教学参考（中旬），2018（10）：2-5.［2］张建华.关注模型特征提升解题能力：“动点路径”中考试题归类解法思考［J］.中国数学教育（初中版），2019（6）：48-52.［3］沈岳夫.洞察试题结构构造基本图形［J］.中国数学教育（初中版），2017（11）：47-50.［4］叶先玖，王胜兰，胡泽明.讲题的关注点：理性、确定、及时、适度［J］.中学数学杂志，2019（8）：48-52.。

中考数学24题专题练习1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H在边BF上，且∠HDF=∠E，连接CH，求证：∠BCH=45°﹣∠EBC．6、如图，直角梯形ABCD中，AD∥BC，∠B=90°，∠D=45°．（1）若AB=6cm，，求梯形ABCD的面积；（2）若E、F、G、H分别是梯形ABCD的边AB、BC、CD、DA上一点，且满足EF=GH，∠EFH=∠FHG，求证：HD=BE+BF．7、已知：如图，ABCD中，对角线AC，BD相交于点O，延长CD至F，使DF=CD，连接BF交AD于点E．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD 为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．（1）求证：AD=BE；（2）试判断△ABF的形状，并说明理由．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．求证：（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．30、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．参考答案1、如图，等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，连接BE，CE（1）求证：BE=CE；（2）若∠BEC=90°，过点B作BF⊥CD，垂足为点F，交CE于点G，连接DG，求证：BG=DG+CD．证明：（1）已知等腰梯形ABCD中，AD∥BC，AB=DC，E为AD中点，∴AB=DC，∠BAE=∠CDE，AE=DE，∴△BAE≌△CDE，∴BE=CE；（2）延长CD和BE的延长线交于H，∵BF⊥CD，∠HEC=90°，∴∠EBF+∠H=∠ECH+∠H=90°∴∠EBF=∠ECH，又∠BEC=∠CEH=90°，BE=CE（已证），∴△BEG≌△CEH，∴EG=EH，BG=CH=DH+CD，∵△BAE≌△CDE（已证），∴∠AEB=∠GED，∠HED=∠AEB，∴∠GED=∠HED，又EG=EH（已证），ED=ED，∴△GED≌△HED，∴DG=DH，∴BG=DG+CD．2、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，E为AB延长线上一点，连接ED，与BC交于点H．过E作CD的垂线，垂足为CD上的一点F，并与BC交于点G．已知G 为CH的中点．（1）若HE=HG，求证：△EBH≌△GFC；（2）若CD=4，BH=1，求AD的长．（1）证明：∵HE=HG，∴∠HEG=∠HGE，∵∠HGE=∠FGC，∠BEH=∠HEG，∴∠BEH=∠FGC，∵G是HC的中点，∴HG=GC，∴HE=GC，∵∠HBE=∠CFG=90°．∴△EBH≌△GFC；（2）解：∵ED平分∠AEF，∠A=∠DFE=90°，∴AD=DF，∵DF=DC﹣FC，∵△EBH≌△GFC，∴FC=BH=1，∴AD=4﹣1=3．3、如图，梯形ABCD中，AB∥CD，AD=DC=BC，∠DAB=60°，E是对角线AC延长线上一点，F是AD延长线上的一点，且EB⊥AB，EF⊥AF．（1）当CE=1时，求△BCE的面积；（2）求证：BD=EF+CE．（2）过E点作EM⊥DB于点M，四边形FDME是矩形，FE=DM，∠BME=∠BCE=90°，∠BEC=∠MBE=60°，△BME≌△ECB，BM=CE，继而可证明BD=DM+BM=EF+CE．（1）解：∵AD=CD，∴∠DAC=∠DCA，∵DC∥AB，∴∠DCA=∠CAB，∴，∵DC∥AB，AD=BC，∴∠DAB=∠CBA=60°，∴∠ACB=180°﹣（∠CAB+∠CBA）=90°，∴∠BCE=180°﹣∠ACB=90°，∵BE⊥AB，∴∠ABE=90°，∴∠CBE=∠ABE﹣∠ABC=30°，在Rt△BCE中，BE=2CE=2，，∴…（5分）（2）证明：过E点作EM⊥DB于点M，∴四边形FDME是矩形，∴FE=DM，∵∠BME=∠BCE=90°，∠BEC=∠MBE=60°，∴△BME≌△ECB，∴BM=CE，∴BD=DM+BM=EF+CE…（10分）4、如图．在平行四边形ABCD中，O为对角线的交点，点E为线段BC延长线上的一点，且．过点E作EF∥CA，交CD于点F，连接OF．（1）求证：OF∥BC；（2）如果梯形OBEF是等腰梯形，判断四边形ABCD的形状，并给出证明．解答：（1）证明：延长EF交AD于G（如图），在平行四边形ABCD中，AD∥BC，AD=BC，∵EF∥CA，EG∥CA，∴四边形ACEG是平行四边形，∴AG=CE，又∵，AD=BC，∴，∴∠ADC=∠ECF，在△CEF和△DGF中，∵∠CFE=∠DFG，∠ADC=∠ECF，CE=DG，∴△CEF≌△DGF（AAS），∴CF=DF，∵四边形ABCD是平行四边形，∴OB=OD，∴OF∥BE．（2）解：如果梯形OBEF是等腰梯形，那么四边形ABCD是矩形．证明：∵OF∥CE，EF∥CO，∴四边形OCEF是平行四边形，∴EF=OC，又∵梯形OBEF是等腰梯形，∴BO=EF，∴OB=OC，∵四边形ABCD是平行四边形，∴AC=2OC，BD=2BO．∴AC=BD，∴平行四边形ABCD是矩形．5、如图，梯形ABCD中，AD∥BC，∠ABC=90°，BF⊥CD于F，延长BF交AD的延长线于E，延长CD交BA的延长线于G，且DG=DE，AB=，CF=6．（1）求线段CD的长；（2）H在边BF上，且∠HDF=∠E，连接CH，求证：∠BCH=45°﹣∠EBC．（1）解：连接BD，由∠ABC=90°，AD∥BC得∠GAD=90°，又∵BF⊥CD，∴∠DFE=90°又∵DG=DE，∠GDA=∠EDF，∴△GAD≌△EFD，∴DA=DF，又∵BD=BD，∴Rt△BAD≌Rt△BFD（HL），∴BF=BA=，∠ADB=∠BDF又∵CF=6，∴BC=，又∵AD∥BC，∴∠ADB=∠CBD，∴∠BDF=∠CBD，∴CD=CB=8．（2）证明：∵AD∥BC，∴∠E=∠CBF，∴∠HDF=∠CBF ，由（1）得，∠ADB=∠CBD ，∴∠HDB=∠HBD ，∴HD=HB ，由（1）得CD=CB ，CBD CDBCBD HDF CDB CBH∴∠=∠∴∠-∠=∠-∠∠∠∴即BDH=HBDHB=HD∴△CDH ≌△CBH ，∴∠DCH=∠BCH ，∴∠BCH=∠BCD==．6、如图，直角梯形ABCD 中，AD ∥BC ，∠B=90°，∠D=45°．（1）若AB=6cm ，，求梯形ABCD 的面积；（2）若E 、F 、G 、H 分别是梯形ABCD 的边AB 、BC 、CD 、DA 上一点，且满足EF=GH ，∠EFH=∠FHG ，求证：HD=BE+BF ．解：（1）连AC ，过C 作CM ⊥AD 于M ，如图，在Rt △ABC 中，AB=6，sin ∠ACB==，∴AC=10，∴BC=8，在Rt △CDM 中，∠D=45°，∴DM=CM=AB=6，∴AD=6+8=14，∴梯形ABCD 的面积=•（8+14）•6=66（cm 2）；（2）证明：过G 作GN ⊥AD ，如图，∵∠D=45°，∴△DNG 为等腰直角三角形，∴DN=GN ，又∵AD ∥BC ，∴∠BFH=∠FHN ，而∠EFH=∠FHG ，∴∠BFE=∠GHN ，∵EF=GH ，∴Rt △BEF ≌Rt △NGH ，∴BE=GN ，BF=HN ，∴DA=AN+DN=AN+DG=BF+BE ．7、已知：如图，▱ABCD 中，对角线AC ，BD 相交于点O ，延长CD 至F ，使DF=CD ，连接BF 交AD 于点E ．（1）求证：AE=ED；（2）若AB=BC，求∠CAF的度数．（1）证明：如图．∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．∵DF=CD，∴AB∥DF．∵DF=CD，∴AB=DF．∴四边形ABDF是平行四边形，∴AE=DE．（2）解：∵四边形ABCD是平行四边形，且AB=BC，∴四边形ABCD是菱形．∴AC⊥BD．∴∠COD=90°．∵四边形ABDF是平行四边形，∴AF∥BD．∴∠CAF=∠COD=90°．8、已知：如图，在正方形ABCD中，点G是BC延长线上一点，连接AG，分别交BD、CD于点E、F．（1）求证：∠DAE=∠DCE；（2）当CG=CE时，试判断CF与EG之间有怎样的数量关系？并证明你的结论．（1）证明：在△DAE和△DCE中，∠ADE=∠CDE（正方形的对角线平分对角），ED=DE（公共边），AE=CE（正方形的四条边长相等），∴△DAE≌△DCE （SAS），∴∠DAE=∠DCE（全等三角形的对应角相等）；（2）解：如图，由（1）知，△DAE≌△DCE，∴AE=EC，∴∠EAC=∠ECA（等边对等角）；又∵CG=CE（已知），∴∠G=∠CEG（等边对等角）；而∠CEG=2∠EAC（外角定理），∠ECB=2∠CEG（外角定理），∴4∠EAC﹣∠ECA=∠ACB=45°，∴∠G=∠CEG=30°；过点C作CH⊥AG于点H，∴∠FCH=30°，∴在直角△ECH中，EH=CH，EG=2CH，在直角△FCH中，CH=CF，∴EG=2×CF=3CF．9、如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．（1）求证：DP平分∠ADC；（2）若∠AEB=75°，AB=2，求△DFP的面积．（1）证明：连接PC．∵ABCD是正方形，∴∠ABE=∠ADF=90°，AB=AD．∵BE=DF，∴△ABE≌△ADF．（SAS）∴∠BAE=∠DAF，AE=AF．∴∠EAF=∠BAD=90°．∵P是EF的中点，∴PA=EF，PC=EF，∴PA=PC．又AD=CD，PD公共，∴△PAD≌△PCD，（SSS）∴∠ADP=∠CDP，即DP平分∠ADC；（2）作PH⊥CF于H点．∵P是EF的中点，∴PH=EC．设EC=x．由（1）知△EAF是等腰直角三角形，∴∠AEF=45°，∴∠FEC=180°﹣45°﹣75°=60°，∴EF=2x，FC=x，BE=2﹣x．在Rt△ABE中，22+（2﹣x）2=（x）2解得x1=﹣2﹣2（舍去），x2=﹣2+2．∴PH=﹣1+，FD=（﹣2+2）﹣2=﹣2+4．∴S△DPF=（﹣2+4）×=3﹣5．10、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，BD=BC，E为CD的中点，交BC的延长线于F；（1）证明：EF=EA；（2）过D作DG⊥BC于G，连接EG，试证明：EG⊥AF．（1）证明：∵AD∥BC，∴∠DAE=∠F，∠ADE=∠FCE．∵E为CD的中点，∴ED=EC．∴△ADE≌△FCE．∴EF=EA．（5分）（2）解：连接GA，∵AD∥BC，∠ABC=90°，∴∠DAB=90°．∵DG⊥BC，∴四边形ABGD是矩形．∴BG=AD，GA=BD．∵BD=BC，∴GA=BC．由（1）得△ADE≌△FCE，∴AD=FC．∴GF=GC+FC=GC+AD=GC+BG=BC=GA．∵由（1）得EF=EA，∴EG⊥AF．（5分）11、如图，直角梯形ABCD中，∠DAB=90°，AB∥CD，AB=AD，∠ABC=60度．以AD 为边在直角梯形ABCD外作等边三角形ADF，点E是直角梯形ABCD内一点，且∠EAD=∠EDA=15°，连接EB、EF．（1）求证：EB=EF；（2）延长FE交BC于点G，点G恰好是BC的中点，若AB=6，求BC的长．（1）证明：∵△ADF为等边三角形，∴AF=AD，∠FAD=60°（1分）∵∠DAB=90°，∠EAD=15°，AD=AB（2分）∴∠FAE=∠BAE=75°，AB=AF，（3分）∵AE为公共边∴△FAE≌△BAE（4分）∴EF=EB（5分）（2）解：如图，连接EC．（6分）∵在等边三角形△ADF中，∴FD=FA，∵∠EAD=∠EDA=15°，∴ED=EA，∴EF是AD的垂直平分线，则∠EFA=∠EFD=30°．（7分）由（1）△FAE≌△BAE知∠EBA=∠EFA=30°．∵∠FAE=∠BAE=75°，∴∠BEA=∠BAE=∠FEA=75°，∴BE=BA=6．∵∠FEA+∠BEA+∠GEB=180°，∴∠GEB=30°，∵∠ABC=60°，∴∠GBE=30°∴GE=GB．（8分）∵点G是BC的中点，∴EG=CG∵∠CGE=∠GEB+∠GBE=60°，∴△CEG为等边三角形，∴∠CEG=60°，∴∠CEB=∠CEG+∠GEB=90°（9分）∴在Rt△CEB中，BC=2CE，BC2=CE2+BE2∴CE=，∴BC=（10分）；解法二：过C作CQ⊥AB于Q，∵CQ=AB=AD=6，∵∠ABC=60°，∴BC=6÷=4．12、如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于点E，F是CD的中点，DG是梯形ABCD的高．（1）求证：AE=GF；（2）设AE=1，求四边形DEGF的面积．（1）证明：∵AB=DC，∴梯形ABCD为等腰梯形．∵∠C=60°，∴∠BAD=∠ADC=120°，又∵AB=AD，∴∠ABD=∠ADB=30°．∴∠DBC=∠ADB=30°．∴∠BDC=90°．（1分）由已知AE⊥BD，∴AE∥DC．（2分）又∵AE为等腰三角形ABD的高，∴E是BD的中点，∵F是DC的中点，∴EF∥BC．∴EF∥AD．∴四边形AEFD是平行四边形．（3分）∴AE=DF（4分）∵F是DC的中点，DG是梯形ABCD的高，∴GF=DF，（5分）∴AE=GF．（6分）（2）解：在Rt△AED中，∠ADB=30°，∵AE=1，∴AD=2．在Rt△DGC中∠C=60°，并且DC=AD=2，∴DG=．（8分）由（1）知：在平行四边形AEFD中EF=AD=2，又∵DG⊥BC，∴DG⊥EF，∴四边形DEGF的面积=EF•DG=．（10分）13、已知，如图在直角梯形ABCD中，AD∥BC，∠ABC=90°，DE⊥AC于点F，交BC于点G，交AB的延长线于点E，且AE=AC，连AG．（1）求证：FC=BE；（2）若AD=DC=2，求AG的长．解答：（1）证明：∵∠ABC=90°，DE⊥AC于点F，∴∠ABC=∠AFE．∵AC=AE，∠EAF=∠CAB，∴△ABC≌△AFE，∴AB=AF．∴AE﹣AB=AC﹣AF，即FC=BE；（2）解：∵AD=DC=2，DF⊥AC，∴AF=AC=AE．∴AG=CG，∴∠E=30°．∵∠EAD=90°，∴∠ADE=60°，∴∠FAD=∠E=30°，∴FC=，∵AD∥BC，∴∠ACG=∠FAD=30°，∴CG=2，∴AG=2．14、如图，直角梯形ABCD中，AD∥BC，∠ABC=90°，点E是AB边上一点，AE=BC，DE⊥EC，取DC的中点F，连接AF、BF．（1）求证：AD=BE；（2）试判断△ABF的形状，并说明理由．（1）证明：∵AD∥BC，∴∠BAD+∠ABC=180°，∵∠ABC=90°，∴∠BAD=∠ABC=90°，∵DE⊥EC，∴∠AED+∠BEC=90°∵∠AED+∠ADE=90°，∴∠BEC=∠ADE，∵∠DAE=∠EBC，AE=BC，∴△EAD≌△EBC，∴AD=BE．（2）答：△ABF是等腰直角三角形．理由是：延长AF交BC的延长线于M，∵AD∥BM，∴∠DAF=∠M，∵∠AFD=∠CFM，DF=FC，∴△ADF≌△MFC，∴AD=CM，∵AD=BE，∴BE=CM，∵AE=BC，∴AB=BM，∴△ABM是等腰直角三角形，∵△ADF≌△MFC，∴AF=FM，∴∠ABC=90°，∴BF⊥AM，BF=AM=AF，∴△AFB是等腰直角三角形．15、（2011•潼南县）如图，在直角梯形ABCD中，AB∥CD，AD⊥DC，AB=BC，且AE⊥BC．（1）求证：AD=AE；（2）若AD=8，DC=4，求AB的长．解答：（1）证明：连接AC，∵AB∥CD，∴∠ACD=∠BAC，∵AB=BC，∴∠ACB=∠BAC，∴∠ACD=∠ACB，∵AD⊥DC，AE⊥BC，∴∠D=∠AEC=90°，∵AC=AC，∴，∴△ADC≌△AEC，（AAS）∴AD=AE；（2）解：由（1）知：AD=AE，DC=EC，设AB=x，则BE=x﹣4，AE=8，在Rt△ABE中∠AEB=90°，由勾股定理得：82+（x﹣4）2=x2，解得：x=10，∴AB=10．说明：依据此评分标准，其它方法如：过点C作CF⊥AB用来证明和计算均可得分．16、如图，已知梯形ABCD中，AD∥CB，E，F分别是BD，AC的中点，BD平分∠ABC．（1）求证：AE⊥BD；（2）若AD=4，BC=14，求EF的长．（1）证明：∵AD∥CB，∴∠ADB=∠CBD，又BD平分∠ABC，∴∠ABD=∠CBD，∴∠ADB=∠ABD，∴AB=AD，∴△ABD是等腰三角形，已知E是BD的中点，∴AE⊥BD．（2）解：延长AE交BC于G，∵BD平分∠ABC，∴∠ABE=∠GBE，又∵AE⊥BD（已证），∴∠AEB=∠GEB，BE=BE，∴△ABE≌△GBE，∴AE=GE，BG=AB=AD，又F是AC的中点（已知），所以由三角形中位线定理得：EF=CG=（BC﹣BG）=（BC﹣AD）=×（14﹣4）=5．答：EF的长为5．17、如图，在梯形ABCD中，AD∥BC，∠D=90°，BE⊥AC，E为垂足，AC=BC．（1）求证：CD=BE；（2）若AD=3，DC=4，求AE．（1）证明：∵AD∥BC，∴∠DAC=∠BCE，而BE⊥AC，∴∠D=∠BEC=90°，AC=BC，∴△BCE≌△CAD．∴CD=BE．（2）解：在Rt△ADC中，根据勾股定理得AC==5，∵△BCE≌△CAD，∴CE=AD=3．∴AE=AC﹣CE=2．18、如图，在梯形ABCD中，AD∥BC，AB⊥AC，∠B=45°，AD=1，BC=4，求DC的长．解：如图，过点D作DF∥AB，分别交AC，BC于点E，F．（1分）∵AB⊥AC，∴∠AED=∠BAC=90度．∵AD∥BC，∴∠DAE=180°﹣∠B﹣∠BAC=45度．在Rt△ABC中，∠BAC=90°，∠B=45°，BC=4，∴AC=BC•sin45°=4×=2（2分）在Rt△ADE中，∠AED=90°，∠DAE=45°，AD=1，∴DE=AE=．∴CE=AC﹣AE=．（4分）在Rt△DEC中，∠CED=90°，∴DC==．（5分）19、已知梯形ABCD中，AD∥BC，AB=BC=DC，点E、F分别在AD、AB上，且．（1）求证：BF=EF﹣ED；（2）连接AC，若∠B=80°，∠DEC=70°，求∠ACF的度数．证明：∵FC=F′C，EC=EC，∠ECF'=∠BCF+∠DCE=∠ECF，∴△FCE≌△F′CE，∴EF′=EF=DF′+ED，∴BF=EF﹣ED；（2）解：∵AB=BC，∠B=80°，∴∠ACB=50°，由（1）得∠FEC=∠DEC=70°，∴∠ECB=70°，而∠B=∠BCD=80°，∴∠DCE=10°，∴∠BCF=30°，∴∠ACF=∠BCA﹣∠BCF=20°．20、如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，且AF⊥AB，连接EF．（1）若EF⊥AF，AF=4，AB=6，求AE的长．（2）若点F是CD的中点，求证：CE=BE﹣AD．解：（1）作EM⊥AB，交AB于点M．∵AE=BE，EM⊥AB，∴AM=BM=×6=3；∵∠AME=∠MAF=∠AFE=90°，∴四边形AMEF是矩形，∴EF=AM=3；在Rt△AFE中，AE==5；（2）延长AF、BC交于点N．∵AD∥EN，∴∠DAF=∠N；∵∠AFD=∠NFC，DF=FC，∴△ADF≌△NCF（AAS），∴AD=CN；∵∠B+∠N=90°，∠BAE+∠EAN=90°，又AE=BE，∠B=∠BAE，∴∠N=∠EAN，AE=EN，∴BE=EN=EC+CN=EC+AD，∴CE=BE﹣AD．．21、如图，四边形ABCD为等腰梯形，AD∥BC，AB=CD，对角线AC、BD交于点O，且AC⊥BD，DH⊥BC．（1）求证：DH=（AD+BC）；（2）若AC=6，求梯形ABCD的面积．解：（1）证明：过D作DE∥AC交BC延长线于E，（1分）∵AD∥BC，∴四边形ACED为平行四边形．（2分）∴CE=AD，DE=AC．∵四边形ABCD为等腰梯形，∴BD=AC=DE．∵AC⊥BD，∴DE⊥BD．∴△DBE为等腰直角三角形．（4分）∵DH⊥BC，∴DH=BE=（CE+BC）=（AD+BC）．（5分）（2）∵AD=CE，∴．（7分）∵△DBE为等腰直角三角形BD=DE=6，∴．∴梯形ABCD的面积为18．（8分）注：此题解题方法并不唯一．22、已知，如图，△ABC是等边三角形，过AC边上的点D作DG∥BC，交AB于点G，在GD的延长线上取点E，使DE=DC，连接AE，BD．（1）求证：△AGE≌△DAB；（2）过点E作EF∥DB，交BC于点F，连AF，求∠AFE的度数．（1）证明：∵△ABC是等边三角形，DG∥BC，∴∠AGD=∠ABC=60°，∠ADG=∠ACB=60°，且∠BAC=60°，∴△AGD是等边三角形，AG=GD=AD，∠AGD=60°．∵DE=DC，∴GE=GD+DE=AD+DC=AC=AB，∵∠AGD=∠BAD，AG=AD，∴△AGE≌△DAB；（2）解：由（1）知AE=BD，∠ABD=∠AEG．∵EF∥DB，DG∥BC，∴四边形BFED是平行四边形．∴EF=BD，∴EF=AE．∵∠DBC=∠DEF，∴∠ABD+∠DBC=∠AEG+∠DEF，即∠AEF=∠ABC=60°．∴△AFE是等边三角形，∠AFE=60°．23、如图，梯形ABCD中，AD∥BC，DE=EC，EF∥AB交BC于点F，EF=EC，连接DF．（1）试说明梯形ABCD是等腰梯形；（2）若AD=1，BC=3，DC=，试判断△DCF的形状；（3）在条件（2）下，射线BC上是否存在一点P，使△PCD是等腰三角形，若存在，请直接写出PB的长；若不存在，请说明理由．解：（1）证明：∵EF=EC，∴∠EFC=∠ECF，∵EF∥AB，∴∠B=∠EFC，∴∠B=∠ECF，∴梯形ABCD是等腰梯形；（2）△DCF是等腰直角三角形，证明：∵DE=EC，EF=EC，∴EF=CD，∴△CDF是直角三角形（如果一个三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形），∵梯形ABCD是等腰梯形，∴CF=（BC﹣AD）=1，∵DC=，∴由勾股定理得：DF=1，∴△DCF是等腰直角三角形；（3）共四种情况：∵DF⊥BC，∴当PF=CF时，△PCD是等腰三角形，即PF=1，∴PB=1；当P与F重合时，△PCD是等腰三角形，∴PB=2；当PC=CD=（P在点C的左侧）时，△PCD是等腰三角形，∴PB=3﹣；当PC=CD=（P在点C的右侧）时，△PCD是等腰三角形，∴PB=3+．故共四种情况：PB=1，PB=2，PB=3﹣，PB=3+．（每个1分）24、如图，在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，AD=DC，E、F分别在AD、DC的延长线上，且DE=CF．AF交BE于P．（1）证明：△ABE≌△DAF；（2）求∠BPF的度数．解答：（1）证明：∵在梯形ABCD中，AD∥BC，∠ABC=∠BCD=60°，∴AB=CD，∵AD=DC，∴BA=AD，∠BAE=∠ADF=120°，∵DE=CF，∴AE=DF，在△BAE和△ADF中，，∴△ABE≌△DAF（SAS）．（2）解：∵由（1）△BAE≌△ADF，∴∠ABE=∠DAF．∴∠BPF=∠ABE+∠BAP=∠BAE．而AD∥BC，∠C=∠ABC=60°，∴∠BPF=120°．25、如图，在梯形ABCD中，AD∥BC，AB=AD=DC，BD⊥DC，将BC延长至点F，使CF=CD．（1）求∠ABC的度数；（2）如果BC=8，求△DBF的面积？解答：解：（1）∵AD∥BC，∴∠ADB=∠DBC，∵AB=AD，∴∠ADB=∠ABD，∴∠DBC=∠ABD，∵在梯形ABCD中AB=DC，∴∠ABC=∠DCB=2∠DBC，∵BD⊥DC，∴∠DBC+2∠DBC=90°∴∠DBC=30°∴∠ABC=60°（2）过点D作DH⊥BC，垂足为H，∵∠DBC=30°，BC=8，∴DC=4，∵CF=CD∴CF=4，∴BF=12，∵∠F+∠FDC=∠DCB=60°，∠F=∠FDC∴∠F=30°，∵∠DBC=30°，∴∠F=∠DBC，∴DB=DF，∴，在直角三角形DBH中，∴，∴，∴，即△DBF的面积为．26、如图，梯形ABCD中，AD∥BC，AB=DC=10cm，AC交BD于G，且∠AGD=60°，E、F分别为CG、AB的中点．（1）求证：△AGD为正三角形；（2）求EF的长度．（1）证明：连接BE，∵梯形ABCD中，AB=DC，∴AC=BD，可证△ABC≌△DCB，∴∠GCB=∠GBC，又∵∠BGC=∠AGD=60°∴△AGD为等边三角形，（2）解：∵BE为△BCG的中线，∴BE⊥AC，在Rt△ABE中，EF为斜边AB上的中线，∴EF=AB=5cm．27、已知，如图，AD∥BC，∠ABC=90°，AB=BC，点E是AB上的点，∠ECD=45°，连接ED，过D作DF⊥BC于F．（1）若∠BEC=75°，FC=3，求梯形ABCD的周长．（2）求证：ED=BE+FC．解：（1）∵∠BEC=75°，∠ABC=90°，∴∠ECB=15°，∵∠ECD=45°，∴∠DCF=60°，在Rt△DFC中：∠DCF=60°，FC=3，∴DF=3，DC=6，由题得，四边形ABFD是矩形，∴AB=DF=3，∵AB=BC，∴BC=3，∴BF=BC﹣FC=3﹣3，∴AD=DF=3﹣3，∴C梯形ABCD=3×2+6+3﹣3=9+3，答：梯形ABCD的周长是9+3．（2）过点C作CM垂直AD的延长线于M，再延长DM到N，使MN=BE，∴CN=CE，可证∠NCD=∠DCE，∵CD=CD，∴△DEC≌△DNC，∴ED=EN，∴ED=BE+FC．28、（2005•镇江）已知：如图，梯形ABCD中，AD∥BC，E是AB的中点，直线CE交DA的延长线于点F．（1）求证：△BCE≌△AFE；（2）若AB⊥BC且BC=4，AB=6，求EF的长．（1）证明：∵AD∥BC，E是AB的中点，∴AE=BE，∠B=∠EAF，∠BCE=∠F．∴△BCE≌△AFE（AAS）．（2）解：∵AD∥BC，∴∠DAB=∠ABC=90°．∵AE=BE，∠AEF=∠BEC，∴△BCE≌△AFE．∴AF=BC=4．∵EF2=AF2+AE2=9+16=25，∴EF=5．29、已知：如图，在梯形ABCD中，AD∥BC，BC=DC，CF平分∠BCD，DF∥AB，BF 的延长线交DC于点E．求证：（1）△BFC≌△DFC；（2）AD=DE；（3）若△DEF的周长为6，AD=2，BC=5，求梯形ABCD的面积．（1）∵DC=BC，∠1=∠2，CF=CF，∴△DCF≌△BCF．（2）延长DF交BC于G，∵AD∥BG，AB∥DG，∴四边形ABGD为平行四边形．∴AD=BG．∵△DFC≌△BFC，∴∠EDF=∠GBF，DF=BF．又∵∠3=∠4，∴△DFE≌△BFG．∴DE=BG，EF=GF．∴AD=DE．（3）∵EF=GF，DF=BF，∴EF+BF=GF+DF，即：BE=DG．∵DG=AB，∴BE=AB．∵C△DFE=DF+FE+DE=6，∴BF+FE+DE=6，即：EB+DE=6．∴AB+AD=6．又∵AD=2，∴AB=4．∴DG=AB=4．∵BG=AD=2，∴GC=BC﹣BG=5﹣2=3．又∵DC=BC=5，在△DGC中∵42+32=52∴DG2+GC2=DC2∴∠DGC=90°．∴S梯形ABCD=（AD+BC）•DG=（2+5）×4=14．30、如图，梯形ABCD中，AD∥BC．∠C=90°，且AB=AD．连接BD，过A点作BD的垂线，交BC于E．（1）求证：四边形ABED是菱形；（2）如果EC=3cm，CD=4cm，求梯形ABCD的面积．解答：解：（1）证明：∵AD∥BC，DE2=CD2+CE2=42+32=25，∴∠OAD=∠OEB，∴DE=5又∵AB=AD，AO⊥BD，∴AD=BE=5，∴OB=OD，∴S梯形ABCD=．又∵∠AOD=∠EOB，∴△ADO≌△EBO（AAS），∴AD=EB，又∵AD∥BE，∴四边形ABCD是平行四边形，又∵AB=AD∴四边形ABCD是菱形．（2）∵四边形ABCD是菱形，∴AD=DE=BE，。

1一道几何题目的演变“变式教学”为学生架起了一座知识的桥梁，引导学生从“变”的现象中发现“不变”的本质；从“不变”的本质中探究“变”的规律，使学生更深刻地理解数学知识，对提高学生思维能力、应变能力大有裨益．所谓变式训练就是保持原命题的本质不变，不断变换原命题的条件、结论、图形等产生新的情境，引导学生从多角度、多方面去探究问题．现以一道课本习题为例，谈谈如何进行变式训练．例题 如图1，已知点C 为线段AB 上的一点，分别以线段AC 、BC 为边作正△ACM 和正△BCN ，求证：AN ＝BM ．简解 由等边三角形的性质可以得出△ACN ，△MCB 两边及其夹角分别对应相等，从而△ACN ≌△MCB ，得出线段AN 与线段BM 相等．点评 三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主．判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．本题考查了等边三角形的性质的运用，全等三角形的判定与性质的运用，解答时证明三角形全等是关键，注意：全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，HL ，全等三角形的对应边、对应角相等．演变1 植入新问：不改变原命题的条件和结论，在原命题中植入新的问题，拓宽对图形性质的进一步研究．(1)求证：DC ＝CE ；(2)图2中，线段AN 与BM 相交于点O ，求∠BON 度数；（3）若连结OC ，如图3，则OC 平分∠AOB 吗？请说明理由．解析 (1)由△ACN ≌△MCB ，可得∠DNC ＝∠EBC ，又∠DCN ＝∠ECB ＝60°，CN ＝CB ，得△DCN ≌△ECB ，结论得证，在此基础上，若连结线段DE ，如图2，可求证DE ∥AB ．(2)由∠BON ＝∠AOM ＝∠NAB ＋∠ABM ＝∠CMB ＋∠CBM ＝∠ACM 而得出结论．(3)过点C 作CG ⊥AN ，CH ⊥BM ，由△ACN ≌△MCB ，得到两三角形面积相等，由2AN ＝BM ，得到CG ＝CH ，再利用角平分线定理即可得证．演变2 克隆变式：原命题条件、结论不变，将正三角形变为正方边形、菱形等．(4)①将原题中“△ACM 和△BCN 两个等边三角形”换成“两个正方形”（如图4），AF 与BD 的关系如何？②如果点C 在线段AB 的延长线上，a 中结论是否成立？请作图，并说明理由．解析（AF 与BD 有数量关系和位置关系．四边形ACDE 、CBGF 是正方形，AC ＝CD ，CF ＝CB ，∠ACF ＝∠DCB ＝90°，可证△ACF ≌△DCB(SAS)，得AF ＝BD ；延长AF 交DB 于点G ，根据∠FAC ＝∠BCD ，对顶角相等，得∠BGN ＝∠MCB ＝90°，即BD ⊥AC ． ②先证△AFC ≌△DBC 可得结论成立．评注 此题主要考查了正方形的性质，全等三角形的性质和判定的应用，以及学生的推理能力．(5)上述问题中，若将其中一个正方形固定，使另一个正方形绕点C 任意旋转一个角度，如图6，上述结论还能成立吗？为什么？解析 抓住运动中不变的元素，证明思路与(4)类似．(6)（2014年南通中考题）如图7，点E 是菱形ABCD 对角线CA 的延长线上任意一点，以线段AE 为边作一个菱形AEFG ，且菱形AEFG∽菱形ABCD ，连结EB、GD ．①求证：EB ＝DG ；②若∠DAB ＝60°，AB＝2，AG ，求GD 的长．3解析 ①利用相似多边形的对应角相等和菱形的四边相等证得三角形全等后即可证得两条线段相等；②连接BD 交AC 于点P(如图8)，则BP ⊥AC ．根据∠DAB ＝60°，BP ＝12AB ＝1，得到EP ＝；利用勾股定理求得EB 的长，即可求得线段GD 的长．点评 本题考查了相似多边形的性质，解题的关键是了解相似多边形的对应边的比相等、对应角相等．演变3 变为探究题：将原命题的题设、结论进行弱化处理，变为条件开放或结论开放题；或在保持图形的某些性质不变的情况下，将图形中的某些元素（点、线等）运动起来，从形外到形内再到形外，在运动中寻找不变关系或变化的规律．(7)已知：如图9所示，在△ABC 和△ADE 中，AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE ，且点B 、A 、D 在一条直线上，连结BE ，CD ，M ，N 分别为BE ，CD 的中点．①求证：(i)BE ＝CD ；(ii)△AMN 是等腰三角形．②在图9的基础上，将△ADE 绕点A 按顺时针方向旋转180°，其他条件不变，如图10．请直接写出①中的两个结论是否仍然成立．解析 ①(i)由∠BAC ＝∠DAE ，等式左右两边都加上∠CAE ，得到一对角相等，再由AB ＝AC ，AF 为公共边，利用SAS 可得出三角形ABE 与三角形ACD 全等，由全等三角形的对应边相等可得出BE ＝CD ；(ii)由M 与N 分别为BE ，CD 的中点，且BE ＝CD ，可得出ME ＝ND ，由△ABE 与△ACD 全等，得到对应边AE ＝AD ，对应角∠AEB ＝∠ADC ，利用SAS 可得出△AME 与△AND 全等，利用全等三角形的对应边相等可得出AM ＝AN ，即△AMN 为等腰三角形． ②结论仍成立，方法类似．点评 此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．(8)已知在△AB.C 中，∠BAC ＝90°，∠ABC ＝45°，点D 为直线BC 上一动点（点D 不与点B 、C 重合），以AD 为边作正方形ADEF ，连结CF ．①如图11，当点D 在线段BC 上时，求证CF ＋CD ＝BC ；②如图12，当点D 在线段BC 的延长线上时，其他条件不变，请直接写出CF ，BC ，CD 三条线段之间的关系；③如图13，当点D 在线段BC 的反向延长线上时，且点A 、F 分别在直线BC 的两侧，其他条件不变，求CF，BC，CD三条线段之间的关系；解析(1)△ABC是等腰直角三角形，利用SAS即可证明△BDD≌△CAF，从而证得CF＝BD，据此即可证得；②同(1)相同，利用SAS即可证得△BAD≌△CAF，从而证得BD＝CF，即可得到CF－CD＝BC；③首先证明△BDD≌△CAF，△FCD是直角三角形，然后根据正方形的性质即可求得DF的长，则OC即可求得．点评本题考查了正方形与全等三角形的判定与性质的综合应用，证明三角形全等是关键．数学教育家波利亚认为：“与其穷于应付烦琐的数学内容和过量的题目，还不如适当选择某些有意义但又不太复杂的题目去帮助学生发掘题目的各个方面，在指导学生解题过程中，提高他们的才智与推理能力．”教学中重视对例题和习题的“改装”或引申，把分散的知识点串成一条线，最大可能地覆盖知识点，有利于知识的建构，当然，变式训练要由浅入深，由简到繁，由特殊到一般，循序渐进，螺旋上升，形成一系列的问题串、知识链、方法链．让学生在变题中，学会探索；在变题中，学会创造；在变题中，把自己变得更聪明，更机智，领略到数学的和谐、奇异与美妙，收到极好的学习效果．4。

考题追本溯源，由习题走向中考作者：***来源：《中学教学参考·理科版》2021年第08期[摘要]對考题开展追本溯源有助于理解问题，发掘结论.中考几何探究题往往与教材的习题、模型、结论有着一定的关联，深入探究可显著提升解题能力，发展数学思维.文章以一道中考几何探究题为例进行考题溯源、解法探究，并开展教学反思.[关键词]习题;几何;相似;模型;探究教材是知识的本源，习题具有强化知识、引导方法的作用.历年的中考压轴题往往“根”源于教材习题，深入研读习题可以获得典型问题的解题思路.因此考题教学中，有必要深入探究考题，对考题进行追本溯源.下面以一道2020年中考压轴题为例进行具体探究.一、考题呈现评析：本题为几何探究题，以“基础巩固→尝试应用→拓展提高”的形式引导学生探究，题目所涉三个小问既相互独立又存在关联.理解“基础巩固”环节问题的结构和解法思路对于后续问题的探究极为关键.二、考题探究1.问题溯源第（1）问，设定[△ABC]的[AB]边上的一点为D，与C相连后形成三个共边共角三角形：[△ABC]、[△ADC]、[△BDC].分析图形结构发现，问题源自人教版教材九年级下册第36题的习题2，其内容如下.虽然考题与习题的条件存在差异，但本质上是一致的，图像所涉三个三角形是相似关系，以第（1）问证明为例，过程如下：实则在该相似模型中，还可以由相似性质转化出线段之间的乘积关系，由于[△ACD∼△ABC]，则[ACAD=ABAC]，所以[AC2=AD·AB]，这也是上述考题“基础巩固”环节结论证明的思路方法.2.问题解析（1）参考问题溯源中习题的解析思路，要证明三线段之间的乘积关系，只需要证明[△ABC∽△ACD]，该对相似三角形存在一个显著特点：含有一个公共角、一条公共边，图形结构为初中数学常见的共边共角相似模型.（2）该问依托平行四边形构建了与（1）问相似的共边三角形，问题突破还需参考上述模型的解析思路.具体突破时可进行图形分割，[EF]将[△BCF]分割为[△BFE]和[△ECF]，三者互为共边共角三角形.求[AD]的长，则可由平行四边形的性质进行等量转化，即[AD=BC]，则后续只需分析[BE]、[BF]和[BC]三线段关系即可，显然可将其转化为分析[△BFE]和[△BCF]的图形关系.参考上述问题，可知只需证明两者相似.（3）该问以菱形为背景，求菱形的边长，根据上述问题突破的思路，显然需要在图形中构建共边共角相似模型，然后利用相似性质进行比例关系转化，进而求出线段长.注意到条件[EF∥AC]，则可分别延长[EF]和[DC]，设两线交点为G，如图6所示，则在[△DEF]中存在共边共角相似模型，具体求解过程如下.3.问题评析上述以探究的形式，依托共边共角相似模型构建了几何综合题，整体难度适中.第（1）问的基础巩固实则就是引导学生回顾教材中的共边共角相似模型，这也是整个问题突破的核心关键，掌握三角形相似比例变换是重点.后续两问所考查的侧重点略有不同，第（2）问侧重复杂图像中的模型提取，而第（3）问侧重模型的综合构建，上述突破过程充分利用菱形、平行四边形等基本图形的性质，有效实现问题转化.三、解后思考1.重视图像解析，追溯问题原型中考几何探究题往往进行阶梯递进设问，图像结构由简单到复杂，充分理解图像、掌握图形特点是关键.因此在读题阶段要重视图像解析，必要时可进行问题溯源，思考问题在教材中的原型，从而联想解题思路，获得对应的解题策略，这也是中考几何探究题的重要考查方向.如上述几何探究题实则是对教材共边共角模型的拓展变式，利用相似模型的结论可直接获得关键条件，从而高效破解.在教学中，教师应重视教材经典习题的讲解，结合数学模型来引导学生掌握问题突破策略.2.重视结论归纳，关注模型变化几何探究题侧重考查学生提炼结论、总结归纳能力，即基于几何问题的条件、特征提取结论，形成问题的解析策略.如上述探究题中提取了共边共角模型，利用相似比例关系推导线段长，模型的结论是后续破解的基础.因此在探究教学中，要注重提升学生的总结归纳能力，引导学生掌握总结问题、归纳结论的方法，提升学生的数学能力.另外，归纳总结是建立在对模型的深层理解上，故教学中教师还应引导学生关注模型变化，从模型的一般性中获得特殊的结论，逐步提升学生的综合能力.3.重视探究过程，发展数学思维“经历探究过程，总结问题结论”是探究型问题的典型特点，即考题以探究形式引导学生思考，进行结论总结，强化应用.因此该类问题更为关注学生的思维过程，教学中教师要注重培养学生发现问题、猜想验证的能力，发展学生的数学思维，可结合具体内容开展探究活动，引导学生操作实践、独立思考.以上述几何探究题的共边共角模型为例，可首先展示习题，让学生思考问题图像的特点，然后讨论问题解析方法，总结并验证结论，在此基础上进行拓展探究，可以函数图像为背景进一步变式探究，帮助学生完成知识融合与思维完善.四、写在最后几何探究题往往注重对教材习题、模型、结论的挖掘，开展考题溯源，挖掘问题本源内容对于理解问题、总结方法有一定的帮助.教学中教师要注重引导学生关注教材，以教材为基础开展探究活动，针对性地提升学生的探究能力，发展学生的数学思维.[ 参考文献 ][1] 李茂辉.解读几何探究，探讨解析思考：以一道几何探究题的思路突破为例[J].数学教学通讯，2020（11）：71-73.[2] 刘媚.中考几何探究性问题研究[J].中学数学，2019（8）：87-88.[3] 徐新.山重水复疑无路，柳暗花明又一村：谈一道中考几何综合题的命制过程[J].中学数学教学参考，2019（15）：57-58+74.（责任编辑陈昕）。

题型09 几何类比、拓展、探究题一、解答题1．如图1，ABC ∆（12AC BC AC <<）绕点C 顺时针旋转得DEC ∆，射线AB 交射线DE 于点F ． （1）AFD ∠与BCE ∠的关系是 ；（2）如图2，当旋转角为60°时，点D ，点B 与线段AC 的中点O 恰好在同一直线上，延长DO 至点G ，使OG OD =，连接GC ．①AFD ∠与GCD ∠的关系是 ，请说明理由；②如图3，连接,AE BE ，若45ACB ∠=o ，4CE =，求线段AE 的长度．2．（问题）如图1，在Rt ABC V 中，90,ACB AC BC ∠=︒=，过点C 作直线l 平行于AB ．90EDF ∠=︒，点D 在直线l 上移动，角的一边DE 始终经过点B ，另一边DF 与AC 交于点P ，研究DP 和DB 的数量关系．（探究发现）（1）如图2，某数学兴趣小组运用“从特殊到一般”的数学思想，发现当点D 移动到使点P 与点C 重合时，通过推理就可以得到DP DB =，请写出证明过程；（数学思考）（2）如图3，若点P 是AC 上的任意一点（不含端点A C 、），受（1）的启发，这个小组过点D 作DG CD ⊥交BC 于点G ，就可以证明DP DB =，请完成证明过程；（拓展引申）（3）如图4，在（1）的条件下，M 是AB 边上任意一点（不含端点A B 、），N 是射线BD 上一点，且AM BN =，连接MN 与BC 交于点Q ，这个数学兴趣小组经过多次取M 点反复进行实验，发现点M 在某一位置时BQ 的值最大．若4AC BC ==，请你直接写出BQ 的最大值．3．小波在复习时，遇到一个课本上的问题，温故后进行了操作、推理与拓展．(1)温故：如图 1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，若BC=6 ，AD=4，求正方形PQMN的边长．(2)操作：能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作：如图 2，任意画△ABC，在AB上任取一点P′，画正方形P′Q′M′N′，使Q′,M′在BC边上，N′在△ABC内，连结B N′并延长交AC于点N，画NM⊥BC于点M，NP⊥NM交AB于点P，PQ⊥BC于点Q，得到四边形PQMN．小波把线段BN称为“波利亚线”．(3)推理：证明图2 中的四边形PQMN是正方形．(4)拓展：在(2)的条件下，于波利业线B N上截取NE=NM，连结EQ，EM(如图 3)．当tan∠NBM=34时，猜想∠QEM的度数，并尝试证明．请帮助小波解决“温故”、“推理”、“拓展”中的问题．4．问题提出：如图，图①是一张由三个边长为1 的小正方形组成的“L”形纸片，图②是一张a×b的方格纸（a×b的方格纸指边长分别为a，b的矩形，被分成a×b个边长为 1 的小正方形，其中a≥2 ，b≥2，且a，b为正整数）．把图①放置在图②中，使它恰好盖住图②中的三个小正方形，共有多少种不同的放置方法？问题探究：为探究规律，我们采用一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，最后得出一般性的结论．探究一：把图①放置在2× 2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图③，对于2×2的方格纸，要用图①盖住其中的三个小正方形，显然有4 种不同的放置方法．探究二：把图①放置在3×2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图④，在3×2的方格纸中，共可以找到2 个位置不同的2 ×2方格，依据探究一的结论可知，把图①放置在3×2 的方格纸中，使它恰好盖住其中的三个小正方形，共有2 ×4＝8种不同的放置方法．探究三：把图①放置在a ×2 的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图⑤，在a ×2 的方格纸中，共可以找到______个位置不同的2×2方格，依据探究一的结论可知，把图①放置在a× 2 的方格纸中，使它恰好盖住其中的三个小正方形，共有______种不同的放置方法．探究四：把图①放置在a ×3 的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图⑥，在a ×3 的方格纸中，共可以找到______个位置不同的2×2方格，依据探究一的结论可知，把图①放置在a ×3 的方格纸中，使它恰好盖住其中的三个小正方形，共有_____种不同的放置方法．……问题解决：把图①放置在a ×b的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？（仿照前面的探究方法，写出解答过程，不需画图．）问题拓展：如图，图⑦是一个由4 个棱长为1 的小立方体构成的几何体，图⑧是一个长、宽、高分别为a，b，c（a≥2 ，b≥2 ，c≥2 ，且a，b，c是正整数）的长方体，被分成了a×b×c个棱长为1 的小立方体．在图⑧的不同位置共可以找到______个图⑦这样的几何体．5．在ABC ∆中，90BAC ∠=︒，AB AC =，AD BC ⊥于点D ,（1）如图1，点M ，N 分别在AD ，AB 上，且90BMN ∠=︒，当30AMN ∠=︒，2AB =时，求线段AM 的长；（2）如图2，点E ，F 分别在AB ，AC 上，且90EDF ∠=︒，求证：BE AF =；（3）如图3，点M 在AD 的延长线上，点N 在AC 上，且90BMN ∠=︒，求证：AB AN +=;6．如图，正方形ABDE 和BCFG 的边AB ，BC 在同一条直线上，且2AB BC =，取EF 的中点M ，连接MD ，MG ，MB ．（1）试证明DM MG ⊥，并求MBMG的值． （2）如图，将如图中的正方形变为菱形，设()2090EAB αα∠=<<︒，其它条件不变，问（1）中MBMG的值有变化吗？若有变化，求出该值（用含α的式子表示）；若无变化，说明理由．7．定义：有一组邻边相等且对角互补的四边形叫做等补四边形． 理解：()1如图1，点A B C ，，在O e 上，ABC ∠的平分线交O e 于点D ，连接AD CD ，．求证：四边形ABCD 是等补四边形； 探究：()2如图2，在等补四边形ABCD 中AB AD ，＝，连接AC AC ，是否平分?BCD ∠请说明理由． 运用：()3如图3，在等补四边形ABCD 中，AB AD ＝，其外角EAD ∠的平分线交CD 的延长线于点105F CD AF ，＝，＝，求DF 的长．8．已知V ABC 内接于O e ，BAC ∠的平分线交O e 于点D ，连接DB ，DC ．（1）如图①，当120BAC ∠=o 时，请直接写出线段AB ，AC ，AD 之间满足的等量关系式： ； （2）如图②，当90BAC ∠=o 时，试探究线段AB ，AC ，AD 之间满足的等量关系，并证明你的结论； （3）如图③，若BC =5，BD =4，求ADAB AC+ 的值．9．如图，在ABC ∆中，AB BC =，AD BC ⊥于点D ，BE AC ⊥于点E ，AD 与BE 交于点F ，BH AB ⊥于点B ，点M 是BC 的中点，连接FM 并延长交BH 于点H ．（1）如图①所示，若30ABC ∠=o ，求证：DF BH +=； （2）如图②所示，若45ABC ∠=o ，如图③所示，若60ABC ∠=o （点M 与点D 重合），猜想线段DF 、BH 与BD 之间又有怎样的数量关系？请直接写出你的猜想，不需证明．10．将在同一平面内如图放置的两块三角板绕公共顶点A旋转，连接BC，DE．探究S△ABC与S△ADC的比是否为定值．（1）两块三角板是完全相同的等腰直角三角板时，S△ABC：S△ADE是否为定值？如果是，求出此定值，如果不是，说明理由．（图①）（2）一块是等腰直角三角板，另一块是含有30°角的直角三角板时，S△ABC：S△ADE是否为定值？如果是，求出此定值，如果不是，说明理由．（图②）（3）两块三角板中，∠BAE+∠CAD＝180°，AB＝a，AE＝b，AC＝m，AD＝n（a，b，m，n为常数），S△ABC：S△ADE是否为定值？如果是，用含a，b，m，n的式子表示此定值（直接写出结论，不写推理过程），如果不是，说明理由．（图③）11．如图1，对角线互相垂直的四边形叫做垂美四边形．(1)概念理解：如图2，在四边形ABCD 中，AB AD =，CB CD =，问四边形ABCD 是垂美四边形吗？请说明理由；(2)性质探究：如图1，四边形ABCD 的对角线AC 、BD 交于点O ，AC BD ⊥．试证明：2222AB CD AD BC +=+；(3)解决问题：如图3，分别以Rt ACB V 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE ，连结CE 、BG 、GE ．已知4AC =，5AB =，求GE 的长．12．（1）数学理解：如图①，△ABC是等腰直角三角形，过斜边AB的中点D作正方形DECF，分别交BC，AC于点E，F，求AB，BE，AF之间的数量关系；（2）问题解决：如图②，在任意直角△ABC内，找一点D，过点D作正方形DECF，分别交BC，AC于点E，F，若AB＝BE+AF，求∠ADB的度数；（3）联系拓广：如图③，在（2）的条件下，分别延长ED，FD，交AB于点M，N，求MN，AM，BN的数量关系．13．如图，正方形ABCD 的边长为2，E 为AB 的中点，P 是BA 延长线上的一点，连接PC 交AD 于点F ，AP FD =．（1）求AFAP的值； （2）如图1，连接EC ，在线段EC 上取一点M ，使EM EB =，连接MF ，求证：MF PF =； （3）如图2，过点E 作EN CD ⊥于点N ，在线段EN 上取一点Q ，使AQ AP =，连接BQ ，BN ．将AQB ∆绕点A 旋转，使点Q 旋转后的对应点'Q 落在边AD 上．请判断点B 旋转后的对应点'B 是否落在线段BN 上，并说明理由．14．在ABC ∆中，90ABC ∠=︒，ABn BC=，M 是BC 上一点，连接AM （1）如图1，若1n =，N 是AB 延长线上一点，CN 与AM 垂直，求证：BM BN =（2）过点B 作BP AM ⊥，P 为垂足，连接CP 并延长交AB 于点Q . ①如图2，若1n =，求证：CP BMPQ BQ=②如图3，若M 是BC 的中点，直接写出tan BPQ ∠的值（用含n 的式子表示）15．⑴如图1，E 是正方形ABCD 边AB 上的一点，连接BD DE 、，将BDE ∠绕着点D 逆时针旋转90°，旋转后角的两边分别与射线BC 交于点F 和点G . ①线段DB 和DG 的数量关系是 ； ②写出线段BE BF 、和DB 之间的数量关系.⑵当四边形ABCD 为菱形，ADC 60∠=o ，点E 是菱形ABCD 边AB 所在直线上的一点，连接BD DE 、，将BDE ∠绕着点D 逆时针旋转120°，旋转后角的两边分别与射线BC 交于点F 和点G .①如图2，点E 在线段上时，请探究线段BE BF 、和BD 之间的数量关系，写出结论并给出证明； ②如图3，点E 在线段AB 的延长线上时，DE 交射线BC 于点M ；若 BE 1,AB 2==,直接写出线段GM 的长度.16．教材呈现：如图是华师版九年级上册数学教材第78页的部分内容．例2 如图，在ABC ∆中，,D E 分别是边,BC AB 的中点，,AD CE 相交于点G ，求证：13GE GD CE AD ==，证明：连结ED ．请根据教材提示，结合图①，写出完整的证明过程．结论应用：在ABCD Y 中，对角线AC BD 、交于点O ，E 为边BC 的中点，AE 、BD 交于点F ． （1）如图②，若ABCD Y 为正方形，且6AB =，则OF 的长为 ． （2）如图③，连结DE 交AC 于点G ，若四边形OFEG 的面积为12，则ABCD Y 的面积为 ．17．如图1，在矩形ABCD 中，BC =3，动点P 从B 出发，以每秒1个单位的速度，沿射线BC 方向移动，作PAB ∆关于直线PA 的对称'PAB ∆，设点P 的运动时间为()t s（1）若AB =①如图2，当点B ’落在AC 上时，显然△PCB ’是直角三角形，求此时t 的值②是否存在异于图2的时刻，使得△PCB ’是直角三角形？若存在，请直接写出所有符合题意的t 的值？若不存在，请说明理由（2）当P 点不与C 点重合时，若直线PB ’与直线CD 相交于点M ，且当t ＜3时存在某一时刻有结论∠P AM =45°成立，试探究：对于t ＞3的任意时刻，结论∠P AM =45°是否总是成立？请说明理由.18．在等腰三角形ABC ∆中，AB AC =，作CM AB ⊥交AB 于点M ，BN AC ⊥交AC 于点N ． （1）在图1中，求证：BMC CNB ∆≅∆；（2）在图2中的线段CB 上取一动点P ，过P 作//PE AB 交CM 于点E ，作//PF AC 交BN 于点F ，求证：PE PF BM +=；（3）在图3中动点P 在线段CB 的延长线上，类似（2）过P 作//PE AB 交CM 的延长线于点E ，作//PF AC 交NB 的延长线于点F ，求证：···AM PF OM BN AM PE +=．19．问题情境：如图1，在正方形ABCD中，E为边BC上一点（不与点B、C重合），垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N．判断线段DN、MB、EC之间的数量关系，并说明理由．问题探究：在“问题情境”的基础上，（1）如图2，若垂足P恰好为AE的中点，连接BD，交MN于点Q，连接EQ，并延长交边AD于点F．求∠AEF的度数；（2）如图3，当垂足P在正方形ABCD的对角线BD上时，连接AN，将△APN沿着AN翻折，点P落在点P'处．若正方形ABCD的边长为4 ，AD的中点为S，求P'S的最小值．问题拓展：如图4，在边长为4的正方形ABCD中，点M、N分别为边AB、CD上的点，将正方形ABCD 沿着MN翻折，使得BC的对应边B'C'恰好经过点A，C'N交AD于点F．分别过点A、F作AG⊥MN，FH⊥MN，垂足分别为G、H．若AG＝52，请直接写出FH的长．20．箭头四角形,模型规律:如图1，延长CO 交AB 于点D ，则1BOC B A C B ∠∠+∠∠+∠+∠＝＝．．因为凹四边形ABOC 形似箭头，其四角具有“BOC A B C ∠∠+∠+∠＝”这个规律，所以我们把这个模型叫做“箭头四角形”．模型应用:（1）直接应用：①如图2，A B C D E F ∠+∠+∠+∠+∠+∠= ．②如图3，ABE ACE ∠∠、的2等分线（即角平分线）BF CF 、交于点F ，已知12050BEC BAC ∠=∠=o o ，，则BFC ∠=③如图4，i i BO CO 、分别为ABO ACO ∠∠、的2019等分线12320172018i =⋯（，，，，，）．它们的交点从上到下依次为1232018O O O O ⋯、、、、．已知BOC m BAC n ∠=∠=o o ，，则1000BO C ∠= 度 （2）拓展应用：如图5，在四边形ABCD 中，2BC CD BCD BAD =∠=∠，．O 是四边形ABCD 内一点，且OA OB OD ==．求证：四边形OBCD 是菱形．21．如图1，在Rt △ABC 中，∠B =90°，BC =2AB =8，点D ，E 分别是边BC ，AC 的中点，连接DE ，将△EDC 绕点C 按顺时针方向旋转，记旋转角为α. （1）问题发现 ① 当0α︒=时，AEBD= ；② 当时，AEBD= （2）拓展探究试判断：当0°≤α＜360°时，AEDB的大小有无变化？请仅就图2的情况给出证明. （3）问题解决当△EDC 旋转至A 、D 、E 三点共线时，直接写出线段BD 的长.22．操作体验：如图，在矩形ABCD中，点E、F分别在边AD、BC上，将矩形ABCD沿直线EF折叠，使点D恰好与点B重合，点C落在点C′处.点P为直线EF上一动点(不与E、F重合)，过点P分别作直线BE、BF的垂线，垂足分别为点M和N，以PM、PN为邻边构造平行四边形PMQN.(1)如图1，求证：BE＝BF；(2)特例感知：如图2，若DE＝5，CF＝2，当点P在线段EF上运动时，求平行四边形PMQN的周长；(3)类比探究：若DE＝a，CF＝b.①如图3，当点P在线段EF的延长线上运动时，试用含a、b的式子表示QM与QN之间的数量关系，并证明；②如图4，当点P在线段FE的延长线上运动时，请直接用含a、b的式子表示QM与QN之间的数量关系.(不要求写证明过程)23．如图，平面内的两条直线l1、l2,点A、B在直线l2上，过点A、B两点分别作直线l1的垂线，垂足分别为A1、B1，我们把线段A1B1叫做线段AB在直线l2上的正投影，其长度可记作T（AB，CD）或T（AB，l2）,特别地，线段AC在直线l2上的正投影就是线段A1C，请依据上述定义解决如下问题.（1）如图1，在锐角△ABC中，AB=5，T（AC，AB）=3，则T（BC，AB）= ；（2）如图2，在Rt△ABC中，∠ACB=90°，T（AC，AB）=4，T（BC，AB）=9，求△ABC的面积；（3）如图3，在钝角△ABC中，∠A=60°，点D在AB边上，∠ACD=90°，T（AD，AC）=2，T（BC，AB）=6，求T（BC，.CD）24．（1）（探究发现）如图1，EOF ∠的顶点O 在正方形ABCD 两条对角线的交点处，90EOF ︒∠=，将EOF ∠绕点O 旋转，旋转过程中，EOF ∠的两边分别与正方形ABCD 的边BC 和CD 交于点E 和点F （点F 与点C ，D 不重合）．则,,CE CF BC 之间满足的数量关系是 ． （2）（类比应用）如图2，若将（1）中的“正方形ABCD ”改为“120BCD ∠=o 的菱形ABCD ”，其他条件不变，当60EOF ∠=o 时，上述结论是否仍然成立？若成立，请给出证明；若不成立，请猜想结论并说明理由． （3）（拓展延伸）如图3，120BOD =o ∠，34OD =，4OB =，OA 平分BOD ∠，AB =且2OB OA >，点C 是OB 上一点，60CAD ∠=o ，求OC 的长．25．根据相似多边形的定义，我们把四个角分别相等，四条边成比例的两个凸四边形叫做相似四边形．相似四边形对应边的比叫做相似比．（1）某同学在探究相似四边形的判定时，得到如下三个命题，请判断它们是否正确（直接在横线上填写“真”或“假”）．①条边成比例的两个凸四边形相似；（ 命题） ②三个角分别相等的两个凸四边形相似；（ 命题） ③两个大小不同的正方形相似．（ 命题）（2）如图1，在四边形ABCD 和四边形A 1B 1C 1D 1中，∠ABC ＝∠A 1B 1C 1，∠BCD ＝∠B 1C 1D 1，111111AB BC CDA B B C C D ==，求证：四边形ABCD 与四边形A 1B 1C 1D 1相似．（3）如图2，四边形ABCD 中，AB ∥CD ，AC 与BD 相交于点O ，过点O 作EF ∥AB 分别交AD ，BC 于点E ，F ．记四边形ABFE 的面积为S 1，四边形EFDE 的面积为S 2，若四边形ABFE 与四边形EFCD 相似，求21S S 的值．26．在△ABC 中，已知D 是BC 边的中点，G 是△ABC 的重心，过G 点的直线分别交AB 、AC 于点E 、F .（1）如图1，当EF ∥BC 时，求证：1BE CFAE AF+=； （2）如图2，当EF 和BC 不平行，且点E 、F 分别在线段AB 、AC 上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.（3）如图3，当点E 在AB 的延长线上或点F 在AC 的延长线上时，（1）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由.27．如图，在等腰Rt ABC V 中，90,ACB AB ∠==o 点D ,E 分别在边AB ,BC 上，将线段ED 绕点E 按逆时针方向旋转90º得到EF ．（1）如图1，若AD BD =，点E 与点C 重合，AF 与DC 相交于点O ．求证：2BD DO =． （2）已知点G 为AF 的中点．①如图2，若,2AD BD CE ==，求DG 的长．②若6AD BD =，是否存在点E ，使得DEG △是直角三角形？若存在，求CE 的长；若不存在，试说明理由．28．(1)方法选择如图①，四边形ABCD 是O e 的内接四边形，连接AC ，BD ，AB BC AC ==．求证：BD AD CD =+. 小颖认为可用截长法证明：在DB 上截取DM AD =，连接AM …小军认为可用补短法证明：延长CD 至点N ，使得DN AD =…请你选择一种方法证明．(2)类比探究（探究1）如图②，四边形ABCD 是O e 的内接四边形，连接AC ，BD ，BC 是O e 的直径，AB AC =．试用等式表示线段AD ，BD ，CD 之间的数量关系，并证明你的结论．（探究2）如图③，四边形ABCD 是O e 的内接四边形，连接AC ，BD ．若BC 是O e 的直径，30ABC ∠=︒，则线段AD ，BD ，CD 之间的等量关系式是______．(3)拓展猜想如图④，四边形ABCD 是O e 的内接四边形，连接AC ，BD ．若BC 是O e 的直径，::::BC AC AB a b c =，则线段AD ，BD ，CD 之间的等量关系式是______．29．（1）证明推断：如图（1），在正方形ABCD 中，点E ，Q 分别在边BC ，AB 上，DQ AE ⊥于点O ，点G ，F 分别在边CD ，AB 上，GF AE ⊥．①求证：DQ AE =； ②推断：GF AE的值为 ； （2）类比探究：如图（2），在矩形ABCD 中，BC k AB =（k 为常数）．将矩形ABCD 沿GF 折叠，使点A 落在BC 边上的点E 处，得到四边形FEPG ，EP 交CD 于点H ，连接AE 交GF 于点O ．试探究GF 与AE CP 之间的数量关系，并说明理由；（3）拓展应用：在（2）的条件下，连接CP ，当23k =时，若3tan 4CGP ∠=，GF =CP 的长．30．在ABC ∆，CA CB =，ACB α∠=．点P 是平面内不与点A ，C 重合的任意一点．连接AP ，将线段AP 绕点P 逆时针旋转α得到线段DP ，连接AD ，BD ，CP ．（1）观察猜想如图1，当60α︒=时，BD CP 的值是 ，直线BD 与直线CP 相交所成的较小角的度数是 ． （2）类比探究如图2，当90α︒=时，请写出BD CP 的值及直线BD 与直线CP 相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当90α︒=时，若点E ，F 分别是CA ，CB 的中点，点P 在直线EF 上，请直接写出点C ，P ，D 在同一直线上时AD CP的值．。

一道平面几何题的十种证法题目：如图1，△ABC中，D、F在AB上，AD=BF，过D作DE∥BC，交AC 于E，过F作FG∥BC交AC于G．求证：BC=DE＋FG．分析：证明一条线段等于另外两条线段的和，常用的方法是将线段的位置平移：（1）延长较短线段与较长线段相等；（2）在较长线段上截取与较短线段相等的线段；（3）将线段适当移动位置后进行比较；（4）采用其它比较方法，如解析法，三角法，面积法等．一、延长较短线段与较长线段相等解法1 如图2，延长FG到H，使FH等于BC，连结CH．（关键证GH=DE即可）．由作法知FH平行且等于BC FBCH是平行四边形CH=BF．在△ADE和△CHG中，CH=BF=AD．由CH∥AB∠A=∠2，又∠1=∠B，∠H=∠B，所以∠1=∠H．∴△ADE≌△CHG，则DE=GH，故BC=FG＋GH=DE＋FG．证法2 如图3，仍延长FG到H，使GH=DE，连结CH．（关键证BC=FH）．由DE∥BC∥FG∠1=∠2=∠3．又AD=FB，所以AE=GC．∴△ADE≌△CHG，（SAS）∴∠A=∠GCH AB∥CH．∴四边形FBCH是平行四边形，所以，BC=FH，∴BC=DE＋FG．证法3 如图4，延长DE到H，使DH=BC，连结CH．（关键证FG=EH）．由DBCH及DH=BC．再△AFG≌△CHE，得FG=EH．二、恰当地将线段平移证法4 如图5找EG的中点K，连接DK并延长DK交FG的延长线于H，可证得△DEK≌△HGK DE=GH．再证得△ADE≌△CHG，（或证△ADK≌△CHK）∠A=∠GCH∴BC=GH＋FG=DE＋FG．证法5 如图6．过D作DH∥AC交BC于H，则DE=HC．不难证得△AFG≌△DBH，可得FG=BH，∴BC＝BH＋HC＝DE＋FG．证法6 如图7过F作FH∥AC交BC于H（或在BC上截取CH=FG）．三、在较长的线段上截取较短的线段证法7 如图8在BC上截取BH=DE．不难得出△ADE≌△FBH．则∠1=∠2=∠3FH∥AC FG=HC．（同理可在BC上截取BH=FG．再证HC=DE）四、利用梯形或三角形的中位线定理题中要证的结论系三角形的底边BC等于梯形DFGE两底之和，可猜想通过梯形DFGE的中位线沟通两者之间的关系．证法8 如图9．又AD=FB，由平行截割定理得MN也是△ABC的中位线，五、利用相似三角形的性质和比例的性质题中要证的边实质是相似三角形的对应边，因此，可从相似三角形的对应边成比例和比例的基本性质入手证明．证法9 如图1．又AD=BF，所以，AD＋AF=AD＋DB=AB．即BC=DF＋FG．六、其它线段变换证法10 如图10．作AH⊥DE于H，作FP⊥BC于P，作GQ⊥BC于Q．易证△ADH≌△FBP，△AHE≌△GQC．DH＋HE=BP＋QC，又FG=PQ．则BC=PQ＋BP＋QC＝FG＋DH＋HE，即BC=DE ＋FG．。

1一道中考题的多证与思考 问题情境如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分∠DAM． 探究展示 (1)证明：AM＝AD＋MC； (2)AM＝DE＋BM是否成立？ 若成立，请给出证明；若不成立，请说明理由． 拓展延伸 (3)若四边形ABCD是长与宽不相等的矩形，其他条件不变，探究展示(1)、(2)中的结论是否成立？请分别作出判断，不需要证明． 证明 (1)方法一（补短法）

方法二（补短法） 延长AD到Q，使DQ＝MC，连结EQ（图略）． 易证Rt△EDQ≌Rt△ECM，

方法三（截长法） 在AM上截取AP＝AD，连结EP、EM(图略)， 易证△APE≌ADE和△EPM≌△ECM． ∴AM＝AP＋PM＝AD＋MC． 方法四 延长AE与BC的延长线相交于点F(图略)，易证Rt△ADE≌Rt△FCE，以下同方法一． 方法五 过点P作EP⊥AM，垂足为P（图略），易证Rt△APF≌Rt△ADE，以下同方法三． 方法六 连结MF并延长与AD的延长线交于点Q（图略），易证 △EDQ≌△EGM， 2

MC＝DQ，ME＝EQ． 又AE平分∠MAD， ∴AM＝AQ＝AD＋MC． 点评 方法一和方法二运用补短法，都要证明三点共线，这是学生容易忽失的；方法四利用了“AD∥BC且DE＝EC”构造全等三角形，间接地达到了补短之目的；方法五表面上与方法三相同，实质上是不同的，方法三运用的是(SAS)来判定两个三角形全等，方法五运用的是(AAS)来判定两个三角形全等；它是根据角平分线上任意一点到角的两边的距离相等构造全等三角形，间接达到截长之目的． (2)AM＝DE＋BM成立． 方法一（截长法） 如图2，在AM上截取MF＝BM，连结BF并延长分别交AF、AD于点G、H．

方法二（补短法） 如图2，延长MB到N，使BN＝DE， 易证△ABN≌△ADE，

方法三（旋转法） 如图2．将ADE绕点A顺时针旋转90°，得到△ABN，△ABN≌△ADE，以下同方法二． 方法四（利用基本图形） 如图2，过点B作BH⊥AE，分别交AM、AF、AD于点F、G、H，