传送带模型和板块模型

传送带模型和板块模型传送带模型”问题的分析思路V o(v o> 0)在另一个匀速运动的物体上开始运动的力学系统可看做“传送6(a)、(b)、(c)所示.2.建模指导传送带模型问题包括水平传送带问题和倾斜传送带问题.(1) 水平传送带问题：求解的关键在于对物体所受的摩擦力进行正确的分析判断.判断摩擦力时要注意比较物体的运动速度与传送带的速度，也就是分析物体在运动位移x(对地)的过程中速度是否和传送带速度相等•物体的速度与传送带速度相等的时刻就是物体所受摩擦力发生突变的时刻.(2) 倾斜传送带问题：求解的关键在于认真分析物体与传送带的相对运动情况，从而确定其是否受到滑动摩擦力作用•如果受到滑动摩擦力作用应进一步确定其大小和方向，然后根据物体的受力情况确定物体的运动情况•当物体速度与传送带速度相等时，物体所受的摩擦力有可能发生突变.【例1 如图7所示，倾角为37°长为I = 16 m的传送带，转动速度为v =10 m/s,动摩擦因数尸0.5，在传送带顶端A处无初速度地释放一个质量为m = 0.5 kg的物体.已知sin 37 = 0.6, cos 37 = 0.8, g= 10m/s2.求：(1) 传送带顺时针转动时，物体从顶端A滑到底端B的时间；(2) 传送带逆时针转动时，物体从顶端A滑到底端B的时间.突破训练1 如图8所示，水平传送带AB长L = 10 m,向右匀速运动的速度V0= 4 m/s，一质量为1 kg的小物块(可视为质点)以V1= 6 m/s的初速度从传送带右端B点冲上传送带，物块与传送；带间的动摩擦因数尸0.4, g取10 m/s2.求：(1) 物块相对地面向左运动的最大距离；(2) 物块从B点冲上传送带到再次回到B点所用的时间.1模型特征一个物体以速度带”模型，如图图6二•“滑块一木板模型”问题的分析思路1模型特点：上、下叠放两个物体，并且两物体在摩擦力的相互作用下发生相对滑动.2 •建模指导解此类题的基本思路：(1)分析滑块和木板的受力情况，根据牛顿第二定律分别求出滑块和木板的加速度；(2)对滑块和木板进行运动情况分析，找出滑块和木板之间的位移关系或速度关系，建立方程.特别注意滑块和木板的位移都是相对地面的位移【例2 如图所示，质量为M，长度为L的长木板放在水平桌面上，木板右端放有一质量为m长度可忽略的小木块，木块与木板之间、木板与桌面之间的动摩擦因数均为。

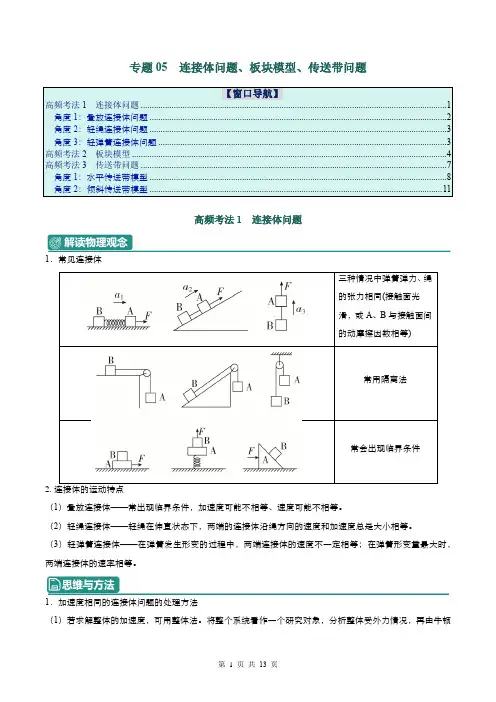
专题05 连接体问题、板块模型、传送带问题【窗口导航】高频考法1 连接体问题 ........................................................................................................................................... 1 角度1：叠放连接体问题 ....................................................................................................................................... 2 角度2：轻绳连接体问题 ....................................................................................................................................... 3 角度3：轻弹簧连接体问题 ................................................................................................................................... 3 高频考法2 板块模型 ............................................................................................................................................... 4 高频考法3 传送带问题 ........................................................................................................................................... 7 角度1：水平传送带模型 ....................................................................................................................................... 8 角度2：倾斜传送带模型 . (11)高频考法1连接体问题1．常见连接体三种情况中弹簧弹力、绳的张力相同(接触面光滑，或A 、B 与接触面间的动摩擦因数相等)常用隔离法常会出现临界条件2. 连接体的运动特点（1）叠放连接体——常出现临界条件，加速度可能不相等、速度可能不相等。

题型专练一 连接体问题、板块模型、传送带模型连接体问题、 板块模型、传送带模型是经典的三种模型，是涉及多个物体发生相对运动的问题，分析这类问题要从受力分析和运动过程分析，分析每个物体的运动情况，由牛顿第二定律分析它们的加速度情况，有时还要结合能量和动量的观点解决问题。

例题1. （2022·全国·高考真题）如图，一不可伸长轻绳两端各连接一质量为m 的小球，初始时整个系统静置于光滑水平桌面上，两球间的距离等于绳长L 。

一大小为F 的水平恒力作用在轻绳的中点，方向与两球连线垂直。

当两球运动至二者相距35L 时，它们加速度的大小均为（ ）A ．58F mB ．25FmC ．38F mD ．310Fm【答案】A【解析】当两球运动至二者相距35L 时，,如图所示由几何关系可知3310sin 52LL θ==设绳子拉力为T ，水平方向有2cos T F θ=解得58T F =对任意小球由牛顿第二定律可得T ma =解得58Fa m=故A 正确，BCD 错误。

故选A 。

例题2. （多选）（2021·全国·高考真题）水平地面上有一质量为1m 的长木板，木板的左端上有一质量为2m 的物块，如图（a ）所示。

用水平向右的拉力F 作用在物块上，F 随时间t 的变化关系如图（b ）所示，其中1F 、2F 分别为1t 、2t 时刻F 的大小。

木板的加速度1a 随时间t 的变化关系如图（c ）所示。

已知木板与地面间的动摩擦因数为1μ，物块与木板间的动摩擦因数为2μ，假设最大静摩擦力均与相应的滑动摩擦力相等，重力加速度大小为g 。

则（ ）A ．111=F m g μB ．2122211()()m m m F g m μμ+=-C ．22112m m m μμ+>D ．在20~t 时间段物块与木板加速度相等【答案】BCD【解析】A ．图（c ）可知，t 1时滑块木板一起刚在从水平滑动，此时滑块与木板相对静止，木板刚要滑动，此时以整体为对象有1112()F m m g μ=+A 错误；BC ．图（c ）可知，t 2滑块与木板刚要发生相对滑动，以整体为对象， 根据牛顿第二定律，有211212()()F m m g m m a μ-+=+以木板为对象，根据牛顿第二定律，有221121()0m g m m g m a μμ-+=>解得2122211()()m m m F g m μμ+=-()12212m m m μμ+>BC 正确；D ．图（c ）可知，0~t 2这段时间滑块与木板相对静止，所以有相同的加速度，D 正确。

3.系统内一对滑动摩擦力做的功等于−f滑∙x相，产生热量Q＝f滑∙x相4.电动机做的功等于F牵∙x传，将电能转化为机械能和内能三、板块模型中的功能关系区分三种位移：板的位移，物块的位移，相对位移内容讲解例 1.如图所示，传送带以v0的速度匀速运动。

将质量为m的物体无初速度放在传送带上的左端，物体将被传送带送到右端，已知物体到达右端之前已和传送带相对静止，则下列说法正确的是()A.传送带对物体做功为12mv02B. 传送带克服摩擦做功12mv02C. 在传送物体过程中产生的热量为12mv02D. 电动机因传送物体而多消耗的能量为12mv02【答案】AC【分析】电动机多消耗的电能转化为内能和物体的动能，根据功能关系分析电动机多做的功；根据运动学公式求出物体与传送带相对运动时，传送带位移与物体位移之间的关系，得出传送带克服摩擦力做的功。

解决本题的关键在于分析清楚物体的运动过程以及相对位移，灵活运动功能关系。

【解答】A.物体受重力支持力和摩擦力，根据动能定理，传送带对物体做的功等于动能的增加量，即12mv02，故A正确；B.根据动能定理得：摩擦力对物体做功大小为12mv02，在物体匀加速运动的过程中，由于传送带的位移大于物体的位移，则传送带克服摩擦力做的功大于摩擦力对物体做功，所以传送带克服摩擦力做的功大于12mv02，故B错误；C.在传送物体过程产生的热量等于滑动摩擦力与相对路程的乘积，即Q=fΔx；设加速时间为t，物体的位移为x1=12v0t，传送带的位移为x2=v0t；根据动能定理，有f·x1=12mv02，故热量Q=fΔx=12mv02，故C正确；D.电动机由于传送物体多消耗的能量等于物体动能增加量和摩擦产生的内能的和，故大于12mv02，故D错误。

故选AC。

例2.如图所示，传送带与水平面之间的夹角为θ=30°，其上A、B两点间的距离为L=5m，传送带在电动机的带动下以V=1m/s的速度匀速运动，现将一质量为m=10kg的小物体(可视为质点)轻放在传送带的A点，已知小物体与传送带之间的动摩擦因数μ为√32，在传送带将小物体从A点传送到B点的过程中，求：(1)传送带对小物体做的功；(2)电动机做的功．【分析】本题为传送带问题，要注意分析物体在传送带上的受力情况及运动情况，综合利用牛顿第二定律及动能定理、功能关系等方法求解。

专题提升九传送带模型和板块模型题组一传送带模型1.如图所示，足够长的水平传送带以v＝2m/s的速度逆时针匀速转动，一个物块以v0＝4m/s的初速度从左端A处水平滑上传送带，物块与传送带间的动摩擦因数μ＝0.2，g取10m/s2，那么物块再次返回到A处所用的时间为()A.4sB.2sC.4.5sD.3s2.(2022·福建省福州高级中学高一期末)如图，水平传送带长为L＝5.3m，运行速率v＝1m/s，在其左端以初速度v0＝2m/s水平滑上一物块。

若物块与传送带间的动摩擦因数μ＝0.5，g取10m/s2，则物块从左到右的运动过程中()A.刚滑上时，物块受到向右的滑动摩擦力B.物块一直做匀减速直线运动C.物块在传送带上的运动时间为5.2sD.物块在传送带上留下的划痕长度为0.3m3.如图所示，在一条倾斜的、静止不动的传送带上，有一个滑块能够自由地向下滑动，该滑块由上端自由地滑到底端所用时间为t1，如果传送带向上以速度v0运动起来，保持其他条件不变，该滑块由上端滑到底端所用的时间为t2，那么() A.t1＝t2B.t1>t2C.t1<t2D.不能确定题组二“滑块—木板”模型问题4.(2022·湖南高一月考)如图所示，物块A和木板B的质量相同，A可以看作质点，木板B长3m。

开始时A、B均静止。

现使A以水平初速度v0从B的最左端开始运动。

已知A与B、B与水平面间的动摩擦因数分别为μ1＝0.3和μ2＝0.1，取重力加速度大小g＝10m/s2，若A刚好没有从B上滑下来，则v0的大小为()A.5m/sB.25m/sC.6m/sD.26m/s5.(2022·江苏扬州市新华中学高一阶段检测)如图所示，两物体A、B叠放在光滑水平面上，两物体间动摩擦因数为μ＝0.2，已知它们的质量m＝2kg，M＝1kg，力F作用在m物体上(设最大静摩擦力等于滑动摩擦力，g＝10m/s2)，则() A.当F＝4N时，两物体即将发生相对运动B.当F＝5N时，两物体一定发生相对运动C.当F＝8N时，物体B的加速度为4m/s2D.当F＝12N时，物体A的加速度为4m/s26.如图所示，在光滑水平面上有一质量为m1的足够长的木板，其上叠放一质量为m2的木块。

两类动力学模型：“板块模型”和“传送带模型”模型1 板块模型[模型解读]1．模型特点涉及两个物体，并且物体间存在相对滑动．2．两种位移关系滑块由滑板的一端运动到另一端的过程中，若滑块和滑板同向运动，位移大小之差等于板长；反向运动时，位移大小之和等于板长．设板长为L，滑块位移大小为x1，滑板位移大小为x2同向运动时：L＝x1－x2反向运动时：L＝x1＋x23．解题步骤[典例赏析][典例1] (2017·全国卷Ⅲ)如图，两个滑块A和B的质量分别为m A＝1 kg和m B＝5 kg，放在静止于水平地面上的木板的两端，两者与木板间的动摩擦因数均为μ1＝0.5；木板的质量为m＝4 kg，与地面间的动摩擦因数为μ2＝0.1.某时刻A、B两滑块开始相向滑动，初速度大小均为v0＝3 m/s.A、B相遇时，A与木板恰好相对静止．设最大静摩擦力等于滑动摩擦力，取重力加速度大小g＝10 m/s2.求：(1)B 与木板相对静止时，木板的速度；(2)A 、B 开始运动时，两者之间的距离．[审题指导] 如何建立物理情景，构建解题路径①首先分别计算出B 与板、A 与板、板与地面间的滑动摩擦力大小，判断出A 、B 及木板的运动情况．②把握好几个运动节点．③由各自加速度大小可以判断出B 与木板首先达到共速，此后B 与木板共同运动． ④A 与木板存在相对运动，且A 运动过程中加速度始终不变．⑤木板先加速后减速，存在两个过程．[解析] (1)滑块A 和B 在木板上滑动时，木板也在地面上滑动．设A 、B 与木板间的摩擦力的大小分别为f 1、f 2，木板与地面间的摩擦力的大小为f 3，A 、B 、木板相对于地面的加速度大小分别是a A 、a B 和a 1.在物块B 与木板达到共同速度前有：f 1＝μ1m Ag ①f 2＝μ1m Bg ②f 3＝μ2(m A ＋m B ＋m )g ③由牛顿第二定律得f 1＝m A a A ④f 2＝m B a B ⑤f 2－f 1－f 3＝ma 1⑥设在t 1时刻，B 与木板达到共同速度，设大小为v 1.由运动学公式有v 1＝v 0－a B t 1⑦v 1＝a 1t 1⑧联立①②③④⑤⑥⑦⑧式，代入数据解得：v 1＝1 m/s(2)在t 1时间间隔内，B 相对于地面移动的距离为s B ＝v 0t 1－12a B t 21⑨设在B 与木板达到共同速度v 1后，木板的加速度大小为a 2，对于B 与木板组成的体系，由牛顿第二定律有： f 1＋f 3＝(m B ＋m )a 2⑩由①②④⑤式知，a A ＝a B ；再由⑦⑧可知，B 与木板达到共同速度时，A 的速度大小也为v 1，但运动方向与木板相反．由题意知，A 和B 相遇时，A 与木板的速度相同，设其大小为v 2.设A 的速度大小从v 1变到v 2所用时间为t 2，根据运动学公式，对木板有v 2＝v 1－a 2t 2⑪对A 有v 2＝－v 1＋a A t 2⑫在t 2时间间隔内，B (以及木板)相对地面移动的距离为s 1＝v 1t 2－12a 2t 22⑬在(t 1＋t 2)时间间隔内，A 相对地面移动的距离为 s A ＝v 0(t 1＋t 2)－12a A (t 1＋t 2)2⑭A 和B 相遇时，A 与木板的速度也恰好相同，因此A 和B 开始运动时，两者之间的距离为 s 0＝s A ＋s 1＋s B ⑮联立以上各式，代入数据得s 0＝1.9 m(也可以用下图的速度－时间图象做)[答案] (1)1 m/s (2)1.9 m滑块滑板类模型的思维模板[题组巩固]1.(2019·吉林调研)(多选)如图所示，在光滑的水平面上放置质量为m 0的木板，在木板的左端有一质量为m 的木块，在木块上施加一水平向右的恒力F ，木块与木板由静止开始运动，经过时间t 分离．下列说法正确的是( )A ．若仅增大木板的质量m 0，则时间t 增大B ．若仅增大木块的质量m ，则时间t 增大C ．若仅增大恒力F ，则时间t 增大D ．若仅增大木块与木板间的动摩擦因数μ，则时间t 增大解析：BD [根据牛顿第二定律得，木块的加速度a 1＝F －μmg m ＝F m －μg ，木板的加速度a 2＝μmg m 0，木块与木板分离，则有l ＝12a 1t 2－12a 2t 2得t ＝2l a 1－a 2.若仅增大木板的质量m 0，木块的加速度不变，木板的加速度减小，则时间t 减小，故A 错误；若仅增大木块的质量m ，则木块的加速度减小，木板的加速度增大，则t 变大，故B 正确；若仅增大恒力F ，则木块的加速度变大，木板的加速度不变，则t 变小，故C 错误；若仅增大木块与木板间的动摩擦因数，则木块的加速度减小，木板的加速度增大，则t 变大，故D 正确．]2．(2019·黑龙江大庆一模)如图，木板静止于水平地面上，在其最右端放一可视为质点的木块．已知木块的质量m ＝1 kg ，木板的质量m 0＝4 kg ，长l ＝2.5 m ，上表面光滑，下表面与地面之间的动摩擦因数μ＝0.2.现用水平恒力F ＝20 N 拉木板，g 取10 m/s 2，求：(1)木板的加速度；(2)要使木块能滑离木板，水平恒力F 作用的最短时间．解析：(1)木板受到的摩擦力为F f ＝μ(m 0＋m )g ＝10 N 木板的加速度为a ＝F －F f m 0＝2.5 m/s 2.(2)设拉力F 作用t 时间后撤去，木板的加速度为 a ′＝－F f m 0木板先做匀加速运动，后做匀减速运动，且有a ＝－a ′＝2.5 m/s 2则有2×12at 2＝l 联立并代入数据解得t ＝1 s ，即F 作用的最短时间是1 s.答案：(1)2.5 m/s2(2)1 s3.(2019·河南中原名校联考)如图所示，质量M＝1 kg的木板静置于倾角θ＝37°、足够长的固定光滑斜面底端．质量m＝1 kg的小物块(可视为质点)以初速度v0＝4 m/s从木板的下端冲上木板，同时在木板上端施加一个沿斜面向上的F＝3.2 N的恒力．若小物块恰好不从木板的上端滑下，求木板的长度l为多少？已知小物块与木板之间的动摩擦因数μ＝0.8，重力加速度g取10 m/s2，sin 37°＝0.6，cos 37°＝0.8.解析：由题意，小物块向上做匀减速运动，木板向上做匀加速运动，当小物块运动到木板的上端时，恰好和木板共速．设小物块的加速度为a，由牛顿第二定律得，mg sin θ＋μmg cos θ＝ma，设木板的加速度为a′，由牛顿第二定律得，F＋μmg cos θ－Mg sin θ＝Ma′，设二者共速时的速度为v，经历的时间为t，由运动学公式得v＝v0－at，v＝a′t；小物块的位移为s，木板的位移为s′，由运动学公式得，s＝v0t－12at2，s′＝12a′t2；小物块恰好不从木板上端滑下，有s－s′＝l，联立解得l＝0.5 m.答案：0.5 m模型2 传送带模型[模型解读]对于传送带问题，分析清楚物体在传送带上的运动情况是解题关键，分析思路是：弄清物体与传送带的相对运动——确定所受摩擦力的方向——确定物体的运动情况，具体分析见下表：1．水平传送带问题[典例2] 如图所示为某工厂的货物传送装置，倾斜运输带AB(与水平面成α＝37°)与一斜面BC(与水平面成θ＝30°)平滑连接，B点到C点的距离为L＝0.6 m，运输带运行速度恒为v0＝5 m/s，A点到B点的距离为x＝4.5 m，现将一质量为m＝0.4 kg的小物体轻轻放于A点，物体恰好能到达最高点C点，已知物体与斜面间的动摩擦因数μ1＝36，(g 取10 m/s2，sin 37°＝0.6，cos 37°＝0.8，空气阻力不计)求：(1)小物体运动到B点时的速度v的大小；(2)小物体与运输带间的动摩擦因数μ；(3)小物体从A点运动到C点所经历的时间t.[审题指导][解析] (1)设小物体在斜面上的加速度为a 1，运动到B 点的速度为v ，由牛顿第二定律得mg sin θ＋ μ1mg cos θ＝ma 1由运动学公式知v 2＝2a 1L ，联立解得v ＝3 m/s.(2)因为v ＜v 0，所以小物体在运输带上一直做匀加速运动，设加速度为a 2，则由牛顿第二定律知 μmg cos α－mg sin α＝ma 2又因为v 2＝2a 2x ，联立解得μ＝78. (3)小物体从A 点运动到B 点经历的时间t 1＝v a 2，从B 点运动到C 点经历的时间t 2＝v 1a 1联立并代入数据得小物体从A 点运动到C 点所经历的时间t ＝t 1＋t 2＝3.4 s.[答案] (1)3 m/s (2)78(3)3.4 s 解传送带问题的思维模板[题组巩固]1.(2019·山东临沂高三上学期期中)(多选)如图所示，绷紧的水平传送带始终以恒定速率v 1运行．初速度大小为v 2(v 1＜v 2)的小物块从与传送带等高的光滑水平地面上滑上传送带，从小物块滑上传送带开始计时，物块在传送带上运动的v －t 图象可能是( )解析：AC [物块滑上传送带，由于速度大于传送带速度，物块做匀减速直线运动，可能会滑到另一端一直做匀减速直线运动，到达另一端时恰好与传送带速度相等，故C 正确．物块滑上传送带后，物块可能先做匀减速直线运动，当速度达到传送带速度后一起做匀速直线运动，速度的方向保持不变，故B 、D 错误，A 正确．]2.如图所示为粮袋的传送装置，已知A 、B 两端间的距离为L ，传送带与水平方向的夹角为θ，工作时运行速度为v ，粮袋与传送带间的动摩擦因数为μ，正常工作时工人在A 端将粮袋放到运行中的传送带上．设最大静摩擦力与滑动摩擦力大小相等，重力加速度大小为g .关于粮袋从A 到B 的运动，以下说法正确的是( )A ．粮袋到达B 端的速度与v 比较，可能大，可能小，也可能相等B ．粮袋开始运动的加速度为g (sin θ－μcos θ)，若L 足够大，则以后将以速度v 做匀速运动C ．若μ≥tan θ，则粮袋从A 端到B 端一定是一直做加速运动D ．不论μ大小如何，粮袋从A 到B 端一直做匀加速运动，且加速度a ≥g sin θ 解析：A [若传送带较短，粮袋在传送带上可能一直做匀加速运动，到达B 端时的速度小于v ；μ≥tan θ，则粮袋先做匀加速运动，当速度与传送带的速度相同后，做匀速运动，到达B 端时速度与v 相同；若μ＜tan θ，则粮袋先做加速度为g (sin θ＋μcos θ)的匀加速运动，当速度与传送带相同后做加速度为g (sin θ－μcos θ)的匀加速运动，到达B 端时的速度大于v ，选项A 正确；粮袋开始时速度小于传送带的速度，相对传送带的运动方向是沿传送带向上，所以受到沿传送带向下的滑动摩擦力，大小为μmg cos θ，根据牛顿第二定律得加速度a ＝mg sin θ＋μmg cos θm＝g (sin θ＋μcos θ)，选项B 错误；若μ≥tan θ，粮袋从A 到B 可能一直是做匀加速运动，也可能先匀加速运动，当速度与传送带的速度相同后，做匀速运动，选项C 、D 均错误．]3．(2019·湖北宜昌高三一模)如图为仓库中常用的皮带传输装置示意图，它由两台皮带传送机组成，一台水平传送，A 、B 两端相距3 m ，另一台倾斜，传送带与地面的倾角θ＝37°，C 、D 两端相距4.45 m ，B 、C 相距很近，水平部分AB 以5 m s 的速率顺时针转动．将质量为10 kg 的一袋大米放在A 端，到达B 端后，速度大小不变地传到倾斜的CD 部分，米袋与传送带间的动摩擦因数均为0.5.试求：(1)若CD 部分传送带不运转，求米袋沿传送带所能上升的最大距离．(2)若要将米袋送到D 端，求CD 部分顺时针运转的速度应满足的条件及米袋从C 端到D 端所用时间的取值范围．解析：(1)米袋在AB 上加速时的加速度a 0＝μmg m＝μg ＝5 m/s 2 米袋的速度达到v 0＝5 m/s 时，滑行距离：s 0＝v 202a 0＝2.5 m ＜AB ＝3 m 因此米袋在到达B 点之前就有了与传送带相同的速度．设米袋在CD 上运动的加速度大小为a ，由牛顿第二定律得：mg sin θ＋μmg cos θ＝ma ，代入数据得：a ＝10 m/s 2所以能上升的最大距离：s ＝v 202a＝1.25 m. (2)设CD 部分运转速度为v 1时米袋恰能达到D 点，则米袋速度减为v 1之前的加速度为： a 1＝－g (sin θ＋μcos θ)＝－10 m/s 2米袋速度小于v 1至减为0前的加速度为a 2＝－g (sin θ－μcos θ)＝－2 m/s 2由v 21－v 202a 1＋0－v 212a 2＝4.45 m. 解得：v 1＝4 m/s.即要把米袋送到D 点，CD 部分的速度v CD ≥v 1＝4 m/s米袋恰能运动到D 点所用时间最长为：t max ＝v 1－v 0a 1＋0－v 1a 2＝2.1 s 若CD 部分传送带的速度较大，使米袋沿CD 上滑时所受摩擦力一直沿皮带向上，则所用时间最短，此种情况米袋加速度一直为a 2，由s CD ＝v 0t min ＋12a 2t 2min 得：t min ＝1.16 s所以，所求的时间t 的范围为1．16 s≤t ≤2.1 s答案：(1)1.25 m (2)v CD≥4 m/s 1.16 s≤t≤2.1 s。

“板块模型”是一类高考常考的题型，其中考察知识点比较综合，对于不同的情形也需要特殊的处理方法，但离不开基础的受力分析、运动分析、以及抓住临界条件、或者加速度突变的点，结合牛顿第二定律进行思考求解！本节主要讲力作用在木块上的情形下的处理方法。

一、经典例题1．如图所示，长木板放置在水平面上，一小物块置于长木板的中央，长木板和物块的质量均为m，物块与木板间的动摩擦因数为μ，木板与水平面间动摩擦因数为13μ，已知最大静摩擦力与滑动摩擦力大小相等，重力加速度为g。

现对物块施加一水平向右的拉力F，则木板加速度大小a可能是( )A.a=μgB.a＝2 3 gC. a＝1 3 gD. a＝1 23 Fg m本题考查板块模型中的临界问题，关键找出临界状态，运用整体法和隔离法，根据牛顿第二定律进行求解．2．如图所示，光滑水平面上有一块木板，质量M = 1.0 kg，长度L = 1.0 m．在木板的最左端有一个小滑块（可视为质点），质量m = 1.0 kg．小滑块与木板之间的动摩擦因数μ = 0.30．开始时它们都处于静止状态．某时刻起对小滑块施加一个F = 8.0 N水平向右的恒力，此后小滑块将相对木板滑动.（1）求小滑块离开木板时的速度；（2）假设只改变M、m、μ、F中一个物理量的大小，使得小滑块速度总是木板速度的2倍，请你通过计算确定改变后的那个物理量的数值（只要提出一种方案即可）。

规律总结：对于这类“板块模型”的题型，一般要寻找隐含关系，挖掘位移之间的几何关系是突破口。

学会使用控制变量法定性分析开放性题型。

对于此类题型要明确是否发生相对滑动的临界条件以及各自获得加速度的合外力由哪些力提供的的情况。

二、练习题1．(多选)(2014·江苏高考)【题号：3200000116】如图1所示，A、B两物块的质量分别为2 m和m，静止叠放在水平地面上。

A、B间的动摩擦因数为μ，B与地面间的动摩擦因数为1μ。

最大静摩擦力等于滑动摩擦力，重力加速度为g。

传送带问题与板块模型（2023.12）例1．如图所示，一水平方向足够长的传送带以恒定的速率v1沿顺时针方向运动，把一质量为m的物体无初速度地轻放在左端，物体与传送带间的动摩擦因数为μ，重力加速度为g，则下列说法正确的是（）A．物体一直受到摩擦力作用，大小为μmgB．物体最终的速度为v1C．物体一直做匀加速直线运动D．物体与传送带间的相对运动时间2v g μ变式1.如图所示，水平传送带以a1=0.5m/s2的加速度水平向右运动，传送带两端距离是s=14m，将一质量为m的物体轻放在传送带左端A，此时传送带的瞬时速度为v0=1m/s，已知传送带与物体间的动摩擦因数为µ=0.1，求物体从传送带一端运动到另一端所需时间。

例2如图所示，传输带与水平间的倾角为θ=37°，皮带以10m/s的速率运行，在传输带上端A处无初速地放上质量为0.5kg的物体，它的传输带间的动摩擦因数为0.5，若传输带A到B的长度为16m，则物体从A运动到B的时间为多少？变式2．如图所示，一浅色传送带与水平面的夹角θ=30°，且以v1=2m/s的速度沿顺时针方向传动。

一质量m=lkg的小炭块以v2=4m/s的速度滑上传送带的底端，最终又从传送带的底端滑出。

已知小炭块与传送带间的动摩擦因数35μ=，传送带足够长。

计算时取7 2.6=，g=10m/s2。

问：（1）小炭块向上滑行的时间？（2）小炭块离开传送带时的速度大小？（3）小炭块在传送带上运动的整个过程中，其相对传送带的位移大小？小炭块在传送带上留下的痕迹长度？A Bv例3．如图所示，在光滑的水平地面上有一个长为L，质量为M=4 kg的木板A，在木板的左端有一个质量为m=2 kg的小物体B，物体A、B之间的动摩擦因数为μ=0.2，当对B施加水平向右的力F时(设A、B之间的最大静摩擦力大小等于滑动摩擦力的大小)，取重力加速度g=10 m/s2。

（1）若F=4.2 N，则A、B的加速度分别为多大？（2）若F=10 N，则A、B的加速度分别为多大？变式3．如图甲，质量M=1 kg的木板静止在水平面上，质量m=1 kg、大小可以忽略的铁块静止在木板的右端．设最大静摩擦力等于滑动摩擦力，已知木板与地面间的动摩擦因数μ1=0.1，铁块与木板之间的动摩擦因数μ2=0.4，取g=10 m/s2.现给木板施加一个水平向右的力F。

高中物理复习：连接体问题、板块模型、传送带模型考点一连接体问题[知能必备]1．连接体问题模型弹力连接、摩擦力连接、轻绳连接、轻杆连接、弹簧连接．2．解题方略：要充分利用“加速度相等”这一条件或题中特定条件，交替使用整体法与隔离法解题．可以先用整体法求出加速度，然后再用隔离法选取合适的研究对象，应用牛顿第二定律求作用力．即“先整体求加速度，后隔离求内力”．[典例剖析](多选)如图，三个质量均为1 kg的物体A、B、C叠放在水平桌面上，B、C用不可伸长的轻绳跨过一光滑轻质定滑轮连接，A与B之间、B与C之间的接触面以及轻绳均与桌面平行，A与B之间、B与C之间以及C与桌面之间的动摩擦因数分别为0.4、0.2和0.1，重力加速度g取10 m/s2，设最大静摩擦力等于滑动摩擦力．用力F沿水平方向拉物体C，以下说法正确的是()A．拉力F小于11 N时，不能拉动CB．拉力F为17 N时，轻绳的拉力为4 NC．要使A、B保持相对静止，拉力F不能超过23 ND．A的加速度将随拉力F的增大而增大【思路点拨】解此题关键有两点：(1)利用整体法和隔离法选取研究对象，进行正确受力分析，注意摩擦因数的不同及摩擦力的大小和方向．(2)正确判断“相对滑动”的临界条件．解析：AC当C物体即将运动时，C物体水平方向受桌面给C的向右的摩擦力f桌，绳子向右的拉力T，B给C向右的摩擦力f BC，其中f桌＝0.1(m A＋m B＋m C)g＝3 N，f BC＝0.2(m A ＋m B)＝4 N，当即将滑动时应有F＝f桌＋f BC＋T，T＝f BC＝4 N，可解得F＝11 N，故A正确；因此B和C的加速度大小相等，在A和B即将发生相对滑动，对A受力分析可得，f AB＝0.4m A g ＝m A a，对AB整体受力分析可得T－f BC＝(m A＋m B)a，对C物体受力分析可得F－T－f BC－f 桌＝m C a ，联立解得F ＝23 N ，说明A 和B 发生相对滑动的临界力大小为F ＝23 N ，故C 正确；当F ＝17 N 时，A 和B 没有发生相对滑动，此时对AB 整体T －f BC ＝(m A ＋m B )a 1，对C 物体受力分析F －T －f BC －f 桌＝m C a 1，联立解得T ＝8 N ，故B 错误；当拉力增大，A 和B 发生相对滑动时，则A 物体受到滑动摩擦力，加速度为a ＝0.4g ＝4 m/s 2，加速度不变，D 错误．[题组精练]1.如图所示，在倾角为30°的光滑斜面上，有质量相等的两物块用轻绳连接，用沿斜面的力F ＝40 N 使两物块一起向上加速运动．则轻绳的拉力为( )A ．10 NB ．20 NC ．30 ND ．40 N解析：B 以两物块为研究对象，利用牛顿第二定律，有F －2mg sin 30°＝2ma ，以靠下的物块为研究对象，设轻绳的拉力为F T ，根据牛顿第二定律，有F T －mg sin 30°＝ma ，代入数据，解得F T ＝20 N ，ACD 错误，B 正确．2.(2021·苏州一模)如图所示，光滑水平面上放置质量分别为m 、2m和3m 的三个木块，其中质量为2m 和3m 的木块间用一不可伸长的水平轻绳相连，轻绳能承受的最大拉力为F T .现用水平拉力F 拉质量为3m 的木块，使三个木块以同一加速度运动，则以下说法正确的是( )A ．质量为2m 的木块受到四个力的作用B ．当F 逐渐增大到F T 时，轻绳刚好被拉断C ．当F 逐渐增大到1.5F T 时，轻绳还不会被拉断D ．轻绳刚要被拉断时，质量为m 和2m 的木块间的摩擦力为23F T 解析：C 质量为2m 的木块受五个力的作用，A 项错误；当绳的拉力为F T 时，对m 和2m 有F T ＝3ma ，此时对整体有F ＝6ma ，可得F ＝2F T ，故B 项错误，C 项正确；轻绳刚要被拉断时，质量为m 和2m 的木块间的摩擦力为13F T ，故D 项错误． 3．如图所示，一根不可伸长的轻绳一端系住小球，另一端固定在光滑直角斜劈顶端O 点，轻绳与斜面平行，斜劈底面水平．使小球和斜劈做下列运动，下面5种运动中，小球对斜面的压力可能为零的是( )①一起水平向左加速； ②一起水平向右加速；③一起竖直向上加速； ④一起竖直向下加速；⑤绕过O点的竖直轴一起匀速转动．A．①②③B．②③⑤C．②④⑤D．①③④解析：C①若一起水平向左加速，小球受合外力水平向左，斜面对小球的支持力的水平分力与绳子拉力的水平分力的合力水平向左，因此支持力不可能为零，①错误；②一起水平向右加速，当绳子拉力的竖直分量恰好等于重力时，斜面的支持力为零，绳子拉力的水平分力就是合外力，②正确；③一起竖直向上加速，绳子拉力与支持力的合力竖直向上，大于重力，绳子拉力不可能为零，因此支持力不可能为零，③错误；④一起竖直向下加速，当加速度等于g时，绳子拉力减小为零时，此时斜面的支持力也为零，④正确；⑤绕过O点的竖直轴一起匀速转动，合力指向转轴，当角速度足够大时，绳子拉力的竖直分量恰好等于重力时，斜面的支持力为零，⑤正确．考点二板块模型[知能必备]1．审题建模：求解时应先仔细审题，弄清楚题目的含义、分析清楚每一个物体的受力情况、运动情况．2．求加速度：准确求出各物体在各运动过程的加速度(注意两过程的连接处加速度可能突变)．3．做好两分析[典例剖析](经典高考题)如图所示，质量相等的物块A和B叠放在水平地面上，左边缘对齐．A与B、B与地面间的动摩擦因数均为μ.先敲击A，A立即获得水平向右的初速度，在B 上滑动距离L后停下．接着敲击B，B立即获得水平向右的初速度，A、B都向右运动，左边缘再次对齐时恰好相对静止，此后两者一起运动至停下．最大静摩擦力等于滑动摩擦力，重力加速度为g.求：(1)A 被敲击后获得的初速度大小v A ；(2)在左边缘再次对齐的前、后，B 运动加速度的大小a B 、a B ′；(3)B 被敲击后获得的初速度大小v B .【解题策略】(1)读题审题：①A 与B 、B 与地面间的动摩擦因数均为μ――→想到地面与B 间的摩擦力是A 与B 间的摩擦力的2倍②左边缘再次对齐时恰好相对静止――→想到B 与A 的位移差等于第一次A 的位移(2)情境转化：①敲击A 后―→A 做匀减速直线运动②敲击B 后―→B 做匀减速直线运动、A 做匀加速直线运动③A 、B 相对静止后―→A 、B 整体做匀减速直线运动解析：(1)由牛顿运动定律知，A 加速度的大小a A ＝μg由匀变速直线运动得2a A L ＝v 2A 解得v A ＝2μgL (2)设A 、B 的质量均为m对齐前，B 所受合外力大小F ＝3μmg由牛顿运动定律F ＝ma B ，得a B ＝3μg对齐后，A 、B 整体所受合外力大小F ′＝2μmg由牛顿运动定律F ′＝2ma B ′，得a B ′＝μg(3)经过时间t ，A 、B 达到共同速度v ，位移分别为x A 、x B ，A 加速度的大小等于a A 则v ＝a A t ，v ＝v B －a B tx A ＝12a A t 2，x B ＝v B t －12a B t 2 且x B －x A ＝L解得v B ＝22μgL答案：(1)2μgL (2)3μg μg (3)22μgL解答“板块”问题时要注意：“一个转折、两个关联”(1)一个转折：即滑块与长木板达到相同的速度时或滑块离开长木板时的受力情况以及运动状态的变化为转折点．(2)两个关联：即发生转折前后滑块和长木板的受力情况以及滑块与长木板的位移之间的关联，必要时要通过作草图把握关系．当有外力作用在木板上的物块或木板上时，一般用动力学观点借助牛顿运动定律和运动学公式就能求解，做好两物体的受力分析和运动过程分析是解决此类问题的关键点和突破口．[题组精练]1．如图所示，静止在水平地面上的木板(厚度不计)质量为m1＝1 kg，与地面间的动摩擦因数μ1＝0.2，质量为m2＝2 kg 且可看成质点的小物块与木板和地面间的动摩擦因数均为μ2＝0.4，以v0＝4 m/s的水平速度从左端滑上木板，经过t＝0.6 s滑离木板，g取10 m/s2，以下说法正确的是() A．木板的长度为1.68 mB．小物块离开木板时，木板的速度为1.6 m/sC．小物块离开木板后，木板的加速度大小为2 m/s2，方向水平向右D．小物块离开木板后，木板与小物块将发生碰撞解析：D由于μ2m2g>μ1(m1＋m2)g，对木板由牛顿第二定律得μ2m2g－μ1(m1＋m2)g＝m1a1，解得a1＝2 m/s2，即物块在木板上以a2＝μ2g＝4 m/s2向右减速滑行时，木板以a1＝2 m/s2向右加速运动，在0.6 s时，物块的速度v2＝1.6 m/s，木板的速度v1＝1.2 m/s，B错误；物块滑离木板时，物块位移为x2＝v0＋v22t＝1.68 m，木板位移x1＝v12t＝0.36 m，两者相对位移为x＝x2－x1＝1.32 m，即木板长度为1.32 m，A错误；物块离开木板后，木板做减速运动，加速度大小为a1′＝2 m/s2，方向水平向左，C错误；分离后，在地面上物块会滑行x2′＝v222a2＝0.32m，木板会滑行x1′＝v212a1′＝0.36 m，所以两者会相碰，D正确．2．如图甲所示，一长方体木板B放在水平地面上，木板B的右端放置着一个小铁块A，在t＝0时刻，同时突然给A、B初速度，其中A的初速度大小为v A＝1 m/s，方向水平向左；B的初速度大小为v B＝14 m/s，方向水平向右，木板B运动的v­t图像如图乙所示．已知A、B的质量相等，A与B及B与地面之间均有摩擦(动摩擦因数不等)，A与B之间的最大静摩擦力等于滑动摩擦力，A始终没有滑出B，取重力加速度g＝10 m/s2.(提示：t＝3 s时刻，A、B达到共同速度v＝2 m/s；3 s时刻至A停止运动前，A向右运动的速度始终大于B的速度)求：(1)小铁块A向左运动相对地面的最大位移；(2)B运动的时间及B运动的位移大小．解析：(1)由题图乙可知，0～3 s内A做匀变速运动，速度由v A＝－1 m/s变为v＝2 m/s则其加速度大小为a A ＝v －v A t 1＝2－（－1）3m/s 2＝1 m/s 2，方向水平向右． 当A 水平向左运动速度减为零时，向左运动的位移最大，则s ＝v 2A 2a A＝0.5 m. (2)设A 与B 之间的动摩擦因数为μ1，由牛顿第二定律得μ1mg ＝ma A则μ1＝a A g＝0.1 由题图乙可知，0～3 s 内B 做匀减速运动，其速度由v B ＝14 m/s 变为v ＝2 m/s则其加速度大小为a B ＝v B －v t 1＝14－23m/s 2＝4 m/s 2 方向水平向左设B 与地面之间的动摩擦因数为μ2，由牛顿第二定律得μ1mg ＋2μ2mg ＝ma B则μ2＝a B －μ1g 2g＝0.15 3 s 之后，B 继续向右做匀减速运动，由牛顿第二定律得2μ2mg －μ1mg ＝ma B ′则B 的加速度大小为a B ′＝2μ2g －μ1g ＝2 m/s 2方向水平向左3 s 之后运动的时间为t 2＝v a B ′＝22s ＝1 s 则B 运动的时间为t ＝t 1＋t 2＝4 s0～4 s 内B 的位移x B ＝v B ＋v 2t 1＋v 2t 2＝25 m ，方向水平向右． 答案：(1)0.5 m (2)4 s 25 m3．(2021·山东省泰安市高三检测)如图所示，水平面上有一长度为L 的平板B ，其左端放置一小物块A (可视为质点)，A 和B 的质量均为m ，A 与B 之间、B 与水平面之间的动摩擦因数均为μ＝0.50，开始时A 和B 都静止，用一个水平推力作用到平板B 上，使A 和B 恰好能保持相对静止一起向右匀加速运动．当位移为x 时，将原来的推力撤去并同时用另一水平推力作用到A 上，使A 保持原来的加速度继续匀加速运动，直到脱离平板．已知重力加速度为g .求：(1)平板B 的最大速度；(2)物块A 脱离平板时的速度大小v .解析：(1)设A 和B 一起做匀加速运动的加速度大小为a ，对A ，有μmg＝ma解得a＝0.5g将原推力撤去时平板B的速度最大，得v2m＝2ax解得B的最大速度v m＝gx(2)推力作用到A上之后，A保持匀加速运动，有x A＝v m t＋12at2v＝v m＋atv2－v2m＝2ax A平板B做匀减速运动，有μ·2mg－μmg＝ma′解得a′＝0.5g讨论两种情况：(a)物块A脱离平板时平板未停下，则对B，有x B＝v m t－12a′t2A、B的位移关系满足x A－x B＝L联立可解得t＝2L g代入数据可得A脱离平板时的速度v＝gx＋0.5gL此时B的速度满足v B＝v m－a′t＞0可解得相应的条件为L＜2x(b)物块A脱离平板时平板停下，则对B，有v2m＝2a′x BA、B的位移关系同样满足x A－x B＝L解得A脱离平板时的速度v＝2gx＋gL相应的条件为L≥2x答案：(1)gx(2)见解析考点三传送带模型[知能必备]1．模型特征一个物体以速度v0(v0≥0)在另一个匀速运动的物体上运动的力学系统可看作“传送带”模型，如图(a)(b)(c)所示．2．解题关键(1)关注两个时刻①初始时刻：物体相对于传送带的速度或滑动方向决定了该时刻的摩擦力方向．②物体与传送带速度相等的时刻：摩擦力的大小、方向或性质(滑动摩擦力或静摩擦力)可能会发生突变．(2)注意过程分解①摩擦力突变点是加速度突变点，也是物体运动规律的突变点，列方程时要注意不同过程中物理量莫混淆．②摩擦力突变点对应的状态是前一过程的末状态，也是后一过程的初状态，这是两个过程的连接点．(3)物体在倾斜传送带上运动，物体与传送带速度相同后需比较tan θ与μ的大小关系：μ>tan θ，速度相等后一起匀速；μ<tan θ，速度相等后物体的加速度向下，根据v与a的方向关系即可判定运动情况．[典例剖析]如图所示，一水平传送带以4 m/s的速度逆时针传送，水平部分长L＝6 m，其左端与一倾角为θ＝30°的光滑斜面平滑相连，斜面足够长，一个可视为质点的物块无初速度地放在传送带最右端，已知物块与传送带间的动摩擦因数μ＝0.2，g取10 m/s2.求物块从放到传送带上到第一次滑回传送带最远端所用的时间．【解题指导】解析：物块在传送带上，根据牛顿第二定律得，μmg＝ma解得a ＝μg ＝2 m/s 2设经过时间t 1物块的速度与传送带的速度相同，则有：v ＝at 1，解得t 1＝v a ＝42 s ＝2 s ； 经过的位移x 1＝v 22a＝4 m<6 m ， 在传送带上匀速运动的时间t 2＝L －x 1v ＝0.5 s物块在斜面上的加速度a ′＝mg sin 30°m＝5 m/s 2， 在斜面上的运动时间t 3＝2v a ′＝85s ＝1.6 s ， 返回传送带在传送带上减速到零(即第一次滑回传送带最远端)的时间t 4＝v a ＝42s ＝2 s 则t ＝t 1＋t 2＋t 3＋t 4＝6.1 s.答案：6.1 s传送带问题的分析技巧(1)理清物体与传送带间的相对运动方向及摩擦力方向是解决传送带问题的关键．(2)传送带问题还常常涉及临界问题，即物体与传送带达到相同速度，这时会出现摩擦力改变的临界状态，对这一临界状态进行分析往往是解题的突破口．[题组精练]1．如图所示，绷紧的水平传送带始终以恒定速率v 1运行．初速度大小为v 2的小物块从与传送带等高的光滑水平地面上的A 处滑上传送带．若从小物块滑上传送带开始计时，小物块在传送带上运动的v ­t 图像(以地面为参考系)如图乙所示．已知v 2＞v 1，则( )A ．t 2时刻，小物块离A 处的距离达到最大B ．t 2时刻，小物块相对传送带滑动的距离达到最大C ．0～t 2时间内，小物块受到的摩擦力方向先向右后向左D ．0～t 3时间内，小物块始终受到大小不变的摩擦力作用解析：B 0～t 1时间内小物块向左做匀减速直线运动，t 1时刻小物块向左速度减为零，此时离A 处的距离达到最大，故A 错误；t 2时刻前小物块相对传送带向左运动，之后小物块相对传送带静止，t 2时刻小物块相对传送带滑动的距离达到最大，故B 正确；0～t 2时间内小物块先减速，后反向加速，小物块受到大小不变，方向始终向右的摩擦力作用，故C 错误；t 2时刻小物块向右速度增加到与传送带相等，t 2时刻之后小物块与传送带保持相对静止随水平传送带一起匀速运动，摩擦力消失，故D 错误．2．(2021·湖北荆州二模)如图所示为货场使用的传送带的模型，传送带倾斜放置，与水平面夹角为θ＝37°，传送带AB 足够长，传送皮带轮以大小为v ＝2 m/s 的恒定速率顺时针转动．一包货物以v 0＝12 m/s 的初速度从A 端滑上倾斜传送带，若货物与皮带之间的动摩擦因数μ＝0.5，且可将货物视为质点．(g ＝10 m/s 2，已知sin 37°＝0.6，cos 37°＝0.8)(1)求货物刚滑上传送带时加速度为多大？(2)经过多长时间货物的速度和传送带的速度相同？这时货物相对于地面运动了多远？(3)从货物滑上传送带开始计时，货物再次滑回A 端共用了多长时间？解析：(1)设货物刚滑上传送带时加速度为a 1，货物受力如图所示：根据牛顿第二定律得沿传送带方向：mg sin θ＋F f ＝ma 1垂直传送带方向：mg cos θ＝F N又F f ＝μF N由以上三式得：a 1＝g (sin θ＋μcos θ)＝10×(0.6＋0.5×0.8) m/s 2＝10 m/s 2，方向沿传送带向下．(2)货物速度从v 0减至传送带速度v 所用时间设为t 1，位移设为x 1，则有：t 1＝v －v 0－a 1＝1 s ，x 1＝v 0＋v 2t 1＝7 m. (3)当货物速度与传送带速度相等时，由于mg sin θ＞μmg cos θ，此后货物所受摩擦力沿传送带向上，设货物加速度大小为a 2，则有mg sin θ－μmg cos θ＝ma 2，得：a 2＝g (sin θ－μcos θ)＝2 m/s 2，方向沿传送带向下．设货物再经时间t 2，速度减为零，则t 2＝0－v －a 2＝1 s 货物沿传送带向上滑的位移x 2＝v ＋02t 2＝1 m 则货物上滑的总距离为x ＝x 1＋x 2＝8 m.货物到达最高点后将沿传送带匀加速下滑，下滑加速度大小等于a 2.设下滑时间为t 3，则x ＝12a 2t 23，代入解得t 3＝2 2 s. 所以货物从A 端滑上传送带到再次滑回A 端的总时间为t ＝t 1＋t 2＋t 3＝(2＋22) s. 答案：(1)10 m/s 2，方向沿传送带向下 (2)1 s 7 m (3)(2＋22) s3. (2021·安徽省马鞍山市高三下学期二模)有一水平足够长的传送带，以3 m/s 的速度沿顺时针方向匀速运转，传送带右端与倾角为37°的粗糙固定斜面底端B 平滑连接，一质量为1 kg 的小滑块从斜面上A 点由静止释放，经过一段时间后，最终停在传送带与斜面的连接处．小滑块与斜面、传送带之间的动摩擦因数均为0.5，A 、B 间距离为4 m ．重力加速度g ＝10 m/s 2，sin 37°＝0.6，cos 37°＝0.8.求：(1)小滑块从释放到第一次到达B 点经历的时间；(2)小滑块第三次通过B 点的速度大小；(3)从释放到最终停止，小滑块运动的总路程．解析：(1)小滑块从A 点由静止释放向下运动mg sin θ－μmg cos θ＝ma 1得a 1＝2 m/s 2s AB ＝12a 1t 21得t 1＝2 s(2)小滑块第一次滑上传送带的速度为v ＝a 1t 1＝4 m/s此后先向左匀减速，而后向右匀加速，v ＝4 m/s>v 0＝3 m/s ，当滑块和传送带速度相同时开始匀速，所以滑块返回B 点时速度为v 0＝3 m/s滑块沿斜面向上运动的加速度为ma 2＝mg sin θ＋μmg cos θ解得a 2＝10 m/s 2滑块第一次以初速度v 0冲上斜面后上升的最大距离x 1，滑块第三次到B 时速度为v 1，则v 20＝2a 2x 1v 21＝2a 1x 1联立得v 1＝v 0 15＝355m/s (3)滑块第一次以v 滑上传送带，向左运动的位移为s 1＝v 22μg＝1.6 m 滑块第二次以初速度v 1滑上传送带，由于v 1<v 0，滑块从传送带上返回B 点时速度大小仍为v 1，由第(2)问的分析知，此后滑块每次滑下斜面的速度大小是滑上斜面速度的 15 v 1＝v 015 v 2＝v 0⎝⎛⎭⎫152 v 3＝v 0⎝⎛⎭⎫153 ……滑块第一次滑上斜面之后在斜面上的总路程s 2＝2v 202a 2＋2v 212a 2＋2v 222a 2＋… 联立可得s 2＝1.125 m滑块第三次滑上传送带之后在传送带上的总路程s 3＝2v 212μg ＋2v 222μg ＋2v 232μg＋… 联立可得s 3＝0.45 m小滑块运动的总路程s 总＝s AB ＋2s 1＋s 2＋s 3＝8.775 m答案：(1)2 s (2)355m/s (3)8.775 m 限时规范训练(三) 连接体问题、板块模型、传送带模型建议用时60分钟，实际用时________一、单项选择题 1．如图所示，质量分别为3 kg 、5 kg 的P 、Q 两滑块，用轻弹簧连接后置于光滑水平地面上．现用大小F ＝8 N 的水平拉力拉Q ，使P 、Q 一起向右做匀加速直线运动．则此过程中弹簧的弹力大小为( )A ．3 NB ．4 NC ．5 ND ．8 N解析：A 对PQ 的整体，由牛顿第二定律F ＝(m P ＋m Q )a ，对P ，T ＝m P a, 解得T ＝3 N ，故选项A 正确．2．(2021·山东省聊城市高三下学期模拟)车厢中用细线悬挂小球，通过细线的倾斜程度来检测车辆在行进过程中的加速度．如图所示，质量相同的两个光滑小球通过轻质细线分别系于车的顶部，左侧小球与车厢左侧壁接触，两细线与竖直方向的夹角相同，拉力大小分别为T 1和T 2.下列说法正确的是( )A ．车可能正在向左做加速运动B ．两细线的拉力T 1＝T 2C ．当汽车加速度增大时，T 1变小D ．当汽车加速度减小时，T 2增大解析：B 对右边小球进行受力分析，沿细线方向斜右上方的拉力，和竖直向下的重力．设细线与竖直方向夹角为θ，根据牛顿第二定律有ma ＝mg tan θ，T 2＝mg cos θ，加速度水平向右，可以判断小车可能向右加速，或者向左减速，故A 错误；同理，对左边小球受力分析，可得ma ＝F N －T 1sin θ，T 1＝mg cos θ，联立可得T 1＝T 2，故B 正确；根据上面选项的分析，可知当汽车加速度增大时， T 1不变，故C 错误；根据上面选项的分析，可知当汽车加速度减小时，小球2的细线的夹角变小，T 2变小．故D 错误．3．如图所示，在平直公路上行驶的厢式货车内，用轻绳AO 、BO 在O 点悬挂质量为5 kg 的重物，轻绳AO 、BO 与车顶部夹角分别为30°、60°.在汽车加速行驶过程中，为保持重物悬挂在O 点位置不动，重力加速度为g ，厢式货车的最大加速度( )A.g 2B ．3g 3 C.3g 2 D ．3g解析：B 对小球受力分析可得F A sin 30°＋F B sin 60°＝mg ，F B cos 60°－F A cos 30°＝ma ，联立解得12·⎝⎛⎭⎫233mg －33F A －32F A ＝ma ，整理得33mg －233F A ＝ma ，当F A ＝0时，a 取得最大值a ＝33g .故选B 项． 4．如图所示，一水平方向足够长的传送带以恒定的速度v 1＝2 m/s 沿顺时针方向转动，传送带右端有一与传送带等高的光滑水平面，一物体以恒定速度v 2＝5 m/s 沿直线向左滑向传送带后，经过一段时间又返回光滑水平面，速率为v 2′，物体与传送带间的动摩擦因数为0.2，则下列说法正确的是( )A ．返回光滑水平面时的速率为v 2′＝2 m/sB ．返回光滑水平面时的速率为v 2′＝5 m/sC ．返回光滑水平面的时间为t ＝3.5 sD ．传送带对物体的摩擦力先向右再向左解析：A 因为传送带足够长，且顺时针转动，又因为v 1<v 2，则物体会先向左减速直到速度为0，再向右加速，最后匀速，则物体返回光滑水平面时的速率为v 2′＝2 m/s ，故A 正确，B 错误；由牛顿第二定律得a ＝f m ＝μmg m ＝μg ＝2 m/s 2，则物体减速的时间为t 1＝v 2a＝2.5 s ，物体减速的位移为x 1＝12at 21＝6.25 m ，物体反向加速的时间为t 2＝v 1a＝1 s ，反向加速的位移为x 2＝12at 22＝1 m ，物体匀速的时间为t 3＝x 1－x 2v 1＝2.625 s ，故物体返回光滑水平面的时间为t ＝t 1＋t 2＋t 3＝6.125 s ，故C 错误；由于物体是先向左减速，后反向加速，最后匀速返回，所以传送带对物体的摩擦力先向右后为0，故D 错误．5．质量为1 kg 的木板B 静止在水平面上，可视为质点的物块A 从木板的左侧沿木板上表面水平冲上木板，如图甲所示．A 和B 经过1 s 达到同一速度，之后共同减速直至静止，A 和B 运动的v ­t 图像如图乙所示，取g ＝10 m/s 2，则物块A 的质量为( )A ．1 kgB ．2 kgC ．3 kgD ．6 kg解析：C 由图像可知，物块在0～1 s 内的加速度大小为a 1＝2 m/s 2，以物块为研究对象，由牛顿第二定律得μ1mg ＝ma 1，解得：μ1＝0.2，木板在0～1 s 内的加速度大小为a 2＝2 m/s 2，在1 s ～3 s 内物块与木板相对静止，一起做匀减速运动，加速度大小为a 3＝1 m/s 2，AB 同速后整体为研究对象，由牛顿第二定律得：μ2(M ＋m )g ＝(M ＋m )a 3，解得：μ2＝0.1，再以B 为研究对象，在0～1 s 内水平方向受到两个滑动摩擦力，由牛顿第二定律得：μ1mg －μ2(M ＋m )g ＝Ma 2代入数据解得A 的质量m ＝3 kg.6．用货车运输规格相同的两层水泥板，底层水泥板固定在车厢内，为防止货车在刹车时上层水泥板撞上驾驶室，上层水泥板按如图所示方式放置在底层水泥板上．货车以3 m/s 2的加速度启动，然后以12 m/s 匀速行驶，遇紧急情况后以8 m/s 2的加速度刹车至停止．已知每块水泥板的质量为250 kg ，水泥板间的动摩擦因数为0.75，最大静摩擦力等于滑动摩擦力，取g ＝10 m/s 2，则( )A ．启动时上层水泥板所受摩擦力大小为1875 NB ．刹车时上层水泥板所受摩擦力大小为2000 NC ．货车在刹车过程中行驶的距离为9 mD ．货车停止时上层水泥板相对底层水泥板滑动的距离为0.6 m解析：C 摩擦力提供给水泥板最大的加速度为a ′＝μg ＝7.5 m/s 2启动时，加速度小于最大加速度，上层水泥板所受摩擦力为静摩擦力，大小为f ＝ma ＝250×3 N ＝750 N ，A 错误；刹车时，加速度大于最大加速度，上层水泥板所受摩擦力为滑动摩擦力，其大小为f ＝μmg＝1875 N ，B 错误；货车在刹车过程中行驶的距离为s ＝v 22a＝9 m ，C 正确；货车停止时间为t ＝v a ＝1.5 s ，该时间内，上层水泥板滑动的距离为s ′＝v t －12μgt 2＝18－8.4375＝9.5625 m ，货车停止时上层水泥板相对底层水泥板滑动的距离为Δs ＝s ′－s ＝0.5625 m ，D 错误．7．(2021·山东济宁高三检测)如图所示，三个物体A 、B 和C 的质量分别为2m 、m 和m ，A 、B 叠放在水平桌面上，A 通过跨过光滑定滑轮的轻绳与C 相连，定滑轮左端的轻绳与桌面平行，A 、B 间的动摩擦因数为μ(μ＜1)，B 与桌面间的动摩擦因数为μ3，A 、B 、桌面之间的最大静摩擦力等于相对应的滑动摩擦力，重力加速度为g ，下列说法正确的是( )A ．三个物体A 、B 、C 均保持静止B ．轻绳对定滑轮的作用力大小为2mgC ．若A 、B 之间发生相对滑动，则需满足μ＜0.2D ．若A 、B 之间未发生相对滑动，则A 受到的摩擦力大小为1＋2μ3mg 解析：C 物块A 与B 之间的最大静摩擦力f 1＝2μmg ，物块B 与桌面间的最大静摩擦力f 2＝3mg ×μ3＝μmg ，显然f 2＜f 1，由于μ＜1，即μmg ＜mg ，物块B 一定与桌面间发生相对滑动，A 错误；由于物块C 加速下降，绳子拉力T ＜mg ，因此轻绳对定滑轮的作用力大小F ＝2T ＜2mg ，B 错误；若A 与B 间恰好将发生相对滑动时，A 与B 的加速度恰好相等，此时对物块B ：f 1－f 2＝ma ，对A 、B 整体：T －f 2＝3ma ，对物块C: mg －T ＝ma ，解得μ＝0.2，因此若A 、B 之间发生相对滑动，则需满足μ＜0.2，C 正确；若A 、B 之间未发生相对滑动，则对整体mg －f 2＝4ma ，对物块B ：f －f 2＝ma ，可得A 受到的摩擦力大小f ＝1＋3μ4mg ，D 错误． 8．(2021·湖北省八市高三下学期3月联考)如图所示，传送带以10 m/s 的速度逆时针匀速转动，两侧的传送带长都是16 m ，且与水平方向的夹角均为37°.现有两个滑块A 、B (可视为质点)从传送带顶端同时由静止滑下，已知滑块A 、B 的质量均为1 kg ，与传送带间动摩擦因数均为0.5，取重力加速度g ＝10 m/s 2，sin 37°＝0.6，cos 37°＝0.8.下列说法正确的是( )A ．滑块A 先做匀加速运动后做匀速运动B ．滑块A 、B 同时到达传送带底端C ．滑块A 、B 到达传送带底端时的速度大小相等D ．滑块A 在传送带上的划痕长度为5 m解析：D 两滑块都以10 m/s 的初速度沿传送带下滑，且mg sin 37°>μmg cos 37°，故传送带对两滑块的滑动摩擦力均沿斜面向上，大小也相等，故两滑块沿斜面向下的加速度大小相同，为a ＝g sin 37°＋μg cos 37°＝10 m/s 2，滑块A 先加速，加速到传送带速度所需位移为x 1＝v 202a ＝5 m<16 m ，所需时间为t 1＝v 0a＝1 s ，加速到传送带速度后，由于mg sin 37°>μmg cos 37°，故不能和传送带保持相对静止，摩擦力反向，之后加速度为a ′＝g sin 37°－μg cos 37°＝2 m/s 2，加速到传送带底端L －x 1＝v 0t 2＋12a ′t 22，解得时间t 2＝1 s ，到达底端共用时t ＝t 1＋t 2＝2 s ，B 滑块一直以加速度a ′加速至传送带底端L ＝12a ′t ′2，解得t ′＝4 s ，AB 错误；A 到达底端时的速度为v A ＝v 0＋a ′t 2＝10 m/s ＋2×1 m/s ＝12 m/s ，B 到达底端时的速度为v B ＝a ′t ′＝2×4 m/s ＝8 m/s ，C 错误；加速到传送带速度之时的相对位移为Δx 1＝v 0t 1－x 1＝10×1 m －5 m ＝5 m ，加速到传送带速度以后，相对位移为Δx 2＝11－v 0t 2＝1 m ，滑块比传送带速度快，会覆盖之前的划痕，滑块A 在传送带上的划痕长度为5 m ，D 正确．二、多项选择题9．如图甲所示，一水平传送带沿顺时针方向旋转，在传送带左端A 处轻放一可视为质点的小物块，小物块从A 端到B 端的速度—时间变化规律如图乙所示，t ＝6 s 时恰好到达B 点，重力加速度g 取10 m/s 2，则( )。