最新人教版高中数学选修4-1《弦切角的性质》自我小测

2021年高中数学 2.4弦切角的性质同步检测试题新人教A版选修4-1►一层练习1．如图所示，经过⊙O上的点A的切线和弦BC的延长线相交于点P，若∠CAP ＝40°，∠ACP＝100°，则∠BAC所对的弧的度数为( )A．40°B．100°C．60° D．30°答：C2．如图所示，圆O的直径AB＝6，C为圆周上一点，BC＝3过C作圆的切线l，过A作l的垂线AD，交圆O于E，垂足为D，则∠DAC＝( )A．15° B．30°C．45° D．60°答：B3．如图所示，AD切⊙O于点F，FB、FC为⊙O的两弦，请列出图中所有的弦切角：________________________________________________________________________.答：∠AFB、∠AFC、∠DFC、∠DFB答：45°135°45°90°►二层练习5．已知⊙O的内接四边形ABCD中，AB是⊙O的直径，∠BCD＝120°，过点D的切线PD 与BA的延长线交于点P，则∠APD的度数是( )A．15° B．30°C．45° D．60°答：B6．如图所示，AB是⊙O的直径，直线EF切⊙O于点B，点C、D在⊙O上，∠CBE＝40°，则∠BCD的度数是( )A ．110°B ．115°C ．120°D ．135° 答：B7．如图所示，已知AB 和AC 分别是⊙O 的弦和切线，点A 为切点，AD 为∠BAC 的平分线，且交⊙O 于点D ，BD 的延长线与AC 交于点C ，AC ＝6，AD ＝5，则CD ＝______.解析：由弦切角定理，有∠CAD ＝∠B . 又∠C ＝∠C ，则△ACD ∽△BCA ， ∴CD AC ＝AC BC，又∠BAD ＝∠CAD ＝∠B ， 则BC ＝CD ＋BD ＝CD ＋AD .设CD ＝x ，则x 6＝6x ＋5，x ＝4或－9(舍去)，故CD ＝4. 答案：48．如图所示，EB ，EC 是圆O 的两条切线，B ，C 是切点，A ，D 是圆O 上两点，如果∠E ＝46°，∠DCF＝32°，试求∠A 的度数．解析：连接OB ，OC ，AC ，根据弦切角定理，可得∠A ＝∠BAC ＋∠CAD ＝12(180°－∠E )＋∠DCF ＝67°＋32°＝99°.►三层练习9．如图所示，直线PB 与圆O 相切于点B ，D 是弦AC 上的点，∠PBA ＝∠DBA .若AD ＝m ，AC ＝n ，则AB ＝________.答：mn10．如图所示，过圆O 外一点P 分别作圆的切线和割线交圆于A ，B ，且PB ＝7，C 是圆上一点使得BC ＝5，∠BAC ＝∠APB ，则AB ＝________.解析：由弦切角定理有∠PAB ＝∠C ， 又∠APB ＝∠BAC ， 则△APB ∽△CAB . 即AB BC ＝PB AB，∴AB ＝BC ·PB ＝35. 答案：3511．如下图，圆O 是△ABC 的外接圆，过点C 的切线交AB 的延长线于点D ，CD ＝27，AB ＝BC ＝3，则AC ＝________.答：37212．如图，已知圆O 的直径AB ＝5，C 为圆周上一点，BC ＝4，过点C 作圆O 的切线l ，过点A 作l 的垂线AD ，垂足为D ，则CD ＝________.解析：由弦切角定理，有∠ACD ＝∠B ， ∴CDAC ＝cos∠ACD ＝cos B ＝BC AB. ∴CD52－42＝45.故CD ＝125. 答案：12513．(xx·珠海二调)如图，AB 是圆O 的直径，直线CE 和圆O 相切于点C ，AD ⊥CE 于D ，若AD ＝1，∠ABC ＝30°，则圆O 的面积是________．解析：由弦切角定理，有∠ACD ＝∠ABC ＝30°，∴AC ＝2AD ，AB ＝2AC ，即AB ＝4，S ⊙O ＝π·⎝ ⎛⎭⎪⎫422＝4π.答案：4π14．如图所示，⊙O 和⊙O ′相交于A ，B 两点，过A 作两圆的切线分别交两圆于C ，D 两点，连接DB 并延长交⊙O 于点E .证明：(1)AC ·BD ＝AD ·AB ；证明：由AC 与⊙O ′相切于A ，得 ∠CAB ＝∠ADB ， 同理∠ACB ＝∠DAB ，所以△ACB ∽△DAB .从而AC AD ＝AB BD， 即AC ·BD ＝AD ·AB .(2)AC ＝AE .证明：由AD 与⊙O 相切于A ，得 ∠AED ＝∠BAD . 又∠ADE ＝∠BDA ，得 △EAD ∽△ABD .从而AE AB ＝AD BD，即AE ·BD ＝AD ·AB . 结合(1)的结论知，AC ＝AE .15．(xx·新课标全国Ⅰ卷)如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.(1)证明：DB＝DC；解析：连接DE，交BC为G，由弦切角定理得，∠ABE＝∠BCE，而∠ABE＝∠CBE，故∠CBE＝∠BCF，BE＝CE.又因为DB⊥BE，所以DE为直径，∠DCE＝90°，由勾股定理可得DB＝DC.(2)设圆的半径为1，BC＝3，延长CE交AB于点F，求△BCF外接圆的半径．解析：由(1)知，∠CDE＝∠BDE，DB＝DC，故DG是BC的中垂线，所以BG＝32，圆心为O，连接BO，则∠BOG＝60°，∠ABE＝∠BCE＝∠CBE＝30°，所以CF⊥BF，故外接圆半径为32./P32841 8049 聉p27844 6CC4 泄23826 5D12 崒23911 5D67 嵧kL 39007 985F 顟30885 78A5 碥26951 6947 楇。

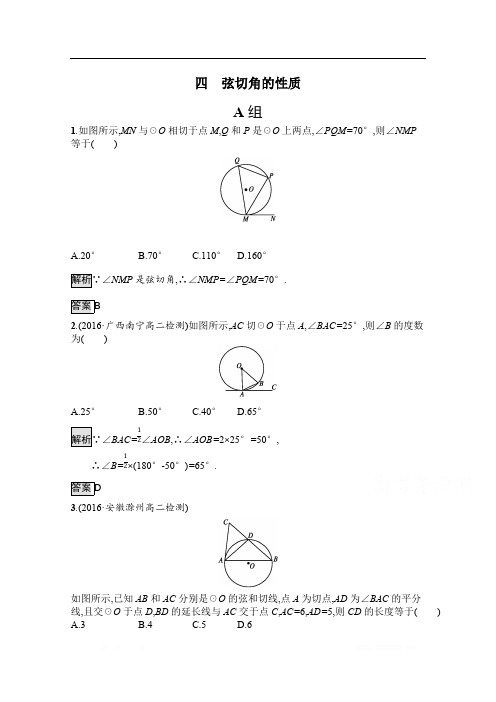
四　弦切角的性质A 组1.如图所示,MN 与☉O 相切于点M ,Q 和P 是☉O 上两点,∠PQM=70°,则∠NMP 等于( )A.20°B.70°C.110°D.160°NMP 是弦切角,∴∠NMP=∠PQM=70°.2.(2016·广西南宁高二检测)如图所示,AC 切☉O 于点A ,∠BAC=25°,则∠B 的度数为( )A.25°B.50°C.40°D.65°BAC=∠AOB ,∴∠AOB=2×25°=50°,12∴∠B=×(180°-50°)=65°.123.(2016·安徽滁州高二检测)如图所示,已知AB 和AC 分别是☉O 的弦和切线,点A 为切点,AD 为∠BAC 的平分线,且交☉O 于点D ,BD 的延长线与AC 交于点C ,AC=6,AD=5,则CD 的长度等于( )A.3B.4C.5D.6∠CAD=∠ABC.又因为AD 为∠BAC 的平分线,所以∠CAD=∠DAB ,从而∠CBA=∠DAB ,所以DB=AD=5,且△ACD ∽△BCA ,于是,即,解CD CA =AC BC CD 6=6CD +5得CD=4(负值舍去).4.如图所示,四边形ABCD 是圆的内接四边形,AB 是直径,MN 是☉O 的切线,切点为C ,若∠BCM=38°,则∠B=( )A.32°B.42°C.52°D.48°如图所示,连接AC.∵∠BCM=38°,MN 是☉O 的切线,∴∠BAC=38°.∵AB 为☉O 的直径,∴∠BCA=90°.∴∠B=90°-38°=52°.5.如图,AB 是☉O 的直径,EF 切☉O 于点C ,AD ⊥EF 于点D ,AD=2,AB=6,则AC 的长为( )A.2B.3C.2D.43连接BC ,如图所示.∵EF 是☉O 的切线,∴∠ACD=∠ABC.又AB 是☉O 的直径,∴∠ACB=90°.又AD ⊥EF ,∴∠ACB=∠ADC.∴△ADC ∽△ACB.∴.ABAC =AC AD ∴AC 2=AD ·AB=2×6=12,∴AC=2.36.(2016·河南禹州高二月考)如图,若AB 切☉O 于A ,AC ,AD 为☉O的弦,且,则∠C 与∠CAB 的关系是 .⏜AC =⏜AD,所以∠ADC=∠ACD.又由弦切角定理可得∠BAC=∠ADC ,故⏜AC =⏜AD ∠C=∠CAB.C=∠CAB7.已知AB 是☉O 的弦,PA 是☉O 的切线,A 是切点,如果∠PAB=30°,那么∠AOB= .弦切角∠PAB=30°,∴它所夹的弧所对的圆周角等于30°,所对的圆心角等于60°.°8.(2016·河北唐山高二检测)已知PA 是圆O 的切线,切点为A ,PO 交圆O 于B ,C 两点,AC=,∠PAB=30°,则线段PB 的长为 .3连接OA ,∵PA 为☉O 的切线,∴∠OAP=90°,∠C=∠PAB=30°,∴∠OBA=∠OAB=60°,∴∠P=∠PAB=30°,∴PB=AB.又AC=,BC 为☉O 的直径,3∴∠CAB=90°,∴AB=1,∴PB=1.9.如图所示,☉O 1与☉O 2交于A ,B 两点,过☉O 1上一点P 作直线PA ,PB 分别交☉O 2于点C 和点D ,EF 切☉O 1于点P ,求证:EF ∥CD.AB ,∵EF 是☉O 1的切线,由弦切角定理知,∠FPA=∠PBA.又在☉O 2中,四边形ABDC 为圆内接四边形,∴∠C=∠ABP ,∴∠FPA=∠C ,∴EF ∥CD.10.(2016·江西赣州高二检测)如图,在△ABC 中,∠B=90°,O 是AB 上一点,以O 为圆心,OB 为半径的圆与AB 交于点E ,与AC 切于点D ,直线ED 交BC 的延长线于F ,若AD ∶AE=2∶1,求tan ∠F 的值.如图所示,连接BD.∵AC 为☉O 的切线,∴∠ADE=∠ABD.∵∠A=∠A ,∴△ADE ∽△ABD ,∴,即,ADAE =BD DE BD DE =21∴.DE BD =12∵BE 为☉O 的直径,∴∠BDE=90°,∴tan ∠ABD=.DE BD =12∵∠F+∠BEF=90°,∠ABD+∠BEF=90°,∴∠ABD=∠F ,∴tan ∠F=tan ∠ABD=.12B 组1.如图,在圆的内接四边形ABCD 中,AC 平分∠BAD ,EF 切☉O 于C 点,则图中与∠DCF 相等的角的个数是( )A.4B.5C.6D.7∠DCF=∠DAC ,∠DCF=∠BAC ,∠DCF=∠BCE ,∠DCF=∠BDC ,∠DCF=∠DBC.2.如图所示,☉O 和☉O'相交于A ,B 两点,过点A 作两圆的切线,分别交两圆于C ,D 两点,若BC=2,BD=4,则AB 的长为( )A.2B.2C.4D.623AC ,AD 分别是两圆的切线,∴∠C=∠BAD ,∠D=∠BAC.∴△ACB ∽△DAB.∴.∴AB 2=BC ·DB=2×4=8.∴AB=2(负值舍去).BCBA =AB DB 23.已知AB切☉O于A点,圆周被AC所分成的优弧与劣弧之比为3∶1,则夹劣弧的弦切角∠BAC= .优弧与劣弧之比为3∶1,∴劣弧所对的圆心角为90°,所对的圆周角为45°,故由弦切角定理可知,弦切角∠BAC=45°.°4.导学号19110038如图,AB是圆O的直径,点C在圆O上.延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则BC= .OC.∵AB为圆O的直径,∴AC⊥BC.又BC=CD,∴AB=AD=6,∠BAC=∠CAD.又CE为圆O的切线,则OC⊥CE.∵∠ACE为弦切角,∴∠ACE=∠B.∴∠ACE+∠CAD=90°.∴CE⊥AD.又AC⊥CD,∴CD2=ED·AD=2×6=12,33即CD=2.∴BC=2.235.(2016·湖南岳阳高二检测)如图所示,△ABC 内接于☉O ,AB=AC ,直线XY 切☉O 于点C ,BD ∥XY ,AC ,BD 相交于E.(1)求证:△ABE ≌△ACD ;(2)若AB=6 cm,BC=4 cm,求AE 的长.XY 是☉O 的切线,所以∠1=∠2.因为BD ∥XY ,所以∠1=∠3,故∠2=∠3.因为∠3=∠4,所以∠2=∠4.因为∠ABD=∠ACD ,又因为AB=AC ,所以△ABE ≌△ACD.∠3=∠2,∠ABC=∠ACB ,所以△BCE ∽△ABC ,,即AC ·CE=BC 2.BCAB =CE CB 因为AB=AC=6 cm,BC=4 cm,所以6·(6-AE )=16,故AE= cm .1036.导学号19110039(2016·吉林长春高二检测)如图,AB 为☉O 的直径,直线CD 与☉O 相切于E ,AD ⊥CD 于D ,BC ⊥CD 于C ,EF ⊥AB 于F ,连接AE ,BE.证明:(1)∠FEB=∠CEB ;(2)EF 2=AD ·BC.由直线CD 与☉O 相切,得∠CEB=∠EAB.由AB 为☉O 的直径,得AE ⊥EB ,从而∠EAB+∠EBF=.π2又EF ⊥AB ,得∠FEB+∠EBF=.π2从而∠FEB=∠EAB ,故∠FEB=∠CEB.(2)由BC ⊥CE ,EF ⊥AB ,∠FEB=∠CEB ,BE 是公共边,则Rt △BCE ≌Rt △BFE ,所以BC=BF.同理可证Rt △ADE ≌Rt △AFE ,得AD=AF.又在Rt △AEB 中,EF ⊥AB ,故EF 2=AF ·BF ,所以EF 2=AD ·BC.。

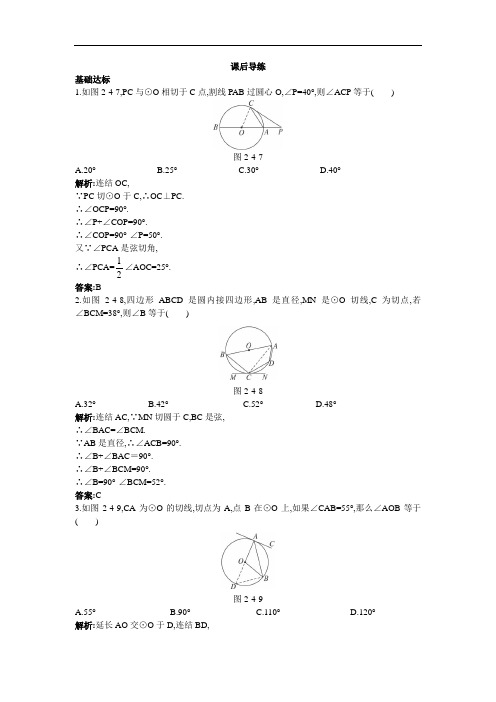
课后导练基础达标1.如图2-4-7,PC 与⊙O 相切于C 点,割线PAB 过圆心O,∠P=40°,则∠ACP 等于( )图2-4-7 A.20° B.25° C.30° D.40° 解析:连结OC,∵PC 切⊙O 于C,∴OC ⊥PC. ∴∠OCP=90°.∴∠P+∠COP=90°. ∴∠COP=90°-∠P=50°. 又∵∠PCA 是弦切角, ∴∠PCA=21∠AOC=25°. 答案:B2.如图2-4-8,四边形ABCD 是圆内接四边形,AB 是直径,MN 是⊙O 切线,C 为切点,若∠BCM=38°,则∠B 等于( )图2-4-8 A.32° B.42° C.52° D.48° 解析:连结AC,∵MN 切圆于C,BC 是弦, ∴∠BAC=∠BCM.∵AB 是直径,∴∠ACB=90°. ∴∠B+∠BAC ＝90°. ∴∠B+∠BCM=90°. ∴∠B=90°-∠BCM=52°. 答案:C3.如图2-4-9,CA 为⊙O 的切线,切点为A,点B 在⊙O 上,如果∠CAB=55°,那么∠AOB 等于( )图2-4-9A.55°B.90°C.110°D.120° 解析:延长AO 交⊙O 于D,连结BD,∵AC 切⊙O 于A,AB 是弦, ∴∠D=∠CAB. 又∵∠D=21∠AOB, ∴∠AOB=2∠CAB=110°. 答案:C4.如图2-4-10,∠ABC=90°,O 是AB 上一点,⊙O 切AC 于D,交AB 于E,连结DB 、DE 、OC,则图中与∠CBD 相等的角共有( )图2-4-10A.1个B.2个C.3个D.4个 解析:∵AB ⊥BC,∴BC 与⊙O 相切,BD 为弦. ∴∠CBD=∠BED. 同理,∠CDB=∠BED. ∴∠CBD=∠CDB. 又OC ⊥BD,DE ⊥BD, ∴DE ∥OC.∴∠BED=∠BOC. ∴∠CBD=∠BOC. ∴共3个. 答案:C5.如图2-4-11,AB 、AC 与⊙O 相切于B 、C,∠A=50°,点P 是圆上异于B 、C 的一动点,则∠BPC 的度数是( )图2-4-11A.65°B.115°C.65°或115°D.130°或50° 解析:点P 可能位置有两种情况,点P 在优弧上或在劣弧上.图2-4-12(1)如图2-4-12,在优弧上, ∵AB 、AC 是切线,∴∠ABC=∠P 1,∠ACB=∠P 1,∠ABC=21(180°-∠A)=65°. (2)如图2-4-13,在劣弧上,可在优弧上任取一点Q,图2-4-13由(1)知∠Q=65°,∵四边形BP 2CQ 内接于圆O, ∴∠BP 2C+∠Q=180°. ∴∠BP 2C=180°-∠Q=115°. 综上,∠BPC=65°或115°. 答案:C 温馨提示本题运用了运动变化思想、分类思想和化归思想. 综合运用6.如图2-4-14,AD 是圆内接△ABC 的∠A 的平分线,交圆于D,E 为BC 中点,BF 为圆的切线,DF ⊥BF. 求证:DE=DF.图2-4-14证明:连结BD,∵BF 是切线,BD 是弦, ∴∠DBF=∠BAD. ∵=,∴∠DBC=∠DAC.又∵AD 是∠BAC 的平分线,∴∠BAD=∠DAC.∴∠DBF=∠DBE, 即BD 是∠EBF 的平分线. ∵∠BAD=∠DAC,∴=,即D 是中点.∵E 是BC 中点,∴DE ⊥BC. ∴DE=DF.7.如图2-4-15,梯形ABCD 中,AB ∥DC,AD=BC,以AD 为直径的⊙O 交AB 于点E,⊙O 的切线EF 交BC 于F,求证:EF ⊥BC.图2-4-15证明:∵AD是直径,∴∠AED=90°.∴∠DEF+∠BEF=90°.∵EF切⊙O于点E,DE是弦,∴∠DEF=∠A.∴∠A+∠BEF=90°.∵AD=BC,AB∥DC,∴∠B=∠A.∴∠B+∠BEF=90°.∴∠BFE=90°.∴EF⊥BC.8.两圆内切于点P,大圆的弦AD交小圆于点B、C.求证:∠APB=∠CPD.图2-4-16证明:过P作两圆的公切线MN.∵PB是小圆弦,MN是切线,∴∠BPM=∠BCP.∵PA是大圆弦,MN是切线,∴∠APM=∠D.∴∠BPM-∠APM=∠BCP-∠D.又∠BCP=∠D+∠CPD,∴∠BCP-∠D=∠CPD.∴∠APB=∠CPD.9.如图2-4-17,AB是⊙O的弦,CD是经过⊙O上一点M的切线.图2-4-17求证:(1)AB∥CD时,AM=MB.(2)AM=MB时,AB∥CD.证明:(1)∵AB∥CD,∴∠A=∠AMC.∵CD切⊙O于M,AM是弦,∴∠AMC=∠B.∴∠A=∠B.∴AM=BM.(2)∵AM=MB,∴∠A=∠B.又∵CD切⊙O于M,AM是弦,∴∠AMC=∠B.∴∠AMC=∠A.∴AB∥CD.拓展探究10.如图2-4-18,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动且总保持PQ=PO,过Q作⊙O的切线交BA的延长线于点C.图2-4-18(1)当∠QPA=60°时,请你对△QCP的形状作出猜想,并证明;(2)当QP⊥AO时,△QCP的形状是___________三角形.(3)由(1)、(2)得出的结论,请你进一步猜想,当点P在线段AM上运动到任何位置时△QCP一定是___________三角形.解析:(1)△QCP是等边三角形,证明:连结OQ,则CQ⊥OQ.∵PQ=PO,∠QPC=60°,∴∠POQ=∠PQO=30°.∴∠C=∠CQO-∠POQ=60°.∴∠CQP=∠C=∠QPC=60°.∴△QPC是等边三角形.(2)等腰直角(解析:略)(3)等腰(解析:略)备选习题11.如图2-4-19,BC为⊙O直径,DE切⊙O于A点,BD⊥DE于D,若∠ABD=50°,则的度数为_________________.图2-4-19解析:∵BD⊥DE,∴∠BDA=90°.∴∠ABD+∠BAD=90°.∴∠BAD=90°-50°=40°.∵AB是弦,AD是切线,∴∠C=∠BAD=40°.∴BC是直径.∴∠BAC=90°.∴∠C+∠ABC=90°.∴∠ABC=90°-∠C=50°.∴的度数为100°.答案:100°12.如图2-4-20,AB为⊙O的直径,DA、DE为⊙O两切线,A、C为切点,A、B、E共线,若的度数为60°,则∠CAD的度数为____________,∠E的度数为_____________.图2-4-20解析:∵度数为60°,∴∠BAC=30°,∠BCE=30°.∵AD为切线,∴BA⊥AD.∴∠BAC+∠CAD=90°.∴∠CAD=90°-∠BAC=60°.∵AB为直径,∴∠ACB=90°.∴∠ABC=90°-∠BAC=30°.∴∠E=∠ABC-∠BCE=30°.答案:60°30°13.两圆内切于点P,大圆的弦AB切小圆于C，求证：∠APC＝∠CPB.图2-4-21证明:过P作两圆公切线MN,设PB交小圆于D,连结CD.∵PC是小圆弦,MN切小圆于P,∴∠MPC=∠PDC.∵PA是大圆弦,MN切大圆于P,∴∠MPA=∠B.∴∠MPC-∠MPA=∠PDC-∠B.∵∠PDC=∠B+∠BCD,∴∠PDC-∠B=∠BCD.∴∠APC=∠BCD.又AB切小圆于C，CD是小圆弦,∴∠BCD=∠CPB.∴∠APC=∠CPB.14.如图2-4-22,△ABC中,过A与BC相切于D的圆分别交AB、AC于E、F,且EF∥BC. 求证:AD平分∠A.图2-4-22证明:连结DF,∵BC 切圆于D,DF 是弦, ∴∠3=∠2.∵EF ∥BC,∴∠3=∠4. 又∠1=∠4,∴∠1=∠2,即AD 平分∠BAC.15.如图2-4-12(1),OA 和OB 是⊙O 的半径,且OA ⊥OB,P 是OA 上任一点,BP 的延长线交⊙O 于Q,过Q 的⊙O 的切线交OA 的延长线于R,易证RP=RQ(不要求证明). (1)现将PA 向上平移至图2-4-23(2)位置,结论还成立吗?若成立,请证明.(2)若将PA 向上平移至⊙O 外,结论还成立吗?如图2-4-23(3),若成立,请证明.(1) (2) (3)图2-4-23解析:(1)成立.证明:连结OQ,则QR ⊥OQ. ∴∠PQR+∠BQO=90°.∵∠RPQ=∠1,∠1+∠B=90°, ∴∠RPQ+∠B=90°.又OB=OQ,∴∠B=∠BQO. ∴∠PQR=∠RPQ.∴RP=RQ. (2)结论仍然成立.证明:连结OQ,则OQ ⊥RQ. ∴∠RQO=90°.∴∠RQP+∠BQO=90°.∵OA ⊥PA,∴∠P+∠ABP=90°. 又∠PBA=∠OBQ,∵OB=OQ, ∴∠OBQ=∠OQB.∴∠P=∠PQR.∴RP=RQ.。

四弦切角的性质课时过关·能力提升基础巩固1如图,已知AB是半圆O的直径,C,D是半圆上的两点,半圆O的切线PC交AB的延长线于点P,∠PCB=25°,则∠ADC为()A.105°B.115°C.120°D.125°,连接BD.∵PC与☉O相切,∴∠BDC=∠BCP=25°.∵AB是直径,∴∠ADB=90°.∴∠ADC=∠ADB+∠BDC=90°+25°=115°.2如图,PQ为☉O的切线,A是切点,若∠BAQ=55°,则∠ADB=()A.55°B.110°C.125°D.155°PQ是切线,∴∠C=∠BAQ=55°.∵四边形ADBC内接于圆,∴∠ADB=180°-∠C=180°-55°=125°.3如图,△ABC内接于☉O,EC切☉O于点C.若∠BOC=76°,则∠BCE等于()A.14°B.38°C.52°D.76°EC为☉O的切线,∴∠BCE=∠BAC=1∠BOC=38°.24如图,四边形ABCD是圆内接四边形,AB是直径,MN是☉O的切线,C为切点,若∠BCM=38°,则∠B等于()A.32°B.42°C.52°D.48°AC,如图.∵MN切☉O于点C,BC是弦,∴∠BAC=∠BCM.∵AB是直径,∴∠ACB=90°.∴∠B+∠BAC=90°.∴∠B+∠BCM=90°,∴∠B=90°-∠BCM=52°.5如图,AD切☉O于点F,FB,FC为☉O的两弦,请列出图中所有的弦切角.AFB,∠AFC,∠DFC,∠DFB6如图,AB是☉O的直径,直线CE与☉O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则☉O的面积是.DE是切线,∴∠ACD=∠ABC=30°.又AD⊥CD,∴AC=2AD=2.∵AB是直径,∴∠ACB=90°.又∠ABC=30°,∴AB=2AC=4,AB=2.∴OA=12∴☉O的面积为S=π·OA2=4π.π7如图,AB是☉O的弦,CD是经过☉O上的点M的切线.求证:(1)如果AB∥CD,那么AM=MB;(2)如果AM=BM,那么AB∥CD.∵CD切☉O于点M,∴∠DMB=∠A,∠CMA=∠B.∵AB∥CD,∴∠CMA=∠A,∴∠A=∠B,∴AM=MB.(2)∵AM=BM,∴∠A=∠B.∵CD切☉O于点M,∴∠CMA=∠B.∴∠CMA=∠A.∴AB∥CD.8如图,四边形ABED内接于☉O,AB∥DE,AC切☉O于点A,交ED延长线于点C.求证:AD∶AB=DC∶BE.ACD和△ABE中,所以只要证明△ACD∽△AEB即可.四边形ABED内接于☉O,∴∠ADC=∠ABE.∵AC是☉O的切线,∴∠CAD=∠AED.∵AB∥DE,∴∠BAE=∠AED.∴∠CAD=∠BAE,∴△ACD∽△AEB.∴AD∶AB=DC∶BE.9如图,已知圆上的,过点C的圆的切线与BA的延长线交于点E.求证:(1)∠ACE=∠BCD;(2)BC2=BE·CD.证明这两个角都等于∠ABC;(2)转化为证明△BDC∽△ECB.∵,∴∠BCD=∠ABC.∵EC与圆相切于点C,∴∠ACE=∠ABC.∴∠ACE=∠BCD.(2)∵∠ECB=∠CDB,∠EBC=∠BCD,∴△BDC∽△ECB.∴,即BC2=BE·CD.10如图,AB是半圆O的直径,C是圆周上异于点A,B的一点,过点C作圆O的切线l,过点A作直线l的垂线AD,垂足为点D,AD交半圆于点E.求证:CB=CE.CBE=∠CEB.方法一)连接BE,如图.因为AB是半圆O的直径,点E为圆周上一点,所以∠AEB=90°,即BE⊥AD.又因为AD⊥l,所以BE∥l.所以∠DCE=∠CEB.因为直线l是圆O的切线,所以∠DCE=∠CBE.所以∠CBE=∠CEB,故CE=CB.(方法二)连接AC,BE,在DC延长线上取一点F,如图.因为AB是半圆O的直径,C为圆周上一点,所以∠ACB=90°,即∠BCF+∠ACD=90°.因为AD⊥l,所以∠DAC+∠ACD=90°,所以∠BCF=∠DAC.因为直线l是圆O的切线,所以∠CEB=∠BCF.又∠DAC=∠CBE,所以∠CBE=∠CEB.所以CE=CB.能力提升1如图,AB是☉O的直径,EF切☉O于点C,AD⊥EF于点D,若AD=2,AB=6,则AC的长为()A.2B.3C.23D.4BC,如图.∵EF是☉O的切线,∴∠ACD=∠ABC.又AB是☉O的直径,∴∠ACB=90°.又AD⊥EF,∴∠ACB=∠ADC.∴△ADC∽△ACB.∴.∴AC2=AD·AB=2×6=12,∴AC=23.★2如图,已知∠ABC=90°,O是AB上一点,☉O切AC于点D,交AB于点E,B,连接DB,DE,OC,则图中与∠CBD相等的角共有()A.1个B.2个C.3个D.4个AB⊥BC,∴BC与☉O相切,BD为弦.∴∠CBD=∠BED.同理可得∠CDB=∠BED,∴∠CBD=∠CDB.连接OD.∵OD=OB,OC=OC,∴Rt△COD≌Rt△COB.∴CB=CD,∠DCO=∠BCO.∴OC⊥BD.又DE⊥BD,∴DE∥OC.∴∠BED=∠BOC,∴∠CBD=∠BOC.∴与∠CBD相等的角共有3个.3如图,AB是☉O的直径,PB,PE分别切☉O于点B,C,若∠ACE=40°,则∠P=.,连接BC,则∠ACE=∠ABC,∠ACB=90°.又∠ACE=40°,则∠ABC=40°.所以∠BAC=90°-∠ABC=90°-40°=50°,∠ACP=180°-∠ACE=140°.又AB是☉O的直径,则∠ABP=90°.又四边形ABPC的内角和等于360°,所以∠P+∠BAC+∠ACP+∠ABP=360°.所以∠P=80°.4如图,已知圆O的直径AB=6,C为圆周上一点,BC=3,过点C作圆的切线l,过点A作l的垂线AD,垂足为点D,则线段CD的长为.直线l是圆O的切线,∴∠ACD=∠ABC.又AB是直径,∴AC⊥BC.∵BC=3,AB=6,∴∠ABC=60°.∴AC=33.又∠ACD=∠ABC,∴∠ACD=60°..又AD⊥l,∴CD=AC cos60°=3325如图,☉O和☉O'相交于A,B两点,过点A作两圆的切线,分别交两圆于C,D两点,若BC=2,BD=4,则AB的长为.AC,AD分别是两圆的切线,∴∠C=∠BAD,∠D=∠BAC.∴△ACB∽△DAB.∴.∴AB2=BC·DB=2×4=8.∴AB=22(负值舍去).26如图,BA是☉O的直径,AD是☉O的切线,切点为A,BF,BD分别交AD于点F,D,交☉O于点E,C,连接CE.求证:BE·BF=BC·BD.BE·BF=BC·BD,只需证,即证明△BEC∽△BDF.由∠DBF为公共角,只需再找一组角相等,为此,过点B作☉O的切线,构造弦切角.,过点B作☉O的切线BG,则AB⊥BG.又AD是☉O的切线,∴AD⊥AB,∴BG∥AD,∴∠GBC=∠BDF.∵∠GBC=∠BEC,∴∠BEC=∠BDF.又∠CBE=∠DBF,∴△BEC∽△BDF.∴.∴BE·BF=BC·BD.7如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E.求证:(1)△ABE≌△ACD;(2)BE=BC.由已知,得∠ABE=∠ACD,只需证明∠BAE=∠CAD,转化为证明∠BAE=∠CDB,∠CDB=∠DCN,∠DCN=∠CAD.(2)转化为证明∠BEC=∠ECB.∵BD∥MN,∴∠CDB=∠DCN.又∠BAE=∠CDB,∴∠BAE=∠DCN.又直线MN是☉O的切线,∴∠DCN=∠CAD.∴∠BAE=∠CAD.又∠ABE=∠ACD,AB=AC,∴△ABE≌△ACD.(2)∵∠EBC=∠BCM,∠BCM=∠BDC,∴∠EBC=∠BDC.∴CB=CD.∵∠BEC=∠EDC+∠ECD,∠ECD=∠ABE,∴∠BEC=∠EBC+∠ABE=∠ABC.又AB=AC,∴∠ABC=∠ECB.∴∠BEC=∠ECB.∴BE=BC.★8如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B.(1)试探索∠BCP与∠P的数量关系.(2)若∠A=30°,则PB与PA有什么关系?(3)∠A可能等于45°吗?为什么?∵PC是切线,∴∠BCP=∠A.∵AB是直径,∴∠ACB=90°.在△ACP中,∠A+∠P+∠ACP=180°,∴∠BCP+∠P+∠ACB+∠BCP=180°.∴2∠BCP+∠P+90°=180°.∴∠P=90°-2∠BCP.(2)若∠A=30°,则∠BCP=∠A=30°,∠ABC=60°.∴∠P=30°,∴PB=BC,BC=1AB.2∴PB=1PA,即PA=3PB.3(3)∠A不可能等于45°.理由如下:设∠A=45°,则∠ABC=45°,∠BCP=45°,∴CP∥AB,与题干中PC与AB交于点P矛盾, ∴∠A不可能等于45°.。

课后训练1．如图，O 的半径为2 cm,O 切AC 于D ，切BE 于E ，∠ACB ＝60°,则CE 的长为（ ）．A ．3cmB ．23cm 3C ．3cm 3D ．23cm2．如图,AB 是O 的直径,直线EF 切O 于B ，C 、D 为O 上的点，∠CBE ＝40°，AD CD =,则∠BCD 的度数是( )．A ．110°B ．115°C ．120°D ．135°3．如图，在圆的内接四边形ABCD 中，AC 平分∠BAD ，EF 切O 于C 点，那么图中与∠DCF 相等的角的个数是( )．A ．4B ．5C ．6D ．74．如图，BD 为O 的直径，AB 、AE 切O 于B 、C ，∠BDC ＝65°,则∠BAC ＝________。

5．如图，已知AB 与O 相切于点M ，MC MD =，且MC 、MD 为14圆周长,则∠AMC ＝__________。

6．已知,如图，△ABC内接于O,DC切O于C点，BC平分∠ACD，则△ABC为________．7．如图，AB是O的直径，CD是O的切线，C为切点，AC 平分∠BAD．求证：AD⊥CD．8．如图，P是O的半径OA上的一点，D在O上，且PD＝PO.过点D作O的切线交OA的延长线于点C，延长DP交O于K，连接KO，OD．(1）证明：PC＝PD；(2)若该圆的半径为5，CD∥KO，求出OC的长．如图,BC为O的直径,AB AD=，过点A的切线与CD的延长线交于点E.(1）试猜想∠AED是否等于90°？为什么？（2）若25AD=，ED∶EA＝1∶2，求O的半径．(3）在（2）的条件下求∠CAD的正弦值．参考答案1.答案：B解析：∵CD、CE是O的切线，∴OC平分∠ECD．∴∠OCE＝12∠ECD＝12(180°－∠ACB)＝12(180°－60°）＝60°.∴CE＝OE cot60°＝323233⨯=(cm）．2。

课时跟踪检测(九) 弦切角的性质一、选择题1．P在⊙O外，PM切⊙O于C，PAB交⊙O于A，B，则()A．∠MCB＝∠B B．∠PAC＝∠PC．∠PCA＝∠B D．∠PAC＝∠BCA解析：选C由弦切角定理知∠PCA＝∠B.2．如图，PC与⊙O相切于C点，割线PAB过圆心O，∠P＝40°，则∠ACP等于()A．20°B．25°C．30°D．40°解析：选B连接OC.∵PC切⊙O于C点，∴OC⊥PC.∵∠P＝40°，∴∠POC＝50°.连接BC，则∠B＝12∠POC＝25°，∴∠ACP＝∠B＝25°.3．如图，AB是⊙O的直径，EF切⊙O于C，AD⊥EF于D，AD＝2，AB＝6，则AC 的长为()A．2 B．3 C．2 3 D．4解析：选C连接BC，则∠ACB＝90°，又AD⊥EF，∴∠ADC＝90°，即∠ADC＝∠ACB，又∵∠ACD＝∠ABC，∴△ABC∽△ACD，∴ACAD＝ABAC，∴AC2＝AD·AB＝12，即AC＝2 3.4．如图，AB是⊙O的直径，P在AB的延长线上，PD切⊙O于C 点，连接AC，若AC＝PC，PB＝1，则⊙O的半径为() A．1 B．2C．3 D．4解析：选A连接BC.∵AC＝PC，∴∠A＝∠P.∵∠BCP＝∠A，∴∠BCP＝∠P.∴BC＝BP＝1.由△BCP∽△CAP得PC PA＝PB PC.∴PC2＝PB·PA，即AC2＝PB·PA.而AC2＝AB2－BC2，设⊙O半径为r，则4r2－12＝1·(1＋2r)，解得r＝1.二、填空题5．如图，AB是⊙O的直径，PB，PE分别切⊙O于B，C，若∠ACE＝40°，则∠P ＝________.解析：连接BC，∵AB是⊙O的直径，∴∠ACB＝90°.又∠ACE＝40°，∴∠PCB＝∠PBC＝50°.∴∠P＝80°.答案：80°6．如图，点P在圆O直径AB的延长线上，且PB＝OB＝2，PC切圆O于C点，CD⊥AB于D点，则CD＝________.解析：连接OC.∵PC切⊙O于C点，∴OC⊥PC.∵PB＝OB＝2，OC＝2.∴PC＝2 3.∵OC·PC＝OP·CD，∴CD＝2×234＝ 3.答案： 37．如图，过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB＝7，C是圆上一点使得BC＝5，∠BAC＝∠APB，则AB＝________.解析：由PA为⊙O的切线，BA为弦，得∠PAB＝∠BCA，又∠BAC＝∠APB，于是△APB∽△CAB，所以PBAB＝ABBC.而PB＝7，BC＝5，故AB2＝PB·BC＝7×5＝35，即AB＝35.答案：35三、解答题8.如图，AB是半圆O的直径，C是圆周上一点(异于A，B)，过C作圆O的切线l，过A作直线l的垂线AD，垂足为D，AD交半圆于点E.求证：CB＝CE.证明：连接AC，BE，在DC延长线上取一点F，因为AB是半圆O的直径，C为圆周上一点，所以∠ACB＝90°，即∠BCF＋∠ACD＝90°.又因为AD⊥l，所以∠DAC＋∠ACD＝90°.所以∠BCF＝∠DAC.又因为直线l是圆O的切线，所以∠CEB＝∠BCF，又∠DAC＝∠CBE，所以∠CBE＝∠CEB，所以CB＝CE.9.如图所示，△ABC内接于⊙O，AB＝AC，直线XY切⊙O于点C，弦BD∥XY，AC，BD相交于点E.(1)求证：△ABE≌△ACD；(2)若AB＝6 cm，BC＝4 cm，求AE的长．解：(1)证明：因为XY是⊙O的切线，所以∠1＝∠2.因为BD∥XY，所以∠1＝∠3，所以∠2＝∠3.因为∠3＝∠4，所以∠2＝∠4.因为∠ABD＝∠ACD，又因为AB＝AC，所以△ABE≌△ACD.(2)因为∠3＝∠2，∠ABC＝∠ACB，所以△BCE∽△ACB，所以BCAC＝CECB，即AC·CE＝BC2.因为AB＝AC＝6 cm，BC＝4 cm，所以6·(6－AE)＝16.所以AE＝103(cm)．10.如图，已知C点在圆O直径BE的延长线上，CA切圆O于A 点，DC是∠ACB的角平分线，交AE于点F，交AB于D点．(1)求∠ADF的度数；(2)若AB＝AC，求AC∶BC.解：(1)∵AC为圆O的切线，∴∠B＝∠EAC.又DC是∠ACB的平分线，∴∠ACD＝∠DCB.∴∠B＋∠DCB＝∠EAC＋∠ACD，即∠ADF＝∠AFD. 又∵BE为圆O的直径，∴∠DAE＝90°，∠ADF＝12(180°－∠DAE)＝45°.(2)∵∠B＝∠EAC，∠ACB＝∠ACE，∴△ACE∽△BCA.∴ACBC＝AEAB.又∵AB＝AC，∴∠B＝∠ACB＝23∠ADF＝30°.∴在Rt△ABE中，ACBC＝AEAB＝tan ∠B＝tan 30°＝33.小课堂：如何培养学生的自主学习能力？自主学习是与传统的接受学习相对应的一种现代化学习方式。

学业分层测评(九)(建议用时：45分钟)[学业达标]一、选择题1．如图2­4­12所示，AB 是⊙O 的直径，MN 与⊙O 切于点C ，AC ＝12BC ，则sin ∠MCA ＝( )图2­4­12A.12 B.22 C.32D.55【解析】 由弦切角定理，得∠MCA ＝∠ABC . ∵sin ∠ABC ＝AC AB ＝AC AC 2＋BC 2＝AC 5AC ＝55，故选D. 【答案】 D2．如图2­4­13，在圆的内接四边形ABCD 中，AC 平分∠BAD ，EF 切⊙O 于C 点，那么图中与∠DCF 相等的角的个数是( )图2­4­13A．4 B．5C．6 D．7【解析】∠DCF＝∠DAC，∠DCF＝∠BAC，∠DCF＝∠BCE，∠DCF＝∠BDC，∠DCF＝∠DBC.【答案】 B3.如图2­4­14所示，AB是⊙O的直径，EF切⊙O于C，AD⊥EF于D，AD＝2，AB＝6，则AC的长为( )图2­4­14A．2 B．3C．2 3 D．4【解析】连接BC.∵AB是⊙O的直径，∴AC⊥BC，由弦切角定理可知，∠ACD＝∠ABC，∴△ABC∽△ACD，∴ACAD＝ABAC，∴AC2＝AB·AD＝6×2＝12，∴AC＝23，故选C.【答案】 C4．如图2­4­15，PC与⊙O相切于C点，割线PAB过圆心O，∠P＝40°，则∠ACP等于( )【导学号：07370043】图2­4­15A ．20°B ．25°C ．30°D ．40°【解析】 如图，连接OC ，BC ，∵PC 切⊙O 于C 点，∴OC ⊥PC ，∵∠P ＝40°，∴∠POC ＝50°. ∵OC ＝OB ，∴∠B ＝12∠POC ＝25°，∴∠ACP ＝∠B ＝25°. 【答案】 B5．如图2­4­16所示，已知AB ，AC 与⊙O 相切于B ，C ，∠A ＝50°，点P 是⊙O 上异于B ，C 的一动点，则∠BPC 的度数是( )图2­4­16A ．65°B ．115°C．65°或115°D．130°或50°【解析】当点P在优弧上时，由∠A＝50°，得∠ABC＝∠ACB＝65°.∵AB是⊙O的切线，∴∠ABC＝∠BPC＝65°.当P点在劣弧上时，∠BPC＝115°.故选C.【答案】 C二、填空题6.如图2­4­17所示，直线PB与圆O相切于点B，D是弦AC上的点，∠PBA＝∠DBA.若AD＝m，AC＝n，则AB＝________.图2­4­17【解析】∵PB切⊙O于点B，∴∠PBA＝∠ACB.又∠PBA＝∠DBA，∴∠DBA＝∠ACB，∴△ABD∽△ACB.∴ABAC＝ADAB，∴AB2＝AD·AC＝mn，∴AB＝mn.【答案】mn7．如图2­4­18，已知△ABC内接于圆O，点D在OC的延长线上．AD是⊙O的切线，若∠B＝30°，AC＝2，则OD的长为__________．图2­4­18【解析】连接OA，则∠COA＝2∠CBA＝60°，且由OC＝OA知△COA为正三角形，所以OA＝2.又因为AD是⊙O的切线，即OA⊥AD，所以OD＝2OA＝4.【答案】 48.如图2­4­19，点P在圆O直径AB的延长线上，且PB＝OB ＝2，PC切圆O于C点，CD⊥AB于D点，则CD＝________.图2­4­19【解析】连接OC，∵PC切⊙O于点C，∴OC⊥PC，∵PB＝OB＝2，OC＝2，∴PC＝23，∵OC·PC＝OP·CD，∴CD＝2×234＝ 3.【答案】 3三、解答题9．如图2­4­20所示，△ABT内接于⊙O，过点T的切线交AB 的延长线于点P，∠APT的平分线交BT，AT于C，D.图2­4­20求证：△CTD为等腰三角形．【证明】∵PD是∠APT的平分线，∴∠APD＝∠DPT.又∵PT是圆的切线，∴∠BTP＝∠A.又∵∠TDC＝∠A＋∠APD，∠TCD＝∠BTP＋∠DPT，∴∠TDC＝∠TCD，∴△CTD为等腰三角形．10．如图2­4­21，AB是⊙O的弦，M是上任一点，过点M 的切线与分别以A，B为垂足的直线AD，BC交于D，C两点，过M点作NM⊥CD交AB于点N，求证：MN2＝AD·BC.图2­4­21【证明】连接AM，MB，因为DA ⊥AB ，MN ⊥CD ， 所以∠MDA ＋∠MNA ＝180°. 又因为∠MNA ＋∠MNB ＝180°， 所以∠MDA ＝∠MNB ，又因为CD 为⊙O 的切线，所以∠1＝∠2， 所以△ADM ∽△MNB ，所以AD MN ＝AM BM ，同理MN BC ＝AM BM ，所以AD MN ＝MNBC，即有MN 2＝AD ·BC .[能力提升]1．在圆O 的直径CB 的延长线上取一点A ，AP 与圆O 切于点P ，且∠APB ＝30°，AP ＝3，则CP ＝( ) 【导学号：07370044】A. 3 B ．2 3 C ．23－1D ．23＋1【解析】 如图，连接OP ，则OP ⊥PA ，又∠APB ＝30°， ∴∠POB ＝60°，在Rt △OPA 中，由AP ＝3， 易知，PB ＝OP ＝1， 在Rt △PCB 中，由PB ＝1，∠PBC ＝60°，得PC ＝ 3. 【答案】 A2．如图2­4­22，AB 是⊙O 直径，P 在AB 的延长线上，PD 切⊙O 于C 点，连接AC ，若AC ＝PC ，PB ＝1，则⊙O 的半径为( )图2­4­22A．1 B．2C．3 D．4【解析】连接BC.∵AC＝PC，∴∠A＝∠P.∵∠BCP＝∠A，∴∠BCP＝∠P，∴BC＝BP＝1.由△BCP∽△CAP，得PC2＝PB·PA，即AC2＝PB·PA.而AC2＝AB2－BC2，设⊙O半径为r，则4r2－12＝1·(1＋2r)，解得r＝1.【答案】 A3．如图2­4­23，过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB＝7，C是圆上一点使得BC＝5，∠BAC＝∠APB，则AB ＝__________.图2­4­23【解析】由PA为⊙O的切线，BA为弦，得∠PAB＝∠BCA.又∠BAC ＝∠APB ， 于是△APB ∽△CAB ，所以PB AB ＝AB BC.而PB ＝7，BC ＝5，故AB 2＝PB ·BC ＝7×5＝35，即AB ＝35. 【答案】354．如图2­4­24，AB 为⊙O 的直径，直线CD 与⊙O 相切于E ，AD 垂直CD 于D ，BC 垂直CD 于C ，EF 垂直AB 于F ，连接AE ，BE .图2­4­24证明：(1)∠FEB ＝∠CEB ； (2)EF 2＝AD ·BC .【证明】 (1)由直线CD 与⊙O 相切，得∠CEB ＝∠EAB. 由AB 为⊙O 的直径，得AE ⊥EB ，从而∠EAB ＋∠EBF ＝π2.又EF ⊥AB ，得∠FEB ＋∠EBF ＝π2. 从而∠FEB ＝∠EAB ，故∠FEB ＝∠CEB.(2)由BC ⊥CE ，EF ⊥AB ，∠FEB ＝∠CEB ，BE 是公共边，得Rt △BCE ≌Rt △BFE ，所以BC ＝BF .类似可证Rt △ADE ≌Rt △AFE ，得AD ＝AF . 又在Rt △AEB 中，EF ⊥AB ，故EF 2＝AF ·BF ， 所以EF 2＝AD ·BC .。

人教新课标A版选修4-1数学2.4弦切角的性质同步检测A卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题；共20分)1. （2分）如图，经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，则∠BAC所对的弧的度数为（）A . 40°B . 100°C . 120°D . 30°2. （2分）如图，在⊙O中，AB是弦，AC是⊙O的切线，A是切点，过 B作BD⊥AC于D，BD交⊙O于E点，若AE平分∠BAD，则∠BAD=（）A . 30°B . 45°C . 50°D . 60°3. （2分）(2016·天津模拟) 如图，圆O的直径AB长度为10，CD是点C处的切线，AD⊥CD，若BC=8，则CD=（）A .B .C .D .4. （2分） PT切⊙O于T，割线PAB经过O点交⊙O于A、B，若PT=4，PA=2，则cos∠BPT=（）A .B .C .D .5. （2分）若图中，PA切⊙O于点A，PCB交⊙O于C、B两点，且PCB过点O，AE⊥BP交⊙O于E，则图中与∠CAP相等的角的个数是（）A . 1B . 2C . 3D . 46. （2分） (2017高一下·河北期末) 如图所示，在圆的内接四边形中，平分，切于点，那么图中与相等的角的个数是（）A . 4B . 5C . 6D . 77. （2分）如图，直线BC切⊙O于B，AB=AC，AD=BD，则∠A=（）A . 35°B . 36°C . 40°D . 50°8. （2分） (2017高二上·信阳期末) 如图，已知四边形ABCD是圆内接四边形，且∠BCD=120°，AD=2，AB=BC=1，现有以下结论：①B，D两点间的距离为；②AD是该圆的一条直径；③CD= ；④四边形ABCD的面积S= ．其中正确结论的个数为（）A . 1B . 2C . 3D . 49. （2分）如图⊙O中，弦AB与弦CD相交于点P，∠B=38°，∠APD=80°，则∠A等于（）A . 38°B . 42°C . 80°D . 118°10. （2分） (2016高二下·五指山期末) 如图，四边形ABCD是⊙O的内接四边形，延长BC到E，已知∠BCD：∠ECD=3：2，那么∠BOD等于（）A . 120°B . 136°C . 144°D . 150°二、填空题 (共5题；共5分)11. （1分）如图，圆O是△ABC的外接圆，过点C的切线交AB的延长线于点D，CD=， AB=BC=3．AC 的长为________ ．12. （1分）如图，已知点D在圆O直径AB的延长线上，过D作圆O的切线，切点为C．若CD=， BD=1，则圆O的面积为________ ．13. （1分）如图，从圆O外一点P作圆O的割线PAB、PCD，AB是圆O的直径，若PA=4，PC=5，CD=3，则∠CBD=________ ．14. （1分）如图，AB的延长线上任取一点C，过C作圆的切线CD，切点为D，∠ACD的平分线交AD于E，则∠CED=________15. （1分）如图，AB、AC是⊙O的两条切线，切点分别为B、C．若∠BAC=60°，BC=6，则⊙O的半径为________ ．三、解答题 (共10题；共70分)16. （10分） (2015高三上·苏州期末) 如图，四边形么BDC内接于圆，BD=CD，过C点的圆的切线与AB的延长线交于E点．（1）求证：∠EAC=2∠DCE；（2）若BD⊥AB，BC=BE，AE=2，求AB的长．17. （5分）(2016·城中模拟) 如图，在△ABC和△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD，⊙O是以AB 为直径的圆，DC的延长线与AB的延长线交于点E．（Ⅰ）求证：DC是⊙O的切线；（Ⅱ）若EB=6，EC=6 ，求BC的长．18. （5分）如图，四边形ABCD内接于⊙O，BD是⊙O的直径，过点A作⊙O的切线AE，与CD的延长线交于E，AE⊥CD，垂足为点E．（Ⅰ）证明：DA平分∠BDE；（Ⅱ）如果AB=4，AE=2，求对角线CA的长．19. （5分）如图，∠PAQ是直角，圆O与射线AP相切于点T，与射线AQ相交于两点B，C．求证：BT平分∠OBA．20. （10分）(2016·大连模拟) 如图所示，已知圆O1与圆O2相交于A，B两点，过点A作圆O1的切线交圆O2于点C，过点B作两圆的割线，分别交圆O1 ，圆O2于点D，E，DE与AC相交于点P．（1）求证：AD∥EC；（2）若AD是圆O2的切线，且PA=3，PC=1，AD=6，求DB的长．21. （10分）(2017·白山模拟) 如图，A，B，C，D四点在同一圆上，BC与AD的延长线交于点E，点F在BA 的延长线上．（1）若 = ， =1，求的值；（2）若EF2=FA•FB，证明：EF∥CD．22. （5分）(2017·镇江模拟) 如图，圆O的直径AB=6，C为圆周上一点，BC=3，过C作圆的切线l，过A 作l的垂线AD，AD分别与直线l、圆交于点D、E．求∠DAC的度数与线段AE的长．23. （5分）(2017·唐山模拟) 如图，A、B、C为⊙O上三点，B为的中点，P为AC延长线上一点，PQ 与⊙O相切于点Q，BQ与AC相交于点D．（Ⅰ）证明：△DPQ为等腰三角形；（Ⅱ）若PC=1，AD=PD，求BD•QD的值．24. （10分）如图，AB切O于点D，直线AD交O于D，E两点，BC⊥DE，垂足为C．（1）证明：CBD=DBA；（2）若AD=3DC，BC=，求O的直径．25. （5分）(2017·榆林模拟) 如图，已知PA与圆O相切于点A，经过点O的割线PBC交圆O于点B，C，∠APC 的平分线分别交AB，AC于点D，E．（Ⅰ）证明：∠ADE=∠AED；（Ⅱ）若AC=AP，求的值．参考答案一、选择题 (共10题；共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题；共5分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共10题；共70分) 16-1、16-2、17-1、18-1、19-1、20-1、20-2、21-1、21-2、22-1、23-1、24-1、24-2、25-1、。

自我小测1．如图，△ABC为⊙O的内接三角形，AB为直径，D为BC延长线上一点，PC切⊙O于C点，∠PCD＝20°，则∠A等于()A．20°B．30°C．40°D．50°2．如图，在圆的内接四边形ABCD中，AC平分∠BAD，EF切⊙O于C点，那么图中与∠DCF相等的角的个数是()A．4 B．5 C．6 D．73．如图所示，四边形ABCD是圆内接四边形，AB是直径，MN是⊙O的切线，C为切点．若∠BCM＝38°，则∠B等于()A．32°B．42°C．52°D．48°4．如图，AB是⊙O的直径，EF切⊙O于点C，AD⊥EF于点D，AD＝2，AB＝6，则AC的长为()A．2 B．3 C．2 3 D．45．如图，AB是⊙O的直径，PB，PE分别切⊙O于B，C，若∠ACE＝40°，则∠P＝__________.6．已知AB是⊙O的弦，PA是⊙O的切线，A是切点，如果∠PAB＝30°，那么∠AOB ＝________.7．如图，AB是圆O的直径，点C在圆O上．延长BC到D使BC＝CD，过C作圆O 的切线交AD于E.若AB＝6，ED＝2，则BC＝__________.8．如图，AB是⊙O的直径，直线CE与⊙O相切于点C，AD⊥CE于D.若AD＝1，∠ABC＝30°，求⊙O的面积．9．如图，EP交圆于E，C两点，PD切圆于D，G为CE上一点且PG＝PD，连接DG 并延长交圆于点A，作弦AB垂直EP，垂足为F.(1)求证：AB为圆的直径；(2)若AC＝BD，求证：AB＝ED.10．如图，BC为⊙O的直径，AB＝AD，过点A的切线与CD的延长线交于点E.(1)试猜想∠AED是否等于90°？为什么？(2)若AD＝25，ED∶EA＝1∶2，求⊙O的半径；(3)在(2)的条件下，求∠CAD的正弦值．参考答案1．A2．解析：∠DCF ＝∠DAC ，∠DCF ＝∠BAC ， ∠DCF ＝∠BCE ，∠DCF ＝∠BDC ，∠DCF ＝∠DBC . 答案：B3．解析：连接AC ，如图所示．∵MN 切圆于C ，BC 是弦，∴∠BAC ＝∠BCM . ∵AB 是直径，∴∠ACB ＝90°.∴∠B ＋∠BAC ＝90°.∴∠B ＋∠BCM ＝90°， ∴∠B ＝90°－∠BCM ＝52°. 答案：C4．解析：连接BC ，如图所示．∵EF 是⊙O 的切线， ∴∠ACD ＝∠ABC . 又AB 是⊙O 的直径， ∴∠ACB ＝90°. 又AD ⊥EF ， ∴∠ACB ＝∠ADC .∴△ADC ∽△ACB .∴AB AC ＝AC AD.∴AC2＝AD·AB＝2×6＝12，∴AC＝2 3.答案：C5．解析：如图所示，连接BC，则∠ACE＝∠ABC，∠ACB＝90°.又∠ACE＝40°，则∠ABC＝40°.所以∠BAC＝90°－∠ABC＝90°－40°＝50°，∠ACP＝180°－∠ACE＝140°.又AB是⊙O的直径，则∠ABP＝90°.又四边形ABPC的内角和等于360°，所以∠P＋∠BAC＋∠ACP＋∠ABP＝360°.所以∠P＝80°.答案：80°6．解析：∵弦切角∠PAB＝30°，∴它所夹的弧所对的圆周角等于30°，所对的圆心角等于60°.答案：60°7．解析：连接OC.∵AB为圆O的直径，∴AC⊥BC.又BC＝CD，∴AB＝AD＝6，∠BAC＝∠CAD.又CE为圆O的切线，则OC⊥CE.∵∠ACE为弦切角，∴∠ACE＝∠B.∴∠ACE＋∠CAD＝90°.∴CE⊥AD.又AC⊥CD，∴CD2＝ED·AD＝2×6＝12，即CD＝2 3.∴BC＝2 3.答案：2 38．解：∵DE是切线，∴∠ACD＝∠ABC＝30°.又∵AD⊥CD，∴AC＝2AD＝2.又∵AB是直径，∴∠ACB＝90°.又∵∠ABC＝30°，∴AB＝2AC＝4，∴OA＝12AB＝2.∴⊙O的面积S＝π·OA2＝4π.9．证明：(1)因为PD＝PG，所以∠PDG＝∠PGD.由于PD为切线，故∠PDA＝∠DBA.又由于∠PGD＝∠EGA，故∠DBA＝∠EGA，所以∠DBA＋∠BAD＝∠EGA＋∠BAD，从而∠BDA＝∠PFA. 由于AF⊥EP，所以∠PFA＝90°.于是∠BDA＝90°.故AB是直径．(2)连接BC，DC.由于AB是直径，故∠BDA＝∠ACB＝90°.在Rt△BDA与Rt△ACB中，AB＝BA，AC＝BD，从而Rt△BDA≌Rt△ACB.于是∠DAB＝∠CBA.又因为∠DCB＝∠DAB，所以∠DCB＝∠CBA，故DC∥AB.由于AB⊥EP，所以DC⊥EP，∠DCE为直角．于是ED为直径．由(1)得ED＝AB.10．解：(1)∠AED＝90°.证明：连接AB，∵BC为直径，∴∠BAC＝90°.又∵AE切⊙O于A，AB＝AD，∴∠EAD＝∠ACB.又∵四边形ABCD内接于⊙O，∠ADE＝∠ABC，∴△AED∽△CAB，∴∠AED＝∠CAB＝90°.(2)∵AD ＝25，DE ∶EA ＝1∶2，∠AED ＝90°， ∴ED ＝2，EA ＝4.又AB ＝AD ＝25，△EAD ∽△ACB ， ∴AD BC ＝ED AB .∴BC ＝AD ·AB ED ＝(25)22＝10. ∴⊙O 的半径为5.(3)连接AB ，过D 作DF ⊥AC 于F .∵在△ABC 中，AC ＝45； 在△AEC 中，CE ＝8，∴CD ＝6. 又△CDF ∽△CBA ， ∴DF AB ＝CD CB. ∴DF ＝CD ·AB CB ＝6×2510＝655.∴sin ∠CAD ＝DF AD ＝65525＝35.备选习题分析：(1)很明显∠ABE ＝∠ACD ，只需证明∠BAE ＝∠CAD ，转化为证明∠BAE ＝∠CDB ，∠CDB ＝∠DCN ，∠DCN ＝∠CAD .(2)转化为证明∠BEC ＝∠ECB .证明：(1)∵BD ∥MN ， ∴∠CDB ＝∠DCN . 又∠BAE ＝∠CDB ， ∴∠BAE ＝∠DCN .又直线MN 是⊙O 的切线，∴∠DCN＝∠CAD.∴∠BAE＝∠CAD.又∠ABE＝∠ACD，AB＝AC，∴△ABE≌△ACD.(2)∵∠EBC＝∠BCM，∠BCM＝∠BDC，∴∠EBC＝∠BDC.∴CB＝CD.∵∠BEC＝∠EDC＋∠ECD，∠ECD＝∠ABE，∴∠BEC＝∠EBC＋∠ABE＝∠ABC.又AB＝AC，∴∠ABC＝∠ECB.∴∠BEC＝∠ECB.∴BE＝BC.。

课时跟踪检测(九) 弦切角的性质一、选择题1．P在⊙O外，PM切⊙O于C，PAB交⊙O于A，B，则()A．∠MCB＝∠B B．∠PAC＝∠PC．∠PCA＝∠B D．∠PAC＝∠BCA解析：选C由弦切角定理知∠PCA＝∠B.2．如图，PC与⊙O相切于C点，割线PAB过圆心O，∠P＝40°，则∠ACP等于()A．20°B．25°C．30°D．40°解析：选B连接OC.∵PC切⊙O于C点，∴OC⊥PC.∵∠P＝40°，∴∠POC＝50°.连接BC，则∠B＝1∠POC＝25°，2∴∠ACP＝∠B＝25°.3．如图，AB是⊙O的直径，EF切⊙O于C，AD⊥EF于D，AD＝2，AB＝6，则AC 的长为()A．2 B．3 C．2 3 D．4解析：选C连接BC，则∠ACB＝90°，又AD⊥EF，∴∠ADC＝90°，即∠ADC ＝∠ACB ，又∵∠ACD ＝∠ABC ，∴△ABC ∽△ACD ，∴AC AD ＝AB AC， ∴AC 2＝AD ·AB ＝12，即AC ＝2 3.4．如图，AB 是⊙O 的直径，P 在AB 的延长线上，PD 切⊙O 于C点，连接AC ，若AC ＝PC ，PB ＝1，则⊙O 的半径为( )A ．1B ．2C ．3D ．4解析：选A连接BC .∵AC ＝PC ，∴∠A ＝∠P .∵∠BCP ＝∠A ，∴∠BCP ＝∠P .∴BC ＝BP ＝1.由△BCP ∽△CAP 得PC PA ＝PB PC. ∴PC 2＝PB ·PA ，即AC 2＝PB ·PA .而AC 2＝AB 2－BC 2，设⊙O 半径为r ，则4r 2－12＝1·(1＋2r )，解得r ＝1.二、填空题5．如图，AB 是⊙O 的直径，PB ，PE 分别切⊙O 于B ，C ，若∠ACE ＝40°，则∠P ＝________.解析：连接BC，∵AB是⊙O的直径，∴∠ACB＝90°.又∠ACE＝40°，∴∠PCB＝∠PBC＝50°.∴∠P＝80°.答案：80°6．如图，点P在圆O直径AB的延长线上，且PB＝OB＝2，PC切圆O于C点，CD ⊥AB于D点，则CD＝________.解析：连接OC.∵PC切⊙O于C点，∴OC⊥PC.∵PB＝OB＝2，OC＝2.∴PC＝2 3.∵OC·PC＝OP·CD，∴CD＝2×23＝ 3.4答案： 37．如图，过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB＝7，C是圆上一点使得BC＝5，∠BAC＝∠APB，则AB＝________.解析：由PA 为⊙O 的切线，BA 为弦，得∠PAB ＝∠BCA ，又∠BAC ＝∠APB ，于是△APB ∽△CAB ，所以PB AB ＝AB BC. 而PB ＝7，BC ＝5，故AB 2＝PB ·BC ＝7×5＝35，即AB ＝35.答案：35三、解答题8.如图，AB 是半圆O 的直径，C 是圆周上一点(异于A ，B )，过C 作圆O 的切线l ，过A 作直线l 的垂线AD ，垂足为D ，AD 交半圆于点E .求证：CB ＝CE .证明：连接AC ，BE ，在DC 延长线上取一点F ，因为AB 是半圆O 的直径，C 为圆周上一点，所以∠ACB ＝90°，即∠BCF ＋∠ACD ＝90°.又因为AD ⊥l ，所以∠DAC ＋∠ACD ＝90°.所以∠BCF ＝∠DAC .又因为直线l 是圆O 的切线，所以∠CEB ＝∠BCF ，又∠DAC ＝∠CBE ，所以∠CBE ＝∠CEB ，所以CB ＝CE .9.如图所示，△ABC 内接于⊙O ，AB ＝AC ，直线XY 切⊙O 于点C ，林老师网络编辑整理 弦BD ∥XY ，AC ，BD 相交于点E .(1)求证：△ABE ≌△ACD ；(2)若AB ＝6 cm ，BC ＝4 cm ，求AE 的长．解：(1)证明：因为XY 是⊙O 的切线，所以∠1＝∠2.因为BD ∥XY ，所以∠1＝∠3，所以∠2＝∠3.因为∠3＝∠4，所以∠2＝∠4.因为∠ABD ＝∠ACD ，又因为AB ＝AC ，所以△ABE ≌△ACD .(2)因为∠3＝∠2，∠ABC ＝∠ACB ，所以△BCE ∽△ACB ，所以BC AC ＝CECB ，即AC ·CE ＝BC 2.因为AB ＝AC ＝6 cm ，BC ＝4 cm ，所以6·(6－AE )＝16.所以AE ＝103 (cm)．10.如图，已知C 点在圆O 直径BE 的延长线上，CA 切圆O 于A 点，DC 是∠ACB 的角平分线，交AE 于点F ，交AB 于D 点．(1)求∠ADF 的度数；(2)若AB ＝AC ，求AC ∶BC .解：(1)∵AC 为圆O 的切线，∴∠B ＝∠EAC .又DC 是∠ACB 的平分线，∴∠ACD ＝∠DCB .∴∠B ＋∠DCB ＝∠EAC ＋∠ACD ，即∠ADF ＝∠AFD .林老师网络编辑整理又∵BE 为圆O 的直径，∴∠DAE ＝90°，∠ADF ＝12(180°－∠DAE )＝45°. (2)∵∠B ＝∠EAC ，∠ACB ＝∠ACE ，∴△ACE ∽△BCA .∴AC BC ＝AE AB .又∵AB ＝AC ，∴∠B ＝∠ACB ＝23∠ADF ＝30°. ∴在Rt △ABE 中，AC BC ＝AE AB ＝tan ∠B ＝tan 30°＝33.。