下载文档原格式
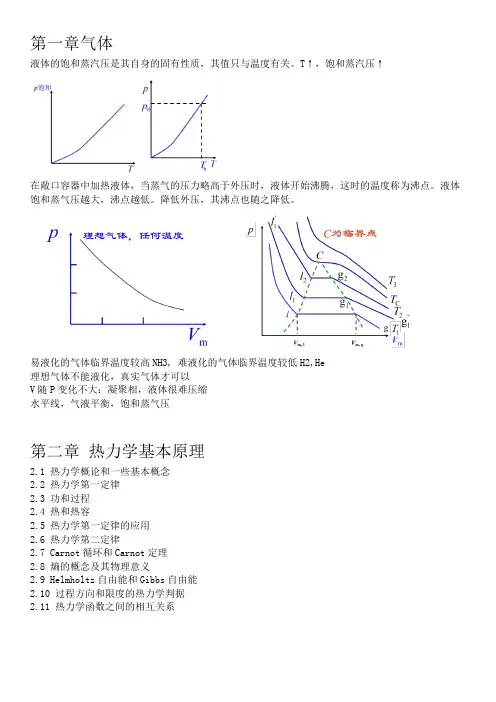
第一章气体液体的饱和蒸汽压是其自身的固有性质，其值只与温度有关。
T↑，饱和蒸汽压↑在敞口容器中加热液体，当蒸气的压力略高于外压时，液体开始沸腾，这时的温度称为沸点。
液体饱和蒸气压越大，沸点越低。
降低外压，其沸点也随之降低。
易液化的气体临界温度较高NH3, 难液化的气体临界温度较低H2,He理想气体不能液化，真实气体才可以V随P变化不大：凝聚相，液体很难压缩水平线，气液平衡，饱和蒸气压第二章热力学基本原理2.1 热力学概论和一些基本概念2.2 热力学第一定律2.3 功和过程2.4 热和热容2.5 热力学第一定律的应用2.6 热力学第二定律2.7 Carnot循环和Carnot定理2.8 熵的概念及其物理意义2.9 Helmholtz自由能和Gibbs自由能2.10 过程方向和限度的热力学判据2.11 热力学函数之间的相互关系2.1 热力学概论和一些基本概念(1) 系统与环境：系统+环境=大的孤立系统(2) 系统的(宏观)性质广度性质具有加和性，强度性质不具有。
(3) 热力学平衡态热平衡、力平衡、相平衡、化学平衡(4) 状态与状态函数状态函数在数学上具有全微分的性质，当系统的状态发生了一个无限小的变化，状态函数 Z 的变化记为dZ ，状态函数 Z 的变化为，非状态函数不能积分，变化用δ，区别于状态函数的d.（5） 过程与途径(6) 热和功热和功是系统和环境间能量交换的两种不同形式。
都与过程相联系，即使始态和终态相同，过程不同，交换的热和功也会不同。
不是状态函数！ 微小变化用δ表示，以区别于d ；某一过程的热（或功）交换用Q (或W)表示，不用ΔQ (或ΔW )。
热是大量分子无规则运动的一种表现。
由于温差,系统与环境之间传递的能量称为热符号Q 单位J ，系统吸热 Q > 0 系统放热 Q < 0除热外,系统与环境间传递的其他能量称为功，是大量分子(或粒子)有序运动的一种表现。
符号W 单位J ，系统得到功W > 0，系统做功W < 0热和功的特点1. 是传递的能量,一定要与过程相联系2. 不是状态函数膨胀功(体积功) We ；非膨胀功Wf ：电功 表面功2.2 热力学第一定律系统的总能量（E ）由T(动能)、V (势能)和系统内部的能量U 三部分构成。
热力学能是状态函数
热力学能是一个重要的概念，它不仅提供了一种定量衡量物理系统所处当前状态的有效方式，而且也为研究热力学系统的变化提出了重要的参考点：热力学能的状态函数。
热力学能是状态函数的一个重要概念，它可以帮助人们理解物理系统的热力学行为以及如何使用其效果。
一. 热力学能是什么？
热力学能（thermodynamic energy）是指热力学系统中存在的能量，它可以在特定的状态函数之间流动。
它通常用特定的单位来衡量，比如焦耳或电子伏特。
二. 热力学能如何作为状态函数利用？
热力学能拥有多种形式，它可以作为物理系统的状态函数来使用，用以说明物理系统可以提供的能量。
例如，可以用热力能来实现热力学过程，从而影响物理系统静止时所包含的势能。
三. 最终
热力学能是一个非常重要的概念，它可以帮助我们理解物理系统，从而利用它的热力学行为。
它也可以用作状态函数，从而推断物理系统所能提供的能量，从而在实际应用中发挥作用。
摘要状态函数是物理化学中计算热力学过程函数变的核心，状态一定，状态函数的值一定，其所得的差值只取决于物质过程的始终态，但本文只是对化学变化中各状态函数的计算方法做的归类总结，即对热力学能变化量(ΔU)、焓变(ΔH)、熵变(ΔS)、亥姆霍兹自由能变(ΔA)、吉布斯自由能变(ΔG) 的计算方法做了总结。
对于个别状态函数的解法附有简单的例题来加以说明。
关键词：状态函数；热力学能变化量；焓变；熵变；亥姆霍兹自由能变；吉布斯自由能变AbstractState function is calculated in physical and chemical thermodynamics process function becomes the core, the state must, state function value must be the difference in value, and its income depends only on material process throughout, but the article just normal for chemical change in each state function calculation method of deflection-proof, i.e. do of thermodynamic energy variation (Δ U), enthalpy getting (Δ H), entropy change (Δ S),helmholtz free can change (Δ A), gibbs free energy getting (Δ G), summarizes the calculation method. The solution for individual state function with simple example to try to explain it.Key words：State function; Thermodynamic energy variation; Enthalpy variable; Entropy change; Helmholtz free can change; Gibbs free energy change目录引言 (1)1 化学变化中涉及的状态函数 (2)2 化学变化中各状态函数的具体计算 (2)2.1热力学能 (2)2.2 热力学能变化量的计算 (2)2.2 焓变的计算 (3)2.2.1 焓的定义 (3)2.2.2 焓变 (3)2.2.3在标准状态下化学反应焓变计算归类如下 (3)2.2.4利用键焓值计算焓变 (4)2.2.5利用燃烧焓值计算焓变 (4)2.2.6利用盖斯定律 (4)2.2.7利用Kirchhoff定律计算化学反应焓变： (5)2.3 熵变的计算 (5)2.3.1 熵的定义 (5)2.3.2 熵变 (5)2.3.3 熵变的计算 (6)2.4 亥姆霍兹自由能变的计算 (7)2.4.1 亥姆霍兹自由能 (7)2.4.2 亥姆霍兹自由能变的计算 (7)2.5 吉布斯自由能变的计算 (8)2.5.1吉布斯自由能与温度的关系—Gibbs-Helmholtz方程 (8)2.5.2吉布斯自由能与压力的关系 (8)2.5.3 根据反应系统中各物质的标准生成吉布斯自由能∆f G mθ，计算反应的∆r G mθ (9)2.5.4根据化学反应等温方程式(霍夫曼等温方程式)计算反应∆r G mθ (9)2.5.5由一些反应的Kθ求算未知反应的∆r G mθ (10)2.5.6根据电池的标准电动势Eθ计算反应的∆r G mθ (11)3 小结 (12)参考文献 (13)致谢 (14)引言状态函数是由系统状态唯一确定的热力学量，又称为热力学函数。
1.1 热力学概论（1）状态与状态函数
1.1.1体系和环境
我们用观察、实验等方法进行科学研究时，必须先确定所要研究的对象，把要研究的那部分物质与其余的分开（分隔面可以是实际的，也可以是想象的），这种被划定的对象就称为体系，而体系以外，与体系密切相关，影响所及的部分则称为环境。
例如:一个热机气缸中的气体，一个反应器中的物质，一个原电池中的物料，这些都是热力学体系，而这些体系以外的部分为环境。
体系又可分为如下几种：
（1）隔离体系（或孤立体系）:体系和环境之间既没有物质交换，也没有能量交换。
（2）封闭体系：体系和环境之间没有物质交换，但有能量交换。
（3）敞开体系：体系和环境之间既有物质交换，也有能量交换。
如一个盖着的热水瓶可近似地认为是一个隔离体系；一个盖着的，但不保温的热水瓶可认为是一个封闭体系；一个没盖的，也不保温的热水瓶可认为是一个敞开体系。
1.1.2 状态和状态函数
1.1.
2.1 状态函数与状态函数法
⏹ 状态：某一热力学系统的状态指体系的物理性质和化学性质的综合表现。
⏹ 体系的性质：描述体系状态的一些变量，如体积、压力和温度等称为性质。
这些性质又可分为两类：
（1）广度性质（或容量性质）：广度性质的数值与体系物质的数量成正比，如体积、内能和熵等。
广度性质具有加和性。
（2）强度性质：强度性质的数值与体系物质的数量无关，如温度、压力、密度和粘度等。
强度性质不具有加和性。
两个广度性质相除就成了强度性质，如摩尔体积和密度等。
⏹ 状态函数：在热力学中，把体系的性质称为状态变量或状态函数.
如:温度、压力、体积、密度和粘度等。
状态函数的特点：状态函数的数值只与体系现在所处的状态有关，而与其过去的历史无关。
如:一大气压下25℃的水，它的密度和粘度都有确定的值，不管这水是由0℃升温来的，还是由100℃降温来的。
1.2.2.2 状态函数法：状态函数的增量只与体系的始末态有关，而与状态变化的过程无关。
如果体系状态变化循环一周，则状态函数的增量为0。
从数学上来说，状态函数的微分是全微分，全微分沿封闭路径积分一周结果为0。
⎰=-=∆0
(12dV V V V 体积） ⎰=-=∆0(dU V V U 初态
末态内能）
X X X X X X X X X ∆=-==⎰⎰始末末
始末始）（途径）（途径对于任意状态函数：d 2d 1
1.1.3 平衡态必须满足条件：以强度性质度量
•热平衡（thermal equilibrium）：
各处温度相等，d T = 0 (以温度度量)
•力平衡（mechanical equilibrium）：
各处压强相等，d p = 0 (以压强度量)
•相平衡（phase equilibrium）：
各处组成数量不变，无净物质转移d m = 0
(以化学势度量)
•化学平衡（chemical equilibrium ）：
各处组成不变;d c = 0 (以化学势度量)。
