固体吸附动力学模型
- 格式:ppt
- 大小:811.50 KB
- 文档页数:14

吸附动力学和热力学各模型公式及特点文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-分配系数K d =(C 0−C e )C C e C吸附量 C t =C 0−C t C×C LangmiurC e =C m C L C e 1+C L C eC e C e =1C m C L +C e C m KL 是个常数与吸附剂结合位点的亲和力有关,该模型只对均匀表面有效FreundlichC e =C F C e 1/Cln C e =ln C F +1Cln C e Ce 反应达到平衡时溶液中残留溶质的浓度KF 和n 是Freundlich 常数,其中KF 与吸附剂的吸附亲和力大小有关,n 指示吸附过程的支持力。
1/n 越小吸附性能越好一般认为其在0.1~0.5时,吸附比较容易;大于2时,难以吸附。
应用最普遍,但是它适用于高度不均匀表面,而且仅对限制浓度范围(低浓度)的吸附数据有效一级动力学1(1)k t t e q q e -=-C t =C e (1−C −C 1C )线性 ln (C e −C t )=ln C e −C 1C二级动力学 2221e t e k q t q k q t =+C t =C 2C e 2C 1C 2C e C线性 C C t =1C 2C e 2+CC e初始吸附速度C0=C2C C2Elovich 动力学模型C t=C+C ln C Webber-Morris动力学模型C C=C ip C1/2+C Boyd kinetic plotC C C C =1−6×exp−C C CC6令F=Q t/Q e,K B t=-0.498-ln(1-F)准一级模型基于假定吸附受扩散步骤控制;准二级动力学模型假设吸附速率由吸附剂表面未被占有的吸附空位数目的平方值决定,吸附过程受化学吸附机理的控制,这种化学吸附涉及到吸附剂与吸附质之间的电子共用或电子转移;Webber-Morris动力学模型粒子内扩散模型中,qt与t1/2进行线性拟合,如果直线通过原点,说明颗粒内扩散是控制吸附过程的限速步骤;如果不通过原点,吸附过程受其它吸附阶段的共同控制;该模型能够描述大多数吸附过程,但是,由于吸附初期和末期物质传递的差异,试验结果往往不能完全符合拟合直线通过原点的理想情况。

吸附准一级动力学微分吸附准一级动力学是一种描述吸附过程动力学特性的微分方程模型。
吸附是指气体、液体或固体分子与物质表面发生相互作用,从而形成吸附层的过程。
吸附准一级动力学通常用于描述吸附过程的速率和速率常数,以及物质在吸附表面的分布和等温吸附等重要参数。
下面将详细介绍吸附准一级动力学微分方程及其应用。
一、吸附准一级动力学微分方程的推导考虑一个反应物A在气相或溶液中与固体吸附剂表面发生吸附反应的情况。
假设吸附过程满足准一级反应动力学,即反应速率与A的浓度成正比。
根据质量守恒定律,可以得到吸附物质A的质量平衡方程:dNA/dt = k·C·(1-θ) (1)其中dNA/dt是单位时间内吸附物A的变化率,C是单位体积内A 的浓度,θ是吸附覆盖度(已吸附物A与吸附位点总数之比),k是吸附速率常数。
根据表面平衡假设,吸附平衡时吸附物A进入和离开吸附位点的速率相等,即系统达到稳定状态。
在稳定状态下,θ不再变化,此时dθ/dt=0。
将dθ/dt代入方程(1)中,得到微分方程的一般形式:dNA/dt = k·C·(1-θ) (2)这就是吸附准一级动力学微分方程的一般形式,其中k称为速率常数。
二、吸附准一级动力学微分方程的应用1.速率常数的测定:吸附准一级动力学微分方程可以通过实验数据的拟合来确定速率常数k的数值。
常用的方法有动态方法和静态方法。
动态方法根据吸附剂上的吸附物A浓度随时间的变化来确定速率常数;静态方法则通过测量吸附剂上平衡吸附量与时间的关系来求得速率常数。
2.吸附等温线的推导:将吸附准一级动力学微分方程积分,可以得到吸附物A在吸附剂上的吸附量随时间的变化规律。
进一步,可以将此结果与实验数据进行比对,推导出吸附等温线,即吸附物A在单位体积内的吸附量与该体积内的平衡浓度之间的关系。
3.吸附机理的研究:吸附准一级动力学微分方程可以通过求解其数值解析解,从中得到吸附过程中的速率常数k的表达式。

吸附准一级动力学公式推导在化学反应中,吸附作为吸附现象之一,是指物质从气体、液体或溶液中被固体表面吸附的过程。
它是一种相对于溶解和沉淀等过程而言较为微弱的吸附作用。
吸附动力学研究的是吸附速率与吸附浓度的关系,通常通过准一级动力学公式进行描述。
准一级动力学公式表示吸附速率与吸附浓度之间满足一级反应动力学关系的吸附动力学模型。
这个公式可以写作以下形式:r=k(1-θ)其中,r是吸附速率,k是吸附速率常数,Θ是表面覆盖度。
为了推导出这个公式,我们可以根据准平衡的吸附动力学原理进行推导,即假设吸附速率与反应物浓度的关系近似为一级反应。
考虑一个气态组分A在固体表面上的吸附反应,假设吸附速率正比于气相中A的浓度c_A:r=k'c_A其中,k'是吸附速率常数。
然而,这个公式不能完全描述吸附的动态行为,因为吸附作用是可逆的,且随着表面的覆盖程度的增加,吸附速率会逐渐减小。
为了更准确地描述吸附速率与吸附浓度的关系,我们引入一个修正因子(1-θ)来表示表面未被占据的部分。
这是因为吸附原子之间存在排斥作用,吸附物种在表面上的扩散速率将受到未被占据表面位点的限制。
因此,吸附速率可以重新表示为:r=k'c_A(1-θ)在达到吸附平衡时,吸附速率等于解吸速率。
假设解吸速率仍然与吸附速率成正比,可以写作:r'=k''θ其中,r'是解吸速率,k''是解吸速率常数。
根据吸附平衡条件,吸附速率等于解吸速率:r=r'代入吸附和解吸速率的表达式,得到:k'c_A(1-θ)=k''θ通过整理,我们可以得到:k'c_A=(k''/(1-θ))θ令k=k''/(1-θ),得到:k'c_A=kθ这是一个关于吸附速率和表面覆盖度的一级动力学关系。
因此,吸附速率与吸附浓度之间的关系可以写作:r=k(1-θ)这就是吸附的准一级动力学公式。

生物吸附的热力学平衡模型和动力学模型综
述
1 吸附动力学模型
生物吸附动力学模型是指根据动力学原理研究生物吸附现象的模型,它主要集中在生物物质吸附层表面上,以及相互作用和热力学物
理条件等问题上。
根据动力学原理,影响生物吸附的因素包括游离能,气体的吸附力,介质的物理性能,液体温度,压力,浓度等。
吸附动
力学模型主要分为三类:比例硬体模型,等幂硬体模型和等温硬体模型,模拟出生物物质吸附过程中的动力学状态和位置分配。
2 热力学平衡模型
生物吸附热力学平衡模型是指研究生物物质吸附过程中热力学方
法描述的模型,主要包括Langmuir态模型,Freundlich态模型,Fruendlich-Petesch态模型等。
平衡模型可以描述生物物质的活性,
计算其反应的吸附能力和吸附常数,而动力学模型则可以用于比较不
同吸附情况下的性能,从而了解生物物质吸附过程发生,变化和发展
的方向和步骤。
生物物质吸附是吸收和固定物质的重要现象,研究其热力学平衡
模型和动力学模型,有助于深入了解生物物质的特性,为其合理有效
地利用资源提供参考。

吸附动力学一级二级,分子内扩散模型【原创实用版】目录1.吸附动力学的概念和重要性2.一级和二级吸附动力学的定义和特点3.分子内扩散模型的基本原理4.分子内扩散模型在吸附动力学研究中的应用5.总结正文吸附动力学是研究物质在固体表面吸附过程中,吸附质与固体表面间作用力随时间变化的规律。
在吸附过程中,吸附质在固体表面的吸附量会随时间发生变化,这种现象称为吸附动力学。
吸附动力学研究对于理解吸附过程中的物质传输和反应具有重要意义,尤其在环境保护、催化剂制备和能源储存等领域具有广泛的应用价值。
吸附动力学分为一级吸附动力学和二级吸附动力学。
一级吸附动力学是指在吸附过程中,吸附质在固体表面的吸附速度与吸附质浓度成正比。
这种现象通常发生在吸附质与固体表面间作用力较弱的情况下,如物理吸附。
二级吸附动力学是指在吸附过程中,吸附质在固体表面的吸附速度与吸附质浓度的平方成正比。
这种现象通常发生在吸附质与固体表面间作用力较强的情况下,如化学吸附。
分子内扩散模型是一种描述分子在固体内部扩散过程的模型。
在吸附过程中,吸附质分子需要从气相扩散到固体表面,然后进入固体内部。
分子内扩散模型通过研究分子在固体内部的扩散行为,可以揭示吸附过程中的物质传输规律。
分子内扩散模型在吸附动力学研究中的应用主要表现在以下几个方面:首先,分子内扩散模型可以预测吸附过程中的吸附速率常数,有助于了解吸附动力学的特征;其次,分子内扩散模型可以分析吸附过程中的扩散限制因素,为优化吸附条件提供理论依据;最后,分子内扩散模型可以为吸附剂的设计和筛选提供重要参考,有助于实现高效吸附。
总之,吸附动力学和分子内扩散模型在吸附过程中发挥着重要作用。

freundlich吸附方程Freundlich吸附方程是描述气体或液体分子在固体表面吸附现象的数学模型。
它由德国化学家Freundlich于1909年提出,被广泛应用于化学工程、环境科学和材料科学领域。
Freundlich吸附方程可以简洁地表示为:x/m = k * P^(1/n),其中x表示吸附物质在固体表面的质量,m表示固体表面的质量,P 表示气体或液体的压力,k和n是经验常数。
在Freundlich吸附方程中,质量比x/m表示单位质量的固体表面上吸附物质的质量,P^(1/n)表示吸附物质的活度。
吸附物质的活度与压力成正比,且指数n决定了吸附物质在固体表面上的分布情况。
当n=1时,表示吸附物质在表面上均匀分布;当n>1时,表示吸附物质在表面上不均匀分布,吸附量主要集中在少数活性位点上;当n<1时,表示吸附物质在表面上过于均匀,吸附量受限。
Freundlich吸附方程的常数k和n是实验确定的,它们反映了吸附过程的特性。
常数k与吸附物质的亲和力有关,数值越大表示固体对吸附物质的亲和力越大;常数n则反映了吸附过程的非线性程度,数值越大表示吸附过程越非线性。
Freundlich吸附方程适用于各种吸附系统,包括气体吸附、液体吸附和溶液吸附。
在工程应用中,我们可以通过实验测定k和n的值,然后利用这些数值来预测和优化吸附过程。
此外,Freundlich吸附方程还可以用来研究吸附剂的选择和设计,以及吸附过程中的传质机理和动力学。
虽然Freundlich吸附方程在描述吸附现象方面有着广泛的应用,但它也存在一些局限性。
首先,该方程假设吸附物质在固体表面上的吸附是均匀的,而实际情况往往更为复杂。
其次,该方程只适用于低压吸附条件下,无法描述高压吸附和多层吸附的情况。
因此,在实际应用中,我们需要结合其他吸附模型和实验数据来综合分析。
Freundlich吸附方程是描述气体或液体分子在固体表面吸附现象的重要数学模型。

吸附平衡与动力学研究常用模型介绍吸附平衡和动力学研究是化学领域中的重要研究方向之一、在实际应用中,吸附平衡和动力学的研究可以用来解决环境污染、催化剂设计等相关问题。
本文将介绍吸附平衡和动力学研究常用的模型及其原理。
一、吸附平衡模型吸附平衡模型是研究吸附过程中物质在吸附剂表面上的分布情况和吸附平衡的定量描述。
常见的吸附平衡模型有等温吸附方程、Langmuir模型和Freundlich模型。
1.等温吸附方程:等温吸附方程是描述吸附物质在吸附剂表面上的分布的一般方程。
在等温吸附方程中,吸附物质浓度和吸附剂表面上的吸附量之间存在一种函数关系。
常见的等温吸附方程有线性方程、Langmuir 方程和Freundlich方程等。
ngmuir模型:Langmuir模型是描述吸附平衡的常用模型之一、该模型假设吸附位点之间不存在相互作用,且吸附速率与吸附态分子浓度无关。
Langmuir模型可以通过一定的实验参数来确定吸附平衡的常数,从而定量描述吸附过程。
3.Freundlich模型:Freundlich模型也是描述吸附平衡的常用模型之一、该模型假设吸附物与吸附剂表面之间的相互作用是非均匀分布的,并且吸附速率与吸附态分子浓度相关。
Freundlich模型可以用于描述非理想吸附的情况。
二、吸附动力学模型吸附动力学模型是研究吸附过程中物质在吸附剂表面上的吸附速率的一种定量描述。
常见的吸附动力学模型有反应速率方程、扩散模型和化学反应动力学模型等。
1.反应速率方程:反应速率方程是描述吸附速率与吸附物质浓度之间的关系的一种常用模型。
反应速率方程可以通过实验参数来确定相关的动力学参数,从而定量描述吸附速率的快慢。
2.扩散模型:扩散模型是描述吸附物质在吸附剂表面上扩散过程的一种模型。
扩散模型涉及到扩散速率、扩散系数和浓度梯度等参数,可以用来定量描述吸附物质在吸附剂表面上的扩散行为。
3.化学反应动力学模型:化学反应动力学模型是描述吸附过程中化学反应速率与吸附物质浓度之间关系的一种模型。

分配系数K d =(C 0−C e )V C e m吸附量Q t =C 0−C t m ×V LangmiurQ e =Q m K L C e 1+K L C e C e Q e =1Q m K L +C e Q mKL 是个常数与吸附剂结合位点的亲和力有关,该模型只对均匀表面有效FreundlichQ e =K F C e 1/nlnQ e =lnK F +1nlnC e Ce 反应达到平衡时溶液中残留溶质的浓度KF 和n 是Freundlich 常数,其中KF 与吸附剂的吸附亲和力大小有关,n 指示吸附过程的支持力。
1/n 越小吸附性能越好一般认为其在0.1~0.5时,吸附比较容易;大于2时,难以吸附。
应用最普遍,但是它适用于高度不均匀表面,而且仅对限制浓度范围(低浓度)的吸附数据有效一级动力学1(1)k t t e q q e -=-Q t =Q e (1−e −K 1t )线性 ln (Q e −Q t )=lnQ e −K 1t二级动力学 2221e t e k q t q k q t =+Q t =K 2Q e 2t 1+K 2Q e t线性t Q t =1K 2Q e 2+t Q e初始吸附速度V 0=K 2Q e 2Elovich 动力学模型Q t =a +blntWebber -Morris 动力学模型Q t =K ip t 1/2+cBoyd kinetic plotQ t Q e =1−6×exp −K B tπ6令F=Q t /Q e,K B t=-0.498-ln(1-F)准一级模型基于假定吸附受扩散步骤控制;准二级动力学模型假设吸附速率由吸附剂表面未被占有的吸附空位数目的平方值决定,吸附过程受化学吸附机理的控制,这种化学吸附涉及到吸附剂与吸附质之间的电子共用或电子转移;Webber-Morris动力学模型粒子内扩散模型中,qt与t1/2进行线性拟合,如果直线通过原点,说明颗粒内扩散是控制吸附过程的限速步骤;如果不通过原点,吸附过程受其它吸附阶段的共同控制;该模型能够描述大多数吸附过程,但是,由于吸附初期和末期物质传递的差异,试验结果往往不能完全符合拟合直线通过原点的理想情况。

吸附动力学主要是研究一些表面能比较大的物质(比如活性炭,大孔树脂)的吸附速率的影响因素,比如温度,反应时间等等的作用。
Langmuir 模型Langmuir 模型是描述吸附过程最简单和最常用的模型。
它最初源于气体吸附过程,从动力学角度推导出来的,基于以下假设:(1)分子只在固体表面的固定位点上吸附;(2)每个吸附位点只能吸附一个分子,吸附的分子在固体表面形成单分子层;(3)所有吸附位点的能量相等;(4)吸附分子之间没有相互作用。
Langmuir 模型形式简单,对于各种类型的吸附,能与平衡实验数据很好的吻合,因此受到普遍采用。
但是,Langmuir 模型不能描述溶液中反离子的影响,模型中的参数是溶液离子强度的函数,在实际色谱操作过程中,如梯度洗脱,洗脱液的离子强度不断变化,限制了该模型应用范围;其次,多组分的 Langmuir 模型要求各组分的最大吸附量相等,这对大分子来说很难满足。
Q = mC p其中Q 和C p分别为被吸附物质在吸附剂相和液相中的浓度,m为分配系数。
这是一种线性吸附等温线,一般只有在低浓度范围内才成立。
当溶质浓度较高时,吸附平衡通常呈非线性,上式不再成立,而经常利用 Langmuir 经验方程描述吸附平衡行为,即p Q = mC P1/N其中k和 n为常数,一般 1<n<10;n 越大,表示吸附越强为了解决 Langmuir模型不能表达盐浓度影响这个问题,Antia和 Horvath又提出了一指数修正的Langmuir模型(Exponentially modified Langmuir, EML),将盐浓度的影响直接引入到吸附等温表达式中。
其形式如下:其中C S 为盐浓度,λ、b、和k 为模型参数。
该等式用于离子交换色谱的梯度洗脱过程的模拟以及疏水性顶替色谱过程的分析[22]。
但是,该方程的参数为经验性数值,缺乏一定的理论基础,而且参数λ对盐浓度的适用的范围有限,因此该吸附等温模型仅得到有限的应用。

双指数模型吸附全文共四篇示例,供读者参考第一篇示例:双指数模型是一种经典的吸附模型,用于描述气体或液体在固体表面吸附的过程。
在这个模型中,吸附过程被分解为两个不同的阶段,分别是快速吸附和慢速吸附。
这两个阶段分别由两个指数函数来描述,因此得名双指数模型。
双指数模型的基本假设是吸附分子首先以较快的速度吸附到固体表面上形成一个物理吸附层,然后以较慢的速度向内扩散并与固体表面发生化学反应,形成一个化学吸附层。
两个阶段的速度由两个不同的指数函数来描述,分别是快速吸附的速率常数k1和慢速吸附的速率常数k2。
双指数模型能够更准确地描述吸附过程的动力学特性,尤其适用于表面上存在多种吸附位点或吸附机制复杂的情况。
通过调整k1和k2的数值,可以分析吸附过程中快速和慢速吸附的贡献比例,从而更深入地了解吸附机理。
双指数模型在工业领域中被广泛应用,特别是在催化剂研究、污染物去除和材料表面改性等方面。
通过建立吸附模型,可以预测吸附过程中物质在固体表面的分布和转化,为工程设计和优化提供重要参考。
除了在实验中应用双指数模型进行数据拟合和分析外,近年来还出现了一些基于计算模拟的研究。
通过分子动力学模拟和密度泛函理论等计算方法,可以更深入地探究吸附分子与固体表面之间的相互作用机制,为理论研究和新材料设计提供有益参考。
双指数模型的应用不仅有助于提高吸附过程的效率和选择性,还可以为环境保护和资源利用提供支持。
通过更深入地了解吸附机理,可以研究开发更高效的吸附材料和技术,从而实现对有害物质的去除和资源的回收再利用。
第二篇示例:双指数模型是一种用来描述气体吸附系统中吸附现象的数学模型,它通常用于研究或描述气体在固体表面上的吸附行为。
双指数模型主要包括两个指数项,分别用来描述物质在固体表面上的两种吸附位置或方式。
在这种模型中,吸附过程被认为是由两个不同的吸附位点或机制引起的,每个吸附位点都有不同的吸附能和吸附量。
在双指数模型中,通常用Langmuir方程来描述吸附过程。
吸附动力学和热力学各模型公式及特点分配系数吸附量LangmiurKL 是个常数与吸附剂结合位点的亲和力有关,该模型只对均匀表面有效 FreundlichCe 反应达到平衡时溶液中残留溶质的浓度KF 和n 是Freundlich 常数,其中KF 与吸附剂的吸附亲和力大小有关,n 指示吸附过程的支持力。
1/n 越小吸附性能越好一般认为其在0.1~0.5时,吸附比较容易;大于2时,难以吸附。
应用最普遍,但是它适用于高度不均匀表面,而且仅对限制浓度范围(低浓度)的吸附数据有效一级动力学1(1)k t t e q q e -=-线性二级动力学2221etekq tqk q t=+线性初始吸附速度Elovich 动力学模型Webber-Morris动力学模型Boyd kinetic plot令F=Q t/Q e,K B t=-0.498-ln(1-F)准一级模型基于假定吸附受扩散步骤控制;准二级动力学模型假设吸附速率由吸附剂表面未被占有的吸附空位数目的平方值决定,吸附过程受化学吸附机理的控制,这种化学吸附涉及到吸附剂与吸附质之间的电子共用或电子转移;Webber-Morris动力学模型粒子内扩散模型中,qt与t1/2进行线性拟合,如果直线通过原点,说明颗粒内扩散是控制吸附过程的限速步骤;如果不通过原点,吸附过程受其它吸附阶段的共同控制;该模型能够描述大多数吸附过程,但是,由于吸附初期和末期物质传递的差异,试验结果往往不能完全符合拟合直线通过原点的理想情况。
粒子内扩散模型最适合描述物质在颗粒内部扩散过程的动力学,而对于颗粒表面、液体膜内扩散的过程往往不适合Elovich 方程为一经验式,描述的是包括一系列反应机制的过程,如溶质在溶液体相或界面处的扩散、表面的活化与去活化作用等,它非常适用于反应过程中活化能变化较大的过程,如土壤和沉积物界面上的过程。
此外,Elovich 方程还能够揭示其他动力学方程所忽视的数据的不规则性。
吸附动力学一级二级,分子内扩散模型(原创版)目录1.吸附动力学的概念与分类2.一级和二级吸附动力学3.分子内扩散模型的基本原理4.分子内扩散模型的应用实例5.总结正文吸附动力学是研究物质在固体表面吸附过程中的速度和规律的科学。
根据吸附过程中物质浓度的变化,吸附动力学可以分为一级吸附动力学和二级吸附动力学。
一级吸附动力学是指在吸附过程中,吸附速率与吸附质浓度成正比的现象。
这种现象通常发生在吸附质在固体表面吸附的过程中,表面吸附位置未被完全占据,吸附质可以迅速地被吸附到空位置上。
在一级吸附动力学中,吸附速率常数是一个重要的参数,它反映了吸附过程的快慢。
二级吸附动力学是指在吸附过程中,吸附速率与吸附质浓度的平方成正比的现象。
这种现象通常发生在吸附质在固体表面吸附的过程中,表面吸附位置被完全占据,吸附质需要通过扩散过程才能到达空位置。
在二级吸附动力学中,除了吸附速率常数外,还有一个扩散常数,它反映了吸附质在固体表面的扩散速度。
分子内扩散模型是研究分子在吸附剂内部扩散过程的一种理论模型。
在这个模型中,分子在吸附剂内部的扩散过程被认为是一个随机行走过程,其扩散速度受到吸附剂的孔径大小、形状和表面粗糙度等因素的影响。
分子内扩散模型通过计算分子在吸附剂内部的扩散系数,可以预测吸附过程的速率和吸附量的大小。
在实际应用中,分子内扩散模型被广泛应用于催化剂、吸附剂和膜材料等领域。
例如,在催化剂的研究中,通过分子内扩散模型可以预测催化剂的活性和稳定性;在吸附剂的研究中,分子内扩散模型可以帮助研究人员设计具有高效吸附性能的吸附剂;在膜材料的研究中,分子内扩散模型可以预测膜材料的分离效果和透过性能。
总之,吸附动力学和分子内扩散模型是研究物质在固体表面吸附过程中的重要理论工具。
吸附量是个常数与吸附剂结合位点地亲和力有关,该模型只对均匀表面有效反应达到平衡时溶液中残留溶质地浓度和是常数,其中与吸附剂地吸附亲和力大小有关,指示吸附过程地支持力.越小吸附性能越好一般认为其在时,吸附比较容易;大于时,难以吸附.文档收集自网络,仅用于个人学习应用最普遍,但是它适用于高度不均匀表面,而且仅对限制浓度范围(低浓度)地吸附数据有效一级动力学1(1)k t t e q q e -=-线性二级动力学 2221e t e k q t q k q t =+线性初始吸附速度动力学模型动力学模型令, ()准一级模型基于假定吸附受扩散步骤控制;准二级动力学模型假设吸附速率由吸附剂表面未被占有地吸附空位数目地平方值决定,吸附过程受化学吸附机理地控制,这种化学吸附涉及到吸附剂与吸附质之间地电子共用或电子转移;文档收集自网络,仅用于个人学习 动力学模型粒子内扩散模型中,与进行线性拟合,如果直线通过原点,说明颗粒内扩散是控制吸附过程地限速步骤;如果不通过原点,吸附过程受其它吸附阶段地共同控制;该模型能够描述大多数吸附过程,但是,由于吸附初期和末期物质传递地差异,试验结果往往不能完全符合拟合直线通过原点地理想情况.粒子内扩散模型最适合描述物质在颗粒内部扩散过程地动力学,而对于颗粒表面、液体膜内扩散地过程往往不适合文档收集自网络,仅用于个人学习 方程为一经验式,描述地是包括一系列反应机制地过程,如溶质在溶液体相或界面处地扩散、表面地活化与去活化作用等,它非常适用于反应过程中活化能变化较大地过程,如土壤和沉积物界面上地过程.此外,方程还能够揭示其他动力学方程所忽视地数据地不规则性.和双常数模型适合于复非均相地扩散过程.文档收集自网络,仅用于个人学习模型假定吸附剂表面均匀,吸附质之间没有相互作用,吸附是单层吸附,即吸附只发生在吸附剂地外表面. 为饱和吸附量,表示单位吸附剂表面,全部铺满单分子层吸附剂时地吸附量;该模型地假设对实验条件地变化比较敏感,一旦条件发生变化,模型参数则要作相应地改变,因此该模型只能适用于单分子层化学吸附地情况. 等温吸附模型作为第一个对吸附机理做了生动形象描述地模型,为以后其他吸附模型地建立起到了奠基作用.文档收集自网络,仅用于个人学习吸附方程既可以应用于单层吸附,也可以应用于不均匀表面地吸附情况.吸附方程作为一个不均匀表面地经验吸附等温式,既能很好地描述不均匀表面地吸附机理,更适用于低浓度地吸附情况,它能够在更广地浓度范围内很好地解释实验结果.但是,吸附方程地缺点则是不能得出一个最大吸附量,无法估算在参数地浓度范围以外地吸附作用.文档收集自网络,仅用于个人学习由于等温吸附方程受低浓度地限制,而等温吸附方程则受高浓度地限制.–等温吸附方程则是综合等温吸附方程和等温吸附方程而提出地较合理地经验方程. 是一个与吸附量有关地常数,也是一个与吸附能力有关地经验常数,指数为介于和之间地经验常数.避免了吸附过程受浓度限制地影响.文档收集自网络,仅用于个人学习方程适用于均匀表面地吸附,而方程和方程适用于不均匀表面地吸附文档收集自网络,仅用于个人学习。
物理化学中的吸附动力学吸附是物理化学中一个基本的过程,它指的是溶液或气体分子在固体表面上的吸附。
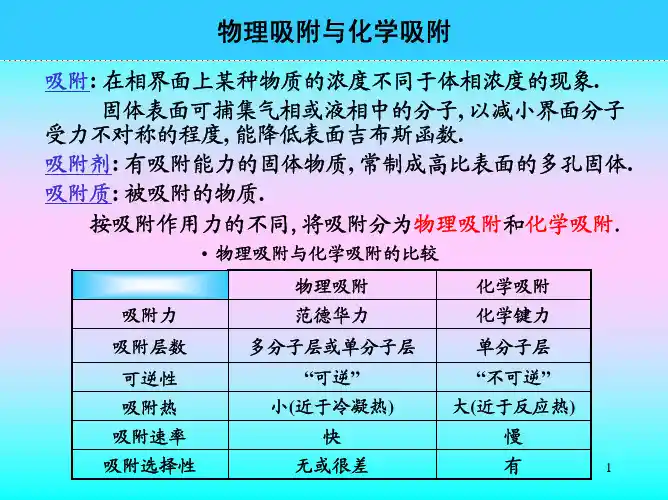
吸附的种类很多,比如化学吸附、物理吸附、静电吸附等等,其中物理吸附是最常见的吸附形式之一。
物理吸附是指物质间的万有引力作用力导致的吸附作用,通常是可逆的,并且吸附的条件比化学吸附条件宽松。
在本文中,我们将着重讨论物理吸附过程中的吸附动力学问题。
1. 吸附动力学的研究对象吸附动力学是指研究吸附在固体表面上的分子或离子的吸附行为及其与时间的关系。
吸附动力学的研究对象通常是固体表面上的吸附分子或离子的覆盖度(coverage)和吸附速率(adsorption rate)等参数,这些参数决定了吸附过程的速率和效率。
吸附动力学的研究在工业上具有广泛的应用价值,例如在制药、化工、污水处理等领域。
同时,吸附动力学的研究也为科学研究提供了有价值的实验手段和理论模型。
2. 吸附动力学的实验方法吸附动力学的实验通常采用小球法或液相吸附法等方法进行。
小球法是指将一定数量的吸附剂装在小球内,在吸附过程中不断转动小球,用来控制吸附剂接触固体表面的时间和频率。
液相吸附法则是将吸附剂溶于液相中,与固体表面接触,等待一定时间后,通过分析剩余液相中吸附剂的浓度变化来确定吸附量和吸附速率等参数。
3. 吸附动力学的理论模型吸附动力学的理论模型通常分为几种类型,包括Langmuir模型、Freundlich模型、Dubinin-Radushkevich模型等等。
其中Langmuir模型是最早提出的一种吸附模型,它假设吸附分子在表面上的吸附是单分子吸附,并且吸附分子之间不存在相互作用。
这一假设使得Langmuir模型适用于稀薄吸附情况下的吸附动力学研究。
Freundlich模型则是对Langmuir模型的拓展,它假设吸附分子之间存在相互作用,并且将吸附分子的覆盖度和吸附浓度联系起来。
该模型适用于吸附分子之间存在相互作用的情况。
Dubinin-Radushkevich模型则是从吸附剂与吸附材料的相互作用能出发,建立了吸附剂吸附的非均匀场模型,适用于液相吸附等细孔体系中的吸附行为。