任意进制计数器(全)

任意进制计数器的设计【摘要】计数器集成芯片一般有4位二进制、8位二进制或十进制计数器，而在实际应用中，往往需要设计一个任意n进制计数器，本文给出它的设计方法和案例。

【关键词】计数器；清零一、利用反馈清零法获得计数器1 集成计数器清零方式异步清零方式：与计数脉冲cp无关，只要异步清零端出现清零信号，计数器立即被清零。

此类计数器有同步十进制加法计数器ct74ls160、同步4位二进制加法计数器ct74ls161、同步十进制加/减计数器ct74ls192、同步4位二进制加/减计数器ct74ls193等。

同步清零方式：与计数脉冲cp有关，同步清零端获得清零信号后，计数器并不立刻被清零，只是为清零创造条件，还需要再输入一个计数脉冲cp，计数器才被清零。

属于此类计数器有同步十进制加法计数器ct74ls162、同步4位二进制加法计数器ct74ls163、同步十进制加/减计数器ct74ls190、同步4位二进制加/减计数器ct74ls191等。

2 反馈清零法对于异步清零方式：应在输入第n个计数脉冲cp后，利用计数器状态sn进行译码产生清零信号加到异步清零端上，立刻使计数器清零，即实现了n计数器。

在计数器的有效循环中不包括状态sn，所以状态sn只在极短的瞬间出现称为过渡状态。

对于同步清零方式：应在输入第n-1个计数脉冲cp后，利用计数器状态sn-1进行译码产生清零信号，在输入第n个计数脉冲cp 时，计数器才被清零，回到初始零状态，从而实现n计数器。

可见同步清零没有过渡状态。

利用计数器的清零功能构成n计数器时，并行数据输入端可接任意数据，其方法如下：①写出n计数器状态的二进制代码。

异步清零方式利用状态sn，同步清零方式利用状态sn-1。

②写出反馈清零函数。

③画逻辑图。

例1 试用ct74ls160的异步清零功能构成六进制计数器。

解：①写出sn的二进制代码。

sn=s6=0110②写出反馈清零函数。

③画逻辑图。

如图1所示。

总结任意进制计数器的实现方法在计算机科学中，计数器是一种用于记录和控制某种计数操作的设备或算法。

通常情况下，我们使用的是十进制计数器，即以10为基数的计数器。

然而，在某些应用中，需要使用其他进制的计数器，例如二进制、八进制或十六进制。

实现任意进制计数器的方法如下：1. 定义计数器的进制：首先，我们需要确定计数器的进制，例如二进制、八进制或十六进制。

进制的选择取决于具体的需求。

2. 确定计数器的位数：接下来，我们需要确定计数器的位数，即计数器可以表示的最大值。

位数决定了计数器可以表示的范围。

3. 初始化计数器：根据选择的进制和位数，初始化计数器。

对于二进制计数器，可以将所有位都设置为0；对于八进制和十六进制计数器，可以将每一位都设置为最小值。

4. 计数器递增：根据选择的进制，实现计数器的递增操作。

对于二进制计数器，可以通过反转位的方式进行递增；对于八进制和十六进制计数器，可以在每一位上递增，并在达到最大值时进位到高位。

5. 计数器输出：根据具体需求，将计数器的当前值以所选进制表示出来。

对于二进制计数器，可以直接输出每一位的值；对于八进制和十六进制计数器，可以将每一位的值转换为对应的字符表示。

拓展部分：1. 递减操作：除了递增操作，我们也可以实现计数器的递减操作。

递减操作的实现与递增操作类似，只是在达到最小值时需要进行借位操作。

2. 范围检查：在实现任意进制计数器时，需要进行范围检查，确保计数器的值在合法范围内。

如果计数器的值超过了最大值，可以选择将其重置为最小值或抛出异常。

3. 多进制切换：在某些情况下，我们需要在不同的进制之间切换计数器的表示。

可以实现一个函数或方法，用于将计数器的值在不同进制之间进行转换。

4. 高位补零：为了使计数器的输出结果具有固定的位数，可以在输出时进行高位补零。

补零操作可以保证计数器的输出结果具有统一的格式。

总的来说，实现任意进制计数器需要确定进制、位数，初始化计数器，实现递增、递减操作，并进行范围检查和输出。

总结任意进制计数器的设计方法一、引言计数器是数字电路中常见的组合逻辑电路，其作用是在一定范围内对输入的信号进行计数。

而进制计数器则是在特定进制下进行计数的计数器，如二进制计数器、十进制计数器等。

本文将总结任意进制计数器的设计方法。

二、基本概念1. 进位：当某一位达到最大值时，需要向高位进位。

2. 借位：当某一位减法结果为负时，需要向高位借位。

3. 余数：在除法中，被除数除以除数所得到的余数即为该数字的个位数字。

4. 商：在除法中，被除数除以除数所得到的商即为该数字的十位以及更高位数字。

三、二进制计数器设计方法1. 同步二进制计数器同步二进制计数器又称为并行加法器或者锁存式加法器。

其实现原理是将多个全加器连接起来，并且每一个全加器都接收同样的时钟信号。

当时钟信号发生变化时，所有全加器同时进行运算。

2. 异步二进制计数器异步二进制计算机又称为Ripple Counters或者Clock-Triggered Flip-Flops。

其实现原理是通过多个D触发器连接起来，每个D触发器都接收上一个触发器的输出信号。

当时钟信号发生变化时，第一个D触发器会先被触发，然后它的输出信号会传递到下一个D触发器中。

四、十进制计数器设计方法1. 二进制编码计数器二进制编码计数器是一种使用二进制代码表示数字的计数器。

其实现原理是通过将BCD码转换成二进制来实现计数。

2. BCD码计数器BCD码计数器是一种使用BCD码表示数字的计数器。

其实现原理是通过多个BCD加法器连接起来，每个加法器都接收同样的时钟信号。

当时钟信号发生变化时，所有加法器同时进行运算。

五、任意进制计数器设计方法1. 基于同步电路设计方法任意进制计算机可以通过同步电路来实现。

其实现原理是将多个全加器连接起来，并且每一个全加器都接收同样的时钟信号。

当时钟信号发生变化时，所有全加器同时进行运算。

2. 基于异步电路设计方法任意进制计算机也可以通过异步电路来实现。

其实现原理是通过多个D触发器连接起来，每个D触发器都接收上一个触发器的输出信号。

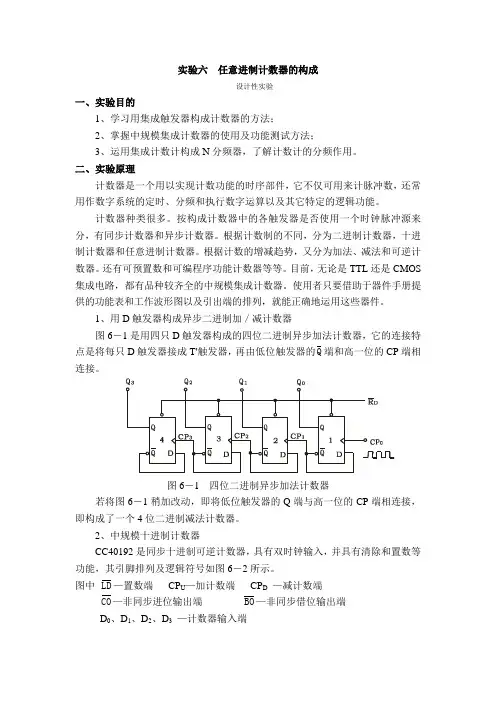
实验六任意进制计数器的构成设计性实验一、实验目的1、学习用集成触发器构成计数器的方法；2、掌握中规模集成计数器的使用及功能测试方法；3、运用集成计数计构成N分频器，了解计数计的分频作用。

二、实验原理计数器是一个用以实现计数功能的时序部件，它不仅可用来计脉冲数，还常用作数字系统的定时、分频和执行数字运算以及其它特定的逻辑功能。

计数器种类很多。

按构成计数器中的各触发器是否使用一个时钟脉冲源来分，有同步计数器和异步计数器。

根据计数制的不同，分为二进制计数器，十进制计数器和任意进制计数器。

根据计数的增减趋势，又分为加法、减法和可逆计数器。

还有可预置数和可编程序功能计数器等等。

目前，无论是TTL还是CMOS 集成电路，都有品种较齐全的中规模集成计数器。

使用者只要借助于器件手册提供的功能表和工作波形图以及引出端的排列，就能正确地运用这些器件。

1、用D触发器构成异步二进制加／减计数器图6－1是用四只D触发器构成的四位二进制异步加法计数器，它的连接特点是将每只D触发器接成T'触发器，再由低位触发器的Q端和高一位的CP端相连接。

图6－1 四位二进制异步加法计数器若将图6－1稍加改动，即将低位触发器的Q端与高一位的CP端相连接，即构成了一个4位二进制减法计数器。

2、中规模十进制计数器CC40192是同步十进制可逆计数器，具有双时钟输入，并具有清除和置数等功能，其引脚排列及逻辑符号如图6－2所示。

图中LD—置数端CP U—加计数端CP D—减计数端CO—非同步进位输出端BO—非同步借位输出端D0、D1、D2、D3—计数器输入端Q 0、Q 1、Q 2、Q 3 —数据输出端 CR图6－2 CC40192引脚排列及逻辑符号CC40192（同74LS192，二者可互换使用）的功能如表6－1，说明如下：当清除端CR 为高电平“1”时，计数器直接清零；CR 置低电平则执行其它功能。

当CR 为低电平，置数端LD 也为低电平时，数据直接从置数端D 0、D 1、D 2、D 3 置入计数器。

任意进制计数器的构成方法从降低成本的角度考虑，集成电路的定型产品必须有足够大的批量。

因此，目前常见的计数器芯片在计数进制上只做成应用较广的几种类型，如十进制、十六进制、7位二进制、12位二进制、14位二进制等。

在需要其他任意一种进制的计数器时识能用已有的计数器产品经过外电路的不同连接方式得到。

假定已有的是N进制计数器，而需要得到的是M进制计数器。

这时有M<NN和M>N两种可能的情况。

下面分别讨论两种情况下构成任意一进制计数器的方法。

1. M<N的情况在N进制计数器的顺序计数过程中，若设法使之跳越N一M个状态，就可以得到M 进制计数器了。

实现跳跃的方法有置零法(或称复位法)和置数法(或称置位法)两种。

置零法适用于有置零输人端的计数器。

对于有异步置零输人端的计数器，它的工作原理是这样的:设原有的计数器为N进制，当它从全0状态S。

开始计数并接收了M个计数脉冲以后，电路进人S}状态。

如果将SM状态译码产生一个置零信号加到计数器的异步置零输人端，则计数器将立刻返回S。

状态，这样就可以跳过N一M个状态而得到M进制计数器(或称为分频器)。

图6. 3.犯(e)为置零法原理示意图。

由于电路一进人s，状态后立即又被置成S。

状态，所以礼状态仅在极短的瞬时出现，在稳定的状态循环中不包括SM状态。

而对于有同步置零输人端的计数器，由于置零输人端变为有效电平后计数器并不会立刻被置零，必须等下一个时钟信号到达后，才能将计数器置零，因而应由sM _,状态译出同步置零信号。

而且，s},;状态包含在稳定状态的循环当中。

例如同步十进制计数器74162、同步十六进制计数器74163就都是采用同步置零方式。

置位法与置零法不同，它是通过给计数器重复置人某个数值的方法跳越N一M个状态，从而获得M进制计数器的，如图6. 3. 32助所示。

置数操作可以在电路的任何一个状态下进行。

这种方法适用于有预置数功能的计数器电路。

对于同步式预置数的计数器(如74160,74161) ,LD' -0的信号应从S‘状态译出，待下一个CGK信号到来时，才将要置入的数据置入计数器中。

第一章一、填空题1.二进制数是以2为基数的计数体制，十进制数是以10 为基数的计数体制，十六进制数是以 16 为基数的计数体制。

2.二进制数只有 0 和 1 两个数码，其计数的基数是 2 ，加法运算进位关系为逢2进一。

3.十进制数转换为二进制数的方法是：整数部分是除2取余法，小数部分用乘2取整法。

4.十进制数（23.76）转换为二进制数为(10111.110)2，8421BCD码(00100011.01110110)8421BCD，余三码为(01010110.10101001)余3BCD。

5.二进制数转换为十进制数的方法为各位加权系数之和。

6.将二进制数（1011011）表示为加权系数之和的形式 2×1+2×1+2×1+2×1+2×1 。

7.格雷码的特点是相连不同，其余各位相邻两组代码只有一位代码不同，其余代码都相同。

8.数字电路主要是输出与输入之间的逻辑关系，故数字电路又称逻辑电路。

二、判断题。

1.二进制数是以2为基数的计数体制（√）2.二进制数的权值是10的幂。

（×）3.十进制数整数转换为二进制数的方法是采用“除2取余法”（√）4.BCD码是用4位二进制数表示1位十进制数。

（√）5.二进制数转换为十进制数的方法是各位加权系数之和。

（√）6.模拟电路又称逻辑电路。

（×）7.余3BCD码是用3位二进制数表示1位十进制数。

（×）8.二进制数整数最低位的权值为2。

（×）三、选择题。

1.1010的基数是（B）A10 B2 C16 D任意数2.下列数中，不是余3码的是（D）A 1011 B1010 C 0110 D 00003.二进制数最低位的权值是（B）A 0B 1C 2D 44.十进制数的权值是（A）A 10的幂B2的幂C16的幂 D 8的幂5.二进制数的权值为（B）A 10的幂B2的幂 C 16的幂 D 8的幂6.在二进制计数系统中每个变量的取值为（A）A 0和1B 0—7C 0—10D 0—167.十进制计数系统包含（B）A 六个数字B 十个数字C 十六个数字D 三十二个数字8.（1000100101110101）8421BCD对应的十进制数为（B）A 8561B 8975 C7AD3 7971第二章一、填空题。