圆的内接正多边形的画法

正五边形尺规作图的画法与其他正五边形的画法第一种：圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O；2、作圆的两条互相垂直的直径AZ和XY；3、作OY的中点M；4、以点M为圆心,MA为半径作圆,交OX于点N；5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形.第二种作法：1. 以O为圆心,半径长为R画圆,并作互相垂直的直径MN和AP；2. 平分半径OM于K,得OK=KM；3. 以K为圆心,KA为半径画弧与ON交于H, AH即为正五边形的边长；4. 以AH为弦长,在圆周上截得A、B、C、D、E各点,顺次连结这些点.五边形ABCDE即为所求.第三种：圆内接正五边形的画法如下:1、作一个圆,设它的圆心为O；2、作圆的两条互相垂直的直径AZ和XY；3、作OY的中点M；4、以点M为圆心,MA为半径作圆,交OX于点N；5、以点A为圆心,AN为半径,在圆上连续截取等弧,使弦AB=BC=CD=DE=AN,则五边形ABCDE即为正五边形.以上两种图形的作法运用了所求图形边长与已知的线段长度的关系,用构造直角三角形的方法作出与所求图形的边长相等的线段,从而作出整个图形,这是尺规作图中常用的一种方法——等线段法,即用已知图形的线段作出与所求图形边长相等的线段.正多边形的尺规作图是大家感兴趣的．正三边形很好做；正四边形稍难一点；正六边形也很好做；正五边形就更难一点,但人们也找到了正五边形的直规作图方法．确实,有的困难一些,有的容易一些．正七边形的尺规作图是容易一些,还是困难一些呢？人们很久很久未找到作正七边形的办法,这一事实本身就说明作正七边形不容易；一直未找到这种作法,也使人怀疑：究竟用尺规能否作出正七边形来？数学不容许有这样的判断：至今一直没有人找到正七边形的尺规作图方法来,所以断言它是不能用尺规作出的．人们迅速地解决了正三、四、五、六边形的尺规作图问题,却在正七边形面前止步了：究竟能作不能作,得不出结论来．这个悬案一直悬而未决两千余年．17世纪的费马,就是我们在前面已两次提到了的那个法国业余数学家,他研究了形如Fi 〔i为右下角标〕＝22i〔底数2指数2的i次幂〕＋1 的数．费马的一个著名猜想是,当n≥3时,不定方程xn＋yn＝zn没有正整数解．现在他又猜测Fi都是素数,对于i＝0,1,2,3,4时,容易算出来相应的Fi：F0＝3,F1＝5,F2＝17,F3=257,F4=65 537验证一下,这五个数的确是素数．F5=225+1是否素数呢？仅这么一个问题就差不多一百年之后才有了一个结论,伟大的欧拉发现它竟不是素数,因而,伟大的费马这回可是猜错了！F5是两素数之积：F5＝641×6 700 417．当然,这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事,不然,何以需要等近百年？何以需要欧拉这样的人来解决问题？更奇怪的是,不仅F5不是素数,F6,F7也不是素数,F8,F9,F10,F11等还不是素数,甚至,对于F14也能判断它不是素数,但是它的任何真因数还不知道．至今,人们还只知F0,F1,F2,F3,F4这样5个数是素数．由于除此而外还未发现其他素数,于是人们产生了一个与费马的猜想大相径庭的猜想,形如22i＋1的素数只有有限个．但对此也未能加以证明．当然,形如Fi=22i+1的素数被称为费马素数．由于素数分解的艰难,不仅对形如Fi=22i+1的数的一般结论很难做出,而且具体分解某个Fi也不是一件简单的事．更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年,一位德国数学家高斯,在他仅20岁左右之时发现,当正多边形的边数是费马素数时是可以尺规作图的,他发现了更一般的结论：正n 边形可尺规作图的充分且必要的条件是n=2k〔2的k次幂〕或2k×p1×p2×…×ps,〔1,2…s为右下角标〕其中,p1,p2,…,ps是费马素数．正7边形可否尺规作图呢？否！因为7是素数,但不是费马素数．倒是正17边形可尺规作图,高斯最初的一项成就就是作出了正17边形．根据高斯的理论,还有一位德国格丁根大学教授作了正257边形．就这样,一个悬而未决两千余年的古老几何问题得到了圆满的解决,而这一问题解决的过程是如此的蹊跷,它竟与一个没有猜对的猜想相关连．正17边形被用最简单的圆规和直尺作出来了,而正多边形可以换个角度被视为是对圆的等分,那么这也相当于仅用圆规和直尺对圆作了17等分,其图形更觉完美、好看．高斯本人对此也颇为欣赏,由此引导他走上数学道路<他早期曾在语言学与数学之间犹豫过>,而且在他逝后的墓碑上就镌刻着一个正17边形图案．高斯把问题是解决得如此彻底,以致有了高斯的定理,我们对于早已知道如何具体作图的正三边形、正五边形,还进而知道了它们为什么能用尺规作图,就因为3和5都是费马素数<3=F0,5＝F1>；对于很久以来未找到办法来作出的正七边形,乃至于正11边形、正 13边形,现在我们能有把握地说,它们不可能由尺规作图,因为7、11、13都不是费马素数；对于正257边形、正65 537边形,即使我们不知道具体如何作,可是理论上我们已经知道它们是可尺规作图的；此外,为什么正四边形、正六边形可尺规作图呢？因为4＝22,因为6= 2· 3而 3=F0．。

正多边形与圆及正多边形的画法内容：1．正多边形和圆的有关概念：正多边形的外接圆，正多边形的中心，•正多边形的半径，正多边形的中心角，正多边形的边心距．2．在正多边形和圆中，圆的半径、边长、边心距中心角之间的等量关系．3．正多边形的画法．问题：1．什么叫正多边形？2．从你身边举出两三个正多边形的实例，正多边形具有轴对称、•中心对称吗？其对称轴有几条，对称中心是哪一点？1．各边相等，各角也相等的多边形是正多边形．2．实例略．正多边形是轴对称图形，对称轴有无数多条；•正多边形是中心对称图形，其对称中心是正多边形对应顶点的连线交点．探究：如果我们以正多边形对应顶点的交点作为圆心，过点到顶点的连线为半径，能够作一个圆，很明显，这个正多边形的各个顶点都在这个圆上，如图，•正六边形ABCDEF，连结AD、CF交于一点，以O为圆心，OA为半径作圆，那么肯定B、C、•D、E、F都在这个圆上．因此，正多边形和圆的关系十分密切，只要把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆．我们以圆内接正六边形为例证明．如图所示的圆，把⊙O•分成相等的6•段弧，依次连接各分点得到六边ABCDEF，下面证明，它是正六边形．根据正多边形的定义，各边相等、各角相等、六边形ABCDEF是⊙O的内接正六边形，⊙O是正六边形ABCDEF的外接圆．为了今后学习和应用的方便，•我们把一个正多边形的外接圆的圆心叫做这个多边形的中心．外接圆的半径叫做正多边形的半径．正多边形每一边所对的圆心角叫做正多边形的中心角．中心到正多边形的一边的距离叫做正多边形的边心距．例1．已知正六边形ABCDEF ，如图所示，其外接圆的半径是a ，•求正六边形的周长和面积．例2．利用你手中的工具画一个边长为3cm 的正五边形．例3．在直径为AB 的半圆内，划出一块三角形区域，如图所示，使三角形的一边为AB ，顶点C 在半圆圆周上，其它两边分别为6和8，现要建造一个内接于△ABC•的矩形水池DEFN ，其中D 、E 在AB 上，如图24-94的设计方案是使AC=8，BC=6． （1）求△ABC 的边AB 上的高h ．（2）设DN=x ，且h DN NFh AB-=，当x 取何值时，水池DEFN 的面积最大？ （3）实际施工时，发现在AB 上距B 点1．85的M 处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为了保护大树，请设计出另外的方案，使内接于满足条件的三角形中欲建的最大矩形水池能避开大树．hF DEC BANG课时作业1．如图1所示，正六边形ABCDEF内接于⊙O，则∠ADB的度数是（）．A．60° B．45° C．30° D．22．5°(1) (2) (3)2．圆内接正五边形ABCDE中，对角线AC和BD相交于点P，则∠APB的度数是（）． A．36° B．60° C．72° D．108°3．若半径为5cm的一段弧长等于半径为2cm的圆的周长，•则这段弧所对的圆心角为（）A．18° B．36° C．72° D．144°4．已知正六边形边长为a，则它的内切圆面积为_______．5．在△ABC中，∠ACB=90°，∠B=15°，以C为圆心，CA长为半径的圆交AB于D，如图2所示，若AC=6，则AD的长为________．6．四边形ABCD为⊙O的内接梯形，如图3所示，AB∥CD，且CD为直径，•如果⊙O 的半径等于r，∠C=60°，那图中△OAB的边长AB是______；△ODA的周长是_______；∠BOC的度数是________．7．等边△ABC的边长为a，求其内切圆的内接正方形DEFG的面积．8．如图所示，•已知⊙O•的周长等于6 cm，•求以它的半径为边长的正六边形ABCDEF 的面积．9．如图所示，正五边形ABCDE的对角线AC、BE相交于M．（1）求证：四边形CDEM是菱形；（2）设MF2=BE·BM，若AB=4，求BE的长．。

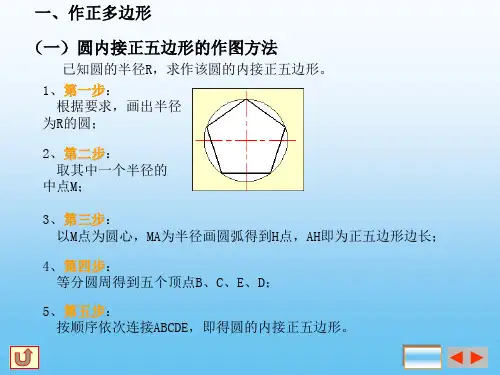
正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆，设它的圆心为O；2、作圆的两条互相垂直的直径AZ和XY；3、作OY的中点M；4、以点M为圆心，MA为半径作圆，交OX于点N；5、以点A为圆心，AN为半径，在圆上连续截取等弧，使弦AB=BC=CD=DE=AN，则五边形ABCDE即为正五边形。

以上两种图形的作法运用了所求图形边长与已知的线段长度的关系，用构造直角三角形的方法作出与所求图形的边长相等的线段，从而作出整个图形，这是尺规作图中常用的一种方法——等线段法，即用已知图形的线段作出与所求图形边长相等的线段。

正多边形的尺规作图是大家感兴趣的．正三边形很好做；正四边形稍难一点；正六边形也很好做；正五边形就更难一点，但人们也找到了正五边形的直规作图方法．确实，有的困难一些，有的容易一些．正七边形的尺规作图是容易一些，还是困难一些呢？人们很久很久未找到作正七边形的办法，这一事实本身就说明作正七边形不容易；一直未找到这种作法，也使人怀疑：究竟用尺规能否作出正七边形来？数学不容许有这样的判断：至今一直没有人找到正七边形的尺规作图方法来，所以断言它是不能用尺规作出的．人们迅速地解决了正三、四、五、六边形的尺规作图问题，却在正七边形面前止步了：究竟能作不能作，得不出结论来．这个悬案一直悬而未决两千余年．17世纪的费马，就是我们在前面已两次提到了的那个法国业余数学家，他研究了形如Fi （i为右下角标）＝22i（底数2指数2的i次幂）＋1 的数．费马的一个著名猜想是，当n≥3时，不定方程xn＋yn＝zn没有正整数解．现在他又猜测Fi都是素数，对于i＝0，1，2，3，4时，容易算出来相应的Fi：F0＝3，F1＝5，F2＝17，F3=257，F4=65 537验证一下，这五个数的确是素数．F5=225+1是否素数呢？仅这么一个问题就差不多一百年之后才有了一个结论，伟大的欧拉发现它竟不是素数，因而，伟大的费马这回可是猜错了！F5是两素数之积：F5＝641×6 700 417．当然，这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事，不然，何以需要等近百年？何以需要欧拉这样的人来解决问题？更奇怪的是，不仅F5不是素数，F6，F7也不是素数，F8，F9，F10，F11等还不是素数，甚至，对于F14也能判断它不是素数，但是它的任何真因数还不知道．至今，人们还只知F0，F1，F2，F3，F4这样5个数是素数．由于除此而外还未发现其他素数，于是人们产生了一个与费马的猜想大相径庭的猜想，形如22i＋1的素数只有有限个．但对此也未能加以证明．当然，形如Fi=22i+1的素数被称为费马素数．由于素数分解的艰难，不仅对形如Fi=22i+1的数的一般结论很难做出，而且具体分解某个Fi也不是一件简单的事．更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年，一位德国数学家高斯，在他仅20岁左右之时发现，当正多边形的边数是费马素数时是可以尺规作图的，他发现了更一般的结论：正n边形可尺规作图的充分且必要的条件是n=2k（2的k次幂）或2k×p1×p2×…×ps，（1，2…s为右下角标）其中，p1，p2，…，ps是费马素数．正7边形可否尺规作图呢？否！因为7是素数，但不是费马素数．倒是正17边形可尺规作图，高斯最初的一项成就就是作出了正17边形．根据高斯的理论，还有一位德国格丁根大学教授作了正257边形．就这样，一个悬而未决两千余年的古老几何问题得到了圆满的解决，而这一问题解决的过程是如此的蹊跷，它竟与一个没有猜对的猜想相关连．正17边形被用最简单的圆规和直尺作出来了，而正多边形可以换个角度被视为是对圆的等分，那么这也相当于仅用圆规和直尺对圆作了17等分，其图形更觉完美、好看．高斯本人对此也颇为欣赏，由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过)，而且在他逝后的墓碑上就镌刻着一个正17边形图案．高斯把问题是解决得如此彻底，以致有了高斯的定理，我们对于早已知道如何具体作图的正三边形、正五边形，还进而知道了它们为什么能用尺规作图，就因为3和5都是费马素数(3=F0，5＝F1)；对于很久以来未找到办法来作出的正七边形，乃至于正11边形、正 13边形，现在我们能有把握地说，它们不可能由尺规作图，因为7、11、13都不是费马素数；对于正257边形、正65 537边形，即使我们不知道具体如何作，可是理论上我们已经知道它们是可尺规作图的；此外，为什么正四边形、正六边形可尺规作图呢？因为4＝22，因为6= 2· 3而 3=F0．。

正多边形和圆【学习目标】1. 了解正多边形和圆的有关概念及对称性；2 .理解并掌握正多边形半径和边长、边心距、中央角之间的关系,会应用正多边形和圆的有关知识画正多边形：3 .会进行正多边形的有关计算.【要点梳理】要点一、正多边形的概念各边相等,各角也相等的多边形是正多边形.要点进阶：判断一个多边形是否是正多边形,必须满足两个条件：(1)各边相等：(2)各角相等；缺一不可.如菱形的各边都相等,矩形的各角都相等,但它们都不是正多边形(正方形是正多边形).要点二、正多边形的重要元素1 .正多边形的外接圆和圆的内接正多边形正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.2 .正多边形的有关概念(1) 一个正多边形的外接圆的圆心叫做这个正多边形的中央.(2)正多边形外接圆的半径叫做正多边形的半径.(3)正多边形每一边所对的圆心角叫做正多边形的中央角.(4)正多边形的中央到正多边形的一边的距离叫做正多边形的边心距.3 .正多边形的有关计算f«-2Y1800(1)正n边形每一个内角的度数是i——L------------------- ；360°(2)正n边形每个中央角的度数是—:n360°(3)正n边形每个外角的度数是—.n要点进阶：要熟悉正多边形的根本概念和根本图形,将待解决的问题转化为直角三角形.要点三、正多边形的性质1 .正多边形都只有一个外接圆,圆有无数个内接正多边形.2 .正n边形的半径和边心距把正n边形分成2 n个全等的直角三角形.3 .正多边形都是轴对称图形,对称轴的条数与它的边数相同,每条对称轴都通过正n边形的中央：当边数是偶数时,它也是中央对称图形,它的中央就是对称中央.4,边数相同的正多边形相似.它们周长的比,边心距的比,半径的比都等于相似比,面积的比等于相似比的平方.5.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆要点进阶：〔1〕各边相等的圆的内接多边形是圆的内接正多边形：〔2〕各角相等的圆的外切多边形是圆的外切正多边形.要点四.正多边形的画法1 .用量角器等分圆由于在同圆中相等的圆心角所对的弧也相等,因此作相等的圆心角〔即等分顶点在圆心的周角〕可以等分圆：根据同圆中相等弧所对的弦相等,依次连接各分点就可画出相应的正n边形.2 .用尺规等分圆对于一些特殊的正n边形,可以用圆规和直尺作图.①正四、八边形.在.0中,用尺规作两条互相垂直的直径就可把圆分成4等份,从而作出正四边形.再逐次平分各边所对的弧〔即作NAOB 的平分线交出于E〕就可作出正八边形、正十六边形等,边数逐次倍增的正多边形.②正六、三、十二边形的作法.通过简单计算可知,正六边形的边长与其半径相等,所以,在.0中,任画一条直径AB,分别以A、B为圆心,以.0的半径为半径画弧与..相交于C、D和E、F,那么A、C、E、B、F、D是..的6等分点.显然,A、E、F〔或C、B、D〕是..的3等分点.要点进阶：面正n边形的方法：〔1〕将一个圆n等份,〔2〕顺次连结各等分点.【典型例题】类型一、正多边形的概念例1.如下图,正五边形的对角线AC和BE相交于点M.〔1〕求证：AC/7ED：〔2〕求证：ME=AE.例2.如图,正方形ABCD内接于OO, E为DC的中点,直线BE交.0于点F,假设OO的半径为小云那么BF的长为.举一反三：【变式】同一个圆的内接正六边形和外切正六边形的周长的比等于〔〕A. 3： 4B. <3： 2C. 2： <3 D・ 1： 2类型二、正多边形和圆的有关计算例3.如图,AG是正八边形ABCDEFGH的一条对角线.〔1〕在剩余的顶点B、C、D、E、F、H中,连接两个顶点,使连接的线段与AG平行,并说明理由：〔2〕两边延长AB、CD、EF、GH,使延长线分别交于点P、Q、M、N,假设AB=2,求四边形PQMN的例4. 如图〔1〕所示,圆内接aABC中,AB=BC=CA, OD、0E为..的半径,OD_LBC于点F, OE±AC于点G,求证：阴影局部四边形OFCG的面积是^畋的面积的3图⑴举一反三：【变式】如下列图,假设NDOE保持120°角度不变,求证：当ND0E绕着0点旋转时,由两条半径和AABC 的两条边围成的图形,图中阴影局部的面积始终是AABC的面积的,.3【稳固练习】一、选择题1 .等边三角形的内切圆半径,外接圆半径和高的比是〔〕A. 1 ： 2：B. 2： 3： 4C. 1 ： 2D. 1： 2： 32 .将边长为3cm的正三角形各边三等分,以这六个分点为顶点构成一个正六边形,那么这个正六边形的面积为〔〕A 30 2 D 3有二「3小：n , 二A. -------- c mB. ----------------- cmC. --------- c mD. 3,3cin2 4 83 .如图,4PQR是.0的内接正三角形,四边形ABCD是.0的内接正方形,BC〃QR,那么NA0Q=〔〕4 .周长是12的正三角形、正方形、正六边形的面积分别是S,、Si、S6,那么它们的大小关系是〔〕.A. S6>S：>S3B. S5>S I>S GC. S6>S3>S ID.5 .如下图,八边形ABCDEFGH是正八边形,其外接..的半径为点,那么正八边形的面积5为〔〕.A. —B. 4及C. 8D.426 .先作半径为杂的圆的内接正方形,接着作上述内接正方形的内切圆,再作上述内切圆的内接正方形,…,那么按以上规律作出的第7个圆的内接正方形的边长为〔〕A.〔劣°13.〔挈C. 〔6〕6 口.〔6〕7二、填空题7 . 一个正方形与圆有相等的周长,那么圆面积与正方形的面积比为.8 .如下图,正六边形内接于圆0,圆0的半径为10,那么图中阴影局部的面积为.9 .半径相等的圆内接正三角形、正方形、正六边形的边长之比为.10 .如图,在边长为2的正六边形ABCDEF中,点P是其对角线BE上一动点,连接PC、PD,那么△ PCD 的周长的最小值是.11 .如下图,有一个圆.和两个正六边形Ti、L. L的6个顶点都在圆周上,工的6条边都和圆0相切〔我们称兀,T：分别为圆0的内接正六边形和外切正六边形〕.〔1〕设L,O的边长分别为a, b,圆.的半径为r,那么r：a二〔2〕正六边形T,, T二的面r：b=积比SjS二的值是.12 .如下图,正方形ABCD中,边长AB=3,.0与.O'外切且与正方形两边相切,两圆半径为R、r,贝lj R+r=.三、解做题13 .如图,正六边形ABCDEF的边长为2必m,点P为六边形内任一点.那么点P到各边距离之和为多少cm?14 .如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是..的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度中O0上逆时针运动.〔1〕求图①中NAPB的度数：〔2〕图②中,NAPB的度数是,图③中NAPB的度数是:〔3〕根据前而探索,你能否将此题推广到一般的正n边形情况？假设能,写出推广问题和结论：假设不能,请说明理由.15 .如图,正三角形、正方形、正六边形等正n边形与圆的形状有差异,我们将正n边形与圆的接近程度称为“接近度〞.在研究“接近度〞时,应保证相似图形的“接近度〞相等.〔1〕设正n边形的每个内角的度数为m°,将正n边形的“接近度〞定义为1180-m .于是,18〔Hn 越小,该正n边形就越接近于圆,①假设"20,那么该正n边形的“接近度〞等于:②当“接近度〞等于时,正n边形就成了圆.〔2〕设一个正n边形的半径〔即正n边形外接圆的半径〕为R,边心距〔即正n边形的中央到各边的距离〕为r,将正n边形的“接近度〞定义为|R-r|,于是|R-r越小,正n边形就越接近于圆. 你认为这种说法是否合理？假设不合理,请给出正n边形“接近度〞的一个合理定义.。

2.6正多边形与圆【推本溯源】1.之间所学到的正多边形是？那什么叫正多边形？正三角形（等边三角形），正方形正多边形：各边相等、各角都相等的多边形叫做正多边形2.认识圆内接正多边形用量角器把一个圆分成n 等分，依次连接各等分点所得的n 边形是这个圆的内接正n 边形，这个圆是这个正n 边形的外接圆。

正多边形的外接圆的圆心叫做正多边形的中心，外接圆的半径叫做正多边形的半径.3.与正多边形的有关概念4.正多边形的计算名称公式内角正n 变形的每个内角都为n 1802n ︒∙-）（中心角正n 边形的每个中心角都为n 360︒外角正n 边形的每个外角都为n360︒边心距正n 边形的边心距222a r ）（-=R 周长正n 边形的周长C=na 面积正n边形的面积r 21C S =5.正多边形的对称性正多边形都是轴对称图形，一个正n 边形共有n 天对称轴，每条对称轴都经过正n 边形的中心.一个正多边形，如果有偶数条边，那么它又是中心对称图形，对称中心就是这个正多边形的中心。

6.正多边形的画法（1）量角器画法在半径为R 的圆中，先用量角器画一个度数为n 360︒的圆心角，这个角所对的弧就是圆周的n1，然后在圆上依次截取这条弧的等弧，就得到圆的n 等分点，顺次连接各等分点即可作出半径为R 的正n 边形。

（2）尺规作图画法①作正方形作法：1.在圆O 中作两条互相垂直的直径AC 、BD.2.依次连接A 、B 、C 、D 四个点，四边形ABCD 即可画出。

②作正六边形作法：1.在圆O 中画出任意一条直径AD ；2.分别以点A 、D 为圆心，圆O 的半径为半径作弧，与圆O点B 、F 和点C 、E ；3.依次连接A 、B 、C 、D 、E 、F 六个点，即可画出正六边形。

【解惑】：如图，A ．23B 【答案】C 【分析】如图所示，由正六边形形，由O 的周长是12π∵正六边形ABCDEF 内接于360==606COD ︒∴∠︒，OCD ∴△是等边三角形，∵O 的周长是12π，在Rt AOG △中，OA ∴122AG OA ==，∴22OG OA AG =-故选：C ．A．3【答案】C【答案】48︒/48度【分析】连接OD ，根据正六边形的性质得出根据正五边形的内角和求出【详解】解：连接OD ,∵点O 是正六边形ABCDEF ∴360,6OD OE DOE =∠=∴DOE 是等边三角形，∴60OED ∠=︒，∵()1521805OEG ∠=⨯-⨯⎡⎣∴1086048DEG ∠=︒-︒=︒，故答案为：48︒．【点睛】此题考查了正多边形的性质，多边形的内角和公式，正确掌握正多边形的性质是解题的关键．例5：如图，正五边形ABCDE 的两条对角线AC BE ，相交于点F ．(1)求FAE ∠的度数；(2)求证：四边形CDEF 为菱形．【点睛】本题考查了正多边形的性质及菱形的判定，利用正五边形的性质得出内角度数是解题关键．【摩拳擦掌】A．4S B．3S【答案】C【分析】如图所示可将正六边形分为6个全等的三角形，拼成的四边形由两个三角形组成，将正六边形可分为6个全等的三角形，∵拼成的四边形的面积为∴每一个三角形的面积为∵剩余部分可分割为4∴剩余部分的面积为4⨯故选C．【点睛】本题考查的是正多边形与圆的含义，本题的关键．2．（2023·安徽·统考中考真题）如图，正五边形A ．60︒B 【答案】D 【分析】先计算正五边形的内角，再计算正五边形的中心角，作差即可．【详解】∵180BAE ∠=︒【答案】126【分析】由正五角星得，ACB BAC ∠=∠360725AOC ︒∠==︒,利用四边形内角和为由正五角星得，∠∴180B BAC ∠=︒-∠360︒【答案】60（答案不唯一）【分析】先求出正六边形的中心角，再根据旋转变换的性质解答即可．【详解】解：360案则这个图案绕着它的中心旋转故答案为：60（答案不唯一）【点睛】本题考查了旋转对称图形、正多边形的性质，掌握正六边形的中心角是关键．8．（2023·湖南·统考中考真题）如图，用若干个全等的正五边形排成圆环状，图中所示的是其中3个正五边形的位置．要完成这一圆环排列，共需要正五边形的个数是【答案】10【分析】先求出正五边形的外角为解．【详解】解：根据题意可得：∵正五边形的一个外角3605︒=∴1272∠=∠=︒，【点睛】本题主要考查了圆的基本性质，角的求法．9．（2022秋·云南昆明·九年级校考期中）如图，点30ADC∠=︒．(1)求BOC ∠的度数；(2)求ACB ∠的度数；【答案】(1)60︒(2)120︒【分析】（1）根据垂径定理得出 AC BC=，再利用圆周角定理得出BOC ∠的度数:（2）连接BD ，根据圆内接四边形的性质便可求得结果．【详解】（1）∵点A 、B 、C 、D 都在O 上，∴ AC BC=，∵30ADC ∠=︒，∴260AOC BOC ADC ∠=∠=∠=︒，∴BOC ∠的度数为60︒（2）连接BD ，∵ AC BC=，∴30ADC BDC ∠=∠=︒，∴60ADB ∠=︒，∵180ACB ADB ∠+∠=︒，∴120ACB ∠=︒【点睛】此题主要考查了圆内接四边形的性质，垂径定理和圆周角定理等知识，熟练掌握和运用这些定理是解决问题的关键．10．（2023春·陕西西安·九年级统考阶段练习）如图，已知O ，请用尺规作图法，求作O 的一个内接正方形（保留作图痕迹，不写作法）．【答案】见解析的【分析】先作直径AC，再作AC的垂直平分线交O于点B，D，则四边形ABCD为O内接正方形．【详解】解：如图，正方形ABCD即为所求．【点睛】本题考查了作图-应用与设计作图：首先要理解题意，弄清问题中对所作图形的要求，结合对应几何图形的性质和基本作图的方法作出图，同时此题也考查了正多边形和圆．11．（2023春·浙江·八年级专题练习）如图，若一个正方形和一个正六边形有一边重合．(1)用无刻度的直尺画出这个图形的对称轴；∠的度数．(2)求BAC【答案】(1)作图见解析(2)150︒【分析】（1）连接AE，BD交于点M，连接DF，AG交于点N，过点M，N作直线MN 即可；（2）根据多边形的内角和可得DAB ∠和DAC ∠的度数，再根据周角是360︒即可求解．【详解】（1）解：如图，连接AE ，BD 交于点M ，连接DF ，AG 交于点N ，∵正方形、正六边形都是轴对称图形，∴对称轴经过点M 和点N ，∴直线MN 是这个图形的对称轴．则直线MN 即为所作．（2）∵正方形的内角和为：()42180=360⨯︒︒-，∴正方形的每一个内角的度数为：360490︒÷=︒，∴90DAB ∠=︒，∵正六边形的内角和为：()62180=720⨯︒︒-∴正六边形一个内角的度数为：7206=120︒÷︒，∴120DAC ∠=︒，∴=360=36090120150BAC DAB DAC ∠︒∠-∠︒-︒-︒=︒-．∴BAC ∠的度数为150︒．【点睛】本题考查作图，正多边形的内角和：()2180n -⨯︒（3n ≥且n 为正整数），角的和差．解题的关键是应用正多边形的性质：正多边形每一个内角都相等，都是轴对称图形，对称轴经过正多边形的中心．12．（2022秋·九年级单元测试）如图，已知O ．(1)求作O 的内接正方形（要求尺规作图，保留作图痕迹，不写作法）；(2)若O 的半径为4，求它的内接正方形的边长．（2）因为O 的半径为所以AC BD ⊥，OA OB =所以224AB OA OB =+=故O 的内接正方形的边长为【点睛】此题主要考查了复杂作图、正多边形和圆、勾股定理；正确掌握正方形的性质是解【知不足】1．（2023·四川南充·四川省南充高级中学校考二模）下列图形中，旋转120︒后能与原图形重合的是（）A ．等边三角形B ．正方形C ．正五边形D ．正八边形【答案】A【分析】确定每个图形的中心角，然后根据旋转的性质确定即可．【详解】解：如图︒÷=︒，∵等边三角形的中心角为3603120∴旋转120︒后即可与原图形重合；∵正方形的中心角为360490︒÷=︒，︒÷=︒，正五边形的中心角为360572︒÷=︒，正八边形的中心角为360845∴正方形、正五边形、正八边形旋转120︒后不能与原图形重合．故选：A．【点睛】本题考查旋转的性质，确定图形的中心角，理解旋转的性质是解题关键．2．（2023·河北沧州·模拟预测）如图，将一个正n边形绕其中心O旋转45︒或60︒都能和其本身重合，则n的最小值是（）A．6B．8C．12D．24【答案】D【分析】根据题意得出正n边形的中心角最大为15︒，然后由圆周角除以中心角即可得出结果．【详解】解：正n边形绕其中心O旋转45︒或60︒都能和其本身重合，∵45︒和60︒最大公约数为15︒，∴正n边形的中心角最大为15︒，︒÷︒=，∴3601524故选D．【点睛】本题考查了旋转对称图形，解答此题的关键是要明确绕其中心O旋转45︒或60︒都能和其本身重合得出正n边形的中心角最大为15︒．，点F在弧AE上．若3．（2023·江苏·九年级假期作业）如图，正五边形ABCDE内接于O∠=︒，则FCDCDF95∠的大小为（）A ．38︒【答案】C 【分析】连接OE ，OD 95CDF ∠=︒，可得∠∵五边形ABCDE 是正五边形，∴()52180CDE ∠=-⨯∵95CDF ∠=︒，∴FDE CDE ∠=∠-∠【答案】90︒/90度【分析】根据AB是O定理得出12P AOB ∠=∠出OCP AOB OAC ∠=∠+∠【答案】36【分析】如图所示，连接周角定理可得APB∠【详解】解：如图所示，连接【点睛】本题主要考查了正多边形与圆，圆周角定理，熟知同圆或等圆中，同弧所对的圆周角度数是圆心角的一半是解题的关键．6（2023·上海·统考中考真题）如果一个正多边形的中心角是为________．【答案】120【分析】根据正多边形内角和公式可求出∠的度数．从而可求出COF(1)在方格纸中画出以AC为对角线的正方形小正方形的顶点上；∠为顶角的等腰三角形(2)在方格纸中画出以GFE格点上，连接AG，并直接写出线段【答案】(1)见详解；（2）解：以GFE ∠为顶角的等腰三角形225334AG =+=．【点睛】本题考查作图−应用与设计、勾股定理、等腰直角三角形的性质等知识，解题的关键是理解题意，学会利用数形结合的思想思考问题，属于中考常考题型．9．（2022秋·九年级单元测试）如图，求边长为【答案】22a 【分析】连接OA ，OB ，根据正方形的性质得到22OA OB a ==即可．【详解】解：如图，连接OA ，OB ∵四边形ABCD 是正方形，∴OA OB ⊥，OA OB =，∵正方形ABCD 边长为a ，∴2222OA OB AB a +==，∴222a OA OB a ===，2【点睛】本题考查了正多边形和圆，勾股定理，正方形的性质，解题的关键是掌握正方形的性质．10．（2023·江苏·九年级假期作业）如图，∠=︒，延长AB30BAC的切线；(1)求证：CD是O(2)以BC为边的圆内接正多边形的周长等于【答案】(1)见解析，=OA OC∴∠=∠=︒，30OAC OCA，AC CD=60BOC ∠=︒ ，∴以BC 为边的圆内接正多边形是圆内接正六边形，132BC AB ∴==，【一览众山小】1．（2023·河北保定·统考二模）如图，一个正多边形纸片被一块矩形挡板遮住一部分，则这个正多边形纸片的边数是（）A．4B．【答案】C【分析】先根据正多边形的定义把图形补充完整，再求解．【详解】解：根据正多边形的定义把多边形补充完整如下图；有图形得：这个正多边形纸片是六边形，故选：C．【点睛】本题考查了正多边形和圆，掌握正多边形的定义是解题的关键．2．（2023·河北承德·统考二模）如图，在边长为∥，则得到的正方形边长最大为GHIJ，若GH ABA．6B．【答案】D【分析】当正方形顶点落在正六边形边上时，正方形面积最大，由此画出图形求解即可．【详解】解析：当正方形顶点落在正六边形边上时，正方形面积最大．此时，OF 垂直平分GJ ，正方形的中心也是∴60GFO ∠=︒，GOF ∠设FM x =，则MO MG =∴32x x +=，解得x =∴33MG =-，∴正方形的边长为：2MG 故选D ．【点睛】本题考查正方形的性质，等边三角形的判定与性质，含关系，正六边形的性质等知识，根据题意画出符合条件的正方形是解题的关键．3．（2023·浙江台州·统考中考真题）如图，半径和正方形的边长都为A ．2【答案】D 【分析】设正方形四个顶点分别为可得，EA 的长度为圆上任意一点到正方形边上任意一点距离的最小值，求解即可．则EA的长度为圆上任意一点到正方形边上任意一点距离的最小值，由题意可得：OE AB=由勾股定理可得：OAA．3,32⎛⎫--⎪⎝⎭B．32⎛⎝【答案】D【分析】如图，连接BD，OD于点G，过点D¢作DH y⊥轴于点≌DGO在正六边形ABCDEF 中，AF 60,30,FAO AFO ∴∠=︒∠=︒11,3,22OA AF BD BD ∴===33,(,3)22OB OA AB D =+=，将正六边形ABCDEF 绕坐标原点360458÷= ，即8次旋转一周，【答案】63由题意可得：360AOB ∠=∵2OA OB ==∴OAB 为等边三角形，∴2AB =【答案】2【分析】连接,,OA OC OE ()ASA BAC OAC ≌ ，得到【详解】如图所示，连接∵六边形ABCDEF 是 ∴AC AE CE ==，∴ACE △是O 的内接正三角形，∵120B ∠=︒，AB BC =∴(11802BAC BCA ∠=∠=【答案】①②③④【分析】连接OA，OB，AOB BOC COD∠=∠=∠角形，利用其性质即可判断结论．∵正八边形ABCDEFGH∴1===，故④OA OB OCAOB BOC COD∠=∠=∠为等腰直角三角形，同理，∴AOC【答案】33【分析】根据正六边形的性质求出正六边形的倍即可．．【详解】解：设正六边形ABCDEF为T，∵正六边形ABCDEF，(1)[定义]我们将正n边形的周长L与正多边形对应的内切圆的周长边形的“正圆度”n k．如图，正三角形ABC的边长为1，求得其内切圆的半径为k=___________；k≈（3）解：3 1.65之的研究，精进π多时，其周长L也与对应的内切圆周长更接近，其比值更接近于(1)在图①中画一个O 的内接正方形ABCD ．(2)在图②中画一个O 的内接四边形ABCD ，使该四边形只是轴对称图形，且点边形内部．(3)在图③中画一个四边形ABCD ，使该四边形对角互补，其中一个内角为该四边形的一条边上．（2）解：如图所示，四边形∵2213AB CD ==+∴四边形ABCD 是等腰梯形，∴四边形ABCD 是轴对称图形；（3）解：如图所示，四边形ABCD 即为所求；由正方形的性质可知45135ABC ADC =︒=︒∠，∠，∴四边形ABCD 对角互补，且BC 经过点O ．【点睛】本题主要考查了正方形的性质与判定，轴对称图形的定义，勾股定理和勾股定理得逆定理，正多边形与圆，数量掌握相关知识是解题的关键．11．（2023·上海静安·统考二模）如图，在矩形ABCD 中，点P 是边BC 的中点，O 是PAD 的外接圆，O 交边AB 于点E ．(1)求证：PA PD =；(2)当AE 是以点O 为中心的正六边形的一边时，求证： AE EP=．【答案】(1)证明见解析；(2)证明见解析．【分析】（1）根据矩形的性质及线段中点的定义得到三角形全等的条件，则ABP DCP ≅ ，根据“全等三角形的对应边相等”得到PA PD =；（2）连接,OA OE OD OP ，，，并延长PO 交AD 于点M ，先证明OP AB ∥，再根据“有一个角是60 的等腰三角形是等边三角形”得到AOE △为等边三角形，然后根据“两直线平行，内错角相等”得到60EOP AEO ∠∠== ，则60AOE EOP ∠∠== ，最后根据“在同圆中，相等的圆心角所对的弧相等”得到 AE EP=．【详解】（1）四边形ABCD 是矩形，且点P 是边BC 的中点，AB DC B C BP CP ∠∠∴===，，，在ABP 和DCP 中，BP CP B C AB DC =⎧⎪∠=∠⎨⎪=⎩，∴()ABP DCP SAS ≅ ，PA PD ∴=；（2）证明：如图，连接,OA OE OD OP ，，，并延长PO 交AD 于点M ，四边形ABCD 是矩形，∴90BAD ∠=︒∵OA OD =，PA PD =，∴点P 、O 都在线段AD 的垂直平分线上，∴PO 垂直平分AD ，∴90DMP BAD ∠∠=︒=，OP AB ∴∥，AE 是以点O 为中心的正六边形的一边，∴由正六边形性质可得∶60 ∠AOE=，∵OA OE =，AOE ∴ 是等边三角形，60AEO ∠∴=又OP AB∥60EOP AEO ∠∠∴== ，60AOE EOP ∠∠∴== ，AE EP∴=．【点睛】本题主要考查了全等三角形的判定及性质，矩形的性质，等边三角形的判定及性质，线段垂直平分线的判定以及正多边形的性质，熟练掌握线段垂直平分线的判定及性质以及等边三角形的判定及性质是解题的关键．12．（2023·山西·校联考二模）如图，正方形ABCD 内接于O ，连接AC ，点F 是 CD的中点，过点D 作O 的切线与AF 的延长线相交于点G ．(1)试判断AC 与DG 的位置关系，并说明理由．(2)求G ∠的度数．【答案】(1)∥AC DG ,理由见解析(2)22.5G ∠=︒【分析】（1）连接OD ，可得90AOD ∠=︒，根据切线的定义可得90ODG ∠=︒，即可得出结论∥AC DG ．（2）根据正方形的性质可得，90ADC ∠=︒，DA DC =，则45CAD ∠=︒．根据点F 是 CD的中点，可得22.5CAF FAD ∠=∠=︒．最后根据平行线的性质可得22.5G CAF ∠=∠=︒．【详解】（1）解：∥AC DG ．理由：如图，连接OD ，。

正五边形尺规作图的画法及其他正五边形的画法圆内接正五边形的画法如下:1、作一个圆，设它的圆心为O；2、作圆的两条互相垂直的直径AZ和XY；3、作OY的中点M；4、以点M为圆心，MA为半径作圆，交OX于点N；5、以点A为圆心，AN为半径，在圆上连续截取等弧，使弦AB=BC=CD=DE=AN，则五边形ABCDE即为正五边形。

以上两种图形的作法运用了所求图形边长与已知的线段长度的关系，用构造直角三角形的方法作出与所求图形的边长相等的线段，从而作出整个图形，这是尺规作图中常用的一种方法——等线段法，即用已知图形的线段作出与所求图形边长相等的线段。

正多边形的尺规作图是大家感兴趣的．正三边形很好做；正四边形稍难一点；正六边形也很好做；正五边形就更难一点，但人们也找到了正五边形的直规作图方法．确实，有的困难一些，有的容易一些．正七边形的尺规作图是容易一些，还是困难一些呢？人们很久很久未找到作正七边形的办法，这一事实本身就说明作正七边形不容易；一直未找到这种作法，也使人怀疑：究竟用尺规能否作出正七边形来？数学不容许有这样的判断：至今一直没有人找到正七边形的尺规作图方法来，所以断言它是不能用尺规作出的．人们迅速地解决了正三、四、五、六边形的尺规作图问题，却在正七边形面前止步了：究竟能作不能作，得不出结论来．这个悬案一直悬而未决两千余年．17世纪的费马，就是我们在前面已两次提到了的那个法国业余数学家，他研究了形如Fi （i为右下角标）＝22i（底数2指数2的i次幂）＋1 的数．费马的一个著名猜想是，当n≥3时，不定方程xn＋yn＝zn没有正整数解．现在他又猜测Fi都是素数，对于i＝0，1，2，3，4时，容易算出来相应的Fi：F0＝3，F1＝5，F2＝17，F3=257，F4=65 537验证一下，这五个数的确是素数．F5=225+1是否素数呢？仅这么一个问题就差不多一百年之后才有了一个结论，伟大的欧拉发现它竟不是素数，因而，伟大的费马这回可是猜错了！F5是两素数之积：F5＝641×6 700 417．当然，这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事，不然，何以需要等近百年？何以需要欧拉这样的人来解决问题？更奇怪的是，不仅F5不是素数，F6，F7也不是素数，F8，F9，F10，F11等还不是素数，甚至，对于F14也能判断它不是素数，但是它的任何真因数还不知道．至今，人们还只知F0，F1，F2，F3，F4这样5个数是素数．由于除此而外还未发现其他素数，于是人们产生了一个与费马的猜想大相径庭的猜想，形如22i＋1的素数只有有限个．但对此也未能加以证明．当然，形如Fi=22i+1的素数被称为费马素数．由于素数分解的艰难，不仅对形如Fi=22i+1的数的一般结论很难做出，而且具体分解某个Fi也不是一件简单的事．更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年，一位德国数学家高斯，在他仅20岁左右之时发现，当正多边形的边数是费马素数时是可以尺规作图的，他发现了更一般的结论：正n边形可尺规作图的充分且必要的条件是n=2k（2的k次幂）或2k×p1×p2×…×ps，（1，2…s为右下角标）其中，p1，p2，…，ps是费马素数．正7边形可否尺规作图呢？否！因为7是素数，但不是费马素数．倒是正17边形可尺规作图，高斯最初的一项成就就是作出了正17边形．根据高斯的理论，还有一位德国格丁根大学教授作了正257边形．就这样，一个悬而未决两千余年的古老几何问题得到了圆满的解决，而这一问题解决的过程是如此的蹊跷，它竟与一个没有猜对的猜想相关连．正17边形被用最简单的圆规和直尺作出来了，而正多边形可以换个角度被视为是对圆的等分，那么这也相当于仅用圆规和直尺对圆作了17等分，其图形更觉完美、好看．高斯本人对此也颇为欣赏，由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过)，而且在他逝后的墓碑上就镌刻着一个正17边形图案．高斯把问题是解决得如此彻底，以致有了高斯的定理，我们对于早已知道如何具体作图的正三边形、正五边形，还进而知道了它们为什么能用尺规作图，就因为3和5都是费马素数(3=F0，5＝F1)；对于很久以来未找到办法来作出的正七边形，乃至于正11边形、正 13边形，现在我们能有把握地说，它们不可能由尺规作图，因为7、11、13都不是费马素数；对于正257边形、正65 537边形，即使我们不知道具体如何作，可是理论上我们已经知道它们是可尺规作图的；此外，为什么正四边形、正六边形可尺规作图呢？因为4＝22，因为6= 2· 3而 3=F0．文案编辑词条B 添加义项?文案，原指放书的桌子，后来指在桌子上写字的人。

圆内接正五边形的画法
1、圆内接正五边形五条边长度相等。

（即圆的五条弦长度相等）。

2、圆内接正五边形的五个内角相等，都是108°。

3、圆内接正五边形的五条边在圆内所对的五条优弧长度相等。

4、圆内接正五边形的五条边在圆内所对的五条优弧的弧度数相等。

扩展资料：
圆外切正多边形判定方法
正多边形的判定,正多边形的定义当然是正多边形的判定方法之一，但如同全等三角形的判定一样,用定义来证明两个三角形全等显然不可取,因此需用判定定理来证。

判定定理:把圆几等分(n>2)
①依次连结各分点所得的多边形是这个圆的内接正n边形。

②经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形，也就是说,若要证明一个多边形是圆内接正多边形，只要证明这个多边形的顶点是圆的等分点即可。

如：要证明一个圆内接n边形ABCDEF……是圆内接正n边形，就要证A、B、C、D、E、F……各点是圆的n等分点，就是要证
AB=BC=CD=DE=EF=…….同样，要证明一个圆外切边形是圆外切正n边形，只要证明各切点是圆的等分点即可。

、[正五边形的画法]圆内接正五边形的画法如下:1、任作一圆O2、任作圆O中互相垂直的两直径AB、CD3、作OD的垂直平分线交OD于E4、以E为圆心，EA长为半径作弧，交CD于F5、在圆O上顺序作弦AG=GH=HM=MN=NA=AF则得正五边形AGHMN已知边长作正五边形的近似画法如下:①作线段AB等于定长l,并分别以A,B为圆心,已知长l为半径画弧与AB的中垂线交于K.②以K为圆心，取AB的2/3长度为半径向外侧取C点，使CK=2/3AB③以C为圆心,已知边长AB为半径画弧,分别与前两弧相交于M,N.④顺次连接A,B,N,C,M各点即近似作得所要求的正五边形.正多边形的尺规作图是大家感兴趣的.正三边形很好做;正四边形稍难一点;正六边形也很好做;正五边形就更难一点，但人们也找到了正五边形的直规作图方法.确实，有的困难一些，有的容易一些.正七边形的尺规作图是容易一些，还是困难一些呢?人们很久很久未找到作正七边形的办法，这一事实本身就说明作正七边形不容易;一直未找到这种作法，也使人怀疑：究竟用尺规能否作出正七边形来?数学不容许有这样的判断：至今一直没有人找到正七边形的尺规作图方法来，所以断言它是不能用尺规作出的.人们迅速地解决了正三、四、五、六边形的尺规作图问题，却在正七边形面前止步了：究竟能作不能作，得不出结论来.这个悬案一直悬而未决两千余年.17世纪的费马，就是我们在前面已两次提到了的那个法国业余数学家，他研究了形如Fi (i为右下角标)=22i(底数2指数2的i次幂)+1 的数.费马的一个著名猜想是，当n≥3时，不定方程xn+yn=zn没有正整数解.现在他又猜测Fi都是素数，对于i=0，1，2，3，4时，容易算出来相应的Fi：F0=3，F1=5，F2=17，F3=257，F4=65 537验证一下，这五个数的确是素数.F5=225+1是否素数呢?仅这么一个问题就差不多一百年之后才有了一个结论，伟大的欧拉发现它竟不是素数，因而，伟大的费马这回可是猜错了!F5是两素数之积：F5=641×6 700 417.当然，这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事，不然，何以需要等近百年?何以需要欧拉这样的人来解决问题?更奇怪的是，不仅F5不是素数，F6，F7也不是素数，F8，F9，F10，F11等还不是素数，甚至，对于F14也能判断它不是素数，但是它的任何真因数还不知道.至今，人们还只知F0，F1，F2，F3，F4这样5个数是素数.由于除此而外还未发现其他素数，于是人们产生了一个与费马的猜想大相径庭的猜想，形如22i+1的素数只有有限个.但对此也未能加以证明.当然，形如Fi=22i+1的素数被称为费马素数.由于素数分解的艰难，不仅对形如Fi=22i+1的数的一般结论很难做出，而且具体分解某个Fi也不是一件简单的事.更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年，一位德国数学家高斯，在他仅20岁左右之时发现，当正多边形的边数是费马素数时是可以尺规作图的，他发现了更一般的结论：正n边形可尺规作图的充分且必要的条件是n=2k(2的k次幂)或2k×p1×p2×…×ps，(1，2…s为右下角标)其中，p1，p2，…，ps是费马素数.正7边形可否尺规作图呢?否!因为7是素数，但不是费马素数.倒是正17边形可尺规作图，高斯最初的一项成就就是作出了正17边形.根据高斯的理论，还有一位德国格丁根大学教授作了正257边形.就这样，一个悬而未决两千余年的古老几何问题得到了圆满的解决，而这一问题解决的过程是如此的蹊跷，它竟与一个没有猜对的猜想相关连.正17边形被用最简单的圆规和直尺作出来了，而正多边形可以换个角度被视为是对圆的等分，那么这也相当于仅用圆规和直尺对圆作了17等分，其图形更觉完美、好看.高斯本人对此也颇为欣赏，由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过)，而且在他逝后的墓碑上就镌刻着一个正17边形图案.高斯把问题是解决得如此彻底，以致有了高斯的定理，我们对于早已知道如何具体作图的正三边形、正五边形，还进而知道了它们为什么能用尺规作图，就因为3和5都是费马素数(3=F0，5=F1);对于很久以来未找到办法来作出的正七边形，乃至于正11边形、正13边形，现在我们能有把握地说，它们不可能由尺规作图，因为7、11、13都不是费马素数;对于正257边形、正65 537边形，即使我们不知道具体如何作，可是理论上我们已经知道它们是可尺规作图的;此外，为什么正四边形、正六边形可尺规作图呢?因为4=22，因为6= 2· 3而3=F0.费马数费马数是以数学家费马命名一组自然数，具有形式：其中 n 为非负整数。

正五边形尺规作图的画法及延伸圆内接正五边形的画法如下：（1）作一个圆，设它的圆心为O；（2）作圆的两条互相垂直的直径AZ和XY；（3）作OY的中点M；（4）以点M为圆心，MA为半径作圆，交OX于点N；有MA=MN.（5）以点A为圆心，AN为半径，在圆上连续截取等弧，使AB=BC=CD=DE=AN。

（6）连接AE.则五边形ABCDE即为正五边形。

证明：设圆的半径为R，由上述正五边形的作法可知：()22222AN AO ON AO AM MO=+=+-∴110252-AN R=.由于半径为R的正五边形的边长a=AN，所以五边形ABCDE即为正五边形。

以上作法运用了所求图形边长与已知的线段长度的关系，用构造直角三角形的方法作出与所求图形的边长相等的线段，从而作出整个图形，这是尺规作图中常用的一种方法——等线段法，即用已知图形的线段作出与所求图形边长相等的线段。

正多边形的尺规作图是大家感兴趣的．正三边形很好做；正四边形稍难一点；正六边形也很好做；正五边形就更难一点，但人们也找到了正五边形的尺规作图方法．那正七边形的尺规作图是容易一些，还是困难一些呢？人们很久很久未找到作正七边形的办法，这一事实本身就说明作正七边形不容易；一直未找到这种作法，也使人怀疑：用尺规究竟能否作出正七边形来？数学不容许有这样的判断：即“至今一直没有人找到正七边形的尺规作图方法来，所以断言它是不能用尺规作出的．”人们迅速地解决了正三、四、五、六边形的尺规作图问题，却在正七边形面前止步了：究竟能作不能作，得不出结论来．这个悬案一直悬而未决两千余年．17世纪的费马，就是我们在前面已两次提到了的那个法国业余数学家，他研究了形如221ii F =+的数．费马的一个著名猜想是，当 n≥3时，不定方程xn ＋yn ＝zn 没有正整数解．现在他又猜测Fi 都是素数，对于i ＝0，1，2，3，4时，容易算出来相应的Fi ： F0＝3，F1＝5，F2＝17，F3=257，F4=65 537验证一下，这五个数的确是素数．F5=225+1是否素数呢？仅这么一个问题就差不多一百年之后才有了一个结论，伟大的欧拉发现它竟不是素数，因而，伟大的费马这回可是猜错了！F 5是两素数之积：F 5＝641×6 700 417．当然，这一事例多少也说明：判断一个较大的数是否素数也决不是件简单的事，不然，何以需要等近百年？何以需要欧拉这样的人来解决问题？更奇怪的是，不仅F5不是素数，F6，F7也不是素数，F8，F9，F10，F11等还不是素数，甚至，对于F14也能判断它不是素数，但是它的任何真因数还不知道．至今，人们还只知F0，F1，F2，F3，F4这样5个数是素数．由于除此而外还未发现其他素数，于是人们产生了一个与费马的猜想大相径庭的猜想，形如22i ＋1的素数只有有限个．但对此也未能加以证明．当然，形如Fi=22i+1的素数被称为费马素数．由于素数分解的艰难，不仅对形如Fi=22i+1的数的一般结论很难做出，而且具体分解某个Fi 也不是一件简单的事．更加令人惊奇的事情发生在距欧拉发现F5不是素数之后的60多年，一位德国数学家高斯，在他仅20岁左右之时发现，当正多边形的边数是费马素数时是可以尺规作图的，他发现了更一般的结论：正n 边形可尺规作图的充分且必要的条件是n=2k （2的k 次幂）或 2k×p1×p2×…×ps ，（1，2…s 为右下角标）其中，p1，p2，…，ps 是费马素数．正7边形可否尺规作图呢？否！因为7是素数，但不是费马素数．倒是正17边形可尺规作图，高斯最初的一项成就就是作出了正17边形．根据高斯的理论，还有一位德国格丁根大学教授作了正257边形．就这样，一个悬而未决两千余年的古老几何问题得到了圆满的解决，而这一问题解决的过程是如此的蹊跷，它竟与一个没有猜对的猜想相关连．正17边形被用最简单的圆规和直尺作出来了，而正多边形可以换个角度被视为是对圆的等分，那么这也相当于仅用圆规和直尺对圆作了17等分，其图形更觉完美、好看．高斯本人对此也颇为欣赏，由此引导他走上数学道路(他早期曾在语言学与数学之间犹豫过)，而且在他逝后的墓碑上就镌刻着一个正17边形图案．高斯把问题是解决得如此彻底，以致有了高斯的定理，我们对于早已知道如何具体作图的正三边形、正五边形，还进而知道了它们为什么能用尺规作图，就因为3和5都是费马素数(3=F0，5＝F1)；对于很久以来未找到办法来作出的正七边形，乃至于正11边形、正13边形，现在我们能有把握地说，它们不可能由尺规作图，因为7、11、13都不是费马素数；对于正257边形、正65 537边形，即使我们不知道具体如何作，可是理论上我们已经知道它们是可尺规作图的；此外，为什么正四边形、正六边形可尺规作图呢？因为4＝22，因为6= 2· 3而3=F0．。