下载文档原格式
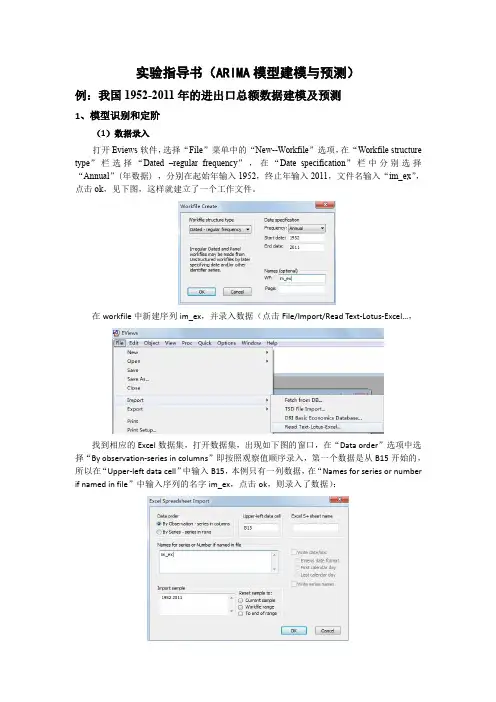
实验指导书（ARIMA模型建模与预测）例：我国1952-2011年的进出口总额数据建模及预测1、模型识别和定阶（1）数据录入打开Eviews软件，选择“File”菜单中的“New--Workfile”选项，在“Workfile structure type”栏选择“Dated–regular frequency”，在“Date specification”栏中分别选择“Annual”(年数据)，分别在起始年输入1952，终止年输入2011，文件名输入“im_ex”，点击ok，见下图，这样就建立了一个工作文件。
在workfile中新建序列im_ex，并录入数据（点击File/Import/Read Text-Lotus-Excel…，找到相应的Excel数据集，打开数据集，出现如下图的窗口，在“Data order”选项中选择“By observation-series in columns”即按照观察值顺序录入，第一个数据是从B15开始的，所以在“Upper-left data cell”中输入B15，本例只有一列数据，在“Names for series or number if named in file”中输入序列的名字im_ex，点击ok，则录入了数据）：（2）时序图判断平稳性双击序列im_ex ，点击view/Graph/line，得到下列对话框：得到如下该序列的时序图，由图形可以看出该序列呈指数上升趋势，直观来看显著非平稳。
40,00080,000120,000160,000200,000240,000556065707580859095000510IM_EX（3）原始数据的对数处理因为数据有指数上升趋势，为了减小波动，对其对数化，在Eviews 命令框中输入相应的命令“series y=log(im_ex)”就得到对数序列，其时序图见下图，对数化后的序列远没有原始序列波动剧烈：45678910111213556065707580859095000510Y从图上仍然直观看出序列不平稳，进一步考察序列y 的自相关图和偏自相关图：从自相关系数可以看出，呈周期衰减到零的速度非常缓慢，所以断定y 序列非平稳。
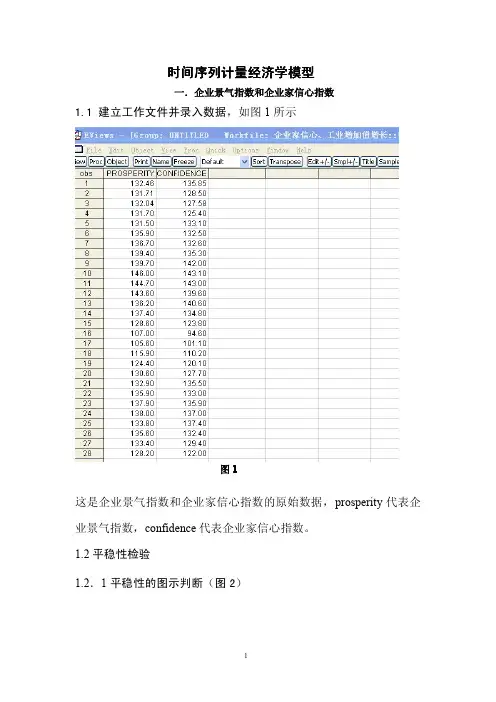
时间序列计量经济学模型一．企业景气指数和企业家信心指数1.1建立工作文件并录入数据，如图1所示图1这是企业景气指数和企业家信心指数的原始数据，prosperity代表企业景气指数，confidence代表企业家信心指数。
1.2平稳性检验1.2．1平稳性的图示判断（图2）图2从图中可以看出企业景气指数和企业家信心指数这两序列都是非平稳的。
1.2.2样本自相关图判断点击主界面Quick\Series Statistics\Correlogram...，在弹出的对话框中输入prosperity，点击OK就会弹出Correlogram Specification对话框，选择Level，并输入要输出的阶数(一般默认为24)，点击OK，即可得到prosperity的样本相关函数图,如图3所示。
图3从上述样本相关函数图，可以看到企业景气指数（prosperity）的样本相关函数是缓慢的递减趋于零的，但随着时间的推移，在0附近波动并呈发散趋势。
所以，通过企业景气指数（prosperity）的样本相关图，可初步判定该企业景气指数（prosperity）时间序列非平稳。
同理得：confidence的样本相关函数图,如图4所示图4从上述样本相关函数图，可以看到企业家信心指数（confidence）的样本相关函数是缓慢的递减趋于零的，但随着时间的推移，在0附近波动并呈发散趋势。
所以，通过企业家信心指数（confidence）的样本相关图，可初步判定该企业家信心指数（confidence）时间序列非平稳。
1.2.3单位跟检验单位跟检验((ADF检验检验))（1）企业景气指数（prosperity）采用ADF检验对prosperity序列进行平稳性的单位根检验。
点击主界面Quick\Series Statistics\Unit Root Test...，在弹出的Series对话框中输入prosperity，点击OK，就会出现UnitRoot Test对话框，如图5所示。
eviews实验指导ARIMA模型建模与预测在数据分析和时间序列预测的领域中，ARIMA 模型是一种非常强大且实用的工具。
通过eviews 软件来实现ARIMA 模型的建模与预测，可以帮助我们更高效地处理和分析数据，做出更准确的预测。
接下来，让我们逐步深入了解如何使用eviews 进行ARIMA 模型的建模与预测。
首先，我们要明白什么是 ARIMA 模型。
ARIMA 全称为自回归移动平均整合模型（Autoregressive Integrated Moving Average Model），它由三个部分组成：自回归（AR）部分、差分（I）部分和移动平均（MA）部分。
自回归（AR）部分是指当前值与过去若干个值之间存在线性关系。
例如，如果说一个时间序列在 AR(2)模型下，那么当前值就与前两个值有关。
移动平均（MA）部分则表示当前值受到过去若干个随机误差项的线性影响。
差分（I）部分用于将非平稳的时间序列转化为平稳序列。
平稳序列在统计特性上，如均值、方差等，不随时间变化而变化。
在 eviews 中进行 ARIMA 模型建模与预测，第一步是数据的导入和预处理。
打开 eviews 软件后，选择“File”菜单中的“Open”选项，找到我们要分析的数据文件。
数据的格式通常可以是 Excel、CSV 等常见格式。
导入数据后，需要对数据进行初步的观察和分析，了解其基本特征，比如均值、方差、趋势等。
接下来，判断数据的平稳性。
这是非常关键的一步，因为 ARIMA 模型要求数据是平稳的。
我们可以通过绘制时间序列图、计算自相关函数（ACF）和偏自相关函数（PACF）来直观地判断数据的平稳性。
如果时间序列图呈现明显的趋势或周期性，或者自相关函数和偏自相关函数衰减缓慢，那么很可能数据是非平稳的。
对于非平稳的数据，我们需要进行差分处理。
在 eviews 中，可以通过“Quick”菜单中的“Generate Series”选项来实现差分操作。
eviews实验指导ARIMA模型建模与预测在当今的数据分析领域，时间序列分析是一项至关重要的技术，而ARIMA 模型则是其中的一种常用且强大的工具。
通过 Eviews 软件来进行 ARIMA 模型的建模与预测，可以帮助我们更好地理解和处理时间序列数据，从而为决策提供有力的支持。
接下来，让我们一起深入了解如何使用 Eviews 进行 ARIMA 模型的建模与预测。
一、ARIMA 模型的基本原理ARIMA 模型，全称为自回归移动平均整合模型（Autoregressive Integrated Moving Average Model），它由三个部分组成：自回归（AR）、差分（I）和移动平均（MA）。
自回归（AR）部分表示当前值与过去若干个值之间的线性关系。
简单来说，如果一个时间序列在当前时刻的值受到过去若干个时刻的值的影响，那么就存在自回归关系。
移动平均（MA）部分则反映了随机干扰项对当前值的影响。
它通过将当前值表示为过去若干个随机干扰项的线性组合，来描述时间序列中的随机波动。
差分（I）操作则用于将非平稳的时间序列转化为平稳序列。
平稳性是时间序列分析中的一个重要概念，指的是时间序列的统计特性（如均值、方差等）不随时间变化而变化。
二、Eviews 软件操作环境介绍在开始建模之前，我们先来熟悉一下 Eviews 软件的操作环境。
打开 Eviews 软件，我们会看到一个简洁明了的界面。
菜单栏提供了各种功能选项，如文件操作、数据处理、模型估计等。
工作区用于显示数据、图表和分析结果。
在进行 ARIMA 模型建模时，我们主要会用到“Quick”菜单中的“Estimate Equation”选项，以及“View”菜单中的各种分析功能。
三、数据准备与导入首先，我们需要准备好要分析的时间序列数据。
数据可以以 Excel表格或其他常见的数据格式保存。
在 Eviews 中，可以通过“File”菜单中的“Import”选项将数据导入到软件中。
eviews实验指导(ARIMA模型建模与预测) eviews实验指导(ARIMA模型建模与预测)ARIMA模型是一种常用的时间序列分析方法，可以用于建模和预测时间序列数据。
在eviews软件中，我们可以利用其强大的功能进行ARIMA模型的建模和预测分析。
一、数据准备与导入在进行ARIMA模型建模之前，首先需要准备好相关的时间序列数据，并导入eviews软件中。
可以通过以下步骤进行操作：1. 创建一个新的工作文件，点击"File" -> "New" -> "Workfile"，选择合适的时间范围和频率。
2. 在eviews软件中，点击"Quick" -> "Read Text"，导入包含时间序列数据的文本文件。
确保文本文件中的数据格式正确，并根据需要设置导入选项。
3. 确认数据已经成功导入，可以通过在工作文件窗口中查看和编辑数据。
二、ARIMA模型建模在eviews中，建立ARIMA模型需要进行以下步骤：1. 点击"Quick" -> "Estimate Equation"，打开方程估计对话框。
2. 在对话框中，选择要建模的时间序列变量，并选择ARIMA模型。
根据数据的特点，可以选择不同的AR、MA和差分阶数。
3. 设置其他参数，如是否包含常数项、是否进行季节性调整等。
根据具体分析需求进行选取。
4. 点击"OK"，进行模型估计。
eviews将自动计算出ARIMA模型的系数估计和相应的统计指标。
5. 检查模型的拟合优度，可以通过观察残差序列的ACF和PACF图、Ljung-Box检验等方法来判断模型是否合适。
三、模型诊断与改进建立ARIMA模型后，需要对模型进行诊断，以确保其满足建模的基本假设。
常见的诊断方法包括：1. 检查模型的残差序列是否为白噪声，可以通过观察残差序列的ACF和PACF图、Ljung-Box检验等方法来判断。
ARIMA Theory （求和自回归移动平均模型理论）求和自回归移动平均模型是简单AR(自回归)模型的推广，它用三种工具来模拟扰动项中的序列相关性。
第一个工具是运用自回归或AR 项。
上面介绍的AR(1)模型仅运用了一阶项，但是，总的来说，可以用更多的、高阶AR 项。
每一个AR 项对应于无条件残差的预测方程中使用的残差滞后值。
一个p 阶自回归模型，AR(p)形式如下：(20.14)t p t p t t t u u u u εϕϕϕ++++=--- (2211)第二个工具是求和项。
求和的阶相当于对预测序列进行差分。
一阶求和表示预测模型对于最初序列进行一次差分。
二阶求和相当于进行二次差分，等等。
第三个工具是运用MA 、移动平均项。
移动平均预测模型用预测误差的滞后值来改善当前预测。
一阶移动平均项运用最近时刻的预测误差，二阶移动平均项运用最近两个时刻的预测误差，等等。
MA(q)的形式如下：(20.15) q t q t t t u -----=εθεθε (11)自回归和移动平均表示可以组合为ARMA(p,q)模型：(20.16) q t q t p t p t t t u u u u --------++++=εθεθεϕϕϕ......1t 12211虽然计量经济学家们常常对回归模型中的残差运用ARIMA 模型，但这一表示可以直接用于一个序列。
后者提供了一种单变量模型，指定序列的条件均值为一个常数，并且用序列与均值的离差作为残差。
ARIMA 模型原理(博克思-詹金斯1976)在ARIMA 模型的预测中，通过对上面描述的三个成分的有机组合构成一个完整的预测模型。
对残差序列建立ARIMA 模型的第一步是看看它的自相关特性。
为此，可以看序列的相关图，正如Correlogram 里大致描述的那样。
ARIMA 建模的这个阶段叫做识别(不要和联立方程中相同的词混淆)。
残差的现值与过去值之间的相关性为选择ARIMA 模型提供指导。
运用Eviews软件进行ARIMA模型的识别、诊断、估计和预测121页word文档Eviews在时间序列建模中的应用一、工作文件的建立、保存和调用（一）工作文件的建立有两种方式创建工作文件，一是菜单方式，另一个是命令方式。
1 菜单方式运行Eviews软件，在打开的主窗口中，进行如下操作：File/new/workfile/在出现的对话框中对workfile structure type 进行选择/Dated-regular frequency/OKWorkfile structure type选项区共有3种类型：Unstructured/Undated（非结构/非日期）、Dated-regular frequency和Balanced Panel（平衡面板）。
其中默认的状态是Dated-regular frequency类型。
（1）Unstructured/Undated此类数据的观测标识代码用整数表示，只需给出总的数据观测值个数，系统将自动从1开始依次为每个样本观测值分配整数型的标识代码。
（2）Dated-regular frequency在默认状态Dated-regular frequency类型下，另一选项区Date specification（日期设定）中有8个选择，分别是Annual（年度的），Semi-annual （半年度的），Quarterly（季度的）、Monthly（月度的）、Weekly（周度的）、Daily-5 day week（一周5个工作日）、Daily-7 day week（一周7工作日）和Integer date（整序数的），其输入格式如下：Annual选项：用四位数表示年份，如2019，2019等。
在start date后输入起始年份，End date后输入终止年份。
在1900和2000年之间的年份可以只输入后2位；semi Annual选项：输入格式同Annual选项，每一年有上半年和下半年两个数据；Quarterly选项：输入格式为年份：季度，如2019：1，或98：1。
