垂径定理第一课时1PPT课件

格式：pptx
大小：5.11 MB
文档页数：18

下载文档原格式

初中数学《垂径定理》公开课课件

C
O
AE
F
B
P
D
A
B
O
自我评价本节课堂自我评价
评价项目及评价结果优
良
合格
不合格
课前预习的主动性以及效果
课堂活动的参与度
独立回答问题以及解决问题的准确性
对整节课所学知识以及数学思想方法的认识与体会
较之上节课的学习表现是
否
是否有了进步
备注：请根据评价项目对自己作出客观的评价,并写在相应的栏目下面。
E
连半径建模思想
F
●
D
O
用勾股方程思想
解这个方程,得R 545.
牛刀小试
1.如图，已知⊙O的半径为30mm,弦AB=36mm,则∠OAB的正弦值是。
0
A
B
辅助线：作垂直，得平分，用勾股
大显身手
2.⊙O的半径为10cm，弦AB∥CD，
AB=16cm，CD=12cm，则AB、CD间的
距离是 2cm或14cm .
.
3.分类讨论思想
1.实际生活中的应用价值
2.自主探索和团队合作精神
当堂检测
必做题
1.如图，⊙O的直径为10，弦AB=8,P为AB上的一个动点，那么
OP长的取值范围是______。
2.已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。求证：AC＝BD。
O
A
PB
O.
AC
DB
当堂检测
动手操作
折一折：把一个圆沿着它的任意一条直径所在的
直线对折，重复几次，你发现了什么？由此你能得到什么结论？
·
可以发现：圆是_轴__对__称_ 图形，任何一条直__径__所__在__的__直__线都是它的对称轴，它有__无__数__条对称轴。

《垂径定理公开课》课件

《垂径定理公开课》PPT 课件
这是一场关于《垂径定理》的公开课，旨在通过清晰的PPT展示，向大家介绍垂径定理的定义、推导过程、应用以及拓展内容，让大家深入了解这一重要的几何概念。
课程介绍
这门课程将为大家详细介绍垂径定理的内容。我们将从基础知识开始，逐步引入更深入的概念和应用。希望通过本课程的学习，大家能够对垂径定理有一个全面的了解。
垂径定理的应用
垂径定理不仅仅是一种几何概念，还具有广泛的应用价值。在多种几何问题中，都可以利用垂径定理来解决具体问题，例如确定直径、垂径的位置，计算相关角度和长度等。
垂径定理的例题分析
通过一些具体的例Βιβλιοθήκη 分析，我们将进一步探究垂径定理的应用。我们将结合实际问题，通过解题的方式，帮助大家更好地理解和掌握垂径定理，并培养灵活运用的能力。
垂径定理的拓展
垂径定理作为一个基础定理，还有许多有趣的拓展内容。这些拓展内容可以进一步丰富和拓宽我们的几何知识，使我们在解决更复杂的几何问题时能够更加游刃有余。
结论和总结
通过这门课程，我们已经全面地学习了垂径定理的相关内容。希望大家通过这次学习，对垂径定理有了更深入的理解，并且能够在实际问题中灵活运用。谢谢大家的参与！
垂径定理的定义
垂径定理是几何学中的一个基本定理，它描述了直径与垂直线的关系。通过垂径定理，我们可以从直径推导出垂直线，以及从垂直线推导出直径，从而建立了直径与垂直线的重要联系。
垂径定理的推导过程
通过推导过程，我们将深入探讨垂径定理的原理和推理。我们将通过几何推导和逻辑推理，引导大家逐步理解垂径定理的推导过程，并梳理其中的关键步骤和思路。

垂径定理ppt课件

沿着直径CD折叠时，CD两侧的两 A
E
B
个半圆重合，A点和B点重合，⌒ AE
和BE重合，AC、AD⌒分别和⌒BC、
D
BD重⌒ 合。⌒因此
⌒
⌒ppt课件⌒.
⌒
4
AE＝BE，AC＝BC，AD＝BD
总结
3、图形语言
A
垂径定理
1、文字语言垂直于弦的直径平分圆，并且平分圆所对的两条弧。
O
C
E
D
B
2、符号语言
ppt课件.
1
问题：左图中AB为圆O

的直径，CD为圆O的弦。
A
相交于点E，当弦CD在
圆上运动的过程中有没有
特殊情况？
O
D
C
E
B
运动CD
直径AB和弦CD互相垂直
ppt课件.
2
特殊情况
C
O
A
E
D
特殊情况
在⊙O中，AB为弦， CD为直径，AB⊥CD
提问：你在圆中还能找到那些相等的量？并证明你猜得的结论。
B
CE=DE
ppt课件.
AC =AD ,BC=BD
3
证明结论
已知：在⊙O中，CD是直径，AB是弦，
证CA明DC：⊥＝连AB⌒结CBO，，A垂A⌒、D足O＝B为B，⌒ED则。。O求⌒A＝证O：BA。E＝BEC，
因为垂直于弦AB的直径CD所在的直线既是等腰三角形OAB的对称轴
.O
又是⊙ O的对称轴。所以，当把圆
ppt课件.
7
例题1
例1 如图，已知在 A ⊙O中，弦AB的长为8 厘米，圆心O到AB的距离为3厘米，求⊙O 的半径。
EB .

数学公开课优质课件精选《垂径定理》

解析
要证明FM垂直于FN，只需证明角MFN等于 90度。根据抛物线的性质可知AF = AM， BF = BN。因此，角 AFM和角BFN均为45 度。所以角MFN等于 90度，即FM垂直于FN
。
例题6
已知椭圆C： (x^2)/a^2 + (y^2)/b^2 = 1 (a > b > 0)的左、右焦点分别为F1、F2，过F1的直线l与椭圆C交于A、B 两点。若|AF1| = 3|F1B|，且|AB| = 4√3 ，求椭圆C的方程。
利用垂径定理求线段中点
01
通过构造以线段为直径的圆，利用垂径定理可求得线段的中点
Hale Waihona Puke 。判定线段中点的性质
02
根据垂径定理，若一条线段是某圆的直径，则该线段的中点是
圆心，从而可判定线段中点的性质。
解决与线段中点相关的几何问题
03
利用垂径定理可以解决与线段中点相关的各种问题，如求线段
的长度、证明线段的平行或垂直等。
应用场景
在解决三维几何问题中，如计算球面上两点的最短距离、判断点到球面的位置关系等问题时，可应用三维空间中的垂径定理。
垂径定理与其他知识点的联系
与勾股定理的联系
在直角三角形中，垂径定理可视为勾股定理的特殊情况，当直角三角形的两条直角边相等时，斜
边上的中线即为垂径。
与圆的性质的联系
垂径定理与圆的性质密切相关，如圆心角、弧长、弦长等概念在证明垂径定理时均有涉及。
解决角平分线问题
1 2 3
利用垂径定理构造角平分线
通过构造以角为顶点的圆，利用垂径定理可求得角的平分线。
判定角平分线的性质
根据垂径定理，若一条射线是某圆的切线，且切点是角的顶点，则该射线是角的平分线，从而可判定角平分线的性质。

演示文档垂径定理课件PPT.ppt

可推得
平分弦
平分弦所对的劣（优）弧
..........
7
在下列图形，符合垂径定理的条件吗？
练习1 D
A
B
E
A
O
O
CE
O
A
E
B
AC
B C
O
O
E
C
D
AE
B
B
D..........
D D
O
AE
B
C
8
C
O
A
A
E
B
A
O
D
B
D
B
O
D
C
A
A
O
C
B
C
C
B
D
O
..........
9
判断下列图形，能否使用垂径定理？
④⑤ ①②③ 平分弦所对的两条弧的直线经过圆心,并且垂直平分弦.
..........
14
一、判断是非：
（1）平分弦的直径，平分这条弦所对的弧。
（2）平分弦的直线，必定过圆心。
（3）一条直线平分弦（这条弦不是直径），
那么这条直线垂直这条弦。
A
C
OD
(1) B
C
•O
A
B
(2) D
..........
拱高(弧的中点到弦的距离)为7.2m，你能求出赵州桥
主桥拱的半径吗？
37.4
C
解：如图，设半径为R，
AB=37.4,CD=7.
7.2
A
18.7
AD 1 AB2 1 37.4 18.7,
2
2
D
R
R-7.2

垂径定理PPT教学课件

曹雪芹
（1715?──1764?)名霑，号雪芹，是我国伟大的现实主义作家。
《红楼梦》是他“披阅
十载，增删五次”，“字字
看来皆是血，十年辛苦不寻
常”的产物。可惜，在他生
前，全书没有完稿。今传《红楼梦》120回本，其中前80回的绝大部分出于他的手笔，后40回则为高鹗所续。 80回以后他已写出一部分初稿，但由于种种原因而没有流传下来。
在文中画出黛玉精要概括律诗要点的句子。
用自己的话进行概括，完成填空：律诗是形式，词句是表象，
只有立意才是精髓
延伸阅读、探究思考
黛玉指导香菱学诗，这对我们学习语文有何借鉴作用
首先，要多读。诵读就是学好诗歌的根基，这是提高鉴赏能力的根本途径。
其次，要学诗就要学一流的。我们在阅读时，也要挑选文质兼美的作品，这对于陶冶情操，培养纯正的文学趣味是非常有益的。
需积累的词语
起承转合以词害意
诲人不倦挖心搜胆
穿凿
揣摩
地灵人杰精血诚聚
你认为香菱是怎样一个人？
香菱咏月诗（三）的鉴赏
精华欲掩料应难，影自娟娟魄自寒。一片砧敲千里白，半轮鸡唱五更残。绿蓑江上秋闻笛，红袖楼头夜倚栏。博得嫦娥应自问，何缘不使永团圆？
思考、讨论：
香菱学诗成功的原因是什么？
AB是弦，垂足为E.
求证：AE=BE
C
AC=BC,AD=BD
AE B D
C O
A
BA E B
D
连结OA,OB, OA=OB
C和D⊙所O在的直对线称是轴等腰三角形C
1 两个半圆重合
2 A,B两点重合
O
3 AE,BE重合 4 AC,BC重合

《垂径定理》课件

,进而判断船能否顺利通过这
座拱桥.
解:如图所示,设所在圆的圆心为 O,半径为 r m,连结 OA,OC,过 O 作 OK⊥AB 于点 K,
交 CD 于点 H,交于点 G.则 OA=OG=r m,GK=2.4 m,OK=OG-GK=(r-2.4)m.

由垂径定理,得 AK= AB= ×7.2=3.6(m).
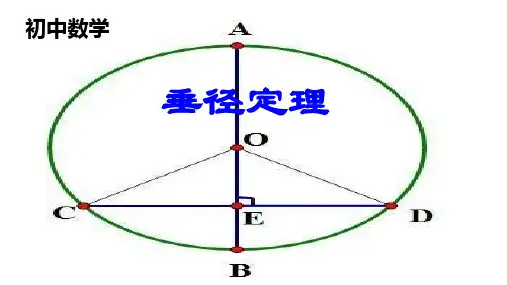
①四变量:如图所示,弦长a,圆心到弦的距离(弦心距)d,半径r,弧的中点到弦
的距离(弓形高)h.这四个变量知任意两个可求其他两个.

2
2
2
②两关系:( ) +d =r ;h+d=r.

(2)垂径定理应用中常作的辅助线:作垂线,连半径,构造直角三角形.
(3)垂径定理应用中常用技巧:设未知数,根据勾股定理列方程.
探究点二
垂径定理的应用
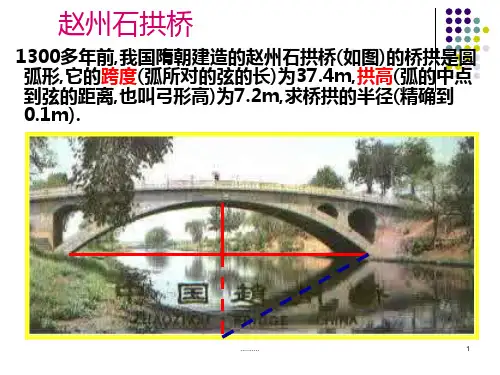
[例2] 某地方有座弧形的拱桥,如图所示,桥下的水面宽为7.2 m,拱顶高出水面
2.4 m,现有一艘宽3 m、船舱顶部为长方形并高出水面2 m 的船要经过这里,此船
能顺利通过这座拱桥吗?
[导学探究]
1.补全拱形圆弧所在圆的圆心,构造直角三角形求出圆的半径 .
2.通过船的宽度求出可以通过的船的最大高度
的长.
[导学探究]
4 ,OP= 2 .
2.要求弦CD的长,需构造由弦心距、半弦(弦的一半)及半径
1.由AP=2,BP=6,可得直径AB=
8 ,半径OA=
形,利用直角三角形的性质解决问题.
围成的直角三角
解:如图所示,作 OH⊥CD 于点 H,连结 OC.
因为 OH⊥CD,所以 HC=HD.
因为 AP=2,BP=6,所以 AB=8.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B
4.如图, 将小圆去掉,
O
已知:AC=BD
求证:△OCD是等腰三角形 A C E D B
例3:如图，CD为圆O的直径，弦 AB交CD于E， ∠ CEB=30°， DE=9㎝，CE=3㎝，求弦AB的长。
A
D
E C
O
B
天下第一桥的主桥拱半径是多少?
它的赵主州桥桥是坐圆落弧在形河,它北的省跨赵度县(弧。所建对于的隋弦代已的，有长由约)著1为3名0307匠年.4师m的,李历拱春史高设。(弧计是的和当中建今点造世到，界弦距现的今存距最离早)、为跨7.径2m最. 大、保存最完善的单孔敞肩型石拱桥。被誉为天下第一桥。
C
C
B
O
O
O
O
D
A D
BA D
BC A
A
B
D
C
不符合不符合
符合符合
C
C
AC B O
E
O
A
B
O
ADB
D
符合
符合
符合
例1. 如图,已知AB是⊙O的弦, OC⊥AB于C, 且AB=8, OC=3,求⊙O的半径。
O
练习：
ACB
1.⊙O的半径为8，OC⊥弦AB于C，且OC=6，求弦长AB. 2.⊙O的半径为6，弦AB=8，求圆心O到AB的距离。
24.1.2 垂直于弦的直径
一、实践探究
把一个圆沿着它的任意一条直径对折，重复几次，你发现了什么？由此你能得到什么结论？
可以发现：
圆是轴对称图形，任何一条直径所在直线都是
它的对称轴．
二、
如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB （1） AE=BE吗？为什么？（2）A⌒C与B⌒C相等吗？ A⌒D与B⌒D相等吗？为什么？
+
a 2
2
C
·O
E
A
B
D
C
·O
E
A
B
D
CD⊥AB CD是直径垂直于弦的直径
AE=BE 平分弦
⌒⌒ AC = BC 平分弦所对的
⌒⌒ AD = BD
两条弧
垂径定理
垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
题设
结论
｝（1）过圆心
（2）垂直于弦
｛（3）平分弦（4）平分弦所对的优弧（5）平分弦所对的劣弧
1.以O为圆心的两个同心圆中,大圆的直径 AB交小圆C,D两点,问（1）AC与BD相等吗?
AC O D B
O A CED B
第1题图
第2题图
（2）若将直径向下移动,变为非直径的弦AB, 交小圆于C,D两点,是否仍有AC=BD呢?
3.如图, 将大圆去掉，
O
已知： OA=OB
求证： AC=BD
A C ED
3.如图,已知⊙O的半径为 6 cm,弦 AB与半径 OC
互相平分,交点为 M , 求弦 AB 的长.
O
r
a
d
a
2
r2 =d2 + 2
A
2
C
B
小结：①作“弦心距”是很重要的一条辅助线，它可以和垂径定理相联系。
②圆的半径,弦的一半及弦心距可构成直角三角形。因此只要知道圆中半径(或直径),弦,弦心距中任意两个量，就可以求出第三个量。
如果把（2），（3）互换呢？
命题:平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧
已知：CD是直径，AB是弦，并且CD平分AB
求证：CD⊥AB，A⌒D＝B⌒D，A⌒C＝B⌒C
A
C
.O
E B
D
推论：平分弦（不是直径）的直径垂直于弦，并且
平分弦所对的两条弧.
判断
（1）垂直于弦的直线平分弦，并且平分弦所对的两条弧……………………………………( × )
天下第一桥的主桥拱半径是多少?
拱高跨度
赵州桥的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗?
主桥拱半径
天下第一桥的主桥拱半径是多少?
赵州桥的主桥拱是圆弧形, 它的跨度(弧所对的弦的长)为 37.4m,拱高(弧的中点到弦的距离)为7.2m,你能求出赵州桥主桥拱的半径吗? C
7.2m
B
A
D
37.4m
方程思想
O
课堂小结
1.圆的轴对称性：圆是轴对称图形,任何一条直径所在的直线
都是它的对称轴。
2.垂径定理：垂直于弦的直径平分弦，并且平分弦所对
的两条弧。
3.在计算题中，垂径定理经常结合勾股定理一起使用。
rO ad
A 2C B
4.在计算过程中，要结
合方程思想解题.
r2
=d2
（2）平分弦的直径垂直于弦，并且平分弦所对的两条弧………………………………………( × )
（3）弦所对的两弧中点的连线，垂直于弦，并且经过圆心……………………………………..( √ )
C
A M└ ●O
D
如图∵ CD是直径,
B
CD⊥AB,
∴AM=BM,
A⌒C =B⌒C, A⌒D=