- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
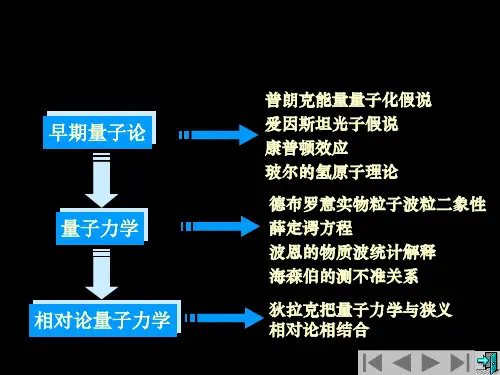
三 、早期的量子论
1 、 Planck 黑体辐射定律 普朗克能量子假说 * 辐射物体中包含大量谐振 子,它们的能量取分立值 * 存在着能量的最小单元 (能量子=h) * 振子只能一份一份地按不连 续方式辐射或吸收能量
2 、光量子及光电效应理论
• 第一个肯定光具有微粒性的是 Einstein,他认为, 光不仅是电磁波,而且还是一种粒子。 • 根据他的理论,电磁辐射不仅在发射和吸收时以能 量 hν的微粒形式出现,而且以这种形式在空间以光
速 C 传播,这种粒子叫做光量子,或光子。
• 由相对论光的动量和能量关系
p = E/C = hv/C = h/λ提出了光子动量 p 与辐射波长
( λ=C/v)的关系。
总结光子能量、动量关系式如下:
E h E h h p n n n k C C h 2n 其中 k 2
由力学可知,频率为ν,波长为λ,沿单位矢量 n 方向 传播的平面波可表为:
2 A cos[ k r t ] 其中 2,k n。
写成复数形式
i A exp[ i(k r t )] A exp ( p r Et)
2
解得: c
2
8 a
2.3 薛定谔方程
三、力场中粒子的波函数方程
P2 力场中E U(r ) 2m P2 E 【 U(r )】 2m
p i,E i t
2 2 i (r , t ) [ U(r , t )] (r , t ) t 2m
ˆ ˆ ˆ LrpLrpr i
§3.2
动量算符和角动量算符
(iii)角动量Z方向的分量
ˆ Lz i
角动量的平方
2 1 1 ˆ2 2 [ L (sin ) 2 ] 2 sin sin
k 2mE
(a x a)
d 2 2 k ( x) 0 2 dx
( x) A coskx B sin kx
( a x a )
2.6 一维无限深势阱
3. 能级与波函数 考虑波函数标准条件 : 单值,有限, 连续 要求波函数在阱内外 V(x) 要连续。所以现在
量子力学
Quantum Mechanics
Heisenberg
Schrodinger
矩阵力学
波动力学
第一章
绪论
§1.1经典物理学的困难 §1.2光的波粒二象性 §1.3原子结构的玻尔理论 §1.4 微观粒子的波粒二象性
§ 1.1 经典物理学的困难
一.经典物理学的成就
解释了大到天体小到原子分子的运动和各种电磁现
U(x)
I -a
II
III a
在阱外有 ( x) 0
0
势阱内的粒子不可能跑到势阱外面来,所以势阱外找 到粒子的几率为零,阱外波函数为零.
2.6 一维无限深势阱
2. 定态薛定谔方程的解: 在势阱内,薛定谔方程为 :
d 2 2mE ( x) 0 2 2 dx
显然E>0 那么方程变成: 它的通解是:
n ka , (n 1,3,5, ) 2
2.6 一维无限深势阱
nHale Waihona Puke k , (n 1,3,5, ) 2a
k 2mE
k 2 h 2 n 2 2 2 E 2m 8m a2
nx ( x) A cos 2a
n k 2a (n 2,4,6, )
(2) A 0, sin ka 0
这种波就是与自由粒子相联系的单色平面波,或称为 描写自由粒子的平面波,这种写成复数形式的波称为 de Broglie 波
二、电子衍射实验
戴维孙
电子衍射实验
正是有了早期的量子论和德布罗意 波才奠定了量子力学的诞生
第二章
波函数和薛定谔方程
§1 波函数的统计解释 §2 态叠加原理 §3 Schrödinger 方程
ˆ ˆ) F (r , p) F (r , p
§3.1
例如
表示力学量的算符
ˆ x i px p x
ˆx x x
2 2 2 ˆ p p ˆ T T 2 2m 2m 2m
2 2 ˆ2 p p 2 ˆ H U (r ) H U (r ) U (r ) 2m 2m 2m
(2)能级简并性
l 0,1,2,, n 1
m 0,1,2,,l
能量只与主量子数 n 有关,而本征函数与 n, , m 有关,故能级存在简并。 当 n 确定后, = n - nr- 1,所以 最大值为 n - 1。当 确定后,m = 0,±1,±2,...., ±。共 2 + 1 个值。所以 对于 E n 能级其简并度为:
i [ n ( r ) n ( r ) n ( r ) n (r )] 2m
J n (r ) 不含时间变量
2.6 一维无限深势阱
1. 势场
0, U ( x)
| x | a | x | a
Ⅰ
Ⅱ
Ⅲ
a
0
a
x
2.6 一维无限深势阱
A coska B sin ka 0, A coska B sin ka 0, (at x a) (at x a)
I -a
II
III
a
A cos ka 0, B sinka 0.
有两种情形的解:
0
A和B不能同 时为零
(1) B 0, coska 0
函数。
2.5 定态薛定谔方程
(四)定态的性质 (1)Hamilton算符的本征值E或En必定是实数
n (r , t ) n n
[ n e xp( iEn t / )] [ n e xp( iEn t / )]
* n n exp[i ( En En )t / ]
n exp(iE t / ) n exp( iEn t / )
* n
n
(r ) n (r )
不含时间变量
2.5 定态薛定谔方程
(3)几率流密度与时间无关 i J n (r , t ) [n n n n ] 2m
i * [ n exp(iEnt / ) n exp( iEn t / ) 2m * n exp( iEn t / ) n exp(iEnt / )]
§3.2
动量算符和角动量算符
(3)、角动量Z分量算符的本征值方程
ˆ Y ( , ) mY ( , ) L z lm lm
L z的本征值是m 本征函数是Ylm ( , )
§3.3 电子在库仑场中的运动
(五)总结
2 4 mZ es E n 1 , 2 , 3 , n 2 2 (1)本征值和本征函数 2 n (r , , ) R (r )Y ( , ) nl lm nlm
2 (r , t ) d 1
归一化波函数
C
归一化因子
把换成的步骤称为归一化
1 2x 例:给定( x) cos 2 a
x (0, a) 将其归一化
解:令以归一化波函数为 ( x), 设( x) c( x)
1 2 a 2 2x ( x) dx 4 c 0 cos a dx x 1 2 a 1 cos 4a 1 2a c dx c 1 0 4 2 4 2
薛定谔波动方程
2.4 粒子流密度和粒子数守恒定律
w J 0 t
几率守恒定律的微分形式
dS
d w(r , t )d J dS S dt
S
w(r , t )d 表示空间中找到粒子的几率随时间的变化 t
J dS 表示单位时间内通过封闭曲面S而流入V的几率
mn [ En Em ] h
量子化条件
假定:与一定能量 E 和动量 p 的实物粒子相联系 的波(他称之为“物质波”)的频率和波长分别为:
• •
E = hν P = h/λ
ν= E/h λ= h/p
该关系称为de. Broglie关系。
因为自由粒子的能量 E 和动量 p 都是常量,所以 由de Broglie 关系可知,与自由粒子联系的波的频率ν 和波矢k(或波长λ)都不变,即它是一个单色平面波
象和光的传播等现象. 牛顿力学 麦克斯韦方程 统计物理学
低速宏观
电磁现象
热现象
§ 1.1 经典物理学的困难 当时物理学家们的世界图样:
物质粒子 + 电磁场 = 世界
物质粒子的运动由经典力学描述 电磁场运动由经典电磁学描述.
二、经典物理学的困难
(1)黑体辐射问题
(2)光电效应
(3)康普顿效应 (4)原子光谱
§1.3波尔(Bohr)的量子论
玻尔假定:
1.原子具有能量不连续的 定态的概念。Bohr提 出了量子化条件: 2.量子跃迁的概念. 原子处于定态时不辐射,但 是因某种原因,电子可以从 一个能级 En 跃迁到另一个较 低(高)的能级 Em ,同时将 发射(吸收)一个光子。光 子的频率为:
电子的角动量 L只能 取的整数倍,即 L n 其中 n 1,2,3
§4 粒子流密度和粒子数守恒定律
§5 定态Schrödinger方程
2.1 波函数的统计解释
(三)波函数的统计解释
物质波是描述粒子在空间的概率分布
的概率波。波函数在空间某点的强度(振
幅绝对值的平方)和在这点找到粒子的概